|
收稿日期: 2015-10-21; 修改日期: 2016-02-18;
优先数字出版日期: 2016-05-25
基金项目: 国家自然科学基金(编号:61303128);河北省自然科学基金(编号:D2014203218)
第一作者简介:
刘帅(1982-),男,博士,讲师,从事遥感图像处理与应用研究。E-mail:liushuai@ysu.edu.cn
中图分类号: TP701
文献标识码: A
文章编号: 1007-4619(2016)03-0420-11
|
摘要
由于城市地表组成的复杂性,基于单核函数的支持向量回归模型很难满足精度。本文结合空间-光谱组合核函数和支持向量回归,提出了一种提取高光谱影像不透水面丰度的改进算法。首先从高光谱遥感图像上提取波谱特征和多通道灰度共生矩阵空间纹理特征,选取研究区10%像元特征数据作为训练数据,以线性加权求和核为多核组合方式,建立结合光谱信息和空间信息的组合核支持向量回归模型。然后,用生成的回归模型预测未知像元不透水面丰度值。最后,对实验结果进行评价。在模拟数据试验中,本文算法比单核回归均方根误差平均降低1.4%,决定系数比单核回归平均提高0.6%。在Hyperion数据两组试验中,该算法比单核回归均方根误差平均降低1.8%,决定系数比单核回归平均提高11.7%。模拟和真实两种高光谱数据实验中,本文算法均得到了空间形态上更准确的不透水面结果,单核回归结果存在失真现象。研究结果表明:本文算法能够有效提取城市不透水面丰度,与单核方法相比有较明显的精度提升。
关键词
支持向量回归 , 空间-光谱核函数 , 特征提取 , 不透水面 , 高光谱
Abstract
Impervious surfaces, such as houses, cement or asphalt roads, parking lots, and other artificial surfaces, can be used as indicators for environment monitoring. Several methods have been proposed to estimate impervious surfaces by using remote sensing images. However, accurate extraction of impervious surfaces remains challenging because of the diversity of urban land covers. Thus, this paper presents an improved hyperspectral remote sensing algorithm for impervious surface extraction by combining spatial-spectral kernel and Support Vector Regression (SVR). The composite kernel support vector regression model estimates impervious surface abundance by fitting an optimal approximating hyper plane to a set of training samples. Basing on the hyperspectral image, we first extract spatial-spectral feature and then select 10% pixels as training data. Spectral features include reflectivity of each pixels, NDVI, greenness and brightness of tasseled cap transformation, soil-adjusted vegetation index, and normalized difference built-up index. Gray level co-occurrence matrix approach is employed to extract spatial features. The first and second moments are identified as effective texture measures. The window size is set as 3×3 pixels for hyperspectral image. SVR method generally uses a single kernel. In this study, instead of using only one single kernel, spatial and spectral kernels are integrated into a kernel framework. Basic kernels include Gaussian, poly, and linear kernels. Using a linear weighted summation kernel as composite kernel combination method, we set the composite kernel SVR model in a manner that combines spatial and spectral features. The values of unknown pixels are predicted using the composite kernel SVR model. Finally, we evaluate the results of the experiments. Two accuracy indices, namely, root mean square error and coefficient of determination, are employed to assess the accuracy of impervious surface extraction. To test the performance of the composite kernel support vector regression model, we conducted experiments on simulated and real hyperspectral datasets. We also compared the performance of the proposed composite kernel SVR with single kernel SVR. On the experiment of simulation range, the root mean square error of the proposed algorithm is lower whereas than the determination coefficient is higher than those of single kernel method (1.4% and 0.6%, respectively). On the Hyperion data experiment, the root mean square error of the algorithm is lower but the determination coefficient is higher than those of single kernel method (1.8% and 11.7%, respectively. On the two kinds of hyperspectral data experiments, the proposed algorithm can obtain spatially explicit results. Furthermore, a distortion phenomenon is observed in the results of single-kernel SVR algorithm. We propose a composite kernel support vector regression model for impervious surface extraction using a hyperspectral image. The results indicate that our algorithm can effectively extract urban impervious surface and exhibits higher accuracy than the single-kernel SVR model. In our future work, we will focus on multisource remote sensing fusion through multiple kernels for impervious surface extraction.
Key words
support vector regression , spatial-spectral kernel , feature extraction , impervious surface , hyperspectral
1 引 言
中国正处于快速城市化时期,巨大的资源、生态环境压力使城市的发展面临着严峻挑战。不透水面是城市中最显著的人工地表特征,一直以来被认为是城市生态环境质量评估的重要指示因子,主要包括房屋、水泥或沥青道路、停车场等人造地表,在城市化监测、水环境监测、热岛效应分析和水文气候建模方面得到了广泛的应用(王浩等,2013; Zhang等,2014)。不透水面丰度是单位面积不透水面所占的比率。由于城市区域地表的组成复杂,空间范围广,传统的城市信息获取手段周期长、费用高、范围小,难以反映城市空间的分布模式及其发展趋势。遥感作为一种非接触、远距离探测技术具备实时性强、监测范围广、相对成本较低的优势,非常有利于对城市环境的监测。由于遥感具备快速、大面积获取地表不透水面信息的能力,并且成本相对较低,因此其在城市不透水面提取中得到了广泛的应用(Deng和Wu,2013; Fan和Deng,2014; Ma等,2014)。最初由Ridd(1995)基于多光谱遥感数据提出了“植被—不透水面—土壤”(V-I-S)模型,将城市土地覆盖表达为植被、不透水面和土壤3种地物光谱端元按一定比率的线性组合。然后,Wu和Murray(2003)采用多光谱数据提出植被、高反照率、低反照率和土壤4种地物光谱为端元光谱,把不透水面丰度归结为高反照率和低反照率丰度相加得到。后来出现的MESMA模型允许改变每个像元端元数目和类型,可减少空间异质性对不透水面提取的影响(Powell等,2007; 王浩等,2011)。上述方法都取得了较大的成功及广泛的应用,然而,不透水面是一种复杂的地表覆盖类型,基于宽波段反射率数据的多光谱遥感影像提取的不透水面、土壤和阴影等地物光谱具有较高的相似性,“异物同谱”现象对提取不透水面精度产生较大影响(王浩等,2013; Lu等,2014)。
随着高光谱遥感卫星发展计划的实施,其对地观测的范围不断扩大,重访周期不断缩短,为城市生态环境研究提供了良好的数据源(Okujeni等,2015)。高光谱数据使不透水面的光谱与其他地物的光谱在一些波段上具有明显的可分性,为提高不透水面提取精度垫定了数据基础。Weng等人(2008)对比了高光谱和多光谱影像反演不透水面的效果,研究表明高光谱影像能更有效的辨识低反照率地物。唐菲和徐涵秋(2014)采用Hyperion高光谱影像研究不透水面丰度,结果表明高光谱影像反演不透水面的能力要优于多光谱遥感影像。高光谱遥感在不透水面研究中具有广阔的前景,但是高光谱数据是一种高维数据,其数据量大、一般有数百个波段,数据处理的要求随着维度的提高和数据量的增大而变高,混合光谱分解中纯净光谱端元获取困难、像元内端元组成可变、“同物异谱”等问题也为后续的信息提取工作带来挑战。支持向量回归SVR(Support Vector Regression)是一种机器学习方法,可以避开端元的提取过程,利用核函数把像元矢量投影到高维特征空间,建立非线性回归模型,提高地物提取的精度(Chang和Lin,2011; Okujeni等,2013,2014,2015)。Esch等人(2009)采用支持向量回归方法研究了德国南部区域的城市不透水面,证明了这种方法能自动提取大范围区域不透水面。程熙等人(2011)采用支持向量回归方法估算天津主城区的不透水面丰度,均方差结果优于线性光谱分解模型。Okujeni等人(2013)采用支持向量回归方法和HyMap高光谱数据对德国柏林地表覆盖信息进行研究,提取屋顶、路面不透水面的精度要高于多端元混合光谱分解模型。然而,大多数研究还仅仅用一个光谱核函数来建立模型,或者基于单核的支持向量回归模型将空间信息和光谱信息堆叠成一个向量。由于空间特征和光谱特征物理意义、量纲和统计特征都不同,简单叠加在一起并不能全面有效利用空谱特征信息,因此很难仅使用一个核函数来反映数据的变化规律(Jun等,2013; 谭熊等,2014)。空间特征是遥感图像处理中的一种重要信息,能够提高分类或信息提取的精度(Fauvel等,2013; 程熙等,2013),如何有效结合空间-光谱信息建立多核回归模型改进不透水面丰度提取精度在已有的研究中并没有讨论,因此有必要在现有光谱核函数的基础上加入空间核函数。
在以往研究的基础上,本文提出一种结合高光谱遥感图像空间特征和光谱特征,以组合核支持向量回归CKSVR(Composite-Kernel Support Vector Regression)为模型提取不透水面丰度的方法。
2 理论与方法
2.1 研究方法
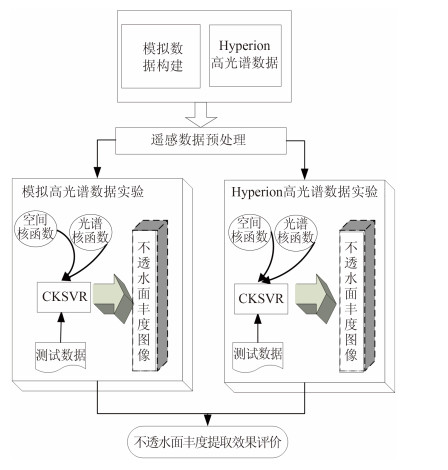
不透水面回归分析需要通过有限的样本集,找出隐藏在随机性后面的统计规律,建立起一个能够反映变量间关系的回归方程,从而可以预测不透水面丰度值。本文在对高光谱数据进行预处理的基础上,主要采用CKSVR模型建立不透水面回归方程,分别利用模拟的高光光谱数据和真实的星载高光谱数据提取不透水面丰度值,并对比单核支持向量回归提取不透水面丰度的效果,对实验的结果进行评价(图 1)。
2.2 空-谱特征提取
将光谱和空间这两种信息分别采用基础核函数(线性核函数、多项式核函数和高斯径向基核函数)组成多核进行处理。光谱信息采用预处理后得到的高光谱图像每个像元的反射率特征信息,以及与不透水面分布相关的NDVI、缨帽变换“绿度”和“亮度”分量、土壤调节植被指数(SAVI)和归一化建筑指数(NDBI)。空间信息采用灰度共生矩阵GLCM(Gray Level Co-occurrence Matrix)提取。GLCM方法是一种提取遥感影像空间特征的概率统计方法,可以提取多种特征,如:均值、方差、对比度、二阶矩、相关性、信息熵等。本文选取GLCM的均值和方差特征,优点在于计算简单,并且包含有效的空间信息。对于多/高光谱影像,传统的GLCM纹理研究通过主成分分析提取的第一个主成分,或者采用全色波段为基础提取GLCM空间特征,这种处理方法会损失大量有用的空间特征信息(Huang等,2014)。针对高光谱遥感影像特点,本文采用一种多通道GLCM提取算法,该方法提取空间信息采用3×3的窗口计算高光谱影像每个波段的灰度共生矩阵特征值,每个像元的空间特征可以用一个向量表示,避免了提取主成分的信息损失,这种方法能够获取更加全面的空间特征信息。
2.3 支持向量回归原理
支持向量回归对观测数据进行训练,得到数据的分布规律后,可以预测未知数据的分布。对于给定的N个训练样本 ${O}{\rm{ = }}\left\{ {\left({{x_i},\,\,{y_i}} \right)} \right.|{x_i} \in {{\bf{R}}^n},\,\,{y_i} \in R$ $i = 1,\cdots,N$,如果可以拟合出一个函数 $y\left({{x}} \right)= {{{w}}^{\rm{T}}}{{\phi}} \left({{x}} \right)+ b$,则此方程构成观测样本集上的SVR模型,w为权系数向量,${{\phi}}$ 将训练样本从输入空间映射到高维特征空间。首先定义ε-不敏感损失函数,给定ε为允许误差,训练样本误差为ξ,当 $\left| \xi \right| < \varepsilon $ 时,损失记为零,否则损失记为 $\left| \xi \right| - \varepsilon $(Smola和Schlkopf,2004)。
在SVR中观测样本到超平面的距离都应小于 $\displaystyle {\varepsilon \over {\sqrt {1 + ||{{w}}|{|^2}} }}$,在满足ε-不敏感函数的前提下,需要极小化 ${||{{w}}|{|^2}}$ 。在实际问题中,考虑到噪声等因素的影响,可以得到相应的目标函数和约束条件,则SVR可以表示为如下凸优化问题:
| $ \begin{aligned} & \min \frac{1}{2}||{ w}|{|^2} + c\sum\limits_{i = 1}^N {\left({{\xi _i} + \xi _i^*} \right)} \\ & \displaystyle s.t. \ \ {y_i} - {{ w}^{\rm{T}}}\phi \left({{x_i}} \right)- b \leqslant \varepsilon + {\xi _i}\\ & \quad\quad \displaystyle {{ w}^{\rm{T}}}\phi \left({{x_i}} \right)+ b - {y_i} \leqslant \varepsilon + \xi _i^*\\ & \quad\quad \displaystyle {\xi _i},\xi _i^* \geqslant 0,i = 1,\cdots,N \end{aligned} $ | (1) |
式中,${\xi _i},\xi _i^*$ 为松弛变量,对应偏离点位于最优回归超平面上和下两种情况。c表示惩罚系数。引入拉格朗日乘数法求解式(1):
| $ \begin{array}{l} L\left({{{w}},b,{\xi _i},\xi _i^*,{\eta _i},\eta _i^*} \right)= \frac{1}{2}||{{w}}|{|^2} + c\sum\limits_{i = 1}^N {\left({{\xi _i} + \xi _i^*} \right)} - \\ [20pt] \displaystyle \sum\limits_{i = 1}^N {{a_i}\left({\varepsilon + {\xi _i} - {y_i} + {{{w}}^{\rm{T}}}\phi \left({{x_i}} \right)+ b} \right)} - \\ [20pt] \displaystyle \sum\limits_{i = 1}^N {a_{_i}^*\left({\varepsilon \! + \! \xi _{_i}^* \! + \! {y_i} - {{{w}}^{\rm{T}}}\phi \left({{x_i}} \right)\! - \! b} \right)} \! - \! \sum\limits_{i = \! 1}^N {\left({{\eta _i}{\xi _i} \! + \! \eta _i^*\xi _i^*} \right)} \end{array} $ | (2) |
式中,$ a $i,$ a $i*,ηi,ηi*是拉格朗日乘子,对上式求各变量的偏导并带入上式,得到原问题的对偶优化问题:
| $ \begin{array}{l} \max \left\{ \begin{array}{l} \sum\limits_{i = 1}^N {{y_i}\left({{a_i} - a_{_i}^*} \right)} - \varepsilon \sum\limits_{i = 1}^N {\left({{a_i} + a_{_i}^*} \right)} \\ [18pt] - \displaystyle \frac{1}{2}\sum\limits_{i = 1,j = 1}^N {\left({{a_i} - a_{_i}^*} \right)\left({{a_j} - a_j^*} \right)K\left({{x_i},{x_j}} \right)} \end{array} \right.\\[18pt] \displaystyle {\rm s.t.} \sum\limits_{i = 1}^N {\left({{a_i} - a_{_i}^*} \right)} = 0,0 \leqslant {a_i} \leqslant c,0 \leqslant a_{_i}^* \leqslant c,\\[18pt] i = 1,\cdots,N \end{array} $ | (3) |
式中,$K\left({{x_i},{x_j}} \right)= \left\langle {\phi \left({{x_i}} \right),\phi \left({{x_j}} \right)} \right\rangle $ 为核函数,根据问题和数据的不同,核函数可以用高斯径向基核函数、多项式核函数和线性核函数3种形式表述,表达式分别为
| $ \begin{array}{*{20}{l}} {K\left( {{x_i},{x_j}} \right) = \exp \left( { - \frac{{||{x_i} - {x_j}|{|^2}}}{{2{\sigma ^2}}}} \right),}\\ {\;\;\;\;K\left( {{x_i},{x_j}} \right) = {{\left( {\left\langle {{x_i},{x_j}} \right\rangle + 1} \right)}^p},}\\ {\;\;\;K\left( {{x_i},{x_j}} \right) = \left\langle {{x_i},{x_j}} \right\rangle } \end{array} $ | (4) |
式中,σ为径向基核函数参数,p为多项式系数。SVR根据选用的核函数,可分为线性SVR和非线性SVR两种。
采用SMO序列最小最优化算法,求解对偶优化问题,最终得到单核支持向量回归SKSVR(Single-Kernel Support Vector Regression)模型为
| $ f\left(x \right)= \sum\limits_{i = 1}^N {\left({{a_i} - a_{_i}^*} \right)} K\left({{x_i},x} \right)+ b $ | (5) |
2.4 空-谱核支持向量回归
空-谱核支持向量回归模型是对单核模型的改进,采用两个核函数代替单一的核函数。空间核对空间纹理信息进行感知,光谱核对光谱信息进行感知,然后再映射到高维特征空间,对空间核和光谱核进行线性加权集成,能够更好的利用空间纹理信息和光谱信息。SKSVR采用单映射函数ϕ,CKSVR则采用多映射函数将样本从输入空间映射到高维特征空间,表示如下:
| $ {{\varPhi}} \left({ x} \right)\!\! = \!\! \left[ {\sqrt {{\mu _1}} {\phi _1}\left({{x}} \right),\sqrt {{\mu _2}} {\phi _2}\left({{x}} \right),\cdots,\sqrt {{\mu _M}} {\phi _M}\left({{x}} \right)} \right] $ | (6) |
式中,M为映射函数的个数,μ1,μ2,⋯,μM是各个功能函数的权重,为了防止过拟合,这里需要限制权重的和为1。因此,多核支持向量回归方程可以转化为以下形式:
| $ \begin{aligned} \min \ \ \frac{1}{2}||{{w}}|{|^2} + c\sum\limits_{i = 1}^N {\left({{\xi _i} + \xi _i^*} \right)} \\ {\rm s.t.} \left\{ {\begin{aligned} & {y_i} - {{{w}}^{\rm{T}}}{{\varPhi}} \left({{x_i}} \right)- b \leqslant \varepsilon + {\xi _i} \\ & {{{w}}^{\rm{T}}}{{\varPhi}} \left({{x_i}} \right)+ b - {y_i} \leqslant \varepsilon + \xi _i^*\\ & {\xi _i},\xi _i^* \geqslant 0,i = 1,\cdots,N\\ & {\mu _s} \geqslant 0,s = 1,\cdots,M\\ & \sum\limits_{s = 1}^M {{\mu _s} = 1} \end{aligned}} \right. \end{aligned} $ | (7) |
经过求解对偶优化问题,最终得到多核支持向量回归模型为
| $ f\left({ x} \right)= \sum\limits_{i = 1}^N {\left({{a_i} - a_i^*} \right)} \tilde K\left({{x_i},{ x}} \right)+ b $ | (8) |
| $ \begin{array}{l} \tilde K\left({{x_i},{ x}} \right)= \left\langle {{ \varPhi} \left({{x_i}} \right),{ \varPhi} \left({ x} \right)} \right\rangle = \\[4pt] {\mu _1}\left\langle {{\phi _1}\left({{x_i}} \right),{\phi _1}\left({ x} \right)} \right\rangle \! + \! {\mu _2}\left\langle {{\phi _2}\left({{x_i}} \right),{\phi _2}\left({ x} \right)} \right\rangle \! + \! \cdots \! + \! \\[4pt] {\mu _M}\left\langle {{\phi _M}\left({{x_i}} \right),{\phi _M}\left({ x} \right)} \right\rangle = \\[4pt] {\mu _1}{K_1}\left({{x_i},{ x}} \right)\! + \! {\mu _2}{K_2}\left({{x_i},{ x}} \right)\! + \!\! \cdots \!\! + \! {\mu _M}{K_M}\left({{x_i},{ x}} \right)\! = \\[4pt] \sum\limits_{s = 1}^M {{\mu _s}{K_s}\left({{x_i},{ x}} \right)} \end{array} $ | (9) |
根据式(9),本文采用的空间-光谱组合核函数可以简化表示为
| $ {{\tilde K}_c} = {\mu _1}{K_1} + {\mu _2}{K_2} $ | (10) |
式中,K1为光谱核函数,K2为空间核函数,μ2=1–μ1。
2.5 精度评价
文中综合采用均方根误差(RMSE)、决定系数(R2)和算法运行平均时间评价算法的实际效果(Xian和Homer,2010; Ma等,2014; Shao和Liu,2014)。相关计算公式如下:
| $ {\rm{RMSE}} = \sqrt {\frac{{\sum\limits_{i = 1}^N {{{\left({{{\hat I}_i} - {I_i}} \right)}^2}} }}{N}} $ | (11) |
| $ {R^2} = \frac{{\sum\limits_{i = 1}^N {{{\left({{{\hat I}_i} - {{\bar I}_i}} \right)}^2}} }}{{\sum\limits_{i = 1}^N {{{\left({{I_i} - {{\bar I}_i}} \right)}^2}} }} $ | (12) |
式中,${{{\hat I}_i}}$ 为第i个像元估算的不透水面丰度值,Ii为第i个像元实际的不透水面丰度值,${{{\bar I}_i}}$ 为所有像元不透水面丰度平均值,N为样本像元总数。
3 实验与分析
本文算法运行的环境为Matlab,硬件环境为CPU Intel i5 1.7 GHZ,内存为4 GB。实验分别从仿真和真实的高光谱数据两个方面对提出的算法进行实验验证。下面分别对数据预处理和实验进行介绍。
3.1 数据预处理
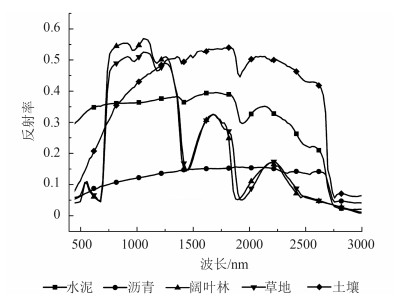
从美国ASTER光谱数据库中选取沥青、水泥、林地、草地、土壤5种特征地物光谱仿真出高光谱影像及不透水面丰度,其中沥青和水泥覆盖的区域为不透水面区域,光谱曲线如图 2所示。选取的特征光谱覆盖从400 nm的可见光区域到3000nm的红外区域,包含301个波段。采用Matlab 仿真出5种地物丰度图和高光谱图像部分。仿真的5种地物丰度满足非负性以及加和为一,沥青、水泥丰度和即为不透水面丰度(图 3)。仿真高光谱图像由线性光谱混合模型生成,为了模拟每个区域局部光谱变化,在生成的高光谱图像上添加40 dB的高斯白噪声,整个图像大小为75(像元)×75(像元)× 301(波段),每个波段包含5行5列共25个大小相同的方型区域(图 4),每个区域包含15×15个像元。整个图像包括两种像元:纯净像元区域和混合像元区域。纯净像元位于第一行的5个区域,从左到右分别表示水泥、沥青、林地、草地和土壤5种纯净地物。第2—5行分别表示2、3、4、5种地物平均混合而成的区域,都是混合像元区域。
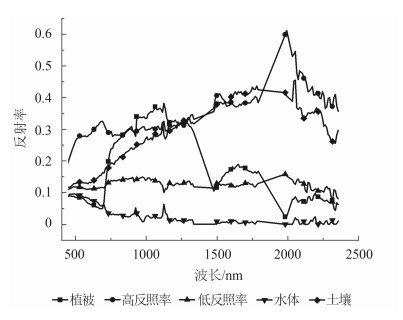
真实的遥感数据采用的是Hyperion高光谱数据。选取的数据为2006年10月2号无云覆盖的美国马里兰州中南部区域的L1T级别影像,包含可见光到红外光谱数据,共有242个波段,波长范围为356—3577 nm。首先针对实验数据各波段进行检查,删除受水汽影响严重和数据质量较差的波段,保留155个有效波段,分别是8—57,79,83—119,133—164,183—184,188—220。然后用ENVI软件对Hyperion进行快速大气校正,获取地物的真实反射率数据。最后选取两块区域为实验区对所提出的算法进行验证,包含植被、水体、土壤、高反射率区域、低反射率区域,高、低反射率区域组成了不透水面,研究区域及相关地物的反射波谱如图 5所示 。
高光谱数据真彩色合成图像如图 6所示。综合高光谱多个波段图像,通过目视解译可以分析出研究区域Hyperion遥感影像大部分被植被所覆盖,不透水面区域主要包括居民地和道路等地物类型。两个研究区内包含不同强度的不透水面丰度信息,对于不透水面提取和精度验证有较好的代表性。
3.2 仿真数据实验
由于仿真数据光谱由线性混合而成并加入了高斯噪声,因此光谱核函数仅采用线性核,空间核函数分别采用多项式核与高斯核。SKSVR方法仅采用光谱核,核函数分别采用线性核、多项式核和高斯核函数。在仿真高光谱影像中随机抽取1457个像元样本数据作为训练数据,12799个像元样本点为测试样本点。需要设置的参数分别为:高斯核参数σ,正则化参数C,多项式系数P,组合核权系数μ和不敏感损失函数ε。为了便于比较,CKSVR与SKSVR相关参数设置保持一致,σ设置为0.1,C设置为100,P设置为2,ε取0.01,μ1的取值为[0–1]区间。验证精度采用的是模拟的真实不透水面丰度值(图 3),实验结果如图 7所示,CKSVR方法有较好的视觉效果,正确反映了不透水面丰度值的空间分布,SKSVR方法图像上存在斑点噪声,图像有较严重失真。
表 1中方法后面括号中表示使用的核函数及其组合方式,算法运行时间为秒。从评价指标的定量对比来看,CKSVR的RMSE比SKSVR方法平均低1.4%,决定系数R2比SKSVR平均高0.6%。实验表明对于仿真数据CKSVR的精度高,视觉效果好,CKSVR中空间核采用RBF核计算时间较长,采用POLY核计算时间平均为0.33 s。
表 1 采用仿真数据比较CKSVR和SKSVR的不透水面提取精度
Table 1 Comparison of impervious surface extraction by CKSVR and SKSVR using simulated hyperspectral data
| 方法 | RMSE | R2 | 时间/s |
| SKSVR(LINE) | 0.00520 | 0.99984 | 0.06485 |
| SKSVR(POLY) | 0.04708 | 0.98156 | 0.70959 |
| SKSVR(RBF) | 0.00584 | 0.99980 | 0.10039 |
| CKSVR(LINE+POLY) | 0.00510 | 0.99988 | 0.328182 |
| CKSVR(LINE+RBF) | 0.00511 | 0.99987 | 5.32881 |
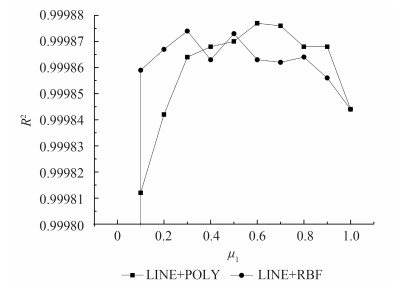
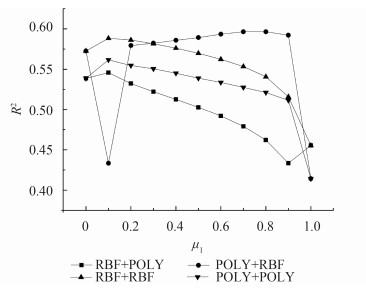
图 8表明组合核中光谱核和空间核权重的取值对CKSVR模型运算结果的精度有较大的影响,组合核LINE+POLY在μ1取0.6时R2取得最大值0.99988,组合核LINE+RBF在μ1取0.3时R2取得最大值0.99987。μ1取0时退化为空间单核函数,μ1取1时退化为光谱单核函数,其结果总体上没有组合核精度高。
3.3 Hyperion数据实验
为进一步验证提出模型的广泛适用性,选择马里兰州城市区域Hyperion影像(图 6)进行实验。对于Hyperion遥感影像,其混合像元中各端元光谱的组合方式大多为非线性组合。因此,实验对光谱信息和空间信息分别采用RBF核函数和POLY核函数构造CKSVR模型,利用核函数把像元矢量投影到高维特征空间,建立非线性回归模型。核函数分别为:高斯核与多项式核组合、多项式核与高斯核组合、高斯核与高斯核组合、多项式核与多项式核组合。同时,将CKSVR模型与仅采用光谱信息的SKSVR(线性核、多项式核和高斯核)模型进行比较。验证采用Hyperion影像及其对应的NLCD(National Land Cover Data)不透水面产品作为测试集。Hyperion影像数据采用NLCD2006的不透水面产品作为验证数据。NLCD2006产品的精度在90%左右(Greenfield等,2009; Xian等,2009),能够有效的对本文方法从Hyperion影像上提取的不透水面精度进行验证。
从影像区域1中随机抽取1467个像元样本数据作为训练数据,1279 9个像元样本点为测试样本点(图 9)。将训练样本特征输入到支持向量回归机进行训练,得到模型,对测试样本的不透水面丰度进行预测,得到最后的不透水面丰度图。CKSVR和SKSVR相关参数设置也保持一致,σ设置为0.1,C设置为100,P设置为2,ε取0.01。
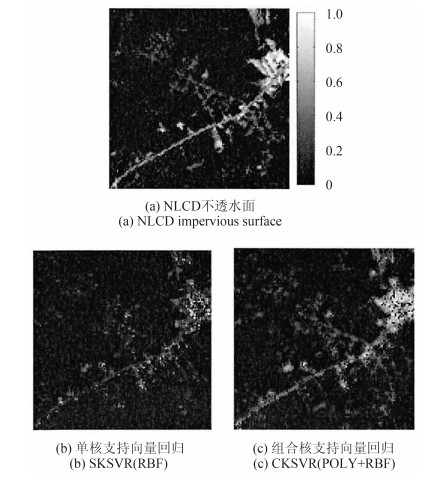
从研究区域1实验结果的目视效果来看,CKSVR方法比SKSVR方法的计算结果更合理地反映了该区域的不透水面丰度的空间分布。表 2中组合核根据μ1取值计算RMSE和R2,取最优的结果。从定量计算结果来看,CKSVR比SKSVR结果均方根误差平均降低约2%,决定系数平均提高近14.2%。
表 2 采用Hyperion数据比较CKSVR和SKSVR的不透水面提取精度
Table 2 Comparison of impervious extraction by CKSVR and SKSVR using hyperion data
| 方法 | RMSE | R2 | 时间/s |
| SKSVR(LINE) | 0.11672 | 0.42508 | 4.17981 |
| SKSVR(POLY) | 0.12798 | 0.41423 | 2.78189 |
| SKSVR(RBF) | 0.12085 | 0.45540 | 2.91523 |
| CKSVR(RBF+POLY) | 0.10318 | 0.54582 | 32.93185 |
| CKSVR(POLY+RBF) | 0.09914 | 0.59646 | 31.14660 |
| CKSVR(RBF+RBF) | 0.09934 | 0.58834 | 58.19055 |
| CKSVR(POLY+POLY) | 0.10193 | 0.56169 | 2.12925 |
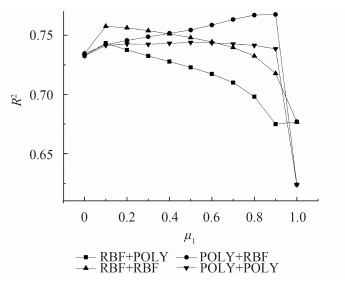
图 10反映了μ1的取值对不透水面提取精度的影响,POLY+RBF组合核在μ1=0.7时取得最优值,均方根误差为0.09914,R2为0.59646。组合核的总体精度要优于单核。
从影像区域2中随机抽取1457个像元样本数据作为训练数据,12740个像元样本点为测试样本点(图 11),实验基本参数设置与区域1实验的参数相同。与研究区域1实验结果相似,CKSVR方法比SKSVR方法的计算结果更合理地反映了该区域的不透水面丰度的空间分布,SKSVR结果中建筑区域不透水面丰度值偏低。从定量计算结果表 3来看,CKSVR比SKSVR结果均方根误差平均降低约1.5%,决定系数平均提高近9.2%。其中组合核根据μ1计算RMSE和R2,取最优的结果。
表 3 采用Hyperion数据比较CKSVR和SKSVR的不透水面提取精度
Table 3 Comparison of impervious extraction by CKSVR and SKSVR using Hyperion data
| 方法 | RMSE | R2 | 时间/s |
| SKSVR(LINE) | 0.09954 | 0.68134 | 4.62331 |
| SKSVR(POLY) | 0.11161 | 0.62394 | 3.81574 |
| SKSVR(RBF) | 0.10089 | 0.67675 | 3.89935 |
| CKSVR(RBF+POLY) | 0.08983 | 0.74337 | 29.56588 |
| CKSVR(POLY+RBF) | 0.08704 | 0.76743 | 30.49732 |
| CKSVR(RBF+RBF) | 0.08823 | 0.75753 | 57.81912 |
| CKSVR(POLY+POLY) | 0.09064 | 0.74381 | 4.21431 |
图 12反映了μ1的取值对不透水面提取精度的影响,4种光谱核和空间核的组合方式中POLY+RBF组合核在μ1=0.9时取得最优值,均方根误差为0.08704,R2为0.76743。
Hyperion遥感影像实验表明:采用支持向量回归模型算法提取不透水面的精度在很大程度上取决于核函数的选择。遥感影像中,光谱信息和空间纹理信息差别很大,不同特征信息在特征空间具有不同的统计特性,因此很难选择一个核函数来表达所有不同来源的特征信息。SKSVR使用单核函数,不能对异构特征区别对待,容易导致异构特征利用效率降低,很难同时具有较高的学习精度和泛化推广能力。因此,在不透水面提取应用中不同的特征信息需要采用不同的核函数以改善模型的精度。空-谱组合核函数可以针对光谱和空间信息采用不同权重的核函数,并使用线性加权的方式进行组合,可以优化融合各基础核函数中的信息,弥补单一核建模的不足,在融合异构特征方面有一定优势,有助于提高不透水面丰度提取的精度。采用CKSVR方法计算得出的R2总体上要高于SKSVR,两区域试验平均提高11.7%;CKSVR方法结果计算的RMSE要低于SKSVR,两次实验平均降低1.8%。
4 结 论
针对单核支持向量回归模型提取不透水面的局限性,本文提出了一种结合光谱信息和空间信息的组合核支持向量回归模型,基于LINE,POLY和RBF三种基础核函数构建组合核函数,模拟高光谱数据实验组合核采用LINE+POLY和LINE+RBF的组合方式,Hyperion数据实验组合核采用RBF+POLY,POLY+RBF,RBF+RBF和POLY+ POLY的组合方式,并对比了不同权重的基础核函数组合在不透水面提取中的精度。通过一组模拟高光谱数据和两组真实高光谱数据实验表明:本文方法能够从高光谱影像有效提取不透水面丰度,与传统的SKSVR相比,由不同核函数组成的CKSVR方法精度都有较大提升,均方根误差RMSE平均降低约1.6%,决定系数平均提高约6.1%。结果表明:该方法改进了SKSVR模型,能够充分挖掘和应用高光谱图像的光谱信息和空间信息,其不透水面提取精度取决于光谱核和空间核采用的基础核函数及其权重的设置。由于该方法受到高光谱波段数、光谱-空间纹理样本特征数和算法复杂度的影响,提取不透水面的计算时间相对单核方法较长。本文仅针对光谱和空间信息提出了以线性加权求和的方式将两个基础核函数进行组合,并且最优核函数权重的选取采用遍历的方法求解,下一步工作考虑采用线性加权的方式组合更多个基础核函数,并优化求解各个核函数的权重,预期会进一步提高复杂地表不透水面提取的精度。
参考文献(References)
-
Chang C-C, Lin C-J.2011.LIBSVM:a library for support vector machines. ACM Transactions on Intelligent Systems and Technology, 2 (3) : [DOI:10.1145/1961189.1961199]
-
Cheng X, Shen Z F, Luo J C, Zhu C M, Zhou Y N, Hu X D.2011.Estimating impervious surface base on comparison of spectral mixture analysis and support vector machine methods. Journal of Remote Sensing, 15 (6) : 1228–1241 . [DOI:10.11834/jrs.20110335] ( 程熙, 沈占锋, 骆剑承, 朱长明, 周亚男, 胡晓东. 2011. 利用混合光谱分解与SVM估算不透水面覆盖率. 遥感学报, 15 (6) : 1228–1241. [DOI:10.11834/jrs.20110335] )
-
Cheng X, Shen Z F, Luo J C, Zhou Y N, Zhang X.2013.A "global-local" impervious surface area extraction model using multispectral remote sensing images. Journal of Remote Sensing, 17 (5) : 1191–1205 . [DOI:10.11834/jrs.20132251] ( 程熙, 沈占锋, 骆剑承, 周亚男, 张新. 2013. "全域-局部"不透水面信息遥感分步提取模型. 遥感学报, 17 (5) : 1191–1205. [DOI:10.11834/jrs.20132251] )
-
Deng C B, Wu C S.2013.A spatially adaptive spectral mixture analysis for mapping subpixel urban impervious surface distribution. Remote Sensing of Environment, 133 : 62–70 . [DOI:10.1016/j.rse.2013.02.005]
-
Esch T, Himmler V, Schorcht G, Thiel M, Wehrmann T, Bachofer F, Conrad C, Schmidt M, Dech S.2009.Large-area assessment of impervious surface based on integrated analysis of single-date Landsat-7 images and geospatial vector data. Remote Sensing of Environment, 113 (8) : 1678–1690 . [DOI:10.1016/j.rse.2009.03.012]
-
Fan F L, Deng Y B.2014.Enhancing endmember selection in multiple endmember spectral mixture analysis (MESMA) for urban impervious surface area mapping using spectral angle and spectral distance parameters. International Journal of Applied Earth Observation and Geoinformation, 33 : 290–301 . [DOI:10.1016/j.jag.2014.06.011]
-
Fauvel M, Tarabalka Y, Benediktsson J A, Chanussot J, Tilton J C.2013.Advances in spectral-spatial classification of hyperspectral images. Proceedings of the IEEE, 101 (3) : 652–675 . [DOI:10.1109/JPROC.2012.2197589]
-
Greenfield E J, Nowak D J, Walton J T.2009.Assessment of 2001 NLCD percent tree and impervious cover estimates. Photogrammetric Engineering and Remote Sensing, 75 (11) : 1279–1286 . [DOI:10.14358/PERS.75.11.1279]
-
Huang X, Liu X B, Zhang L P.2014.A multichannel gray level co-occurrence matrix for multi/hyperspectral image texture Representation. Remote Sensing, 6 (9) : 8424–8445 . [DOI:10.3390/rs6098424]
-
Jun L, Reddy M P, Plaza A, Bioucas-Dias J M, Atli B J.2013.Generalized composite kernel framework for hyperspectral image classification. IEEE Transactions on Geoscience and Remote Sensing, 51 (9) : 4816–4829 . [DOI:10.1109/TGRS.2012.2230268]
-
Lu D S, Li G Y, Kuang W H, Moran E.2014.Methods to extract impervious surface areas from satellite images. International Journal of Digital Earth, 7 (2) : 93–112 . [DOI:10.1080/17538947.2013.866173]
-
Ma Q, He C Y, Wu J G, Liu Z F, Zhang Q F, Sun Z X.2014.Quantifying spatiotemporal patterns of urban impervious surfaces in China:an improved assessment using nighttime light data. Landscape and Urban Planning, 130 : 36–49 . [DOI:10.1016/j.landurbplan.2014.06.009]
-
Okujeni A, van der Linden S, Hostert P.2015.Extending the vegetation-impervious-soil model using simulated EnMAP data and machine learning. Remote Sensing of Environment, 158 : 69–80 . [DOI:10.1016/j.rse.2014.11.009]
-
Okujeni A, van der Linden S, Jakimow B, Rabe A, Verrelst J, Hostert P.2014.A comparison of advanced regression algorithms for quantifying urban land cover. Remote Sensing, 6 (7) : 6324–6346 . [DOI:10.3390/rs6076324]
-
Okujeni A, van der Linden S, Tits L, Somers B, Hostert P.2013.Support vector regression and synthetically mixed training data for quantifying urban land cover. Remote Sensing of Environment, 137 : 184–197 . [DOI:10.1016/j.rse.2013.06.007]
-
Powell R L, Roberts D A, Dennison P E, Hess L L.2007.Sub-pixel mapping of urban land cover using multiple endmember spectral mixture analysis:Manaus, Brazil. Remote Sensing of Environment, 106 (2) : 253–267 . [DOI:10.1016/j.rse.2006.09.005]
-
Ridd M K.1995.Exploring a V-I-S (vegetation-impervious surface-soil) model for urban ecosystem analysis through remote sensing:comparative anatomy for cities. International Journal of Remote Sensing, 16 (12) : 2165–2185 . [DOI:10.1080/01431169508954549]
-
Shao Z F, Liu C.2014.The integrated use of DMSP-OLS nighttime light and MODIS data for monitoring large-scale impervious surface dynamics:a case study in the Yangtze River Delta. Remote Sensing, 6 (10) : 9359–9378 . [DOI:10.3390/rs6109359]
-
Smola A, Schölkopf B.2004.A tutorial on support vector regression. Statistics and Computing, 14 (3) : 199–222 . [DOI:10.1023/B:STCO.0000035301.49549.88]
-
谭 熊, 余 旭初, 张 鹏强, 秦 进春.2014.基于多核支持向量机的高光谱影像非线性混合像元分解. 光学精密工程, 22 (7) : 1912–1920 . [DOI:10.3788/OPE.20142207.1912]
-
Tang F, Xiu H Q.2014.Comparison of performances in retrieving impervious surface between hyperspectral (Hyperion) and multispectral (TM/ETM+) images. Spectroscopy and Spectral Analysis, 34 (4) : 1075–1080 . [DOI:10.3964/j.issn.1000-0593(2014)04-1075-06] ( 唐菲, 徐涵秋. 2014. 高光谱与多光谱遥感影像反演地表不透水面的对比——以Hyperion和TM/ETM+为例. 光谱学与光谱分析, 34 (4) : 1075–1080. [DOI:10.3964/j.issn.1000-0593(2014)04-1075-06] )
-
王 浩, 卢 善龙, 吴 炳方, 李 晓松.2013.不透水面遥感提取及应用研究进展. 地球科学进展, 28 (3) : 327–336 . [DOI:10.11867/j.issn.1001-8166.2013.03.0327]
-
Wang H, Wu B F, Li X S, Lu S L.2011.Extraction of impervious surface in Hai Basin using remote sensing. Journal of Remote Sensing, 15 (2) : 388–400 . [DOI:10.11834/jrs.20110288] ( 王浩, 吴炳方, 李晓松, 卢善龙. 2011. 流域尺度的不透水面遥感提取. 遥感学报, 15 (2) : 388–400. [DOI:10.11834/jrs.20110288] )
-
Weng Q H, Hu X F, Lu D S.2008.Extracting impervious surfaces from medium spatial resolution multispectral and hyperspectral imagery:a comparison. International Journal of Remote Sensing, 29 (11) : 3209–3232 . [DOI:10.1080/01431160701469024]
-
Wu C S, Murray A T.2003.Estimating impervious surface distribution by spectral mixture analysis. Remote Sensing of Environment, 84 (4) : 493–505 . [DOI:10.1016/S0034-4257(02)00136-0]
-
Xian G, Homer C.2010.Updating the 2001 national land cover database impervious surface products to 2006 using landsat imagery change detection methods. Remote Sensing of Environment, 114 (8) : 1676–1686 . [DOI:10.1016/j.rse.2010.02.018]
-
Xian G, Homer C, Fry J.2009.Updating the 2001 National Land Cover Database land cover classification to 2006 by using Landsat imagery change detection methods. Remote Sensing of Environment, 113 (6) : 1133–1147 . [DOI:10.1016/j.rse.2009.02.004]
-
Zhang Y Z, Zhang H S, Lin H.2014.Improving the impervious surface estimation with combined use of optical and SAR remote sensing images. Remote Sensing of Environment, 141 : 155–167 . [DOI:10.1016/j.rse.2013.10.028]