Print

出版日期: 2016-05-25
点击次数：
下载次数：
DOI: 10.11834/jrs.20165200
2016 | Volumn20 | Number 3





                              上一篇|





下一篇
技术方法
优化子空间SVM集成的高光谱图像分类
expand article info 杨凯歌 , 冯学智 , 肖鹏峰 , 朱榴骏
南京大学 地理信息科学系, 江苏省地理信息技术重点实验室, 卫星测绘技术与应用国家测绘地理信息局重点实验室, 南京 210023
收稿日期: 2015-08-15; 修改日期: 2015-01-12; 优先数字出版日期: 2016-05-25
基金项目: 江苏省自然科学基金项目(编号:BK20131056);福建省自然科学基金项目(编号:2015J01175)
第一作者简介: 杨凯歌(1996-),女,本科生,主要研究方向为遥感数字图像处理、资源环境遥感。E-mail:yangkaige@smail.nju.edu.cn
通讯作者简介: 肖鹏峰(1979-),男,副教授。主要研究方向为遥感数字图像处理、资源环境遥感。E-mail:xiaopf@nju.edu.cn
中图分类号: TP751.1
文献标识码: A
文章编号: 1007-4619(2016)03-0409-11

摘要

随机子空间集成是很有前景的高光谱图像分类技术,子空间的多样性和单个子空间的性能与集成后的分类精度密切相关。传统方法在增强单个子空间性能的同时,往往会获得大量最优但相似的子空间,因而减小它们之间的多样性,限制集成系统的分类精度。为此,提出优化子空间SVM集成的高光谱图像分类方法。该方法采用支持向量机(SVM)作为基分类器,并通过SVM之间的模式差别对随机子空间进行k-means聚类,最后选择每类中J-M距离最大的子空间进行集成,从而实现高光谱图像分类。实验结果显示,优化子空间SVM集成的高光谱图像分类方法能够有效解决小样本情况下的Hughes效应问题;总体精度达到75%-80%,Kappa系数达到0.61-0.74;比随机子空间集成方法和随机森林方法分类精度更高、更稳定,适合高光谱图像分类。

关键词

高光谱图像分类 , 随机子空间 , 优化子空间 , 支持向量机

Optimal subspace ensemble with SVM for hyperspectral image classification
expand article info YANG Kaige , FENG Xuezhi , XIAO Pengfeng , ZHU Liujun
Department of Geographic Information Science, Jiangsu Provincial Key Laboratory of Geographic Information Science and Technology, Key Laboratory for Satellite Mapping Technology and Applications of State Administration of Surveying, Mapping and Geoinformation of China, Nanjing University, Nanjing 210023, China

Abstract

Promoting the accuracy of hyperspectral image classification is a crucial and complex issue. Hyperspectral image provides details of spectral variation of land surface with continuous spectral data. On the one hand, this characteristic is widely utilized to analyze and interpret different land-cover classes. On the other hand, the availability of large amounts of spectral space introduces challenging methodological issues, such as curse of dimensionality. Subspace ensemble systems, such as random subspace method (RSM), significantly outperform single classifiers in classifications involving hyperspectral image. However, two issues should be addressed to improve robustness and overall accuracy of the system. The first issue is diversity within subspace ensemble systems, and the second one is the classification accuracy of individual subspaces. In this paper, we adopt Support Vector Machine (SVM) as base classifier and proposed a novel subspace ensemble method, namely, optimal subspace SVM Ensemble, for hyperspectral image classification to improve the performance of RSM. Based on random subspace selection as the initial step, a two-step procedure is designed to avoid similarity within ensemble systems during the optimization of individual subspace accuracy. Instead of maximizing the diversity of ensemble by using a specific diversity measure, the first step employs the k-means cluster procedure according to the similarity of SVM patterns to classify random base classifiers. Second, an optimization process is implemented with Jeffries-Matusita (J-M) distance as criterion by selecting the optimal subspace from each group in the formal phase. The final label is decided based on majority voting of optimal subspaces. Experiments on two hyperspectral datasets reveal that the proposed OSSE obtains sound, robust, and overall accuracy compared with RSM and random forest method. In the first hyperspectral image, namely, the Pavia university data set, the maximum increases in Kappa coefficient and overall accuracy are about 0.04 and 2.64%, respectively, compared with those in RSM and about 0.15 and 12.75%, respectively, compared with those in random forest method. In the second hyperspectral image, namely, the Indian Pines data set, the maximum increases in Kappa coefficient and overall accuracy are about 0.02 and 1.00%, respectively, compared with those in RSM and about 0.13 and 11.12%, respectively, compared with those in random forest method. The combination of optimal subspaces improves the diversity of subspace system and the accuracy of individual classifiers and thus exhibits better performance, particularly when using limited samples, which is common in hyperspectral image classification. Basing on the results of different parameter settings in OSSE, we found two interesting issues related to the number of clustering and initial size of random subspaces. First, the optimal number of clusters in OSSE is stable when using specific hyperspectral remote sensing data. Hence, the optimal number of cluster could be assessed using the characteristics of remote sensing images. Second, similar to RSM, increasing the number of random subspaces minimally contributes to the improvement of classification accuracy in OSSE. Consequently, to decrease the time cost of computing, we should avoid selecting numerous random subspaces.

Key words

hyperspectral image classification , random subspace , optimal subspace , support vector machine

1 引 言

高光谱遥感影像能够提供丰富的地表光谱信息,是当前人类研究地球资源环境的重要数据源,已被成功地应用于土壤类别制图(Chabrillat等,2002)、植被种类识别(Underwood等,2003)、矿物识别(Kruse等,2003)等领域。高光谱影像具有维数高、数据量大和数据不确定性大等特点(谭琨和杜培军,2008),在小样本情况下,传统的统计分类方法常出现严重的Hughes效应(Pal和Foody,2010)。

子空间集成方法利用多个子空间对样本的预测差异,采用一定的集成策略实现分类,为解决高光谱图像中高光谱维数与小样本之间的矛盾,以及波段之间较强的冗余性等问题提供了新的研究思路。随机子空间方法RSM(Random Subspace Method)(Ho,1998)是子空间集成的重要泛型,它通过随机从原始光谱空间中抽取若干个波段组成子空间的方式来降低图像维度,并采用随机子空间集成来提高最终的分类性能,目前已被广泛应用于高光谱图像的分类中。对于随机子空间集成,在子空间上训练的基分类器的差异性越大、识别精度越高,集成效果越好(Xu等,1992)。

目前已有不少研究试图通过扩大子空间的多样性来获得比RSM更优的性能。Yang等人(2010)提出动态子空间方法,通过动态决定子空间的维度并随机选取组成子空间的波段,极大地改善了RSM在高光谱图像分类中的性能。还有许多学者试图通过增强每个子空间的分类性能来提升RSM的分类精度。Chen等(2014)提出一个基于最优子空间SVM集成的方法,通过特征选择算法优化RSM中随机获取的子空间。实验证明,该方法能够极大地提高RSM的表现性能。然而,由于子空间的分类精度和子空间的多样性存在负相关(Skurichina和Duin,2002),大多数特征选择算法都试图得到一个局部或全局最优的子空间(Jain等,2000；Liu和Yu,2005),导致一组最优但相似的子空间出现,从而破坏集合内部的多样性,进而影响分类性能。

除此之外,有些研究同时考虑子空间的多样性和单个子空间的分类性能。Opitz(1999)将子空间的多样性和子空间的分类精度组成线性方程,对随机子空间进行优化,并通过遗传算法获取优化的子空间。也有研究利用熵和交叉熵作为寻找多样化和最优子空间的量度(Cunningham和Carney,2000)。然而,这类研究需要给出度量标准中子空间的多样性和单个子空间的分类性能所占的权重,且目前对于子空间多样性的定义存在较大分歧(Kuncheva和Whitaker,2003)。

本文在RSM的基础上,采用SVM作为基分类器,提出一个优化子空间支持向量机集成OSSE(Optimal Subspace SVM Ensemble)算法。该算法同时考虑子空间之间的多样性和单个子空间的分类性能两方面的影响因素,利用SVM模式之间的区别,对在随机子空间上训练得到的基分类器进行k-means聚类分析,将子空间划分为若干类,并采用J-M距离作为度量标准,从每类中选择性能最优的分类器进行集成。避免了子空间多样性度量方法不统一和最优子空间相似度高的问题。

2 SVM与RSM

2.1 SVM

SVM具有小样本学习、抗噪声性能强、推广性好等优点,已经作为基分类器被成功应用于大量集成学习方法中,是最稳定有效的基分类器之一(Melgani和Bruzzone,2004；Bertoni等,2004；Chen等,2014；Fauvel等,2008)。对于一个二分类问题,线性可分样本集可表述为： $\{({{x}}_i,\ y_i),\ i = 1,2,\cdot \cdot \cdot,N\} $,其中 $ {{x}}_i = [x_i,1,\ x_i,\ 2,$ $ \cdot \cdot \cdot,x_i,d{]^{\bf{T}}} \in {{{R}}^{{d}}}$ 是波段数为d的像元,${y_i} \in \left\{ { - 1,- 1} \right\}$ 是类别标号。在d维特征空间中,SVM训练得到的最优分类函数为：

$ f({{x}})= \sum\limits_{i = 1}^N {{\alpha_i}{y_i}K({{x}}_i,{{x}})} + b $ (1)

式中,αi为拉格朗日乘子,αi不为零的xi即为支持向量(SV)。k(xi,x)为核函数,本研究采用高斯径向基函数(RBF)为核函数。b为分类阈值, 可通过任意一个或两类中任意一对支持向量求得。

由SVM的分类函数可知,SVM的分类结果主要由SV决定,OSSE正是利用支持向量来度量SVM之间的差异性。

2.2 RSM

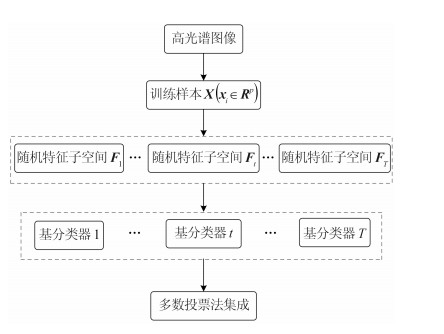
RSM是Ho(1998)提出的一种分类器集成方法。它通过对训练数据集的特征空间采取无放回的随机采样,来获得维度低于原始训练集特征维度的特征子空间,并采用多数投票法进行子空间集成,从而提高分类精度。对于训练样本${{X}} = \left\{ {\left({{{{x}}_i},{y_i}} \right)} \right.,\left. {i = 1,2,\cdots,N} \right\},$ ${{{x}}_i} \in {{{R}}^p},{y_i} = \left\{ {1,2,\cdots,l} \right\}$,RSM实现包含以下步骤(如图 1)：首先,对训练样本的特征空间进行随机采样,得到新的特征子空间,重复T次得到T个特征子空间${{{F}}_{{t}}} = \left({{{x'}_t},{y_t}} \right)$ ；然后,由T个特征子空间训练得到T个基分类器；最后,采用多数投票法将所有基分类器的输出结果集成以完成分类任务。实验证明,与一个分类器及其他集成方法相比,RSM拥有更高的分类精度和更稳定的性能(Ho,1998)。


图 1 RSM执行流程图
Fig. 1 The execution flow chart of RSM

3 研究方法

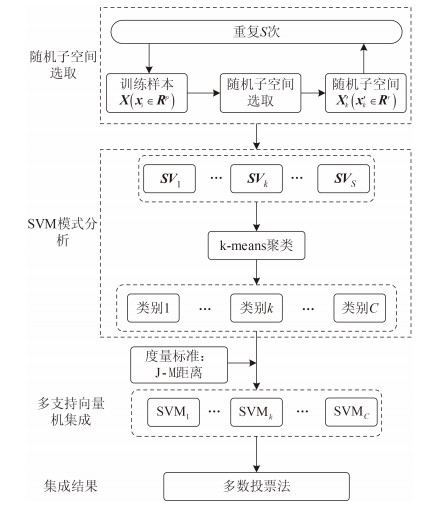
OSSE利用随机方式产生多个子空间,并对子空间进行优化,它包含两个核心步骤：对SVM间差异性的度量；性能最优的子空间的选择。图 2是OSSE的执行流程图。


图 2 OSSE执行流程图
Fig. 2 The execution flow chart of OSSE

3.1 SVM差异性度量

Thomas(1997)将集成差异性定义为“对于新的数据样本,各个分类器做出不同预测的趋势”。在OSSE中,由SVM组成的基分类器之间的差异性被定义为它们对于测试样本的预测差别。

由式(1)最优分类函数可以看出,SVM对测试样本的预测差别由支持向量决定。因此,本文将训练样本中作为支持向量的样本编码为1,非支持向量编码为0。特别地,对于OSSE中的SVM来说,其训练样本都是相同的,如果两个SVM的支持向量有很大的区别,说明它们对于样本的预测差别就会很大。

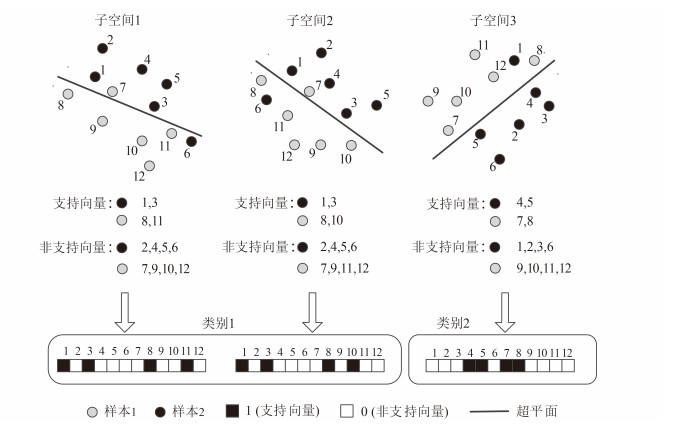
为了获得差异性较大的子空间,OSSE采用k-means方法对每个SVM的支持向量进行聚类。聚类结果中,同一类的SVM因共享更多的支持向量所以对样本的预测差别也就越小。图 3是这一过程的示例。首先,根据不同的特征子空间训练得到3个SVM,并根据训练样本是否为支持向量,将其编码为0和1。然后,根据支持向量之间的差异,将3个子空间聚成两类。这里,子空间1和2属于一类,因为他们共享4个支持向量中的3个,说明它们的预测结果将更相似。


图 3 多SVM的模式分类示例
Fig. 3 The classification of multiple SVMs pattern

3.2 子空间分类性能的度量

目前已经有很多方法可以用来判断特定的波段组合对地物的区分能力,如J-M距离(王长耀等,2006；Bruzzone等,1995)、B距离(De Backer等,2005)、样本间平均距离、类别间相对距离、离散度(陈桂红等,2006；Ball等,2007)等。相对于其他方法,J-M距离被认为更适宜表达地物类别可分性。

J-M距离是基于条件概率理论的光谱可分性指标,其表达公式如下：

$ {J_{ij}} = {\{ {\textstyle \int\limits_{{X}} {[\sqrt {p({{X}}/{\omega _i})} - \sqrt {p({{X}}/\omega {}_j)} ]} ^2}{\bf{d}}{{X}}\} ^{1/2}} $ (2)

式中,$p({{X}}/{\omega _i})$和$p({{X}}/\omega {}_j)$ 是当样本类别分别为${\omega _i}$和${\omega _j}$时,样本X的条件概率密度。

J-M距离是一种成对类别间的距离量度,可以直接用来度量两种地物类别间的可分性,已有大量研究将J-M距离有效地推广到多类别可分性的测量(Bruzzone等,1995)中。其中,平均J-M距离(Bruzzone等,1995)稳定性最强、应用范围最广。因此,本研究采用平均J-M 距离作为特征子空间分类性能的量度标准,平均J-M距离越大,子空间的分类性能越好。平均J-M距离的计算如式(3)：

$ {J_{\rm{ave}}} = \sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {p\left({{\omega _i}} \right)p\left({{\omega _j}} \right){J_{ij}}} } $ (3)

式中,n是所有地物类别的数目,$p\left({{\omega _i}} \right)$和$p\left({{\omega _j}} \right)$ 是当样本类别分别为ωi和ωj时的先验概率。

3.3 OSSE

与RSM类似,OSSE首先对训练样本的特征空间进行随机采样生成大量子空间,并在每个子空间上分别训练SVM。然后OSSE利用k-means方法对SV进行聚类,并以平均J-M距离作为度量标准,从每个类中选出分类性能最佳的子空间参与集成。最终参与集成的子空间数目由聚类数决定,特别的,当聚类数与随机子空间数目相同时,所有的随机子空间都被保留,OSSE等同于RSM。

OSSE的伪代码如下：

输入：

• ${{X}} = \{ \left({{{{x}}_{{i}}},{y_i}} \right)\} _{i = 1}^N$ 其中X为高光谱图像,yi为图像类别标号

• k：每种地物类别训练样本数目

• $r \in \left({{r_{\min }},{r_{\max }}} \right)$ 其中rmin为随机采样的最少波段,rmax为随机采样的最多波段

• S：随机子空间数目

• Z：聚类数

训练样本获取过程：

For i=1,2,···,n

• 从原始图像中类别标签为yi的样本中随机抽取k个作为训练样本

End

• 得到 ${{I}} = \{ \{({{{x}}_{{{ij}}}},{y_i})\} _{j = 1}^k\} _{i = 1}^n$ 其中I为大小为 $\left({n \times k} \right)\times p$ 的训练样本

基分类器训练过程：

For i=1,2,···,S

• 对训练样本子空间随机采样获得维数为r,$r \in \left({{r_{\min }},{r_{\max }}} \right)$,的特征子空间Fi

• 计算平均J-M距离 J-Mave

• 根据SVM学习方法,由Fi训练得到支持向量SVi及基分类器BCi

End

聚类寻优过程：

• 利用k-means方法将S个支持向量机聚成Z类

For i=1,2,···,N

• 寻找每类中平均J-M距离最大的基分类器OBCi

End

识别过程：

• 给定测试样本x,x∈X且x $\notin$ I

For i=1,2,···,N

• 得到集成分类器EC表示为：

$ EC\left({{x}} \right)= \mathop {\arg \max }\limits_{y = \phi } \sum\limits_{i = 1}^Z {I\left({OB{C_i}\left({{x}} \right)= y} \right)} $

End

需要注意的是,J-M距离是在训练样本服从高斯分布的假设下才成立的,当高光谱数据的维度超过样本数目时,训练样本的协方差矩阵不可逆(Hoffbeck和Landgrebe；1996),此时无法得到J-M距离。

4 实验设计

4.1 实验数据集

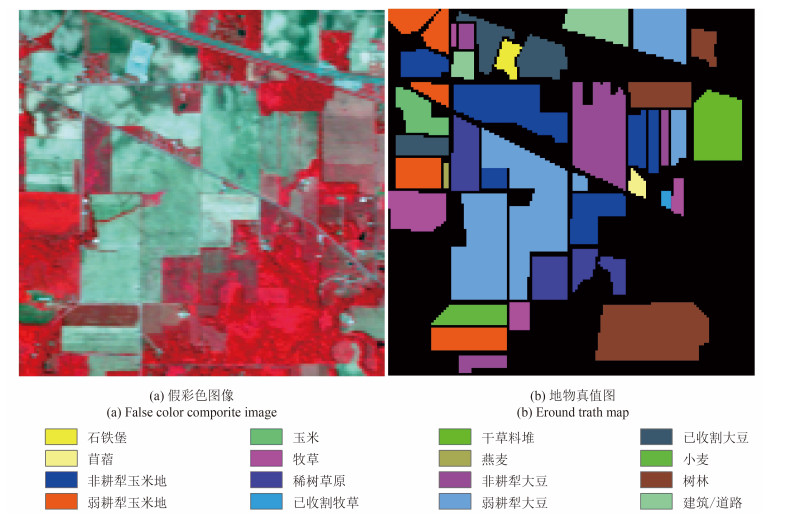
本文采用由不同传感器获取的两幅高光谱遥感影像来评价OSSE的性能。第1组数据为Pavia University高光谱遥感影像,由ROSIS-3获取,共103个波段,光谱范围为0.43—0.86 μm,空间分辨率为1.3 m,大小为610×340像元,覆盖意大利Pavia大学城。图 4展示了成像区域的假彩色合成图像及9种地物类别,详细的地物和样本信息如表 1所示。


图 4 Pavia University数据集假彩色图像(波段80、波段45和波段10) 及Pavia University数据集地物真值图
Fig. 4 Test image of the Pavia university data set with false-color composite (band 80, band 45 and band 10) and corresponding ground truth map

表 1 avia University数据集地物类别详细信息
Table 1 Detailed ground objects information of Pavia University

下载CSV 
类别标号 类别名称 样本数
1 苜蓿 6631
2 草地 18649
3 砂砾 2099
4 树木 3064
5 涂色金属板 1345
6 裸土 5029
7 沥青 1330
8 闭合砖体 3682
9 阴影 947

第2组数据为Indiana Pines高光谱遥感影像,如图 5所示。由AVIRIS获取,覆盖美国西北部印第安纳州的印第安纳松树试验田,包含145×145个像元和220个光谱波段。原始图像共有16种地物类别,其中,第7、9类样本由于数目过少无法计算J-M距离被舍弃。详细的地物和样本信息如表 2所示。


图 5 Indiana Pines数据集假彩色图像(波段50、波段27和波段17) 及Indiana Pines数据集地物真值图
Fig. 5 Test images of the Indian Pines data set with false-color composite (band 50, band 27 and band 17) and corresponding ground truth map

表 2 Indiana Pines数据集地物类别详细信息
Table 2 Detailed ground objects information of Indiana Pines

下载CSV 
类别标号 类别名称 样本数
1 苜蓿 46
2 非耕犁玉米地 1428
3 弱耕犁玉米地 830
4 玉米 237
5 牧草 483
6 稀树草原 730
7 已收割牧草 28
8 干草料堆 478
9 燕麦 20
10 非耕犁大豆 972
11 弱耕犁大豆 2455
12 已收割大豆 593
13 小麦 205
14 树林 1265
15 建筑/道路 386
16 石铁堡 93

4.2 参数设置

为了保证分类结果具有可比性,本文涉及的以SVM作为基分类器的分类算法均采用RBF为核方程,并通过基于5重交叉验证的网格搜寻方法来获得RBF核方程中的gamma数值以及规则化参数C(谭琨和杜培军,2008)。

在小样本情况下,设置不同的随机子空间数目和聚类数对OSSE的性能进行评估,并与相同随机子空间数目的RSM算法、随机森林算法进行比较。其中随机子空间数目S的取值为100、200、300、400和500,聚类数占随机子空间数目的比例从2.5%,以2.5%为步长增加到12.5%。Pavia University数据集中每种地物训练样本数k的取值为20、30和40；由于Indiana Pines数据集的波段数目较多,为了得到正确的J-M距离,只取k为30和40的情况。两幅图像中有类别标号的所有非训练样本均作为测试样本。分类结果用总体精度和Kappa系数评价。为获取算法的统计特征,每个实验采用不同的初始随机子空间重复10次,并同时计算总体精度和Kappa系数的均值和标准差。

5 实验结果分析

5.1 实验结果

表 3和表 4分别为Pavia University数据集和Indiana Pines数据集的分类结果,使用实验所得均值±标准差表示,粗体部分为当样本数目k和随机子空间数目S一定时每次实验中所得最优总体精度。可见,在两个数据集中,对于不同的样本数目k和随机子空间数目S,最优的总体精度和Kappa 系数均由OSSE获得。

表 3 Pavia University数据集实验结果
Table 3 The experiment results of Pavia University database

下载CSV 
样本数k 随机子空间数目S 统计值 OSSE RSM 随机森林
聚类数占随机子空间数目的比例/%
2.50 5.00 7.50 10.00 12.50
100总体精度/%68.83±0.3269.36±0.4270.45±0.4470.21±0.3869.69±0.4369.10±0.4266.70±0.80
Kappa系数 0.6125±0.0346 0.6200±0.0457 0.6311±0.0480 0.6285±0.0414 0.6236±0.0470 0.6163±0.0461 0.5836±0.0086
200 总体精度/% 71.02±0.43 72.30±0.40 72.05±0.37 71.78±0.32 71.27±0.32 69.93±0.42 66.59±0.59
Kappa系数 0.6355±0.0450 0.6492±0.0425 0.6473±0.0393 0.6440±0.0338 0.6384±0.0339 0.6232±0.0434 0.5822±0.0062
20 300 总体精度% 72.61±0.32 71.40±0.39 71.38±0.35 72.16±0.29 71.57±0.24 70.45±0.33 66.80±0.38
Kappa系数 0.6546±0.0337 0.6422±0.0412 0.6414±0.0360 0.6498±0.0297 0.6432±0.0247 0.6307±0.0338 0.5845±0.0039
400 总体精度% 73.39±0.30 72.92±0.27 72.52±0.28 72.32±0.27 72.21±0.26 71.18±0.26 66.81±0.28
Kappa系数 0.6623±0.0341 0.6575±0.0304 0.6537±0.0319 0.6512±0.0297 0.6496±0.0292 0.6378±0.0284 0.5846±0.0030
500 总体精度/% 72.45±.42 72.53±0.41 72.37±0.41 72.10±0.42 71.95±0.43 71.34±0.40 67.02±0.33
Kappa系数 0.6525±0.0485 0.6534±0.0469 0.6515±0.0467 0.6482±0.0479 0.6470±0.0485 0.6390±0.0450 0.5867±0.0034
100 总体精度/% 75.69±0.31 74.84±0.33 76.83±0.30 75.59±0.39 74.29±0.44 73.93±0.39 67.78±0.33
Kappa系数 0.6929±0.0360 0.6838±0.0377 0.7062±0.0340 0.6925±0.0447 0.6781±0.0493 0.6735±0.0437 0.6002±0.0039
200总体精度/% 76.27±0.3476.95±0.3376.36±0.2776.03±0.3475.60±0.3274.08±0.3267.97±0.26
Kappa系数0.6988±0.04010.7058±0.03910.6991±0.03160.6953±0.03910.6906±0.03770.6727±0.03680.6019±0.0030
30300总体精度/% 77.25±0.3576.31±0.3175.90±0.3376.04±0.3076.33±0.3174.81±0.3567.94±0.25
Kappa系数0.7090±0.04090.6987±0.03640.6939±0.03740.6951±0.03410.6986±0.03670.6807±0.03950.6020±0.0029
400总体精度/% 78.18±0.4377.62±0.3977.39±0.4177.56±0.3877.08±0.3775.80±0.3768.06±0.25
Kappa系数0.7205±0.05270.7141±0.04790.7116±0.04980.7136±0.04660.7078±0.04530.6927±0.04470.6033±0.0026
500总体精度/%76.49±0.3876.68±0.3876.31±0.3576.10±0.4075.80±0.3974.74±0.3968.21±0.30
Kappa系数0.7021±0.04290.7044±0.04310.6996±0.04020.6973±0.04560.6937±0.04440.6811±0.04430.6049±0.0034
100 总体精度/% 78.10±0.28 78.20±0.25 79.41±0.23 78.87±0.23 78.05±0.27 76.50±0.29 67.38±0.36
Kappa系数 0.7208±0.0335 0.7219±0.0297 0.7358±0.0264 0.7296±0.0266 0.7209±0.0319 0.7024±0.0333 0.5945±0.0041
200 总体精度/% 78.59±0.20 79.71±0.24 79.17±0.21 78.98±0.23 78.44±0.24 77.07±0.23 67.54±0.48
Kappa系数 0.7269±0.0237 0.7396±0.0290 0.7335±0.0248 0.7315±0.0273 0.7255±0.0272 0.7090±0.0263 0.5966±0.0053
40 300 总体精度/% 79.69±0.31 78.75±0.29 78.82±0.30 78.64±0.26 78.54±0.28 76.72±0.24 67.45±0.33
Kappa系数 0.7392±0.0369 0.7287±0.0345 0.7295±0.0365 0.7271±0.0306 0.7259±0.0338 0.7044±0.0279 0.5958±0.0033
400 总体精度/% 80.12±0.27 79.71±0.24 78.89±0.24 79.02±0.22 78.90±0.22 76.85±0.23 67.37±0.22
Kappa系数 0.7450±0.0315 0.7404±0.0285 0.7308±0.0278 0.7319±0.0253 0.7308±0.0251 0.7063±0.0257 0.5950±0.0023
500 总体精度/% 80.10±0.13 79.91±0.09 79.86±0.11 79.52±0.13 79.45±0.11 77.46±0.16 67.64±0.24
Kappa系数 0.7445±0.0152 0.7423±0.0111 0.7414±0.0125 0.7374±0.0153 0.7366±0.0124 0.7127±0.0178 0.5977±0.0028

表 4 Indiana Pines数据集实验结果
Table 4 The experiment results of Indiana Pines database

下载CSV 
样本数k 随机子空间数目S 统计值 OSSE RSM 随机森林
聚类数占随机子空间数目的比例/%
2.50 5.00 7.50 10.00 12.50
100 总体精度/% 69.27±0.29 70.19±0.19 70.99±0.19 71.59±0.17 72.19±0.15 71.76±0.16 64.40±0.18
Kappa系数0.6532±0.03200.6636±0.02090.6726±0.02060.6792±0.01850.6859±0.01650.6809±0.01760.5805±0.0018
200总体精度/%70.30±0.1772.07±0.1472.50±0.1772.71±0.1772.82±0.1872.21±0.1765.83±0.18
Kappa系数0.6650±0.01900.6849±0.01590.6898±0.01900.6920±0.01910.6932±0.02040.6863±0.01990.5813±0.0019
30300总体精度/%71.84±0.1673.06±0.1773.24±0.1973.54±0.1973.68±0.1773.05±0.1766.00±0.17
Kappa系数0.6827±0.01640.6962±0.01780.6982±0.02040.7016±0.02000.7032±0.01830.6961±0.01710.5851±0.0017
400总体精度/%72.85±0.1373.72±0.1573.79±0.1573.82±0.1673.91±0.1773.18±0.1865.97±0.15
Kappa系数0.6934±0.01480.7031±0.01700.7038±0.01670.7042±0.01720.7052±0.01930.6970±0.02000.5995±0.0019
500总体精度%72.52±0.2573.18±0.2273.39±0.2573.34±0.2573.48±0.2472.59±0.2665.18±0.14
Kappa系数0.6897±0.02700.6970±0.02430.6994±0.02690.6988±0.02670.7003±0.02640.6904±0.02870.6020±0.0019
100总体精度/%71.99±0.2372.92±0.1773.60±0.1374.19±0.1574.62±0.1474.53±0.1765.77±0.14
Kappa系数0.6834±0.02560.6940±0.01820.7017±0.01380.7084±0.01660.7130±0.01550.7119±0.01820.5994±0.0022
200总体精度/%73.27±0.1374.85±0.0975.42±0.1075.47±0.1175.59±0.1075.27±0.1164.69±0.13
Kappa系数0.6834±0.02560.6940±0.01820.7017±0.01380.7084±0.01660.7130±0.01550.7119±0.01820.5935±0.0021
40300总体精度/%73.55±0.1474.28±0.1574.85±0.1675.06±0.1375.21±0.1274.22±0.1465.89±0.13
Kappa系数0.7006±0.01590.7086±0.01700.7152±0.01870.7176±0.01490.7193±0.01410.7082±0.01610.5964±0.0020
400总体精度/%74.03±0.1075.13±0.1175.30±0.0875.34±0.0975.49±0.1074.83±0.0964.37±0.13
Kappa系数0.7064±0.01070.7188±0.01190.7206±0.00880.7210±0.00920.7227±0.01110.7153±0.00940.5889±0.0018
500总体精度/%74.28±0.1174.93±0.1575.10±0.1575.09±0.1675.16±0.1574.33±0.1464.92±0.12
Kappa系数0.7094±0.01300.7166±0.01690.7186±0.01670.7183±0.01830.7192±0.01700.7099±0.01610.6023±0.0021

与RSM相比,在Pavia University数据集中,OSSE所得结果的总体精度和Kappa系数均高于RSM且增幅较大,总体精度的最大增幅可达到2.64%,Kappa系数的最大增幅可达到0.04；在Indiana Pines数据集中,当随机子空间数目S及聚类数较小时,OSSE所得结果的总体精度和Kappa系数略小于RSM,但随着其中任意一个的增加,OSSE的分类性能快速提升从而超越RSM,总体精度的最大增幅可达到1.00%。与随机森林方法相比,两幅影像中OSSE所得结果的总体精度和Kappa系数均较高且增幅较大。在Pavia University 数据集中,总体精度的最大增幅可达到12.75%,Kappa系数的最大增幅可达到0.15。在Indiana Pines数据集中,总体精度的最大增幅可达到11.12%,Kappa系数的最大增幅可达到0.13。下面将从聚类数和随机子空间数目对实验结果进行分析。

5.2 OSSE中不同参数设置分析

5.2.1 聚类数分析

由表 3、表 4可知,在OSSE中,当样本数目k和随机子空间数目S一定时,聚类数的不同对分类精度产生了较大的影响,但分类精度的变化趋势与子空间数目S有关。

由表 3,对于Pavia University数据集,在样本数目k一定时,随着随机子空间数目S的增大,最优总体精度有向较小聚类比例偏移的趋势。将聚类比例与随机子空间数目相乘得到聚类数Z,可以发现,不同S的最优总体精度出现的聚类数稳定在10左右。并且随着聚类数从较小值增大到10,分类精度迅速增加,之后随聚类数的增大分类精度迅速下降。

由表 4可知,对于Indiana Pines数据集,在样本数目k和随机子空间数目S一定时,随着聚类比例的增大整体分类精度增加,最优总体精度出现的聚类比例稳定在12.5%。但是分类精度增加的速度以聚类数15左右为分界点,随着聚类数从较小值增大到15,分类精度迅速增加,之后随聚类数的增大分类精度缓慢增长甚至不变。

由此可见,针对特定的高光谱图像,当样本数目k和随机子空间数目S一定时,OSSE方法存在一个最佳的聚类数Z使分类性能达到最优。并且,这个最优的聚类数不随训练样本大小和随机子空间数目而改变。

5.2.2 随机子空间数目分析

根据实验所得结果,保持样本数目k和随机子空间数目S不变,将不同聚类数所得总体精度和Kappa系数相加取平均值得到结果如表 5和表 6所示。

表 5 Pavia University数据集OSSE精度平均值
Table 5 The average accuracy of Pavia University dataset in OSSE

下载CSV 
样本数目k初始集成规模S平均总体精度/%平均Kappa系数
10069.71 0.6976
20071.69 0.7147
2030071.82 0.7139
400 72.67 0.7223
500 72.28 0.7206
100 75.45 0.7510
200 76.24 0.7580
30 300 76.36 0.7588
400 77.57 0.7709
500 76.28 0.7593
100 78.52 0.7821
200 78.98 0.7867
40 300 78.89 0.7830
400 79.33 0.7867
50079.770.7924

表 6 Indiana Pines数据集OSSE精度平均值
Table 6 The average accuracy of Indiana Pines dataset in OSSE

下载CSV 
样本数目k 初始集成规模S 平均总体精度/% 平均Kappa系数
100 70.85 0.6709
20072.08 0.6850
3030073.07 0.6964
40073.62 0.7019
50073.18 0.6971
10073.47 0.7001
20074.92 0.7001
4030074.59 0.7123
40075.06 0.7179
50074.91 0.7164

如表 5所示,对于Pavia University数据集,当样本数目k为20和30时,随着随机子空间数目S从100增加到400,平均总体精度和Kappa系数逐渐增大,但增大的幅度逐渐降低。当S从400增大到500时,平均总体精度和Kappa系数不但没有增大,反而减小。不同的是,当样本数目k为40时,随着S 的增大平均总体精度和Kappa系数逐渐增加,在S为500时达到峰值。但整体来看,随着S的增大平均总体精度和Kappa系数增加的幅度逐渐降低。

如表 6所示,Indiana Pines数据集出现了与Pavia University数据集相似的趋势。随着随机子空间数目S从100增加到400,平均总体精度和Kappa 系数逐渐增大,但增大的幅度逐渐降低。当集成规模从400增加到500时,平均总体精度和Kappa系数不但没有增大,反而减小。

由此可见,与RSM相似,在OSSE中设置较大的随机子空间数目,不但不能保证更高的分类精度,而且会大大增加时间成本。因此,OSSE并不适宜设置过大的随机子空间数目。但同时,根据Pavia University数据集的实验结果,训练样本的大小对适宜随机子空间数目的选取有一定的影响,且随着训练样本的增大,适宜随机子空间数目呈现增大的趋势。

6 结 论

通过优化随机子空间的方式对现有的随机子空间集成方法进行了改进,提出了OSSE方法。该方法同时考虑子空间之间的差异性和单个子空间的分类性能,并以支持向量在训练样本中的分布差异作为子空间差异性的表征,采用k-means聚类的方法获取具有较大预测差值的最优子空间。同时,实验分析比较了训练样本大小、随机子空间数目和聚类数对OSSE性能的影响。实验表明：

(1) 在相同的参数设置条件下,与RSM算法相比,OSSE在总体分类精度和Kappa系数上均有所提高,对于Pavia University数据集,提高的幅度更大。说明OSSE算法的分类性能及稳定性更好。

(2) 与随机森林算法相比,OSSE算法的优越性更加明显。对于Pavia University数据集和Indiana Pines数据集,总体分类精度的最大增幅分别为12.75%和11.12%,说明OSSE算法的分类性能及稳定性优于随机森林算法。

(3) 对于OSSE算法,当训练样本大小和随机子空间数目一定时,其总体分类精度随聚类比例的变化而变化。同时,对分类结果的分析表明：当训练样本大小一定时,随机子空间数目不同,总体分类精度随聚类比例变化的规律不同；当随机子空间数目一定时,训练样本大小的改变不会对总体分类精度随聚类比例变化的规律产生影响。进一步分析发现,训练样本大小和随机子空间数目的改变均不影响总体分类精度随聚类数变化的规律,即：对于不同的训练样本大小和随机子空间数目,均存在一个非常接近的聚类数Z,并且,当聚类数逐渐增加至Z时,总体分类精度逐渐增大；当聚类数由Z逐渐增加时,总体分类精度逐渐减小。

此外,根据实验结果提出了一些有待进一步深入的工作：

(1) 对于同一个数据集,当训练样本大小和随机子空间数目改变时,最佳的聚类数是不变的,如何根据数据集的特点自动选取最佳聚类数需要进一步探索。

(2) 本研究表明,更大的随机子空间数目并不一定会导致更优的分类精度,同时训练样本的大小对最优随机子空间数目的选择有一定的影响,如何根据数据集的特点选择时间效率高、分类性能好的随机子空间数目需要进一步研究。

参考文献(References)

  • Ball J E, West T, Prasad S and Bruce L M. 2007. Level set hyperspectral image segmentation using spectral information divergence-based best band selection//Proceedings of the IEEE International Geoscience and Remote Sensing Symposium. Barcelona:IEEE:4053-4056 [DOI:10.1109/IGARSS.2007.4423739]
  • Bertoni A, Folgieri R and Valentini G. 2004. Feature selection combined with random subspace ensemble for gene expression based diagnosis of malignancies//Proceedings of the 15th Italian Workshop Neural Nets. Netherlands:Springer:29-35 [DOI:10.1007/1-4020-3432-6_4]
  • Bruzzone L, Roli F, Serpico S B.1995.An extension of the Jeffreys-Matusita distance to multiclass cases for feature selection. IEEE Transactions on Geoscience and Remote Sensing, 33 (6) : 1318–1321 . [DOI:10.1109/36.477187]
  • Chabrillat S, Goetz A F H, Krosley L, Olsen H W.2002.Use of hyperspectral images in the identification and mapping of expansive clay soils and the role of spatial resolution. Remote Sensing of Environment, 82 (2/3) : 431–445 . [DOI:10.1016/S0034-4257(02)00060-3]
  • Chen G H, Tang L, Jiang X G.2006.Feature selection and extraction of hyperspectral data——Based on HyMap data of Barrax in Spanish. Arid Land Geography, 29 (1) : 143–149 . ( 陈桂红, 唐伶俐, 姜小光. 2006. 高光谱遥感图像特征选择和提取方法的比较——基于试验区Barrax的HyMap数据. 干旱区地理, 29 (1) : 143–149. )
  • Chen Y S, Zhao X, Lin Z H.2014.Optimizing subspace SVM ensemble for hyperspectral imagery classification. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 7 (4) : 1295–1305 . [DOI:10.1109/JSTARS.2014.2307356]
  • Cunningham P and Carney J. 2000. Diversity versus quality in classification ensembles based on feature selection//Proceedings of the 11th European Conference on Machine Learning. Catalonia, Spain:Springer:109-116 [DOI:10.1007/3-540-45164-1_12]
  • De Backer S, Kempeneers P, Debruyn W, Scheunders P.2005.A band selection technique for spectral classification. IEEE Geoscience and Remote Sensing Letters, 2 (3) : 319–323 . [DOI:10.1109/LGRS.2005.848511]
  • Fauvel M, Benediktsson J A, Chanussot J, Sveinsson J R.2008.Spectral and spatial classification of hyperspectral data using SVMs and morphological profiles. IEEE Transactions on Geoscience and Remote Sensing, 46 (11) : 3804–3814 . [DOI:10.1109/TGRS.2008.922034]
  • Ho T K.1998.The random subspace method for constructing decision forests. IEEE Transactions on Pattern Analysis and Machine Intelligence, 20 (8) : 832–844 . [DOI:10.1109/34.709601]
  • Hoffbeck J P and Landgrebe D A.1996.Covariance matrix estimation and classification with limited training data. IEEE Transactions on Pattern Analysis and Machine Intelligence, 18 (7) : 763–767 . [DOI:10.1109/34.506799]
  • Jain A K, Duin R P, Mao J C.2000.Statistical pattern recognition:a review. IEEE Transactions on Pattern Analysis and Machine Intelligence, 22 (1) : 4–37 . [DOI:10.1109/34.824819]
  • Kruse F A, Boardman J W, Huntington J F.2003.Comparison of airborne hyperspectral data and EO-1 Hyperion for mineral mapping. IEEE Transactions on Geoscience and Remote Sensing, 41 (6) : 1388–1400 . [DOI:10.1109/TGRS.2003.812908]
  • Kuncheva L I, Whitaker C J.2003.Measures of diversity in classifier ensembles and their relationship with the ensemble accuracy. Machine Learning, 51 (2) : 181–207 . [DOI:10.1023/A:1022859003006]
  • Liu H, Yu L.2005.Toward integrating feature selection algorithms for classification and clustering. IEEE Transactions on Knowledge and Data Engineering, 17 (4) : 491–502 . [DOI:10.1109/TKDE.2005.66]
  • Melgani F, Bruzzone L.2004.Classification of hyperspectral remote sensing images with support vector machines. IEEE Transactions on Geoscience and Remote Sensing, 42 (8) : 1778–1790 . [DOI:10.1109/TGRS.2004.831865]
  • Opitz D W. 1999. Feature selection for ensembles//Proceedings of the 16th National Conference on Artificial Intelligence and the 11th Innovative Applications of Artificial Intelligence Conference Innovative Applications of Artificial Intelligence. Menlo Park, CA, USA:AAAI:379-384
  • Pal M, Foody G M.2010.Feature selection for classification of hyperspectral data by SVM. IEEE Transactions on Geoscience and Remote Sensing, 48 (5) : 2297–2307 . [DOI:10.1109/TGRS.2009.2039484]
  • Skurichina M, Duin P W.2002.Bagging, Boosting and the random subspace method for linear classifiers. Pattern Analysis & Applications, 5 (2) : 121–135 . [DOI:10.1007/s100440200011]
  • Tan K, Du P J.2008.Hyperspectral remote sensing image classification based on support vector machine. Journal of Infrared and Millimeter Waves, 27 (2) : 123–128 . ( 谭琨, 杜培军. 2008. 基于支持向量机的高光谱遥感图像分类. 红外与毫米波学报, 27 (2) : 123–128. )
  • Thomas G D.1997.Machine learning research:four current directions. AI Magazine, 18 (4) : 97–136 .
  • Underwood E, Ustin S and DiPietro D, DiPietro D.2003.Mapping nonnative plants using hyperspectral imagery. Remote Sensing of Environment, 86 (2) : 150–161 . [DOI:10.1016/S0034-4257(03)00096-8]
  • Wang C Y, Liu Z J, Yan C Y.2006.A experimental study on imaging spectrometer data feature selection and wheat type identification. Journal of Remote Sensing, 10 (2) : 249–255 . ( 王长耀, 刘正军, 颜春燕. 2006. 成像光谱数据特征选择及小麦品种识别实验研究. 遥感学报, 10 (2) : 249–255. )
  • Xu L, Krzyzak A, Suen C Y.1992.Methods of combining multiple classifiers and their applications to handwriting recognition. IEEE Transactions on Systems, Man and Cybernetics, 22 (3) : 418–435 . [DOI:10.1109/21.155943]
  • Yang J M, Kuo B C, Yu P T, Chuang C H.2010.A dynamic subspace method for hyperspectral image classification. IEEE Transactions on Geoscience and Remote Sensing, 48 (7) : 2840–2853 . [DOI:10.1109/TGRS.2010.2043533]