|
收稿日期: 2015-08-18; 修改日期: 2016-01-29;
优先数字出版日期: 2016-05-25
基金项目: 国家自然科学基金(编号:41322010,41171292);教育部博士研究生学术新人奖项目(编号:5052012213002,5052012213001)
第一作者简介:
黄旭(1987-),男,博士研究生,主要研究方向为密集匹配。E-mail:huangxu.chess@163.com
通讯作者简介: 张永军(1975-),教授,主要研究方向为数字摄影测量与遥感、计算机视觉等。E-mail:zhangyj@whu.edu.cn
中图分类号: P23
文献标识码: A
文章编号: 1007-4619(2016)03-0431-10
|
摘要
传统的后方交会最小二乘解法需要良好的外方位元素初值。在无初值或者初值不够精确的情况下,最小二乘迭代不容易收敛。在近景摄影测量或者计算机视觉等领域,往往不提供良好的初值,无法适用传统的后方交会解法。针对上述情况,本文提出了一种基于单应性矩阵的后方交会直接解法,在不需要初值的情况下,获取外方位元素的直接解。该方法根据单应性矩阵所描述的平面几何关系,利用单应性矩阵内在的约束条件,将后方交会问题转换为一个二元二次方程组的求解问题。该方法受舍入误差影响小,在无偶然误差的情况下,解算精度能达到10-9量级,能够避免传统直接解法计算复杂的问题,为传统的平差迭代解法提供良好的初值。此外,在多个控制点共面的情况下,该方法能够直接获得外方位元素的精确解。实验结果表明:在各种不同倾角拍摄的情况下,该方法均能够获得稳定的外方位元素,为后续的后方交会最小二乘算法提供良好的初值。采用本文方法计算的初值参与平差,能够达到与人工给定初值平差一致的精度,且迭代收敛速度是人工给定初值平差的2倍以上。在控制点共面的情况下,该方法的反投影精度能够达到亚像素级,且精度优于大部分主流的直接解法。
关键词
后方交会 , 单应性矩阵 , 直接解 , 四元数 , 共面点
Abstract
Space resection is the method of acquiring the exterior orientation parameters of a camera based on three ground control points (GCPs) at least and the corresponding image points. The traditional least squares method of space resection needs good initial values of exterior orientation parameters. However, good initial values are difficult to obtain in the oblique photogrammetry condition. The objective of this study is to compute accurate exterior orientation parameters automatically to provide good initial values for the least squares method of space resection. Solving the space resection problem needs three GCPs and the corresponding image points at least. This study initially starts from three GCPs and then derives a direct solution model of space resection. The three GCPs must be coplanar and the corresponding image points must also be coplanar. Thus, the homography matrix can be used to describe the geometric relationship between a set of coplanar points and another set of coplanar points. This study transforms the collinearity equation into a homography matrix model and derives two constraints based on the orthogonality of the rotation matrix. When only three GCPs exist, the space resection problem can be transformed into a set of binary quadratic equations. The binary quadratic equations have four solutions at most. An additional GCP is necessary to decide the unique solution. When three ground control points exist, the unique solution can be directly computed based on a set of linear equations, which are derived from the homography matrix model. After computing the homography matrix solution, the exterior orientation parameters can be obtained using the relationship between the homography matrix and collinearity equation. Three experiments tested the effectiveness and reliability of the proposed method. The first experiment aimed to test the performance of the proposed method when only three GCPs exist. The experimental data comprise done oblique image of the Yangjiang area and four evenly distributed GCPs. Three of the GCPs were used to compute the exterior orientation parameters, and the remaining one was used to decide the unique solution. The proposed method was compared with the traditional range and imaging equation models. In the first experiment, the proposed method showed the best back substitution accuracy, which reached as high as 9.908010E-9 pixels. However, the back substitution accuracies of the range and imaging equation models were merely 5.891172E-6 pixels and 9.285811E-4 pixels, respectively. The second experiment aimed to show the influence of the proposed method on the least squares result of space resection in different camera angle conditions. Two different datasets were used in the second experiment. The first dataset was still the oblique image of the Yangjiang area. The initial values using the proposed method were compared with the values from the traditional method and the man-made methods. In the large camera angle condition, the least squares iteration based on the traditional method was unable to converge. The accuracy of the least squares results based on the proposed method was as good as that of the man-made initial values. Both methods had back projection accuracies of 0.03592 pixels. However, the convergence rate of the proposed method was good. The second dataset was an aerial image of the Toronto area. Given that the camera angle was small, the traditional method achieved good initial values. Accordingly, the proposed method was compared with the traditional method. In the small camera angle condition, the back projection accuracy of the proposed method was as good as that of the traditional method. The accuracy of both methods was 0.02525 pixels, but the convergence rate of the proposed method is better than the traditional one. The third experiment compared the proposed method with currently popular direct solution models of space resection in the case of multiple coplanar GCPs. Camera calibration data were used in the third experiment. The accuracy of the proposed method was better than that of the coordinate transformation and polynomial models, and was as good as the accuracy of the virtual GCP model. This study proposes a new direct solution model of space resection based on the homography matrix. It transforms the space resection model into a set of binary quadratic equations and acquires the direct solution of exterior orientation parameters. When multiple coplanar GCPs exist, the proposed method is able to transform the collinearity equation into a set of linear equations. Experimental results show that the proposed method can provide good initial values for the least squares method of space resection, which can be applied in oblique photogrammetry, close-range photogrammetry, and so on. Future studies will focus on acquiring direct solutions in the case of non-coplanar GCP s to improve the universality of the proposed method.
Key words
space resection , homography matrix , closed-form solution , unit quaternions , co-planar points
1 引 言
后方交会即已知相机内方位元素的情况下,给定单张影像的像点及其对应的控制点坐标,恢复相机的位置和姿态的过程(Wu和Hu,2006)。相机的位置和姿态是测绘和目标重建的不可或缺的信息,因此后方交会在摄影测量、计算机视觉、目标识别、机器人导航等领域有着广泛的应用(Abidi和Chandra,1995; Yuan,1989; Lowe,1987)。
鉴于共线方程的非线性特征,传统方法采用泰勒展开,将共线方程线性化,根据外方位元素良好的初值,采用最小二乘平差的方法得到外方位元素的精确解(张剑清等,2003)。传统的最小二乘方法解算精度较高,能够同时处理多个控制点,但是其结果受制于初值条件。当初值较差时,往往迭代不收敛(江刚武等,2007)。然而在近景摄影等情况下,良好的初值通常不容易获取。
因此,如何摆脱初值的约束,直接得到外方位元素的解成为一个研究课题。目前主流的研究包括基于3个控制点的后方交会直接解法和基于多个控制点的后方交会直接解法。
后方交会至少需要3个控制点,因此理论上,只需3个控制点,就可以确定相机的外方位元素。可以从成像模型出发,以像点在像空间坐标系下的深度为未知数,构建成像方程直接解模型(Wu和Hu,2006; Závoti和Fritsch,2011);也可以从控制点与相机之间的距离出发,构建距离方程直接解模型(Wu和Hu,2006; Gao等,2003; Haralick等,1994; Fischler和Bolles,1981)。上述两种方法皆把后方交会问题转化为一个三元二次方程组的求解问题,计算较为繁琐,且最多产生4种解,需要额外一个控制点来确定唯一解。
3个控制点的直接解模型存在多解问题,需要额外一个控制点来确定唯一解。额外的控制点并不参与外方位元素的实际计算过程,即该控制点仅仅用于确定唯一解,而不参与解的计算。实际上,控制点尽管精度很高,但仍存在偶然误差。仅仅依靠3个控制点,其解算结果会受到偶然误差的影响。但是,若存在多个(≥4个)控制点参与计算,可以削弱偶然误差的影响,提高外方为元素的解算精度。因此,研究多个(≥4个)控制点情况下,如何直接得到相机唯一的外方位元素成为一个研究方向(Xu等,2008; Quan和Lan,1999; Ansar和Daniilidis,2003; Moreno-Noguer等,2007)。上述基于多个控制点的算法均引入了额外的附加参数,从而将共线方程模型转化为线性方程组,从而直接获得外方位元素的唯一解。但是若引入不适当的附加参数,会导致模型不稳定,降低解算精度。
本文提出了一种基于单应性矩阵的后方交会直接解法,能够将后方交会问题转化为二元二次方程组的计算问题,与传统直接解法相比,不仅受舍入误差影响小,而且简化了计算步骤,能够为传统的最小二乘迭代解法提供良好的初值。此外,在多个控制点(大于等于4个)共面的情况下,本文算法可以直接得到外方位元素的唯一解。
2 数学模型
2.1 单应性几何关系
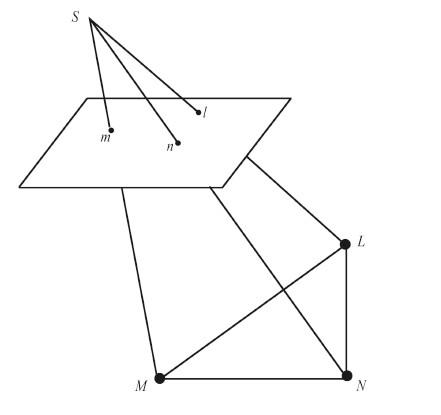
后方交会问题至少需要3个控制点。3个控制点必定共面,而对应的像点也一定共面(都在一个像平面上),如图 1所示,S表示摄影中心;m、n、l和M、N、L分别表示像点和对应的控制点。因此,可以采用一个单应性矩阵来描述一簇共面点与其一一对应的另外一簇共面点之间的几何关系(Hartley和Zisserman,2003):
| $ \lambda p'=H{{P}_{xy}}\ \ H=\left(\begin{matrix} {{h}_{11}} & {{h}_{12}} & {{h}_{13}} \\ {{h}_{21}} & {{h}_{22}} & {{h}_{23}} \\ {{h}_{31}} & {{h}_{32}} & {{h}_{33}} \\ \end{matrix} \right)$ | (1) |
式中,H表示3×3的单应性矩阵;p'表示像点的齐次坐标;Pxy表示对应平面控制点的齐次坐标;${ \lambda} $表示齐次因子。
2.2 后方交会直接解模型
定义Xs、Ys、Zs表示外方位线元素,phi、omega、kappa表示外方位角元素。采用摄像机矩阵的形式,可以将共线方程表达为(Hartley和Zisserman,2003)
| $ \begin{array}{l} { \lambda} { p} = { K}({{ R}^{\rm T}},- {{ R}^{\rm T}}{ t}){ P}\\[5pt] \begin{array}{*{20}{c}} {{ p} = {{(x,y,1)}^{\rm T}}} & {{ P} = {{(X,Y,Z,1)}^{\rm T}}} \end{array} \end{array} $ | (2) |
式中,K表示相机的内参数矩阵;R表示旋转矩阵;t表示外方位线元素向量。为了后续计算的方便,定义R' = RT,t' = – RTt:
| $ {\lambda} { p} = { K}({ R}',{ t}'){ P} $ | (3) |
式中,
| $K=\left(\begin{matrix} -f & 0 & {{x}_{0}} \\ 0 & -f & {{y}_{0}} \\ 0 & 0 & 1 \\ \end{matrix} \right);\text{ }$ |
f、x0、y0表示相机的内方位元素;R'表示旋转矩阵,与外方位角元素有关:
| $ { R}{'} = \left({\begin{aligned} {{a_1}{'}} \quad & {{a_2}{'}} & {{a_3}{'}}\\ {{b_1}{'}} \quad & {{b_2}{'}} & {{b_3}{'}}\\ {{c_1}{'}} \quad & {{c_2}{'}} & {{c_3}{'}} \end{aligned}} \right) $ |
t'表示3×1的平移向量:
| $ { t}' = {\left({\begin{array}{*{20}{c}} {{t_x}},& {{t_y}},& {{t_z}} \end{array}} \right)^{\rm T}} $ |
令p'表示归一化坐标,即${ p}{'} = {{ K}^{ - 1}}{ p}$,式(3)可以表示为
| $ \lambda { p}' =({ R}',{ t}'){ P} $ | (4) |
在空间中,由于三点确定一个平面,所以控制点M、N、L确定一个平面,设为
| $ AX + BY + CZ + D = 0 $ | (5) |
式中,A、B、C、D表示平面方程系数。由式(5),可以将坐标Z表达为
| $ Z = - \frac{{AX + BY + D}}{C} $ | (6) |
将式(6)代入式(4),整理可以得到形如式(1)的公式
| $ \lambda { p}' = { H}{{ P}_{xy}} $ | (7) |
式中,
| $ \begin{aligned} {{ H} = \left({\begin{aligned} { - \displaystyle\frac{{{a_3}'A}}{C} + {a_1}'} & {{a_2}' - \displaystyle\frac{{{a_3}'B}}{C}} & {{t_x} - \displaystyle\frac{{{a_3}'D}}{C}}\\[5pt] { - \displaystyle\frac{{{b_3}'A}}{C} + {b_1}'} & {{b_2}' - \displaystyle\frac{{{b_3}'B}}{C}} & {{t_y} - \displaystyle\frac{{{b_3}'D}}{C}}\\[5pt] { - \displaystyle\frac{{{c_3}'A}}{C} + {c_1}'} & {{c_2}' - \displaystyle\frac{{{c_3}'B}}{C}} & {{t_z} - \displaystyle\frac{{{c_3}'D}}{C}} \end{aligned}} \right)}\\[5pt] {{{ P}_{xy}} = {{\left({X,Y,1} \right)}^{\rm T}}} \quad\quad\quad\quad\quad \end{aligned} $ |
式(7)即为2维射影变换模型,是一个从平面到平面的透视变换模型。式(7)中,单应性矩阵H的9个元素相互之间不独立,根据旋转矩阵的正交性,可以得到两个约束条件:
| $ \begin{array}{l} \displaystyle\frac{{h_{11}^2 + h_{21}^2 + h_{31}^2}}{{{h_{11}}{h_{12}} + {h_{21}}{h_{22}} + {h_{31}}{h_{32}}}} = \displaystyle\frac{{{C^2} + {A^2}}}{{AB}}\\[20pt] \displaystyle\frac{{h_{12}^2 + h_{22}^2 + h_{32}^2}}{{{h_{11}}{h_{12}} + {h_{21}}{h_{22}} + {h_{31}}{h_{32}}}} = \displaystyle\frac{{{C^2} + {A^2}}}{{AB}} \end{array} $ | (8) |
只要将单应性矩阵H计算出来,就可以直接获得相机的外方位元素。
2.3 解算过程
式(7)是一个齐次线性方程组,可以通过除法运算来消除齐次因子λ,即:
| $ \begin{array}{*{20}{c}} {x' = \displaystyle\frac{{{h_{11}}X + {h_{12}}Y + {h_{13}}}}{{{h_{31}}X + {h_{32}}Y + {h_{33}}}}} \\[20pt] {y' = \displaystyle\frac{{{h_{21}}X + {h_{22}}Y + {h_{23}}}}{{{h_{31}}X + {h_{32}}Y + {h_{33}}}}} \end{array} $ | (9) |
式中,x'、y'表示经过归一化的影像坐标;X、Y表示控制点的物方坐标。
分别将3个控制点坐标代入式(9),可以列出6个线性方程:
| $ \begin{array}{l} { M}{\left(\!\! {\begin{array}{*{20}{c}} {{h_{11}}},\!\! & \! \!{{h_{12}}},\!\!& \!\!{{h_{13}}},\!\! & \!\! {{h_{21}}},\!\! & \!\! {{h_{22}}},\!\! & \!\! {{h_{23}}},\!\! & \!\! {{h_{31}}},\! \!& \!\! {{h_{32}}},\! \!& \!\! {{h_{33}}} \end{array}} \!\!\right)^{\rm T}}\!= 0 \end{array} $ | (10) |
式中,
| $ \begin{array}{l} { M} = \left(\!\!\!\!\!\! {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {{X_i}} & {{Y_i}} & 1 & 0 & 0 & 0 & { - {x_i}'{X_i}} & { - {x_i}'{Y_i}} & { - {x_i}'} \end{array}}\\ {\begin{array}{*{20}{c}} 0 & 0 & 0 & {{X_i}} & {{Y_i}} & 1 & { - {y_i}'{X_i}} & { - {y_i}'{Y_i}} & { - {y_i}'} \end{array}}\\ {.......} \end{array}} \!\!\!\!\!\! \right) \end{array} $ |
是一个6×9的矩阵,i=1,2,3。Xi、Yi表示控制点的物方X、Y坐标;X'i、Y'i表示经过归一化的影像坐标。
式(10)是一个不定方程组,所以只能求其通解。令未知参数为h13、h23,考虑单应性矩阵H的齐次性,可令h33 = 1,则有:
| $ {{ X}_h} = {h_{13}}{{ v}_1} + {h_{23}}{{ v}_2} + {{ v}_3} $ | (11) |
式中,${{ X}_h} = {\left({{h_{11}},{h_{12}},{h_{21}},{h_{22}},{h_{31}},{h_{32}}} \right)^{\rm T}}$,v1、v2、v3分别表示6×3系数矩阵:
| $ \begin{aligned} {\left({\begin{array}{*{20}{c}} {{X_i}} & {{Y_i}} & 0 & 0 & { - {x_i}'{X_i}} & { - {x_i}'{Y_i}}\\ 0 & 0 & {{X_i}} & {{Y_i}} & { - {y_i}'{X_i}} & { - {y_i}'{Y_i}} \end{array}} \right)^{ - 1}} \cdot \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left({\begin{array}{*{20}{c}} { - 1} & 0 & {{x_i}'}\\ 0 & { - 1} & {{y_i}'} \end{array}} \right) \end{aligned} $ |
的第1列,第2列和第3列向量。
将式(11)代入式(8),可以得到一个关于h13、h23的二元二次方程组,从而将后方交会问题,转化为一个二元二次方程组的求解问题:
| $ \left\{ {\begin{array}{*{20}{c}} \begin{array}{l} {A_1}h_{13}^2 + {B_1}h_{23}^2 + {C_1}{h_{13}}{h_{23}}+\\[3pt] \;\;\;\;\;\;\; {D_1}{h_{13}} + {E_1}{h_{23}} + {F_1} = 0 \end{array}\\[8pt] \begin{array}{l} {A_2}h_{13}^2 + {B_2}h_{23}^2 + {C_2}{h_{13}}{h_{23}}+\\[3pt] \;\;\;\;\;\;\;\; {D_2}{h_{13}} + {E_2}{h_{23}} + {F_2} = 0 \end{array} \end{array}} \right. $ | (12) |
式中,Ai、Bi、Ci、Di、Ei、Fi(i = 1、2)分别表示二元二次方程组的系数。
上述解算过程中,定义矩阵H的最后一项为1,因此求解的单应性矩阵H,与式(7)中的单应性矩阵,相差一个齐次因子h33。h33可通过下述公式求得:
| $ \begin{aligned} {h_{33}} = & \pm \sqrt {\displaystyle\frac{{{A^2} + {C^2}}}{{{C^2}(h_{11}^2 + h_{21}^2 + h_{31}^2)}}}= \\ & \pm \sqrt {\displaystyle\frac{{{B^2} + {C^2}}}{{{C^2}(h_{12}^2 + h_{22}^2 + h_{32}^2)}}}= \\ & \pm \sqrt {\displaystyle\frac{{AB}}{{{C^2}({h_{11}}{h_{12}} + {h_{21}}{h_{22}} + {h_{31}}{h_{32}})}}} \end{aligned} $ | (13) |
由于控制点必须位于相机的前方,所以必须满足如下条件:
| $ {h_{33}}({h_{31}}X + {h_{32}}Y + 1)= 0 $ | (14) |
从而判断出式(13)中h33的正负号。
根据式(12),可以计算出h13、h23;根据式(11),可以计算出h11、h12、h 21、h 22、h 31、h32;再将h11–h32各乘以齐次因子h33,即可得到式(7)中的单应性矩阵H。
2.4 恢复外方位元素
当单应性矩阵H计算出来后,可根据H推导出旋转矩阵R'和平移向量t'。
旋转矩阵R'可以通过h11、h12、h21、h22、h31、h32求出,根据式(7)单应性矩阵H的前两列元素,可得:
| $ \begin{array}{l} { R}'\left({\begin{array}{*{20}{c}} 1\\ 0\\ { - A/C} \end{array}} \right)= \left({\begin{array}{*{20}{c}} {{h_{11}}}\\ {{h_{21}}}\\ {{h_{31}}} \end{array}} \right)\\ { R}'\left({\begin{array}{*{20}{c}} 0\\ 1\\ { - B/C} \end{array}} \right)= \left({\begin{array}{*{20}{c}} {{h_{12}}}\\ {{h_{22}}}\\ {{h_{32}}} \end{array}} \right) \end{array} $ | (15) |
定义四元数q =(q0,q1,q2,q3)T,用四元数表示旋转矩阵,则式(15)可以表示为
| $ \begin{array}{l} { q} ^{\land} \left({\begin{array}{*{20}{c}} 1\\ 0\\ { - A/C} \end{array}} \right){^ \land} {{ q}^ *} = \left({\begin{array}{*{20}{c}} {{h_{11}}}\\ {{h_{21}}}\\ {{h_{31}}} \end{array}} \right)\\ { q} ^{\land} \left({\begin{array}{*{20}{c}} 0\\ 1\\ { - B/C} \end{array}} \right){^ \land} {{ q}^ *} = \left({\begin{array}{*{20}{c}} {{h_{12}}}\\ {{h_{22}}}\\ {{h_{32}}} \end{array}} \right) \end{array} $ | (16) |
式中,^表示四元数乘法;q*表示共轭四元数。
展开式(16),得到条件方程:
| $ \left({\begin{array}{*{20}{c}} 0 & { - {h_{11}} + 1} & { - {h_{21}}} & { -({h_{31}} + A/C)}\\[4pt] {{h_{11}} - 1} & 0 & { - {h_{31}} + A/C} & {{h_{21}}}\\[4pt] {{h_{21}}} & {{h_{31}} - A/C} & 0 & { -({h_{11}} + 1)}\\[4pt] {{h_{31}} + A/C} & { - {h_{21}}} & {{h_{11}} + 1} & 0\\[4pt] 0 & { - {h_{12}}} & { - {h_{22}} + 1} & { -({h_{32}} + B/C)}\\[4pt] {{h_{12}}} & 0 & { - {h_{32}} + B/C} & {{h_{22}} + 1}\\[4pt] {{h_{22}} - 1} & {{h_{32}} - B/C} & 0 & { - {h_{12}}}\\[4pt] {{h_{32}} + B/C} & { - {h_{22}} - 1} & {{h_{12}}} & 0 \end{array}} \right)\left({\begin{array}{*{20}{c}} {{q_0}}\\[4pt] {{q_1}}\\[4pt] {{q_2}}\\[4pt] {{q_3}} \end{array}} \right)= 0 $ | (17) |
式(17)是一个超定方程组,可根据SVD方法进行计算(鲁铁定等,2007)。将SVD计算结果归一化,即可得到单位四元数q,从而计算出对应的旋转矩阵R'。
平移向量分量tx、ty、tz的计算可以参照式(7)的最后一列,即:
| $ \begin{array}{l} {t_x} = \displaystyle\frac{{{a_3}'D}}{C} + {h_{13}}\\[5pt] {t_y} = \displaystyle\frac{{{b_3}'D}}{C} + {h_{23}}\\[5pt] {t_z} = \displaystyle\frac{{{c_3}'D}}{C} + {h_{33}}\\[5pt] \end{array} $ | (18) |
旋转矩阵R和外方位线元素向量t可以通过R'、t'计算得到:
| $ \begin{array}{*{20}{c}} {{ R} = { R}{'^{\rm T}}}& {{ t} = - { Rt}'} \end{array} $ | (19) |
2.5 多个控制点共面的情况
在实际应用中,常出现控制点共面的情况,比如相机的实验室检校、文物壁画测量等等。在这些场合中,良好的初值往往不容易获取。单应性矩阵可以描述平面与平面之间的几何关系,因此可以通过单应性矩阵直接获得相机的外方位元素。
当控制点个数大于等于4个时,将控制点及其对应的像点坐标代入式(7),可以得到形如式(10)的线性方程组:
| $ \begin{aligned} { M}{\left(\!\! {\begin{array}{*{20}{c}} {{h_{11}}},\!\!& \!\!{{h_{12}}},\!\! & \!\!{{h_{13}}},\!\! & \! \!{{h_{21}}},\!\! & \!\!{{h_{22}}},\!\! & \!\!{{h_{23}}},\!\! & \!\!{{h_{31}}},\!\! & \!\!{{h_{32}}},\!\! & \!\!{{h_{33}}} \end{array}} \!\!\right)^{\rm T}}\!= 0 \end{aligned} $ | (20) |
式中,
| $ \begin{aligned} { M} = \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\quad\; \\ \left(\!\!\!\! {\begin{array}{*{20}{c}} {{X_i}} & {{Y_i}} & 1 & 0 & 0 & 0 & { - {x_i}'{X_i}} & { - {x_i}'{Y_i}} & { - {x_i}'}\\ 0 & 0 & 0 & {{X_i}} & {{Y_i}} & 1 & { - {y_i}'{X_i}} & { - {y_i}'{Y_i}} & { - {y_i}'} \end{array}} \!\!\!\! \right)\\ i = 1,2,\cdot \cdot \cdot,n \qquad\qquad\qquad\qquad\qquad\qquad\qquad \end{aligned} $ | (21) |
式(20)和式(10)的区别在于:式(10)是一个未定方程组,需要计算通解;式(20)是一个超定方程组,可以得到齐次条件下的唯一解。
根据式(20),只需至少4个控制点,就可以得到单应性矩阵H。然后再根据2.4节介绍的方法,恢复外方位元素。
3 试验结果与分析
3.1节和3.2节试验的目的是验证基于3个控制点的单应性矩阵模型的可靠性和有效性。试验分别采用广东省阳江地区的倾斜影像数据和加拿大多伦多市的航空影像数据。
广东省阳江地区数据的倾斜相机为SWDC-5,飞行高度约800 m,相机焦距为99.88 mm,像素大小为0.006 mm。在阳江地区采集了6个控制点,用于外方位元素的计算;采集了17个检查点,用于检验解算精度,控制点和检查点的分布如图 2所示。
多伦多市数据的航空相机为UltraCam-D,飞行高度约1500 m,相机焦距为101.4 mm,像素大小为0.009 mm。在多伦多市采集均匀分布的9个控制点,用于外方位元素计算;采集了21个检查点,用于检验解算精度,控制点和检查点的分布如图 3所示。
在3.1节实验中,将采用阳江地区的控制点数据,对本文算法、成像方程直接解模型(Wu和Hu,2006)和距离方程直接解模型(Wu和Hu,2006)进行实验对比分析。在3.2节实验中,将分别采用阳江地区数据和多伦多市数据,进行后方交会最小二乘迭代实验,在不同倾斜镜头的条件下,比较传统方法提供的初值、人为提供初值以及本文算法计算初值的平差结果。
在3.3节试验中,采用多个平面控制点,以验证本文提出的基于多个共面控制点的单应性矩阵模型的解算精度。试验采用相机检校数据。总共有140个平面点,其中70个控制点用于计算外方位元素,另外70个控制点作为检查点,检验解算精度。70个平面控制点的分布如图 4所示。
本文的单应性矩阵模型是用于恢复针孔相机的方位元素,没有考虑影像畸变的情况。在3组实验中,所有的影像均事先经过了影像畸变改正。
3.1 与主流直接解法的比较试验
在本次试验中,采用阳江地区的4个控制点数据,其中3个控制点用于解算相机的外方位元素,分别采用成像方程直接解模型(Wu和Hu,2006)、距离方程直接解模型(Wu和Hu,2006)和本文提出的单应性矩阵直接解模型获得外方位元素的直接解。由于会产生多解的情况,需要额外一个控制点来确定唯一解。相机外方位元素的解算结果如表 1所示。外方位线元素和回代精度的解算结果均保留6位小数。外方位角元素的解算结果保留8位小数。在根据第4个控制点确定唯一的相机外方位元素以后,将参与计算的3个控制点重新代入成像方程直接解模型、距离方程直接解模型和单应性矩阵直接解模型,统计真实像点坐标和计算出来的像点坐标之间距离的平均值,作为回代精度。3个模型都是严格模型,均采用3个控制点来解算外方位元素,在没有多余观测的情况下,理论上回代精度应该为0。但是受到数据舍入误差的影响,会造成极其微小的误差,如表 1最后一列所示。
表 1 三种模型的外方位元素解算结果
Table 1 Results of exterior orientation of the three models
| 解算模型 | 解算结果 | 回代精度/像素 | |||||
| Xs/m | Ys/m | Zs/m | Phi/rad | Omega/rad | Kappa/rad | ||
| 成像方程 | 605876.3732 | 2420396.8526 | 854.6341 | –0.78811539 | 0.13447479 | 1.45759191 | 5.89E–6 |
| 距离方程 | 605876.3731 | 2420396.8525 | 854.6341 | –0.78811529 | 0.13447484 | 1.45759163 | 9.29E–4 |
| 单应性矩阵 | 605876.3731 | 2420396.8525 | 854.6341 | –0.78811529 | 0.13447486 | 1.45759196 | 9.91E–9 |
| 注:Xs, Ys, Es为外方位线元素坐标;Phi, Omega, Kappa为空间角坐标。 | |||||||
从表 1可以看出,3种方法计算出来的结果基本一致。外方位线元素最大偏差在10–4量级,外方位角元素的最大偏差在10–7量级。本文提出的单应性矩阵模型的回代精度最高,说明单应性矩阵直接解模型受舍入误差的影响最小,模型最为稳定。此外,距离方程直接解模型和成像方程直接解模型均需要求解一个三元二次方程组,与本文提出的方法相比,计算更为复杂。在3.1节实验中,并没有采用检查点来评价3种方法的精度。因为检查点本身存在偶然误差,而偶然误差一般远远大于舍入误差。所以,采用检查点,只能检测出检查点本身的偶然误差,而3种模型的解算结果仅仅受舍入误差影响,所以采用检查点是无法判断哪个模型更加稳定。
3.2 用作最小二乘迭代解法初值的比较试验
分别采用阳江地区数据和多伦多市数据,进行后方交会最小二乘试验。其中,阳江地区数据为倾斜影像,镜头侧摆较大;而多伦多市数据为航空影像,镜头侧摆较小。结合不同倾斜镜头获得的影像进行试验,能够更全面的比较分析本文算法的特点。两组试验的平差中,最大迭代次数设为100。两组试验均从迭代收敛性、控制点反投影精度和检查点反投影精度3个方面进行比较分析。其中,控制点反投影精度是统计控制点的真实像点坐标和计算出来的像点坐标之间距离的平均值;检查点反投影精度是统计检查点的真实像点坐标和计算出来的像点坐标之间距离的平均值。外方位线元素、控制点反投影精度和检查点反投影精度的计算结果保留3位小数,外方位角元素的解算结果保留6位小数。
3.2.1 阳江地区数据试验
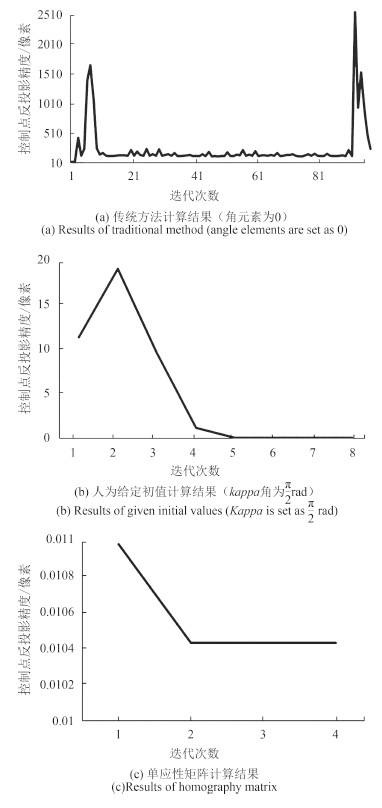
在试验中,分别根据单应性模型计算的初值(如表 1所示)、文献(张剑清等,2003)中传统方法计算的初值(外方位角元素均设为0;外方位线元素Xs、Ys取控制点的重心坐标;外方位线元素Zs取拍摄时的飞行高度)和人为给定初值(Kappa角设为 $\frac{\pi }{2}{\rm{rad}}$,其余与传统方法计算的初值一致),采用全部6个控制点,进行最小二乘迭代计算。试验结果如图 5和表 2所示。
表 2 阳江数据最小二乘迭代比较试验
Table 2 Comparison experiment of least squares for Yangjiang data
| 解算初值模型 | 解算结果 | 控制点反投影精度/像素 | 检查点反投影精度/像素 | |||||
| Xs/m | Ys/m | Zs/m | Phi/rad | Omega/rad | Kappa/rad | |||
| 传统方法(角元素为0) | 604773.8 | 2420666.0 | 40.0 | –0.988 | –1.475 | 2.552 | 243.8 | 498.7 |
| 人为给定初值(kappa角为90°) | 605881.7 | 2420397.1 | 844.6 | –0.797 | 0.134 | 1.454 | 1.0E–2 | 3.6E–2 |
| 单应性矩阵 | 605881.7 | 2420397.2 | 844.6 | –0.797 | 0.134 | 1.454 | 1.0E–2 | 3.6E–2 |
| 注:Xs, Ys, Es为外方位线元素坐标;Phi, Omega, Kappa为空间角的坐标。 | ||||||||
试验数据采用倾斜影像,影像倾角较大。从图 5和表 2可以看出,采用传统方法计算出来的初值,在最小二乘平差过程中,迭代无法收敛,解算结果精度很差,完全无法满足倾斜摄影的需求。而采用本文提出的单应性矩阵模型可以提供良好的初值,迭代收敛速度快,精度高,可以适用于倾斜摄影、近景摄影等应用。在人为给定初值的情况下,外方位元素的解算精度与单应性矩阵方法一致。但是人为给定的初值本身精度有限,因此需要更多的迭代才能使平差收敛,如图 5(b)所示。在一般的工程实践中,初值往往由POS系统提供。但是在近景摄影测量应用中,在没有POS系统的情况下,良好的初值往往不容易确定。在无POS系统提供初值的应用中,可以采用单应性矩阵的方法直接得到较为精确的初值。
比较表 1和表 2可以看出,表 1给出的直接解与表 2给出的迭代解不是完全一样。这是因为直接解是通过3个控制点来解算外方位元素,没有多余观测。由于控制点本身就存在误差,所以直接解的解算精度取决于控制点误差。而迭代解采用了6个控制点,可以通过平差理论来降低控制点误差的影响。所以,迭代解的计算结果更加精确。尽管直接解的结果不是最准确的,但是作为平差迭代的初值是足够了。因此,在控制点数目大于3个的情况下,可以联合直接解模型与平差迭代模型,获得最精确的外方位元素。
3.2.2 多伦多市数据试验
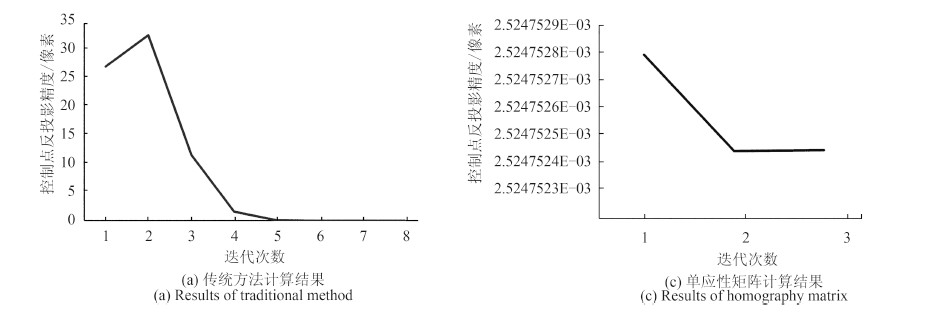
由于多伦多市数据为传统的航空影像,影像倾角较小,采用传统方法就能够得到用于平差解算的初值(张剑清等,2003),所以试验分别根据单应性模型计算的初值和文献(张剑清等,2003)中传统方法计算的初值,采用全部9个控制点,进行平差解算。试验结果如图 6和表 3所示。
表 3 多伦多数据最小二乘迭代比较试验
Table 3 Comparison experiment of least squares toronto data
| 解算初值模型 | 解算结果 | 控制点反投影精度/像素 | 检查点反投影精度/像素 | |||||
| Xs/m | Ys/m | Zs/m | Phi/rad | Omega/rad | Kappa/rad | |||
| 传统方法 | 630403.6 | 4834066.7 | 1631.5 | –2.385E–3 | 1.035E–3 | –1.573 | 2.1E–2 | 2.5E–2 |
| 单应性矩阵 | 630403.6 | 4834066.7 | 1631.5 | –2.385E–3 | 1.035E–3 | –1.573 | 2.1E–2 | 2.5E–2 |
从表 3可以看出,采用传统方法计算出来的初值,解算的外方位元素与单应性矩阵方法一致。这是因为试验数据是传统的航空影像,影像倾角较小。在这种情况下,传统方法能够给出较好的初值,使得最小二乘平差迭代收敛。但是从图 6的对比可以看出,采用单应性矩阵方法计算出来的初值,收敛速度更快,说明单应性矩阵方法提供的初值更加接近于真实值。综合解算精度和收敛速度两方面考虑,即使针对传统的航空影像,单应性矩阵方法提供的初值同样优于传统方法提供的初值。
3.3 与主流的基于平面控制点的直接解法比较试验
将本文提出的模型分别与坐标系转换模型(Xu等,2008)、多项式模型(Quan和Lan,1999)和虚拟控制点模型(Moreno-Noguer等,2007)进行比较。其中,坐标系转换模型是通过坐标系转换的方式,达到对成像方程模型消参的目的;多项式模型直接引入附加参数,将三元二次方程组(可以根据成像方程模型或者距离方程模型得到)线性化,引入控制点共面的约束条件,消除参数之间的冗余性,得到直接解;虚拟控制点模型将后方交会问题转化为相似变换问题,获得直接解。
本次试验分别采用4个控制点、10个控制点、20个控制点直至70个控制点,计算相机的外方位元素,所有控制点均是均匀分布;采用所有的检查点统计解算精度。其中,解算精度是统计检查点的真实像点坐标和计算出来的像点坐标之间距离的平均值。解算结果如表 4所示。所有解算结果均保留6位小数。
表 4 与主流直接解法比较试验
Table 4 Comparison with popular closed-form solutions
| 控制点数目 | 解算精度/像素 | |||
| 单应性矩阵模型 | 坐标系转换模型 | 多项式模型 | 虚拟控制点模型 | |
| 4 | 0.347 | 0.453 | 0.336 | 0.353 |
| 10 | 0.347 | 1.106 | 1.057 | 0.353 |
| 20 | 0.244 | 0.368 | 1.360 | 0.237 |
| 30 | 0.260 | 0.650 | 1.759 | 0.259 |
| 40 | 0.226 | 0.307 | 3.079 | 0.228 |
| 50 | 0.241 | 0.459 | 1.152 | 0.238 |
| 60 | 0.233 | 0.414 | 3.196 | 0.236 |
| 70 | 0.234 | 0.466 | 2.970 | 0.234 |
从表 4可以看出,本文提出的单应性矩阵模型的解算精度优于坐标系转换模型和多项式模型,与虚拟控制点模型较为一致。当控制点在20个以内时,随着控制点数目的增多,单应性矩阵模型的解算结果更加稳定可靠,精度也更高。当控制点超过20个,随着控制点数目的增多,单应性矩阵模型的解算结果趋近一致,并无实质变化。基于平面控制点的单应性矩阵方法可以用于多个控制点共面的场合,比如实验室的相机检校、壁画测量等(Zhang等,2012)。
4 结 论
传统的后方交会最小二乘迭代解法需要良好的外方位元素初值。在初值不够精确或者无初值的情况下,最小二乘解法无法保证迭代收敛。针对上述问题,本文提出了一种基于单应性矩阵的后方交会直接解模型,当控制点数目为3个的情况下,本文算法利用单应性模型的内在约束条件,将后方交会问题转化为二元二次方程组的计算问题;在多个控制点共面的情况下,本文算法能够将共线方程直接转化为线性方程组。该算法无需初值,能够获得相机外方位元素的直接解,解决了传统后方交会方法的初值问题,能够为传统最小二乘方法提供精确的初值。
与现有直接解法相比,本文算法的优势在于:
(1) 在3个控制点的情况下,传统的成像方程直接解模型和距离方程直接解模型,均将后方交会问题转换为三元二次方程组的计算问题;但是本文所提出的单应性矩阵模型,将后方交会转换为二元二次方程组的计算问题,降低了计算复杂度。
(2) 与成像方程直接解模型和距离方程直接解模型相比,本文提出的单应性矩阵模型更加稳定,受舍入误差更小,在无偶然误差的情况下,外方位元素的解算精度能达到10–9像素量级。
(3) 多个控制点共面的情况下,本文提出的单应性模型的反投影精度能够达到亚像素级,且精度优于大部分主流的直接解法,与虚拟控制点模型精度基本一致。
(4) 本文提出的单应性模型能够为传统的后方交会最小二乘方法提供良好的初值,采用本文方法计算的初值参与平差,能够达到与人工给定初值平差一致的精度,且迭代收敛速度是人工给定初值平差的2倍以上。
本文算法可以应用于倾斜摄影、近景摄影、壁画量测等领域。目前,该算法仅仅适用于多个控制点共面的情况下,获取直接解。在未来的工作中,需要进一步研究控制点不共面的情况下,如何获取直接解,以进一步提高本文算法的普适性。
参考文献(References)
-
Abidi M A, Chandra T.1995.A new efficient and direct solution for pose estimation using quadrangular targets:algorithm and evaluation. IEEE Transactions on Pattern Analysis and Machine Intelligence, 17 (5) : 534–538 . [DOI:10.1109/34.391388]
-
Ansar A, Daniilidis K.2003.Linear pose estimation from points or lines. IEEE Transactions on Pattern Analysis and Machine Intelligence, 25 (5) : 578–589 . [DOI:10.1109/TPAMI.2003.1195992]
-
Fischler M A, Bolles R C.1981.Random sample consensus:a paradigm for model fitting with applications to image analysis and automated cartography. Communications of the ACM, 24 (6) : 381–395 . [DOI:10.1145/358669.358692]
-
Gao X S, Hou X R, Tang J L, Cheng H F.2003.Complete solution classification for the perspective-three-point problem. IEEE Transactions on Pattern Analysis and Machine Intelligence, 25 (8) : 930–943 . [DOI:10.1109/TPAMI.2003.1217599]
-
Haralick R M, Lee C N, Ottenberg K, Nölle M.1994.Review and analysis of solutions of the three point perspective pose estimation problem. International Journal of Computer Vision, 13 (3) : 331–356 . [DOI:10.1007/BF02028352]
-
Hartley R, Zisserman A.2003.Multiple View Geometry in Computer Vision.. Cambridge:Cambridge University Press, : 107–110 .
-
Jiang G W, Jiang T, Wang Y, Gong H.2007.Space resection independent of initial value based on unit quaternions. Acta Geodaetica et Cartographica Sinica, 36 (2) : 169–175 . ( 江刚武, 姜挺, 王勇, 龚辉. 2007. 基于单位四元数的无初值依赖空间后方交会. 测绘学报, 36 (2) : 169–175. )
-
Lowe D G.1987.Three-dimensional object recognition from single two-dimensional images. Artificial Intelligence, 31 (3) : 355–395 . [DOI:10.1016/0004-3702(87)90070-1]
-
鲁 铁定, 陶 本藻, 周 世健.2007.矩阵的SVD分解性质及其在秩亏网平差中的应用. 大地测量与地球动力学, 27 (5) : 63–67 .
-
Moreno-Noguer F, Lepetit V and Fua P. 2007. Accurate non-iterative o(n) solution to the pnp problem//Proceedings of the IEEE 11th International Conference on Computer Vision. Rio de Janeiro:IEEE:1-8 [DOI:10.1109/ICCV.2007.4409116]
-
Quan L, Lan Z D.1999.Linear n-point camera pose determination. IEEE Transactions on Pattern Analysis and Machine Intelligence, 21 (8) : 774–780 . [DOI:10.1109/34.784291]
-
Wu Y H, Hu Z Y.2006.PnP problem revisited. Journal of Mathematical Imaging and Vision, 24 (1) : 131–141 . [DOI:10.1007/s10851-005-3617-z]
-
Xu D, Li Y F, Tan M.2008.A general recursive linear method and unique solution pattern design for the perspective-n-point problem. Image and Vision Computing, 26 (6) : 740–750 . [DOI:10.1016/j.imavis.2007.08.008]
-
Yuan J S C.1989.A general photogrammetric method for determining object position and orientation. IEEE Transactions on Robotics and Automation, 5 (2) : 129–142 . [DOI:10.1109/70.88034]
-
Závoti J, Fritsch D.2011.A first attempt at a new algebraic solution of the exterior orientation of photogrammetry. Acta Geodaetica et Geophysica Hungarica, 46 (3) : 317–325 . [DOI:10.1556/AGeod.46.2011.3.4]
-
Zhang J Q, Pan L, Wang S G. Photogrammetry. Wuhan: Wuhan University Press 2003 : 23 -27. ( 张剑清, 潘励, 王树根. 2003. 摄影测量学. 武汉: 武汉大学出版社 : 23 -27. )
-
Zhang Y J, Hu K, Huang R Y.2012.Bundle adjustment with additional constraints applied to imagery of the dunhuang wall paintings. ISPRS Journal of Photogrammetry and Remote Sensing, 72 : 113–120 . [DOI:10.1016/j.isprsjprs.2012.06.008]