|
收稿日期: 2015-06-16; 修改日期: 2015-12-22;
优先数字出版日期: 2016-05-25
基金项目: 国家自然科学基金项目(编号:41371436);国家重点基础研究发展计划(973计划)(编号:2012CB720001)
第一作者简介:
夏琴(1990-),女,硕士研究生,现从事遥感图像处理和稀疏表示理论研究。E-mail:xianduan007@163.com
中图分类号: TP701
文献标识码: A
文章编号: 1007-4619(2016)03-0441-9
|
摘要
常规的去噪方法在去除遥感卫星影像噪声时,往往会造成影像模糊和空间分辨率下降。本文将稀疏表示理论应用于遥感卫星影像去噪,提出了一种改进算法,能够保留低频信息不变,仅对影像的高频信息进行稀疏重建。算法核心是按照是否能够从过完备字典中选择较少原子进行稀疏表示的原则来区分高频信息中的有效信息和噪声。通过3组实验对改进算法与传统去噪方法进行对比检测,实验结果表明,改进算法在去除噪声的同时,能较好地突出影像的边缘和细节信息。
关键词
遥感影像 , 稀疏表示 , 去噪 , K-SVD , 质量评价
Abstract
Considerable noise is present in some multispectral images acquired by remote-sensing satellites. The current traditional de-noising methods not only fail to completely remove the noise, but also cause image blurring and spatial-resolution degradation. This study aims to mitigate the tradeoff between the removal of noise and the reservation of information. To solve this problem, we propose an improved and high-performing sparse representation approach that processes the high-frequency portions in the difference images based on the initial image and the Gaussian-filtered image to remove the noise. In this study, sparse representation is applied to the information in a remote-sensing image to accurately represent important information, which includes edge and texture. By contrast, the noise that is mainly concentrated in the high-frequency portion cannot be represented. We used data sparsity to reconstruct the high-frequency portion without noise. The algorithm completely preserves the low-frequency information and reconstructs the high-frequency information by sparse representation based on whether or not such information can be represented by fewer atoms from the over-complete dictionary. Theoretical analysis and experimental results show that the proposed method outperforms the traditional de-noising methods and the sparse representation method. In terms of visual quality, the proposed method reconstructs the image with clear color and apparent structure. The results of the objective assessment show that the proposed method can achieve a higher peak signal-to-noise ratio than the other methods and provide a feasible solution to remove noise effectively and considerably highlight the details of the original images.
Key words
remote sensing images , sparse representation , image de-noising , K-SVD , quality evaluation
1 引 言
遥感影像在获取和传输过程中,经常会引入噪声。由于影像存在较大的噪声,严重影响了影像的后续处理和应用。因此,在遥感影像预处理中,有效去除噪声并尽可能多地保留影像原有的有用信息尤为关键。
传统的去噪方法可分为空间域滤波和频率域滤波两类。基于空间域的去噪方法是把影像信号和滤波函数进行卷积来完成的,通常是先通过不同的滤波函数得到不同的模板,再利用模板对原始图像上每一个像素的灰度值进行处理。经典的空间域去噪方法有均值滤波、中值滤波、维纳滤波等。这类方法是用同一种方式去处理图像中的每一个像素,而没有顾及每个像素自身的特性,在去除随机噪声方面有很好的效果,但在降低噪声的同时,也会产生较为严重的影像模糊,尤其是在影像的边缘和细节部分。基于频率域的去噪方法是利用噪声和信号在变换域上分布不同的特点,先将原始图像转换到变换域,在变换域对数据进行处理,再进行逆变换将其转换回空间域,从而降低图像中的噪声。常见的变换域方法有傅里叶变换、离散余弦变换、沃尔什变换、小波变换以及多尺度几何分析方法等。实际上,在变换域中信号和噪声是不可能完全分离的。在去除噪声所在的部分时,也去除了信号在此部分的信息。因此,基于频率域的去噪方法的关键在于如何在去除噪声和保留细节上达到平衡,而目前并无十分有效的解决方案。
近年来,随着稀疏表示理论的迅速兴起,基于稀疏表示的去噪方法快速发展起来,被认为在去噪方面具有较强的优势,是目前最受关注的图像去噪算法。该方法按照是否是影像中的稀疏成分,把图像中的信息和噪声分开。由于过完备字典中的原子是有特定结构的,图像中有一定结构的成分构成图像的有用信息,能够用原子来表示,但是图像中噪声是随机分布的,没有结构特征,不能用原子来表示。由此,稀疏重建过程可以将影像的有用信息与噪声分开,从而达到图像去噪的目的(姜鹏飞,2011)。基于稀疏表示的去噪算法使得信号具有更强的自适应性,而且使得信号的表示更加的简单明了(王瑶,2014)。基于稀疏表示的去噪算法都是对影像块进行处理,目前,国内外研究人员提出了基于块处理的多种算法,如K-SVD算法(Aharon等,2006),Block-Matching and 3D filtering(BM3D)算法(Dabov等,2007),Learned Simultaneous Sparse Coding(LSSC)算法(Mairal等,2009),Expected Patch Log Likelihood(EPLL)算法(Sulam & Elad,2015)等。LSSC结合了自适应稀疏先验和局部最近搜索,后者假设每个图像块都有其相似的图像块,再建立相似块集的联合表示,这不仅考虑了图像块的结构还考虑了图像块间的内在关系,BM3D算法与其也有类似之处。然而,尽管其具有有效的局部处理,但是BM3D与LSSC算法对块重叠部分都不能很好处理,因此同样存在局部-整体不一致的问题。K-SVD方法的主要改进在于字典的更新步骤,它通过简单而有效地逐列更新的方式,同步更新字典原子和相关的表示系数使得计算复杂度大大降低。近年来,也产生了不少改进的算法,如Sulam等人提出的小波变换与K-SVD相结合的训练字典方法,在小波分解的不同尺度上分别训练字典,并联合单尺度与多尺度方法得到视觉效果较好的图像(Sulam等,2014)。这些方法在一定程度上取得了成功,但仍存在一些缺陷,如结合多尺度的算法在改善效果的同时更增加了计算复杂度。
目前,基于稀疏表示的去噪方法在对含有噪声的自然图像已做了大量实验和研究,且主要针对高斯噪声、泊松噪声等。而卫星影像由于是从高空获取,具有与自然图像不同的特点:成像距离远、过程复杂、相机焦距长;其在获取和传输过程中受大气散射和折射、CCD感光值偏差、大气湍流、相机抖动等因素的影响会引入多种噪声,能否利用稀疏表示理论去除这些噪声是值得研究的问题。本文将稀疏表示去噪方法引入到卫星影像的去噪过程中,由于K-SVD算法具有良好的耦合性,能够与大多数分解算法一同使用(魏雅丽,2013),因此考虑用K-SVD算法实现卫星影像去噪。然而,基于超完备字典稀疏分解的K-SVD算法虽然收敛速度较快,但是随着噪声的逐渐增大,使用该算法进行去噪后的影像因纹理细节的丢失会产生模糊的效果。由于卫星影像噪声较多,为了避免去噪后影像模糊的现象,本文提出一种改进方法。原始影像与低通滤波后的影像进行差值运算,对差值影像进行基于K-SVD方法的稀疏重建,将重建结果与滤波后的影像进行叠加。实验结果表明,基于稀疏表示的去噪方法可以应用于卫星影像的去噪,且改进的方法保留了较丰富的边缘信息,效果较好,有效地解决了K-SVD去噪带来的模糊现象。
2 图像的稀疏表示去噪方法
2.1 稀疏去噪的基本原理
假设一幅理想的图像表示为F′,V表示图像噪声,此时带有噪声的图像F可以表示为
| $ {{F}}={{{F}}^{'}}+{{V}} $ | (1) |
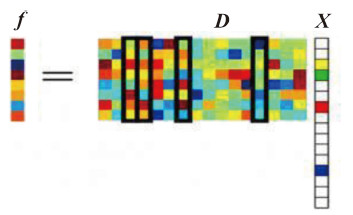
基于稀疏表示去噪方法的核心是将信号通过某个过完备字典D进行稀疏表示,即用若干个基信号来线性表示原始信号F(王瑶,2014),其中列向量f的表达形式如图 1所示。
稀疏去噪的过程包括两个关键的步骤,一是对影像信号进行稀疏分解,使其有效地提高信号稀疏分解的运算效率。要建立此类稀疏分解模型需要满足下式:
| $ \min ||{{{x}}_0}||\,\,\,\,\,\,{\rm{s.}}{{\rm{t.}}^{}}{\rm{}}{{\rm{}}^{}}||{\textbf{f}} - {{Dx}}|{|_2} \leqslant {\bf{\varepsilon }} $ | (2) |
式中,f为列向量信号,x为稀疏表示系数,d为字典,ε为表示误差。
从理论上讲,稀疏编码可以实现,Davis等人(1997)证明稀疏分解均是NP-Hard问题,计算量非常大,因此稀疏编码均采用近似逼近的思想。
稀疏去噪的第二个关键步骤是构造用于稀疏分解的过完备字典,使其更好地体现影像信号的特征(魏雅丽,2013)。字典的选择需满足以下函数:
| $ \mathop {\min }\limits_{{{D}},{{X}}} \left\{ {||{{F}} - {{DX}}||_F^2} \right\}\;\;{\rm{s.}}\;{\rm{t.}}\;\;\forall i,||{{{x}}_i}|| \leqslant T{}_{\rm{0}} $ | (3) |
假设图像块均满足稀疏模型 $M({D},\varepsilon,{{T}_{0}})$,则存在字典 ${D}\in {{{R}}^{n\times m}}(m \geqslant n)$,及每一列 f 对应的表达系数 ${x}\in {{{R}}^{m}}$ 满足式 $||{Dx-f}|{{|}_{2}} \leqslant \bf{\varepsilon }$,即可以近似还原原始信号。
下面以K-SVD算法为例,介绍稀疏表示去噪的基本流程。
2.2 基于K-SVD的稀疏去噪方法
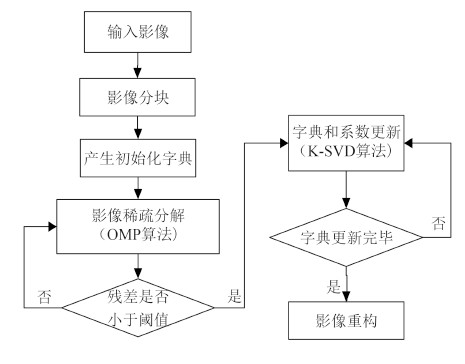
基于K-SVD的稀疏去噪方法其基本流程如图 2所示。下面将详细介绍该方法的具体步骤,其中步骤2、3即为稀疏分解和字典更新这两个关键步骤。
步骤1 影像分块
在进行影像去噪时,采用对影像分块处理的形式,将图像分成具有重叠的N块且大小为 $\sqrt n \times \sqrt n$,其中n << N。将每块影像的像素值设置成一个列向量fi,得到矩阵 ${F}=[{{{f}}_{1}},{{{f}}_{2}},\cdots,{{{f}}_{N}}]$ 。
步骤2 通过OMP算法行稀疏编码
正交匹配追踪(OMP)(Pati等,1993)算法采用最小二乘法计算所有的稀疏系数得到正交化的结果,其过程如下。
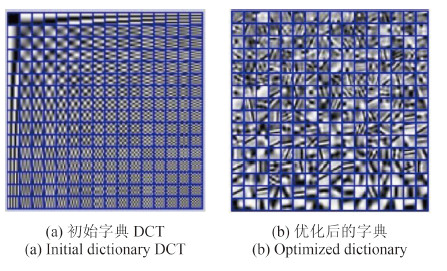
对步骤1中分块得到的每一影像块f通过逐步逼近的方法对信号进行稀疏分解。首先需给定初始字典 ${{G}} = \{ {{{g}}_i}\},$$i = 1,2,\cdots,n$(本文采用DCT为初始字典,如图 3(a)所示),设定初始残差R1=f,f为原始信号,所选原子构成的正交集为D = $\{ {d_p}\} ,p = 1,2, \cdots ,k$,在迭代过程中按一定的原则选择原子以保证稀疏表示的结果与原信号间残差最小。
(1) 依次选择残差与原子内积结果最大时所对应的原子:
| $ {g_{{i_m}}}_{}{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\rm{s}}{\rm{.t}}{\rm{.}}{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} | < {R^m},{g_{{i_m}}} > | = \mathop {\max }\limits_{i \in \Gamma } |{\rm{ < }}{R^m},{g_i} > | $ | (4) |
式中,$m = 1,2,\cdots\!,$ n: $i = 1,2,\cdots n$ 。
(2) 采用Gram-Schmidt正交化方法对式(4)选取的原子进行正交化处理:
| $ {d_m} = {g_{{i_m}}} - \sum\limits_{p = 0}^{m - 1} {\frac{{ < {g_{{i_m}}},{d_p} > }}{{||{d_p}|{|^2}}}} {d_p} $ | (5) |
(3) 并对dm进行归一化处理:
| $ {{{d}}_m} = {{{{{d}}_m}} \over {||{{{d}}_m}|{|^2}}} $ | (6) |
(4) 此时残余分量Rm投影到dm上:
| $ {{{R}}^m} = < {{{d}}_m},{{{R}}^m} > {{{d}}_m} + {{{R}}^{m + 1}} $ | (7) |
依次循环对残余的分量进行分解,当残余分量满足一定的阈值时,停止迭代,此时所有选择的原子构成原子集D,用所选择的原子可得到初步的影像稀疏表示。此时信号f表示如式(8)所示。
| $ {{f}} = \sum\limits_{i = 0}^{k - 1} { < {{{d}}_i},{{{R}}^i} > {{{d}}_i} + {{{R}}^k}} {\kern 1pt} {\kern 1pt} = {{D\hat x}} + {{{R}}^k} $ | (8) |
步骤3 采用K-SVD算法更新字典
使用OMP稀疏分解算法已近似求得稀疏表示系数 $\widehat x$和原子集D,根据已选择的原子,采用K-SVD算法对已选择的所有原子一一更新处理,此时原子与系数同时更新,并使两者都能够达给定的要求。
此过程需要求解的函数如式(3)所示。字典D固定的条件下,上述最优化问题即为寻求稀疏表示系数矩阵,其中:
| $ ||{{F}} - {{DX}}||_F^2 = \sum\limits_{i = 1}^N {||{{{f}}_i} - {{D}}{{{x}}_i}||_2^2} $ | (9) |
因此,对于分块处理的N个影像块,式(3)可解耦为N个独立的问题:
| $ \begin{array}{*{20}{l}} {\min \{ ||{{\bf{f}}_i} - D{x_i}||_2^2\} \;{\rm{s}}.\;{\rm{t}}.\;\;||{x_i}|| \le {T_0},\;\;}\\ {i = 1,2, \cdots ,N} \end{array} $ | (10) |
在OMP算法处理后得到固定的X与D,此时需对原子集中的所有原子进行更新,首先考察字典中的一列dk(即第k个原子)以及和dk对应的系数矩阵中的第k行,记为 $x_T^k$(不是X中的第k个向量xk)。考虑式(3),${\rm{||}}{{F}} - {{DX}}||_F^2$ 可以写成如式(11)所示。
| $ \begin{array}{l} \displaystyle ||{{F}} - {{DX}}||_F^2 = ||{{F}} - \sum\limits_{j = 1}^K {{{{d}}_j}{{x}}_T^j} ||_F^2 = \\ [10pt] \displaystyle ||({{F}} - \sum\limits_{j \ne k}^K {{{{d}}_j}{{x}}_T^j})- {{{d}}_k}{{x}}_T^k||_F^2 = \\ [10pt] \displaystyle ||{{{E}}_k} - {{{d}}_k}{{x}}_T^k||_F^2 \end{array} $ | (11) |
由式(11),可利用奇异值分解(SVD)来求解dk和$x_T^k$ 。
定义 ${{\omega }}_k$ 为指向样本{fi}中使用原子dk的指标集,即 $x_T^k(i)$ 中非零的位置。由此,
| $ {{{\omega }}_k} = \{ i|\;1 \leqslant i \leqslant K,x_T^k \ne 0\} $ | (12) |
定义 $N \times {{{\omega }}_k}$ 大小的矩阵k,矩阵中 $({{{\omega }}_k}(i),i)$ 位置为1,其余位置为0。当执行时 ${{x}}_R^k = {{x}}_T^k{\Omega _k}$,由于忽略零元素使行向量 ${ x}_T^k$ 缩小,得到的结果为长度为| ${{\omega }}_k$ |的行向量 ${ x}_k^R$ 。同理,对F执行 $F_k^R = { F}{\Omega _k}$ 得到一个长度为 $n \times |{{{\omega }}_k}|$ 的矩阵,其中包含使用了原子dk的样本子集; ${{E}}_k^R = {{{E}}_k}{\Omega _k}$ 得到对应于使用dk的子集的误差矩阵。由此,式(11)等同于式(13)。
| $ ||{{{E}}_k}{\Omega _k} - {{{d}}_k}{{x}}_T^k{\Omega _k}||_F^2 = ||{{E}}_k^R - {{{d}}_k}{{x}}_R^k||_F^2 $ | (13) |
于是可利用SVD直接进行求解。通过SVD,将其分解为 ${{E}}_k^R = {{U}}\Delta {{{V}}^{\rm T}}$,更新原子 ${{{d}}_k} = {{{u}}_1}$,更新系数 ${{x}}_R^k = \Delta(1,1)\cdot {{{v}}_1}$ 。
上述为对原子集中第k列原子更新过程,对于原子集D中的所有原子,从第一列原子开始对所有原子依次进行上述过程的更新处理,直到所有原子更新完毕,得到优化的字典DF如图 2(b)所示,此时得到的原子集及稀疏系数 ${{\hat x}}{}_F$ 全局最优,可以很好地描述原始信号的有用信息,稀疏表示的结果如式(14)所示。
| $ {{f}} \approx {{{D}}_F}{{{\hat x}}_F} $ | (14) |
步骤4 影像重构
经过步骤3、4的计算,对 ${{F}} = [{{{f}}_1},{{{f}}_2},\cdots,{{{f}}_N}]$ 进行稀疏分解得到稀疏系数和优化后的字典,经重构后 ${{{F}}^{'}} = [{{{f}}_1}^{'},{{{f}}_2}^{'},\cdots,{{{f}}_N}^{'}]$,将其每一列重新设置为一个影像块,合并所有的影像块,在重叠区域做均值处理,此时的影像即为稀疏去噪后的影像。
3 卫星影像的稀疏去噪方法
经过上述K-SVD算法去噪处理后,结果影像中噪声去除明显,但是边界信息丢失较为严重,视觉上有明显的模糊现象。考虑到K-SVD算法直接对影像的灰度值处理,不能充分体现K-SVD对结构特征的敏感性,未能充分利用其算法对结构特征进行很好的表达。因此,本文借鉴传统的空间域低通滤波的思想,将影像的低频和高频信息分开处理,保留低频信息不变,对高频信息进行K-SVD算法稀疏重建。由于高频信息包含大量边界信息,同时也几乎包括了全部的噪声,采用K-SVD对高频信息处理,这样做能够对影像的低频信息进行保护,防止其在稀疏重建的过程中丢失;同时也能充分利用K-SVD对结构特征敏感的特性,在对高频信息稀疏重建过程中去除噪声并更好地恢复结构特征。
另外对于遥感卫星彩色影像,本文采用对高频信息分波段进行处理的形式,每个波段训练不同的字典来去除各个波段的不同噪声,以获得每个波段的最优解。分波段处理是为了保证各波段和整体信息量的最大化,获得相对于原始影像更好的估计。
本文改进算法的基本流程图如图 4所示,下面介绍该方法的详细步骤。
(1) 获取差值影像
通过对原始影像进行低通滤波获得背景影像,用原始影像减去背景影像得到差值影像。此时差值影像包含大量的边界信息和噪声,由于灰度数值较小,反差不明显,因此为了增大差值影像反差,突出边界信息,对差值影像做线性拉伸处理,拉伸的范围设定为原始影像的灰度动态范围。
| $ {{{I}}_1} = {{{I}}_{\text{in}}} - G({{{I}}_{\text{in}}}){,_{}}_{}{{{I}}_2} = X({{{I}}_1}) $ | (15) |
式中,Iin为输入影像,G(*)为低通滤波,I1为差值影像,X为线性拉伸,I2为拉伸后的差值影像。
(2) 计算拉伸前后差值影像的均值
| $ mea{n_i} = {1 \over {m*n}}\sum\limits_{y = 0}^m {\sum\limits_{x = 0}^n {{{{I}}_i}(x,y)} },i = 1,2 $ | (16) |
式中,mean1为拉伸前差值影像的均值,mean2为拉伸后差值影像的均值。
(3) 稀疏去噪
对处理后的差值影像各个波段分别做K-SVD稀疏去噪处理,得到去噪后的差值影像。
| $ {{{I}}_{\bf{k - svd}}} = P({{{I}}_2}) $ | (17) |
式中,P为K-SVD稀疏处理。
(4) 影像的叠加
将去噪后的差值影像叠加到背景影像上获取结果影像,采用式(18)的处理方式。由于差值影像的拉伸处理会造成灰度值的变化,计算灰度均值差,保持差值影像处理前后灰度均值不变。
| $ {{{I}}_{\bf{out}}} = G({{{I}}_{\bf{in}}})+ {{{I}}_{\bf{k - svd}}} -(mea{n_2} - mea{n_1}) $ | (18) |
式中,Iin为输入影像,G(*)为低通滤波处理,Iout为输出结果。
4 实验结果与分析
为了验证稀疏去噪方法能否应用于遥感卫星影像去噪中以及验证本文改进算法的有效性,利用真实遥感卫星影像数据进行了以下3组实验。
4.1 实验1
第1组实验,以某地区一景天绘卫星5 m高分辨率全色影像的局部区域为例,对清晰的3个类型区域先进行加噪处理(
稀疏去噪的方法在自然图像去噪上取得了较好的成果,本组实验的目的是为了验证其在卫星遥感影像上的适用性。从图 5中区域1的目视效果看,对于高斯滤波,去噪后影像仍存在较多的噪声且轮廓不清晰;小波阈值法去噪效果有所提升,轮廓较清楚,但仍存在一定的噪声,而BM3D去噪后结果影像亮度变暗,与原始影像差别较大;K-SVD算法处理的结果中噪声基本去除,表面很光滑,但去除噪声的同时也模糊了边界。从影像下半部分的农田区域可以看出,K-SVD处理后表面过于平滑,部分田埂边界已经模糊不可见;而经过本文的改进算法去噪后,边界信息得到较好的保留。
5种方法处理的峰值信噪比和平均梯度统计结果如表 1所示。从统计的多区域影像去噪的评价指标来看,各区域中,K-SVD算法的峰值信噪比均高于传统算法,说明K-SVD算法去除高斯噪声的效果明显优于传统算法。采用本文算法也得到了与K-SVD算法基本接近的峰值信噪比,本文认为改进算法在去噪方面与K-SVD算法效果相当。另外比较各区域不同算法的平均梯度可以看出,本文算法具有最高的梯度值,说明在去噪过程中,本文算法保留了更多的边界信息,具有更强的纹理特征,较K-SVD有更好的视觉感受。因此,可以从实验得出结论,K-SVD算法同样适用在遥感影像的去噪处理上,且改进的算法也得到了较好的验证。
表 1 去噪影像质量评价指标统计表
Table 1 The quality parameters of the de-noising image
| 峰值信噪比 | 平均梯度 | |||||
| 区1 | 区2 | 区3 | 区1 | 区2 | 区3 | |
| 原影像 | — | — | — | 2.6 | 6.1 | 9.7 |
| 高斯3×3 | 33.9 | 34.5 | 24.4 | 2.3 | 3.5 | 1.7 |
| 小波法 | 32.2 | 32.4 | 25.4 | 3.0 | 5.9 | 5.0 |
| BM3D | 20.9 | 30.1 | 22.4 | 2.9 | 5.8 | 5.9 |
| K-SVD | 35.1 | 35.8 | 28.8 | 2.1 | 5.8 | 5.4 |
| 本文算法 | 35.3 | 35.9 | 28.6 | 3.4 | 6.4 | 6.3 |
4.2 实验2
为了验证稀疏去噪方法对于实际含噪声的遥感卫星多光谱影像去噪的效果,进行了第2组实验。以某地区一景天绘卫星10 m分辨率多光谱影像为例,天绘卫星多光谱影像存在较多的噪声,不同区域的表现不同,对此采用上述五种算法对影像分别做去噪处理,结果如图 6所示。图 7所示为红色方框区域的局部影像。其中高斯滤波窗口大小为11×11,小波阈值法阈值为[10.28,24.08],BM3D算法σ值为10,K-SVD算法字典大小为64×64,迭代次数为10次,本文算法的低通滤波选择窗口大小为8×8的高斯滤波。由于本组实验中没有标准的影像作为参考影像,本实验采用均值、方差、信息熵及平均梯度作为评价指标。5种方法的评价指标结果如表 2所示。
表 2 去噪影像质量评价指标统计表
Table 2 The quality parameters of the de-noising image
| 去噪方法 | 均值 | 标准方差 | 熵 | 平均梯度 |
| 高斯 | 107.35 | 33.63 | 11.64 | 2.92 |
| 小波 | 106.95 | 35.82 | 11.78 | 4.06 |
| BM3D | 92.17 | 38.90 | 11.68 | 4.41 |
| K-SVD | 108.20 | 35.40 | 11.69 | 3.35 |
| 本文 | 105.48 | 39.30 | 11.95 | 4.56 |
从图 6和图 7的实验结果可看出,高斯滤波都造成了过渡平滑现象,丢失了大量的边缘信息,相对而言小波阈值法和BM3D法保留了较多的细节信息,但去噪效果并不彻底。K-SVD算法去除了大量的噪声,但边界部分不够清晰,视觉效果较为模糊。而本文算法中影像内部信息丰富,从局部放大图可以看出地物纹理丰富、亮度鲜明且轮廓特征非常明显,影像上表现为道路、屋顶面清晰且轮廓突出。
从表 2的评价指标统计结果来看,本文算法处理后的灰度均值与其他算法处理后的基本一致,说明去噪过程基本没有影响原影像的灰度分布,去噪后影像并没有失真。本文算法的标准方差较高说明本文算法影像内部灰度变化更明显,细节信息更突出。同时,本文算法有最高的信息熵值和平均梯度,说明本文算法的结果影像信息量丰富且边界特征最为明显。由此可看出,本文的改进算法在去噪时,由于只对影像的高频信息进行稀疏重建,在保护了低频信息的同时恢复了影像的结构特征,得到了比直接利用K-SVD算法进行处理更好的效果,证明了改进算法的可行性,且其适用于遥感卫星影像的实际去噪过程中。
4.3 实验3
影像去噪的目的是为了能得到更好的数据以便后期处理与应用,因此为了分析小波阈值法、K-SVD算法与本文方法的优劣性,本文进行第3组实验,对图 6(a)的结果影像进行边缘检测,重点比较去噪处理后影像的边缘检测效果。
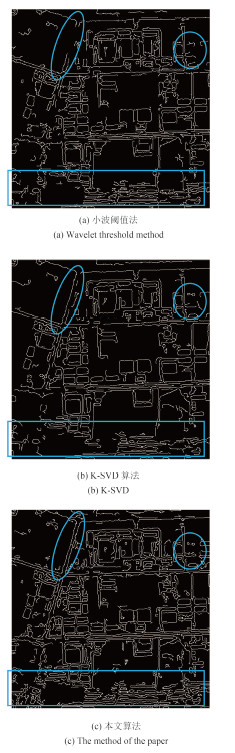
边缘检测采用Canny算子,选取阈值参数[50,150]对3幅去噪后的影像分别进行边缘检测,图 8所示为检测结果。
从图 8中可看出,本文算法去噪后的影像边缘检测结果最好,K-SVD算法次之,小波阈值法的结果在一些地方存在较大的缺失。如图 8中蓝色椭圆区域,本文算法的结果能检测出较为完整的道路边缘,K-SVD算法的结果中道路右侧边缘未能检测出来,而小波阈值法的结果道路中间出现断裂,未能检测到。图 8中的蓝色圆圈区域也显示了本文算法的结果比其他两种方法的结果更为完整,且小波阈值法处理后的影像检测出的边缘存在较多毛刺、线条不连续。在图 8中的蓝色方框区域,K-SVD算法处理的影像底部的地物轮廓丢失较多,而本文算法检测到的边缘较完整、准确。由此说明,本文算法处理后的影像残留噪声较少,道路房屋边界明显,有利于后期的检测、分类等应用,因此可以看出本文算法在去噪方面要优于小波阈值法和K-SVD算法。
4.4 实验总结
从对加噪影像的处理,对实际含噪声影像的处理以及对去噪结果的边缘检测来看,实验结果都证明了稀疏表示去噪方法可以用于遥感卫星影像的去噪过程中,且证明了改进算法的可行性与有效性,解决了传统方法去噪时去噪结果与细节信息难以平衡的问题。
5 结 论
稀疏表示理论在图像表示方面具有较大的优势,在图像压缩、去噪以及超分辨率重建等多个方面得到了广泛的应用。本文将稀疏表示去噪方法引入到遥感卫星影像去噪中,拓展了稀疏表示去噪方法在图像处理上的应用范围。对于复杂多变的卫星影像去噪,稀疏表示的去噪方法表现了其相对于传统算法的适用性及优越性。本文提出的改进的稀疏去噪方法,将影像的低频信息和高频信息分开处理,对高频部分进行基于K-SVD的稀疏去噪,在去除噪声的同时保留了较强的边缘信息,取得了较好的去噪效果,对于影像的后期处理和应用具有重要的实际意义。
本文研究了稀疏表示去噪方法在遥感卫星影像上的应用,进一步可以研究稀疏表示理论在遥感卫星影像融合、超分辨率重建等方面的应用。另外,基于稀疏表示的去噪方法其算法复杂度高且计算量较大,后续需要考虑如何解决对遥感卫星影像处理时运算时间长和占用内存大的问题。
参考文献(References)
-
Aharon M, Elad M, Bruckstein A.2006.K-SVD:An algorithm for designing overcomplete dictionaries for sparse representation. IEEE Transactions on Image Processing, 54 (11) : 4311–4322 . [DOI:10.1109/TSP.2006.881199]
-
Dabov K, Foi A, Katkovnik V, Egiazarian K.2007.Image denoising by sparse 3-D transform-domain collaborative filtering. IEEE Transactions on Image Processing, 16 (8) : 2080–2095 . [DOI:10.1109/TIP.2007.901238]
-
Davis G, Mallat S, Avellaneda M.1997.Adaptive greedy approximations. Constructive Approximation, 13 (1) : 57–98 . [DOI:10.1007/BF02678430]
-
Jiang P F. Image Denoising Based Sparse Representation and Dictionary Learned. Xi'an: Xi'an Electronic and Science University 2011 . ( 姜鹏飞. 2011. 基于稀疏表示与字典学习的图像去噪算法研究. 西安: 西安电子科技大学 . )
-
Mairal J, Bach F, Ponce J, Sapiro G and Zisserman A. 2009. Non-local sparse models for image restoration//Proceedings of the 2009 IEEE 12th International Conference on Computer Vision. Kyoto:IEEE:2272-2279 [DOI:10.1109/ICCV.2009.5459452]
-
Sulam J, Ophir B and Elad M. 2014. Image denoising through multi-scale learnt dictionaries//Proceedings of the 2014 IEEE International Conference on Image Processing. Paris:IEEE:808-812 [DOI:10.1109/ICIP.2014.7025162]
-
Sulam J and Elad M. 2015. Expected patch log likelihood with a sparse prior//Energy Minimization Methods in Computer Vision and Pattern Recognition. Switzerland:Springer International Publishing:99-111 [DOI:10.1007/978-3-319-14612-6_8]
-
Wang Y. Research on Image Denoising Algorithm based on Sparse Representation. Hefei: Anhui University 2014 . ( 王瑶. 2014. 基于稀疏表示的图像去噪算法研究. 合肥: 安徽大学 . )
-
Wei Y L. Research on Image Denoising based on Sparse Representation. Tianjin: Tianjin University of Technology 2013 . ( 魏雅丽. 2013. 基于稀疏表示的图像去噪方法研究. 天津: 天津理工大学 . )
-
Pati Y C, Rezaiifar R., Krishnaprasad P S.1993.Orthogonal Matching Pursuit:Recursive Function Approximation with Applications to wavelet decomposition. The 27th Annual Asilomar Conference on Signal System and Computer, 1 : 40–44 .