2009)。定量热红外遥感研究的主要目的是精确获取地表(包括植被、土壤、岩石和水体)的表面温度和地物发射率(张仁华,1991),然而温度与发射率的分离方法没有考虑大气影响(Zhou等,2012)。如果大气校正不准确,将严重干扰地表温度和地物发射率的反演结果(田国良,2014),大气校正已成为地表参数定量分析的基本前提(袁金国等,2009)。

在针对热红外高光谱数据的大气校正计算中,主要有两类获取大气参数的方法：一是利用经验或实测的大气廓线,借助成熟的大气辐射传输模型来获取。如LOWTRAN(http//www.researchgate.net/publication/235203858_Uer_guide_to_LDWTRAN_7)、MODTRAN(Ber等,1999)等大气辐射传输模型及相关的大气廓线数据库、分子光谱数据库等。由于实测大气模式参数往往难以获得,经验参数无法有效反映时相差异和局地差异,使得依赖经验大气廓线参数驱动的模拟计算精度面临较大的不确定性。二是从高光谱数据空间和光谱信息出发,由星载/机载传感器数据反演出大气透过率和路径辐射等大气参数。Gu等(2000)提出了Autonomous Atmospheric Compensation(AAC)算法,运用经验关系式反演得到大气透过率和路径辐射；Young等(2002)提出In-scene Atmospheric Compensation(ISAC)算法,内置了黑体像元标定的方法；Borel(2008)利用查找表,确定出ISAC算法反演结果中的最佳波谱；Distasio和Resmini(2010)比较了ISAC算法和EELM方法,认为两种反演得到的地面辐射波谱形状相似,仅在细节处有些许差异,反演得到的大气透过率和路径辐射有时存在较大差异。

AAC算法和ISAC算法较好地发挥了机载热红外高光谱数据高空间分辨率和波谱分辨率的特点,使大气辐射传输模型有效反映了时相差异和局地差异。但AAC算法和ISAC算法均是建立在模拟数据的基础之上,易受影像噪声的影响,易受波谱分辨率的限制。其中,AAC算法抗噪性较弱,当影像噪声较大时,线性拟合参数不趋向于定值,使得大气反演计算结果存在多样性问题。ISAC算法内置了黑体像元标定方法,反演计算的理论基础可以解决AAC算法出现的多样性问题。

本文针对TASI实测数据,使用AAC算法时,反演结果呈现出多样性问题,为克服该问题,结合ISAC算法,提出了大气校正复合改进算法。

假设大气处于局地热平衡状态,热红外大气辐射传输方程可表示为：

$L\left({x,{\lambda _\theta }} \right)= {L_s}\left({x,{\lambda _\theta }} \right)\tau \left({x,{\lambda _\theta }} \right)+ {L_P}\left({x,{\lambda _\theta }} \right)$

(1)

${L_s}\left({x,{\lambda _\theta }} \right)= \varepsilon \left({x,{\lambda _\theta }} \right)B\left({T\left(x \right),{\lambda _\theta }} \right)+ [1 - \varepsilon \left({x,{\lambda _\theta }} \right)]{L_{SKY}}\left({x,{\lambda _\theta }} \right)$

(2)

式中,L(x,λ_θ)为传感器观测辐射亮度,L^S(x,λ_θ)为地面辐射亮度,x为空间位置,λ_θ为第θ个通道的波长,(x,λ_θ)为大气透过率,L^P(x,λ_θ)大气路径辐射,L^SKY(x,λ_θ)为大气下行辐射、L^SKY(x,λ_θ)为地物发射率,B(T(x),λ)为地物黑体辐射亮度。利用[L(x,λ_θ)-L^P(x,λ_θ)]/(x,λ_θ),得到,即为大气校正。

假设大气参数横向稳定性明显优于地物,同时地物辐射率波谱显著平滑于大气辐射/吸收波谱,在此基础上选择两个毗邻通道,以λ_S和λ_W表示。通过式(1)可以推导出任意两个波段满足方程(3)所示关系。

$\eqalign{ & L\left({x,{\lambda _S}} \right)= {{{L_s}\left({x,{\lambda _S}} \right)\tau \left({x,{\lambda _S}} \right)} \over {{L_s}\left({x,{\lambda _W}} \right)\tau \left({x,{\lambda _W}} \right)}}L\left({x,{\lambda _W}} \right)+ {L_P}\left({x,{\lambda _s}} \right)\cr & - {{{L_s}\left({x,{\lambda _S}} \right)\tau \left({x,{\lambda _S}} \right)} \over {{L_s}\left({x,{\lambda _W}} \right)\tau \left({x,{\lambda _W}} \right)}}{L_P}\left({x,{\lambda _W}} \right)\cr} $

(3)

当两者波谱分辨率足够高时,传感器观测辐射亮度L_S(x,_S)和L_S(x,_W)则近似相等,即${L_s}\left({x,{\lambda _S}} \right)\approx {L_s}\left({x,{\lambda _W}} \right)$ 。相应地,方程(3)可以简化为方程(4)。

$L\left({x,{\lambda _S}} \right)= {{\tau \left({x,{\lambda _S}} \right)} \over {\tau \left({x,{\lambda _W}} \right)}}L\left({x,{\lambda _W}} \right)+ {L_P}\left({x,{\lambda _s}} \right)- {{\tau \left({x,{\lambda _S}} \right)} \over {\tau \left({x,{\lambda _W}} \right)}}{L_P}\left({x,{\lambda _W}} \right)$

(4)

由方程(4)可以看出,相邻两通道传感器观测辐射亮度差异主要由大气参数在两个相邻通道的差异引起,则定义

$Tr = {{\tau \left({x,{\lambda _S}} \right)} \over {\tau \left({x,{\lambda _W}} \right)}}$

(5)

$Pd = {L_P}\left({x,{\lambda _s}} \right)- Tr \cdot {L_P}\left({x,{\lambda _W}} \right)$

(6)

$L\left({x,{\lambda _S}} \right)= Tr \cdot L\left({x,{\lambda _W}} \right)+ Pd$

(7)

方程(5)和(6)中Tr为两通道透过率之比,Pd为路径辐射加权差。两通道的辐射亮度为线性关系,斜率为Tr,截距为,Pd。通过对局部影像数据块中L_S(x,_S)、L_S(x,_W)波段辐射亮度值进行线性拟合,得到方程(7),从而获得参数、的值。

利用经验关系式(8),求出所有通道的大气透过率和路径辐射。

$y\left(\lambda \right)= \sum\limits_{i = 1}^3 {\sum\limits_{j = 1}^3 {{c_{ij}}} } \left(\lambda \right)T{r^{i - 1}}P{d^{i - 1}}$

(8)

式(8)中,y()为大气透过率和路径辐射,c_ij()为随波长变化的系数。这个经验关系式构成了AAC算法的核心,从根本上决定了AAC算法的精度水平。

ISAC算法的核心工作为计算地表等效温度,并可标定黑体像元。ISAC算法假设大气参数横向稳定性明显优于地物,即大气在一定区域范围内均一不变,而对应的地表温度及地物类型变化较大。在热红外波段,很多地物,诸如水体、植被及粗糙的地表,具有高且平滑的比辐射率谱。对于这些热红外行为近似黑体的地物,传感器接收辐射亮度对应的方程(1)和(2)可简化为:

$L(x,{y_\theta })\cong B\left({T\left(x \right),{\lambda _\theta }} \right)\tau \left({x,{\lambda _\theta }} \right)+ {L_P}\left({x,{\lambda _\theta }} \right)$

(9)

在局地范围内$L\left({x,{\lambda _\theta }} \right)$、${L_P}\left({x,{\lambda _\theta }} \right)$可以认为是常数 ,对传感器接收的辐射亮度与近黑体地表发射辐射亮度进行线性拟合,便可获得λ波段的参数、值。

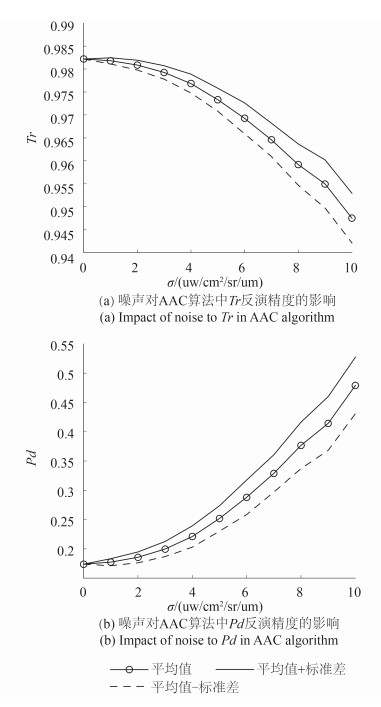
本文使用美国Johns Hopkins University地物波谱库(JHU光谱库)中56种地物的发射率信息及MODTRAN 4.0模拟的大气波谱合成模拟数据,定量评价不同噪声水平对AAC算法中参数、反演精度的影响效果。

在合成数据中添加均值为0,标准差为0- 10的高斯白化噪声,对AAC算法参数、进行实验,噪声对AAC算法中Tr和Pd反演精变的影响。如图 1,一方面,随着噪声水平变大,参数、反演稳定性变差；另一方面,参数均值亦随噪声水平而发生变化。这两方面造成反演精度迅速退化。TASI的实验数据集在28、29波段具有较高的噪声水平(≈8),而AAC算法经验关系式具有较大的系数(如图 7,数量级达到10³-10⁴),说明大气反演结果对波谱失真高度敏感。

2.3节的分析表明：AAC算法的抗噪性较弱,当TASI实测数据噪声水平较高时,反演结果呈现出多样性问题。针对此问题,提出大气校正复合改进算法：利用ISAC算法标定黑体像元的方法得到Tr、Pd,替代AAC算法线性拟合得到的Tr、Pd,进而由经验关系式得到最终的大气反演结果。复合改进算法拟改善噪声扰动的TASI实测数据的大气校正计算结果,提高计算结果的稳定性。

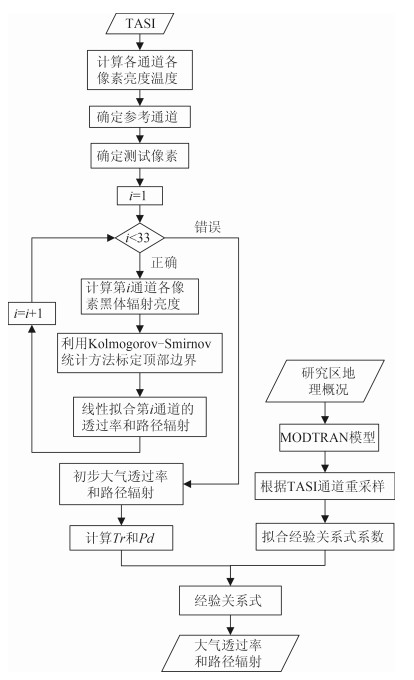
复合改进算法的具体步骤如下：

(1) 计算TASI数据各通道各像素的亮度温度,分析每个像素最大亮度温度所在通道,将比例最高者作为参考通道₀,将通道的像素标记为测试像素₀,计算测试像素对应地表近似温度T_s。

(2) 依据,调用普朗克函数,计算测试像素对应通道的黑体辐射亮度值${B\left({{T_s},{\lambda _\theta }} \right)}$ ,构建各通道$\left({L\left(\lambda \right),B\left({{T_s},{\lambda _\theta }} \right)} \right)$ 散点群,利用Kolmogorov-Smirnov(KS)统计方法,标定去除噪声效应后的散点顶部边界,对标定后的顶部边界做加权线性拟合,斜率为该通道对应的大气透过率,截距为该通道对应的路径辐射,进而得到相另邻通道之间的关系参数和。

(3) 根据研究区地理位置及气象状况,利用MODTRAN 4.0,模拟得到多组大气波谱,并重采样至TASI波段。

(4) 利用多元线性回归,拟合得到经验关系式2.8中各波段大气透过率及路径辐射与、的系数,拟合判定系数和均方误差等。

(5) 调用经验关系式(8)来构建完整的大气透过率和路径辐射波谱。

以甘肃柳园为研究区,选取热红外航空成像光谱仪TASI(Thermal Airborne Hyperspectral Imager)为实验数据集,成像时间为2010-09-08T15:00—2010-09-08T18:00,飞行航高为1.875 km,获取14个条带。研究区范围,为95°10′E- 95°46′E,41°8′N - 41°16′N之间如图 3,研究区面积746 km²。

TASI传感器是加拿大研制的机载热红外高光谱设备,在8-11.5μm波段范围内设置了32个通道,波谱分辨率为0.1095μm,空间分辨率为2.25 m,飞行时仪器采用垂直对地观测,各航带间的旁向重叠为25%(Hu等,2015)。

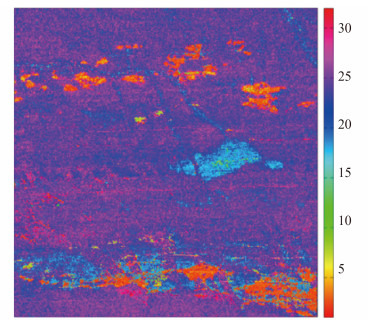
将TASI数据划分成不同的数据块,利用普朗克逆函数计算给定TASI数据块各通道亮度温度,得到最大亮度温度通道分布影像图(如图 4),通道25(中央波长10.6828μm)反演的亮度温度占据了所有通道反演的最大亮温中的最多数,说明该通道对应大气透过率较高,且大部分地物在该通道处具有较高的比辐射率,因此选取其为求取地表温度的最优通道₀。

将以通道₀为最大亮温通道的像素标记为测试像素,并设通道₀对应的地物比辐射率为常数ε₀(如0.95),利用方程(10)计算测试像素对应地表近似温度T_s。

${T_{\rm{s}}} = {B^{ - 1}}\left( {{\lambda _0},L({\lambda _0}){\varepsilon _0}} \right) $

(10)

以T_s调用普朗克函数计算测试像素各通道黑体辐射亮度值${B\left({{T_s},{\lambda _\theta }} \right)}$,针对各通道构建$\left({L\left(\lambda \right),B\left({{T_s},{\lambda _\theta }} \right)} \right)$散点群,进行线性拟合并且移除该线性趋势。

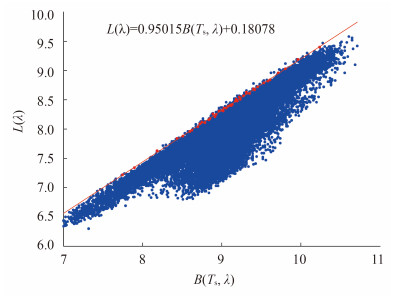
根据取值${B\left({{T_s},{\lambda _\theta }} \right)}$,将移除线性趋势的散点划分为N个数据箱(如N=45),每个数据箱包含相同数目的散点。假设传感器噪声服从高斯分布,地物比辐射率于_max一端服从Dense分布,则由噪声引起的散点顶部边界分布符合$erf\left({u/\sqrt 2 \cdot NESR} \right)$ (Yong等,2002),该函数中U为权重,NESR为噪声等效辐射亮度。根据该理论分布,利用Kolmogorov-Smirnov(KS)统计方法标定去除噪声效应后的散点顶部边界。恢复线性趋势,对标定的各数据区间顶部边界进行加权线性拟合(以KS检验相伴概率为权重),如图 5,斜率即为该通道对应大气透过率(_θ),截距为路径辐射L_P(_θ)。

根据AAC算法波段选取原则、地物发射率特征以及TASI通道参数特征,选取波段28(中央波长11.0113 μm)、29(中央波长11.1208 μm)作为和通道,由方程(5)和(6)可以获得大气参数和,本文分别采用0.9808和0.1838W·m^-2sr^-1·μm^-1。

根据TASI数据获取的地理位置及气象状况,MODTRAN 4.0主要选用的参数包括：中纬度夏季大气模式、热红外辐射模型、乡村气溶胶、能见度23km、春夏季季节模式、航高1.875km以及波段范围8-11.5um,从而得到研究区的大气透过率和路径辐射等参数。根据大气有效温度的不同将获得的110条大气波谱分为6组,每组对应的相对湿度从标准大气模式0.1变化至2倍不等,较好地覆盖了大气湿度可能的取值范围。每组大气波谱有效温度范围及数量见表 1。

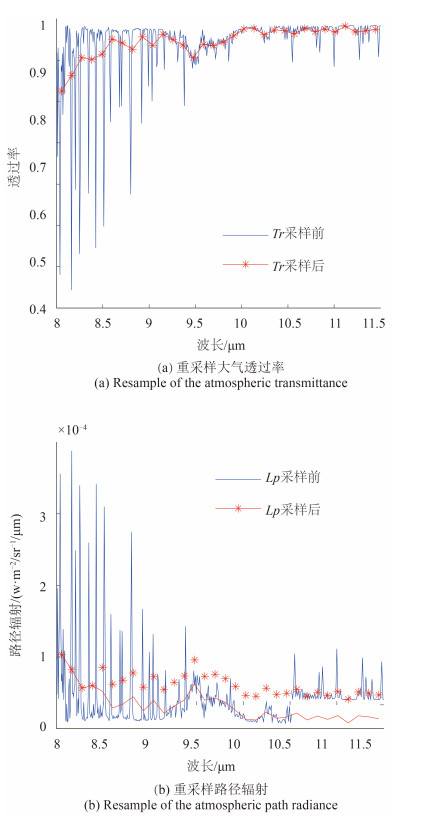
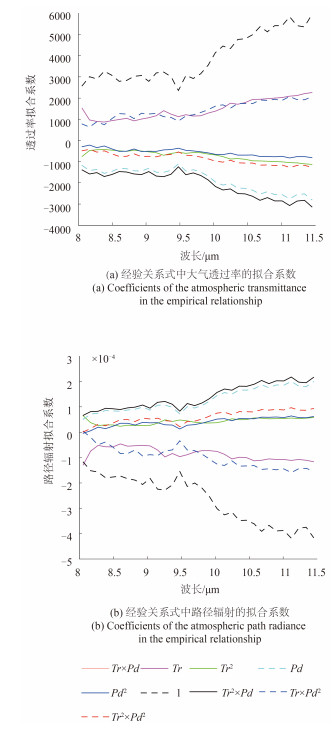
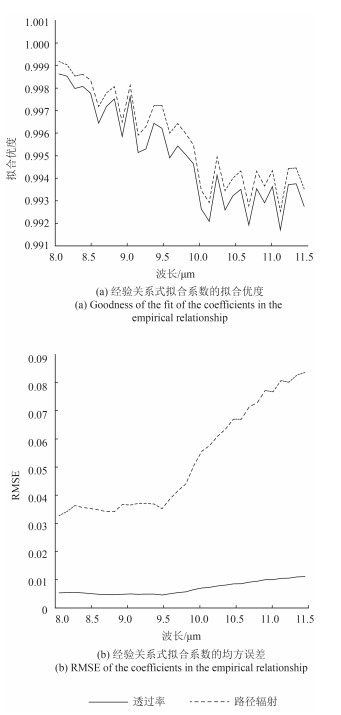
将MODTRAN模拟得到的大气透过率和路径辐射分别重采样至TASI波段图 6。将重采样后的110条大气波谱利用多元线性回归拟合得到经验关系式中各波段大气透过率及路径辐射与、的系数,结果如图 7所示；拟合的判定优度如图 8(a),均方误差如图 8(b)。

通过分析拟合系数的拟合优度和均方误差可以看出,大气透过率波谱与路径辐射波谱以较高的精度服从式(8)所示的经验关系。但经验关系式的拟合系数数值较大,其中大气透过率的数量级达到10³,路径辐射的数量级达到10⁴,说明AAC算法反演结果对参数和较为敏感,反演效果在很大程度上依赖于参数Tr和Pd的反演精度,因而采用ISAC算法约束AAC算法中参数Tr和Pd的浮动性很有必要。

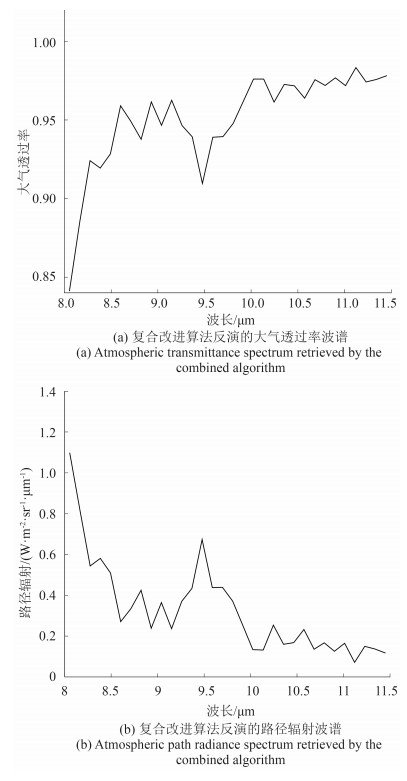
在得到参数、线性拟合结果以及经验关系式系数的基础上,调用经验关系式来构建完整的大气透过率和路径辐射波谱。图 9即为复合改进算法反演的大气透过率和路径辐射波谱。

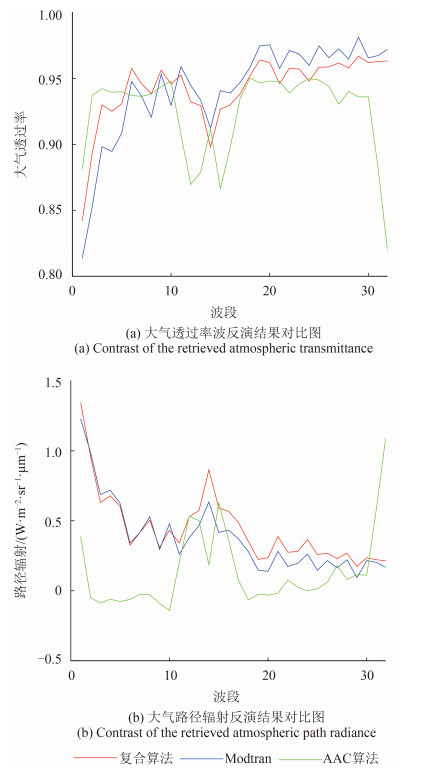
将复合改进算法的反演结果、AAC算法的反演结果和MODTRAN模型的模拟结果进行比较图 10,可以看出：

一方面,复合改进算法的反演结果较AAC算法更具有稳定性。AAC算法由于TASI数据噪声水平较高,而且地物发射率波谱相对于大气波谱并不足够平滑,使得以不同地物分布区为数据源提取的参数是离散的,即、并不趋向于定值,反演结果具有多样性。当波长大于11.3μm时,出现严重偏离现象。

复合改进算法利用ISAC算法中内置黑体像元标定的方法,约束了AAC算法中参数和的浮动性,增强了稳定性。图 10可以看出,其反演的大气波谱与MODTRAN模拟的结果谱形相似,在第8波段、第9波段、第14波段和第22波段等出现相同的吸收峰。

另一方面,复合改进算法的反演结果较MODTRAN模型的模拟结果更具可靠性。由于复合改进算法中不仅包含大气辐射传输模型的参数信息,还包含遥感影像的信息,反演结果理应反映这两部分信息。

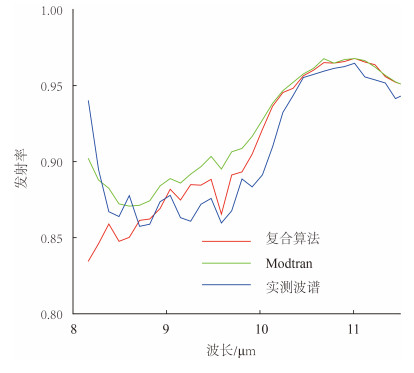
在研究区选取部分花岗岩区域(图 11),分别应用复合改进算法的反演结果及MODTRAN模型的模拟结果进行大气校正,采用ASTER-TES算法(Gillespie等,1998)进行温度与发射率分离,并将生成的发射率波谱与野外实测波谱进行对比,结果显示三者谱形相似(如图 12),但应用复合改进算法进行大气校正之后生成的发射率波谱更接近野外实测波谱,反演结果更加准确,从而进一步证明复合改进算法的有效性(野外实测光谱数据使用美国D&P Instruments公司生产的102F便携式傅里叶变换热红外光谱仪获得,数据采集时间为2014-10-18—2014-10-19)。

由AAC算法原理可知,参数、是TASI辐射定标数据中与两个邻近通道的线性拟合方程的斜率和截距。因TASI数据噪声水平较高,和的实际反演结果存在多样性特征。ISAC算法内置了黑体像元标定方法,本文结合AAC和ISAC两种算法的优点,提出了大气校正的复合改进算法。实验证明,算法能够有效约束影像噪声引起的AAC算法和的多样性问题,使反演结果相对稳定。

(1) 在大气波谱反演方面,相较于MODTRAN模型,复合改进算法结合了大气辐射传输模型和影像两部分信息,提高了反演结果的准确性,有效反映了时相差异和局地差异。同时,相较于AAC算法,复合改进算法提高了抗噪能力,约束了参数和的浮动性,提升了反演结果的稳定性,有效制约了反演结果的多样性。

(2) 在温度与发射率分离方面,分别应用复合改进算法和MODTRAN模型进行大气校正后,再进行温度与发射率分离试验,结果显示复合改进算法得到的发射率波谱更接近实测波谱,取得了预期效果,证明了复合改进算法的有效性。

复合改进算法利用ISAC算法中黑体像元的标定方法,有效改善了AAC算法应用于TASI数据时出现的反演结果多样性的问题,表现出较高的抗噪性,具有较强的实用性,有望进一步推广到其它数据类型。