|
收稿日期: 2015-07-07; 修改日期: 2015-11-05;
优先数字出版日期: 2016-05-25
基金项目: 国家自然科学基金(编号:41371348)
第一作者简介:
孙锐(1988-),男,硕士研究生,研究方向为遥感时空数据融合研究。E-mail:sunrui11@126.com
中图分类号: TP79
文献标识码: A
文章编号: 1007-4619(2016)03-0361-13
|
摘要
遥感数据反演高时空分辨率NDVI对监测植被动态变化过程具有重要意义,然而受天气影响,单颗卫星难以提供时间连续的高空间分辨率NDVI数据。以华北平原中东部为实验区,联合HJ-1 CCD数据和MODIS数据,对STARFM算法进行了改进,(1)考虑了不同地物对光谱响应的差异,为减少分类错误利用统计学上($\overline x \pm 2\sigma $)对分类数据进行筛选,按照不同地物类型分别利用线性拟合方法修改光谱距离权重;(2)定义了预测半径,对HJ-1 CCD数据因外界影响而缺失的影像进行了预测。结果表明,与真实影像相比,预测结果呈现了较好的空间一致性,相关系数均达到了极显著相关,改进算法的预测精度要高于原算法。利用该方法将HJ-1 CCDNDVI的空间变化信息与MODIS NDVI时间变化信息有机结合重构了高时空分辨率NDVI序列,有效补充了HJ-1CCD NDVI的缺失数据集。
关键词
NDVI序列 , 时空融合 , HJ-1 CCD , MODIS , STARFM
Abstract
Retrieval of Normalized Difference Vegetation Index (NDVI)with high spatial and temporal resolutions from remote-sensing data is important for monitoring the dynamic changes in vegetation. However, owing to the impact of weather, a single satellite cannot provide a time series with high-spatial-resolution NDVI data. An effective solution to this problem is to fuse the NDVI with various resolutions retrieved from different sensor data to produce a dataset that has both high spatial and high temporal resolutions. In this study, the middle east part of North China Plain is selected as the experiment area, and HJ-1 CCD and MODIS NDVI data are used. The spatial and temporal adaptive reflectance fusion model is improved in two ways:(1)The difference of the spectral responses between different objects is considered using the confidence interval ($\overline x \pm 2\sigma $) to filter the data and consequently reduce classification errors, and the linear regression method is used to modify the spectral distance weight according to different objects. (2) The predicted radius is defined to predict the missing HJ-1 satellite data whose unavailability is caused by external influences. Results indicate that the distribution of high and low NDVI values of the six studied dates is highly consistent between the observed and predicted images. According to the results of the correlation analysis, the scatter points concentrate along the line of y=x. The correlation coefficients of the six pairs of observed and predicted NDVI images are 0.957, 0.962, 0.935, 0.964, 0.913, and 0.933, which are all significant at 0.01 levels, and all RMSEs are less than 0.07, which indicates good fusion results. According to the difference images and their histograms, the averages of the six difference images are -0.02, 0.001, -0.012, -0.025, 0.023, and -0.02, with standard deviations of 0.049, 0.044, 0.049, 0.036, 0.056 and 0.043, respectively. The pixel values concentrate around 0, and 90% of the pixels have absolute values smaller than 0.1. The percentages of pixels that have absolute values smaller than 0.2 are 99.80%, 99.97%, 99.95%, 99.98%, 99.79%, and 100% for the six images. The accuracy of results tends to decrease as the time intervals increase between the base and prediction dates. The comparison of the results of IR shows that the prediction accuracy of the improved algorithm is higher than that of the original algorithm. The results also show that the base and predicted images have similar seasonal characteristic. If the time interval is extremely long, however, similar seasonal characteristics are not obvious or exhibit significant differences, which reduce the accuracy and precision of the prediction results. Therefore, an appropriate reference image should be selected. In summary, the improved method is employed to reconstruct NDVIs with high temporal and high spatial resolutions by combining the spatial details of HJ-1 CCD data and the temporal variation of MODIS data to effectively supplement the missing HJ-1 CCD NDVI dataset.
Key words
NDVI series , spatial and temporal fusion , HJ-1 CCD , MODIS , STARFM
1 引 言
植被指数是根据植物叶面在可见光波段的强吸收特性和在近红外波段的强反射特性来组合遥感卫星不同波段得到能反映植物生长状况的指数。植被指数已经成功用于全球和区域土地覆盖、植被分类与监测、环境监测、作物和牧草估产、荒漠化研究等各个领域。通过不同波段的组合,目前已经得到40多种植被指数,而归一化植被指数NDVI是最常用的一个。
遥感数据是获取高时空分辨率NDVI序列的重要途径,可以在多个时空尺度和范围上进行大规模植被生物物理特性和物候特征的监测(Coops等,2012;Washington-Allen等,2006),然而受技术的限制,遥感数据在空间分辨率,时间分辨率和重访周期方面优势各异,高空间分辨率遥感数据覆盖范围通常较小且重访周期往往较长(Coops等,2006),不足以对植被的生长过程进行长期动态和实时监测;而高时间分辨率的卫星能以较短的重访周期对植被进行大范围的观测,但空间分辨率往往较低(Holben,1986;Justice等,1985)。例如MODIS数据覆盖范围大,时间分辨率高,但MODIS数据最高250 m的空间分辨率在反映空间异质区域和空间尺度较小的植被状况变化情况时能力有限(Huete等,2002;Kennedy等,2009)。另外,单一传感器易受云污染,例如HJ-1卫星,CCD多光谱相机空间分辨率为30 m,HJ-1A星和HJ-1B星联网可以实现重访周期2天,但受天气影响,数据出现不同程度的缺失。
将不同空间分辨率、时间分辨率和光谱分辨率的传感器数据进行时空融合,生成同时具有高空间分辨率和高时间分辨率特征的遥感数据,是解决上述问题的重要途径。目前时空融合方法主要有小波变换(Malenovsk等,2007)和线性光谱混合模型。小波方面,Malenovsk等人(2007)用小波变换融合了MODIS和Landsat TM影像,融合结果继承了MODIS的大部分特征与Landsat TM的空间细节信息,通过影像融合技术提升了MODIS时间序列影像的空间分辨率。Wu和Wang(2011)通过小波变换进行Landsat TM与MODIS融合,获得了同时具有中空间分辨率影像空间特征和低空间分辨率影像光谱特征的结果。实验结果表明融合影像对于分割、分类以及变化监测具有较强的实用性,但结果像元值并不具有物理意义,不能用于定量的研究。线性光谱混合模型方面,Busetto等人(2008)基于混合像元分解技术,融合TM数据和多时相的MODIS-NDVI,得到了具有TM空间尺度的NDVI时间序列。Roy等人(2008)提出利用ETM+数据和MODIS BRDF产品借助半物理模型方法预测ETM数据的算法,可以有效的捕捉季相变化信息。李大成等人(2014)提出了一种拓展的半物理时空融合算法,在Roy等人(2008)的基础上改进了乘性调制融合机制,最终生成区域尺度的高时空分辨率地表反射率数据集。Gao等人(2006)提出了时空适应性反射率融合模型STARFM(The Spatial and Temporal Adaptive Reflectance Fusion Model),该模型利用同日期的Landsat和MODIS反射率影像,结合预测日期的MODIS反射率影像对预测日期的Landsat 30 m空间分辨率的反射率影像进行预测。该模型有效的利用了高时间分辨率MODIS的时间变化信息和高空间分辨率Landsat的空间变化信息,进而估算高时空分辨率的地表反射率(Gao等,2006)。STARFM算法在数据源选择上未限制使用Landsat和MODIS数据,但目前研究较少选择其他影像作为数据源(Olexa和Lawrence,2014),且算法的参数化均是考虑了国外卫星数据特点,很少用于国产卫星数据(Meng等,2013)。蒙继华等人(2011)在STARFM算法基础上,提出了不同时空分辨率NDVI数据的时空融合算法(STAVFM),将时间变化信息与空间差异信息有机结合,生成了每16天的高分辨率NDVI数据集。Cai等人(2012)利用MODIS BRDF/Albedo产品和HJ-1数据采用同化的方法生成每8天的HJ-1数据空间分辨率的NDVI数据,弥补了HJ-1 NDVI数据缺失。邬明权等(2010)利用遥感时空数据融合技术成功的对水稻种植面积进行提取。王来刚等人(2012)利用HJ-1 CCD数据和SPOT 5数据时空数据融合结果,对冬小麦叶面积指数进行了估算。蔡德文等人(2012)利用遥感时空融合技术,对STARFM算法在农作物监测中的应用进行了适用性验证,结果表明得到的融合影像与真实影像间的相关性较高,且预测精度与土地利用类型是否发生变化有关。Meng等人(2013)利用STAVFM算法,结合HJ-1 CCD影像、MODIS影像生成高时空分辨率NDVI并对作物生物量进行估产,取得很好预测效果。
本文选取国产卫星HJ-1 CCD影像和MOD09GQ作为数据源,对STARFM算法进行修改,包括两个方面:将不同地物类型进行分类拟合,优化光谱距离权重,降低因传感器参数差异带来的误差;定义了预测半径,分时段对影像进行预测。利用改进后的算法预测因受天气影响而缺失的NDVI数据。通过与真实影像对比,利用像元的回归分析和差分影像分析,评价了预测结果的可靠性与真实性,结果表明,改进算法比原始STARFM算法可进一步提高预测精度。
2 数据与方法
2.1 研究区域与数据源
(1) 研究区域概况
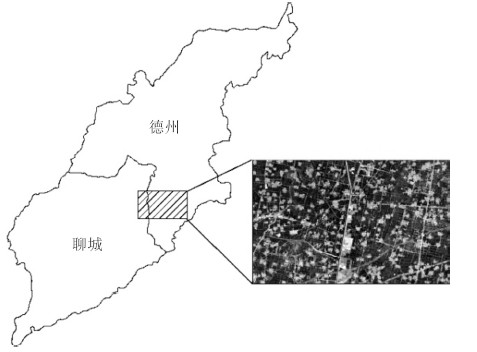
研究区位于山东省西北部,聊城市与德州市的交界处。实验区的中心坐标为116°30′45.94″E,36°42′21.90″N,实验区大小约为35×20 km,如图 1所示。
实验区属于华北平原中东部,平均海拔28m,年平均气温13.3℃,年平均降水量约为520mm,年均无霜期202天。实验区内主要的土地覆盖类型为农田、居民地、道路,还有少量的水体和林地。
(2) HJ-1 CCD数据
共获取2009年4月至2009年6月覆盖研究区的无云或云量很少的9景HJ-1 CCD影像(2009-04-09、2009-04-16、2009-04-21、2009-04-26、2009-05-04、2009-05-08、2009-05-23、2009-05-31、2009-06-02)。HJ-1 CCD影像是由中国资源卫星应用中心提供的经过系统几何校正的第2级产品数据(Cai等,2012)。产品数据依次经过辐射定标、几何校正和大气校正后得到反射率数据,从而计算NDVI。辐射定标采用中国资源卫星应用中心提供的2009年HJ-1A/B星绝对辐射定标系数,几何精纠正利用ENVI软件以15 m Landsat 8全色波段为参照,通过选取地物同名点采用二次多项式校正算法,确保影像校正误差小于0.5个像元,大气校正采用ENVI自带的FLAASH模块进行。
(3) MODIS数据
与HJ-1 CCD影像对应日期的MODIS 250 m日反射率产品(MOD09GQ),利用USGS提供的MODIS Reprojection Tool(MRT)version 4.0工具将所有MODIS影像进行UTM-WGS84投影转换,确保与HJ-1 CCD影像具有相同的坐标系统,采用三次卷积的方法重采样到30 m空间分辨率,对MODIS影像进行几何精校正,保证MODIS影像与HJ-1 CCD影像在空间上配准。最后利用MODIS影像红波段和近红外波段计算NDVI数据。
2.2 研究方法
2.2.1 STARFM算法
STARFM算法在忽略空间位置配准误差、大气校正误差的情况下,t时刻的低空间分辨率遥感数据的像元反射率可以用同期高空间分辨率遥感数据像元反射率的加权和来计算:
| $\begin{equation} {C_t}=\sum {\left({{F_t}^i \times {A_t}^i} \right)}\end{equation}$ | (1) |
式中,Fti为t时刻高空间分辨率遥感数据像元在位置i的像元反射率;Ati为各像元的覆盖面积权重;Ct为对应时刻的低空间分辨率据像元反射率。
STARFM算法首先获取同一时刻tk的高低空间分辨率影像(L和M),得到该时刻tk的高低空间分辨率像元反射率之间的偏差值,反射率偏差值是由系统误差和地物变化引起,同时结合预测时刻t0的低空间分辨率影像M进行预测对应时刻t0高空间分辨率影像L。在反射率偏差值不随时间变化的假设下,t0时刻高空间分辨率像元反射率L(xi,yi,t0)计算公式如下:
| $\begin{array}{l}L\left({{x_i},{y_i},{t_0}} \right)=M\left({{x_i},{y_i},{t_0}} \right)+L\left({{x_i},{y_i},{t_k}} \right)- \\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;M\left({{x_i},{y_i},{t_k}} \right)\end{array}$ | (2) |
为了考虑像元的临边效应,计算反射率时选择移动窗口内与中心像元光谱相似且无云的像元参与计算。中心像元反射率计算公式如下:
| $\begin{array}{l}L\left({{x_{w/2}},{y_{w/2}},{t_0}} \right)=\sum\limits_{i=1}^w {} \sum\limits_{j=1}^w {} \sum\limits_{k=1}^w {{W_{ijk}}} \times \left({M\left({{x_i},{y_j},{t_0}} \right)} \right.+\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;L\left({{x_i},{y_j},{t_k}} \right)- \left.{M\left({{x_i},{y_j},{t_k}} \right)} \right)\end{array}$ | (3) |
式中,w为移动窗口的大小,(xw/2,yw/2)为移动窗口中心像元的位置,Wijk为窗口内相似像元对中心像元的权重系数,由窗口内相似像元的光谱距离权重、时间距离权重和空间距离权重经过归一化处理得到,3种权重的计算请参考Gao等人(2006)的文献。
2.2.2 算法改进
算法中高低空间分辨率像元反射率差值不随时间而变化的假定,忽略了不同传感器之间的系统差异,这种差异可能是因光谱范围的大小、不同波段光谱响应函数的差异造成的。为了尽量避免这种差异对预测值的影响,假定研究时间段内地物类型不会受到人为因素的干扰,针对不同地物类型采用分类拟合的方法进行光谱距离权重的计算。采用Shen等人(2013)提出的计算光谱差异的公式:
| ${S_{ijkc}}=|{a_c} \times {L_c}\left({{x_i},{y_j},{t_k}} \right)+{b_c} - {M_C}\left({{x_i},{y_j},{t_k}} \right){\rm{|}}$ | (4) |
式中,c代表土地覆盖类型,可以通过高空间分辨率影像分类获取,ac和bc通过最小二乘法进行线性拟合得到,Lc代表第c类高空间分辨率像元,Mc代表第c类对应的低空间分辨率像元。
该算法预测结果对分类算法不敏感并且当分类数量大于5时,对分类数量也不敏感(Shen等,2013),因此实验中采用非监督分类方法。根据研究区实际情况分为5类,同时简化Shen等人(2013)提出的式(4)的计算方法。利用最小二乘法对分类数据进行线性拟合,获得不同地物类型的a和b。为了尽量降低分类误差异常值对线性拟合系数的影响,采用统计学上($\overline x \pm 2\sigma $)的方法对分类像元进行再次筛选,假定相同地物类型NDVI差异不大且正态分布,利用($\overline x \pm 2\sigma $)可覆盖95.4%的像元数量,减少了因分类错误而引入的过大或者过小的NDVI数值像元。
蔡德文等人(2012)研究表明融合影像的预测精度与土地利用类型是否发生变化有关,土地利用类型未发生变化时融合预测精度高,土地类型发生变化时则预测精度较差。根据研究区的实际情况和研究时段,4月到6月是研究区主要作物(小麦)的快速生长和成熟期,NDVI会快速的增大或者减小,因此需要对时间距离权重进行修改,为此引入预测半径的概念,具体为:
(1) 定义16天为有效预测半径,4月到6月作物的NDVI变化较大,不宜扩大预测半径长度。
选择16天作为有效预测半径的原因有3个:首先,16天是HJ-1A星和HJ-1B联网的8个重访周期,单颗卫星的4个重访周期,基本可以保证前后两个预测半径内可以获得多期数据。其二,MODIS陆地标准产品MOD13均为16天合成,即使每16天的预测半径内仅成功预测一景数据也可以在环境变化监测中进行应用。其三,4月到6月是研究区内小麦快速生长和成熟期,NDVI会发生较大的变化,若预测半径过大,土地覆盖类型发生变化则会严重影响预测精度。
(2) 当有效预测半径内存在多景数据时,可以选取其中一景作为基准影像进行预测半径内的其他影像日期的预测。
(3) 当有效预测半径内无法获取遥感卫星数据时,此时选取预测时间前后两对基准影像对距离预测时间最近的两景影像进行预测,并对预测结果进行时间距离的加权平均,计算公式如下:
| $ L\left({{T_1}} \right)={{{T_1} - {T_0}} \over {{T_2} - {T_0}}} \times L\left({{T_2}} \right)+{{{T_2} - {T_1}} \over {{T_2} - {T_0}}} \times L\left({{T_0}} \right)$ | (5) |
式中,T0和T2分别为预测时间T1以前和以后的时间距离最小的两期数据的时间,L(T2)为预测时间以后的T2基准影像预测的时刻的结果,L(T0)为预测时间以前的基准影像预测的T0时刻的结果,L(T1)为T0和T2时刻预测结果时间距离加权平均值,是最终结果。
3 结果与分析
3.1 整体性分析
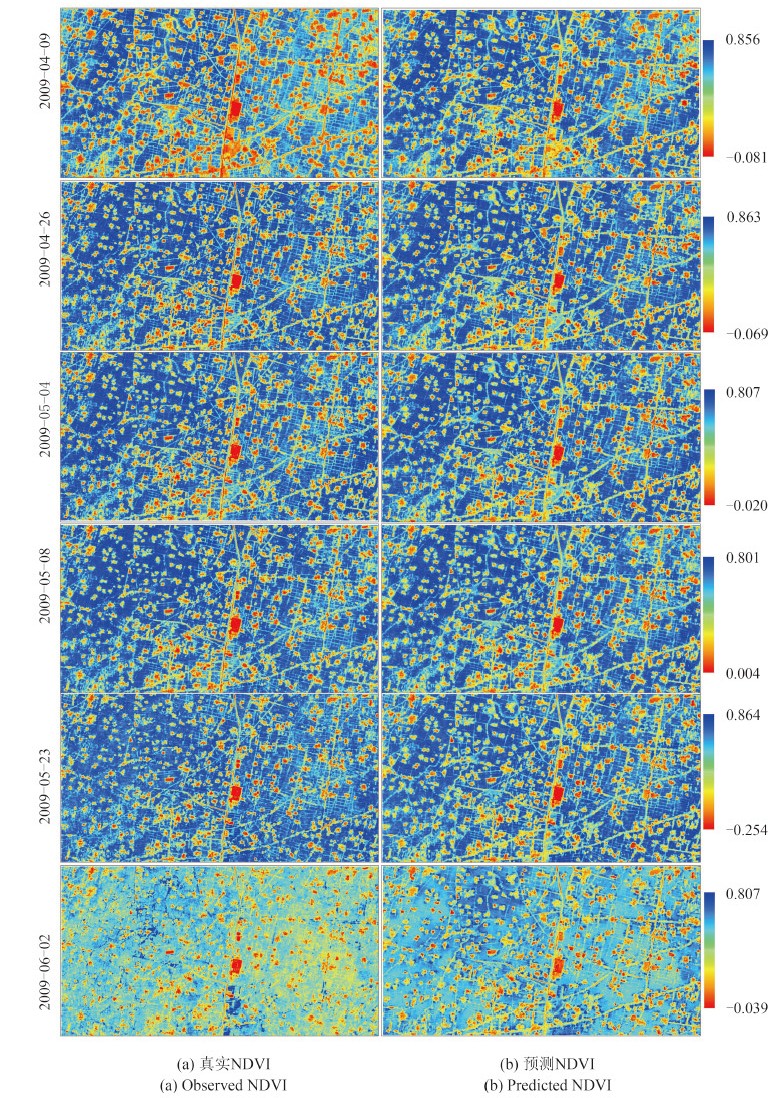
因篇幅所限,仅列举了以2009-04-16为单一基准影像,分别对2009-04-09、2009-04-26、2009-05-04、2009-05-08、2009-05-23和2009-06-02进行NDVI的预测,对融合结果进行了目视检验。图 2(a)为不同时刻的真实HJ-1 CCD NDVI影像,图 2(b)列为预测的对应时刻的NDVI影像。
通过分析真实HJ-1 CCD NDVI和预测HJ-1 CCD NDVI二者的影像图,可以发现利用时空融合技术进行预测得到的预测HJ-1 CCD NDVI像元高低值不仅在空间分布上与同期的真实HJ-1 CCD NDVI是一致的,而且很好的捕捉MOD09GQ NDVI在不同时刻之间的变化特征,此外又能在30 m空间分辨率像元尺度上反映空间细节分布差异。从预测结果可以看出,以2009-04-16为单一基准影像对2009-06-02进行预测,得到的NDVI数据,部分区域NDVI值偏高,这可能是因为2009-06-02为正处于主要作物(小麦)的成熟期或收获期,MODIS 250米空间分辨率数据不能有效的捕捉这种快速的变化,即两种传感器分辨率的差异,也可能是由于预测时间间隔过长造成的。总体上说时空数据融合技术可以将高空间分辨率影像的空间细节分布特征与低空间分辨率影像的高时间分辨率的时间变化信息进行有机的结合。
3.2 相关性分析
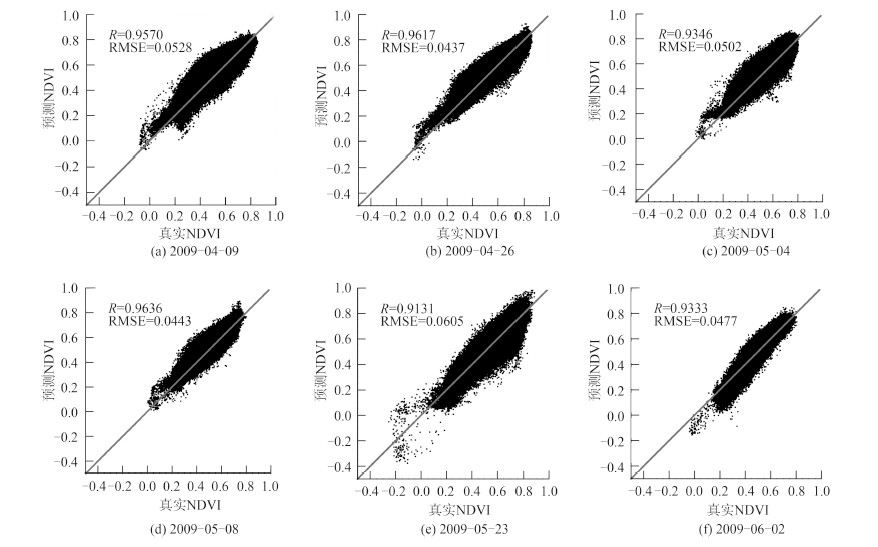
利用2009-04-16和2009-05-31的HJ-1 CCD NDVI数据,结合相应时间的MOD09GQ NDVI数据,对2009-04-09、2009-04-26、2009-05-04、2009-05-08、2009-05-23以及2009-06-02的HJ-1 CCD NDVI进行预测。图 3显示了不同时刻的真实NDVI与预测NDVI之间的像元散点分布。从相关性上来看,预测影像与真实影像的散点分布很集中,绝大数分布在y=x直线附近,6个不同预测时刻的R和RMSE统计情况如表 1所示。由表 1可知,R均为极显著相关,这表示预测影像与真实影像对应像元值的大小的空间分布很一致,融合效果很好。RMSE均小于0.061,这也表明线性拟合程度很好,离散程度很小,预测值与真实值具有很好的一致性。
表 1 预测结果的R与RMSE
Table 1 R and RMSE of prediction results
| 预测指标 | 预测时间 | |||||
| 2009-04-09 | 2009-04-26 | 2009-05-04 | 2009-05-08 | 2009-05-23 | 2009-06-02 | |
| R | 0.957 | 0.962 | 0.935 | 0.964 | 0.913 | 0.933 |
| RMSE | 0.053 | 0.044 | 0.050 | 0.044 | 0.061 | 0.048 |
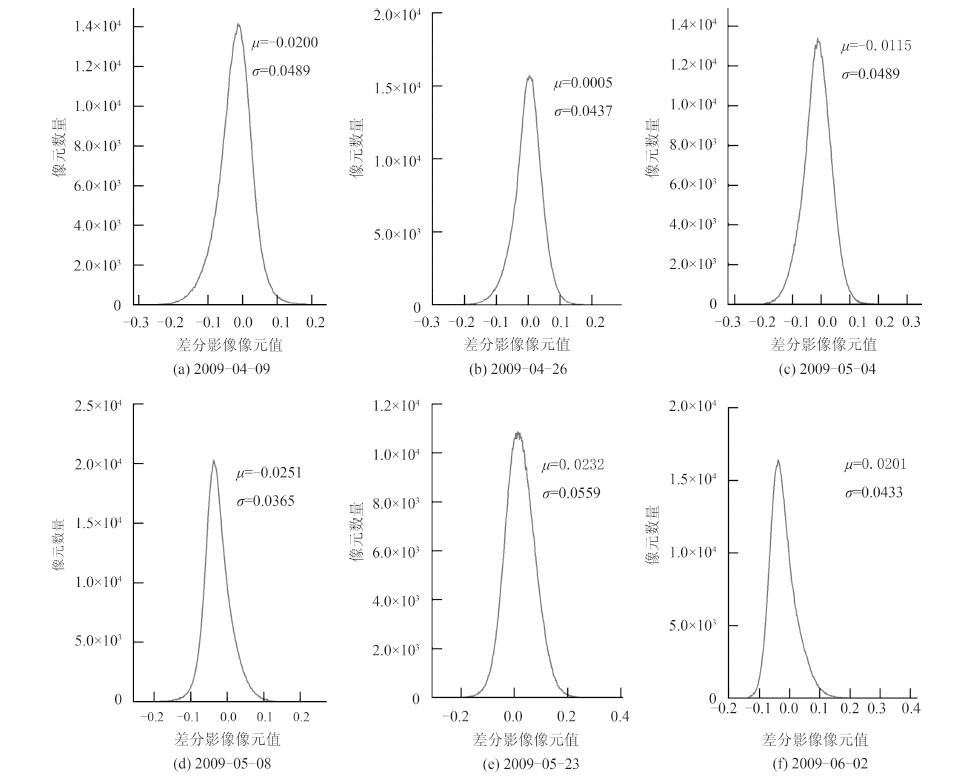
另外,图 4显示了上述6景真实NDVI影像与预测NDVI影像的差分影像的像元直方图分布情况。差分影像的平均值、标准偏差、像元绝对值小于0.1和0.2的百分比统计情况如表 2。由表 2可知,差分影像像元的平均值和标准偏差较小,6景差分影像的像元绝对值小于0.1所占的比例均超过90%以上,几乎所有的差分影像值的绝对值小于0.2,预测结果整体上精度很高。因此认为该方法可以有效的对缺失HJ-1 CCD NDVI时间序列进行重构。
表 2 差分影像分析
Table 2 Analysis of difference image
| 预测时间 | ||||||
| 2009-04-09 | 2009-04-26 | 2009-05-04 | 2009-05-08 | 2009-05-23 | 2009-06-02 | |
| 平均值 | –0.020 | 0.001 | –0.012 | –0.025 | 0.023 | –0.020 |
| 标准偏差 | 0.049 | 0.044 | 0.049 | 0.036 | 0.056 | 0.043 |
| P<0.1 | 93.20% | 96.90% | 94.70% | 98.17% | 90.00% | 97.80% |
| P<0.2 | 99.80% | 99.97% | 99.95% | 99.98% | 99.79% | 100.00% |
| 注:P为差分影像的像元绝对值。 | ||||||
3.3 整体回归分析与差分影像分析
当HJ-1 CCD NDVI基准影像不同时,得到相似像元的数量和位置也可能存在差异,为了确定基准影像的选择对融合结果的影响,利用改进的算法,仅考虑传感器差异的影响,暂时不引入预测半径,选择不同时刻的单一影像作为基准影像进行预测,对预测结果利用相关系数R、平均绝对差值AAD(Average Absolute Difference)、平均差值AD(average difference)(Gao等,2006;Walker等,2012;Zhu等,2010),差分影像标准差SD等评价指标进行分析(表 3)。
表 3 不同基准影像的结果精度比
Table 3 Accuracy comparison of prediction results of different base image
| 基准时间 | 评价标准 | 预测时间 | ||||||||
| 2009-04-09 | 2009-04-16 | 2009-04-21 | 2009-04-26 | 2009-05-04 | 2009-05-08 | 2009-05-23 | 2009-05-31 | 2009-06-02 | ||
| 2009-04-09 | AAD | - | 0.042 | 0.078 | 0.060 | 0.039 | 0.062 | 0.057 | 0.064 | 0.083 |
| AD | - | 0.023 | 0.066 | 0.048 | –0.001 | –0.045 | –0.004 | –0.024 | –0.039 | |
| SD | - | 0.049 | 0.067 | 0.056 | 0.052 | 0.059 | 0.074 | 0.077 | 0.091 | |
| R | - | 0.952 | 0.929 | 0.934 | 0.932 | 0.901 | 0.863 | 0.707 | 0.641 | |
| 2009-04-16 | AAD | 0.040 | - | 0.071 | 0.043 | 0.041 | 0.063 | 0.053 | 0.061 | 0.077 |
| AD | –0.020 | - | 0.061 | 0.027 | –0.020 | –0.056 | –0.019 | –0.035 | –0.049 | |
| SD | 0.049 | - | 0.056 | 0.045 | 0.049 | 0.046 | 0.064 | 0.067 | 0.078 | |
| R | 0.957 | - | 0.954 | 0.960 | 0.939 | 0.935 | 0.896 | 0.764 | 0.716 | |
| 2009-04-21 | AAD | 0.068 | 0.059 | - | 0.038 | 0.077 | 0.114 | 0.088 | 0.080 | 0.098 |
| AD | –0.057 | –0.050 | - | –0.017 | –0.070 | –0.113 | –0.077 | –0.068 | –0.078 | |
| SD | 0.062 | 0.049 | - | 0.048 | 0.054 | 0.047 | 0.064 | 0.068 | 0.083 | |
| R | 0.937 | 0.960 | - | 0.952 | 0.940 | 0.955 | 0.922 | 0.800 | 0.762 | |
| 2009-04-26 | AAD | 0.057 | 0.040 | 0.047 | - | 0.052 | 0.084 | 0.061 | 0.070 | 0.090 |
| AD | –0.047 | –0.025 | 0.031 | - | –0.044 | –0.082 | –0.045 | –0.057 | –0.071 | |
| SD | 0.056 | 0.045 | 0.053 | - | 0.041 | 0.045 | 0.055 | 0.061 | 0.078 | |
| R | 0.946 | 0.963 | 0.956 | - | 0.967 | 0.956 | 0.941 | 0.937 | 0.782 | |
| 2009-05-04 | AAD | 0.043 | 0.046 | 0.093 | 0.055 | - | 0.043 | 0.035 | 0.045 | 0.061 |
| AD | 0.001 | 0.021 | 0.084 | 0.045 | - | –0.034 | 0.003 | –0.018 | –0.029 | |
| SD | 0.057 | 0.054 | 0.065 | 0.044 | - | 0.041 | 0.047 | 0.054 | 0.068 | |
| R | 0.941 | 0.939 | 0.938 | 0.965 | - | 0.946 | 0.940 | 0.840 | 0.779 | |
| 2009-05-08 | AAD | 0.063 | 0.064 | 0.130 | 0.084 | 0.042 | - | 0.044 | 0.045 | 0.053 |
| AD | 0.041 | 0.053 | 0.127 | 0.080 | 0.031 | - | 0.034 | 0.025 | 0.017 | |
| SD | 0.064 | 0.051 | 0.060 | 0.047 | 0.041 | - | 0.046 | 0.051 | 0.066 | |
| R | 0.925 | 0.945 | 0.953 | 0.957 | 0.954 | - | 0.942 | 0.861 | 0.814 | |
| 2009-05-23 | AAD | 0.061 | 0.056 | 0.104 | 0.062 | 0.034 | 0.044 | - | 0.037 | 0.048 |
| AD | 0.003 | 0.018 | 0.090 | 0.045 | –0.003 | –0.037 | - | –0.015 | –0.021 | |
| SD | 0.079 | 0.067 | 0.076 | 0.056 | 0.045 | 0.044 | - | 0.045 | 0.057 | |
| R | 0.883 | 0.904 | 0.917 | 0.941 | 0.945 | 0.938 | - | 0.888 | 0.855 | |
| 2009-05-31 | AAD | 0.093 | 0.088 | 0.115 | 0.094 | 0.059 | 0.049 | 0.047 | - | 0.040 |
| AD | 0.033 | 0.050 | 0.099 | 0.076 | 0.026 | –0.026 | 0.023 | - | –0.020 | |
| SD | 0.108 | 0.094 | 0.092 | 0.081 | 0.069 | 0.058 | 0.056 | - | 0.043 | |
| R | 0.768 | 0.807 | 0.861 | 0.857 | 0.867 | 0.894 | 0.913 | - | 0.933 | |
| 2009-06-02 | AAD | 0.113 | 0.104 | 0.130 | 0.112 | 0.074 | 0.058 | 0.059 | 0.040 | - |
| AD | 0.054 | 0.067 | 0.106 | 0.089 | 0.038 | –0.016 | 0.030 | 0.018 | - | |
| SD | 0.120 | 0.102 | 0.106 | 0.095 | 0.081 | 0.072 | 0.067 | 0.045 | - | |
| R | 0.703 | 0.761 | 0.819 | 0.804 | 0.809 | 0.822 | 0.864 | 0.891 | - | |
如表 3所示,以不同时刻为基准影像进行预测,预测结果随着基准日期与预测日期之间时间间隔的增加,预测结果精度趋于降低。当基准影像获取时间处于植被生长高峰期时,预测结果质量较高,但随着时间距离推移,植被生长状况发生显著变化时,其精度会明显降低。前8景基准影像(除2009-04-21外)的预测结果只有个别预测日期的平均绝对差值大于0.1,且同为2009-04-21;以2009-04-21为基准影像预测,只有2009-05-08的平均绝对差值大于0.1;前8景的预测结果精度要高于以2009-06-02为基准影像的预测结果。预测相同日期影像,以不同的基准日期进行预测,通过对比NDVI预测结果,发现使用距离预测日期最近的影像作为基准影像比使用单一时刻作为基准影像,预测结果精度更高更准确。通过对比相关系数R发现,不同基准影像预测结果的相关系数R,随着预测时间间隔的增加而趋于降低。通过对比AAD、SD和相关系数R发现,不同方向的预测,预测结果精度也有明显差异,如以2009-04-16为基准影像预测2009-06-02和以2009-06-02为基准影像预测2009-04-16,预测结果的精度有明显差异。因此应选择距离预测时刻较近的影像对作为基准影像对,同时需要考虑预测方向从而确保预测结果精度。
为了更准确地比较改进算法与原始STARFM算法预测结果精度,采用IR定量化的表示预测结果精度的提高程度,计算公式为
| $IR=\left({1 - \frac{{{\rm{STARF}}{{\rm{M}}_G}}}{{{\rm{STARF}}{{\rm{M}}_Y}}}} \right)\times 100\% $ | (6) |
或者
| $\begin{equation} IR=\left({1 - {{{\rm{STARF}}{{\rm{M}}_G}} \over {{\rm{STARF}}{{\rm{M}}_Y}}} - 1} \right)\times 100 \textrm{%} \end{equation}$ | (7) |
式中,STARFMY表示利用原始STARFM算法得到的预测结果的指标,STARFMG表示利用文章提出的算法得到的预测结果的指标。根据不同的评价指标选择不同的计算公式,如AAD和RMSE的IR计算选择式(6),R的IR计算选择式(7)。
利用改进后的算法,考虑传感器差异同时引入预测半径,为便于分析,以2009-05-31为改进算法中的固定基准影像,分别选取2009-04-16、2009-04-21、2009-04-26为另一对基准影像,原始STARFM算法中仅需要一对基准影像,因此也选择以2009-04-16、2009-04-21、2009-04-26为基准影像进行预测,两种算法的预测结果如表 4所示。
表 4 改进方法与原始方法预测结果分析
Table 4 Results analysis between improved and original methods
| 预测时间 | 基准时间 | |||||||||
| 2009-04-16 | 2009-04-21 | 2009-04-26 | ||||||||
| 原始算法 | 改进算法 | IR/% | 原始算法 | 改进算法 | IR/% | 原始算法 | 改进算法 | IR/% | ||
| 2009-04-09 | AAD | 0.042261 | 0.039930 | 5.52 | 0.073266 | 0.067966 | 7.23 | 0.059918 | 0.057012 | 4.85 |
| R | 0.955528 | 0.956969 | 0.15 | 0.935439 | 0.937030 | 0.17 | 0.944262 | 0.945633 | 0.15 | |
| RMSE | 0.055629 | 0.052825 | 5.04 | 0.089566 | 0.084220 | 5.97 | 0.076184 | 0.073046 | 4.12 | |
| 2009-04-16 | AAD | - | - | - | 0.063675 | 0.058528 | 8.08 | 0.041445 | 0.040420 | 2.47 |
| R | - | - | - | 0.958830 | 0.960153 | 0.14 | 0.961688 | 0.962682 | 0.10 | |
| RMSE | - | - | - | 0.074989 | 0.069749 | 6.99 | 0.052648 | 0.051462 | 2.25 | |
| 2009-04-21 | AAD | 0.071217 | 0.071101 | 0.16 | - | - | - | 0.047350 | 0.047286 | 0.14 |
| R | 0.943884 | 0.953929 | 1.06 | - | - | - | 0.955472 | 0.955662 | 0.02 | |
| RMSE | 0.082308 | 0.081416 | 1.08 | - | - | - | 0.061571 | 0.061482 | 0.14 | |
| 2009-04-26 | AAD | 0.043672 | 0.042786 | 2.03 | 0.040530 | 0.037904 | 6.48 | - | - | - |
| R | 0.959691 | 0.961706 | 0.21 | 0.950766 | 0.952070 | 0.14 | - | - | - | |
| RMSE | 0.051352 | 0.043730 | 14.84 | 0.053979 | 0.050901 | 5.70 | - | - | - | |
| 2009-05-04 | AAD | 0.041978 | 0.038963 | 7.18 | 0.082106 | 0.077025 | 6.19 | 0.052597 | 0.051861 | 1.40 |
| R | 0.932912 | 0.934551 | 0.18 | 0.938671 | 0.939996 | 0.14 | 0.966110 | 0.966517 | 0.04 | |
| RMSE | 0.053761 | 0.050188 | 6.65 | 0.093723 | 0.088444 | 5.63 | 0.061177 | 0.060388 | 1.29 | |
| 2009-05-08 | AAD | 0.063535 | 0.036739 | 42.18 | 0.119164 | 0.068783 | 42.28 | 0.084561 | 0.084361 | 0.24 |
| R | 0.935454 | 0.963569 | 3.01 | 0.954351 | 0.966341 | 1.26 | 0.945623 | 0.955556 | 1.05 | |
| RMSE | 0.073442 | 0.044296 | 39.69 | 0.127714 | 0.076648 | 39.98 | 0.093319 | 0.093193 | 0.13 | |
| 2009-05-23 | AAD | 0.053108 | 0.047393 | 10.76 | 0.092831 | 0.047393 | 48.95 | 0.061150 | 0.047393 | 22.50 |
| R | 0.895690 | 0.913050 | 1.94 | 0.910447 | 0.913050 | 0.29 | 0.900284 | 0.913050 | 1.42 | |
| RMSE | 0.066540 | 0.060492 | 9.09 | 0.104814 | 0.060492 | 42.29 | 0.071097 | 0.060492 | 14.92 | |
| 2009-05-31 | - | - | - | - | - | - | - | |||
| 2009-06-02 | AAD | 0.080413 | 0.039813 | 50.49 | 0.102712 | 0.039813 | 61.24 | 0.094019 | 0.039813 | 57.65 |
| R | 0.714558 | 0.933308 | 30.61 | 0.759705 | 0.933308 | 22.85 | 0.779749 | 0.933308 | 19.69 | |
| RMSE | 0.095249 | 0.047733 | 49.89 | 0.119008 | 0.047733 | 59.89 | 0.109822 | 0.047733 | 56.54 | |
由表 4可知,改进的算法比原始STARFM算法产生的AAD和RMSE有所降低,R有所提高。以2009-04-16、2009-04-21、2009-04-26为基准影像进行预测,评价指标均有不同程度的提高,AAD的IR平均提高分别为16.90%、25.78%、12.75%;R的IR平均提高分别为5.31%、3.57%、3.21%;RMSE的IR平均提高分别为18.04%、23.78%、11.34%。改进算法中以2009-04-16和2009-05-31为基准影像,对不在预测半径内的2009-05-04和2009-05-08的预测结果精度明显高于原始算法,同理2009-04-21和2009-05-31为基准影像预测的2005-05-08的预测结果精度也明显高于原算法,因此认为利用两对基准影像的预测结果要好于单一基准影像。此外分别对比在基准影像2009-04-16、2009-04-21、2009-04-26和2009-05-31预测半径内的预测结果评价指标,可知预测精度比原始算法有不同程度的提高。这表明由光谱范围的大小、不同波段光谱响应函数的差异等因素所造成的预测误差,改进后的算法比原始的STARFM算法得到更好的预测精度。
3.4 预测半径精度分析
通过上文分析可知使用单一基准影像进行预测,当预测时间跨度较大时预测结果的精度会有所下降,为了验证预测半径对结果的影响,做了一组实验:(1)仅考虑传感器差异的影响,暂时不引入预测半径以2009-04-16、2009-05-31为单一基准影像对2009-05-04和2009-05-08进行预测;(2)考虑传感器差异同时引入预测半径,以2009-04-16和2009-05-31为基准影像对不在预测半径内的2009-05-04和2009-05-08影像进行预测。对预测结果进行差分影像分析和回归分析,结果如表 5所示。
表 5 预测精度分析
Table 5 Analysis results of prediction accuracy
| 预测时间 | 指标 | 基准时间 | IR/% | |||
| 2009-04-16 | 2009-05-31 | 2009-04-16+ 2009-05-31 | 2009-04-16 | 2009-05-31 | ||
| 2009-05-04 | AAD | 0.041146 | 0.059111 | 0.038963 | 5.31 | 34.09 |
| AD | –0.019730 | 0.026406 | –0.011497 | 41.73 | 56.46 | |
| SD | 0.049110 | 0.068749 | 0.048854 | 0.52 | 28.94 | |
| R | 0.938521 | 0.867241 | 0.934551 | –0.42 | 7.80 | |
| RMSE | 0.052932 | 0.073614 | 0.050188 | 5.10 | 31.79 | |
| 2009-05-08 | AAD | 0.063099 | 0.048956 | 0.036739 | 41.78 | 24.96 |
| AD | –0.056378 | –0.026168 | –0.025074 | 55.52 | 4.18 | |
| SD | 0.046420 | 0.058155 | 0.036515 | 21.34 | 37.21 | |
| R | 0.935448 | 0.893937 | 0.963569 | 3.01 | 7.80 | |
| RMSE | 0.073271 | 0.062249 | 0.044296 | 39.32 | 28.78 | |
从表 5可知,改进算法得到的预测结果精度要远大于仅使用单一基准影像进行预测的结果,其中IR表示改进后的算法比单一基准影像预测结果精度的提高的比例。通过对比2009-04-16和2009-05-31的预测结果,改进算法预测结果AAD的提高比例IR在5.31%到41.78%范围内;AD的提高比例IR在4.18%到56.46%范围内;SD的提高比例IR在0.52%到37.21%范围内;RMSE的提高比例IR在5.1%到39.32%范围内。对比相关系数R,改进后的算法在2009-05-04的预测结果的相关系数为0.9346,虽然小于2009-04-16为基准所得到相关系数0.9385,但是高于2009-05-31为基准所得到的相关系数0.867,且其他评估指标均有不同程度提高,预测精度明显提高。其他时刻R的提高比例IR在3.01%到7.80%范围内,均有不同程度的提高。因此认为利用两对基准影像的预测结果进行时间距离加权可以有效的保证那些不在预测半径内的预测影像的精度。
4 结论
本文以STARFM算法为基础,对相似像元权重进行修改,选取华北平原小范围的MODIS和HJ-1 CCD数据,进行时空融合开展NDVI时间序列重构研究。改进后的算法得到的预测结果精度要高于原始STARFM算法。利用该方法将HJ-1 CCD NDVI的空间变化信息与MODIS NDVI时间变化信息相结合,生成具有高时空分辨率NDVI数据,有效补充了HJ-1 CCD NDVI的缺失数据集。
基准影像日期的选择与预测日期影像应当具有相似的季相特征,若时间跨度过大,相似季相特征不明显或者有明显差异,则会加大预测结果的不确定性,从而降低预测结果精度和质量,应该考虑基准影像的选择对预测结果的影响差异。
由于大气条件以及BRDF等因素的干扰,经过图像预处理得到像元反射率再进行NDVI的计算,无意间将一些噪声引入NDVI影像,同时MOD09GQ数据集的一些噪声,将通过算法引入到预测日期影像中,影响了预测结果的精度。因此以后工作中会引入去除影像除噪声的方法,进一步提高预测结果精度。
改进后的算法比原始STARFM算法有更高的精度,但在异质性区域,如农田与村庄的交错地带、狭窄的道路等等,影像中的混合像元会干扰融合结果的精度,所以将引入混合像元分解机制到影像时空融合技术中进行研究。
文中所选研究区域的主要覆盖类型为耕地,时间段为主要作物(小麦)的一个生育期,下一步工作将进行跨作物生育期研究,同时选择异质性更高的区域类型,例如山区、农林混合、城市等,进行融合算法有效性的检验。
文中考虑不同传感器系统差异对预测结果的影响,采用分类线性拟合的方法进行控制,然而不能提取出有效的参数。因此下一步工作将针对不同传感器光谱响应函数的差异,进行参数提取,并引入到融合算法中进一步提高预测精确度。
参考文献(References)
-
Busetto L, Meroni M, Colombo R.2008.Combining medium and coarse spatial resolution satellite data to improve the estimation of sub-pixel NDVI time series. Remote Sensing of Environment, 112 (1) : 118–131 . [DOI:10.1016/j.rse.2007.04.004]
-
Cai D W, Niu Z, Wang L.2012.Adaptability research of spatial and temporal remote sensing data fusion technology in crop monitoring. Remote Sensing Technology and Application, 27 (6) : 927–932 . ( 蔡德文, 牛铮, 王力. 2012. 遥感数据时空融合技术在农作物监测中的适应性研究. 遥感技术与应用, 27 (6) : 927–932. )
-
Cai W W, Song J L, Wang J D, Xiao Z Q.2012.High spatial-and temporal-resolution NDVI produced by the assimilation of MODIS and HJ-1 data. Canadian Journal of Remote Sensing, 37 (6) : 612–627 . [DOI:10.5589/M12-004]
-
Coops N C, Johnson M, Wulder M A, White J C.2006.Assessment of QuickBird high spatial resolution imagery to detect red attack damage due to mountain pine beetle infestation. Remote Sensing of Environment, 103 (1) : 67–80 . [DOI:10.1016/j.rse.2006.03.012]
-
Coops N C, Hilker T, Bater C W, Wulder M A, Nielsen S E, McDermid G, Stenhouse G.2012.Linking ground-based to satellitederived phenological metrics in support of habitat assessment. Remote Sensing Letters, 3 (3) : 191–200 . [DOI:10.1080/01431161.2010.550330]
-
Gao F, Masek J, Schwaller M, Hall F.2006.On the blending of the Landsat and MODIS surface reflectance:predicting daily Landsat surface reflectance. IEEE Transactions on Geoscience and Remote Sensing, 44 (8) : 2207–2218 . [DOI:10.1109/Tgrs.2006.872081]
-
Holben B N.1986.Characteristics of maximum-value composite images from temporal Avhrr data. International Journal of Remote Sensing, 7 (11) : 1417–1434 . [DOI:10.1080/01431168608948945]
-
Huete A, Didan K, Miura T, Rodriguez E P, Gao X, Ferreira L G.2002.Overview of the radiometric and biophysical performance of the MODIS vegetation indices. Remote Sensing of Environment, 83 (1/2) : 195–213 . [DOI:10.1016/S0034-4257(02)00096-2]
-
Justice C O, Townshend J R G, Holben B N , Tucker C J.1985.Analysis of the phenology of global vegetation using meteorological satellite data. International Journal of Remote Sensing, 6 (8) : 1271–1318 . [DOI:10.1080/01431168508948281]
-
Kennedy R E, Townsend P A, Gross J E, Cohen W B, Bolstad P, Wang Y Q , Adams P.2009.Remote sensing change detection tools for natural resource managers:understanding concepts and tradeoffs in the design of landscape monitoring projects. Remote Sensing of Environment, 113 (7) : 1382–1396 . [DOI:10.1016/j.rse.2008.07.018]
-
Li D C, Tang P, Hu C M, Zheng K.2014.Spatial-temporal fusion algorithm based on an extended semi-physical model and its preliminary application. Journal of Remote Sensing, 18 (2) : 307–319 . [DOI:10.11834/jrs.20143213] ( 李大成, 唐娉, 胡昌苗, 郑柯. 2014. 一种拓展的半物理时空融合算法及其初步应用. 遥感学报, 18 (2) : 307–319. [DOI:10.11834/jrs.20143213] )
-
Malenovský Z, Bartholomeus H M, Acerbi-Junior F W, Schopfer J T, Painter T H, Epema G F, Bregt A K.2007.Scaling dimensions in spectroscopy of soil and vegetation. International Journal of Applied Earth Observation and Geoinformation, 9 (2) : 137–164 . [DOI:10.1016/j.jag.2006.08.003]
-
Meng J H, Wu B F, Du X, Xu L M, Zhang F F.2011.Method to construct high spatial and temporal resolution NDVI DataSet-STAVFM. Journal of Remote Sensing, 15 (1) : 44–59 . ( 蒙继华, 吴炳方, 杜鑫, 钮立明, 张飞飞. 2011. 高时空分辨率NDVI数据集构建方法. 遥感学报, 15 (1) : 44–59. )
-
Meng J H, Du X, Wu B F.2013.Generation of high spatial and temporal resolution NDVI and its application in crop biomass estimation. International Journal of Digital Earth, 6 (3) : 203–218 . [DOI:10.1080/17538947.2011.623189]
-
Olexa E M, Lawrence R L.2014.Performance and effects of land cover type on synthetic surface reflectance data and NDVI estimates for assessment and monitoring of semi-arid rangeland. International Journal of Applied Earth Observation and Geoinformation, 30 : 30–41 . [DOI:10.1016/j.jag.2014.01.008]
-
( RoyD P, JuJ C, LewisP, SchaafC, GaoF, HansenM , LindquistE. 2008. Multi-temporal MODIS-Landsat data fusion for relative radiometric normalization, gap filling, and prediction of Landsat data. Remote Sensing of Environment, 112 (6) : 3112–3130. [DOI:10.1016/j.rse.2008.03.009] )
-
Shen H F, Wu P H, Liu Y L, Ai T H, Wang Y, Liu X P.2013.A spatial and temporal reflectance fusion model considering sensor observation differences. International Journal of Remote Sensing, 34 (12) : 4367–4383 . [DOI:10.1080/01431161.2013.777488]
-
Walker J J, de Beurs K M, Wynne R H, Gao R H.2012.Evaluation of Landsat and MODIS data fusion products for analysis of dryland forest phenology. Remote Sensing of Environment, 117 : 381–393 . [DOI:10.1016/j.rse.2011.10.014]
-
Wang L G, Tian Y C, Zhu Y, Yao X, Zheng G Q, Cao W X.2012.Estimation of winter wheat leaf area index by fusing different spatial and temporal resolution remote sensing data. Transactions of the Chinese Society of Agricultural Engineering, 28 (17) : 117–124 .
-
( 王来刚, 田永超, 朱艳, 姚霞, 郑国清, 曹卫星. 2012. 不同时空分辨率遥感数据融合估算冬小麦叶面积指数. 农业工程学报, 28 (17) : 117–124. [DOI:10.3969/j.issn.1002-6819.2012.17.017] )
-
Washington-Allen R A, West N E, Ramsey R D, Efroymson R A.2006.A protocol for retrospective remote sensing-based ecological monitoring of rangelands. Rangeland Ecology & Management, 59 (1) : 19–29 . [DOI:10.2111/04-116r2.1]
-
Wu M Q, Niu Z , Wang C Y.2010.Mapping paddy fields by using spatial and temporal remote sensing data fusion technology. Transactions of the CSAE, 26 (S2) : 48–52 . [DOI:10.3969/j.issn.1002-6819.2010.z2.010] ( 邬明权, 牛铮, 王长耀. 2010. 利用遥感数据时空融合技术提取水稻种植面积. 农业工程学报, 26 (S2) : 48–52. [DOI:10.3969/j.issn.1002-6819.2010.z2.010] )
-
Wu M Q and Wang C Y. 2011. Spatial and Temporal Fusion of Remote Sensing Data using wavelet transform//Proceedings of the 2011 International Conference on Remote Sensing, Environment and Transportation Engineering (RSETE). Nanjing:IEEE:1581-1584[DOI:10.1109/RSETE.2011.5964589]
-
Zhu X L, Chen J, Gao F, Chen X H, Masek J G.2010.An enhanced spatial and temporal adaptive reflectance fusion model for complex heterogeneous regions. Remote Sensing of Environment, 114 (11) : 2610–2623 . [DOI:10.1016/j.rse.2010.05.032]