|
收稿日期: 2015-07-29; 修改日期: 2015-11-18;
优先数字出版日期: 2016-05-25
基金项目: 国家自然科学基金项目(编号:41201336;41471353);中央高校基础科研专项(编号:15CX05056A,14CX02143A)
第一作者简介:
马红章(1977-),男,博士,讲师,主要从事多源遥感数据协同反演研究。E-mail:mahzh@upc.edu.cn
中图分类号: TP79
文献标识码: A
文章编号: 1007-4619(2016)03-0374-8
|
摘要
建立适用于多类型植被场景的热辐射方向性模型是进行地表热辐射方向性研究的一种手段。利用真实植株几何及生理参数的统计平均值来刻画理念植株,并给定其空间分布特征,进行不同生长期植被冠层的描述。基于冠层双向孔隙率思想构建了冠层热辐射方向性3维模型,模型继承了孔隙率模型在计算冠层热辐射方向性上的简洁优势同时以几何光学的思想考虑了冠层空间异质性对冠层热辐射方向性的影响。以玉米冠层为例,进行了不同生长期玉米冠层热辐射方向亮温的模拟,通过与实地测量数据的比对表明,本文发展的模型能够较准确地模拟不同生长期玉米植被场景的方向亮温变化规律,模拟误差主要来自理念株的刻画误差、玉米叶片形状的近似以及忽略了多次散射贡献等3个方面。模型的构建方法对稀疏植被场景、浓密植被场景、多类型植被的混合场景均可适用,不同观测几何下的植被场景4组份面积比计算结果有望应用于复杂地表条件下地表返照率的研究。
关键词
热辐射 , 3维模型 , 理念株 , 孔隙率 , 组分温度
Abstract
Plant canopy temperature and soil temperature can be used to estimate canopy transpiration. The sensible heat flux and latent heat flux of the soil are crucial in predicting drought and estimating crop yield. In reality, land vegetation has multiple types with different shapes and spatial distributions; thus, a general model suitable for variety of vegetation types is important to investigate the thermal radiation directivity of the surface covered by vegetation. Based on the theory of bidirectional gap probability, a three-dimensional simulation model for hermal radiation directivity of a nouniform canopy was established in this study. The ideal plant given the special distribution was employed to form the canopy observation scene. The ideal plant is the basic unit for describing the observation scene, which possesses the statistical averages of the parameters of all the plants in the observed area. The multi-angle thermal infrared field data of different growth periods of a corn crop was used to verify the results of the simulation model proposed in this paper. Encouraging results have been obtained. The results show that the model can accurately simulate the change trend in the canopy temperature distribution with only a small deviation, which may be attributed to the following factors:(1) The deviation in the parameters used to establish the ideal plant affects the simulation result. (2) The roughness of the soil layer and the shape of the leaf are not considered in the process of simulation. (3) The model does not consider multiple scattering in the canopy body. Moreover, the quantity of the plants in the observation area is limited, and the spatial distribution of the plants differs to a certain extent from the statistical average used in the simulation. Given the parameters of the ideal plant and its spatial distribution, the model can calculate the area ratios of the four components in asparse vegetation scene, dense vegetation scene, and a mixed vegetation scene. The results combined with the Li-Strahlergeometric-optical model could be applied to the study of the surface albedo under complex surface conditions.
Key words
thermal radiation , three dimensional model , ideal plant , gap probability , component temperature
1 引 言
作物冠层组分温度与土壤组分温度的精确获取可用于计算冠层蒸腾以及土壤的显热和潜热通量,对于干旱预测和作物产量估算至关重要。进行非同温混合像元的热辐射空间分布模拟,掌握其热辐射方向性规律是实现像元组分温度反演的前提和基础。
在针对单一植被类型或冠层具有规则几何形态的冠层热辐射方向性模型的研究中,Jackson等人(1979)提出了均一冠层四组分模型;Kimes和Kirchner(1983)对行状结构几何形态的冠层简化为‘箱体’来研究冠层热辐射方向性;chen等人(2002)在Kimes模型的基础上,建立了行播作物的热辐射方向性间隙率模型等。现实中,地表植被类型多样,冠层形态各异,建立适用于多植被类型和复杂冠层空间异质性的冠层热辐射方向性模拟模型对地表热辐射方向性研究至关重要。Qin和Gerstl(2000)基于植被真实场景,建立了计算机真实结构模型(RGM),用于短波太阳辐射分布与BRDF的模拟,Liu等人(2007)将RGM模型拓展至热红外波段,进行冠层热辐射的方向性模拟。RGM模型克服了四组分模型及箱体模型仅适用于单一植被类型或冠层需具有规则几何特征的局限性,RGM模型理论上可适用于任意植被场景,但是刻画场景所需的参数极为繁杂并且模型的模拟精度又完全依赖于植被场景刻画是否真实。
本文基于三维冠层双向孔隙率思想构建了非均一冠层热辐射方向性三维模型,模型通过构造理念植株并给定植株的空间分布来描述冠层场景,大大降低了对冠层空间异质性刻画的难度。模型继承了孔隙率模型在计算冠层热辐射方向性上的简洁优势同时兼顾了冠层空间异质性对冠层热辐射方向性的影响。以玉米作物为例进行了不同生长期玉米植被场景的热辐射方向亮温的模拟,并基于玉米多角度热红外观测数据对模型进行了验证。
2 理念株刻画
理念株是刻画观测场景的基本单位,用于刻画理念株的参数具有观测区内所有植株对应参数的统计平均意义(杜永明,2006)。理念株是对观测区内所有植株几何特征及生理参数的抽象与平均,其空间边界是所有植株相对各自中心的几何空间边界平均,冠层叶片体密度与角度分布也是所有单植株相对各自中心相应位置处对应参数的平均。
2.1 外包络线几何特征
外包络是理念株叶片空间分布的外边界线,外包络线绕茎中心轴线旋转所形成的立体空间为理念株叶片分布空间。理念株外包络线可用植株最外层叶片到植株中轴线平均距离(叶展宽)随植株高度的变化来表示。设植株最大叶展宽为Rmax,依据植株几何形态的先验知识,给定植株垂直向10等分层叶展宽与最大叶展宽Rmax的比值ri=1-10,采用线性内插法可确定N分层($N\geqslant 10$)情形下各层叶展宽相对比值${{r}_{n=1,\cdots,N}}$,则第n层的叶展宽为Rn=Rmax·rn。
2.2 叶片体密度
假定理念株叶片体密度分布具有轴对称性且在径向的分布规律不随高度发生变化,对Rn水平向进行10等分段,以植株叶片体密度分布为先验知识设定各段叶片体密度的相对变化比例${{g}_{i=1,\cdots,10}}$,采用线性内插法确定M分段($M\geqslant 10$)情形下,每段的叶片体密度相对变化比例${{g}_{i=1,\cdots,M}}$。设定垂直向10等分层各层叶片体密度最大值的相对变化比例${{f}_{i=1,\cdots,10}}$,采用线性内插法确定N分层情形下,每层的叶片体密度最大值相对变化比例${{g}_{i=1,\cdots,N}}$。第n分层叶片总面积为
| ${{S}_{n}}=S\frac{{{f}_{n}}{{R}_{n}}^{2}}{\sum\limits_{i=1}^{N}{({{f}_{i}}{{R}_{i}}^{2})}}$ | (1) |
式中,S为单理念植株叶片总面积(或由植株平均占地面积S'与样地叶面积指数LAI计算,S=S'×LAI)。
第n层第m段处单位体积内的叶片面积为
| ${\rho _{n,m}}={{{d_{n,m}}N} \over {{s_{n,m}}H}}$ | (2) |
式中,H为植株高度,Sn,m为第n层第m段的环形面积,dn,m为Sn,m内叶片总面积,分别由式(3)(4)计算:
| ${S_{n,m}}=\left\{ \begin{array}{l}\pi \left[ {{{({R_n}\frac{m}{M})}^2} - {{({R_n}\frac{{m - 1}}{M})}^2}} \right],m > 1\\{\rm{ }}\pi {(\frac{{{R_n}}}{M})^2},m=1\end{array} \right.$ | (3) |
| ${d_{n,m}}={S_n}{{{g_m}{s_{n,m}}} \over {\sum\limits_{i=1}^M {{g_i}{s_{n,i}}} }}$ | (4) |
2.3 观测场景构建
植被场景可看作是由众多单理念植株按照一定的空间分布组成的场景,场景大小可根据需求设定。以水平地面相互垂直的两个方向为X、Y轴,以垂直地面向上为Z轴,给定场景中各理念植株的坐标(xi,yi),则场景任意空间点P(xp,yp,zp)的叶片体密度由(xp,yp)到(xi,yi)距离Li以及zp与理念株高度H的关系共同决定,其中,zp决定P点所处的理念株垂直分层数n,Li与Rn的关系确定P点所处径向分段值m,由式(2)可得到P点叶片体密度值,如果点P处于多理念植株的重叠空间,则P点处叶片体密度为各理念株在P点处体密度值的累加。
3 冠层孔隙率计算
3.1 冠层孔隙率计算理论
对于一个植被场景,冠层是按一定规律分布的叶片介质层。对某个方向的截面面积为a的观测路径圆柱,冠层孔隙率不仅与圆柱内叶片面积有关而且与叶片的角度分布亦有关。设观测路径圆柱内存在单位面积的叶片个数为n,叶片法线与观测方向的夹角为θn,且角度为θn叶片出现的归一化比例fn满足:$\sum\limits_{n=1}^n {{f_n}}=1$,令$\sum\limits_{n=1}^n {{f_n}\cos {\theta _n}}=\gamma $。冠层叶片在观测路径圆柱内位置随机,满足Boolean原理(Li和Strahler,1988;Strahler和Jupp,1990),则观测路径冠层孔隙率为
| $gap={{\rm{e}}^{ -({{n \cdot \gamma } \over a})}}$ | (5) |
3.2 四组份比例计算
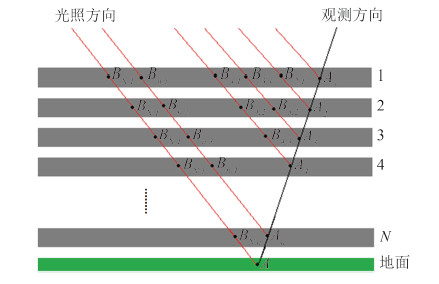
在观测区域土壤层给定一随机点A(x,y),观测方向天顶角和方位角分别为αo和βo,光照方向天顶角和方位角分别为αs和由βs,A点沿观测方向反向延长线与冠层各分层的交点An,由An点沿光照方向反向延长线与冠层各分层交点分别为Bn,j,j取1—(n-1),如图 1所示。由An和Bn,j点坐标结合式(2)可得各点处叶片体密度值${\rho _{{A_n}}}$和${\rho _{{B_{n,j}}}}$。
设观测圆柱和光照圆柱共底且为圆,水平截面面积为Sa,Sa取值与叶片平均大小有关,一般取单叶片平均面积,对于玉米类长条形叶片取叶片的平均宽度作为圆的直径;观测向An点处的可视比例为Pn可由下式计算
| ${P_n}=\left\{ \begin{array}{l}{{\rm{e}}^{ - \left[ {\frac{H}{N} \cdot \frac{{{S_a}}}{{{S_a}\cos({\alpha _o})}} \cdot \sum\limits_{n=1}^{n - 1} {({\rho _{{A_n}}})} } \right]\gamma }} - {{\rm{e}}^{ - \left[ {\frac{H}{N} \cdot \frac{{{S_a}}}{{{S_a}\cos({\alpha _o})}} \cdot \sum\limits_{n=1}^n {({\rho _{{A_n}}})} } \right]\gamma }},n > 1\\1 - {{\rm{e}}^{ - \left[ {\frac{H}{N} \cdot \frac{{{S_a}}}{{{S_a}\cos({\alpha _o})}} \cdot \sum\limits_{n=1}^n {({\rho _{{A_n}}})} } \right]\gamma }},n=1\end{array} \right.$ | (6) |
光照向An点处光照概率为Sn可表示为
| ${S_n}=\left\{ \begin{array}{l}{{\rm{e}}^{ - \left[ {\frac{H}{N} \cdot \frac{{{S_a}}}{{{S_a} \cdot \cos({\alpha _s})}} \cdot \sum\limits_{j=1}^{n - 1} {({\rho _{{B_{n,j}}}})} } \right]\gamma }},n > 1\\1,n=1.\end{array} \right.$ | (7) |
则,土壤层A点处可视比例P为
| $P={{\rm{e}}^{ - \left[ {{H \over N} \cdot {{{S_a}} \over {{S_a} \cdot \cos({\alpha _o})}} \cdot \sum\limits_{n=1}^{n - 1} {({\rho _{{A_n}}})} } \right]\gamma }}$ | (8) |
土壤层A点处光照概率S为
| $S={{\rm{e}}^{ - \left[ {{H \over N} \cdot {{{S_a}} \over {{S_a} \cdot \cos({\alpha _s})}} \cdot \sum\limits_{j=1}^N {({\rho _{{B_{N,j}}}})} } \right]\gamma }}$ | (9) |
假设观测向孔隙率与光照向孔隙率完全独立,则A点处可视光照地表的概率为Psoil1=P·S,可视阴影地表概率为Psoil2=P(1-S);冠层An点处可视光照叶片的概率为Pleaf1n=Pn·Sn,可视阴影叶片概率为Pleaf2n=Pn(1-Sn)。
取观测区域随机点K个(经模拟发现K>500即可得到稳定结果),场景四组分的概率值为每个随机点沿观测路径的四组分比例值的平均。则场景可视光照地表比例为
| ${S_1}={1 \over k} \cdot(\sum\limits_{i=1}^k {P{\rm{soil}}{1_i}})$ | (10) |
场景可视阴影地表比例为
| ${S_2}={1 \over k} \cdot(\sum\limits_{i=1}^k {P{\rm{soil}}{2_i}})$ | (11) |
场景可视光照叶片比例为
| $ {L_1}={1 \over k} \cdot(\sum\limits_{i=1}^k {\sum\limits_{n=1}^{N - 1} {P{\rm{leaf}}{1_n}_i} })$ | (12) |
场景可视阴影叶片比例为
| ${L_2}={1 \over k} \cdot(\sum\limits_{i=1}^k {\sum\limits_{n=1}^{N - 1} {P{\rm{leaf}}{2_n}_i} })$ | (13) |
对于实际情况,观测向孔隙率与光照向孔隙率是相关的,即热点的考虑。两方向夹角越小则相关性越高,相关性取决于两路径中叶片空间分布姿态。Kuusk(1991)用一个交叉函数,而Jupp和Strahler(1991)则用重叠函数来考虑两者之间的相关性。Verstraete等人(1990)提出了物理上严格的热点定义,并用两个共底圆柱重叠部分与观测路径方向圆柱的体积比值来定量热点效应。在本文的模型中,考虑到关于两者相关性,采用Verstraete Verstraete等人(1990)的思想。设在第n层光照立体柱与观测立体柱相交体积内的叶片总面积与光照立体柱内叶片的总面积比值为bn,则光照向An点处的光照概率修正为
| ${S_n}=\left\{ \begin{array}{l}{{\rm{e}}^{ - \left[ {\frac{H}{N} \cdot \frac{{{S_a}}}{{{S_a} \cdot \cos({\alpha _s})}} \cdot \sum\limits_{j=1}^{n - 1} {({\rho _{{B_{n,j}}}} \cdot(1 - {b_j}))} } \right]\gamma }},n > 1\\1,n=1.\end{array} \right.$ | (14) |
土壤层A点处光照概率修正为
| $S={{\rm{e}}^{ - \left[ {{H \over N} \cdot {{{S_a}} \over {{S_a} \cdot \cos({\alpha _s})}} \cdot \sum\limits_{j=1}^N {({\rho _{{B_{N,j}}}} \cdot(1 - {b_j}))} } \right]\gamma }}$ | (15) |
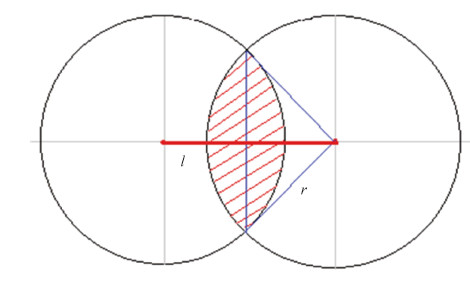
当观测线与光照线重合时,有sn=1和s=1,即可以看到的即是被照亮的。相交比例bn可用如图 2所示的两圆重叠面积Aoverlap和Sa的比值表示:
| ${b_n}=\left\{ \begin{array}{l}\frac{{2\left[ {\frac{{\arccos(\frac{{{l_n}}}{{2r}})}}{\pi } \cdot \pi {r^2} - \frac{{{l_n}}}{2} \cdot \sqrt {{r^2} - {{\left({\frac{{{l_n}}}{2}} \right)}^2}} } \right]}}{{\pi {r^2}}},{l_n} <2r\\0,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{l_n} \ge 2r{\rm{ }}\end{array} \right.$ | (16) |
式中,ln为第n层两圆心距离,r为圆半径。
4 模型模拟与验证
4.1 方向亮温计算
若已知场景四组分发射率及温度数据,则场景方向性热辐射亮温Tb满足下式:
| $ {T_b}^4={e_{\rm{v}}} \cdot({T_{v1}}^4 \cdot {L_1}+{T_{v2}}^4 \cdot {L_2})+{e_s} \cdot({T_{s1}}^4 \cdot {s_1}+{T_{s2}}^4 \cdot {s_2})$ | ((17)) |
式中,ev和es表示植被和土壤组分发射率;TL和Ts表示植被和土壤温度;L1和L2分别表示有光照和无光照的植被可视概率,S1和S2分别表示有光照和无光照土壤的可视概率。
4.2 模型验证
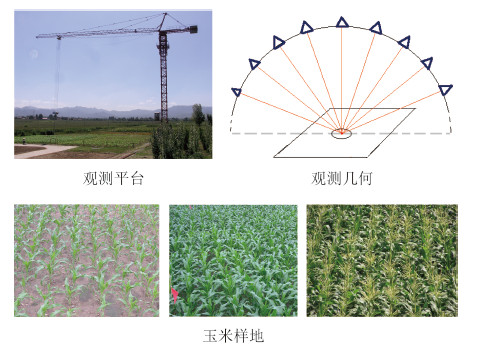
实验数据取自2010年6月- 7月在河北省怀来实验场测量的玉米热红外多角度数据,实验共进行了玉米样地3个生长期(离散期、垄行期、均一期)的热红外多角度数据的测量(图 3),垄为东西走向,平均行间距为60 cm,株间距为38 cm。每期均测量顺垄(近似垂直太阳主平面)、垂直垄(近似太阳主平面)两个平面,同步测量了样地四组分的温度数据以及LAI等。
红外辐射测温仪视场角10°,光谱相应范围7—14 um,测温仪安装在高架塔3维测量平台上,垂直观测高度17 m,天底观测尺度为约3 m直径的圆(含玉米5—6垄)。观测天顶角-60°至60°,角度间隔10°。测量平台完成一个平面的测量需时间8- 10 min,每个平面测量的中间时刻测量太阳的高度角和与垄向的夹角。叶片与土壤的宽波段发射率由多波段红外波谱仪测量数据提取,组分温度数据采用手持红外辐射计测量。冠层亮温观测值中包含了大气下行辐射经地表散射部分,因此观测数据值减掉了大气下行辐射测量亮温与地表平均反射率的乘积值,地表在热红外波段的平均反射率以0.03近似。
离散分布期,植株之间相互无遮蔽;垄行分布期,玉米高度接近1 m,玉米叶面积指数为1.56,处于半封垄状态。均一分布期,玉米高度超过1.6米,玉米叶面积指数为2.88,垄向以及垂直垄向相邻植株间叶片均出现遮蔽。表 1给出了各生长期植株参数,表 2给出了各生长期场景四组分温度及观测几何数据。
表 1 场景主要参数
Table 1 Main parameters of corn canopy
| 生长期 | LAI | 行间距 /cm | 株间距/cm | 株高/cm | 杆高/cm | 杆直径/cm |
| 离散期 | 0.39 | 60 | 38 | 30 | 15 | 0.92 |
| 垄行期 | 1.56 | 60 | 38 | 106 | 57 | 2.43 |
| 均一期 | 2.88 | 60 | 38 | 157 | 97 | 2.8 |
表 2 组分温度与观测几何数据
Table 2 Component temperature and observation geometry data
| 生长期 | 测量平面 | 光照 土壤温度/℃ | 阴影 土壤温度/℃ | 光照 叶片温度/℃ | 阴影 叶片温度/℃ | 太阳天顶角/(°) | 与垄向夹角/(°)(顺时针方向) |
| 离散期 | 太阳主平面 (垂直垄向) | 36.5 | 26.4 | 25.5 | 24.8 | 20 | 91 |
| 垂直主平面 (顺垄向) | 36.6 | 26.8 | 25.5 | 24.8 | 20 | 96 | |
| 垄行期 | 太阳主平面 (垂直垄向) | 37.8 | 27.4 | 25.6 | 24.8 | 21 | 89 |
| 垂直主平面 (顺垄向) | 37.7 | 26.8 | 25.5 | 24.6 | 21 | 95 | |
| 均一期 | 太阳主平面 (垂直垄向) | 35.8 | 27.4 | 27.7 | 26.5 | 22 | 86 |
| 垂直主平面 (顺垄向) | 35.6 | 27.7 | 27.5 | 26.3 | 22 | 94 |
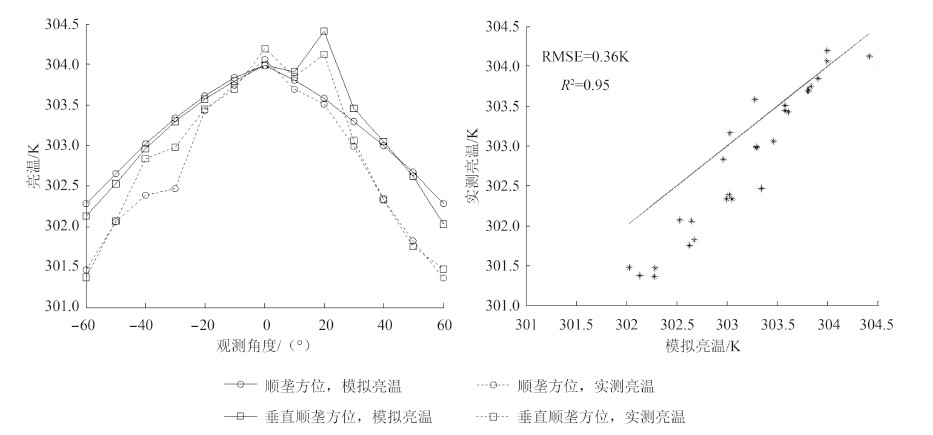
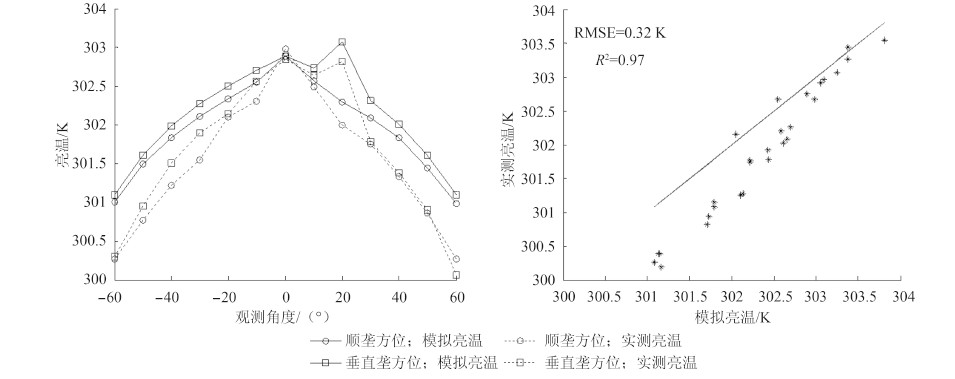
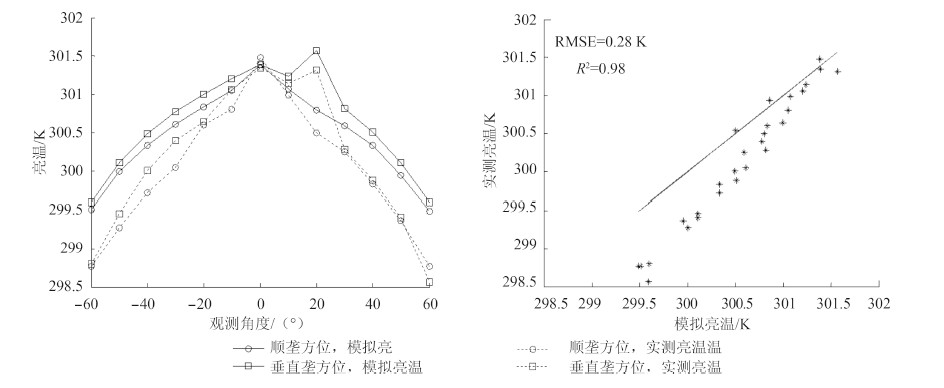
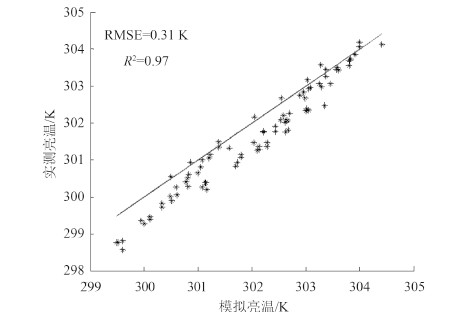
从3个生长期的观测数据与模拟结果的对比发现,模型结果与观测数据偏差较小,RMSE为0.31 K,相关系数达0.97。从每个时期的数据对比图(图 4-图 7)可以看出,模型模拟的方向性亮温变化趋势与观测数据一致,热点效应在观测数据中有明显的体现,模型也能准确模拟其特征。相比较而言,模型的热点效应比实际观测略偏高,随着观测天顶角的增加模拟值偏高于观测值,这说明在天顶角较大时,模型对冠层的孔隙率的估算略偏低,另外,热点时由于仪器平台吊篮遮挡了部分观测视场(正方形吊篮边长为40cm),导致观测的热点效应有所下降。
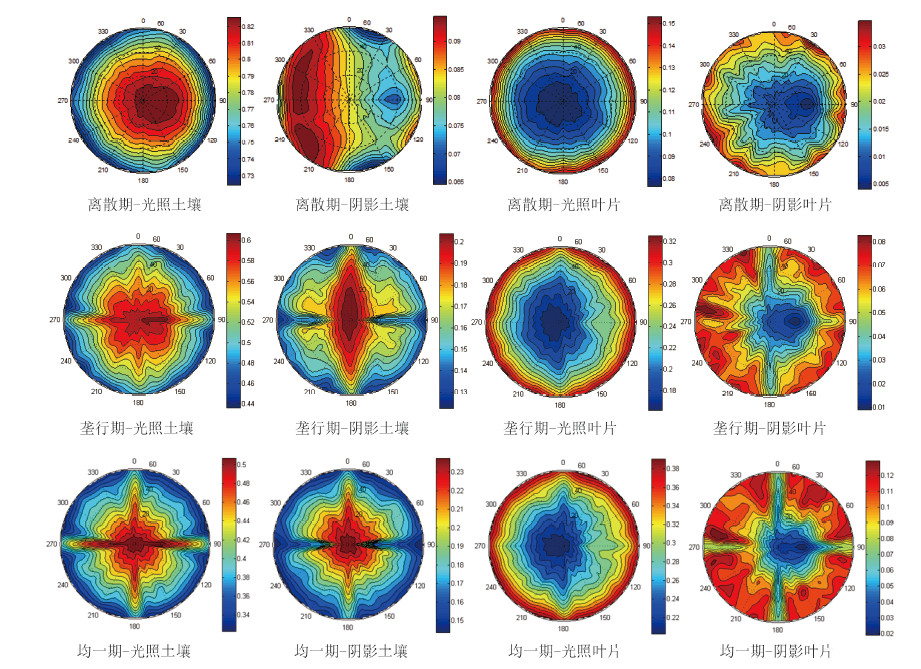
通过设定理念株和空间分布参数,模型可计算不同植被场景任意观测几何下的视场四组份比例分布(图 8),模型计算的三生长期下玉米植被场景不同方位不同天顶角观测方向的视场四组份比例分布。植被场景任意观测几何下的视场四组份比例结合Li-strahler几何光学模型有望进一步应用于复杂地表条件下的地表返照率的计算。
5 结论
本文通过构建理念植株,给定植株空间的分布,基于冠层双向孔隙率的计算来研究非均一冠层的热辐射方向性。通过与实地测量数据的比对,模型能够准确模拟植被场景的方向亮温变化规律,存在的偏差主要来源:(1)描述理念株的各个参数应该是观测场景内所有植株对应参数的平均值,本文玉米理念样株的构造是利用了样地10植株的测量数据平均得到,另外,由于缺失玉米叶片角度分布的实测数据,理念株叶片角度分布上采用了球面分布来近似,因此,理念株构建上的偏差对模拟结果有一定的影响;(2)模拟中并没有考虑土壤层的粗糙度以及玉米叶片狭长属性特征;(3)植被冠层内以及植被冠层与地表之间的热辐射多次散射会导致场景的热辐射方向性变的略微平滑,在模拟中并没有考虑多次散射项的贡献。
通过理念株来构建观测场景,计算量不受场景大小的影响,理论上场景大小可以任意设定;场景的模拟结果在随机点数达到500以上基本稳定,一般取1000随机点即可得到理想结果,模型的运行速度较快;可以通过构建不同植被类型的理念株,并按一定比例进行混合来组建多植被类型的混合场景,进行混合场景的热辐射方向性模拟;植被场景由理念株按给定的空间分布来构建,因此热辐射方向性计算过程不受植被类型和植株密度所限制;模型可输出场景任意观测几何下的四组份面积比例,计算结果进一步结合Li-strahler几何光学模型可有望应用于复杂地表条件下的地表返照率的计算。
参考文献(References)
-
Chen L F, Liu Q H, Fan W J, Li X W, Xiao Q, Yan G J , Tian G L.2002.A bi-directional gap model for simulating the directional thermal radiance of row crops. Science in China Series D:Earth Sciences, 45 (12) : 1087–1098 . [DOI:10.1360/02yd9106]
-
Du Y M. 2006. A study of seasonal variation and models of directional thermal radiance over row-planted winter wheat canopy. Institute of Remote Sensing Applications, Chinese Academy of Science
-
Jackson R D, Reginato R J, Printer P J , Idso S B.1979.Plant canopy information extraction from composite scene reflectance of row crops. Applied Optics, 18 (22) : 3775–3782 . [DOI:10.1364/AO.18.003775]
-
Jupp D L B, Strahler A H.1991.A hotspot model for leaf canopies. Remote Sensing of Environment, 38 (3) : 193–210 . [DOI:10.1016/0034-4257(91)90089-O]
-
Kimes D S, Kirchner J A.1983.Directional radiometric measurements of row-crop temperatures. International Journal of Remote Sensing, 4 (2) : 299–311 . [DOI:10.1080/01431168308948548]
-
Kuusk A. 1991. The hot spot effect in plant canopy reflectance.//Myneni R B and Ross J, eds. Photon-Vegetation Interactions:Applications in Optical Remote Sensing and Plant Ecology. Berlin Heidelberg:Springer-Verlag:139-159[DOI:10.1007/978-3-642-75389-3_5]
-
Li X, Strahler A H.1988.Modeling the gap probability of a discontinuous vegetation canopy. IEEE Transactions on Geoscience and Remote Sensing, 26 (2) : 161–170 . [DOI:10.1109/36.3017]
-
Liu Q H, Huang H G, Qin W, Fu K H, Li X W.2007.An extended 3-D radiosity-graphics combined model for studying thermal-emission directionality of crop canopy. IEEE Transactions on Geoscience and Remote Sensing, 45 (9) : 2900–2918 . [DOI:10.1109/TGRS.2007.902272]
-
Qin W H , Gerstl S A W.2000.3-D scene modeling of semidesert vegetation cover and its radiation regime. Remote Sensing of Environment, 74 (1) : 145–162 . [DOI:10.1016/S0034-4257(00)00129-2]
-
Strahler A H , Jupp D L B.1990.Modeling bidirectional reflectance of forests and woodlands using Boolean models and geometric optics. Remote Sensing of Environment, 34 (3) : 153–166 . [DOI:10.1016/0034-4257(90)90065-T]
-
Verstraete M M, Pinty B , Dickinson R E.1990.A physical model of the bidirectional reflectance of vegetation canopies:1:Theory. Journal of Geophysical Research, 95 (D8) : 11755–11765 . [DOI:10.1029/JD095iD08p11755]