压电驱动器具有位移分辨率高、响应快等优点[1-2],经常被用作原子力显微镜等微纳操作与成像工具的驱动单元[3-5]。然而,由于压电驱动器固有的迟滞特性,以及蠕变和热漂移等其他干扰的影响,导致其实际位移和期望位移之间存在着偏差,从而降低了压电驱动器的定位精度。迟滞特性导致压电驱动器输出位移和输入电压之间产生复杂的非线性关系。此外,迟滞特性还具有记忆性[6],具体体现在其输出位移不仅和当前时刻的输入电压值相关,还和输入电压的变化情况相关[7],该性质导致驱动器在电压增大和减小阶段产生的位移不一致,其典型表现为输出位移和输入电压之间形成一个迟滞环[8]。另外,迟滞非线性会随着输入电压频率的增大而更为显著。因此,迟滞特性对压电驱动器的定位精度产生了严重的影响。
针对上述问题,研究人员尝试建立了多种压电驱动器迟滞模型,并据此对迟滞非线性进行补偿。总体而言,这些模型可以分为基于机理的模型和基于数据的模型。Preisach模型、Duhem模型、Maxwell模型等都是基于机理而建立的模型。具体而言,Xiao等[9]基于Preisach逆模型对变频率迟滞特性进行建模和补偿;Chen等[10]基于Duhem模型对压电驱动器动态迟滞现象进行建模;Liu等[11]基于Maxwell模型实现了对压电驱动器的迟滞建模。然而,基于机理的建模方法在进行参数辨识时需要大量计算,且其应用受限于模型的具体形式。与此相反,基于数据的建模方法不考虑模型具体的物理意义,而是利用神经网络或模糊系统等方式,通过数据驱动建立模型。例如,Cheng等[12]使用Takagi-Sugeno模糊模型准确模拟了压电驱动器的迟滞特性。此外,研究人员也建立了各种神经网络模型来拟合迟滞特性。例如:Ling等[13]改进了传统的神经网络模型对迟滞非线性进行在线辨识;Zhao等[14]利用埃尔曼神经网络对压电驱动器进行建模。在各种不同的神经网络模型当中,循环神经网络(recurrent neural network, RNN)[15]由于其所具有的特殊结构,更适合于辨识具有记忆特性的系统。例如:Xie等[16]利用传统的循环神经网络构建逆模型,在高频电压驱动时得到更为准确的模型;Wu等[17]使用门控循环单元对压电驱动器进行建模,并利用反向传播神经网络提升了模型对频率特性的泛化能力。尽管利用迟滞模型能够减弱迟滞特性对压电驱动器跟踪精度的影响,但是其他动态特性以及外部扰动仍会对驱动器的性能造成影响。为此,需要进一步设计控制器对压电驱动器进行跟踪控制。许多研究人员采用模型预测控制器对驱动器进行跟踪控制。例如:Cheng等[12]分别设计了基于神经网络和Takagi-Sugeno模糊模型的模型预测控制器。Xie等[16]在循环神经网络逆模型的基础上,采用预测控制器对压电驱动器进行跟踪控制。此外,研究人员也针对压电驱动器设计了各种滑模控制策略。例如:Chouza等[18]提出了带有扰动估计的滑模控制方法;Soleymanzadeh等[19]使用自适应滑模控制提高了压电驱动器的跟踪精度。
基于上述工作,本文针对压电驱动器的迟滞建模与跟踪控制展开研究,提出一种基于循环神经网络逆模型的单神经元自适应控制方法,以提高驱动器的定位精度。具体而言,本文首先基于循环神经网络建立了压电驱动器的迟滞逆模型,该模型由迟滞子模型和频率子模型串联而成[20]。在此基础上,利用该逆模型对驱动器进行前馈补偿,并设计了单神经元自适应比例−积分−微分(proportional-integral-derivative,PID)控制器,从而消除模型误差以及蠕变和热漂移等其他干扰对驱动器跟踪性能的影响。本文通过实验验证了建模精度和控制器的跟踪性能。
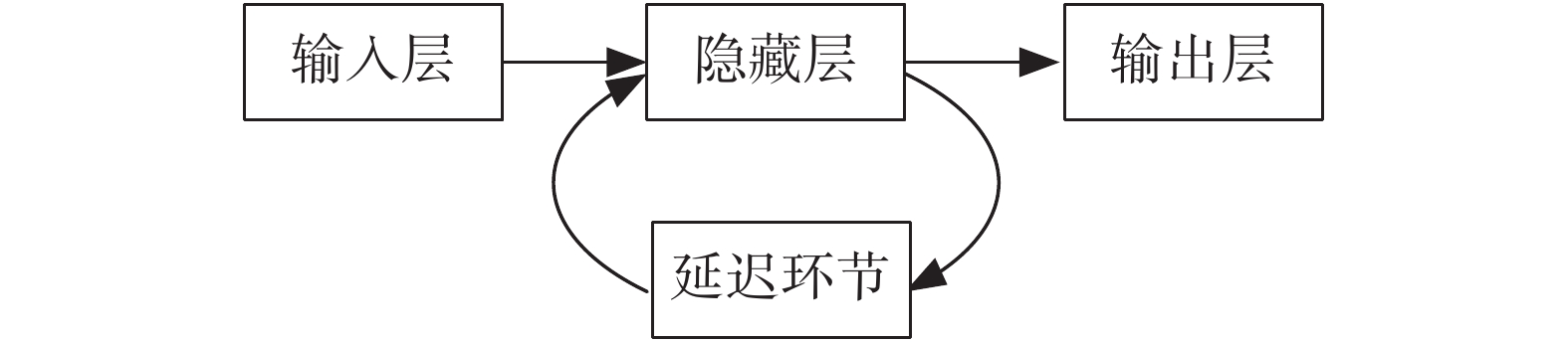
1 基于循环神经网络迟滞逆模型循环神经网络是一种以序列数据作为输入的神经网络。与普通的神经网络相比,循环神经网络在每个隐藏层神经元上包含了一个如图1所示的反馈输入,这使得循环神经网络中隐藏层神经元的输入不仅包含当前时刻的输入,而且和过去一段时间的输入也有一定的相关性,因此循环神经网络拥有“记忆性”。
|
Download:
|
| 图 1 循环神经网络的结构 Fig. 1 Structure of recurrent neural network | |
压电驱动器的输出位移不仅与当前时刻的输入电压相关,而且与输入电压的变化过程密切相关。因此,对于这种输入数据是序列模式,且对于过去时刻的输入数据具有一定依赖性的系统,采用循环神经网络进行建模能够得到更加符合压电驱动器迟滞特性的精确模型[21]。同时,不同频率的输入电压也会对压电驱动器的输出位移产生影响,迟滞非线性会随着频率的增大而更加严重。因此,本文设计了一种级联结构,将压电驱动器的迟滞逆模型拆分为迟滞子模型和频率子模型两部分,其中,迟滞子模型用来拟合迟滞非线性,而频率子模型则将频率相关性引入到模型中,由于采用了循环神经网络结构,所建立的模型更加符合迟滞效应的记忆特性。所建立的逆模型的结构如图2所示,其中,
具体而言,首先采用循环神经网络建立迟滞子模型,其结构如图3所示。在该子模型中,当前时刻驱动器的位移
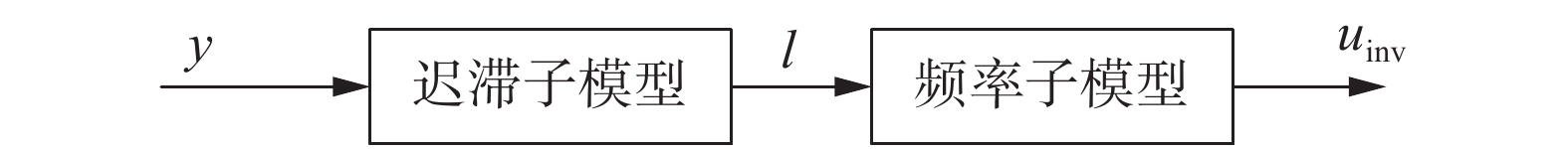
|
Download:
|
| 图 2 压电驱动器迟滞逆模型结构 Fig. 2 Structure of the inverse hysteresis model of the piezoelectric actuator | |

|
Download:
|
| 图 3 基于RNN的迟滞子模型结构 Fig. 3 Structure of the hysteresis submodel based on RNN | |
随后,根据单个循环神经网络神经元的数学模型,可以得到输入层节点和隐藏层节点之间的关系[22]:
| $h\left( t \right) = \tanh \left( {{\alpha _{{h}}}h\left( {t - 1} \right) + {\beta _h}y\left( t \right) + {\lambda _h}} \right)$ | (1) |
| $\tanh \left( x \right) = \frac{{{{\rm{e}}^x} - {{\rm{e}}^{ - x}}}}{{{{\rm{e}}^x} + {{\rm{e}}^{ - x}}}}$ | (2) |
式中:
| $l\left( t \right) = p\left( {{\theta _{{h}}}h\left( t \right) + {\gamma _h}} \right)$ | (3) |
| $\begin{aligned}p\left( x \right) = \left\{\begin{aligned} &{x,\quad x \geqslant 0} \\ &{0,\quad x < 0} \end{aligned}\right.\end{aligned}$ | (4) |
式中:
| $\begin{gathered} l\left( t \right) = p({\theta _{{h}}}\tanh ({\alpha _{{h}}}h(t - 1) + {\beta _h}y(t) + {\lambda _h}) + {\gamma _h}) \end{gathered} $ | (5) |
此外,本文中频率子模型和迟滞子模型采用结构相同的循环神经网络,于是可以得到频率子模型的输入输出关系:
| $\begin{gathered} {u_{\rm{inv}}}\left( t \right) = p({\theta _{f}}\tanh ({\alpha _{f}}{h_f}(t - 1) + {\beta _{f}}l(t) + {\lambda _{f}}) + {\gamma _{f}}) \end{gathered} $ | (6) |
式中:
根据式(5)、(6)即可得到压电驱动器位移和电压之间的关系,随后,采用Levenberg-Marquart算法[23]对网络进行训练,辨识网络中的权重和偏置,即可得到迟滞逆模型的具体形式。
2 组合控制器设计在得到基于循环神经网络的迟滞逆模型之后,利用其对压电驱动器进行前馈补偿,能够减弱迟滞非线性对驱动器跟踪精度的影响。然而,建模误差以及蠕变、热漂移等其他干扰仍然在实际实验中影响压电驱动器的跟踪性能。因此,需要进一步设计相应的控制器提高压电驱动器的跟踪精度。
单神经元自适应PID控制器是一种利用神经元的学习特性和增量式PID的控制器[24],神经元的学习特性可以通过自适应的方式得到更优的PID控制参数。因此,本文在迟滞逆模型前馈的基础上,设计了单神经元自适应PID控制器进一步提升压电驱动器的跟踪精度,控制系统的结构如图4所示。

|
Download:
|
| 图 4 控制系统的结构 Fig. 4 Structure of the control system | |
图4中,
| $u\left( t \right) = {u_{\rm{inv}}}\left( t \right) + {u_c}\left( t \right)$ | (7) |
具体而言,自适应控制器通过以下迭代方式产生输出:
| ${u_c}\left( t \right) = {u_c}\left( {t - 1} \right) + K\sum\limits_{i = 1}^3 {w'_i\left( t \right){\xi _i}\left( t \right)} $ | (8) |
式中:
| $w_i'\left( t \right) = \frac{{{w_i}\left( t \right)}}{{\displaystyle\sum\limits_{i = 1}^3 {\left| {{w_i}\left( t \right)} \right|} }}$ | (9) |
| ${\xi _1}\left( t \right) = e\left( t \right) - e\left( {t - 1} \right)$ | (10) |
| ${\xi _2}\left( t \right) = e\left( t \right)$ | (11) |
| ${\xi _3}\left( t \right) = e\left( t \right) - 2e\left( {t - 1} \right) + e\left( {t - 2} \right)$ | (12) |
式中:
| $\begin{gathered} {w_i}\left( t \right) = {w_i}(t - 1) + {\eta _i}e(t) \times {u_c}(t - 1)(2e(t) - e(t - 1)) \end{gathered} $ | (13) |
式中:
| ${{e}}\left( t \right) = r\left( t \right) - y\left( t \right)$ | (14) |
在单神经元自适应PID控制器中,神经元增益
| $\left\{ {\begin{aligned} &K\left( t \right) = K\left( {t - 1} \right) + \varphi \frac{{K\left( {t - 1} \right)}}{{{T_v}\left( {t - 1} \right)}} \\ &{\rm{sgn}} \left[ {e\left( t \right)} \right] = {\rm{sgn}} [e\left( {t - 1} \right)] \end{aligned}} \right.$ | (15) |
| $\left\{ {\begin{aligned} &K\left( t \right) = 0.75K\left( {t - 1} \right) \\ &{\rm{sgn}} \left[ {e\left( t \right)} \right] \ne {\rm{sgn}} \left[ {e\left( {t - 1} \right)} \right] \end{aligned}} \right.$ | (16) |
式中
| ${\rm{sgn}} \left( x \right) = \left\{ {\begin{aligned} {1,\quad x > 0} \\ {0,\quad x = 0} \\ { - 1,\quad x < 0} \end{aligned}} \right.$ | (17) |
| $\begin{gathered} {T_v}\left( t \right) = {T_v}\left( {t - 1} \right) + \mu {\rm{sgn}} [\left| {\Delta e\left( t \right)} \right| - \\ {T_v}\left( {t - 1} \right)\left| {{\Delta ^2}\left( {e\left( t \right)} \right)} \right|] \\ \end{gathered} $ | (18) |
式中:
为了验证提出方法的有效性,本文分别对模型的拟合效果和控制系统的跟踪性能进行了实验验证。本文采用的激励信号为不同频率的正弦波信号,激励信号经过电压放大器后作为输入驱动压电驱动器。电压放大器采用的是Physik Instrument(PI)公司的E505.00电压放大器,压电驱动器选用的是PI公司的P-517.3CL商用压电驱动器,上位机采用的是基于Matlab/Simulink环境电压放大器和上位机都连接到研华科技有限公司的PCI-1716输入输出数据采集卡进行数据通信。本文在实验中所选取的采样时间为0.025 ms。
3.1 迟滞逆模型训练为了得到迟滞逆模型的具体参数,首先对迟滞子模型进行训练。在低频输入电压的驱动下,频率变化对压电驱动器造成的影响并不明显,因此,对于迟滞子模型,本文选取的激励信号的频率为1 Hz,隐藏层神经元的数量被设置为5。本文采用均方误差作为损失函数,其具体表达式为
| $J\left( {{W}} \right) = \frac{1}{{2N}}{\left( {{{U}} - {{L}}} \right)^{\rm{T}}}\left( {{{U}} - {{L}}} \right)$ | (19) |
式中:
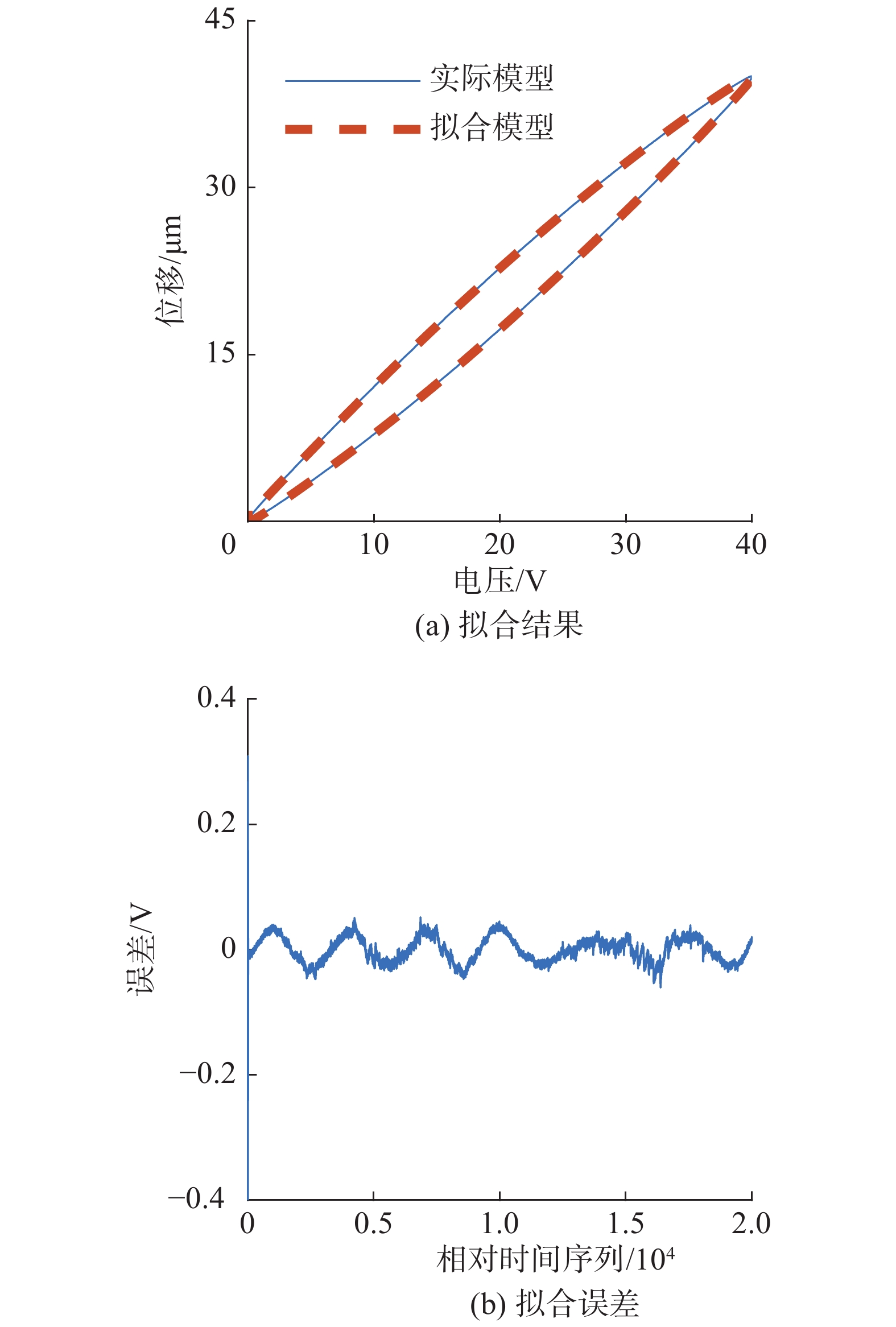
迟滞子模型的拟合效果和训练误差如图5所示。图5(a)为迟滞子模型的拟合效果,蓝色实线为实际测量数据形成的迟滞环,红色虚线为迟滞子模型的模型输出;图5(b)为迟滞子模型输出与实际系统输出位移之间的误差。训练结果表明了,本文所设计的迟滞子模型能够准确拟合迟滞非线性。
|
Download:
|
| 图 5 迟滞子模型训练结果 Fig. 5 Training results of the hysteresis submodel | |
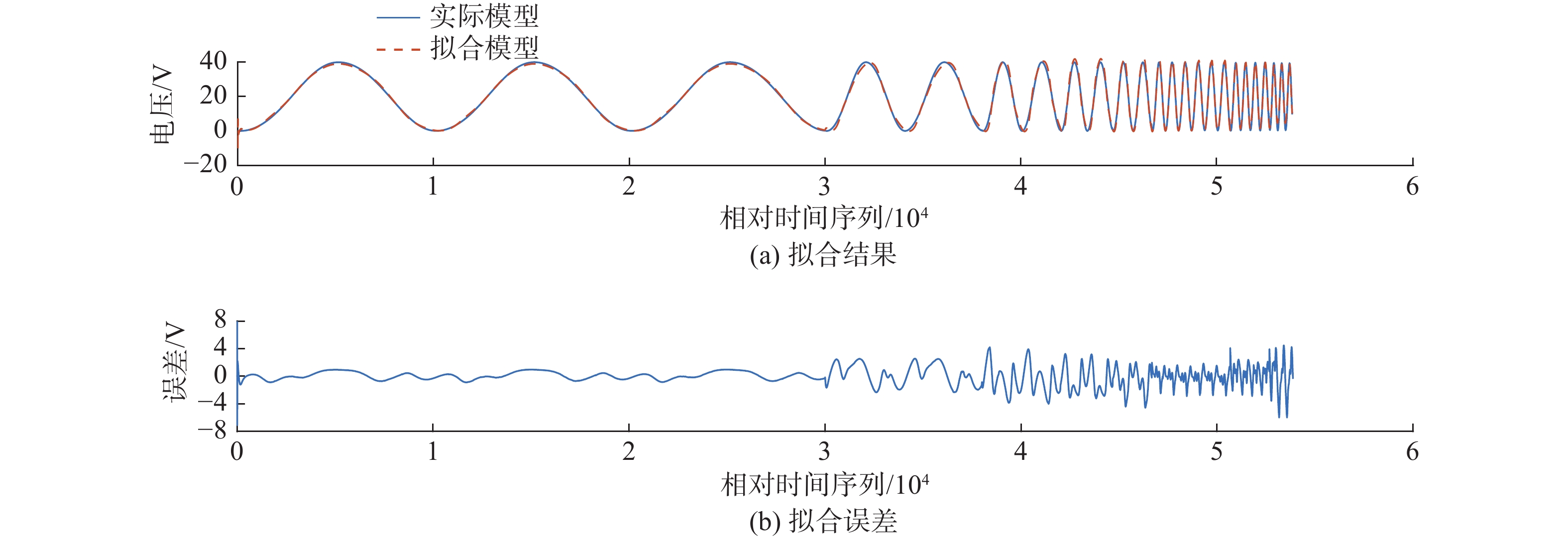
在得到迟滞子模型的具体形式之后,以迟滞子模型的输出作为频率子模型的输入,对频率子模型进行训练,频率子模型的隐藏层神经元数目为8个,选取的损失函数与迟滞子模型相同。对于频率子模型,选取激励信号频率分别为2、5、10、15、20、30、40、50 Hz的数据作为训练组。频率子模型的训练结果如图6所示,其中,(a)图为频率子模型的拟合结果,蓝色实线为实际电压随时间的变化曲线,红色虚线为通过循环神经网络拟合出的电压变化曲线,(b)图为模型输出与实际系统输出之间的误差。训练结果表明,本文设计的迟滞逆模型能够准确拟合压电驱动器在不同频率下的迟滞特性。
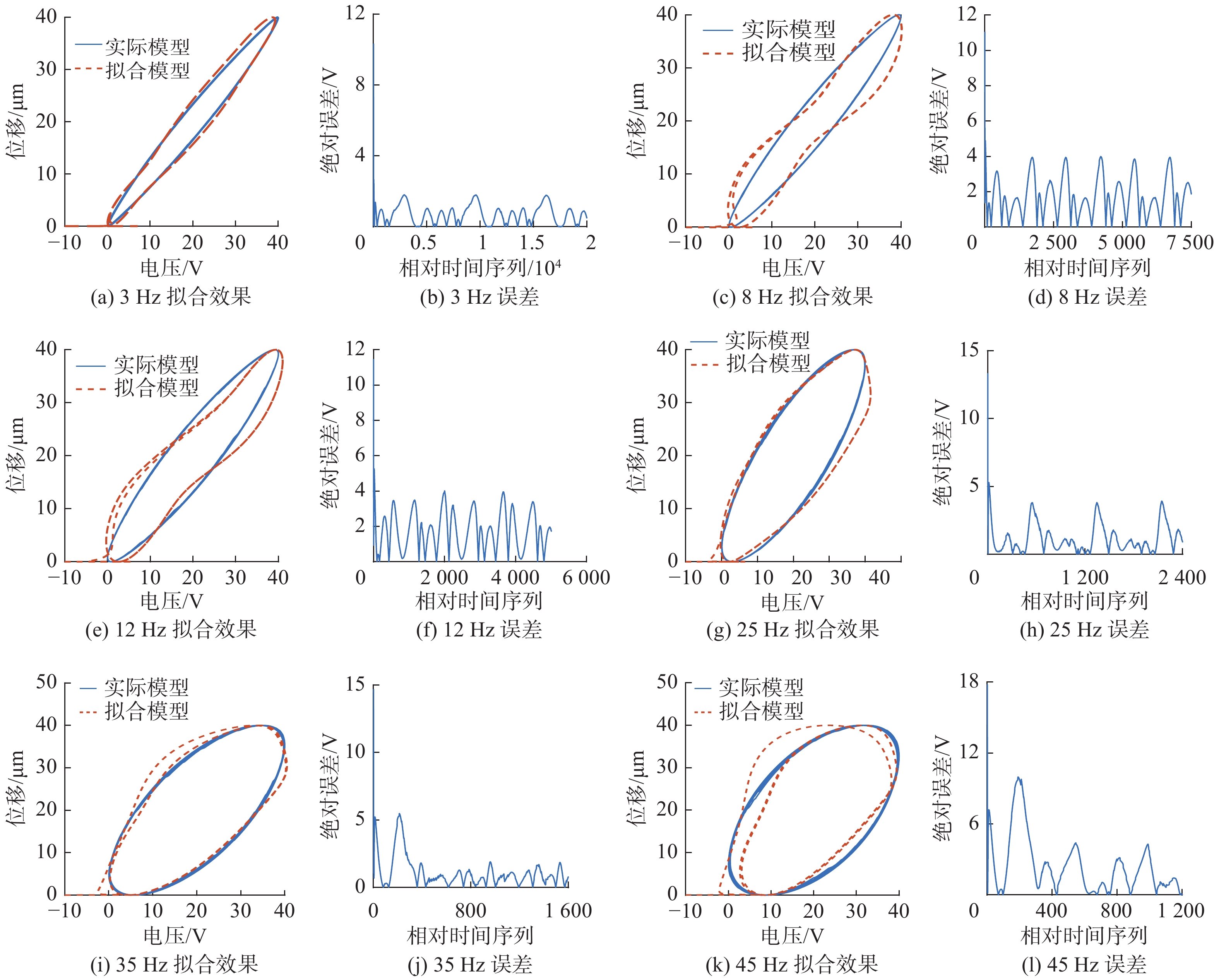
3.2 迟滞逆模型性能测试为了测试模型的泛化能力,本文选取了未进行训练的数据对建模结果进行测试。所选取激励信号的频率分别为3、8、12、25、35和45 Hz。测试结果如图7所示,其中,在拟合效果图中,蓝色实线是实际系统的迟滞环,红色虚线为模型拟合出的迟滞环,在拟合误差图中,拟合误差为拟合模型和实际模型之间的绝对误差。结果表明,由于所建立的模型具有记忆存储能力以及频率相关性,模型能够在一定程度上拟合未用于训练的数据,但是存在明显的误差。因此,需要进一步通过单神经元自适应控制,实现驱动器对于期望轨迹的准确跟踪。
|
Download:
|
| 图 6 频率子模型训练结果 Fig. 6 Training results of the frequency submodel | |
|
Download:
|
| 图 7 测试数据的模型拟合结果和误差 Fig. 7 Model fitting results and errors of the testing data | |
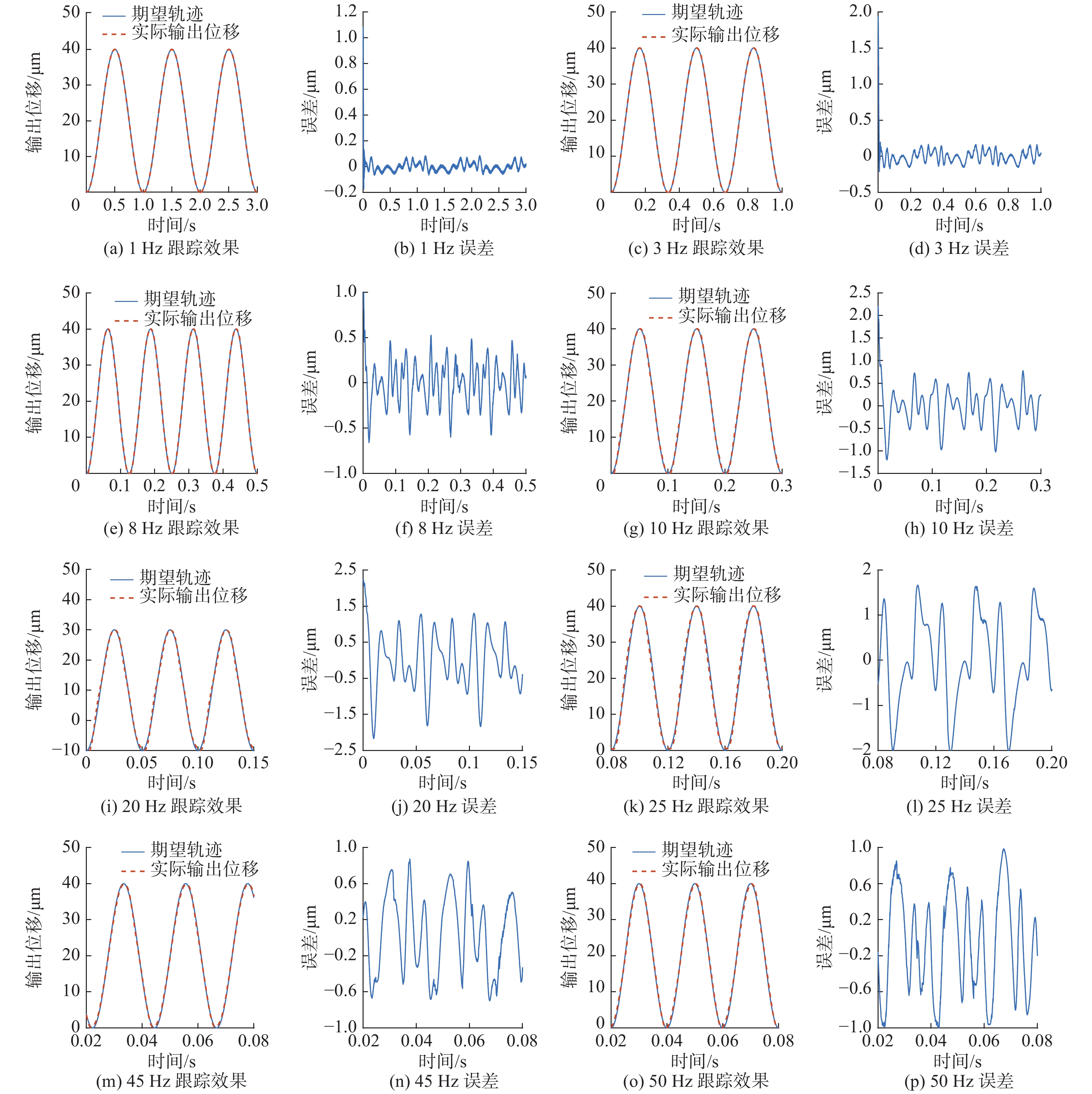
在验证了循环神经网络模型的拟合效果后,本文针对设计的控制系统的跟踪精度进行验证,所选取的激励信号为
|
Download:
|
| 图 8 控制系统的跟踪效果和跟踪误差 Fig. 8 Tracking performance and tracking error of the control system | |
本文设计了一种基于循环神经网络的建模方法,建立了具有记忆特性和频率相关性的压电驱动器迟滞逆模型,该模型能够准确模拟迟滞效应,并具有一定的泛化能力。在此基础上,设计了逆模型前馈补偿与单神经元自适应反馈控制相结合的控制策略,有效地消减了压电驱动器的跟踪误差。实验结果验证了所建立模型的准确性以及所设计控制方法的跟踪性能。未来的研究工作将关注于实现模型参数的在线辨识。
| [1] |
张鑫, 孙小飞, 周文松, 等. 基于压电阻抗和主成分分析的斜拉索覆冰监测[J]. 哈尔滨工程大学学报, 2020, 41(12): 1765-1771. ZHANG Xin, SUN Xiaofei, ZHOU Wensong, et al. Monitoring of stay-cable icing based on electro-mechanical impedance and principal component analysis[J]. Journal of Harbin Engineering University, 2020, 41(12): 1765-1771. (  0) 0)
|
| [2] |
许延峰, 周天放, 蓝宇. 低频弯曲式水听器研究[J]. 应用科技, 2020, 47(1): 99-104. XU Yanfeng, ZHOU Tianfang, LAN Yu. Research on the low frequency curved hydrophone[J]. Applied science and technology, 2020, 47(1): 99-104. (  0) 0)
|
| [3] |
WU Yinan, FAN Zhi, FANG Yongchun, et al. An effective correction method for AFM image distortion due to hysteresis and thermal drift[J]. IEEE transactions on instrumentation and measurement, 2021, 70: 5004212. ( 0) 0)
|
| [4] |
黄心汉. 微装配机器人: 关键技术、发展与应用[J]. 智能系统学报, 2020, 15(3): 413-424. HUANG Xinhan. Microassembly robot: key technology, development, and applications[J]. CAAI transactions on intelligent systems, 2020, 15(3): 413-424. (  0) 0)
|
| [5] |
莫喜平, 刘永平. 纵向换能器的频率方程[J]. 哈尔滨工程大学学报, 2019, 40(7): 1245-1250. MO Xiping, LIU Yongping. Frequency equations for a longitudinal transducer[J]. Journal of Harbin Engineering University, 2019, 40(7): 1245-1250. (  0) 0)
|
| [6] |
GU Guoying, ZHU Limin, SU Chunyi, et al. Modeling of piezoelectric-actuated nanopositioning stages involving with the hysteresis[M]//RU Changhai, LIU Xinyu, SUN Yu. Nanopositioning Technologies: Fundamentals and Applications. Cham: Springer, 2016: 183−212.
( 0) 0)
|
| [7] |
ANG W T, GARMON F A, KHOSLA P K, et al. Modeling rate-dependent hysteresis in piezoelectric actuators[C]//Proceedings 2003 IEEE/RSJ International Conference on Intelligent Robots and Systems. Las Vegas, USA, 2003: 1975−1980.
( 0) 0)
|
| [8] |
STEPANENKO Y, SU Chunyi. Intelligent control of piezoelectric actuators[C]//Proceedings of the 37th IEEE Conference on Decision and Control. Tampa, USA, 1998: 4234−4239.
( 0) 0)
|
| [9] |
XIAO Shunli, LI Yangmin. Modeling and high dynamic compensating the rate-dependent hysteresis of piezoelectric actuators via a novel modified inverse preisach model[J]. IEEE transactions on control systems technology, 2013, 21(5): 1549-1557. DOI:10.1109/TCST.2012.2206029 ( 0) 0)
|
| [10] |
CHEN Hui, TAN Yonghong, ZHOU Xingpeng, et al. Identification of dynamic hysteresis based on duhem model[C]//2011 Fourth International Conference on Intelligent Computation Technology and Automation. Shenzhen, China, 2011: 810−814.
( 0) 0)
|
| [11] |
LIU Yanfang, SHAN Jinjun, GABBERT U, et al. Hysteresis and creep modeling and compensation for a piezoelectric actuator using a fractional-order Maxwell resistive capacitor approach[J]. Smart materials and structures, 2013, 22(11): 115020. DOI:10.1088/0964-1726/22/11/115020 ( 0) 0)
|
| [12] |
CHENG Long, LIU Weichuan, HOU Zengguang, et al. An adaptive Takagi-Sugeno fuzzy model-based predictive controller for piezoelectric actuators[J]. IEEE transactions on industrial electronics, 2017, 64(4): 3048-3058. DOI:10.1109/TIE.2016.2644603 ( 0) 0)
|
| [13] |
LING Jie, FENG Zhao, ZHENG Dongdong, et al. Robust adaptive motion tracking of piezoelectric actuated stages using online neural-network-based sliding mode control[J]. Mechanical systems and signal processing, 2021, 150: 107235. DOI:10.1016/j.ymssp.2020.107235 ( 0) 0)
|
| [14] |
ZHAO Xinlong, SHEN Shuai, SU Liangcai, et al. Elman neural network-based identification of rate-dependent hysteresis in piezoelectric actuators[J]. Journal of intelligent material systems and structures, 2020, 31(7): 980-989. DOI:10.1177/1045389X20905987 ( 0) 0)
|
| [15] |
SERVAN-SCHREIBER D, CLEEREMANS A, MCCLELLAND J L. Learning sequential structure in simple recurrent networks[M]//TOURETZKY D S. Advances in Neural Information Processing Systems 1. San Francisco: Morgan Kaufmann Publishers Inc., 1989: 643−652.
( 0) 0)
|
| [16] |
XIE Shengwen, REN Juan. Predictive control of nano-positioning stage using recurrent-neural-network-based inversion model[C]//2019 IEEE 58th Conference on Decision and Control (CDC). Nice, France, 2019: 7764−7769.
( 0) 0)
|
| [17] |
WU Yinan, FANG Yongchun, LIU Cunhuan, et al. Gated recurrent unit based frequency-dependent hysteresis modeling and end-to-end compensation[J]. Mechanical systems and signal processing, 2020, 136: 106501. DOI:10.1016/j.ymssp.2019.106501 ( 0) 0)
|
| [18] |
CHOUZA A, BARAMBONES O, CALVO I, et al. Sliding mode-based robust control for piezoelectric actuators with inverse dynamics estimation[J]. Energies, 2019, 12(5): 943. DOI:10.3390/en12050943 ( 0) 0)
|
| [19] |
SOLEYMANZADEH D, GHAFARIRAD H, ZAREINEJAD M. Sensorless adaptive sliding mode position control for piezoelectric actuators with charge leakage[J]. Journal of intelligent material systems and structures, 2020, 31(1): 40-52. DOI:10.1177/1045389X19880009 ( 0) 0)
|
| [20] |
CHENG Long, LIU Weichuan, HOU Zengguang, et al. Neural-network-based nonlinear model predictive control for piezoelectric actuators[J]. IEEE transactions on industrial electronics, 2015, 62(12): 7717-7727. DOI:10.1109/TIE.2015.2455026 ( 0) 0)
|
| [21] |
LIN F J, SHIEH H J, HUANG P K, et al. Adaptive control with hysteresis estimation and compensation using RFNN for piezo-actuator[J]. IEEE transactions on ultrasonics, ferroelectrics, and frequency control, 2006, 53(9): 1649-1661. DOI:10.1109/TUFFC.2006.1678193 ( 0) 0)
|
| [22] |
SCHÄFER A M, ZIMMERMANN H G. Recurrent neural networks are universal approximators[C]//Proceedings of the 16th International Conference on Artificial Neural Networks. Athens, Greece, 2006: 632−640.
( 0) 0)
|
| [23] |
MORÉ J J. The Levenberg-Marquardt algorithm: implementation and theory[M]//WATSON G A. Numerical Analysis. Berlin, Heidelberg: Springer, 1997: 105−116.
( 0) 0)
|
| [24] |
XU Baochang, WU Jianzhang, CHEN Yongkun. An improved single neuron adaptive PID control algorithm[C]//2009 Fifth International Conference on Natural Computation. Tianjin, China, 2009: 558−562.
( 0) 0)
|
| [25] |
MARŠÍK J, STREJC V. Application of identification-free algorithms for adaptive control[J]. Automatica, 1989, 25(2): 273-277. DOI:10.1016/0005-1098(89)90081-2 ( 0) 0)
|
 2021, Vol. 16
2021, Vol. 16


