聚类^[1-3]是一种将数据集划分为若干组或类，使类内相似性最大，类间相似性最小的方法。现有文献提出，传统的聚类方法有k均值算法(k-means)^[4]、FCM算法^[5]、子空间聚类等。它们虽然简单，但缺乏处理复杂数据结构的能力，当样本为凸型时，这些算法对数据的处理有较好的效果，当样本空间为非凸时，算法容易陷入局部最优。为解决这一难题，谱聚类应运而生，它不受样本空间形状限制，聚类结果为全局最优解。在这些算法中，由于谱类算法便于实现、性能良好，已被广泛应用于图像分割、信息检索、人脸识别等领域。

谱聚类来源于图论中的最小切割问题^[6-8]。众所周知，数据通过非线性变换，将数据映射到高维特征空间后，数据将变得线性可分。因此，可以通过各种非线性变换，例如基于核的方法，提高高维特征空间中输入数据的特征表示能力。然而，以往的谱聚类方法一般只注重数据降维、优化时间复杂度等，而不是进一步提高数据特征的表示能力。在聚类任务中，数据的特征表示是至关重要的，通过反复的实验和一系列的工作，获得良好的数据特征表示是提高聚类准确度的保证。

ELM^[9-11]最初用于训练“广义”单隐层前馈神经网络(SLFN)，具有快速学习、良好的泛化能力和特征表示能力，被广泛应用于各种机器学习任务，如回归和分类等^[12-14]。近年来，ELM已经扩展到聚类，一般是在ELM获得的嵌入特征空间中进行聚类。ELM的隐层参数选择是随机的，和输入数据无关，与常用的反向传播训练算法相比，ELM最大限度地减小了训练误差和输出权的范数。根据Bartlett理论^[15]，最小化输出权值范数将产生更好的泛化能力。

自编码器(Auto Encoder AE)^[16-17]是深度学习中的一种无监督学习方法，能够从大量数据中自动学习到数据中的有效特征^[18-20]。传统自编码器就是一种在输出层重建输入数据并且结构对称的神经网络。常见的自编码器有降噪自编码器、稀疏自编码器、收缩自编码器和卷积自编码器等^[21]。使用自编码器进行特征提取要比特征分解快，并让目标值等于输入值，是一种尽可能复现输入信号的神经网络。

基于以上启发，本文将极限学习机(ELM)和自编码器(AE)结合起来改进谱聚类，提出了一种基于ELM-AE嵌入特征空间的谱聚类算法。

1 相关工作 1.1 谱聚类算法

谱聚类的概念起源于谱划分，将数据聚类转化为无向图的多路划分问题求解，尤其适用于数据集非凸的情况^[22-23]。假设数据集有n个数据点，目标是将所有数据点划分到c个簇中。谱聚类^[24]首先将数据点看作图的顶点，根据数据点成对相似性，先用欧氏距离计算距离矩阵，再使用高斯核函数将距离矩阵构造为相似矩阵并计算出所对应的拉普拉斯矩阵，谱方法是基于相似拉普拉斯矩阵的特征值和特征向量进行聚类的方法，将这些特征向量构造为低维的特征子空间，再在这个特征子空间上使用诸如k-means的聚类方法进行聚类，NJW谱聚类算法^[24]是一个典型的谱聚类算法。下面简单介绍该方法的原理。

给定一组数据集 ${{X}} = ({{{x}}_1},{{{x}}_2}, \cdots ,{{{x}}_n})$ ，要把这些数据点分成k类，使用谱聚类的一般过程是：

1)根据一定的相似矩阵生成方式构建样本的相似矩阵， ${{W}}$ 中的每一项表示每一对点之间的相似性:

${{{W}}_{{ij}}} = \exp ( - ||{{{x}}_{{i}}} - {{{x}}_{{j}}})|{|^2}/2{\sigma ^2})$

式中：当 ${{i}} = {{j}}$ 时， ${{{W}}_{ij}} = 0$ 。

2)根据相似矩阵 ${{W}}$ 计算度矩阵 ${{D}}$ ， ${{D}}$ 是一个对角矩阵，它的非零元素是 ${{W}}$ 的所有行元素(或者列元素)的总和：

${{{d}}_{{ii}}} = \sum _{{j}}{{{w}}_{{ij}}} $

3)根据 ${{D}}$ 和 ${{W}}$ 计算出拉普拉斯矩阵 ${{L}}$ ，定义拉普拉斯矩阵有很多种方法。非标准化的拉普拉斯矩阵为

${{L}} = {{D}} - {{W}}$

4)对 ${{L}}$ 进行标准化会产生更好的聚类效果，因此一般将拉普拉斯矩阵标准化形式表示为

${{{L}}_{{\rm{norm}}}} = {{{D}}^{{{ - 1} / 2}}}{{{LD}}^{ - 1/2}}$

还可以表示为

${{{L}}_{{\rm{norm}}}}{\rm{ = }}{{{D}}^{{\rm{ - }}1/2}}{{{WD}}^{{\rm{ - }}1/2}}$

5)接下来计算标准化后的拉普拉斯矩阵的前k个最小特征值对应的特征向量 ${{f}}$ ，将各自对应的特征向量 ${{f}}$ 组成的矩阵按行标准化，最终组成 $n \times k$ 维的特征矩阵 ${{F}}$ ；

6)将 ${{F}}$ 中的每一行作为一个k维的样本(共n个样本)，用k-means算法进行聚类得到最终聚类结果。

1.2 极限学习机自编码器

极限学习机自编码器^[19]是一种既可以再现输入数据也可以自行编码的神经网络方法，具有极限学习机的计算速度快、精确率高等特点。与传统的极限学习机相似，ELM-AE包含输入层、单隐含层以及输出层；不同的是，ELM-AE的输出层与输入层相等。给定一个训练样本，ELM-AE的模型结构包括M个输入层节点、J个隐层节点和M个输出层节点。ELM-AE的隐含层输出可以用式(1)表示：

$ {{h}} = {{g}}({{ax}} + {{b}}),\;\; {{{{a}}^{\rm{T}}}{{a}} = {{I}},{{{b}}^{\rm{T}}}{{b}} = 1} $

(1)

式中： ${{a}}$ 是输入层和隐含层之间的输入； ${{b}}$ 是隐含层的偏置。隐含层输出与ELM-AE的输出层之间的数值关系可以用式(2)表示：

$ {{h}}({{{x}}_{{i}}}){{\beta }} = {{{x}}_{{i}}}^{\bf{T}},\;\;{{i}}=1,2,\cdots ,N $

(2)

式中： ${{\beta }}$ 是连接隐含层和输出层的输出权值； ${{g}}( \cdot )$ 是激活函数。ELM-AE的目标是通过最小化正则化最小二乘估计成本函数得到输出权重，其公式为

$\mathop {\min }\limits_{{\beta }} \;\;{{{L}}_1} = \frac{1}{2}{\left\| {{\beta }} \right\|^2} + \frac{C}{2}{\left\| {{{X}} - {{H\beta }}} \right\|^2}$

(3)

式中：C是平衡经验风险与结构风险的参数。通过取 ${{{L}}_{{1}}}$ 对 ${{\beta }}$ 的偏导数并令其等于零，则输出权值矩阵 ${{\beta }}$ 为

${{\beta }} = \left\{ {\begin{array}{*{20}{c}} {{{\left( {\dfrac{{{I}}}{C} + {{{H}}^{\rm{T}}}{{H}}} \right)}^{ - 1}}{{{H}}^{\rm{T}}}{{X}},}\quad{N \geqslant J} \\ {{{{H}}^{^{\rm{T}}}}{{\left( {\dfrac{{{I}}}{C} + {{H}}{{{H}}^{\rm{T}}}} \right)}^{ - 1}}{{X}},}\quad{N < J} \end{array}} \right.$

(4)

2 ELM-AE特征空间的谱聚类算法

前面从理论层面分析了谱聚类及ELM-AE的特征提取方法。传统的谱聚类是将原始数据样本作为聚类初始值，而在实际应用中数据通常冗余且复杂，能够从原始数据中充分挖掘内在信息，通过机器学习算法进行特征学习，使用获得的数据特征空间进行谱聚类将有效提高聚类质量。ELM可以随机初始化输入权重和偏置并得到相应的输出权重，然而随机生成的输入权值和偏差会导致ELM隐层的输出不能很好地代表原始样本的特征。ELM-AE是一种能够重建输入信号的人工神经网络算法，和自动编码器一样，ELM-AE无需迭代可以获得原始样本的主要特征，与传统的ELM不同的是，ELM-AE通过选择随机权重和随机偏差正交，可以获得更高的性能。通过ELM-AE的输出β实现从特征空间到原始输入数据的转换，使得输出数据等于输入数据。

本文提出的基于ELM-AE嵌入特征空间的谱聚类是将ELM-AE的特征空间作为聚类原始值，从而提高聚类性能。SC-ELM-AE模型包含输入层、单隐层和输出层，其模型结构如图1，也具有M个输入层节点，J个隐藏层节点和M个输出层节点，然后如图所示通过ELM-AE获得输出层权值β，ELM-AE输出层的嵌入特征(embedding feature,EF)可由式(5)计算：

$ {\bf{EF}} = {{f}}\left( {{{X}}{{{\beta }}^{\rm{T}}}} \right) $

(5)

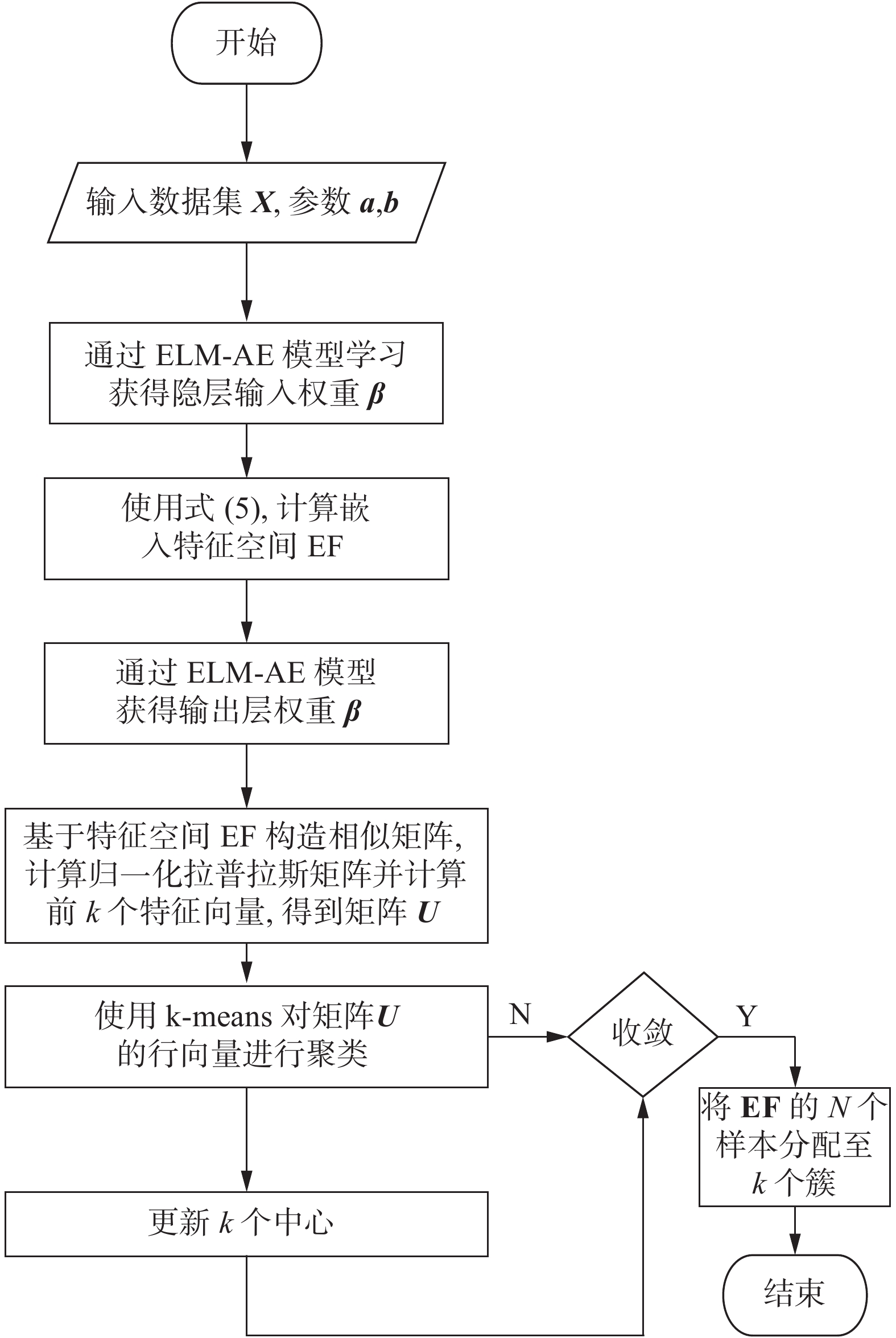
然后采用归一化谱聚类算法将ELM-AE的嵌入特征(EF)作为聚类输入数据点进行聚类。SC-ELM-AE算法流程如图1所示。基于ELM-AE嵌入特征空间的谱聚类算法(SC-ELM-AE)流程详见算法1。

算法1　基于ELM-AE嵌入特征空间的谱聚类

输入　数据集样本 $(x_1,x_2,\cdots,x_n) $ ，参数a和b；

输出　基于EF空间的N个样本的k个簇。

1)初始化由N个隐藏层神经元组成的ELM-AE网络，计算隐藏层的输出 ${{{H}}_{{\rm{ELM - AE}}}} \in {{\bf{R}}^{{{n}} \times {{n}}}}$ ，激活函数使用 $ {\rm{Sigmod}}(\cdot)$ ；

2)使用式(3)、(4)计算ELM-AE的输出层权值；

3)使用式(5)计算嵌入特征EF，激活函数使用 $ {\rm{Sigmod}}(\cdot)$ ；

4)得到嵌入特征样本 ${\bf{EF}} = \left( {{\bf{E}}{{\bf{F}}_1},{\bf{E}}{{\bf{F}}_2}, \cdots, {\bf{E}}{{\bf{F}}_{{n}}}} \right)$ ，初始化高斯相似度函数的参数 $ \sigma $ ，k个聚类；

5)在 ${\bf{EF}}$ 样本空间上，使用高斯相似度函数 $\left. {{{G}}({{x}},{{y}}) = \exp \left( { - {{\left\| {{{f}}\left( {{{{\beta}} ^{\rm{T}}}{{{x}}_{{i}}}} \right) - {{f}}\left( {{\beta ^{\rm{T}}}{{{x}}_{{j}}}} \right)} \right\|}^2}} \right)/2{\sigma ^2}} \right)$ 构造相似度矩阵 ${{S}}\in {{\bf{R}}^{{{n}} \times {{n}}}}$ ，当 $ i=j$ 时， ${{{S}}_{{{ij}}}} = {{G}}\left( {{\bf{E}}{{\bf{F}}_{{i}}},{\bf{E}}{{\bf{F}}_{{j}}}} \right)$ ，否则 $ {{{S}}_{{{ij}}}}=0$ ；

6)构造归一化对称拉普拉斯矩阵 ${{{L}}_{{\rm{norm }}}} = $ $ {{{D}}^{ - {{1}}/{{2}}}}{{S}}{{{D}}^{ - {{1}}/{{2}}}}$ ，其中 $ {{D}}$ 是对角矩阵，其 $ (i,j)$ 元素是 $ S$ 的第i行元素的和；

7)将矩阵 $ {{{L}}_{{\rm{norm }}}}$ 前k个最大特征向量作为列构造矩阵 ${{Y}} \in {{\bf{R}}^{{{n}} \times {{k}}}}$ ；

8)归一化矩阵 $ {{Y}}$ 的行，得到矩阵 ${{U}} \in {{\bf{R}}^{{{n}} \times {{k}}}}$ ，其中 ${{{u}}_{{{ij}}}} = {{{y}}_{{{ij}}}}/{\left( {\displaystyle\sum\limits_{{k}} {{{y}}_{{{ik}}}^{{2}}} } \right)^{{{1}}/{{2}}}}$ ；

9)利用k-means算法对矩阵 $ {{U}}$ 的行向量聚类，得到k个簇。

3 实验结果与分析 3.1 实验环境及数据集说明

为了验证基于ELM-AE嵌入特征空间的谱聚类算法的有效性，选取了UCI机器学习数据库中的5个常用数据集进行验证测试，数据集的基本特征如表1所示。

实验在MATLAB R2016b环境下实现，运行在Windows 10上，实验中使用的计算机CPU 型号为Inter(R)Core(TM)i5-8250U @1.60 GHz，内存为8 GB。本文所有实验中，ELM-AE模型包含输入层、输出层、隐藏层，为了方便实验，隐藏层、输出层的激活函数都采用sigmoid函数。

实验使用的对比算法分别为：传统谱聚类^[25](spectral clustering，SC)、k-means聚类、基于无监督极限学习机(unsupervised extreme learning machine US-ELM)的K-means聚类、基于ELM-AE嵌入特征的无监督极限学习机^[26](unsupervised extreme learning machine based on embedded features of ELM-AE, US-EF-ELM)k-means聚类算法。

本文中，k-means、SC、US-ELM和US-EF-ELM所有算法在数据集上运行10次，记录平均结果和标准差。根据文献[20]在所有数据集上，US-ELM隐藏节点数和US-EF-ELM隐藏节点数均设置为2 000，US-ELM和US-EF-ELM的激活函数均为sigmoid函数。在SC-EF-ELM中，从{100、200、500、1000、2 000}中选择隐藏节点个数，激活函数也为sigmoid函数。在US-ELM、US-EF-ELM和SC-EF-ELM中，正则化参数选取范围为{10⁻⁴, 10⁻³, 10⁻², 10⁻¹, 10⁰, 10¹, 10², 10³, 10⁴}，在SC和SC-EF-ELM中，核函数为高斯核函数，其中高斯核函数的参数为样本间的中值距离。

3.2 性能指标

假设数据集 ${{X}} = \{ {{{x}}_1},{{{x}}_2}, \cdots ,{{{x}}_{{n}}}\}$ ，通过聚类划分得到类簇 ${{C}} = \{ {{{C}}_1},{{{C}}_2}, \cdots ,{{{C}}_{{k}}}\}$ ，真实的类划分为 ${{C}}' = \{ {{C}'_1},{{{C}}'_2}, \cdots ,{{{C}}'_{{k}}}\}$ ，同时，令Y和 ${{Y}}'$ 分别表示与C和 ${C}'$ 对应的分配标签。实验中，采用F-measure ( $ F_1$ )、聚类准确性(cluster accuracy, ACC) 和标准化互信息(normalized mutual information, NMI) 这3个评价标准来衡量聚类结果的质量及算法的有效性。对于这3个评价标准，值越大，聚类性能越好。 $ F_1$ 表示精确率(precision)和召回率(recall)的加权调和平均值：

$ {{F}} = \frac{{\left( {{{{a}}^2} + 1} \right){{PR}}}}{{{{{a}}^2}({{P}} + {{R}})}} $

当参数 $ a=1$ 时，就是 $ F_1$ 指标

$ {{{F}}_1} = \frac{{2{{PR}}}}{{{{P}} + {{R}}}} $

式中：P是精确率(precision)度量值；R是召回率(recall)度量值。 $ F_1$ 综合了P和R的结果，当 $ F_1$ 较大时则比较说明实验结果比较理想。

ACC表示聚类结果中被正确划分的数据点比例：

${\rm{ACC}} = \sum\limits_{{i}}^{{N}} {\delta ({{{y}}_{{i}}},{\rm{map}}({{y}}_{{i}}'))} /{{n}}$

式中：n表示数据样本的个数；当x=y时,则 $\delta ({{x}},{{y}}) = 1$ ，否则 $\delta ({{x}},{{y}}) = 0$ 。 ${\rm{map}}( \cdot )$ 表示通过Hungarian算法将每个聚类标签映射到一个类标签，并且映射是最佳。

NMI 衡量的是算法的划分质量：

${\rm{NMI}} = \frac{{\displaystyle\sum\limits_{{i}}^{{k}} {\displaystyle\sum\limits_{{j}}^{{{{k}}'}} {\left| {{{{C}}_{{i}}} \cap {{C}}_{{j}}'} \right|\log \dfrac{{{{n}}\left| {{{{C}}_{{i}}} \cap {{C}}_{{j}}'} \right|}}{{|{{{C}}_{{i}}}||{{C}}_{{j}}'|}}} } }}{{\sqrt {\displaystyle\sum\limits_{{{i}} = 1}^{{k}} {|{{{C}}_{{i}}}|\log \dfrac{{|{{C}}{}_{{i}}|}}{{{n}}} \cdot \displaystyle\sum_{{{j}} = 1}^{{{{k}}'}} {|{{C}}_{{j}}'|\log \dfrac{{|{{C}}_{{j}}'|}}{{{n}}}} } } }}$

NMI的值越大，聚类有效性越好。

3.3 实验结果

所提出的SC-ELM-AE与k-means、SC、US-ELM和US-EF-ELM在5个数据集上的表现对比见表2。

从表2中可以看出，本文所提出的SC-ELM-AE算法在聚类准确率上与对比算法相比在5个数据集上都有了较大提升。例如，对于高维数据集PEMS-SF，本文所提算法与对比算法相比在ACC上分别提升了33.2%、32.75%、31.46%、26.68%平均提升了31.02%。

SC-ELM-AE聚类算法利用ELM-AE模型无需迭代即可获得低维特征表示空间，尽可能多地保留了原始数据集的丰富信息，使获得的聚类结果更加准确。实验数据结果表明，本文提出的SC-ELM-AE算法在进行实验的数据集上与对比算法相比聚类精度有较大的提升，这也验证了本文所提算法的合理性和有效性。

为了验证提出的SC-ELM-AE算法在增加隐含层节点后的表现，在实验中将ELM-AE模型结构的隐含层节点数从100增加到2 000，并在数据集WDBC和PEMS-SF上基于ELM-AE的嵌入特征空间进行快速谱聚类，实验结果如图2、3所示。

从图2可以看出：将ELM-AE特征表示空间作为谱聚类输入，从(10⁻⁴,10⁻³,10⁻²)中选取正则化参数，当隐藏节点较小，ACC、F-measure和NMI值较低。而在(10⁻¹,10⁰,10¹,10²,10³,10⁴)选取正则化参数时，隐藏节点数量的变化基本不会引起算法性能的波动。

从图3可以看出，本文提出的SC-ELM-AE始终是稳定的。因此，可以推断参数的选择对算法性能的影响不大，在合适的正则化参数下，采用很少的隐藏节点即可实现较高的聚类精度，与传统的聚类方法相比，所提出的SC-ELM-AE算法具有更强的实用性。此外，在UCI的其他3个基准数据集上进行验证，实验结果与推断一致，也证明了所提SC-ELM-AE的性能的有效性。

4 结束语

本文提出了一种通过ELM-AE特征表示空间的谱聚类算法。它利用ELM-AE将输入的原始数据集转化为数据特征表示空间，再对特征表示空间样本集进行谱聚类，利用ELM-AE获得的特征空间可以更好地反映出原始数据的主要信息且计算成本较低；使用ELM-AE进行特征提取，提高了聚类的准确性。通过实验验证了本文算法在有效性和准确性两方面优于现有的谱聚类算法，能够快速有效地处理复杂高维数据。在未来的工作中需要考虑如何在保证聚类精确的情况下进一步提高聚类的速度以及对大规模数据的处理。