2. 北京建筑大学 建筑大数据智能处理方法研究北京市重点实验室,北京 100044;
3. 哈尔滨工业大学 计算机科学与技术学院,黑龙江 哈尔滨 150001
2. Beijing Key Laboratory of Intelligent Processing for Building Big Data, Beijing University of Civil Engineering and Architecture, Beijing 100044, China;
3. School of Computer Science and Technology, Harbin Institute of Technology, Harbin 150001, China
活动语义识别是指从人类的时空轨迹数据或离散的位置序列中挖掘出人类的活动信息[1]。智能移动终端的广泛应用提供了海量的个体位置相关的时空数据,如社交媒体签到数据、GPS(global positioning system)轨迹数据和手机信令数据等[2]。这些数据为精细粒度下个体的活动识别提供了有力支撑。相比原始的时空轨迹数据或位置序列信息,带有语义的活动轨迹数据更能直观地反应人类的具体活动,这有助于深入了解每个个体的生活模式,发现个体的个性需求,为个体提供定制化服务,也可以发现与个体活动模式相同或相似的群体,进而识别群体的共性特征和需求[3]。这些信息的挖掘可以用于配置交通资源和资源规划[4],如公交车的班次和地点的设定、共享单车的投放量和投放地点、商场的选址等,从而达到优化社会资源配置、精细化满足各种群体的不同需求的目的[1, 5-6]。
人类的活动轨迹在空间上是多重交叉的[7],在时间上表现出序列性和一定的周期性[8-10]。已有的大部分方法都是在GPS轨迹数据的空间特征—活动地点的POI(point of interest)数据和运动特征(速度、加速度)之上构建分类模型,进而识别用户的活动语义[11-15]。该类方法忽略了活动轨迹的时间特性,导致该类方法的识别结果过度依赖于POI获取的准确性,而忽视了用户某些活动,难以准确获取相应POI的实际问题,而且容易混淆用户在不同时间访问相近的地方发生的不同活动,本文在文献[16-17]提取用户活动轨迹周期模式的方法上使用LombScargle[18-19]方法挖掘用户轨迹数据的周期作为用户活动特征中的周期特征,再结合用户活动的持续时间、活动中心点附近POI,及活动发生的年份、月份、季节、日期、是否是节假日和是否是周末等时间特征[15],使用随机森林分类器挖掘用户活动语义。
1 相关研究现有的活动语义识别方法可以分为:基于空间特征的识别方法和基于运动特征的识别方法。文献[11]从用户活动的空间角度,采用活动地点的POI数据挖掘语义信息。并且考虑到POI数据不均匀以及POI在不同地区主题下对用户活动的影响度不同等因素,引入隐含狄利克雷分布 (latent dirichlet allocation,LDA)主题模型提取活动地点POI的主题特征。通过地区内POI与主题的相关程度来确定在该主题下POI对用户活动的影响度,从而确定用户在活动地点产生的活动模式。文献[12]使用移动基站提供的数据集结合OpenStreetMap上的POI信息对用户的行为进行识别和预测。文献[13]设计自助数据采集系统,以志愿者的方式采集数据,并利用用户的轨迹、年龄、收入、居住等特征和支持向量机(support vector machine, SVM)模型来识别用户的活动语义。文献[14]利用社交签到数据,融合签到地点频次等信息识别活动语义。文献[15]采用聚类方法获取空间热度特征并利用极限梯度提升 (eXtreme gradient boosting,XGBoost)建模识别用户活动模式。文献[20]逐步提取用户的实时位置,将运动过程中访问的地点与人类的活动相关联起来,进而推断用户进行的活动。上述方法的核心思想是从活动轨迹点的空间信息提取特征来建模,但是用户的轨迹信息在空间和时间上是紧密相连的,因此该类方法忽略了时间特性,导致该类方法的识别结果过度依赖于POI获取的准确性而忽视了用户某些活动难以准确获取相应POI的实际问题,而且容易混淆用户在不同时间访问相近的地方发生的不同活动。
人类活动具有显著的周期性特征[9],已有的研究就轨迹的周期性进行挖掘,如文献[16]中就移动对象频繁访问某一地方的核心点(reference spot)提取用户空间信息,并融合傅里叶变换(fourier transform)获取用户的时间信息。通过提取核心点提取用户的空间信息,再通过傅里叶变换检测活动发生的周期,提取用户的时间信息。使用傅里叶变换挖掘用户活动周期时必须获取轨迹数据的均值采样,但是由于天气的原因无法获取均值采样的轨迹数据。此时必须通过线性插值的方法使不规则的样本变成均值的轨迹。但是由于轨迹数据量庞大的原因,这种插值会带来巨大的计算量。文献[17]在此基础上,先将单个用户轨迹数据运用基于密度的带噪声应用空间聚类 (density based spatial clustering of application with noise,DBSCAN),聚类后获取用户的活动轨迹点,再结合OpenStreetMap中的POI信息进行地点匹配得到带有地点特征的轨迹数据,最后使用LombScargle[18, 21]算法挖掘用户活动的周期。该算法可以直接从非规则采样的轨迹中挖掘出用户的活动周期。但是文献[16-17]均是挖掘用户轨迹的周期模式,并没有结合用户活动产生的轨迹点的空间信息挖掘用户的活动语义。
2 周期模式挖掘针对个体的部分活动存在周期性这一特征,本文从访问位置的周期性挖掘出发,将周期性活动的周期提取、停留时间、周期性活动的相关POI进行提取,构成以时空周期性为核心的特征表示。
单个用户产生的活动轨迹表示为一个三维的时空序列,则用户一天的活动序列
| $ \begin{split} S =& \left\{ {{S_1},{S_2}, \cdots ,{S_m}} \right\} \\ {S_i} =& \{ ({{\rm{lng}}_{{i_1}}},{{\rm{lat}}_{{i_1}}},{t_{{i_1}}}),({{\rm{lng}}_{{i_2}}},{{\rm{lat}}_{{i_2}}},{t_{{i_2}}}), \cdots , \\ &({{\rm{lng}}_{{i_n}}},{{\rm{lat}}_{{i_n}}},{t_{in}})\} ,i \in [1,m] \end{split} $ |
式中:
活动地点匹配是将原始的轨迹序列
| $ \begin{split} {\rm{space}\_d}_{ij}=&\sqrt{({\rm{lng}}_{i}-{\rm{lng}}_{j}{)}^{2}+({\rm{lat}}_{i}-{\rm{lat}}_{j}{)}^{2}} \\ {\rm{time}}\_{d}_{ij}=&\left|{\rm{time}}_{i}-{\rm{time}}_{j}\right| \\ {d}_{ij}=&\frac{({\rm{space}}\_i{d}_{ij}+{\rm{time}}\_{d}_{ij})}{2} \end{split} $ |
算法1 DBSCAN算法。
输入 样本集
1) 初始化核心对象集合
2) for
3) 通过距离度量方式,找到
4) if
5)
6) end for
7) while
8) 随机选取
9) if
10)
continue
11) else
12)
13) end if
14)在
15) end while
输出 簇划分
对于GPS轨迹数据,一个连续采样的轨迹满足在某个轨迹簇
对于时间序列来说,
| $ \begin{aligned} {P_{\rm{LS}}}\left( f \right) = \frac{1}{{2{\sigma ^2}}}\left\{ \frac{{{{\left[\displaystyle\sum _{j = 1}^N\left( {\left( {{x_j} - \bar x} \right){\rm{cos}}(2{\rm{{\text{π}}}} f\left( {{t_j} - \tau } \right)} \right)\right]}^2}}}{{\displaystyle\sum _{j = 1}^N{\rm{co}}{{\rm{s}}^2}\left(2{\rm{{\text{π}}}} f({t_j} - \tau )\right)}} + \right.\\ \left. \frac{{\left[\displaystyle\sum _{j = 1}^N(({x_j} - \bar x){\rm{sin}}(2{\rm{{\text{π}}}} f({t_j} - \tau ))\right]^2}}{{{\rm{si}}{{\rm{n}}^2}(2{\rm{{\text{π}}}} f({t_j} - \tau ))}} \right\}\quad\quad\quad\quad \end{aligned} $ | (1) |
式中:
| $ \begin{split} \overline {x}&=\frac{1}{N}\sum\limits_{j=1}^{N}{x}_{j}\\ {\sigma ^2} &= \frac{1}{{N - 1}}\sum\limits_{j = 1}^N ( {x_j} - \bar x{)^2} \end{split}$ |
式中
| $ {\rm{tan}}(2\left(2{\rm{{\text{π}} }}f\right)\tau )=\dfrac{\displaystyle\sum\limits_{j=1}^{N}{\rm{sin}}(2\left(2{\rm{{\text{π}} }}f\right){t}_{j})}{\displaystyle\sum\limits_{j=1}^{N}{\rm{cos}}(2\left(2{\rm{{\text{π}} }}f\right){t}_{j})} $ |
对于LombScargle图,图中每个峰值表示一个周期。LombScargle图是通过错误预警概率(false alarm probability)来表示该峰值的显著性,其计算为
| $ {P}_{r}\left({p}_{{\rm{max}}}\right)=1-{\left[1-{\rm{exp}}\left(-{p}_{{\rm{max}}}\right)\right]}^{N} $ | (2) |
从式(2)的分布得出,一个有效的功率峰值
| $ z=-{\rm{ln}}\left[1-(1-\alpha {)}^{\frac{1}{N}}\right] $ | (3) |
算法2 周期模式挖掘算法。
输入
1) for
2) for
3) if
4)将
5) end for
6)
7)按照式(2)求出
8)
9) end for
输出 带有周期的GPS轨迹序列
基于周期模式挖掘的语义识别流程如图1。首先,将用户的活动轨迹聚类成若干个轨迹簇,然后为不同轨迹簇中的每个轨迹点分配一个独特的ID作为识别周期模式的地点标识。之后使用这些地点标识识别出每个活动发生的周期模式,计算活动轨迹中心点,利用轨迹中心点获取活动地点附近的POI信息,最后将这些特征作为随机森林分类器的输入识别用户的活动义。

|
Download:
|
| 图 1 本文提出的方法总体流程 Fig. 1 Overall procedure of our proposed method | |
时空轨迹具有序列性、时空紧密性、不规矩的时间间隔、空间层次性和包含背景语义信息等特征。序列性指前后2个相邻的轨迹点在时间上有先后顺序。紧密性指轨迹的空间特征和时间特征紧密相连,不能分割。不规则的时间间隔指现实生活中由设备采集到的数据是非均值采样。空间层次性指人的时空轨迹是区域聚集性和在不同板块下有不同的层次表示。背景语义能一定程度上反映活动者在这个地方进行的活动类型。针对这些特性,本文加入了用户活动参考点的经纬度作为空间特征。通过地图API (application programming interface)获得的POI信息,作为背景语义特征。进行活动的起始时间、活动的时长、活动的日期(活动发生的年份、月份、日期、是否周末)作为时间特征,以及活动的周期特征(包含识别周期过程中每个周期对应的错误预警概率)。
3.2 模型选择随机森林是采用有放回抽样的方式从训练集中选取一定比例的样本和一定个数的特征作为子训练集,使用多个决策树在不同的子训练集中进行分类,并且将最后多数分类器得到的分类结果作为最终分类结果的分类器。该分类器有较好的抗噪性,并且在高维和大数据的数据集下有很好的分类性能,本文采用随机森林算法识别活动语义。
3.2.1 决策树决策树模型呈树形结构,在分类问题中,表示基于特征对实例进行分类的过程。决策树学习过程包含3个步骤:特征选择、决策树的生成和决策树的剪枝。
1)特征选择。
通过计算并比较特征的信息熵或者基尼系数进行特征选择。在分类问题中,设有
| $ {\rm{Gini}}\left(p\right)=1-\sum\limits_{k=1}^{K}{p}_{k}^{2} $ | (4) |
样本集合
| $ {\rm{Gini}}\left(D\right)=1-{\sum\limits_{k=1}^{K}\left(\frac{\left|{C}_{k}\right|}{\left|D\right|}\right)}^{2} $ | (5) |
式中
| $ {\rm{Gini}}(D,A)=\frac{\left|{D}_{1}\right|}{\left|D\right|}{\rm{Gini}}\left({D}_{1}\right)+\frac{\left|{D}_{2}\right|}{\left|D\right|}{\rm{Gini}}\left({D}_{2}\right) $ | (6) |
2)决策树生成。
决策树生成有ID3、C4.5和分类回归树 (classification and regression tree,CART)。
本文用到的是CART算法构建分类树。CART算法采用基尼系数作为评判准则,通过式(6)选取使得基尼系数最小的特征和对应特征取值递归构建二叉树分类树进行分类。
3)决策树的剪枝。
决策树生成算法递归地产生决策树,直到不能进行下去为止。这样的算法产生的树对训练数据分类很准确,但对未知数据集的分类往往没有那么准确—过拟合。解决过拟合的方式是考虑生成树的复杂度,对已经生成的决策树进行简化—剪枝。
3.2.2 基于随机森林的活动语义分类随机森林是由很多独立的决策树组成的一个森林,每棵树之间相互独立,在最终模型组合时,通过投票的方式决定最终的分类结果。
算法3 活动语义识别算法。
输入 提取完的活动轨迹特征矩阵
1)将特征矩阵分成训练集
2)从训练集
3)通过CART方法构建n个决策树,将所有决策树的分类结果概率最高的作为随机森立分类器的结果。
4) n从1~200变化,得到分类器最好精度时对应的决策树的个数。
5)将训练完成的分类器放在测试集上测试。输出模型的训练和测试精度。
输出 模型的精度。
4 实验结果与分析 4.1 实验设置本文采用的数据是来自Yang等[24]通过Foursquare提供的开发者API收集的来自纽约和东京2个城市用户的签到数据,数据有8个特征:用户ID、活动地点ID、场地类别ID、场地类别名称、经度、纬度、UTC时间、时间偏移量。东京数据集TKY包含57万条数据,纽约数据集NYC包含22万条数据,这2个城市的签到数据集时间跨度超过10个月,从2012年4月12日—到2013年2月16日纽约1 083个用户和东京2 293个用户的签到数据记录。在有无周期对比实验中本文根据签到地点名称采用多专家决策的方法最终标记为12类(Shopping, Restaurant, Work, Travel, Entertainment, Service, Meeting, Education, Sports, Rest, Medical, Art)。实验中,为了能识别用户的周期,设定少于5次访问次数的地点为用户不常去的地点,没有周期性,实验中去除了这些数据。TKY签到数据中标签分布如图2,标记完的签到数据如图3。

|
Download:
|
| 图 2 签到数据种类分布 Fig. 2 Distribution of check-ins categories | |

|
Download:
|
| 图 3 签到数据样式 Fig. 3 Examples of check-ins data | |
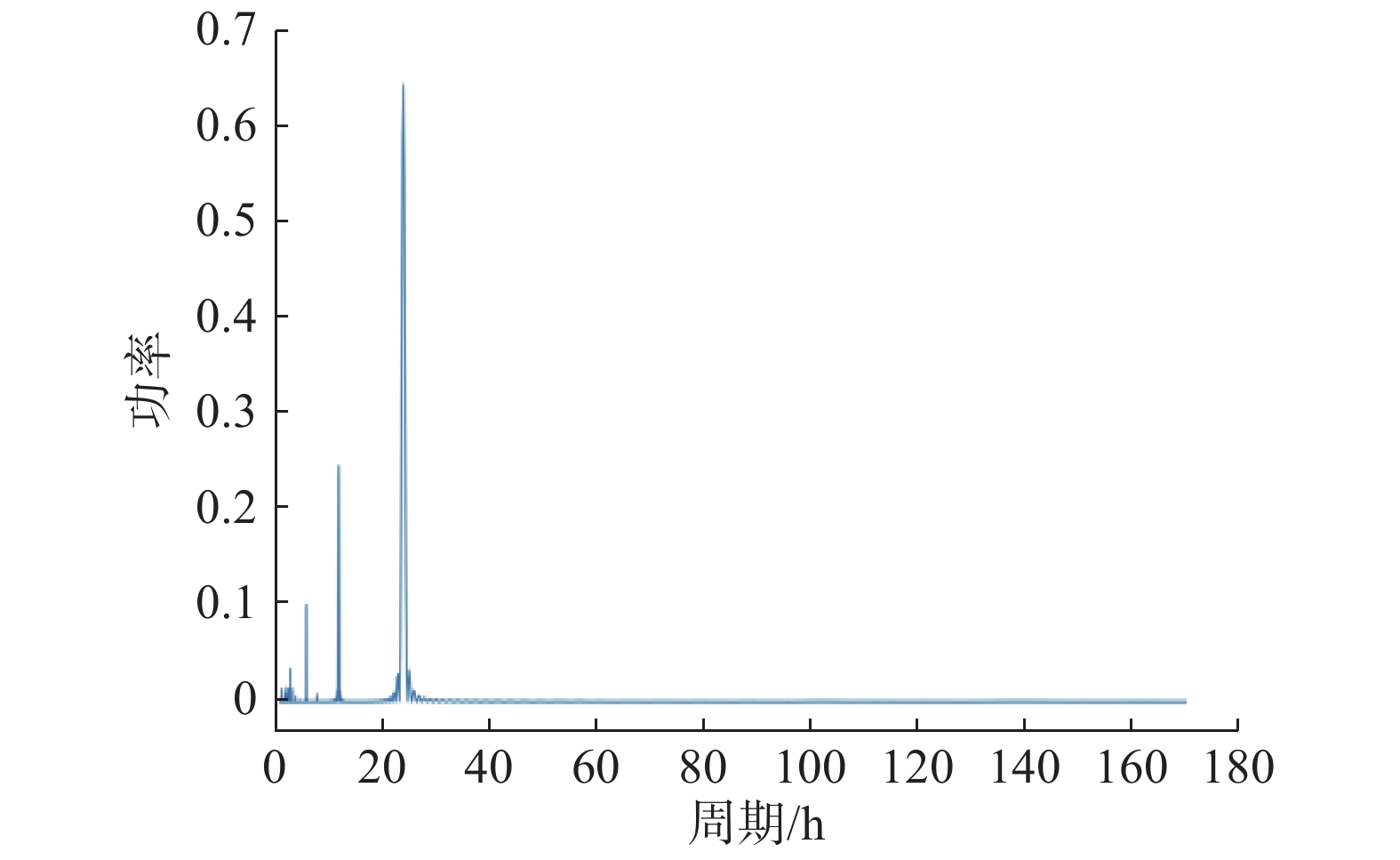
识别周期模式中,识别的周期通常指最小正周期,因此需要传入周期的取值范围限制识别出周期的大小。去除10个月少于5次签到的数据周期为(0, 1440)小时(1个月按30 d计算),某个用户的某个活动周期—频率图如图4所示,通过图5中周期—频率图得到最大峰值对应的周期为24.15 h。这表明用户在这个地方的活动每隔24.15 h会发生一次。
4.2.2 活动语义识别结果为了验证周期特征对活动语义识别的有效性,本文在相同的实验条件下,对比了加入和不加入周期模式特征进行活动语义的识别的性能。分别使用准确度、精准率、召回率、F1值对分类结果进行的评价,其计算为
| $ {\rm{precison}} = \frac{{{\rm{TP}}}}{{({\rm{TP}} + {\rm{FP}})}} $ | (7) |
| $ {\rm{accuracy}} = \frac{{({\rm{TP}} + {\rm{TN}})}}{{({\rm{TP}} + {\rm{FP}} + {\rm{TN}} + {\rm{FN}})}} $ | (8) |
| $ {\rm{recall}} = \frac{{{\rm{TP}}}}{{({\rm{TP}} + {\rm{FN}})}} $ | (9) |
| $ {{F}}_{1} = \frac{{{\rm{precison}} \times {\rm{recall}}}}{{2({\rm{precison}} + {\rm{recall}})}} $ | (10) |
式中:TP、FP、TN、FN表示将正类分正确、将正类分错误、将负类分正确、负类分错误的个数。
|
Download:
|
| 图 4 某个特定活动对应的LombScargle功率—频率 Fig. 4 LombScargle power-frequency diagram corresponding to a specific activity | |
|
Download:
|
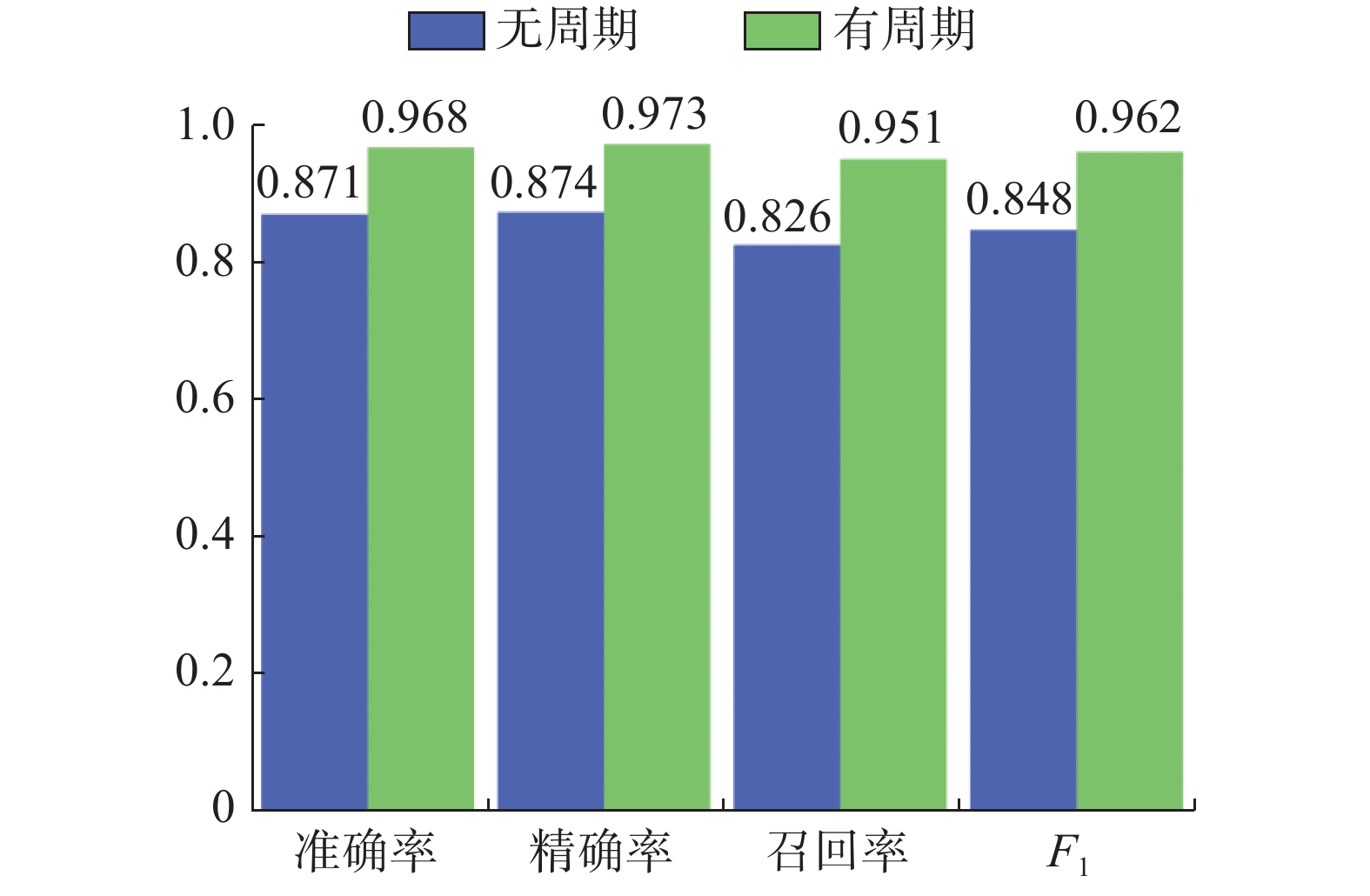
| 图 5 有无周期的分类结果 Fig. 5 The histogram without or with period | |
在周期模式特征中加入错误预警概率作为联合周期特征,随机森林最后参数设置为n-estimator=84,在TKY数据集上得到的实验结果如图5所示。加入周期特征后准确率从0.871提升到0.968,精准率从0.874提升到0.973,召回率从0.826提升到0.951,F1值从0.848提升到0.962。由数值结果可以看出加入周期特征后在各个分类结果中都取得了10%以上的提升。
分别绘制每个分类的结果,得到加入周期特征前后的混淆矩阵如图6、图7,矩阵横轴表示预测的类别,纵轴表示真实的类别。方格对角线的值表示识别正确的类别占总类别的比值,其中空白表示值为0,即在预测样本中完成分类正确。从图6中可以看出,没有加入周期前模型对Edu(Education)、Spo(Sport)、Res(Restaurant)这几种活动的识别精度较低(0.726,0.689,0.707),加入周期模式特征后这些活动的识别效果得到了20%左右的提升,识别精度均超过0.9。从图6可以看出,Edu和Sho、Spo和Sho、Res和Ser(Service)混淆得最为严重,其原因在于人类在学习、运动的活动中,进行活动的时间和场所受个人偏好影响比较大,这些活动的持续时间较长,在特征方面容易与购物、饮食和社会服务(银行,派出所,居委会,政府等社会公共设施内进行的活动)等行为混淆。由于人类的这些行为周期性比较明显,加上周期模式特征后,这些行为会被更加准确地识别出来。

|
Download:
|
| 图 6 不加入周期特征的混淆矩阵 Fig. 6 The confusion matrix without period | |

|
Download:
|
| 图 7 加入周期特征的混淆矩阵 Fig. 7 The confusion matrix with period | |
为了验证本文方法有更好的识别精度,本文和文献[24-25]在相同的数据集下(东京市签到数据集、纽约市数据集)进行实验。本文和文献[24-25]都采签到地点名称作为用户的活动语义标签,TKY数据集包含的标签个数为247个,NYC包含的标签个数为251个。实验结果如表1,LIAO等[25]采用2个基学习器和一个元学习器将时间特征和序列特征整合用于预测用户的活动目的和活动位置,YANG等[24]提出一种上下文感知框架对用户活动偏好进行推理,从而识别用户的活动语义。实验结果如表1所示,在NYC数据集上本文的识别方法相对于LIAO提升精度35.9%,相对于YANG提升了10.8%。在TKY数据集上分别提升了37.8%和23.7%。实验结果表明周期模式挖掘算法具有更好的识别精度,也验证了用户在长时间活动轨迹中周期性的重要作用。
| 表 1 识别算法对比结果 Tab.1 The comparison results of recognition algorithms |
本文通过对比是否加入周期特征的方法,验证了加入周期模式能有效提高活动语义的识别性能;同时,在与LIAO、YANG方法的对比中可以发现本文的方法具有更好的识别精度,验证了本文方法的有效性。本文充分利用了人的部分活动带有显著的周期性这一特点,挖掘了历史活动的周期模式,来提高对当前活动的识别的准确性。因此本文方法更适合个体活动记录的时间跨度较大的数据场景,以便更好地捕捉活动的周期特征。本文的活动语义识别方法是基于周期模式特征为主要特征,因此对于人的部分不频繁的活动模式识别效果不佳,这也是未来要研究的方向之一。
| [1] |
ZHENG Yu. Trajectory data mining: an overview[J]. ACM transactions on intelligent systems and technology, 2015, 6(3): 1-41. ( 0) 0)
|
| [2] |
SIŁA-NOWICKA K, VANDROL J, OSHAN T, et al. Analysis of human mobility patterns from GPS trajectories and contextual information[J]. International journal of geographical information science, 2016, 30(5): 881-906. DOI:10.1080/13658816.2015.1100731 ( 0) 0)
|
| [3] |
郭黎敏, 高需, 武斌, 等. 基于停留时间的语义行为模式挖掘[J]. 计算机研究与发展, 2017, 54(1): 111–122. GUO Limin, GAO Xu, WU Bin, et al. Discovering common behavior using staying duration on semantic trajectory[J]. Journal of computer research and development, 2017, 54(1): 111–122. (  0) 0)
|
| [4] |
姚迪, 张超, 黄建辉, 等. 时空数据语义理解: 技术与应用[J]. 软件学报, 2018, 29(7): 2018–2045.YAO Di, ZHANG Chao, HUANG Jianhui, et al. Semantic understanding of spatio-temporal data: technology and application[J]. Journal of software, 2018, 29(7): 2018–2045.
( 0) 0)
|
| [5] |
LU Mingqi, CHEN Ling, XU Zhenxing, et al. The discovery of personally semantic places based on trajectory data mining[J]. Neurocomputing, 2016, 173: 1142–1153.
( 0) 0)
|
| [6] |
WAN Chengcheng, ZHU Yanmin, YU Jiadi, et al. SMOPAT: mining semantic mobility patterns from trajectories of private vehicles[J]. Information sciences, 2018, 429: 12–25.
( 0) 0)
|
| [7] |
ZHANG Dongzhi, LEE K, LEE I. Mining hierarchical semantic periodic patterns from GPS-collected spatio-temporal trajectories[J]. Expert systems with applications, 2019, 122: 85–101.
( 0) 0)
|
| [8] |
ZHANG Dongzhi, LEE K, LEE I. Hierarchical trajectory clustering for spatio-temporal periodic pattern mining[J]. Expert systems with applications, 2018, 92: 1–11.
( 0) 0)
|
| [9] |
SONG Chaoming, KOREN T, WANG Pu, et al. Modelling the scaling properties of human mobility[J]. Nature physics, 2010, 6(10): 818–823.
( 0) 0)
|
| [10] |
SONG Chaoming, QU Zehui, BLUMM N, et al. Limits of predictability in human mobility[J]. Science, 2010, 327(5968): 1018–1021.
( 0) 0)
|
| [11] |
苏杭. 基于电信位置数据的用户活动推测及行为模式分析[D]. 北京: 北京邮电大学, 2018: 1–84.SU Hang. User activity inference and behavior pattern analysis based on mobile phone data[D]. Beijing: Beijing University of Posts and Telecommunications, 2018: 1–84.
( 0) 0)
|
| [12] |
崔家祥. 基于移动通信数据的用户移动行为分析与位置预测[D]. 北京: 北京邮电大学, 2018: 1–73.CUI Jiaxiang. User mobility analysis and location prediction based on mobile communication data[D]. Beijing: Beijing University of Posts and Telecommunications, 2018: 1–73.
( 0) 0)
|
| [13] |
周超然. 基于大规模GPS轨迹数据的活动链信息分析方法研究[D]. 长春: 吉林大学, 2017: 80–88.ZHOU Chaoran. Research on methods of activity-chain information analysis based on large scale GPS tracking data[D]. Changchun: Jilin University, 2017: 80–88.
( 0) 0)
|
| [14] |
殷浩腾, 刘洋. 基于社交属性的时空轨迹语义分析[J]. 中国科学: 信息科学, 2017, 47(8): 1051–1065.YIN Haoteng, LIU Yang. Semantic analysis of spatial temporal trajectory in LBSNs[J]. Scientia sinica informationis, 2017, 47(8): 1051–1065.
( 0) 0)
|
| [15] |
郭茂祖, 张彬, 赵玲玲, 等. 基于联合特征和XGBoost的活动语义识别方法[J]. 计算机应用, 2020, 40(11): 3159–3165.GUO Maozu, ZHANG Bin, ZHAO Lingling, et al. Active semantic recognition method based on joint features and XGBoost[J]. Journal of computer applications, 2020, 40(11): 3159–3165.
( 0) 0)
|
| [16] |
LI Zhenhui, DING Bolin, HAN Jiawei, et al. Mining periodic behaviors for moving objects[C]//Proceedings of the 16th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. Washington, USA, 2010: 1099–1108.
( 0) 0)
|
| [17] |
ZHANG Dongzhi, LEE K, LEE I. Semantic periodic pattern mining from spatio-temporal trajectories[J]. Information sciences, 2019, 502: 164–189.
( 0) 0)
|
| [18] |
LOMB N R. Least-squares frequency analysis of unequally spaced data[J]. Astrophysics and space science, 1976, 39(2): 447–462. .
( 0) 0)
|
| [19] |
SCARGLE J D. Studies in astronomical time series analysis. II-Statistical aspects of spectral analysis of unevenly spaced data[J]. Astrophysical journal, 1982, 263: 835–853.
( 0) 0)
|
| [20] |
BOUKHECHBA M, BOUZOUANE A, BOUCHARD B, et al. Online recognition of people's activities from raw GPS data: semantic trajectory data analysis[C]//Proceedings of the 8th ACM International Conference on Pervasive Technologies Related to Assistive Environments. Corfu, Greece, 2015: 1–8.
( 0) 0)
|
| [21] |
GLYNN E F, CHEN Jie, MUSHEGIAN A R. Detecting periodic patterns in unevenly spaced gene expression time series using Lomb–Scargle periodograms[J]. Bioinformatics, 2006, 22(3): 310–316.
( 0) 0)
|
| [22] |
BERMINGHAM L, LEE I. Mining place-matching patterns from spatio-temporal trajectories using complex real-world places[J]. Expert systems with applications, 2019, 122: 334-350. DOI:10.1016/j.eswa.2019.01.027 ( 0) 0)
|
| [23] |
VANDERPLAS J T. Understanding the Lomb–Scargle periodogram[J]. The astrophysical journal supplement series, 2018, 236(1): 1–15.
( 0) 0)
|
| [24] |
YANG Dingqi, ZHANG Daqing, ZHENG V W, et al. Modeling user activity preference by leveraging user spatial temporal characteristics in LBSNs[J]. IEEE transactions on systems, man, and cybernetics: systems, 2015, 45(1): 129–142.
( 0) 0)
|
| [25] |
LIAO Dongliang, ZHONG Yuan, LI Jing. Location prediction through activity purpose: integrating temporal and sequential models[C]//Proceedings of the 21st Pacific-Asia Conference on Knowledge Discovery and Data Mining. Jeju, South Korea, 2017: 711–723.
( 0) 0)
|
 2021, Vol. 16
2021, Vol. 16


