2. 浙江警察学院 公共基础部,浙江 杭州 310053;
3. 西安电子科技大学 计算机学院,陕西 西安 710071
2. Basic Courses Department, Zhejiang Police College, Hangzhou 310053, China;
3. School of Computer Science and Technology, Xidian University, Xi’an 710071, China
精确的位置信息,是为许多集群网络,包括机器人网络[1-3]、车联网[4]、无人机集群[5-6]、无人水面艇[7]等,提供服务或者实现完全自主导航[8]的基础。为了获取位置信息,一种可能的方案是为集群网络中的每个节点安装GPS或BDS[9]接收机,但部分应用场景在室内[10]、太空、下水管道、水下[11]等环境中,GPS信号容易受到多径干扰、遮挡等因素的影响,往往只有少部分节点能够得到精确的绝对位置信息,这一部分节点被称为锚节点,而没有位置信息的节点一般被称为未知节点。利用集群网络节点之间通信交互的过程中获得的相对测量信息辅助网络节点定位是解决缺少蜂窝系统基站和在GPS缺失环境下高精度定位的一种新思路[12-13]。相对测量信息包括相对距离测量、相对角度测量、相对速度测量等。本文只考虑基于相对距离测量的定位算法。基于测距的定位算法主要可分为两大类,单点定位和协同定位[14]。基于距离测量的协同定位按照建模思路的不同,可划分为两大类:1)将定位问题建模为一个非凸优化问题[15-17],可通过基于半定规划[15](semidefinite programming,SDP)的算法或基于MDS[16-17](multi-dimensional scaling)的算法求解;2)将定位问题建模为一个非线性最小二乘问题[18],可通过Gauss–Newton、Levenberg– Marquardt算法(LM)以及Powell’s Dog Leg 算法(DL)求解。
基于测距的协同定位算法给出的是集群网络的相对位置信息,这是因为当依据某种算法给出位置估计后,作任意的平移和旋转,依然能够满足距离约束。评价定位算法性能常用的两个指标是平均绝对误差(mean absolute error,MAE)和均方根误差(root mean square error,RMSE),而这两个指标的计算都需要绝对位置信息。实际上,坐标配准可以通过锚节点的绝对位置信息与相对位置信息实现。理论上,对于
考虑具有
三维空间中坐标配准至少需要4个锚节点,假设
| ${{Q}} = {({{C'C}})^{{\rm{ - }}1}}({{C'd}})$ |
此时,
普氏分析的部分推导方法参考了文献[25]。本文将普氏分析应用于坐标配准之中,其基本思想是把坐标配准问题建模为优化问题,即
| $[s,{{Q}},{{T}}] = \arg\min \left\| {s{{BQ}} + {{T}} - {{A}}} \right\|$ | (1) |
如无特殊说明,本文中的
平移后的矩阵
| ${{{l}}_{ci}} = {{{l}}_i} - {\frac{1}{m}}\sum\limits_{j = 1}^m {{{{l}}_j}} $ | (2) |
| ${\hat{ l}}_{ci}^{{\rm{re}}} = {\hat{ l}}_i^{{\rm{re}}} - \frac{1}{m}\sum\limits_{j = 1}^m {{\hat{ l}}_j^{{\rm{re}}}} $ | (3) |
式中:
当把矩阵
| ${{{A}}_0} = \frac{1}{{\left\| {{{{A}}_c}} \right\|}}{{{A}}_c}$ | (4) |
| ${{{B}}_0} = \frac{1}{{\left\| {{{{B}}_c}} \right\|}}{{{B}}_c}$ | (5) |
在进行了2步预处理之后,可以先将式(1)所示的最小化问题简化为式(6)来求解
| ${{Q}} = {\rm{argmin}} \left\| {{{{B}}_0}{{Q}} - {{{A}}_0}} \right\|$ | (6) |
| $\begin{array}{l} {\left\| {{{{B}}_0}{{Q}} - {{{A}}_0}} \right\|^2} = {\rm{tr}}\left( {({{{B}}_0}{{Q}} - {{{A}}_0})^{\rm{T}}({{{B}}_0}{{Q}} - {{{A}}_0})} \right) =\\ \quad{\rm{tr}}({{Q}}^{\rm{T}}{{{B}}_0}^{\rm{T}} {{{B}}_0}{{Q}}) + {\rm{tr}}({{{A}}_0}^{\rm{T}} {{{A}}_0}) - 2{\rm{tr}}({{{A}}_0}^{\rm{T}} {{{B}}_0}{{Q}}) = \\ \quad\quad{\rm{tr}}({{{B}}_0}^{\rm{T}} {{{B}}_0}) + {\rm{tr}}({{{A}}_0}^{\rm{T}} {{{A}}_0}) - 2{\rm{tr}}({{{A}}_0}^{\rm{T}} {{{B}}_0}{{Q}}) \\ \end{array} $ | (7) |
式中:
| ${\rm{tr}}({{{A}}_0}^{\rm{T}} {{{B}}_0}{{Q}}) = {\rm{tr}}({{UWV}}^{\rm{T}}{{Q}}) = {\rm{tr}}({{WV}}^{\rm{T}}{{QU}}) = {\rm{tr}}({{WH}})$ | (8) |
式中
| ${\rm{tr}}({{WH}}) = \sum\limits_{i = 1}^p {{\sigma _i}{h_{ii}}} $ | (9) |
对于三维坐标配准,
| ${{Q}} = {{VU}}^{\rm{T}}$ | (10) |
不存在测距误差的理想环境下,大部分协同定位算法可求得网络相对位置的精确解,此时
| ${s_0} = {\rm{argmin}} \left\| {{s_0}{{{B}}_0}{{Q}} - {{{A}}_0}} \right\|$ | (11) |
由式(11)可得:
| $\begin{array}{l} {\left\| {{s_0}{{{B}}_0}{{Q}} - {{{A}}_0}} \right\|^2} = {\rm{tr}}\left( {({s_0}{{{B}}_0}{{Q}} - {{{A}}_0})^{\rm{T}}({s_0}{{{B}}_0}{{Q}} - {{{A}}_0})} \right) = \\ \quad {\rm{tr}}({{Q}}^{\rm{T}}{{{B}}_0}^{\rm{T}} {{{B}}_0}{{Q}}){s_0}^2 - 2{\rm{tr}}({{{A}}_0}^{\rm{T}} {{{B}}_0}{{Q}}){s_0} + {\rm{tr}}({{{A}}_0}^{\rm{T}} {{{A}}_0}) \\ \end{array} $ | (12) |
式(12)实际是一个关于
| ${s_0} = \frac{{{\rm{tr}}({{{A}}_0}^{\rm{T}} {{{B}}_0}{{Q}})}}{{{\rm{tr}}({{Q}}^{\rm{T}}{{{B}}_0}^{\rm{T}} {{{B}}_0}{{Q}})}} = \frac{{{\rm{tr}}({{UWV}^{\rm{T}}{{VU}^{\rm{T}}}})}}{{{\rm{tr}}({{QQ}^{\rm{T}}}{{{B}}_0}^{\rm{T}} {{{B}}_0})}} = {\rm{tr}}({{W}})$ | (13) |
由式(11)和式(13),可以近似认为
| ${s_0}\frac{{{{B}} - {{{T}}_B}}}{{\left\| {{{{B}}_c}} \right\|}}{{Q}} \approx \frac{{{{A}} - {{{T}}_A}}}{{\left\| {{{{A}}_c}} \right\|}}$ | (14) |
| $\left({s_0}\frac{{\left\| {{{{A}}_c}} \right\|}}{{\left\| {{{{B}}_c}} \right\|}}\right){{BQ}} + \left({{{T}}_A} - {s_0}\frac{{\left\| {{{{A}}_c}} \right\|}}{{\left\| {{{{B}}_c}} \right\|}}{{{T}}_B}{{Q}}\right) \approx {{A}}$ | (15) |
由式(15)得到放缩因子
| $s = {s_0}\frac{{\left\| {{{{A}}_c}} \right\|}}{{\left\| {{{{B}}_c}} \right\|}}$ | (16) |
| ${{T}} = {{{T}}_A} - {s_0}\frac{{\left\| {{{{A}}_c}} \right\|}}{{\left\| {{{{B}}_c}} \right\|}}{{{T}}_B}{{Q}}$ | (17) |
基于普氏分析的坐标配准,需要计算旋转矩阵
输入
输出 旋转矩阵
1)根据式(2)、(3)对矩阵
2)根据式(4)、(5)对
3)根据式(7)~(9)求得旋转矩阵
4)若考虑放缩因子
5)根据式(16)求得放缩因子
6)根据式(17)求得平移向量
普氏分析的计算复杂度比最小二乘法高,一般来说,
本节通过仿真实验来分析锚节点数量、测距误差、网络节点平均连通度对配准精度的影响,比较基于最小二乘与基于普氏分析的坐标配准精度。配准精度用平均绝对误差MAE来评价,MAE的定义为
| ${\rm{MAE}} = \frac{1}{N}\sum\limits_{i = 1}^N {\left\| {{{{\hat{ X}}}_i} - {{{X}}_i}} \right\|} $ | (18) |
实验软件是Windows10系统下Matlab2017a。协同定位算法选择经典MDS+ LM算法,即经典MDS求解初始输入,LM算法迭代求精。基于普氏分析的配准算法,用PA表示。基于最小二乘的配准算法作为对比算法,用LS表示。
在2D和3D环境下分别进行实验,以测试不同锚节点数量对配准精度的影响。理论上,2D空间坐标配准至少需要3个锚节点,3D至少需要4个,然而2D空间中锚节点可能存在的共线问题(3D空间中锚节点的共面问题)会放大配准误差,从而影响本文对LS和PA的比较。因此,分别令
|
Download:
|
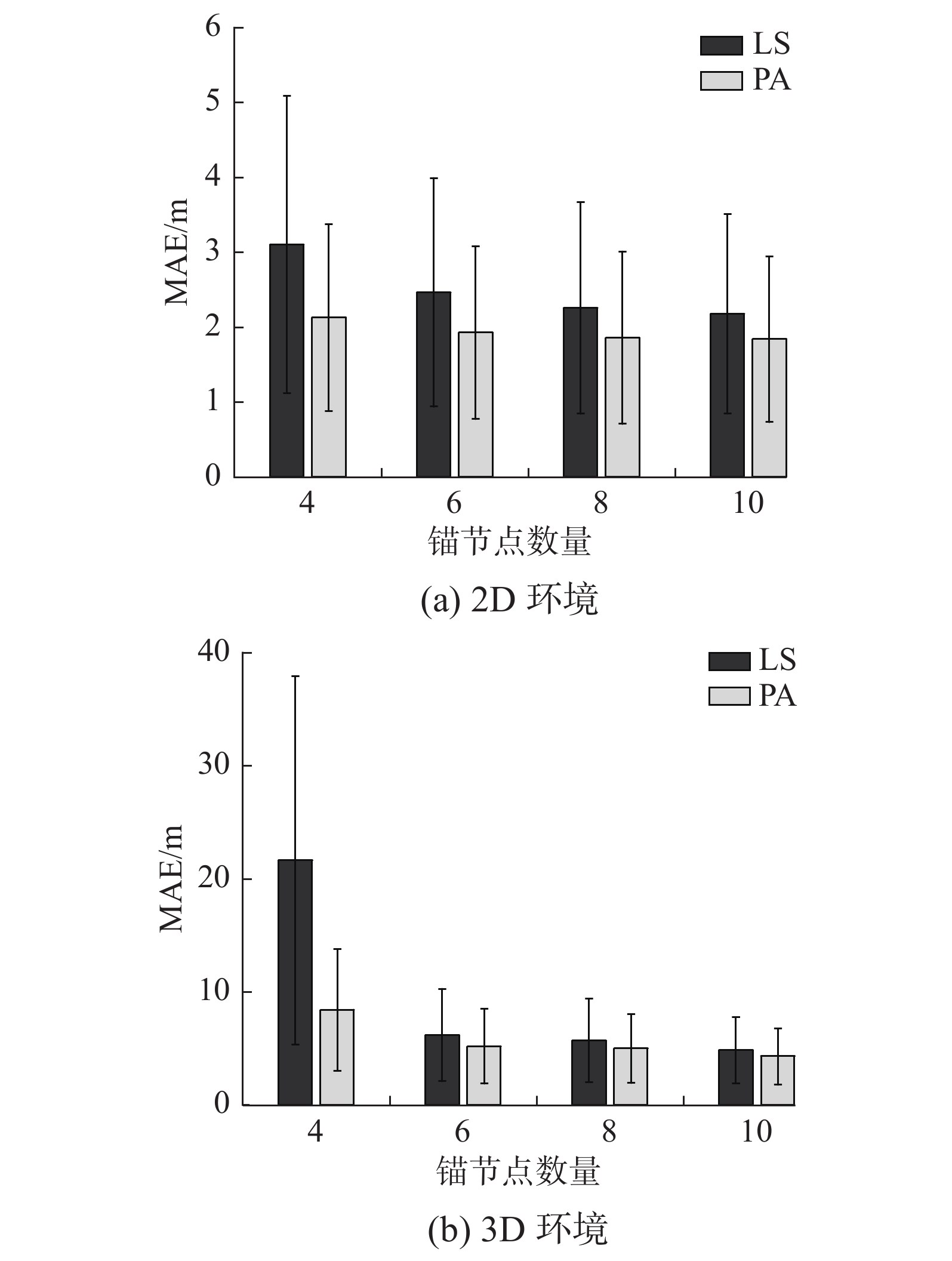
| 图 1 不同锚节点数量对配准精度的影响 Fig. 1 Influence of the number of anchor nodes on the registration accuracy | |
由图1可知,随着锚节点数量的增加,无论在2D环境还是3D环境下,2种配准方法的MAE都呈下降趋势,也即配准误差在降低。在3D环境下,当只有4个锚节点参与配准时(理论上的最小值),配准精度很低,且标准差很大,配准精度不稳定。这充分说明了坐标配准是协同定位的重要组成部分。将锚节点的数量增加至6个,相较于4个锚节点时,无论在2D还是在3D环境下,配准精度都有较大幅度的提高。继续增加锚节点数量,配准精度有提高的趋势,但收益不再明显。在进行坐标配准时,可以在满足最低要求的条件下,增加2~3个冗余锚节点来降低配准误差。对于2种算法,在不同的维数、不同的锚节点数量下,PA的配准精度均高于LS,且标准差更小,更加稳定。以2D环境下6个锚节点为例,LS的MAE是2.465 m,PA的MAE是1.928 m,相较于LS算法,其MAE下降了约22%。在3D环境4个锚节点下,PA算法的优势更加明显。PA算法的计算复杂度高于LS,但考虑到锚节点数量较少,求解
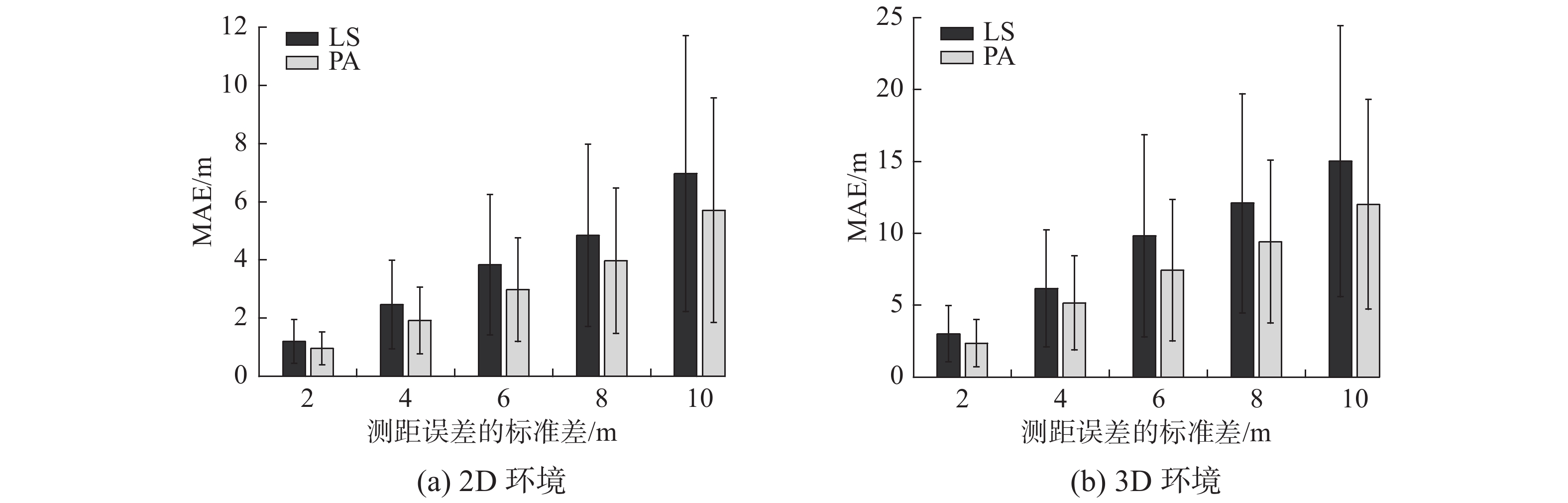
在2D和3D环境下分别进行实验,以测试不同测距误差对配准精度的影响。锚节点数量
|
Download:
|
| 图 2 不同测距误差对配准精度的影响 Fig. 2 Influence of ranging errors on the registration accuracy | |
在2D环境下进行实验,以测试不同节点平均连通度对配准精度的影响,节点平均连通度用deg表示。节点随机布置后,

|
Download:
|
|
图 3 网络平均连通度为6时的坐标配准
Fig. 3 Coordinate registration of
|
|
|
Download:
|
|
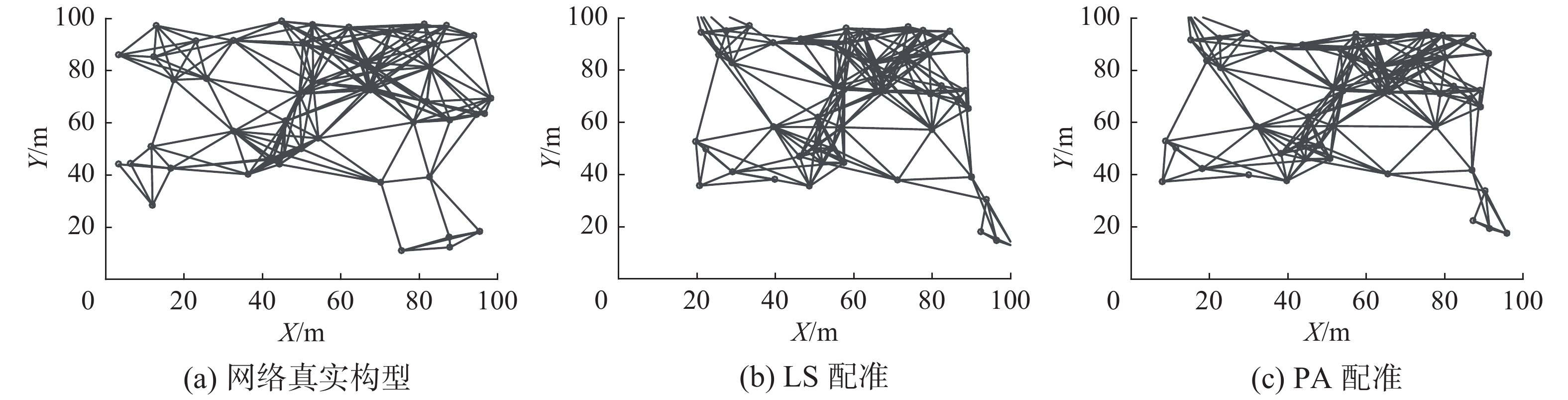
图 4 网络平均连通度为8时的坐标配准
Fig. 4 Coordinate registration of
|
|
如图3,当

|
Download:
|
|
图 5 网络平均连通度为10时的坐标配准
Fig. 5 Coordinate registration of
|
|

|
Download:
|
|
图 6 网络平均连通度为16时的坐标配准
Fig. 6 Coordinate registration of
|
|
本文介绍了协同定位中的坐标配准问题,给出了基于最小二乘与基于普氏分析的坐标配准算法的主要步骤。通过大量的仿真实验证明,坐标配准是协同定位的重要组成部分,一个合理的坐标配准体系可以体现协同定位算法的性能,否则可能会放大定位算法的误差。本文的主要结论有2个方面:1)在不同维数的环境、不同锚节点数量、不同测距误差、不同网络节点平均连通度下,基于普氏分析的坐标配准均优于基于最小二乘的坐标配准,配准误差降低约20%;2)设置配准所用的锚节点数量,2D环境下建议设置4~5个,3D环境下建议设置6~7个。在实验的过程中,不论采用哪种配准算法,锚节点的构型都会对配准精度产生一定影响。目前采用的方法是适当增加锚节点数量来降低这种影响,进一步工作希望能够定量地研究锚节点的构型对配准精度的影响。
| [1] |
WANASINGHE T R, MANN G K I, GOSINE R G. Distributed leader-assistive localization method for a heterogeneous multirobotic system[J]. IEEE transactions on automation science and engineering, 2015, 12(3): 795-809. DOI:10.1109/TASE.2015.2433014 ( 0) 0)
|
| [2] |
YAN Yuan, MOSTOFI Y. Robotic router formation in realistic communication environments[J]. IEEE transactions on robotics, 2012, 28(4): 810-827. DOI:10.1109/TRO.2012.2188163 ( 0) 0)
|
| [3] |
SUN Qian, TIAN Yu, DIAO Ming. Cooperative localization algorithm based on Hybrid topology architecture for multiple mobile robot system[J]. IEEE internet of things journal, 2018, 5(6): 4753-4763. DOI:10.1109/JIOT.2018.2812179 ( 0) 0)
|
| [4] |
WANG Chunxiang, HUANG Hairu, JI Yang, et al. Vehicle localization at an intersection using a traffic light map[J]. IEEE transactions on intelligent transportation systems, 2019, 20(4): 1432-1441. DOI:10.1109/TITS.2018.2851788 ( 0) 0)
|
| [5] |
DENTLER J, KANNAN S, BEZZAOUCHA S, et al. Model predictive cooperative localization control of multiple UAVs using potential function sensor constraints: a workflow to create sensor constraint based potential functions for the control of cooperative localization scenarios with mobile robots[J]. Autonomous robots, 2019, 43(1): 153-178. DOI:10.1007/s10514-018-9711-z ( 0) 0)
|
| [6] |
WANG Xianpeng, YANG L T, MENG Dandan, et al. Multi-UAV cooperative localization for marine targets based on weighted subspace fitting in SAGIN environment[EB/OL]. (2021−3−17)[2021−4−30]https://ieeexplore.ieee.org/document/9380358.
( 0) 0)
|
| [7] |
朱健楠, 虞梦苓, 杨益新. 无人水面艇感知技术发展综述[J]. 哈尔滨工程大学学报, 2020, 41(10): 1486-1492. ZHU Jiannan, YU Mengling, YANG Yixin. Overview of development of unmanned-surface-vehicle sensing technology[J]. Journal of Harbin Engineering University, 2020, 41(10): 1486-1492. (  0) 0)
|
| [8] |
SHIT R C. Precise localization for achieving next- generation autonomous navigation: State-of-the-Art, taxonomy and future prospects[J]. Computer communications, 2020, 160: 351-374. DOI:10.1016/j.comcom.2020.06.007 ( 0) 0)
|
| [9] |
ZHU Yanbo, LIU Yuan, WANG Zhipeng. Evaluation of GBAS flight trials based on BDS and GPS[J]. IET radar, sonar & navigation, 2020, 14(2): 233-241. ( 0) 0)
|
| [10] |
席志红, 占梦奇. 基于位置范围限定的WiFi-KNN室内定位算法[J]. 应用科技, 2020, 47(4): 66-70. XI Zhihong, ZHAN Mengqi. WiFi-KNN indoor positioning algorithm based on location range limitation[J]. Applied science and technology, 2020, 47(4): 66-70. (  0) 0)
|
| [11] |
JIN Bonan, XU Xiaosu, ZHU Yongyun, et al. Single-source aided semi-autonomous passive location for correcting the position of an underwater vehicle[J]. IEEE sensors journal, 2019, 19(9): 3267-3275. DOI:10.1109/JSEN.2019.2892840 ( 0) 0)
|
| [12] |
WYMEERSCH H, LIEN J, WIN M Z. Cooperative localization in wireless networks[J]. Proceedings of the IEEE, 2009, 97(2): 427-450. DOI:10.1109/JPROC.2008.2008853 ( 0) 0)
|
| [13] |
FAN Yingsheng, QI Xiaogang, LIU Lifang. Fault-tolerant cooperative localization of 3D mobile networks via two-layer filter multidimensional scaling[J]. IEEE sensors journal, 2021, 21(6): 8354-8366. DOI:10.1109/JSEN.2020.3046736 ( 0) 0)
|
| [14] |
SHIT R C, SHARMA S, PUTHAL D, et al. Ubiquitous Localization (UbiLoc): a survey and taxonomy on device free localization for smart world[J]. IEEE communications surveys & tutorials, 2019, 21(4): 3532-3564. ( 0) 0)
|
| [15] |
PIOVESAN N, ERSEGHE T. Cooperative localization in WSNs: a hybrid convex/nonconvex solution[J]. IEEE transactions on signal and information processing over networks, 2018, 4(1): 162-172. DOI:10.1109/TSIPN.2016.2639442 ( 0) 0)
|
| [16] |
SHANG Y, RUMI W, ZHANG Y, et al. Localization from connectivity in sensor networks[J]. IEEE transactions on parallel and distributed systems, 2004, 15(11): 961-974. DOI:10.1109/TPDS.2004.67 ( 0) 0)
|
| [17] |
COSTA J A, PATWARI N, HERO A O. Distributed weighted multi-dimensional scaling for node localization in sensor networks[J]. ACM transactions on sensor networks, 2006, 2(1): 39-64. DOI:10.1145/1138127.1138129 ( 0) 0)
|
| [18] |
NOCEDAL J, WRIGHT S J. Numerical optimization[M]. 2nd ed. Berlin: Springer, 2006: 250−274.
( 0) 0)
|
| [19] |
FAN Yingsheng, QI Xiaogang, LI Bo, et al. Fast clustering-based multidimensional scaling for mobile networks localisation[J]. IET communications, 2020, 14(1): 135-143. DOI:10.1049/iet-com.2019.0444 ( 0) 0)
|
| [20] |
马兰芝, 管亮, 冯新泸, 等. 基于普鲁克分析的润滑油红外光谱指纹区相似度评价方法[J]. 石油学报(石油加工), 2013, 29(5): 891-898. MA Lanzhi, GUAN Liang, FENG Xinlu, et al. The method of similarity determination for lubricating Oil infrared fingerprint by Procrustes Analysis[J]. Acta petrolei sinica (petroleum processing section), 2013, 29(5): 891-898. (  0) 0)
|
| [21] |
陈智强, 王作伟, 方龙伟, 等. 基于机器学习和几何变换的实时2D/3D脊椎配准[J]. 自动化学报, 2018, 44(7): 1183-1194. CHEN Zhiqiang, WANG Zuowei, FANG Longwei, et al. Real-time 2D/3D registration of vertebra via machine learning and geometric transformation[J]. Acta automatica sinica, 2018, 44(7): 1183-1194. (  0) 0)
|
| [22] |
成翔昊, 达飞鹏, 汪亮. 基于融合约束局部模型的三维人脸特征点定位[J]. 浙江大学学报(工学版), 2019, 53(4): 770-776. CHENG Xianghao, DA Feipeng, WANG Liang. Feature fusion based constrained local model for three- dimensional facial landmark localization[J]. Journal of Zhejiang University (engineering science), 2019, 53(4): 770-776. DOI:10.3785/j.issn.1008-973X.2019.04.018 (  0) 0)
|
| [23] |
熊玉雪, 杨慧芳, 赵一姣, 等. 两种评价面部三维表面数据不对称度方法的比较[J]. 北京大学学报(医学版), 2015, 47(2): 340-343. XIONG Yuxue, YANG Huifang, ZHAO Yijiao, et al. Comparison of two kinds of methods evaluating the degree of facial asymmetry by three-dimensional data[J]. Journal of Peking University (health sciences), 2015, 47(2): 340-343. (  0) 0)
|
| [24] |
BAI Xuefeng, CAO Hailong, CHEN Kehai, et al. A bilingual adversarial autoencoder for unsupervised bilingual lexicon induction[J]. IEEE/ACM transactions on audio, speech, and language processing, 2019, 27(10): 1639-1648. DOI:10.1109/TASLP.2019.2925973 ( 0) 0)
|
| [25] |
GOWER J C, DIJKSTERHUIS G B. Procrustes problems[M]. Oxford: Oxford University Press, 2004: 29−48.
( 0) 0)
|
| [26] |
MOHAMMADREZA D. Minimal driver nodes for structural controllability of large-scale dynamical systems: node classification[J]. IEEE systems journal, 2020, 14(3): 4209-4216. DOI:10.1109/JSYST.2019.2956501 ( 0) 0)
|
 2021, Vol. 16
2021, Vol. 16


