国家体育总局棋牌运动管理中心以“创新、协调、绿色、开放、共享”的发展理念为指导，以提升国民素质与人民健康水平为发展目标，提出了“传统棋牌项目趣味化”和“趣味棋牌项目竞技化”的重要发展战略。在巩固传统五棋一牌项目(围棋^[1-3]、象棋^[4]、国际象棋^[5]、国际跳棋^[6]、五子棋^[7]、桥牌^[8])基础的同时，针对趣味棋牌竞技化的发展战略，国家体育总局棋牌运动管理中心首先推出了以民间趣味棋牌运动“斗地主”^[9]为原型的竞技二打一扑克项目。2016年9月3日，举办了首届全国竞技二打一扑克锦标赛(China competitive poker championship，CCPC)^[10]，锦标赛中引入了复式赛制^[11]，复式赛制就是在不同的牌桌上，同一个方位的选手发一模一样的牌，把相同牌面下打出的成绩进行汇总，看谁能打出最好的效果，这样就完全避免了发牌的偶然性，达到竞技化的目的。复式赛制的这些特点决定了二打一游戏等项目能够被纳入智力运动这一体系。但与传统线下的比赛不同，在互联网环境下，复式赛制尚存在一些不公平因素，例如，两个不同方位的人很容易通过语音、视频等方式互相告知自己的手牌，存在网上作弊的问题。同等牌力赛制不需要把同样的牌发给每个参赛的人，而是发同样牌力的牌，以此杜绝网络上打相同牌带来的作弊问题。同时，在同等牌力赛制中，用户不再需要同时开赛，可以充分利用其碎片时间随时参赛，也可以中途停顿，而不会影响整个竞赛的过程，等完成打牌的人数满足比赛要求时就计算排名，比复式赛制更加方便。同时，同等牌力的相关研究成果还能应用于能力评测系统。目前该项目已列入中国大学生计算机博弈大赛暨全国锦标赛竞标赛中^[12-14]。因此，本文拟对竞技二打一比赛中的同等牌力问题进行研究。

1 相关工作

竞技二打一是一种玩法简单、娱乐性强的3人扑克牌游戏。一局牌需3个玩家，1个玩家称为地主，地主的逆时针第1个农民称为下家，逆时针第2个农民称为上家或顶家。在每一局游戏中，地主独立存在，而其他两名玩家以农民的身份组成一队与地主对抗。农民队伍只要有一人比地主先出完手中的牌，农民便可获得游戏胜利，否则地主胜，并计算本局地主得分。

一副完整的纸牌共54张牌，由1张红色小丑牌、1张黑色小丑牌和52张标准牌组成。52张标准牌共包括大小不同的13种牌(2、A、K、Q、J、T(10)、9、8、7、6、5、4、3)，每一种牌各有4张，且大小相同。在每一轮开始时，地主将持有20张牌，其他人每人有17张牌。地主先出牌，且可以打一张牌或任何合法的组合。按逆时针顺序玩家依次出牌，每个后续玩家必须要么“过”(不打牌)，要么通过打出相同数量的牌和相同类型的牌的更高组合来击败前一个玩家。最先出完手中的所有牌的玩家为获胜者。如果对局结束，统计此次对局每个玩家的得分。

对于竞技游戏，每一场牌局可以被视为一次考试，给选手发的初始手牌可以看作考试试题。试题的区分度计算可以参照心理学著名的经典测试理论^[15-16](classical test theory，CTT)，在CTT框架下，通过每个试题与总测试分数的相关关系来反映试题区分度。基于此想法，文献[17]通过统计真人牌谱，计算初始手牌的得分均值和方差，利用得分的均值和方差划分将初始手牌划分为10个分类，认为同一类中的手牌具有同等牌力。然而，这种用得分均值和方差来划分区间的分类方法存在较大的误差，为此文献[18]对其进行了改进，通过统计真人牌谱计算初始手牌的得分概率分布，并以得分概率分布为特征进行聚类从而将初始手牌划分成若干个分类。然而，其仍存在两个问题：1)通过统计不同批玩家的得分分布，来计算不同初始手牌的得分概率分布，作为该初始手牌的特征，这个方法在小样本的情况下，由于不同批玩家统计的得分概率分布不同，实验结果难以验证；2)聚类个数是人为预设定的，无法在实际应用中准确地设定出准确的类别数。为解决第1个问题，本文训练了多个不同水平的“竞技二打一AI程序”，作为固定的“玩家”，打牌生成大量的牌谱，易于同等牌力的验证；为解决第2个问题，本文提出同等牌力的选取方法。

2 同等牌力系统设计与实现 2.1 同等牌力系统设计思想

同等牌力就是初始手牌的难度近似。本文通过等级评估指标(grade difficulty index，GDI)来表示初始手牌的难度。等级难度评估指标的含义是：假设一局牌玩完对应的得分共有k种，得分按从小到大排列，将它们看成k个等级。本文认为如果玩家能达到第i个等级，则玩家必能达到第i−1个等级，不必考虑比他低的等级。故玩家能达到第i个等级的难度就是玩家能达到第i个及其以上等级的概率。由于玩家达到第1个等级的概率是100%，所以不考虑玩家达到第1个等级的难度。等级评估指标由k−1个等级概率值组成。

定义1　等级难度评估指标。衡量一副牌难易程度的指标，记为 $G = ({g_1},{g_2}, \cdots ,{g_{k - 1}})$ ，其中 ${g_i}$ 表示固定玩家能达到第i个及其以上等级的概率，k表示二打一规则中规定得分的数量。

定义2　具有同等牌力的初始手牌。两副初始手牌，由同一批玩家打，得到的两个GDI的欧氏距离小于一定阈值，则两副初始手牌具有同等牌力。

然而，从现有的真人打牌数据中难以找到同一批玩家打若干副初始手牌的数据集，短时间内召集一批玩家打若干副初始手牌同样不现实。因此，本文提出生成多个不同水平的“二打一AI程序”来代替真人打牌，以保证一副牌所得等级难度评估指标的可靠性。

利用“二打一AI程序”生成的大量牌谱数据，本文构建了一个可指定难度的同等牌力生成系统。同等牌力生成系统主要由4部分构成：1)训练多个不同水平的DDZAI来产生大量牌谱；2)统计牌谱，计算每个初始手牌的等级难度评估指标；3)基于等级难度评估指标，指定1个或几个难度作为同等牌力的中心，设定阈值，进行不同牌谱分类，即得到不同级别的同等牌力；4)验证同等牌力生成方法的可靠性。同等牌力系统框架如图1所示。

2.2 训练多个不同水平的“二打一AI程序”

笔者将真人打牌日志进行整理，依据输赢次数进行归类，使用文献[19-25]中提出的竞技二打一出牌算法，该算法通过真人打牌日志使用CNN模型训练出具有似人智能的出牌策略。训练n个不同水平的“二打一AI程序”，具体如算法1。

算法1　训练n个不同水平的DDZAI程序

输入　真人打牌日志；

输出　 n个不同水平DDZAI程序。

1)将同一玩家的牌谱划分到同一个牌谱集；

2)清洗掉牌谱集中数据量少于10局的牌谱集；

3)统计玩家的胜率，并按照胜率对玩家进行非递减排序；

4)将水平接近玩家对应的牌谱集划分到同一个DDZAI训练集中，共分为n个训练集，要求每个训练集中数据量尽量均衡。

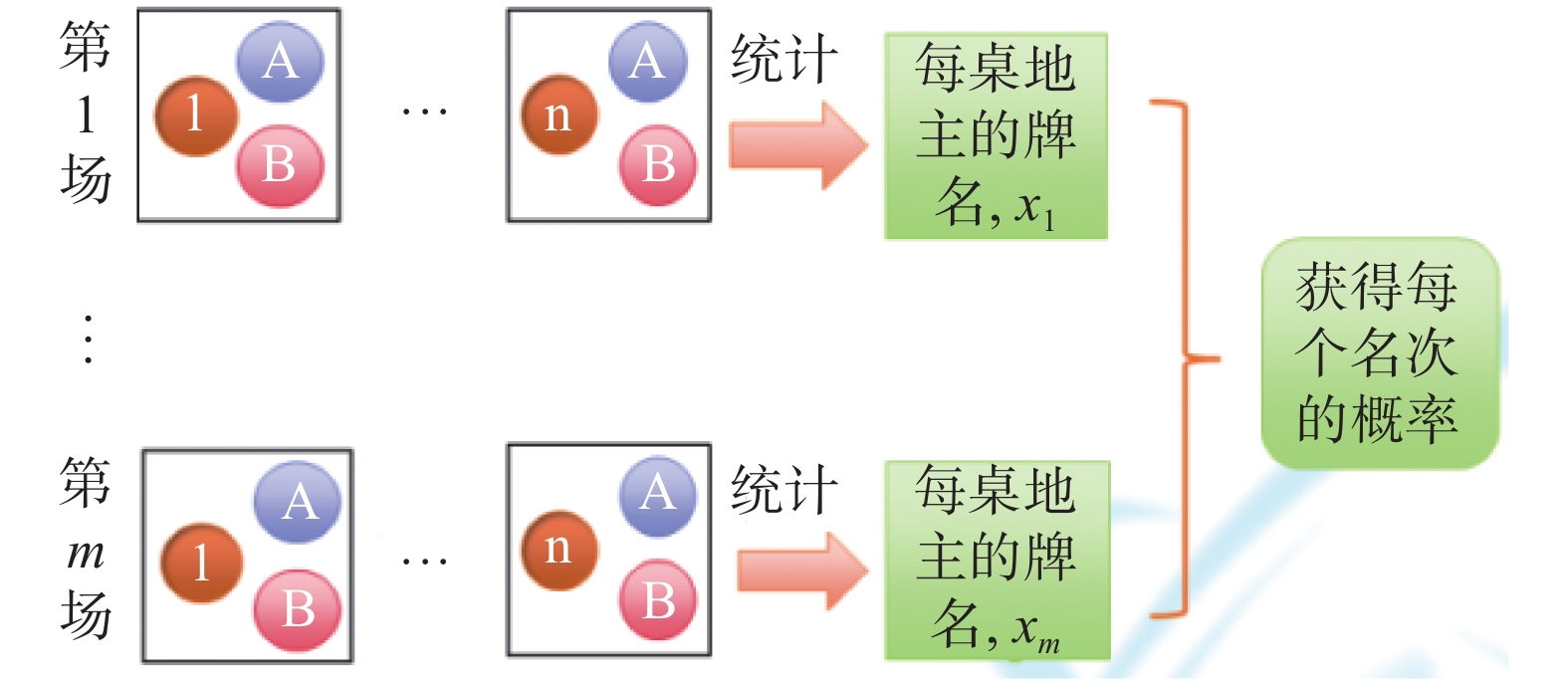
使用文献[21]中提出的竞技二打一出牌算法，分别训练出n个具有不同水平的DDZAI程序。为了验证用上述方法选出的n个DDZAI水平是否有差异，本文通过让这n个DDZAI进行复式赛，其中n个DDZAI的对手相同，并组成n桌。复式赛包括m场比赛，每一场比赛包括多轮比赛来保证n桌DDZAI的地主 ${a_1},{a_2}, \cdots ,{a_n}$ 的排名满足： ${a_i}$ 的水平高于 ${a_j}$ 的水平，i<j，这表明用上述方法选出的n个DDZAI水平有异。具体验证方法如图2所示。

2.3 计算初始手牌的等级难度评估指标

为了对指定难度挑选同等牌力的初始手牌，需要将每副牌难度量化为GDI，初始手牌h的GDI的计算过程为：假设一局牌玩完对应的得分共有k种可能的分值，即 ${s_1},{s_2}, \cdots ,{s_k}$ ；选取n个地主DDZAI，每个地主DDZAI，与同1个下家DDZAI和1个顶家DDZAI组成1桌，共构成n桌AI牌局。为每桌分发同一副初始手牌h，对局后记录每桌的地主得分，假设得分分别为 ${c_1},{c_2}, \cdots ,{c_n}$ ，其中 ${{{c}}_u} \in {\rm{\{ }}{s_1},{s_2}, \cdots ,{s_k}{\rm{\} }}$ ， $u{\rm{ = 1,2,}} \cdots $ ，n按等级排序，统计得分对应的等级次数记为 ${l_1},{l_2}, \cdots ,{l_k}$ 。计算初始手牌h对应的等级难度评估指标 ${G_{\rm{h}}} = ({g_1},{g_2}, \cdots ,{g_k})$ ， ${g_j}$ 的计算公式为

${g_j} = \dfrac{{\displaystyle\sum\limits_{{l_i} \geqslant j + {\rm{1}}} {{l_i}} }}{n}$

(1)

例1　根据比赛规则，得分计算公式为：分数=胜负系数×本局出现的炸弹数量+胜负系数。若地主胜利则胜负系数为1，否则胜负系数为−1。本局出现的炸弹数量为1，则本局的分数为集合R={−2，−1，1，2}中的数之一。这4个分数从小到大排序，定义它们对应的等级分别是1、2、3、4，那么一副牌对应的等级难度评估指标 $G = ({g_1},{g_2},{g_3})$ ，结束后统计得分情况：1桌地主获得−2分，3桌地主获得−1分，2桌地主获得1分，4桌地主获得2分，则 ${g_1} = \dfrac{{3 + 2 + 4}}{{10}} = 0.9$ ， ${g}_{2}=\dfrac{2+4}{10}=0.6$ ， ${g}_{3}=\dfrac{4}{10}=0.4$ ，这副牌对应的等级难度 ${{{G}}_k} = (0.9,0.6, $ $ 0.4)$ 。

一般来说， ${g_i}$ 值表示玩家能达到等级i的概率，某等级对应的值越大代表能获胜的难度越小。如例1， ${{{G}}_k}$ 的难度就表示地主的获胜的难度是0.6，出炸弹能够胜利的难度是0.4。

2.4 选取具有同等牌力的初始手牌

若两副初始手牌的GDI值完全相同或差距足够小，就认为这两副牌的难度相同，即它们具有同等牌力。等级难度评估指标的n个值之间的差距可用欧氏距离计算，计算公式为

${d_{12}} = \sqrt {\sum\limits_{j = {\rm{1}}}^n {{{({g_{1j}} - {g_{2j}})}^2}} } $

(2)

式中两副初始手牌的等级难度评估指标分别为 ${G_1} = ({g_{11}},{g_{12}}, \cdots ,{g_{1n}})$ 和 ${G_2} = ({g_{21}},{g_{22}}, \cdots ,{g_{2n}})$ ，若 ${d_{{\rm{12}}}}$ 值小于预设距离阈值，则 $ {G}_{1} $ 与 $ {G}_{2} $ 具有同等牌力值，否则不具有同等牌力。

系统中也可以任意地或者有目的性地指定一个难度 ${G_c}$ 。比如一轮同等牌力比赛中决定分发一副难度中等的手牌，就可以指定 ${G_c} = (0.75, 0.52, $ $ 0.25)$ ， ${{{G}}_{{c}}}$ 的难度就表示地主获胜的难度是0.52，出炸弹能够胜利的难度是0.25。然后设定一个阈值，通过找出GDI与 ${G_c}$ 的距离小于ε的初始手牌，来生成与这个难度相对应的同等牌力的牌。

为验证同等牌力生成方法的可靠性，本文指定了n个不同水平的地主DDZAI，与相同的1个下家DDZAI和1个上家DDZAI组成n桌，作为同一批比赛选手，分别进行复式赛、同等牌力赛和随机发牌赛。复式赛指每一轮为每桌分发相同的初始手牌。同等牌力赛是指每一轮为每桌分发不同的具有同等牌力的初始手牌。随机发牌赛指每一轮为每桌随机分发不同的初始手牌。

3种比赛都采用同一批选手，分别进行r场比赛，每场比赛进行m轮。每轮比赛记录每桌DDZAI的地主得分。m轮比赛后，统计每桌DDZAI地主总得分，并记录每桌DDZAI的地主名次。r场比赛后，统计每桌DDZAI地主获得每个名次的概率，并以概率最大对应的名次作为地主DDZAI的排名。由于比赛选手固定，如果r场比赛后，同等牌力赛后选手排名与复式赛后选手的排名基本一致，而与随机发牌比赛后选手的排名不一致，就表明同等牌力生成方法是有效的，同等牌力赛代替复式赛是可行的。

3 实验与分析

本文使用Intel Xeon E5-2640 CPU，NVIDIA 2080Ti GPU和Ubuntu 16.04系统的服务器，Python语言，对所提方法进行了3个实验。

实验1　生成多个具有区分度的DDZAI

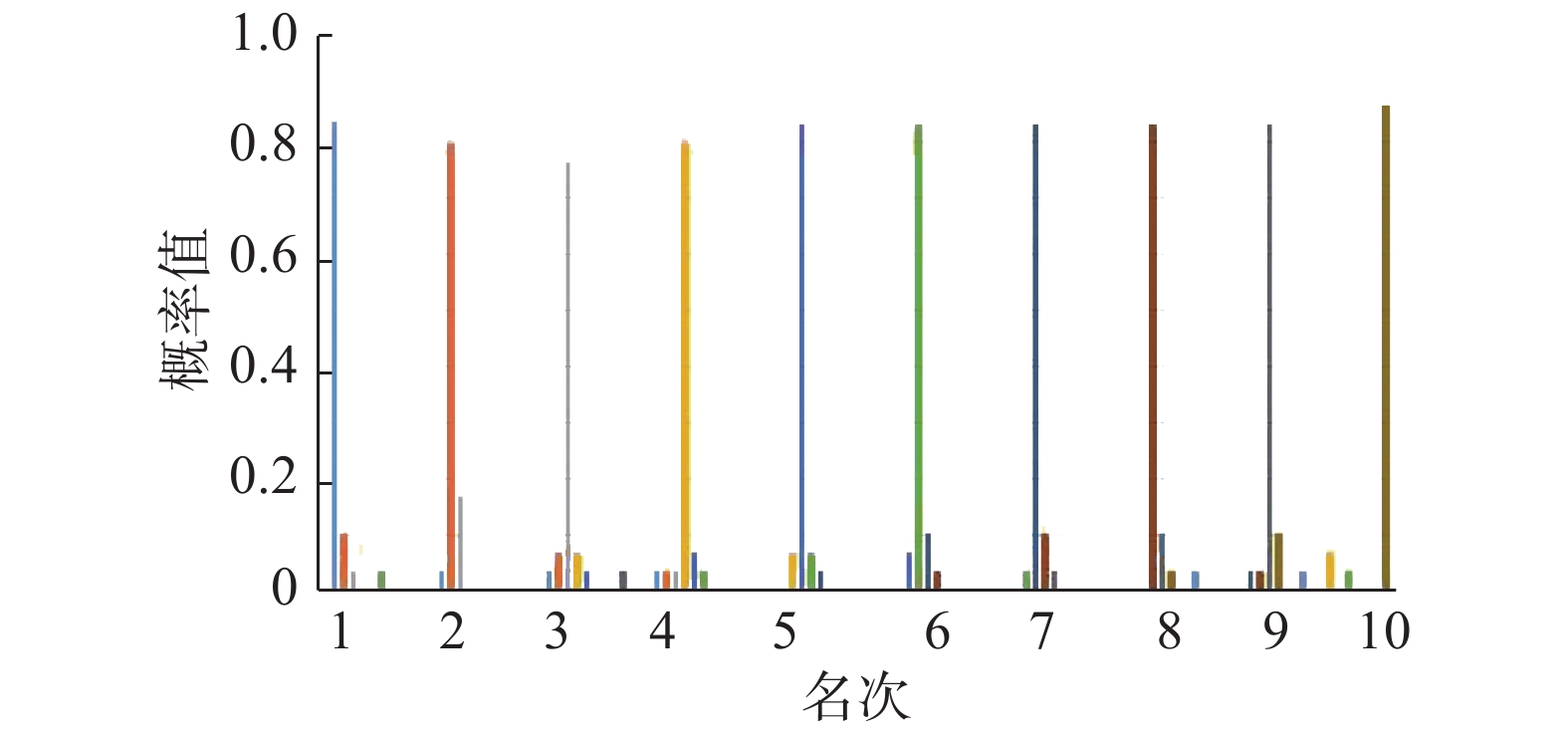
利用国内某著名竞技二打一游戏平台提供的7 000万条游戏日志，使用算法1，将地主的数据集划分为70个，分别训练了70个地主DDZAI；另外利用下家和顶家数据，训练了1个下家DDZAI和1个顶家DDZAI。每桌固定下家和顶家DDZAI，与不同的地主共组成70桌牌局。本文随机选取了其中的10桌DDZAI，根据图2所示进行复式赛。10个DDZAI获得每个名次的概率以及每个DDZAI的排名如图3所示。

实验结果表明：10个DDZAI在不同名次的概率值是不同的，与复式赛得出的排名基本一致，表明生成的DDZAI是具有一定区分度的。

实验2　具有同等牌力的初始手牌测试

随机生成20万副3家持有的炸弹总和数为1的初始手牌，发给70桌，共生成1400万个牌谱，分别计算20万副初始手牌的GDI。

本文以初始手牌Center难度GDI=(0.96,0.91,0.79)作为参照，设置参数ε=0.15，选取了5个具有不同难度的GDI，如表1所示。利用式(2)，分别计算与center的距离，计算结果显示前3个都小于0.15，这表明三者具有同等牌力。后2个计算与center的距离大于0.15，表明这两者不具有同等牌力。

首先从手牌对应的难度值上分析同等牌力情况。手牌Center难度GDI=(0.96,0.91,0.79)表明此牌有91%的概率赢得比赛，有79%的概率出炸弹^[14]并赢得比赛，对于地主来说获胜难度很小。Center1对应的初始手牌有95%的概率赢得比赛，有95%的概率出炸弹并赢得比赛，对于地主来说获胜难度很小。Center2获胜的概率是97%，出炸弹并能胜利的概率为82%，对于地主来说获胜难度小。Center3获胜的概率是85%，出炸弹并能胜利的概率为72%，对于地主来说获胜难度较小。Center4获胜的概率是67.7%，出炸弹并能胜利的概率为61.8%，对于地主来说打牌难度很大。Center5获胜的概率是100%，出炸弹并能胜利的概率为100%，对于地主来说打牌获胜过于简单。

对应表1生成的初始手牌事例，如表2所示，下面从牌面对这5副初始手牌的难度进行分析。

第1副初始手牌：地主持有最大的3张，且地主出顺子6789TJ或者56789TJ后会将农民的手牌拆散，若农民的水平不够，只要放走地主一手小单牌或者小对子，则地主能够出炸弹并胜利，因此第1副初始手牌符合Center的难度。

第2副初始手牌：地主持有最大的3张，且2家农民掉张过多，会放走地主的小牌，地主能够大概率出炸弹并胜利，因此第2副初始手牌符合Center的难度。

第3副初始手牌：地主持有最大的对子，如果农民拆AAA管地主的QQ，则地主的KKK又变成最大，地主能够大概率出炸弹并胜利，因此第3副初始手牌符合Center的难度。

第4副初始手牌：农民持有最大的对子，且地主不善于打对子，农民有控制牌权的能力，且地主小牌较多，但是地主持有KKKAAA2D大牌和炸弹，能够大概率胜利，但是难度要高于前3副牌。

第5副初始手牌：地主持有3个3张带单，1个炸弹，2个对子，地主必能出炸弹胜利，此手牌过于简单，因此第5副初始手牌也不符合Center的难度。

实验结果表明，根据不同初始手牌GDI值的相近程度，来认定哪些牌具有同等牌力的方法是可行的。

实验3　验证同等牌力应用于比赛的可行性

本文共选取了5桌DDZAI参加比赛，复式赛、随机发牌赛和同等牌力赛的比赛场数都为20，一场比赛的轮数分别设置为5、10、20。选取同等牌力的初始手牌时，设置Center难度为GDI=(0.96,0.91,0.79)，ε的取值分别设置为0.15、0.20、0.25。复式赛每个DDZAI获得排名1~5的概率如表3所示。

随机发牌赛每个DDZAI获得排名1~5的概率如表4所示，参数ε不同取值的同等牌力赛后，每个DDZAI获得排名1~5的概率如表5所示。

实验结果分析：1)对比表3、4、5，可以看出当ε = 0.15时，同等牌力赛的DDZAI排名与复式赛的DDZAI排名一致，与随机发牌赛的DDZAI排名不一致，说明了同等牌力生成方法的可靠性；2)从表4可以看出，当ε增大时，DDZAI获得每个名次的概率分布越均衡，评估出AI名次的难度越大，ε<0.15是合适的取值，所以ε的选择较关键。3)对比表3、4、5，可以看出当ε确定时，随着比赛轮数的增加，DDZAI获得每个名次的概率分布没有变化，因此增加比赛轮数不会降低同等牌力赛评估出AI名次的难度。

4 结束语

本文创新性地提出由多个不同水平的“二打一AI程序”来代替真人打牌，产生牌谱，生成同等牌力并进行验证的方法，以保证实验结果的可靠性；提出了用等级难度评估指标GDI来表示初始手牌的难度，给出了判定具有同等牌力的初始手牌的方法；通过指定DDZAI分别进行随机发牌赛、复式赛和同等牌力赛。实验表明，在选择合适阈值情况下，提出的同等牌力生成方法是有效的，用同等牌力赛代替当前的复式赛是可行的。

本文提出的方法需要通过DDZAI计算每一副初始手牌的GDI，消耗的时间较多，只能将得出的具有同等牌力的初始手牌提前存储在牌库中用于比赛，这就需要建立一个可动态、随机生成指定难度的初始手牌系统。本文在接下来的研究中，将对动态的“同等牌力”生成系统进行研究。