2. 东北大学 信息科学与工程学院,辽宁 沈阳 816819
2. Faculty of Information Science and Engineering, Northeastern University, Shenyang 816819, China
随着信息技术的发展,很多制造型企业将物流业务外包给第三方物流代理商(third party logistics, 3PL),由他们承担仓储、运输等任务。对于一些大型企业,多元化、国际化的趋势逐渐增强,供应链策略的设计、优化要与企业的竞争策略相辅相成,考虑内外环境因素的影响,这一问题已然成为一个规模庞大、构造复杂的系统工程[1]。但是3PL只承担实际的物流操作业务,在资源配置、统筹规划、集成技术、综合技能等方面存在一定的局限性,无法实现整个物流系统的优化[2]。美国埃森哲(Accenture)咨询公司在1996年最先提出了第四方物流(fourth party logistics, 4PL)的概念[3],4PL是在3PL的基础上发展起来的,通过集合资源、技术、能力来构建一套完整的供应链解决方案[4]。与3PL相比,4PL具备获取资源和协调规划的能力[5]。企业将供应链的整体优化外包给4PL,4PL通过一系列的考察、分析、规划、设计,将具体的物流作业外包给3PL,进一步提升物流运输的效率,同时使企业能够将自身的资源用于其核心业务[6]。
4PL具有明显的优势,在物流领域中起到举足轻重的作用,得到了国内外学者的广泛研究。同时,4PL也面临着巨大挑战,归结起来可分为2个方面:1)黄敏等[7]提出4PL如何激励3PL提高物流服务质量并降低配送过程中的风险问题;2)如何对资源进一步整合优化使得3PL在可以接受的配送成本条件下提高物流服务质量,使得3PL切实感受到4PL的加入可以使它们能够将自身资源用于其核心业务。因此,考虑在委托商可接受的最大成本约束下,提高加入4PL后的3PL的物流服务质量具有重要研究价值。本文对4PL的路径优化问题进行研究,缩短配送时间,提高物流服务质量。关于4PL的运输路径优化问题,综合考虑3PL的能力、信誉、转运时间及运输成本等因素的影响,如黄敏等[7]充分考虑不确定环境的影响,将3PL代理商的配送时间设定为不确定变量,建立了4PL路径规划模型,并采用多种改进的遗传算法进行求解;崔研等[8]考虑中转发车时间,以运输时间为约束条件,以总成本最小为目标函数,建立了基于一点到多点的多任务第四方物流路径优化模型,并设计蚁群优化算法求解模型;薄桂华等[9]将嵌入删除算法和声搜索算法两阶段算法,用于加快求解带时间窗约束的4PL路径优化问题的运行时间;王勇等[10]考虑了时间和风险因素的约束,研究多任务、多代理商的4PL作业整合优化,采用柔性禁忌算法求解模型[10];崔研等[11]结合模糊的转运时间和最小的成本约束,研究多点到单点的4PL路径优化问题,设计文化基因算法求解模型;陈建清等[12]建立了赋予多维权的有向图模型,描述第四方物流中路径优化、3PL代理商选择等问题,并提出基于Dijkstra算法的求解方法。对于4PL的路径优化问题,既要考虑委托商提出的成本约束,又要满足客户对运输时间的期望。同时,由于运输环境的不确定性,各个3PL代理商运输能力的不同,城市节点中存在的转运时间,4PL路径优化已然成为一个复杂、影响因素相互制约的系统工程问题。在一定的成本预算约束下,如何设计运输路径,选择合适的3PL代理商,形成一套完整的供应链解决方案以实现客户期望的时间,已经成为4PL亟待解决、不断优化的问题。
本文针对4PL运作中的运输时间优化问题,建立了4PL运输时间优化模型。引入收敛因子和隶属度函数,对基本粒子群优化算法(particle swarm optimization, PSO)进行改进,设计收敛模糊粒子群优化算法(convergence fuzzy particle swarm optimization, CFPSO)对4PL运输时间优化问题进行求解。通过3个规模逐渐增大的算例对CFPSO算法的性能进行验证,并且将实验结果与基本PSO、枚举算法(enumeration algorithm, EA)、遗传算法(genetic algorithm, GA)和量子粒子群优化算法(quantum-behaved particle swarm optimization, QPSO)对本问题的求解结果进行比较分析。
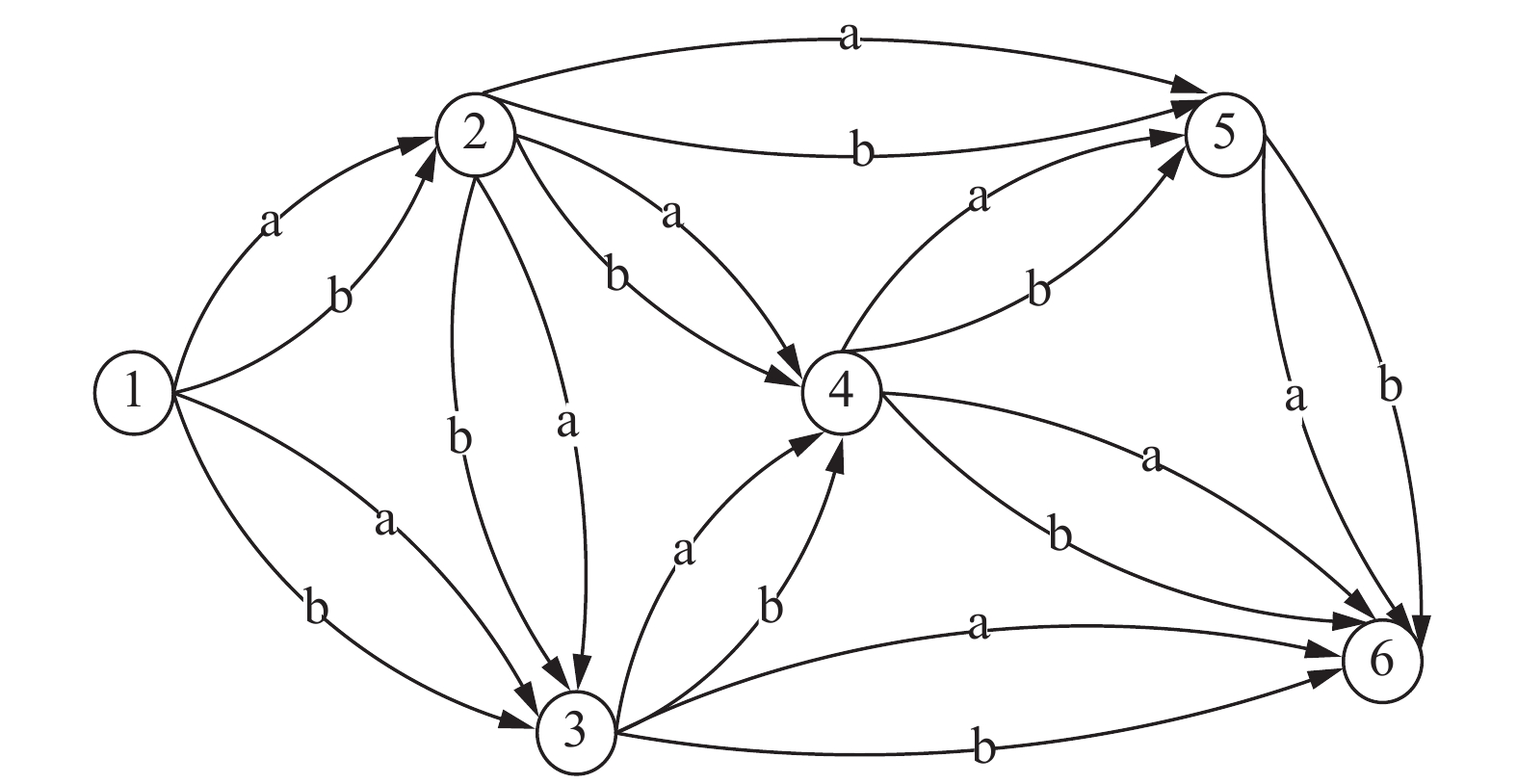
1 第四方物流运输时间优化问题 1.1 第四方物流运输问题在4PL运作中,第四方物流公司通过路径网络图选择合适的路线,将货物从起点城市运输到终点城市。图1为运输路线网络图。
|
Download:
|
| 图 1 运输路线网络 Fig. 1 Transport route network | |
图1中的每个节点表示一个城市,节点1表示起点,节点6表示终点。在物流运输路线上,每两个连通的节点之间有2个备选的代理商,分别是代理商a和代理商b。本文考虑在一定的运输成本约束下,通过选择最佳路径和合适的代理商,实现整体物流作业运输时间最短的目标。
1.2 运输时间优化模型 1.2.1 模型假设与符号定义1)模型假设
①每个作业任务至多由一个代理商负责完成。
②本问题是单任务问题,且只有一个起点和一个终点。
③从出发点运送到终点的过程中,任务需要完成的总运输量不会改变。
2)符号定义
| $ {{\rm{Min}}}\;\;\mathop \sum \limits_{{{g}} = 1}^G \mathop \sum \limits_{i = 1}^N \mathop \sum \limits_{j = 1}^N t_{ij}^gx_{ij}^g $ | (1) |
| $ {{\rm{s}}{\rm{.t}}.}\;\;\mathop \sum \limits_{g = 1}^G \mathop \sum \limits_{i = 1}^N \mathop \sum \limits_{j = 1}^N {d_{ij}}c_{ij}^gQx_{ij}^g \leqslant C $ | (2) |
| $ \begin{array}{c} {\displaystyle\sum_{j = 1}^N} x_{ij}^g \leqslant 1,i \in \left\{ {N - \left\{ 1 \right\}} \right\}, j \in \left\{ {1,2, \cdots ,N} \right\},\\ g \in \left\{ {1,2, \cdots ,G} \right\} \end{array} $ | (3) |
| $ Q \leqslant {Q_g},g \in \left\{ {1,2, \cdots ,G} \right\} $ | (4) |
| $ \left\{ {\begin{array}{*{20}{l}} {1,\;\;\;\;\;{\text{作业在节点}}i{\text{与}}j{\text{之间选代理商}}g}\\ {0,\;\;\;\;\;{\text{作业在节点}}i{\text{与}}j{\text{之间未选代理商}}} \end{array}} \right. $ | (5) |
式(1)为目标函数,表示最小化物流运输时间;式(2)表示各段路径的运输成本之和不超过委托人所能承担的最大成本;式(3)表示至多有一个代理商负责节点
4PL运输时间优化问题的自变量众多,且对算法的运行时间和运行结果的精度要求高,因此采用PSO算法进行求解。PSO算法是一种模拟自然界鸟类觅食过程的生物启发式算法[12-13]。PSO初始化为一群随机粒子,这些粒子在搜索空间中4处移动来寻找问题最佳的解。Shi等[14]引入惯性权重的概念,被大家认为是标准的粒子群优化算法。
模糊粒子群优化算法(fuzzy particle swarm optimization, FPSO)[15]通过改变影响粒子飞行速度、方向的状态更新公式,保持了种群的活跃度,使得算法的精确度大大提升。但是,FPSO需要较长的收敛时间。为了缩短收敛时间,可以引入收缩因子,形成收敛粒子群优化算法(convergence particle swarm optimization, CPSO),相关实验表明此举可以大大提升整个种群的收敛速度[16]。本文考虑吸收FPSO和CPSO的长处,将隶属度函数和收缩因子引入PSO的速度更新公式,从而设计收敛模糊粒子群优化算法(convergence fuzzy particle swarm optimization, CFPSO)。CFPSO不仅可以保证算法的收敛速度,加快全局收敛,还能丰富种群的多样性,减小搜索粒子陷入局部最优的概率,提升算法的整体运算精确度,涵盖了众多改进PSO算法的优势与特点。
2.1 基本PSO算法求解将基本的PSO算法应用到第四方物流运输时间控制问题中,在编码方面,每个粒子被设定为一个备选方案,搜索空间的维数为运输问题中的城市个数,粒子的位置状态信息即是从起点城市向终点城市运输货物的路径。因此,本文采用多进制的编码方式,0表示运输路径不经过该城市,1表示运输路径经过该城市且选择1号代理商承担此段运输任务,2、3等数字与上述意义相同;在初始化种群方面,采用随机初始化的方式,若有两个代理商可供选择,则粒子每一维搜索空间的初始位置在0、1、2中随机产生。第一维与最后一维空间除外,因为这两维代表的是运输路线的起点城市与终点城市,粒子的位置在1、2中随机选取。在选择策略方面,采取优胜劣汰的选择策略。首先,将粒子当前的适应值与自身历史最优值得出的适应值进行比较,若当前的适应值优于自身历史最优值,则更新该粒子的个体历史最优值。然后,对所有粒子的个体历史最优值进行比较,择优选取当代全局最优值,若优于原值,则进行更新,否则进入下次循环,并且以最大迭代次数为终止条件。
2.2 PSO算法改进策略通过加入隶属度函数和收敛因子来更新飞行速度与状态。
| $ v_i^{t + 1} = k\Big[ \omega v_i^t + {c_1}{r_1}\left( {p_i^t - x_i^t} \right) + \displaystyle\sum_{h \in B\left( {i,k} \right)} \varphi \left( h \right){c_2}{r_2}\left( {p_h^t - x_i^t} \right) \Big] $ | (6) |
| $ \begin{array}{l} k = 2/\left| {2 - \phi - \sqrt {\left| {{\phi ^2} - 4\phi } \right|} } \right|,\quad \phi = {c_1} + {c_2}{\rm{}} \end{array} $ | (7) |
| $x_i^{t + 1} = x_i^t + v_i^{t + 1}$ | (8) |
式中:
式(6)为粒子的速度更新公式,式(8)是粒子的位置更新公式[16]。隶属度表示为一个模糊变量,本文基于Bell函数建立隶属度函数[17],如式(9)所示:
| ${\rm{\varphi }}\left( h \right) = \dfrac{1}{{1 + {{\left( {\dfrac{{f\left( {{p_h}} \right) - f\left( {{p_g}} \right)}}{\beta }} \right)}^2}}}{\rm{}}$ | (9) |
式中:
设计罚函数来构造适应度函数:
| $ \begin{array}{l} F = \displaystyle\sum\limits_{g = 1}^G {\sum\limits_{i = 1}^N {\sum\limits_{j = 1}^N {t_{ij}^g} } } x_{ij}^g - \\ {w_1}{\left( {\displaystyle\sum\limits_{g = 1}^G {\sum\limits_{i = 1}^N {\sum\limits_{j = 1}^N {{d_{ij}}c_{ij}^gQx_{ij}^g} - C} } } \right)^ + } - \\ {w_2}{\left( {\displaystyle\sum\limits_{j = 1}^N {x_{ij}^g - 1} } \right)^ + } - {w_3}{\left( {Q \leqslant {Q_g}} \right)^ + } \end{array} $ | (10) |
式中:w1、w2、w3都为惩罚项的系数。
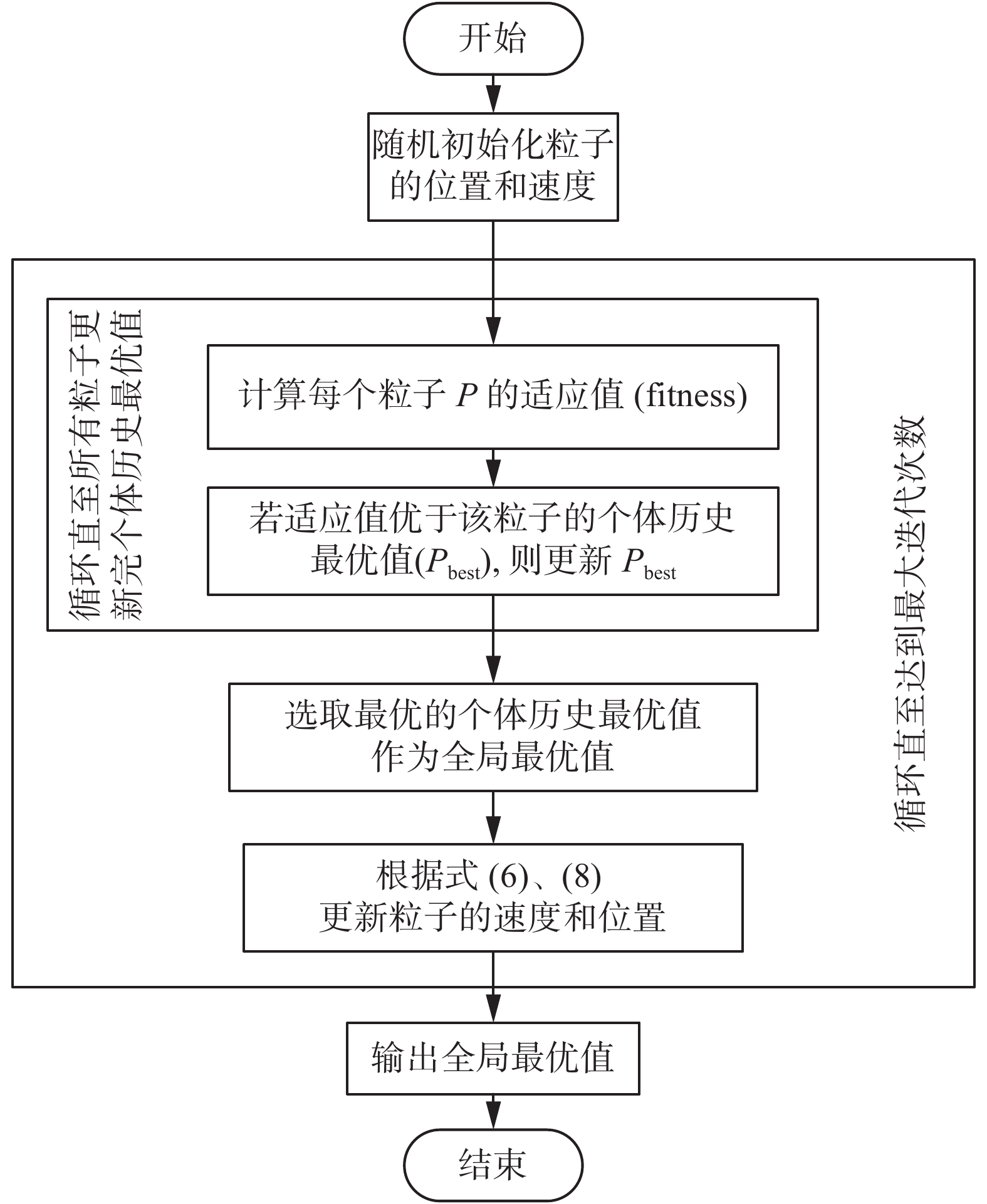
2.4 CFPSO算法流程CFPSO算法流程见图2。
|
Download:
|
| 图 2 CFPSO的流程 Fig. 2 Solution procedeure of the CFPSO | |
本节给出3个不同规模的算例,某物流公司承担运量为100 t的运输任务,在3个规模不同的运输网络中,要求给出在不同的运输成本约束下最小的运输时间、运输路线方案。
3.1 算例1运输网络有6个节点城市,起点城市是杭州,终点城市是淮安。有2种代理商可以承担每段路径具体的运输任务,代理商的运输能力、报价信息如表1所示,每两个相通城市节点之间的距离如表2所示。
| 表 1 算例1代理商运输信息 Tab.1 Details of the transportation agency in case 1 |
| 表 2 算例1城市间距离 Tab.2 Distances between cities in case 1 |
运输网络有12个节点城市,起点城市是杭州,终点城市是石家庄。有3种代理商可以承担每段路径具体的运输任务,代理商的运输能力、报价信息如表3所示,每两个相通城市节点之间的距离如表4所示。
| 表 3 算例2代理商运输信息 Tab.3 Details of the transportation agency in case 2 |
| 表 4 算例2城市间距离 Tab.4 Distances between cities in case 2 |
运输网络有18个节点城市,起点城市是杭州,终点城市是石家庄。每两个相通城市节点之间的距离如表5所示,有3种代理商可以承担每段路径具体的运输任务,代理商的运输能力、报价信息和算例2中相同。
| 表 5 算例3城市间距离 Tab.5 Distances between cities in case 3 |
为了确定收敛因子

|
Download:
|
| 图 3 学习因子对适应值的影响 Fig. 3 Influence of learning factors on fitness value | |
可以看出,随着
设自学习因子
| 表 6 适应值与
|
本节仿真实验参数
|
Download:
|
|
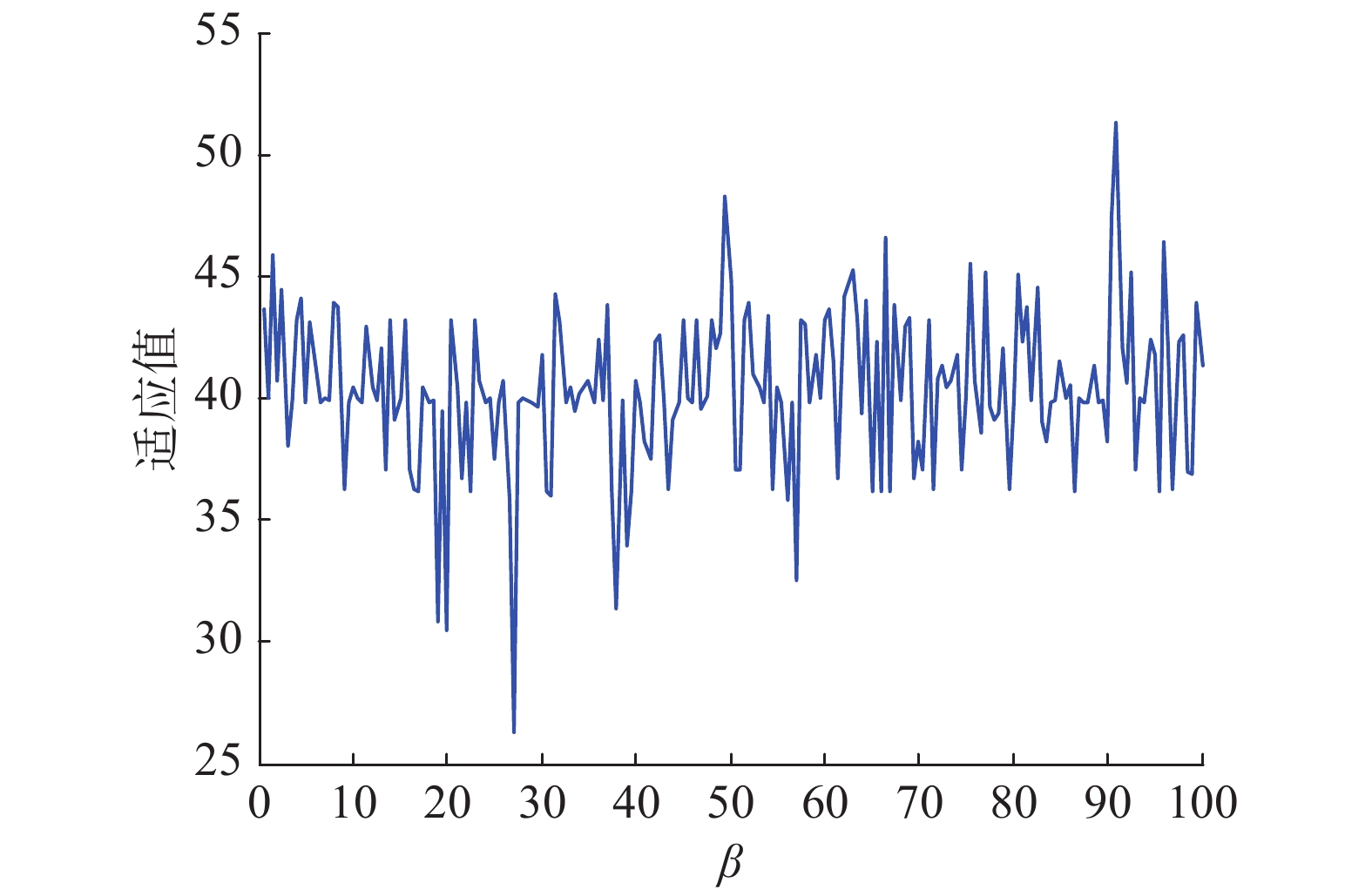
图 4 参数
|
|
从图4中可以看出,随着参数

|
Download:
|
|
图 5 参数
|
|
从图5可以看出,当
为了说明问题这里仅给出算例3的实验结果,见表7。从实验结果可以看出:1)随着运输成本约束的增加,负责每段路径的代理商在不断地变化,最小运输时间也逐渐减少,通过不同的成本约束来控制货物的运输时间;2)委托商给出的整个运输方案的成本预算越多,CFPSO算法运行出的最佳运输路径越倾向于选择速度快的代理商承担运输任务,即花更多的钱来实现运输时间的最优化。
| 表 7 实验结果(算例3) Tab.7 Experimental results (case 3) |
为了验证CFPSO算法的性能,本节采用枚举算法(EA)、基本PSO算法、GA算法和量子粒子群优化(QPSO)算法[18-25]求解上述3个算例,并从最小运输时间、CPU时间等方面进行对比分析。各算例实验结果的对比分别列于表8、9、10中。
| 表 8 各算法运行结果(算例1) Tab.8 Results obtained from the algorithm (case 1) |
| 表 9 各算法运行结果(算例2) Tab.9 Results obtained from the algorithm (case 2) |
| 表 10 各算法运行结果(算例3) Tab.10 Results obtained from the algorithm (case 3) |
综合以上5个算法对3个算例的实验结果,可以得出以下结论:
1)实验结果角度
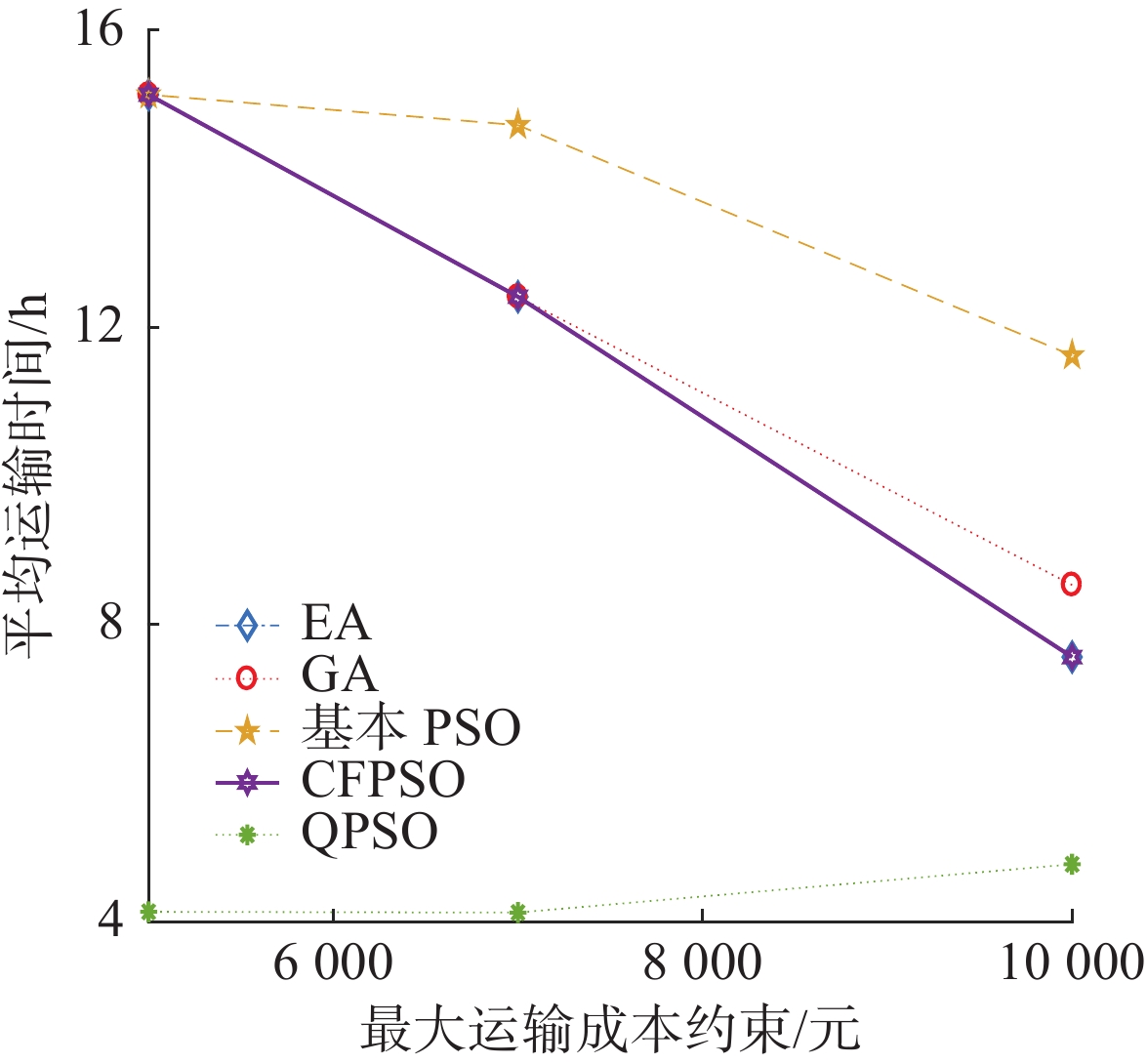
当算例的规模比较小时,如算例1,根据5个算法得到的平均运输时间的优劣性,如图6所示,可以将算法按照收敛能力排序为:
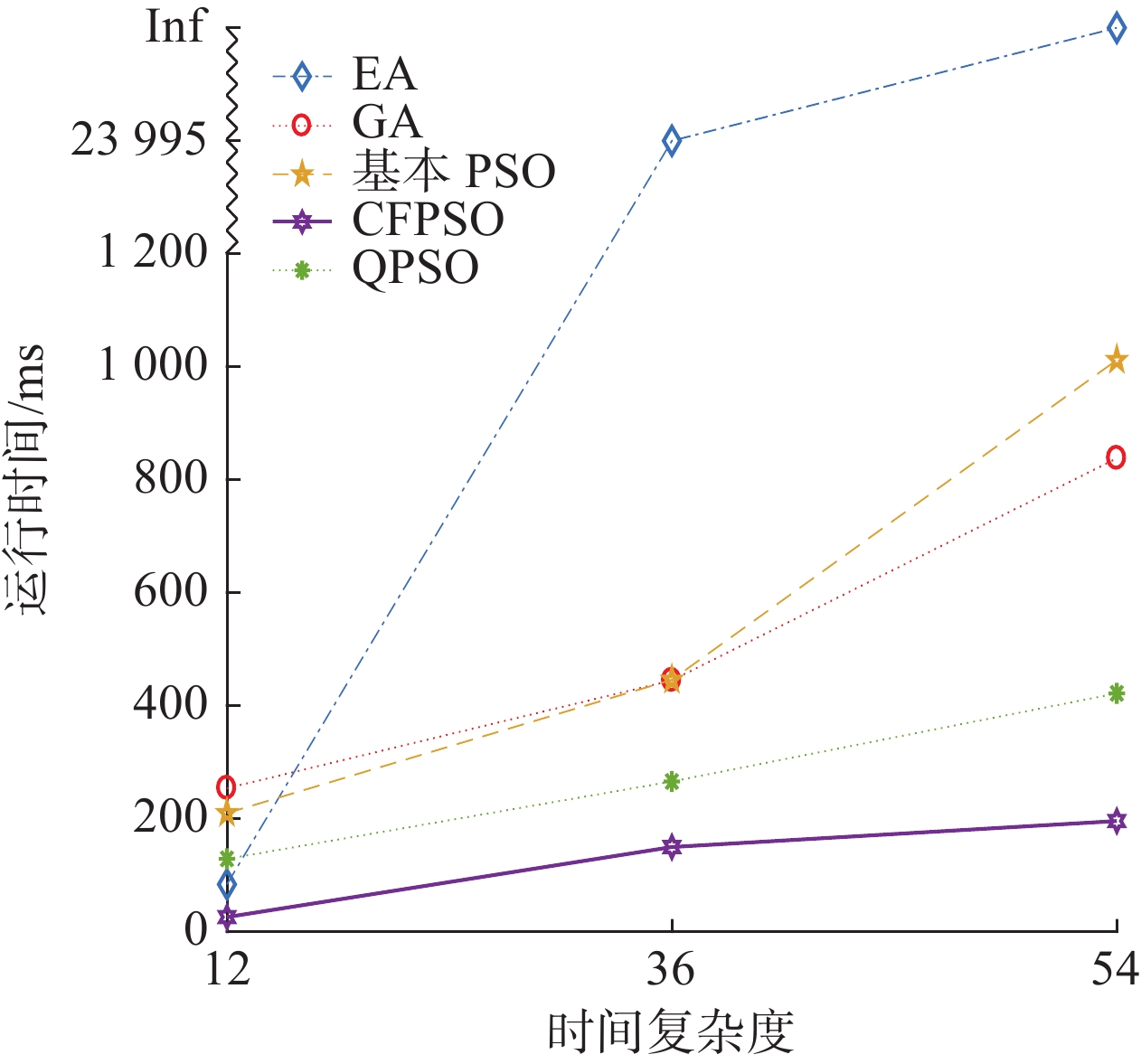
2)CPU时间角度
随着3个算例规模的逐渐增大,算法程序的复杂度也显著增加,在这里将城市个数、代理商个数这两个变量的乘积作为各算例程序的时间复杂度,即
|
Download:
|
| 图 6 算例1实验结果对比 Fig. 6 Comparison of experimental results in case 1 | |
|
Download:
|
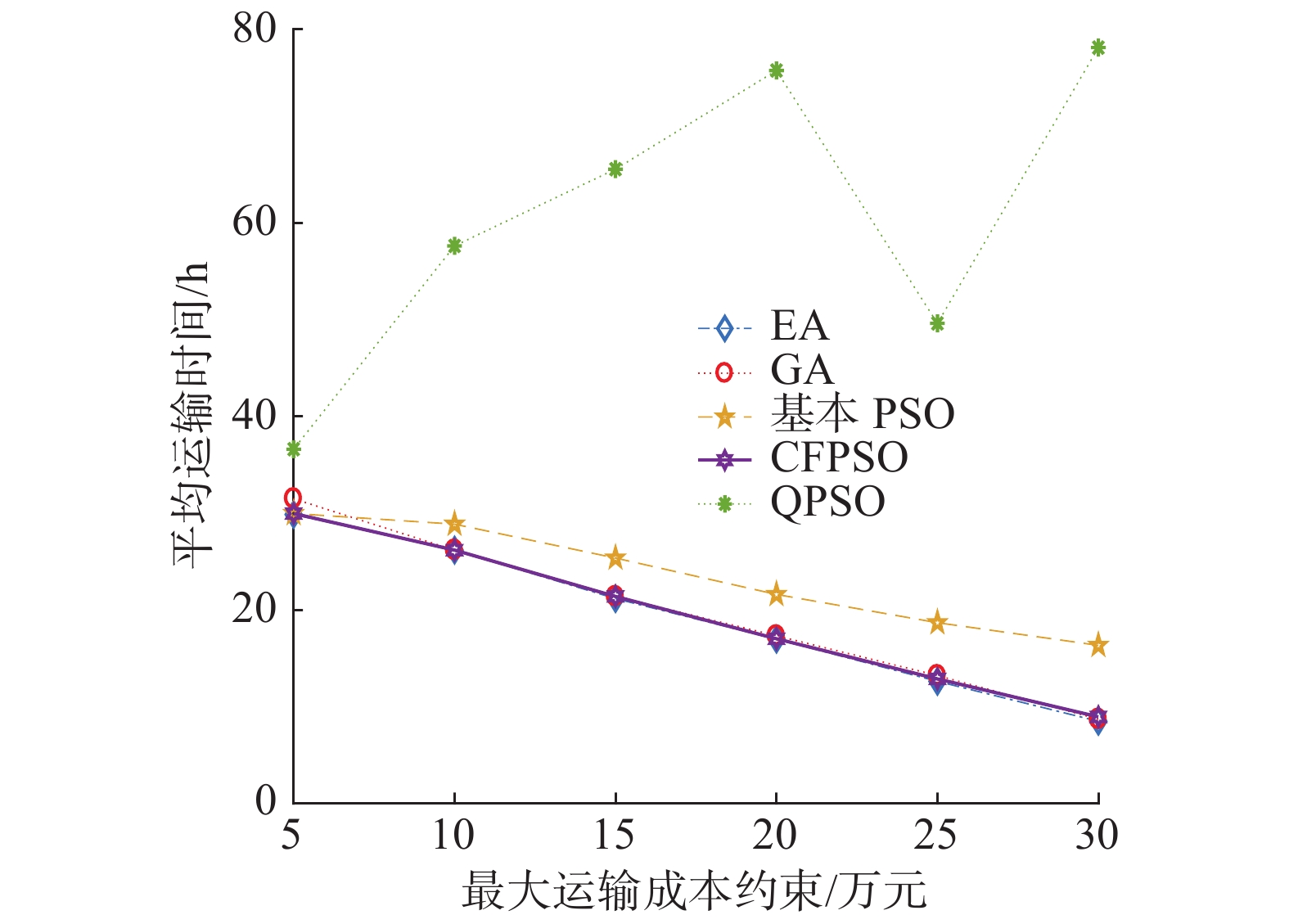
| 图 7 算例2实验结果对比 Fig. 7 Comparison of experimental results in case 2 | |
|
Download:
|
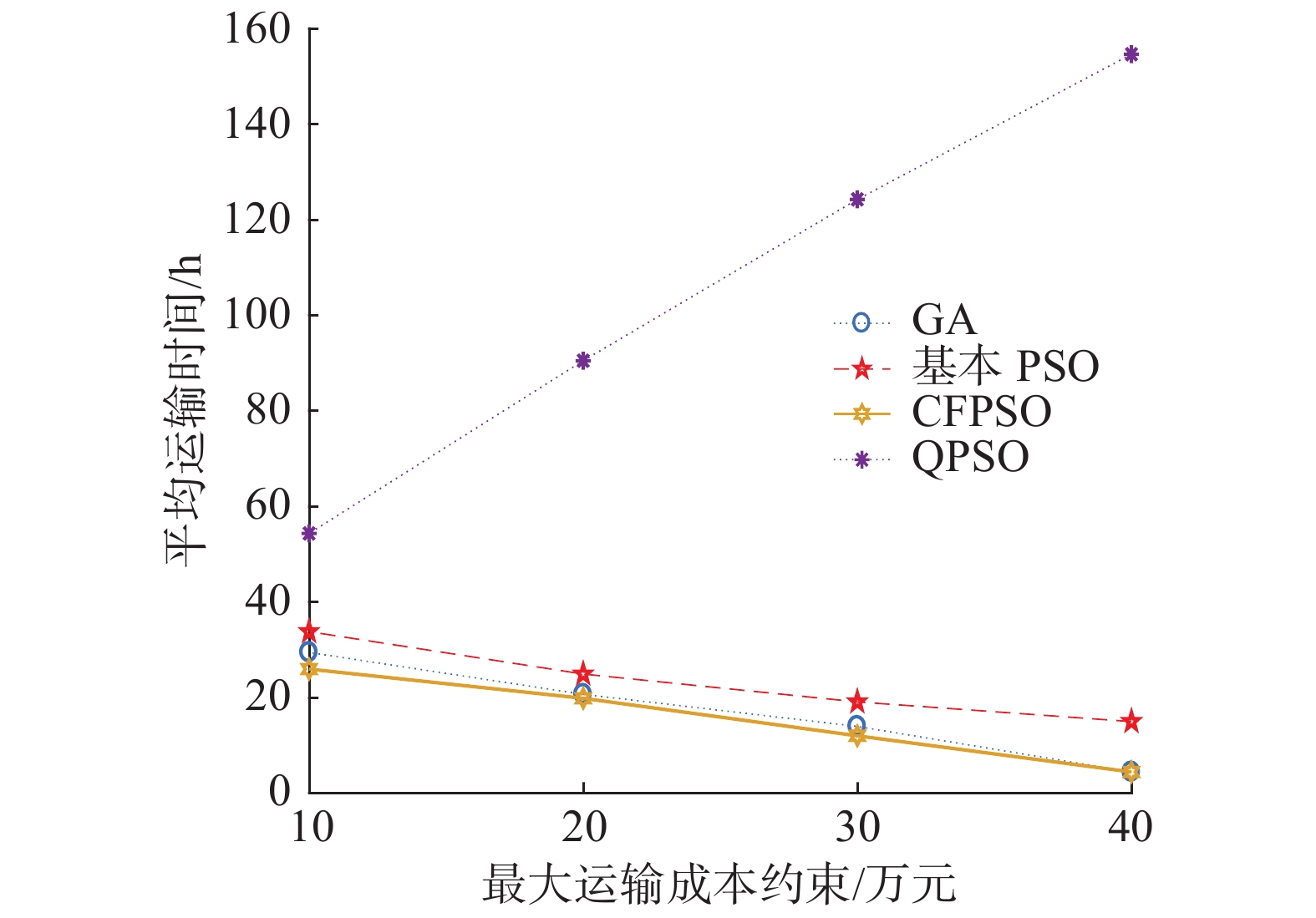
| 图 8 算例3实验结果对比 Fig. 8 Comparison of experimental results in case 3 | |
|
Download:
|
| 图 9 各算法运行时间对比分析 Fig. 9 Comparison of the algorithm’s run time | |
综上所述,CFPSO、QPSO、GA、基本PSO和EA求解本优化问题时各有优劣。针对第四方物流运输时间控制问题,选取最适合的求解算法应从实验结果、CPU时间这两个方面来衡量。通过以上的分析,可以将这4种算法的性能进行排序:
本文针对第四方物流运输时间优化问题,建立了数学模型,设计了收敛模糊粒子群优化算法,设计了多个算例进行实验分析。实验结果分析表明,建立的数学模型合理,能够辅助决策,提供满足运输成本和运输时间要求的决策方案。所设计的收敛模糊粒子群优化算法与枚举算法、基本粒子群优化算法、遗传算法和量子粒子群优化算法相比具有更好的收敛能力和更快的收敛速度,能够有效地解决第四方物流运输时间优化问题,具备可行性。
| [1] |
杨宝军, 李华增. 第四方物流剖析[J]. 工业工程与管理, 2003, 8(3): 49-51, 76. YANG Baojun, LI Huazeng. Analysis of the fourth party logistics[J]. Industrial engineering and management, 2003, 8(3): 49-51, 76. DOI:10.3969/j.issn.1007-5429.2003.03.012 (  0) 0)
|
| [2] |
姚建明, 刘丽文. 4PL模式下的供应链资源整合决策分析[J]. 系统工程, 2007, 25(4): 1-8. YAO Jianming, LIU Liwen. A decision analysis on supply Chain resource integration in 4PL mode[J]. Systems engineering, 2007, 25(4): 1-8. DOI:10.3969/j.issn.1001-4098.2007.04.001 (  0) 0)
|
| [3] |
BADE D J, MUELLER J K. New for the millenium -- 4PL[J]. Transportation & distribution, 1999, 40(2): 78-80. ( 0) 0)
|
| [4] |
HUANG Min, TU Jun, CHAO Xiuli, et al. Quality risk in logistics outsourcing: a fourth party logistics perspective[J]. European journal of operational research, 2019, 276(3): 855-879. DOI:10.1016/j.ejor.2019.01.049 ( 0) 0)
|
| [5] |
YAO Jianming. Decision optimization analysis on supply chain resource integration in fourth party logistics[J]. Journal of manufacturing systems, 2010, 29(4): 121-129. DOI:10.1016/j.jmsy.2010.12.002 ( 0) 0)
|
| [6] |
张新, 田澎. 第四方物流及对物流规划功能的外包[J]. 工业工程与管理, 2002, 7(2): 38-40. ZHANG Xi, TIAN Peng. Fourth party logistics and outsourcing of planning function in logistics[J]. Industrial engineering and management, 2002, 7(2): 38-40. DOI:10.3969/j.issn.1007-5429.2002.02.009 (  0) 0)
|
| [7] |
HUANG Min, REN Liang, LEE L H, et al. Model and algorithm for 4PLRP with uncertain delivery time[J]. Information sciences, 2016, 330: 211-225. DOI:10.1016/j.ins.2015.10.030 ( 0) 0)
|
| [8] |
崔妍, 黄敏, 王兴伟. 考虑中转发车时间4PLRP的模糊规划模型与算法[J]. 系统工程学报, 2012, 27(4): 535-542. CUI Yan, HUANG Min, WANG Xingwei. Fuzzy programming model and algorithm of 4PLRP considering travel schedule[J]. Journal of systems engineering, 2012, 27(4): 535-542. DOI:10.3969/j.issn.1000-5781.2012.04.015 (  0) 0)
|
| [9] |
薄桂华, 黄敏. 考虑拖期风险的第四方物流路径优化问题模型与求解[J]. 复杂系统与复杂性科学, 2018, 15(3): 66-74. BO Guihua, HUANG Min. Model and solution of routing optimization problem in the fourth party logistic eith tardiness risk[J]. Complex systems and complexity science, 2018, 15(3): 66-74. (  0) 0)
|
| [10] |
王勇, 赵骅, 李勇. 用禁忌算法求解第四方物流作业整合优化模型[J]. 系统工程学报, 2006, 21(2): 143-149. WANG Yong, ZHAO Hua, LI Yong. Tabu search algorithm for optimization model of integration of job of 4th party logistics[J]. Journal of systems engineering, 2006, 21(2): 143-149. DOI:10.3969/j.issn.1000-5781.2006.02.006 (  0) 0)
|
| [11] |
CUI Yan, HUANG Min, YANG Shengxiang, et al. Fourth party logistics routing problem model with fuzzy duration time and cost discount[J]. Knowledge-based systems, 2013, 50: 14-24. DOI:10.1016/j.knosys.2013.04.020 ( 0) 0)
|
| [12] |
陈建清, 刘文煌, 李秀. 第四方物流中基于多维权的有向图模型及算法[J]. 工业工程与管理, 2003, 8(3): 45-48, 59. CHEN Jianqing, LIU Wenhuang, LI Xiu. The directed graph model with multi dimensions in the fourth party logistics and its algorithm[J]. Industrial engineering and management, 2003, 8(3): 45-48, 59. DOI:10.3969/j.issn.1007-5429.2003.03.011 (  0) 0)
|
| [13] |
KENNEDY J, EBERHART R C, SHI Y. Swarm intelligence[M]. San Francisco: Morgan Kaufmann Publishers, 2001: 1−10.
( 0) 0)
|
| [14] |
SOMPRACHA C, JAYAWEERA D, TRICOLI P. Particle swarm optimisation technique to improve energy efficiency of doubly-fed induction generators for wind turbines[J]. The journal of engineering, 2019, 2019(18): 4890-4895. DOI:10.1049/joe.2018.9348 ( 0) 0)
|
| [15] |
LAN Rushi, ZHU Yu, LU Huimin, et al. A two-phase learning-based swarm optimizer for large-scale optimization[J]. IEEE transactions on cybernetics, 2020, 2020:1−10.
( 0) 0)
|
| [16] |
ABDELBAR A M, ABDELSHAHID S, WUNSCH II D C. Fuzzy PSO: A generation of particle swarm optimization[C]//Proceedings of International Joint Conference on Neural Networks. Montreal, Canada, 2005: 1086−1091.
( 0) 0)
|
| [17] |
CHEN Chen, XU Junqi, LIN Guobin, et al. Fuzzy adaptive control particle swarm optimization based on T-S fuzzy model of maglev vehicle suspension system[J]. Journal of mechanical science and technology, 2020, 34(1): 43-54. DOI:10.1007/s12206-019-1247-4 ( 0) 0)
|
| [18] |
伍永健, 陈跃东, 陈孟元. 量子粒子群优化下的RBPF-SLAM算法研究[J]. 智能系统学报, 2018, 13(5): 829-835. WU Yongjian, CHEN Yuedong, CHEN Mengyuan. Research on RBPF-SLAM algorithm based on quantum-behaved particle swarm optimization[J]. CAAI transactions on intelligent systems, 2018, 13(5): 829-835. (  0) 0)
|
| [19] |
GUANG He, LU Xiaoli. An improved QPSO algorithm and its application in fuzzy portfolio model with constraints[J]. Soft computing, 2021, 25(12): 7695-7706. DOI:10.1007/s00500-021-05688-3 ( 0) 0)
|
| [20] |
ZHAO Xingang, LIANG Ji, MENG Jin, et al. An improved quantum particle swarm optimization algorithm for environmental economic dispatch[J]. Expert systems with applications, 2020, 152: 113370. DOI:10.1016/j.eswa.2020.113370 ( 0) 0)
|
| [21] |
CHENG Jiatang, XIONG Yan, AI Li. Fault diagnosis of wind turbine gearbox based on neighborhood QPSO and improved D-S evidence theory[J]. Recent advances in computer science and communications, 2020, 13(2): 248-255. DOI:10.2174/2213275912666181218124805 ( 0) 0)
|
| [22] |
CAI Yujie, SUN Jun, WANG Jie, et al. Optimizing the codon usage of synthetic gene with QPSO algorithm[J]. Journal of theoretical biology, 2008, 254(1): 123-127. DOI:10.1016/j.jtbi.2008.05.010 ( 0) 0)
|
| [23] |
XU Xinzheng, SHAN Dong, WANG Guanying, et al. Multimodal medical image fusion using PCNN optimized by the QPSO algorithm[J]. Applied soft computing, 2016, 46: 588-595. DOI:10.1016/j.asoc.2016.03.028 ( 0) 0)
|
| [24] |
LIN Sen, NAN Yurong. Optimization of rolling schedule in tandem cold mill based on QPSO algorithm[J]. Advanced materials research, 2010, 145: 165-170. DOI:10.4028/www.scientific.net/AMR.145.165 ( 0) 0)
|
| [25] |
FAN Qiufeng, WANG Tao, CHEN Yang, et al. Design and application of interval Type-2 TSK fuzzy logic system based on QPSO algorithm[J]. International journal of fuzzy systems, 2018, 20(3): 835-846. DOI:10.1007/s40815-017-0357-3 ( 0) 0)
|
 2021, Vol. 16
2021, Vol. 16


