多智能体系统控制技术是人工智能时代的研究热点之一[1],其成果可用于多个领域,如智能交通、机器人编队,甚至是军事用途,如无人机蜂(狼)群作战等。无人机集群作为一种特殊的多智能体系统,个体无需全局通信,仅通过对其周围一定范围内个体间的通信、合作和协调等就可以表达集群整体结构和功能。它在自组织能力、推理能力,以及对未知环境的适应性等方面有很多潜在应用。
无论是地面起飞式无人机集群,还是空投式无人机集群,其控制技术的难点都在于队形控制,核心在于解决可行性和有效性两个问题[2]:可行性是研究无人机集群能不能全局可控,使之形成所有预定队形;有效性则回答了最少需要输入多少信号,才能达到全局可控。最小领航集选取与这2个问题密切相关。
对于通信网络拓扑结构图为有向图的领航跟随网络系统,文献[3]通过引进匹配概念,使有向网络的可控性问题已得到较好解决。但是,对于无向领航跟随网络系统控制而言,正如Kumar等[4]于2019年所指出的那样:如何选取领航顶点、如何选取最少个数的领航顶点都是尚待解决的难题。
目前,无向网络控制技术已经引起人们的广泛关注。文献[5]是一篇较早关注无向网络可控性的文章,该文通过Kalman秩条件给出了无向网络可控的充要条件。研究无向网络领航集常用的图结构有:强制零点集(zero forcing set, ZFS)[4, 6-8]、约束匹配(constraint matching, CM)[8-11]和非平凡等价划分(nontrivial equitable partition,NEP)[12-15]等。已有的研究成果表明无向网络可控当且仅当领航集是推广的ZFS,且Shima等[8, 10]发现了网络中ZFS与CM之间具有等价关系。基于NEP概念人们给出了网络可控的必要条件,同时也证明了网络可控当且仅当它的每个连通分支可控。
Ji等[16-17]则是通过Laplace矩阵的特征向量研究无向网络的可控性,其中文献[16]给出了无向网络可控的充要条件,文献[17]则给出DCD、TCD等破坏网络可控性的顶点集图特征。文献[18-19]证明了高阶时不变系统的可控性等价于一阶(线性)时不变系统的可控性,通过Laplace矩阵的特征向量给出了无向网络可控的充要条件,同时指出了使网络可控的2个方法:增加领航顶点和修改网络权值。
这些研究关注重点在于从理论上给出领航集的代数特征或图论特征,所举算例规模较小。对于仅具有单特征值的无向网络系统,可以从代数角度给出领航集。理论研究表明,当网络中个体数量趋向无穷时,网络Laplace矩阵仅具有单特征值的概率趋向1。但是,对于无人机集群系统,个体数量大多在几十至几百之间,这类系统的Laplace矩阵具有多重特征值的可能性很大。现有的研究很少涉及求解这种规模无向网络领航集的算法。
复杂网络的相关研究值得借鉴。Hamdan等[20-21]采用启发式算法求复杂网络的领航集,之所以采用启发式算法求领航集是因为这一问题是NP难问题。在无向复杂网络的可控性研究中,多采用携带更多信息的可控性Gramian矩阵[22-23]。Katherine等[24]研究了平均可控性以及可控性与鲁棒性的关系,并给出使树图可控的领航集选取方法。2020年,基于顶点分类文献[25]提出大规模动态系统的最小领航顶点选取问题的算法。
本文针对具有几十个个体的无向领航跟随模式无人机集群领航顶点选取问题,研究领航顶点的图特征,解决具有何种图特征的顶点必须成为领航顶点,以及如何求出最小领航集这2个问题;给出求领航集的算法并用数值仿真实验验证算法的有效性,分析无人机集群领航集的数值特征。
1 基本理论 1.1 无人机集群通信网络的图论模型无人机个体间的通信关系可用图表示。设图
对于领航跟随模式的无人机集群,接收外界输入控制信号的个体称为领航顶点,其余顶点则称为跟随顶点。本文考虑有n个无人机个体的线性时不变系统,个体的动力学方程描述为
| $ {x_i}^\prime = \left\{ \begin{split} &\displaystyle\sum\limits_{{v_i},{v_j} \in E(G)} {({x_j} - {x_i})} ,\quad{x_i}{\text{为跟随顶点}}\\ &\displaystyle\sum\limits_{{v_i},{v_j} \in E(G)} {({x_j} - {x_i})} + {u_i},\quad{x_i}{\text{为领航顶点}} \end{split} \right. $ | (1) |
式中:
|
Download:
|
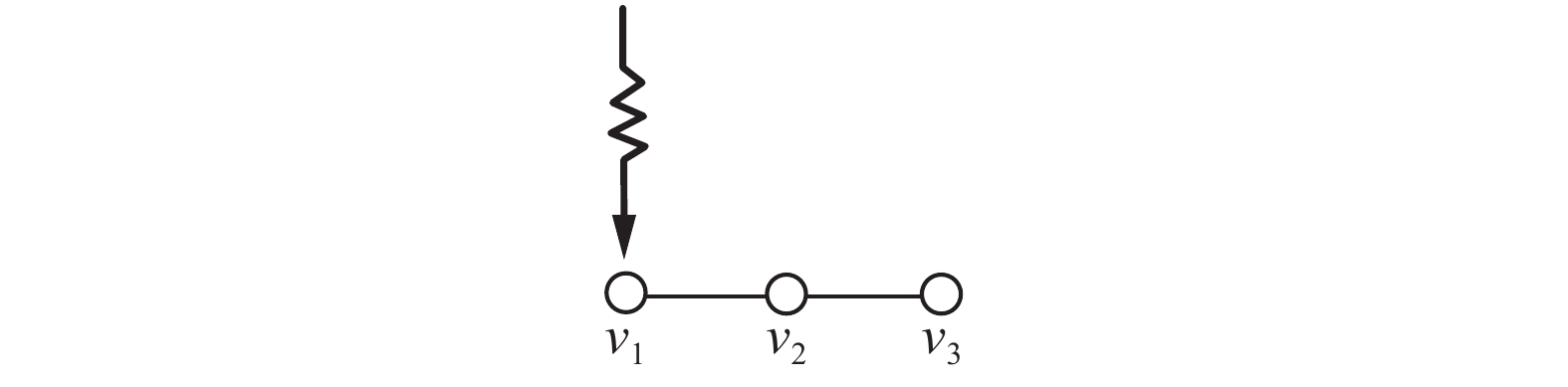
| 图 1 领航集的选取对系统可控性影响 Fig. 1 Influence of leader’s selection on the controllability of the systems | |
设
研究结果表明,无向网络可控性与Laplace矩阵
性质1[16-18] 设F为跟随集,则无向网络线性时不变系统式(1)可控,当且仅当
性质2 设
性质2给出领航集的代数特征。值得注意的是,性质2中的特征向量
由性质2可知,对于非空顶点集
定义1 关键集。设非空顶点集
定义2 完美关键集。设S为关键集,若存在
定义3 最小完美关键集。设S为关键集,若它的任何真子集都不再是关键集,则称S为最小完美关键集(minimal perfect critical set, MPCS)。若
若通信网络拓扑结构图为非连通图,则考虑它的连通分支,故不失一般性,本节讨论的通信网络拓扑结构图均为连通图。连通图的Laplace矩阵的零特征值是单重特征值,且其特征向量为
由k关键集的定义可知,k为正整数且
定理1 n阶连通无向网络不存在1关键集。
证明 设
| $ {{1}}_n^{\rm{T}}{{y}} = \sum\limits_{i = 1}^n {{y_i}} = 0 $ | (2) |
若S为1关键集,不防设
由性质2及定理1知推论1、2成立。
推论1 设G为n阶连通无向网络,
推论2 设n阶无向网络G为非连通图,则G有1关键集的充要条件是
由定理1可知,对于n阶连通无向网络的k关键集,必有
定理2 设顶点集
证明 设
情况1 若矩阵
此时必有
情况2 若矩阵
此时取
设
| ${{Ly}} = \left[ {\begin{array}{*{20}{c}} {{{{L}}_{S \to S}}}&{{{{L}}_{S \to \bar S}}} \\ {{{{L}}_{\bar S \to S}}}&{{{{L}}_{\bar S \to \bar S}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{{y}}_S}} \\ {{0}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\lambda {{{y}}_S}} \\ {{{{L}}_{\bar S \to S}}{{{y}}_S}} \end{array}} \right]$ | (3) |
由
| $ {{1}}_{|S|}^{\rm{T}}{{{L}}_{S \to S}}{{{y}}_S} = m{{1}}_{|S|}^{\rm{T}}{{{y}}_S} = \lambda {{1}}_{|S|}^{\rm{T}}{{{y}}_S} $ |
再由
由定理2可知图1中的顶点集
在一定条件下,运用定理2判断一个顶点子集S是否为关键集时,可以不考虑
设特征向量
引理1 设S为k完美关键顶点集,则
证明 设
| ${{{L}}_{\{ v\} \to V}}{{y}} = \sum\limits_{i = 1}^{k - 1} {{y_i}} $ |
再由式(2)知
由定理1知,2关键集是2完美关键集,也是2最小完美关键集。
定理3 设
证明 由定理2知充分性成立。只须证明必要性。
设S为2关键集,由引理1知
定理4 设
证明 由定理2知充分性成立。只须证明必要性。
设S为3关键集,由引理1知
由定理3可知,2关键集实际上就是文献[26]给出的twins顶点对,由此可见,2关键集是twins顶点对的推广。但与文献[17]中所提出的DCD顶点对不同,DCD顶点对考虑的是在跟随集中的2个顶点,而2关键集考虑的对象则是所有顶点。
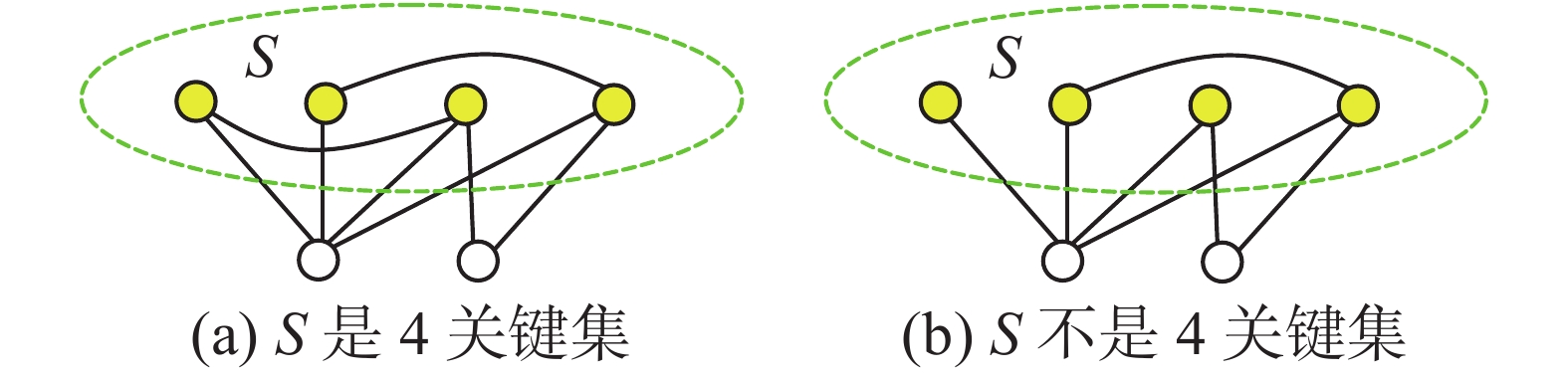
另外,定理3和定理4表明顶点集S能否成为2关键集或3关键集与S中的顶点是否相邻无关。但是,当S中顶点数更多时,该结论不一定成立。如图2中4个深色顶点构成的顶点集S,当S中顶点的相邻关系如图(a)时,它是4关键集;但当S中顶点的相邻关系如图(b)时,它不再是4关键集。
|
Download:
|
| 图 2 4关键集与G[S]的关系 Fig. 2 Relationship between four critical set an G[S] | |
对于顶点集S,按照定理2,删除
若
| ${{y}} = {[{y_1}\; \; \; {y_2}\; \; \cdots \; \; {y_k}\; \; 0\; \; \; \cdots \; \; \; \; 0]^{\rm{T}}}$ |
| ${y_i} \ne 0,\quad i = 1,2, \cdots ,k$ |
由S为独立集知
| ${L_{\{ {v_i}\} \to V}}{{y}} = {d_G}({v_i}){y_i} = \lambda {y_i},\quad i = 1,2, \cdots ,k$ |
即
定理5 设S为独立集,
证明 不防设
我们断言
| ${{1}}_{1 \times |{{\bar S}_{{G_s}}}|}^{\rm{T}}{{{L}}_{{{\bar S}_{{G_S}}} \to S}}{{x}} = [d'\; \; d'\; \; \cdots \; \; \; d']{{x}} = d'\sum\limits_{i = 1}^k {{x_i}} = 0$ |
即有
取
| ${{{L}}_{S \to V}}{{y}} = [{{{L}}_{S \to S}}\; \; \; {{{L}}_{S \to \bar S}}]\left[ {\begin{array}{*{20}{c}} {{x}} \\ {{0}} \end{array}} \right] = {{{L}}_{S \to S}}{{x}} = $ |
| ${[d{x_1}\; \; \; d{x_2}\; \; \cdots \; \; \; d{x_k}]^{\rm{T}}} = \lambda {{x}}$ |
对
| ${{{L}}_{\{ v\} \to V}}{{y}} = [{{{L}}_{\{ v\} \to S}}\; \; \; \; {{{L}}_{\{ v\} \to \bar S}}]\left[ {\begin{array}{*{20}{c}} {{x}} \\ {{0}} \end{array}} \right] = {{{L}}_{\{ v\} \to S}}{{x}} = 0$ |
综上可知
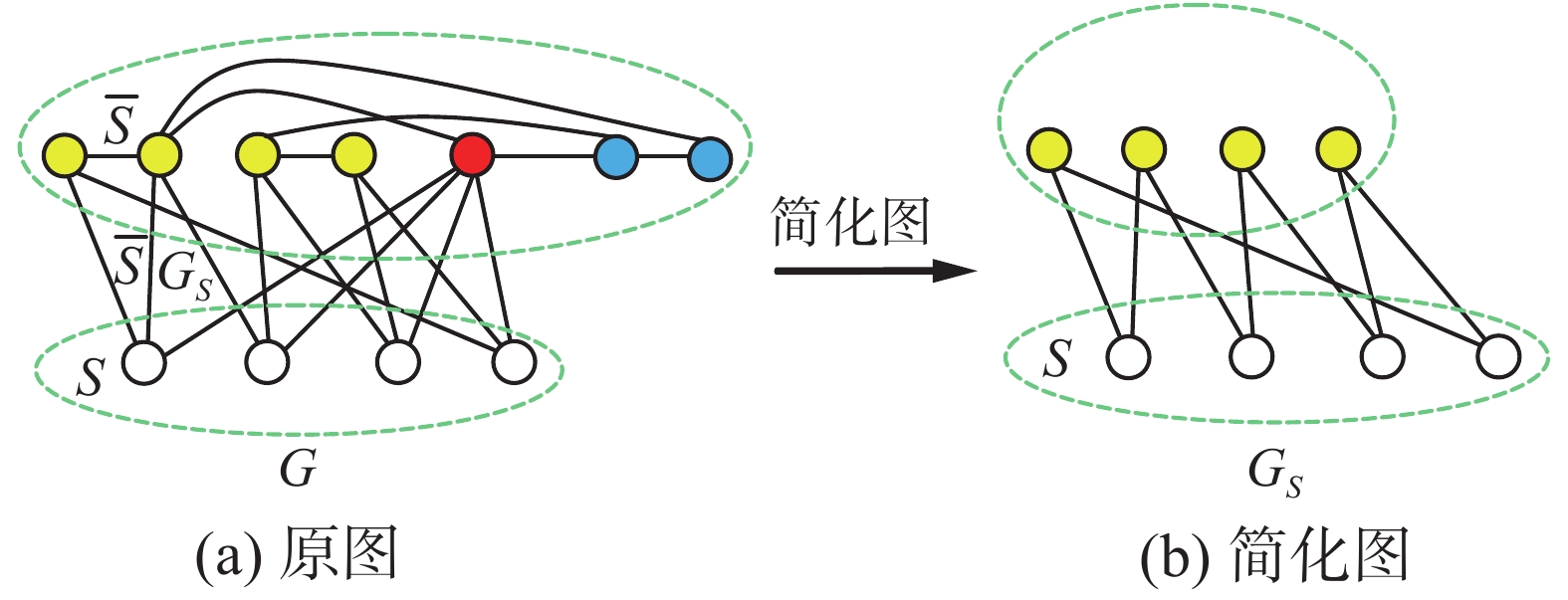
例如,图3中的独立集S,考虑其简化图
|
Download:
|
| 图 3 简化图及其关键集 Fig. 3 Simplification of graph G and its CS | |
基于关键集的概念,本节讨论如何求出无人机集群最小领航集的算法。
3.1 算法理论基础由性质2及关键集的定义知定理6成立。
定理6 设F为跟随集,
证明 由性质2知系统(见式(1))可控当且仅当
设
基于定理6,本节给出求领航集的算法(critical set algorithm, CSA):
1)求出无人机集群通信网络拓扑结构图G的所有k关键集
2)构造二部图
3)求最小顶点集
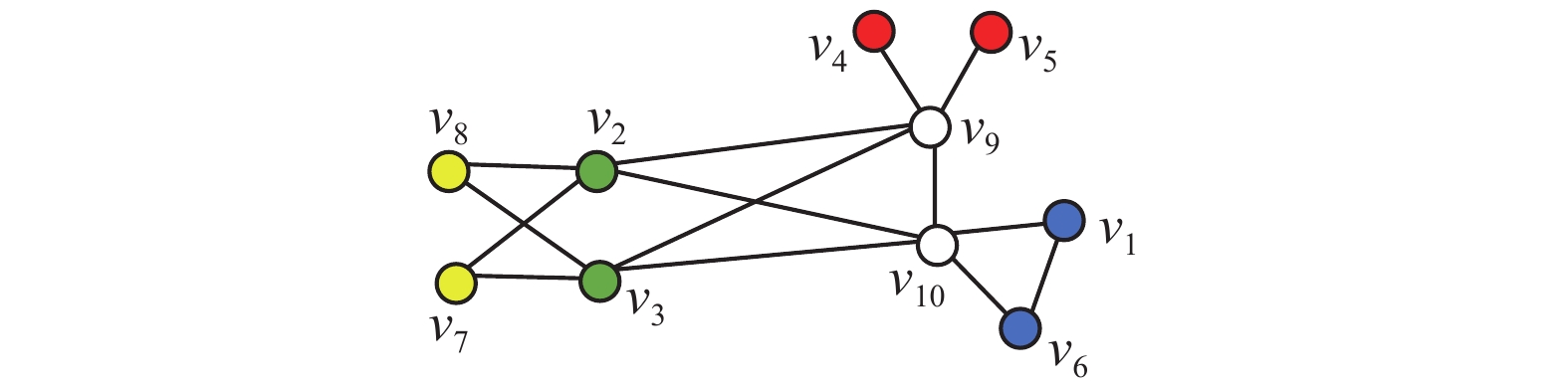
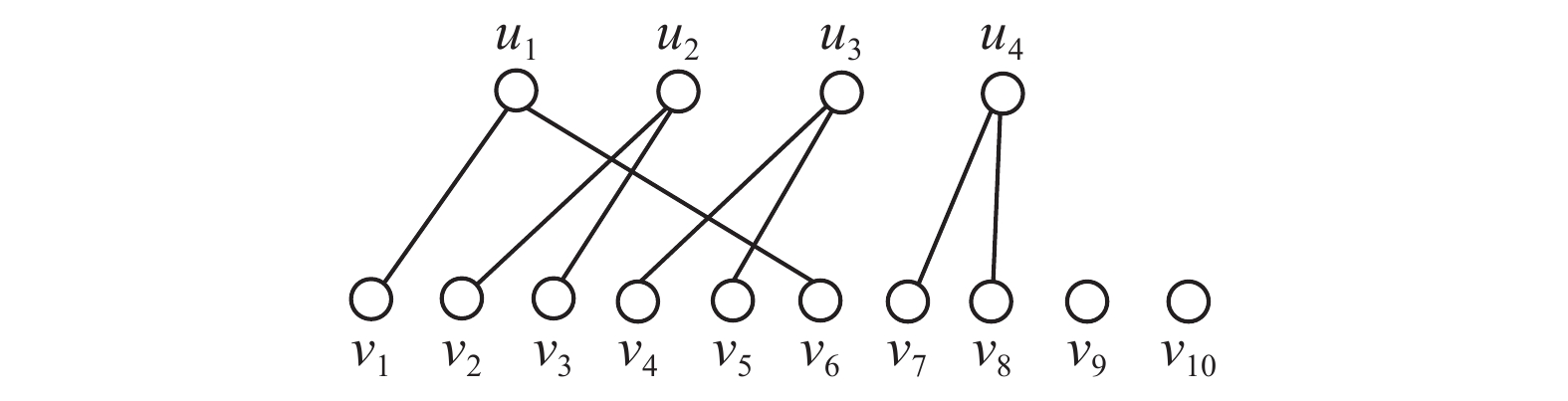
例如,图4中G来自文献[15],由定理3知它有2关键集
|
Download:
|
| 图 4 图G及其关键集 Fig. 4 Graph G it’s critical set | |
于是可构造二部图
|
Download:
|
| 图 5 二部图 Fig. 5 Bipartite graph | |
本算例说明如何运用关键集求出无人机集群通信网络拓扑结构图的最小领航集。
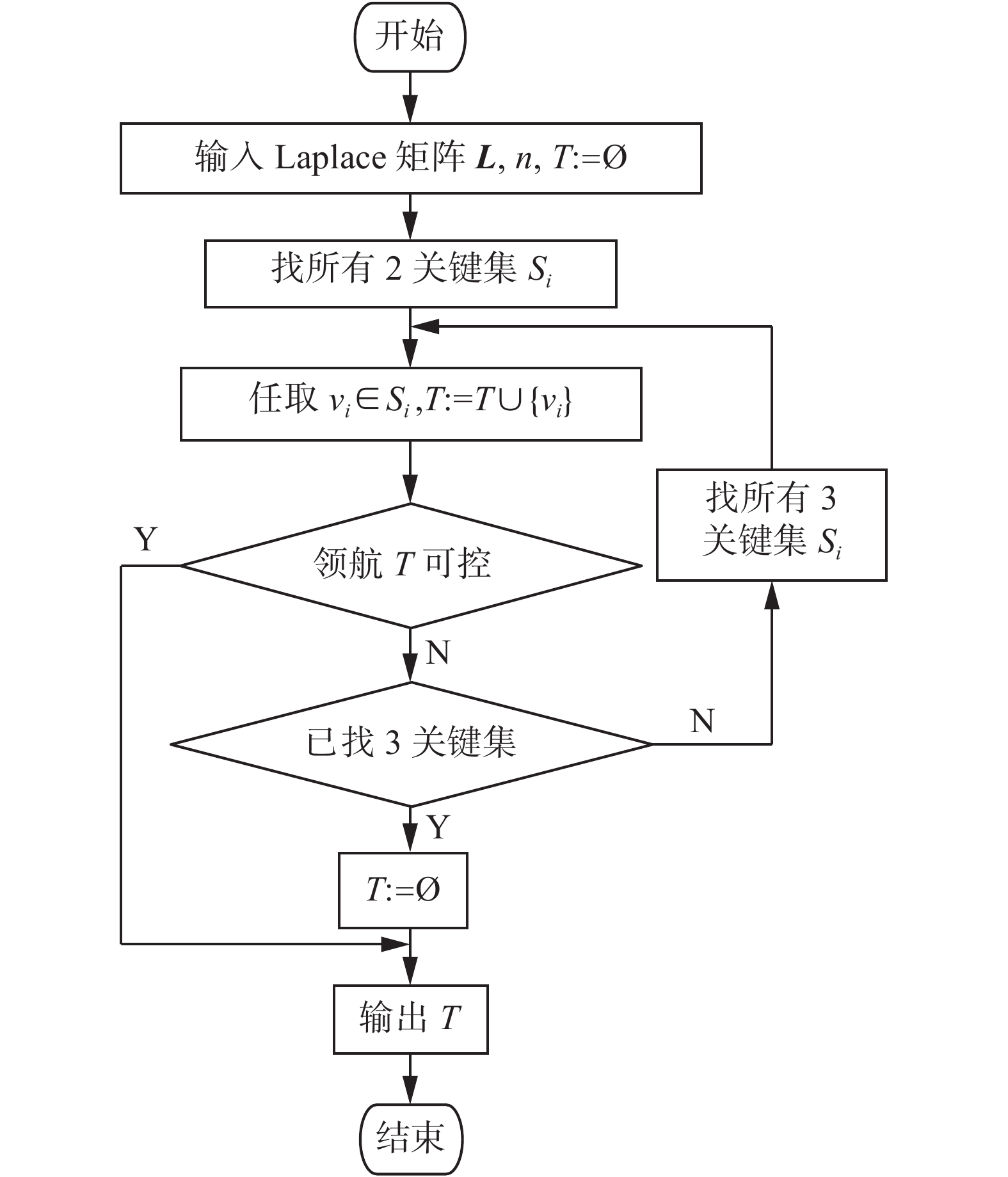
3.3 CSA算法复杂性分析一般地,CSA算法的1)和3)都不是多项式时间的算法。但是,基于本文给出的定理,求出相应特殊的关键集及领航集则是多项式时间算法,具体的算法流程如图6所示。
|
Download:
|
| 图 6 CSA算法流程 Fig. 6 Flow chart of CSA | |
由定理3知,在CSA算法流程图中找出所有2关键集的算法复杂性为
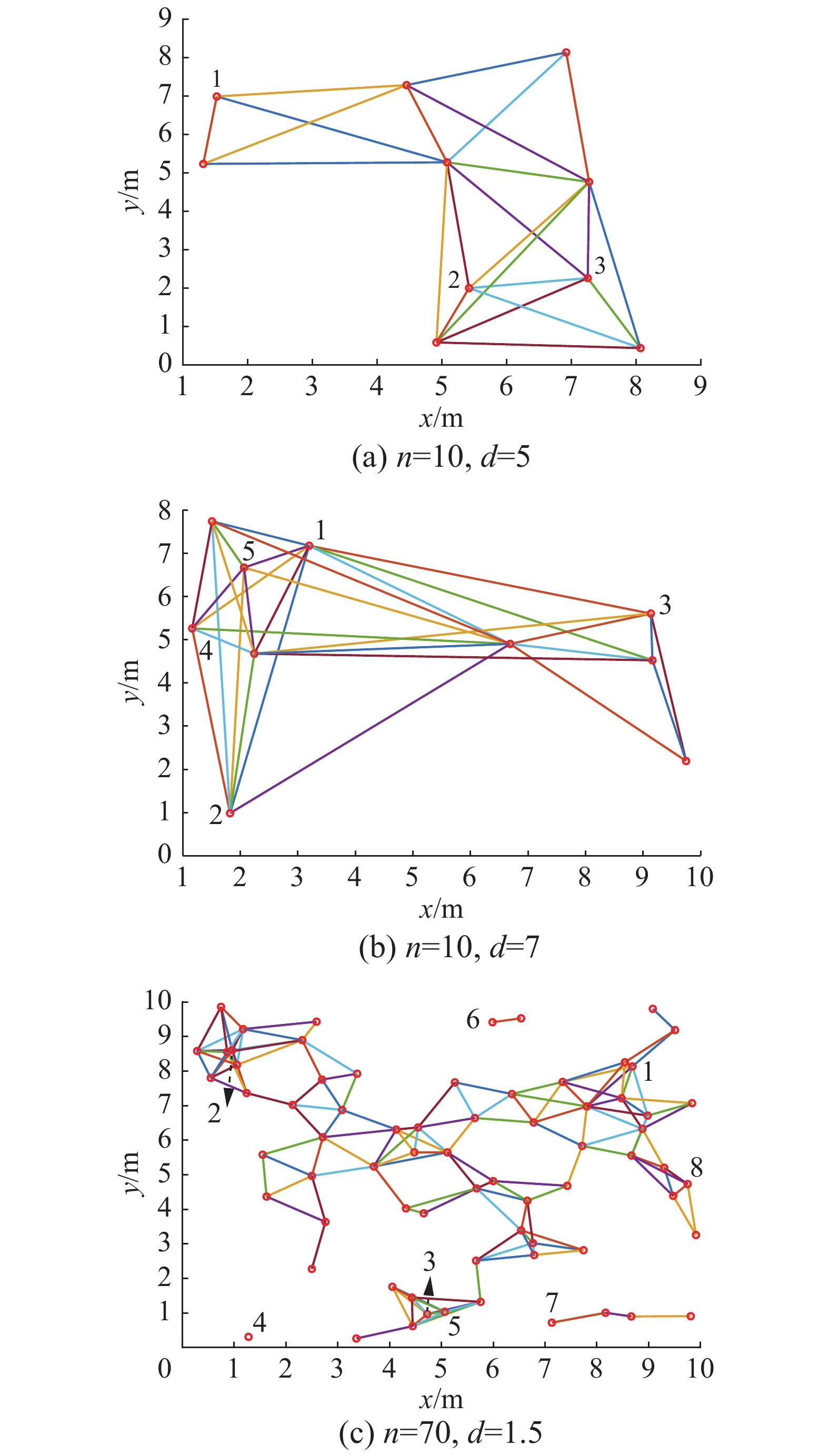
在实验中,设无人机集群的初始位置随机,经过一段时间后形成稳定的通信网络拓扑结构图,并在后续保持通信关系不变。在具体的数值实验中,程序将在
|
Download:
|
| 图 7 无人机集群的通信网络拓扑结构 Fig. 7 Topology of communication network for UAVs | |
其中,图7(a)是通信半径为5时随机生成的具有10个无人机个体的通信网络拓扑结构图,CSA算法求出的领航集为
实验1 代数方法、图论方法及CSA算法的对比实验。
在代数方法中,首先对于单重特征值,先求它的1个特征向量,若该特征向量的非零分量对应的顶点集不是顶点集V,由定义1知,这些非零分量对应的顶点集是1个关键集,在该关键集中任取1个顶点放入领航顶点集;其次,对于多重特征值,设它的重数为
在图论方法中,程序基于本文给出的定理2~5,求出2关键集、3关键集和孤立关键集等一些特殊的关键集。然后,在每个关键集中任取一个顶点放入领航顶点集。
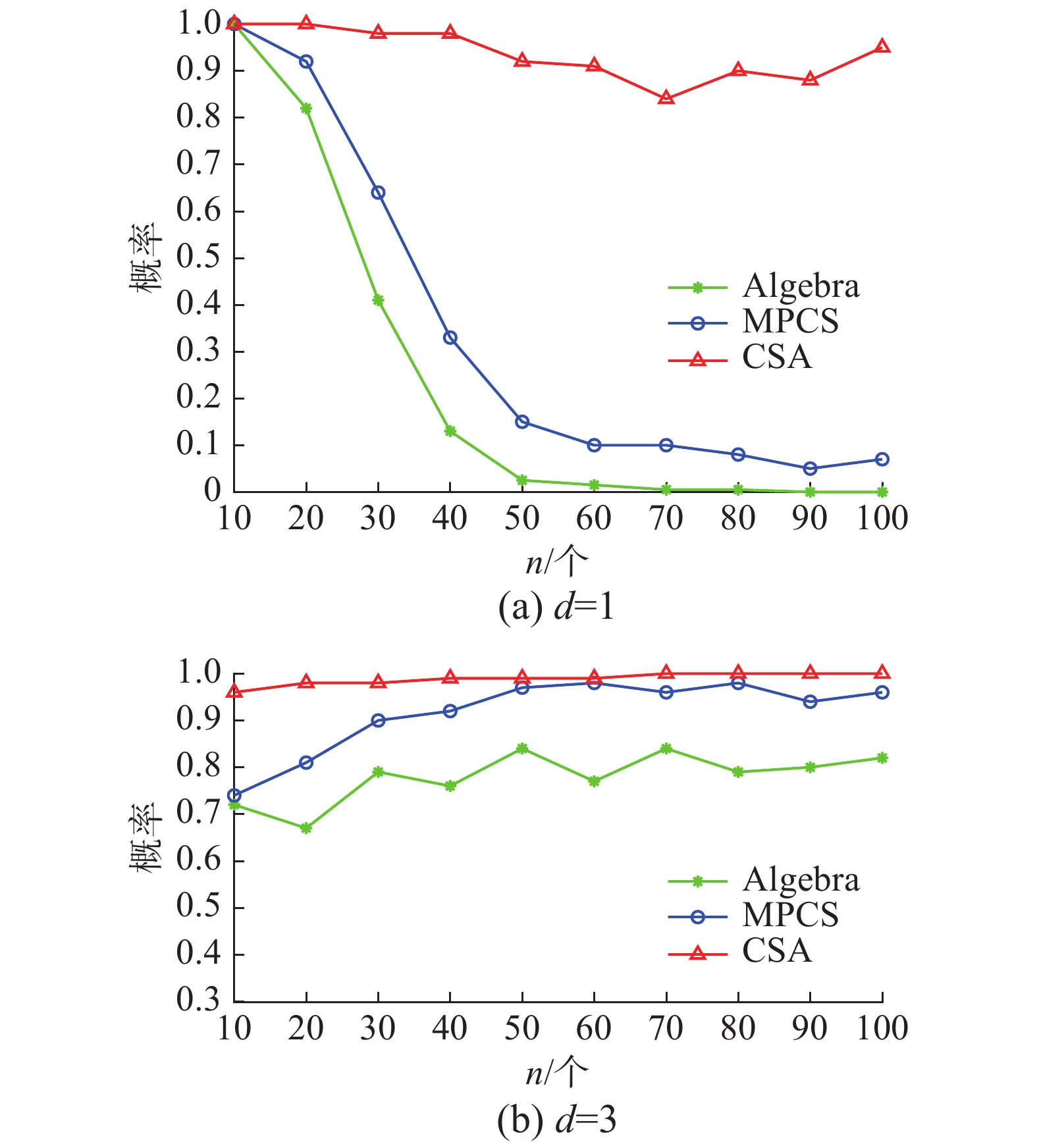
CSA算法则是将代数方法和图论方法相结合求关键集。对于单重特征值,程序用代数方法求它的关键集;对于多重特征值,则用图论方法求出2关键集、3关键集。实验结果如图8所示。
|
Download:
|
| 图 8 对比实验 Fig. 8 Comparison of experimental results | |
从图8中可以看出,通过引入图论理论求关键集,使得求解效率得到大幅度提高,特别是当通信半径
实验2 CSA算法的求解效率与无人机个体通信半径间关系。
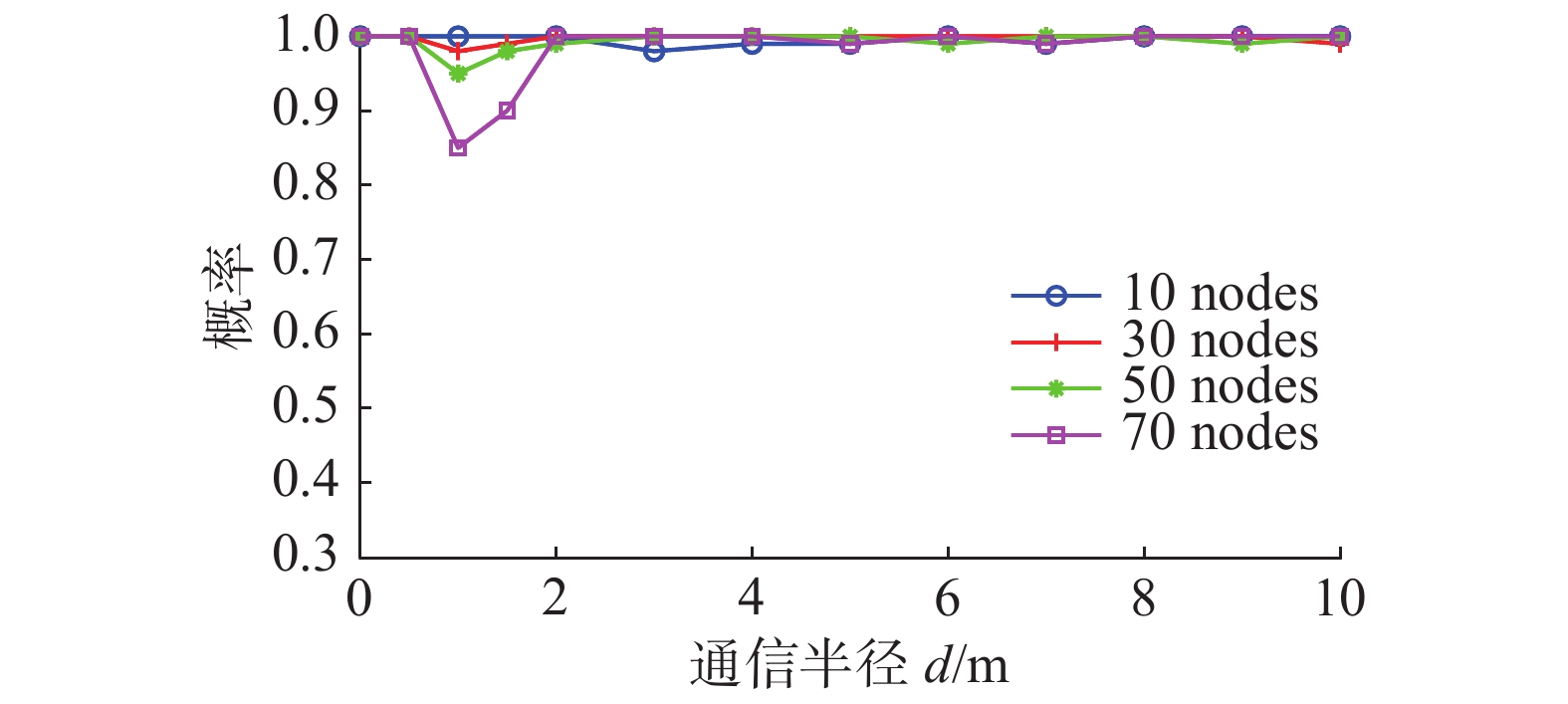
在本实验中,针对不同的无人机个体数目,测试CSA算法在不同通信半径条件下的求解效率,实验结果如图9所示。
|
Download:
|
| 图 9 CSA算法求解效率与通信半径的关系 Fig. 9 Relationship between the efficiency of CSA and communication radius of UAV | |
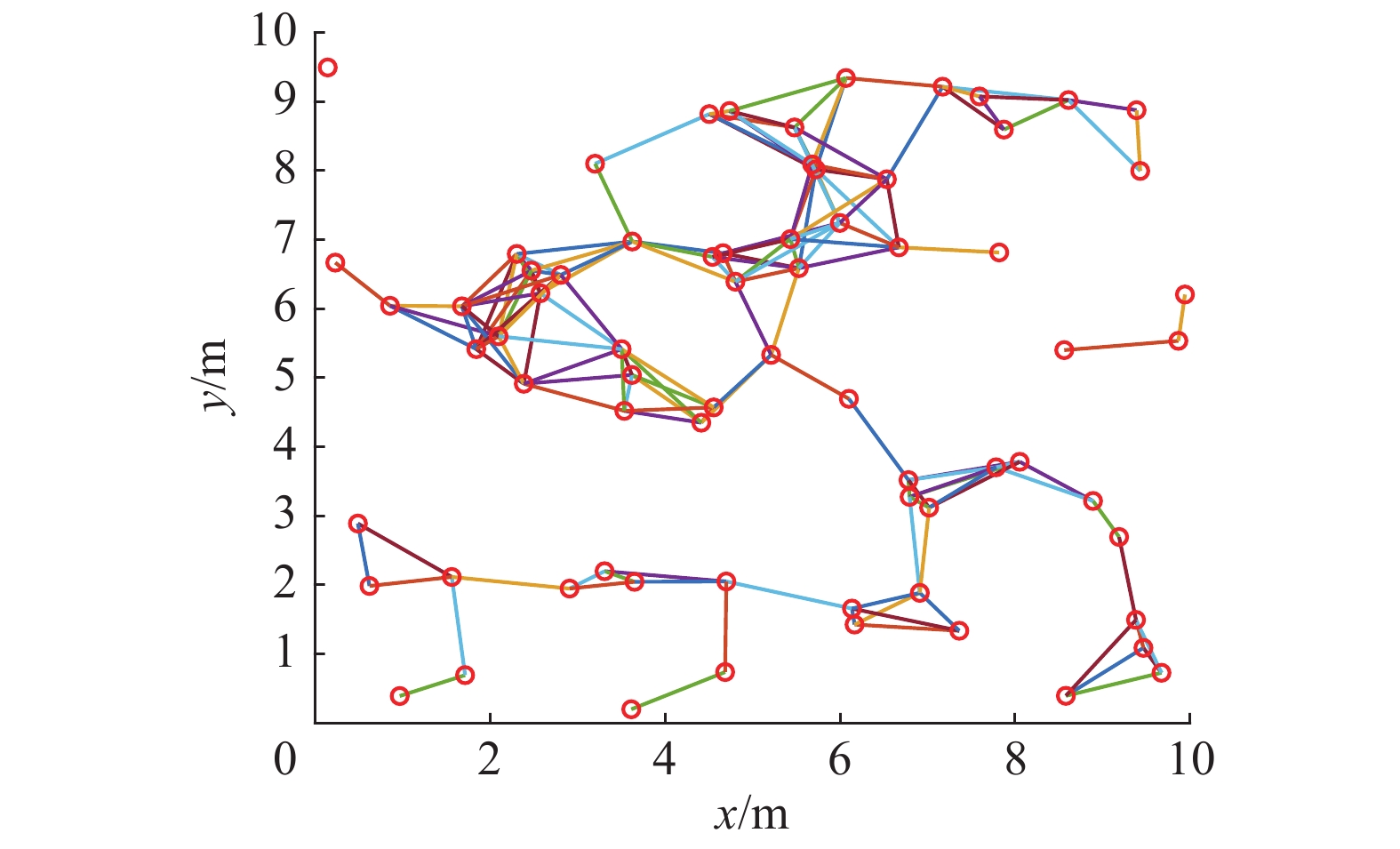
从图9中可以看出,尽管CSA算法在求解过程有一定程度的抖动,但当顶点个数小于30时,求解效率在95%上。一个有趣的现象是,当顶点个数大于30时,若其通信半径介于3~9,则CSA算法几乎100%可以找到领航集;若通信半径小于3或大于9,则CSA算法都出现了不同程度的抖动,特别是当通信半径介于0.5~3时,算法求解效率较差。出现这一现象的原因在于,此时图中单重特征值减少而多重特征值增加,这使得同一特征值对应的关键集增加,而基于本文给出的定理2~5,CSA算法只求出2关键集、3关键集和孤立关键集等一些特殊的关键集,从而使得算法难以找到领航集。例如,见图10,该无向网络的特征值中,除单重特征值外,还有1个3重特征值、1个4重特征值和1个5重特征值,CSA算法难以找到它的领航集。这说明,当顶点个数多且通信半径较小时,图中的关键集情况较复杂,需要进一步从理论上研究
|
Download:
|
| 图 10 复杂特征值情况的网络结构 Fig. 10 Description of networks with multiple eigenvalues | |
实验3 领航顶点个数与边数关系。
随着无人机个体和边数的变化,领航顶点的个数也会相应地变化,因此,本实验不考虑领航顶点个数的绝对值,而是考虑“领航顶点个数/无人机个体数量
实验结果如图11所示。从图11中可以看出,随着边数占比趋于1,领航顶点占比趋于

|
Download:
|
| 图 11 领航顶点个数与边数的关系 Fig. 11 Relationship between the number of leaders and edges | |
本文以几十架无人机构成的无人机集群为应用背景,利用Laplace矩阵的特征向量提出关键集概念,指出领航集所必须具备的图特征,即领航集需覆盖所有关键集。给出了2关键集和3关键集的图特征,从图论角度给出独立集成为关键集的一个充分条件。数值实验表明,基于关键集,CSA算法在大多数情况下能以90%以上的概率搜索到领航集。
如何刻画
另外,从图论角度给出领航集的充要条件,最小领航顶点数的上、下界等也都是值得进一步研究的问题。
| [1] |
DORRI A, KANHERE S S, JURDAK R. Multi-agent systems: a survey[J]. IEEE access, 2018, 6: 28573-28593. DOI:10.1109/ACCESS.2018.2831228 ( 0) 0)
|
| [2] |
肖延东, 老松杨, 侯绿林, 等. 基于节点负荷失效的网络可控性研究[J]. 物理学报, 2013, 62(18): 180201. XIAO Yandong, LAO Songyang, HOU Lülin, et al. Network controllability based on node overloaded failure[J]. Acta Physica Sinica, 2013, 62(18): 180201. DOI:10.7498/aps.62.180201 (  0) 0)
|
| [3] |
LIU Yangyu, SLOTINE J J, BARABÁSI A L. Controllability of complex networks[J]. Nature, 2011, 473(7346): 167-173. DOI:10.1038/nature10011 ( 0) 0)
|
| [4] |
KUMAR Y, SHARA M, PRASANNA C. Minimizing inputs for strong structural controllability[C]//Proceedings of 2019 American Control Conference. Philadelphia, PA, USA, 2019: 2048−2053.
( 0) 0)
|
| [5] |
TANNER H G. On the controllability of nearest neighbor interconnections[C]//Proceedings of the 43rd IEEE Conference on Decision and Control (CDC) (IEEE Cat. No. 04CH37601). Nassau, Bahamas, 2004: 2467−2472.
( 0) 0)
|
| [6] |
MONSHIZADEH N, ZHANG Shou, CAMLIBEL M K. Zero forcing sets and controllability of dynamical systems defined on graphs[J]. IEEE transactions on automatic control, 2014, 59(9): 2562-2567. DOI:10.1109/TAC.2014.2308619 ( 0) 0)
|
| [7] |
MOUSAVI S S, CHAPMAN A, HAERI M, et al. Null space strong structural controllability via skew zero forcing sets[C]//Proceedings of 2018 European Control Conference. Limassol, Cyprus, 2018: 1845−1850.
( 0) 0)
|
| [8] |
MOUSAVI S S, HAERI M, MESBAHI M. On the structural and strong structural controllability of undirected networks[J]. IEEE transactions on automatic control, 2018, 63(7): 2234-2241. DOI:10.1109/TAC.2017.2762620 ( 0) 0)
|
| [9] |
CHAPMAN A, MESBAHI M. On strong structural controllability of networked systems: a constrained matching approach[C]//Proceedings of 2013 American Control Conference. Washington, DC, USA, 2013: 6126−6131.
( 0) 0)
|
| [10] |
TREFOIS M, DELVENNE J C. Zero forcing number, constrained matchings and strong structural controllability[J]. Linear algebra and its applications, 2015, 484: 199-218. DOI:10.1016/j.laa.2015.06.025 ( 0) 0)
|
| [11] |
OLESKY D D, TSATSOMEROS M, VAN DEN DRIESSCHE P. Qualitative controllability and uncontrollability by a single entry[J]. Linear algebra and its applications, 1993, 187: 183-194. DOI:10.1016/0024-3795(93)90134-A ( 0) 0)
|
| [12] |
JI Meng, EGERSTEDT M. A graph-theoretic characterization of controllability for multi-agent systems[C]//Proceedings of 2007 American Control Conference. New York, NY, USA, 2007: 4588−4593.
( 0) 0)
|
| [13] |
RAHMANI A, JI Meng, MESBAHI M, et al. Controllability of multi-agent systems from a graph-theoretic perspective[J]. SIAM journal on control and optimization, 2009, 48(1): 162-186. DOI:10.1137/060674909 ( 0) 0)
|
| [14] |
MARTINI S, EGERSTEDT M, BICCHI A. Controllability analysis of multi-agent systems using relaxed equitable partitions[J]. International journal of systems, control and communications, 2010, 2(1/2/3): 100-121. DOI:10.1504/IJSCC.2010.031160 ( 0) 0)
|
| [15] |
AGUILAR C O, GHARESIFARD B. Almost equitable partitions and new necessary conditions for network controllability[J]. Automatica, 2017, 80: 25-31. DOI:10.1016/j.automatica.2017.01.018 ( 0) 0)
|
| [16] |
JI Zhijian, WANG Zidong, LIN Hai, et al. Interconnection topologies for multi-agent coordination under leader-follower framework[J]. Automatica, 2009, 45(12): 2857-2863. DOI:10.1016/j.automatica.2009.09.002 ( 0) 0)
|
| [17] |
JI Zhijian, YU Haisheng. A new perspective to graphical characterization of multiagent controllability[J]. IEEE transactions on cybernetics, 2017, 47(6): 1471-1483. DOI:10.1109/TCYB.2016.2549034 ( 0) 0)
|
| [18] |
WANG Long, JIANG Fangcui, XIE Guangming, et al. Controllability of multi-agent systems based on agreement protocols[J]. Science in China series F: information sciences, 2009, 52(11): 2074-2088. DOI:10.1007/s11432-009-0185-7 ( 0) 0)
|
| [19] |
JIANG Fangcui, WANG Long, XIE Guangming, et al. On the controllability of multiple dynamic agents with fixed topology[C]//Proceedings of the 2009 Conference on American Control Conference. St. Louis, Missouri, USA, 2009: 5665−5670.
( 0) 0)
|
| [20] |
HAMDAN A M A, NAYFEH A H. Measures of modal controllability and observability for first-and second-order linear systems[J]. Journal of guidance, control, and dynamics, 1989, 12(3): 421-428. DOI:10.2514/3.20424 ( 0) 0)
|
| [21] |
OLSHEVSKY A. Minimal controllability problems[J]. IEEE transactions on control of network systems, 2014, 3(1): 249-258. DOI:10.1016/S0005-1098(00)00181-3 ( 0) 0)
|
| [22] |
PASQUALETTI F, ZAMPIERI S, BULLO F. Controllability metrics, limitations and algorithms for complex networks[J]. IEEE transactions on control of network systems, 2014, 1(1): 40-52. DOI:10.1109/TCNS.2014.2310254 ( 0) 0)
|
| [23] |
SUMMERS T H, CORTESI F L, LYGEROS J. On submodularity and controllability in complex dynamical networks[J]. IEEE transactions on control of network systems, 2016, 3(1): 91-101. DOI:10.1109/TCNS.2015.2453711 ( 0) 0)
|
| [24] |
FITCH K, LEONARD N E. Optimal leader selection for controllability and robustness in multi-agent networks[C]//Proceedings of 2016 European Control Conference. Aalborg, Denmark, 2016: 1550−1555.
( 0) 0)
|
| [25] |
MOHAMMADREZA D. Minimal driver nodes for structural controllability of large-scale dynamical systems: node classification[J]. IEEE systems journal, 2020, 14(3): 4209-4216. ( 0) 0)
|
| [26] |
BIYIKOĞU T, LEYDOLD J, STADLER P F. Laplacian eigenvectors of graphs: perron-frobenius and faber-krahn type theorems[M]. New York: Springer, 2007.
( 0) 0)
|
 2021, Vol. 16
2021, Vol. 16


