特征选择的目标是在给定评价标准下选择非冗余的特征子集，其作为一项重要的数据预处理步骤，能够有效地提高数据分析模型的准确性和高效性，在数据挖掘与知识发现中起着重要的作用^[1]。

数据中存在一些缺失值是一种非常普遍的现象，缺失值给数据中的分类知识带来了不一致性问题^[2]。粗糙集理论是一种能够有效应对不精确、不一致信息的数据建模与知识获取工具。近年来，人们基于粗糙集理论针对不完备数据的特征选择问题进行了深入的分析和讨论。Kryszkiewicz^[3]认为不完备数据中缺失值应是已有值域中的某一特征值，进而提出了一种基于广义差别矩阵的特征选择方法。Parthalin等^[4]为了保留分类所产生的不一致决策区域，研究了基于容差粗糙集的特征选择方法。Meng等^[5]讨论了不一致不完备决策系统中基于区分矩阵的特征选择方法。Grzymala-Busse等^[6]将缺失值考虑为丢失值和不在乎值，提出了基于广义特征关系粗糙集模型的特征选择方法。Qian等^[7]提出了一种高效的正向近似加速器，用于加速不完备数据特征选择的启发式特征搜索过程。Dai^[8]为了处理不完备数值型数据，建立了一种新的容差模糊粗糙集模型，并提出了基于差别矩阵的特征选择方法。Yang等^[9]定义了多准则决策系统中相似优势关系的概念，提出了4种基于差别矩阵的近似分布约简方法。Liang等^[10]提出了一种不完备信息系统中基于粗糙熵的启发式特征选择算法。Qian等^[11]基于不完备信息系统中的最大一致块概念，提出了一种新的组合信息熵用于度量信息系统的不可分辨能力。Dai等^[12]在不完备决策系统中提出一种新的满足单调性约束的条件信息熵。Zhao等^[13]提出了一种新的邻域容差条件熵，并将其应用于混合不完备数据中的特征选择问题。

另一方面，实际应用中数据随时间的推移呈现出动态更新的变化趋势，数据的采集与分析是一个不断优化升级的动态过程。面向动态数据的高效特征选择方法成为了当前人们普遍关注的一个研究热点。增量技术可以利用已有计算结果进行特征选择增量计算，以发现新的特征子集，从而避免重新计算整个特征空间以获取新的特征子集^[14-15]。近年来，许多学者通过将增量学习技术引入到特征选择问题中，对动态数据环境下的高效特征选择方法进行了广泛深入的研究。Xu等^[16]将特征选择问题转化为0-1整数规划问题，提出了一种对象更新条件下的动态特征选择方法。Qian等^[17]设计了一种新的基于相对不可辨识对象对的属性重要度度量方式，并提出了动态粒度空间下的基于序贯三支决策模型的增量特征选择方法。Yang等^[18]分析了对象动态变化时相对可辨识关系的增量更新机制，提出了基于模糊粗糙集的动态特征选择算法。Lang等^[19]提出了覆盖信息系统中基于相关族的动态特征选择方法。Wei等^[20]设计了基于辨识矩阵和压缩辨识矩阵的增量特征选择算法，以获得数据动态变化时最优的特征子集。Zeng等^[21]基于高斯核模糊粗糙集模型，研究了混合信息系统的动态特征选择方法。Liang等^[22]提出了信息熵的批增量递推计算机制，可用于多个数据集之间信息熵的高效融合。Shu等^[23]针对含有缺失值的不完备数据，提出了基于正域的增量特征选择算法。Xie等^[24]提出了3种不完备数据中相容类的更新策略，并设计了相应的增量特征选择算法。考虑到动态数据中特征值存在频繁的修改和更新操作，Wang等^[25]针对完备数据集研究了特征值动态更新时信息熵的增量更新机制，进一步设计了相应的动态特征选择算法。刘吉超等^[26]针对不完备数据中数据集维数动态增加的情形，分析了互补信息熵的更新机制，进而提出了一种增量特征约简算法。钱进等^[27]提出一种基于正域处理面向成组对象集的增量式特征选择算法。综合上文所述，大部分研究者针对完备决策系统的动态更新特征选择问题进行深入的研究，鲜有对不完备决策系统动态更新特征问题研究。基于正域处理不完备决策系统的特征选择存在无法处理边界域中的样本分类的不确定性问题。信息熵作为度量信息不确定性的度量标准，有助于不完备数据特征选择问题研究，而引入增量计算机制可以加速特征选择过程，有效减少计算时间。本文针对不完备决策系统，设计了一种面向特征值动态更新的特征选择算法。文中首先分析了特征值更新时不完备决策系统中相容类和决策类的动态变化模式，并以此给出了条件信息熵的增量计算机制，进而设计了基于增量条件信息熵的动态特征算法，最后通过实验验证进一步说明了算法的有效性和高效性。

1 基本概念

粗糙集理论中，信息系统表示为一个四元组 $S = (U,A,V,f)$ ，其中， $U$ 表示对象的非空有限集合，称为论域； $A$ 表示特征的非空有限集合，即特征集； ${V_a}$ 表示特征 $a \in A$ 的值域，并且有 $V = { \cup _{a \in A}}{V_a}$ ；对任意 $a \in A$ 和 $x \in U$ ， $f:U \times A \to V$ 是一个信息函数，通过信息函数给每一个对象 $x \in U$ 一个特定的特征值 $f(x,a) \in {V_a}$ ， $a \in A$ 。决策系统表示为 ${\rm{DS}} = (U,C \cup \{ d\} ,V,f)$ ，其中， $C$ 代表条件特征的非空有限集合； $d$ 表示决策特征。在实际应用中，信息系统中某些对象的特征值容易丢失，如果一个信息系统中 $V$ 包含缺失的特征值，记作“*”，那么该信息系统被称为不完备信息系统(incomplete information system，IIS)；对于决策系统来说，如果 $* \in {V_C},* \notin {V_d}$ ，称这样的决策系统为不完备决策系统(incomplete decision system，IDS)；对于 $* \notin {V_C},* \notin {V_d}$ 这样的决策系统，称为完备决策系统。

完备信息系统中条件特征的任何子集 $P \subseteq C$ 可诱导一种不可辨识关系 ${\rm{IND}}(P)$ ，定义为

${\rm{IND}}(P) = \{ (x,y) \in U \times U|\forall a \in P,f(x,a) = f(y,a)\} $

${\rm{IND}}(P)$ 是具有自反性、对称性与传递性的等价关系。等价关系 ${\rm{IND}}(P)$ 将论域 $U$ 划分为等价类的集合，表示为 $U/{\rm{IND}}(P) = \{ {[x]_P}|x \in U\} $ ，其中 ${[x]_P} = $ $\{ y|(x,y) \in {\rm{IND}}(P)\} $ 。为了处理含有缺失值的不完备决策系统，Kryszkiewicz提出一种新的二元关系 $T(P),P \subseteq C$ ，定义为

$\begin{array}{l} T(P) = \{ (x,y) \in U \times U|\forall a \in P,f(x,a) = f(y,a) \vee \\ \quad\quad\quad f(x,a) = * \vee f(y,a) = *\} \end{array} $

$T(P)$ 是具有自反性和对称性，但不具有传递性的相容关系。在P下任意一个对象 $x \in U$ 的相容类定义为 ${T_P}(x) = \{ y \in U|(x,y) \in T(P)\} $ 。 $U/T(P)$ 表示相容类集合 $\{ T(P)|x \in U\} $ 。 $U/T(P)$ 中构成论域 $U$ 上的一个覆盖，对于论域中任意一个对象 $x \in U,{T_P}(x) \ne \text{Ø}$ ，并且 ${ \cup _{x \in U}}{T_P}(x) = U$ 。给定一个不完备决策系统 ${\rm{IDS}} = (U,C \cup \{ d\} ,V,f)$ ，决策属性 $d$ 将对象分类为 $m$ 个确定互斥的子集 $U/d = \{ {D_1},{D_2}, \cdots ,{D_m}\} $ 。目标决策概念 ${D_i} \in U/D$ 的上、下近似集定义为

$\begin{array}{l} \quad\underline {{\rm{apr}}} ({D_i}) = \{ x \in U|{T_P}(x) \subseteq {D_i}\} \\ \overline {{\rm{apr}}} ({D_i}) = \{ x \in U|{T_P}(x) \cap {D_i} \ne \text{Ø}\} \end{array} $

基于粗糙集理论的特征选择方法根据特征重要度的不同度量标准，可笼统地归纳为依赖性度量、一致性度量、距离度量和信息度量。前面3种度量方法都局限于数据的实际值，对含有噪声或缺失值的数据处理十分敏感。而基于信息论的度量方法仅关注随机变量的概率分布，不关注其实际值，成为了高维数据中常用的特征重要度度量方式。借鉴香农熵的传统定义形式，Dai等^[8,12]定义了一种新的满足单调性的条件熵来度量不完备决策系统协调程度的不确定性。给定一个不完备决策系统 ${\rm{IDS}} = (U,C \cup \{ d\} ,V,f)$ ，其中， $U = \{ {x_1},{x_2}, \cdots , $ $ {x_n}\}$ ； $U/T(P) = \{ {T_P}({x_i})|i = 1,2, \cdots ,n\} $ ； $U/d = \{ {D_1},{D_2}, \cdots , $ $ {D_m}\}$ 。决策特征 $d$ 关于条件特征子集 $ P $ 的条件熵定义为

$H(d|P) = - \sum\limits_{i = 1}^n {\sum\limits_{j = 1}^m {\frac{{|{T_P}({x_i}) \cap {D_j}|}}{{|U|}}{\log_2} } } \frac{{|{T_P}({x_i}) \cap {D_j}|}}{{|{T_P}({x_i})|}}$

(1)

根据式（1），通过从特征子集 $P$ 删除某个特征 $a$ 引起的条件熵的变化大小，可定义特征的重要度度量函数：

${\rm{sig}}(a,P,d) = H(d|P) - H(d|P - \{ a\} )$

2 不完备数据集中特征值更新的增量特征选择

当不完备决策系统中特征值发生动态更新时，由特征子集所诱导的相容关系和由决策特征所诱导的等价关系会随之变化，进而使得特征度量准则条件熵发生变化。下面，首先分析一组对象的特征值发生更新时相容类和决策类的变化情况。由于条件熵的计算与相容类和决策类中的对象顺序无关，为了方便阐述，下文中假设决策系统中发生特征值修改的对象集合为 $\left\{ {{x_i}{\rm{|}}i = p + 1,p + {\rm{2}}, \cdots ,q} \right\}$ ，则更新后不完备决策系统中相容类的更新为

$\begin{array}{l} U/T'(P) = \{ {{T'}_P}({x_i})|i = 1,2, \cdots ,p,p + 1, \cdots ,\\ \quad\quad\quad q,q + 1, \cdots ,k, k + 1, \cdots ,n\} \end{array} $

式中： ${x_i}(i = 1,2, \cdots ,p)$ 表示相容类保持不变的对象，即 ${T'_P}({x_i}) = {T_P}({x_i})$ ； ${x_i}(i = p + 1,p + 2, \cdots ,q)$ 表示特征值发生变化的对象，其相容类需根据定义计算，即 ${T'_P}({x_i}) = \{ {x_l} \in U|({x_i},{x_l}) \in T'(P)\} $ ； ${x_i}(i = q + 1,q + 2, \cdots ,$ $k)$ 和 ${x_i}(i = k + 1,k + 2, \cdots ,n)$ 分别表示相容类可能出现的两种更新模式的对象集合。对于对象集合 ${x_i}(i = q + 1,q + 2, \cdots ,k)$ ，相容类更新为 ${T'_P}({x_i}) = $ $({T_P}({x_i}) - $ $ T_P^ - ({x_i})) \cup T_P^{\rm{ + }}({x_i})$ ，对于对象集合 ${x_i}(i = k + 1,$ $k + 2, \cdots ,n)$ ，相容类更新方式为 ${T'_P}({x_i}) = {T_P}({x_i}) - $ $T_P^ - ({x_i})$ ，其中， $T_P^ - ({x_i}) \!=\! \{ {x_l}|\{ {x_i},{x_l}\} \!\in\! T(P),p + 1 \!\leqslant \!l \!\leqslant \!q\}$ ； $T_P^ + ({x_i}) \!=\! \{ {x_l}|\{ {x_i},{x_l}\} \!\in\! $ $ T'(P), p + 1 \leqslant l \leqslant q\}$ 。

不完备决策系统中决策特征值发生变化后决策类的更新为

$U/d = \{ {D'_j}|j = 1,2, \cdots ,{q_1},{q_1} + 1, \cdots ,{q_2},{q_2} + 1, \cdots ,m\} $

式中： ${D'_j}(j = 1,2, \cdots ,{q_1})$ 表示决策类保持不变的对象，即 ${D'_j} = {D_j}$ ； ${D'_j}(j = {q_1} + 1,{q_1} + 2, \cdots ,{q_2})$ 表示需要从当前决策类中删除特征值更新的可辨识对象，即 ${D'_j} = {D_j} - D_j^ - $ ； ${D'_j}(j = {q_2} + 1,{q_2} + 2, \cdots ,m)$ 表示不仅需要删除特征值发生更新的可辨识对象集合，同时要增加新特征值下不可辨识的对象集合，即 ${D'_j} = ({D_j} - $ $D_j^ - ) \cup D_j^ + $ ，其中 $D_j^ - = \{ {x_l}|\exists {x_r} \in {D_j},f({x_l},d) = $ $ f({x_r},d),$ $p + 1 \!\leqslant \!l\! \leqslant \!q\}\;\;$ ， $D_j^ + = \{ {x_l}|\exists {x_r} \in {D_j}, f({x_l},d) = f({x_r},d)$ $, $ $ p + 1 \leqslant l \leqslant q\}$ 。

根据上文中不完备决策系统中特征值动态修改后相容类和决策类的更新模式，下面进一步可得相容类与决策类交集的动态更新方式。

对于任意对象 ${x_i}(i = 1,2, \cdots ,p)$ 的相容类和决策类 ${D'_j}(j = 1,2, \cdots ,m)$ ，有 $|{T'_P}({x_i}) \cap {D'_j}| = |{T_P}({x_i}) \cap {D_j}|$ 成立，对于任意对象 ${x_i}(i = p + 1,p + 2, \cdots ,q)$ ，由于其相容类需根据定义计算，无法利用已有结果，因此相容类和决策类 ${D'_j}(j = 1,2, \cdots ,m)$ 的交集表示为 $|{T'_P}({x_i}) \cap {D'_j}|$ 。

对于任意对象 ${x_i}(i = q + 1,q + 2, \cdots ,k)$ 的相容类和决策类 ${D'_j}(j = 1,2, \cdots ,m)$ ，其交集的更新模式为

$ \begin{array}{l}\quad\quad\quad\quad\quad\quad\quad \left|{{T}^{\prime }}_{P}({x}_{i})\cap {D}^{\prime }\right|=\\ \left\{\begin{array}{*{20}{l}}|{T}_{P}({x}_{i})\cap {D}_{j}|,\quad 1\leqslant j\leqslant {q}_{1}\\ \begin{array}{l}|{T}_{P}({x}_{i})\cap {D}_{j}|-|{T}_{P}^-({x}_{i})\cap {D}_{j}|-\\ |{T}_{P}({x}_{i})\cap {D}_{j}^-|+|{T}_{P}^-({x}_{i})\cap {D}_{j}^-|,\end{array}\quad {{q}_{1}+1\leqslant j\leqslant {q}_{2}}\\ |{T}_{P}({x}_{i})\cap {D}_{j}|-|{T}_{P}^-({x}_{i})\cap {D}_{j}|-\\ \begin{array}{l}|{T}_{P}({x}_{i})\cap {T}_{P}^-({x}_{i})|+|{T}_{P}^-({x}_{i})\cap {D}_{j}^-|+\\ |{T}_{P}^+({x}_{i})\cap {D}_{j}^+|\end{array},\quad{q}_{2}+1\leqslant j\leqslant m \end{array}\right.\end{array}$

对于任意对象 ${x_i}(i = k + 1,k + 2, \cdots ,n)$ 的相容类和决策类 ${D'_j}(j = 1,2, \cdots ,m)$ ，其交集的更新模式为

$\begin{array}{l} \quad\quad\quad\quad\quad\quad\quad|{{T'}_P}({x_i}) \cap {{D'}_j}| = \\ \left\{ {\begin{array}{*{20}{l}} {|{T_P}({x_i}) \cap {D_j}|,}\quad{1 \leqslant j \leqslant {q_1}} \\ \begin{array}{l} \!\!\!\!\!|{T_P}({x_i}) \cap {D_j}| - |T_P^ - ({x_i}) \cap {D_j}| - \\ \!\!\!\!\!|{T_P}({x_i}) \cap D_j^ - | + |T_P^ - ({x_i}) \cap D_j^ - |, \\ \end{array} \quad{{q_1} + 1 \leqslant j \leqslant m} \end{array}} \right. \end{array} $

通过分析不完备决策系统中相容类和决策类，以及其交集的动态更新模式，可得特征值发生修改时决策特征 $d$ 关于任意条件特征子集 $P$ 的条件熵的增量计算机制为

${H'_U}(d|P) = {H_U}(d|P) + \varDelta $

其中 $\varDelta $ 的值如下所示：

$ \begin{split}\varDelta =-{\displaystyle\sum\limits_{i=p+1}^{q}{\displaystyle\sum\limits_{j=1}^{m}\dfrac{|{{T}^{\prime }}_{P}({x}_{i})\cap {{D}^{\prime }}_{j}|}{\left|U\right|}\mathrm{log_2}\dfrac{|{{T}^{\prime }}_{P}({x}_{i})\cap {{D}^{\prime }}_{j}|}{|{{T}^{\prime }}_{P}({{x}^{\prime }}_{i})|}+}}\\ {\displaystyle\sum\limits_{i=p+1}^{n}{\displaystyle\sum\limits_{j=1}^{m}\dfrac{|{T}_{P}({x}_{i})\cap {D}_{j}|}{\left|U\right|}}} \mathrm{log_2}\dfrac{|{T}_{P}({x}_{i})\cap {D}_{j}|}{|{T}_{P}({x}_{i})|}+\quad\quad\\ {\displaystyle\sum\limits_{i=q+1}^{n}{\displaystyle\sum\limits_{j={q}_{1}+1}^{m}\Bigg(\frac{|{T}_{P}^-({x}_{i})\cap {D}_{j}|+|{T}_{P}({x}_{i})\cap {D}_{j}^-|}{\left|U\right|}}}- \quad\quad\\ \dfrac{|{T}_{P}^-({x}_{i})\cap {D}_{j}^-|+|{T}_{P}({x}_{i})\cap {D}_{j}|+|{T}_{P}^+({x}_{i})\cap {D}_{j}^+|}{\left|U\right|}\Bigg) \cdot \quad\\ \mathrm{log_2}\dfrac{|{{T}^{\prime }}_{P}({x}_{i})\cap {D}^{\prime }|}{|{{T}^{\prime }}_{P}({x}_{i})|}\quad\quad\quad\quad\quad\quad\quad\quad\end{split}$

基于上述分析，算法1给出了不完备决策系统中特征值更新时基于条件熵的增量式特征选择算法来计算新的特征子集。

算法1　不完备决策系统中基于条件熵的增量式特征选择算法(IFS-CE-IDS)

输入　不完备决策系统 ${\rm{IDS}} = (U,C \cup \{ d\} ,V,f)$ ，原始数据 $U$ 上的特征子集 ${\rm{RED}} \in C$ ，以及数据中发生修改对象的集合 $\Delta U$ ；

输出　特征选择后的特征子集 $A$ 。

1)初始化特征子集 $A = {\rm{RED}}$ ；

2)根据特征值更新对象集合 $\Delta U$ 更新后 $U/d = $ $ \{ {D'_i},{D'_2},\;\cdots ,\;{D'_m}\} ,U/T'(C) = \{ {T'_C}({x_1}),\;{T'_C}({x_2}), \;\cdots ,\; {T'_C}({x_n})\}$ ， $U/T'(A) = \{ {T'_A}({x_1}),{T'_A}({x_2}), \cdots ,{T'_A}({x_n})\} $ ，计算 $T_P^ - ({x_i})$ 、 $T_P^ + ({x_i}) $ 、 $D_j^ - $ 、 $D_j^ + $ ；

3)计算 ${H'_U}(d|C)$ 和 ${H'_U}(d|A) $ ；

4)如果 ${H'_U}(d|C) \ne {H'_U}(d|A)$ 进入7)，否则进入5)；

5)当 ${H'_U}(d|C) \ne {H'_U}(d|A)$ 时，对任意 $a \in C - A$ ，计算 ${\rm{sig}}(a,A \cup \{ a\} ,d)$ ，并且选择其中拥有最大 ${\rm{sig}}(a,A \cup \{ a\} ,d)$ 的 $a$ ， $A = A \cup \{ a\} $ ；

6)对任意特征 $a \in A$ 计算 ${\rm{sig}}(a,A,d)$ ,如果 ${\rm{sig}}(a,A,d) = 0$ ，则 $A = A - \{ a\} $ ；

7)返回A。

该算法中条件熵的计算时间是 $O(|C||U||\Delta U|)$ ，在算法IFS-CE-IDS中，步骤1)~3)的计算时间是 $O(|C||U||\Delta U|)$ ，步骤5)的向特征集A中添加特征的计算时间为 $O(|C{|^2}|U||\Delta U|)$ ，步骤6)中删除掉冗余特征的时间复杂度为 $O(|A||C||U||\Delta U|)$ 。因此，算法IFS-CE-IDS总的时间复杂度为 $O(|C||U||\Delta U|+ $ $ |C{|^2}|U||\Delta U| +$ $|A||C||U||\Delta U|) = O(|C{|^2}|U||\Delta U|)$ 。

3 实验及分析

本文选取了9组UCI数据集进行性能测试，数据集详细信息如表1所示。对于完备数据集Car和kr-vs-kp，随机删除原始数据集中5%的已知特征值变为缺失值，使原始完备数据集变为不完备数据集。对含有数值型数据的数据集Hepatitis、Wisconsin、Dermatology和Ozone，将数值型特征进行了离散化处理。如数据集Hepatitis包含19个特征，其中6个为数值型特征；数据集Wisconsin含有1个数值型特征；数据集Dermatology包含1个数值型特征；数据集Ozone都是数值型特征。实验环境配置为：Intel(R)Core(TM)i5-4210M CPU 2.60 GHz，8 GB内存，操作系统为Windows 10，程序开发平台为IntelliJ IDEA，编程语言为Java。

为验证本文所提出算法IFS-CE-IDS处理数据集特征值更新问题具有高效性和可行性，使用传统批量式特征选择算法HFS-CE-IDS与算法IFS-CE-IDS在9组UCI数据集上进行测试，从分类精度、决策性能以及计算效率三方面对传统批量式特征选择算法HFS-CE-IDS和IFS-CE-IDS进行比较。

3.1 分类精度分析

为比较算法HFS-CE-IDS与算法IFS-CE-IDS所得特征子集的分类精度，对表1中9组数据集选择其中50%对象，并且更新其特征值，然后分别运行传统批量式算法HFS-CE-IDS和增量式算法IFS-CE-IDS对特征值更新数据集进行特征选择。使用决策树J48、Naïve Bayes、SVM(support vector machines)分类器验证这两种算法的分类性能。实验结果如表2~4所示。

见表2，从两种算法在J48分类器的分类精度比较可知，算法IFS-CE-IDS在数据集Hepatitis、Audiology和Soybean上所得的分类精度相较算法HFS-CE-IDS所得分类精度差一些，而在其他6个数据集上算法IFS-CE-IDS所得分类精度与算法HFS-CE-IDS所得分类精度相同甚至更好。从表3可知，在Naïve Bayes分类器中，算法IFS-CE-IDS在9个数据集上的分类精度结果表明新提出算法在大部分数据集上的分类精度不比算法HFS-CE-IDS的分类精度差，例如在数据集Cancer、Car和kr-vs-kp上两种算法的分类精度基本相同。

从表4可知，在SVM分类器中，与算法HFS-CE-IDS相比，新提出算法的分类精度在Hepatitis、Audiology、Cancer、Soybean、Dermatology、Wisconsin、Car、Ozone、kr-vs-kp等7个数据集上相等甚至更好。

实验结果表明，算法IFS-CE-IDS在大部分数据集上能够在特征子集和分类精度上取得和算法HFS-CE-IDS相接近的，甚至更好的结果，可以证明算法IFS-CE-IDS是一种有效的特征选择算法。

3.2 决策性能分析

为检验算法IFS-CE-IDS的决策性能，本文使用文献[28]中对不完备数据进行评估所提出的6种评估函数评估算法HFS-CE-IDS以及算法IFS-CE-IDS计算的特征子集的决策性能。

6种评估函数中，特征集合 $C$ 下不完备决策系统 ${\rm{IDS}} = (U,C \cup \{ d\} ,V,f)$ 近似准确评估函数定义为

${a_C}(F) = \frac{{\displaystyle\sum_{{D_j} \in U/D} {|{{\underline {{\rm{apr}}} }_C}({D_j})|} }}{{\displaystyle\sum_{{D_j} \in U/D} {|{{\overline {{\rm{apr}}} }_C}({D_j})|} }}$

式中： ${{\underline {{\rm{apr}}} }_C} \!=\! \cup \{ x \in U|{\rm{M}}{{\rm{C}}_C} \subseteq {D_j},$ ${D_j} \in U/D\} ,1 \leqslant i \leqslant n$ ，是下近似值； ${\overline {{\rm{apr}}} _C} = \cup \{ x \in U|{\rm{M}}{{\rm{C}}_C} \cap {D_j} \ne \text{Ø} , {D_j} \in U/D\} , $ $ 1 \leqslant i \leqslant n$ ，是上近似值； $F = U/D$ 。其中， ${\rm{M}}{{\rm{C}}_C}$ 表示在特征子集 $C$ 下所得最大一致块集合。

不完备决策系统 ${\rm{IDS}} = (U,C \cup \{ d\} ,V,f)$ 特征集合 $C$ 下的一致性度量评估函数的定义为

${c_C}(D) = \frac{{\displaystyle\sum\nolimits_{{D_j} \in U/D} {|{{\underline {{\rm{apr}}} }_C}({D_j})|} }}{{|U|}}$

不完备决策系统 ${\rm{IDS}} = (U,C \cup \{ d\} ,V,f)$ 在 ${\rm{RULE}} = \{ {Z_{ij}}|{Z_{ij}}:{\rm{des}}({X_i}) \to {\rm{des}}({D_j}),{X_i} \in {\rm{M}}{{\rm{C}}_C},{D_j} \in {\rm{M}}{{\rm{C}}_d}\} $ 下的确定性度量 $\alpha $ 评估函数定义为

$\alpha ({\rm{IDS}}) = \frac{1}{m}\sum\limits_{{N_i}}^m {\frac{1}{{{N_i}}}} \sum\limits_{j = 1}^{{N_i}} {\frac{{|{X_i} \cap {D_j}|}}{{|{X_i}|}}} $

式中： ${N_i}$ 是在不完备决策表中由最大一致块 ${X_i}$ 所诱导得到的决策类数目； ${X_i} \in U$ 表示在 $P \subseteq C$ 下， $(u,v) \in T(P),\forall u,v \in {X_i}$ ，且不存在一个子集 $Y \in U$ ， ${X_i} \subset Y$ ， $(u,v) \in T(P),\forall u,v \in Y$ ，称 ${X_i}$ 为最大一致块。

不完备决策系统 ${\rm{IDS}} = (U,C \cup \{ d\} ,V,f)$ 在 ${\rm{RULE}} = $ $ \{ {Z_{ij}}|{Z_{ij}}:{\rm{des}}({X_i}) \to {\rm{des}}({D_j}),{X_i} \in {\rm{M}}{{\rm{C}}_C},{D_j} \in $ ${\rm{M}}{{\rm{C}}_d}\} $ 下的一致性度量 $\beta $ 评估函数定义为

$ \beta ({\rm{IDS}})=\frac{1}{m}[1-\frac{4}{\left|{X}_{i}\right|}{\sum\limits_{j=1}^{{N}_{i}}|{X}_{i}\cap {D}_{j}|\mu ({Z}_{ij})(1-\mu ({Z}_{ij}))}]$

式中： ${N_i}$ 是在不完备决策表中由最大一致块 ${X_i}$ 所诱导得到决策类数目，且 $\mu ({Z_{ij}}) = |{X_i} \cap {D_j}|/|{X_i}|$ 。

不完备决策系统 ${\rm{IDS}} = (U,C \cup \{ d\} ,V,f)$ 在 ${\rm{RULE}} = $ $ \{ {Z_{ij}}|{Z_{ij}}:{\rm{des}}({X_i}) \to {\rm{des}}({D_j}),{X_i} \in {\rm{M}}{{\rm{C}}_C},{D_j} \in $ ${\rm{M}}{{\rm{C}}_d}\} $ 下的支持度量 $\gamma $ 评估函数定义为

$\gamma ({\rm{IDS}}) = \sum\limits_{j = 1}^n {\frac{{|{D_j}|}}{{{N_j}|U|}}\sum\limits_{k = 1}^{{N_j}} {\frac{{|{X_k} \cap {D_j}|}}{{|U|}}} } $

式中 ${N_j}$ 是条件部分关于 ${D_j}$ 的最大一致块数。

不完备决策系统 ${\rm{IDS}} = (U,C \cup \{ d\} ,V,f)$ 在 ${\rm{RULE}} = \{ {Z_{ij}}|{Z_{ij}}:{\rm{des}}({X_i}) \to {\rm{des}}({D_j}),{X_i} \in {\rm{M}}{{\rm{C}}_C},{D_j} \in $ ${\rm{M}}{{\rm{C}}_d}\} $ 下的覆盖度量 $\vartheta $ 评估函数定义为

$\vartheta ({\rm{IDS}}) = \frac{1}{{|U|}}\sum\limits_{i = 1}^m {\frac{{|{X_i}|}}{{|U|}}} $

选择表1中每组数据集中50%数据对象，更新其特征值，然后分别运行算法HFS-CE-IDS和算法IFS-CE-IDS对特征值更新数据集进行特征选择。并且使用上述6种评估函数评估每组数据集更新后两种算法特征选择的特征子集的决策性能，实验结果如表5所示。

从表5的实验结果可知，算法IFS-CE-IDS与算法HFS-CE-IDS相比，在近似准确评估 ${a_C}$ 、一致性度量评估 ${c_C}$ 以及覆盖度量评估 $\vartheta $ 这3种评估函数下的评估值是相同的；在数据集Soybean上，算法IFS-CE-IDS与算法HFS-CE-IDS在确定性度量 $\alpha $ 评估函数以及一致性度量 $\beta $ 评估函数下的评估值不相同，而在其他8个数据集上两种算法的确定性度量 $\alpha $ 评估函数以及一致性度量 $\beta $ 评估函数的评估值是相同的；在支持度量 $\gamma $ 评估函数所得评估值结果中，两种算法在Cancer、Dermatology、Wisconsin、Car、Ozone、kr-vs-kp这6个数据集上的评估值相同，虽然在其余3个数据集上的评价值不同，但是评估值十分接近。

结合两种算法在6种评估函数下的结果，表明算法IFS-CE-IDS在大部分数据集下能够取得与算法HFS-CE-IDS相同的决策性能。

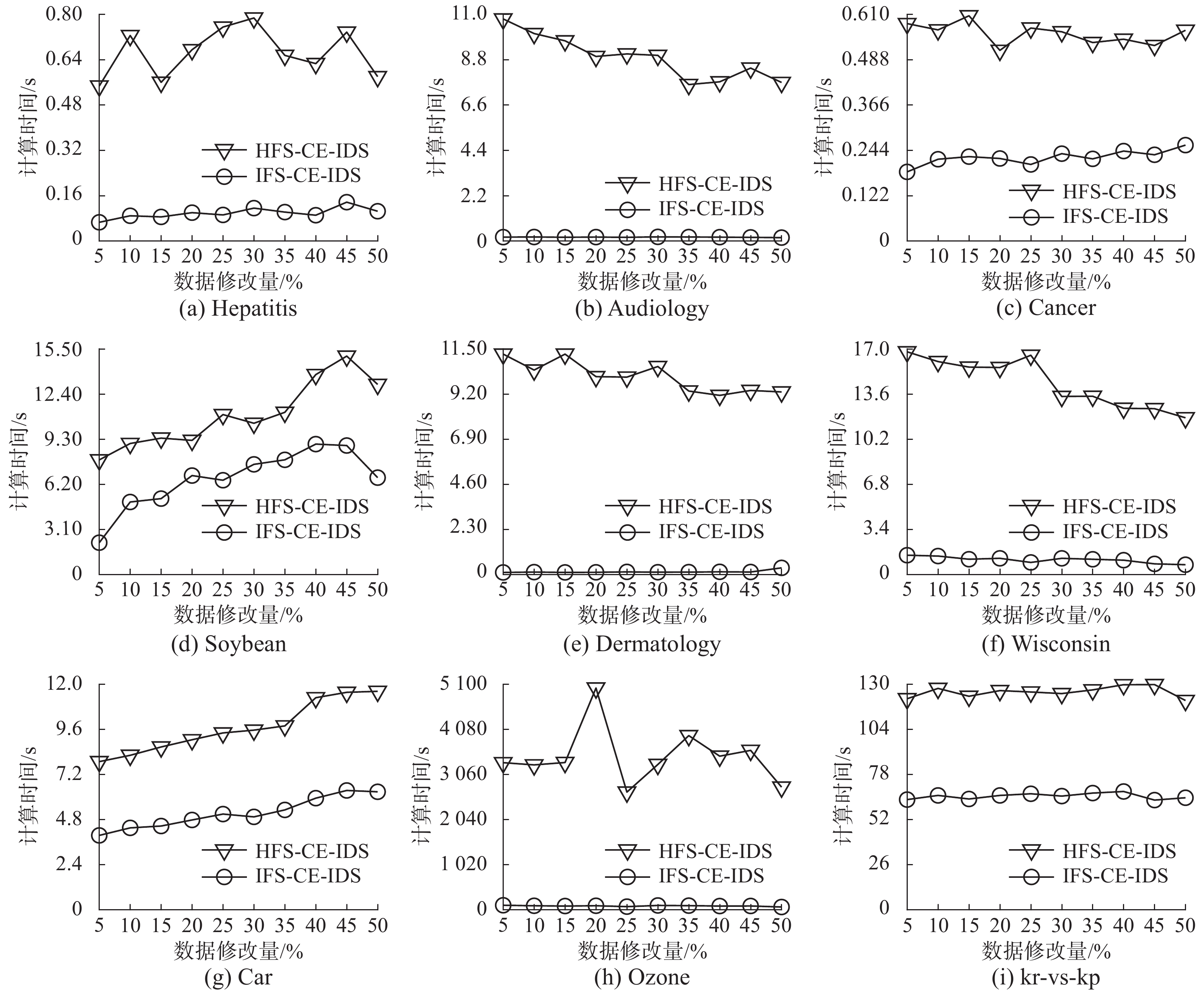
3.3 效率分析

为验证本文提出的增量式特征选择算法IFS-CE-IDS的高效性，采用传统的批量式特征选择算法HFS-CE-IDS作比较，该算法是一种与所提出算法基于相同特征评估准则的非增量方法。对表1中的每组数据集，依次选择其中的5%, 10%, 15%, ···, 50%数据对象并更新其对象特征值。同时发生变化的特征值取决于对象特征的值域。当有不同规模的数据对象特征值发生更新，分别使用增量式特征选择算法IFS-CE-IDS和传统批量式特征选择算法HFS-CE-IDS对数据集进行特征选择，求解特征选择结果。计算时间的比较结果如图1所示，图中详细给出两种算法计算时间随数据对象特征值更新规模的变化而发生的变化。

从图1可知，当不同规模的数据对象特征值发生更新后，传统批量式特征选择算法HFS-CE-IDS比增量式特征选择算法IFS-CE-IDS花费更多时间来选择特征值更新后的特征子集，主要的原因是增量式算法IFS-CE-IDS能够避免重复的计算，可以利用之前已有的计算结果，从而使得特征选择的计算效率得以提高。算法IFS-CE-IDS在9组数据集上的计算效率普遍比算法HFS-CE-IDS高，尤其是在一些数据规模较大的数据集上，算法IFS-CE-IDS的高效性更加明显。比如在Ozone数据集上算法IFS-CE-IDS的计算效率远优于算法HFS-CE-IDS的计算效率。图1中两种特征选择算法的计算时间都存在一些波动，如数据集Ozone中对象数据对象特征值更新20%时，算法HFS-CE-IDS的计算时间突然变得比其他比例耗时更大，因为数据集的数值对象特征值发生更新后，它的相容类与决策类因数据对象特征更新而产生变化，从而导致计算时间发生波动。

在实验分析中，通过算法HFS-CE-IDS与算法IFS-CE-IDS的分类精度、决策性能和计算效率三部分实验结果可知，算法IFS-CE-IDS与算法HFS-CE-IDS相比，在大部分数据集上进行特征选择所得特征子集数量相接近，两种算法分类精度和决策性能基本相同，但算法IFS-CE-IDS的计算时间小于算法HFS-CE-IDS，尤其在数据规模较大的数据集上计算时间的优势更加明显。通过本节分类精度、决策性能和计算效率三部分实验分析，证明IFS-CE-IDS是一种高效的处理数据对象特征值更新问题的增量式特征选择算法。

4 结束语

本文提出了不完备决策系统中面向特征值动态更新的增量式特征选择算法。通过分析不完备决策系统中条件特征值和决策特征值同时更新时相容类和决策类的动态更新模式，构造了条件信息熵的增量计算机制，并进一步设计了一种基于动态不完备决策系统的增量式特征选择算法。实验选取了9组UCI公共数据集，并通过分类精度、决策性能以及计算效率3个方面与传统批量式特征选择算法进行了性能对比。实验结果表明，本文算法所选择的特征子集与批量式算法在分类精度和决策性能具有基本一致的性能表现。同时，在面对不完备数据中特征值的动态变化环境下，本文算法的计算效率远优于传统批量式算法，可在较短时间内计算出一个可行的特征子集。实验中部分数据集使用算法IFS-CE-IDS需要进行特征转化，导致失去部分有效信息，降低算法结果质量，未来将致力于寻求更有效处理混合数据的增量特征算法。