2. 华侨大学 现代应用统计与大数据研究中心,福建 厦门 361021
2. Research Center of Applied Statistics and Big Data, Huaqiao University, Xiamen 361021, China
时间序列数据是指一系列时间及其对应属性值组成的序列集合,常见于医学、金融、水文等领域[1]。通过分析这些数据,如疾病[2]、股票[3-4]和水文数据[5]等,研究者可以发现相关问题的潜在信息,进而为相关部门或企业的工作提供指导性建议。关联规则是由Agrawal等[6]首次提出的,先找出频繁项集,再通过项集的支持度和置信度等指标,分析被研究对象间的关联关系。例如,购物篮分析案例就是关联规则的一个经典应用。Apriori算法是由Agrawal等[7]提出的,在挖掘频繁项集的过程中,该算法不仅要多次扫描数据库,还会产生大量的候选频繁项集,因而导致算法的挖掘效率低。为解决这一问题,很多学者从不同角度提出相应的方法。魏玲等[8]借鉴文献[9]的MapReduce框架,提出了基于MapReduce的Apriori改进算法(MapReduce算法),算法的基本思想是将频繁K−1项集的前K−2项作为键,将最后一项作为值,并将具有相同键的频繁K−1项集合并,以实现快速挖掘出候选频繁K项集。此外,他们还提出性能更高的基于Bigtable与MapReduce的Apriori改进算法(BM_Apriori算法),算法以事务集序号记录每个项出现的位置,通过求频繁K−1项集间的序号列表交集,即可快速获取候选频繁K项集。Zhang[10]基于概率论知识,通过参数a和b估算数据项集同时出现的概率,进而确定频繁项集,最终实现对Apriori算法的改进,但是该算法存在频繁项集缺失的可能性。Tran等[11]为了减少Apriori算法扫描数据库的次数,将事务集转化成事务矩阵,但是在矩阵运算过程中需要消耗较长时间。杨秋翔等[12]基于1和0表示数据项出现和未出现的数据集表示法创建权值向量矩阵,提出可以在数据挖掘过程中不断缩减矩阵的算法(WV_Apriori算法),以此达到提高挖掘频繁K项集速率的目的,但是当数据量越来越大时,创建的矩阵也会随之扩大,进而降低挖掘速率。Han等[13]提出能快速挖掘频繁项集的FP-growth算法,该算法将原数据存储到FP-tree中,从中挖掘频繁项集,从而不会产生候选频繁项集,但是该算法不能给出频繁项集的支持度和置信度。此外,上述算法不能直接用于时间序列数据的关联规则挖掘。Das等[14]于1998年首次提出挖掘时间序列数据的关联规则,此后该研究成为数据挖掘领域的热门方向。Velumani等[15]在数据预处理阶段,先将时间序列数据转为多个事务集,再用Apriori算法挖掘关联规则。赵益[16]提出了Improved-Apriori算法,算法通过计算位置列表的方式可避免多次扫描数据库。然而这2个算法均是基于Apriori,它们都会产生大量的候选频繁项集,会导致其挖掘效率不高。针对时间序列数据,其他学者也做出了相应的努力。Das等[14]先将一条时间序列等分成多条子序列,再挖掘多个时间序列的项间关联规则,但是他并没有给出3支及以上股票的实验结果。Chen等[17]所提的CEMiner算法基于区间数据,发现多个项间的闭合时态模式。Ruan等[18]提出一种可以在大规模区间型时态数据上并行和定量挖掘时间序列模式的算法。然而,这2种方法不能给出频繁项集的支持度和置信度。由于树形结构分支明确,直观易懂,因而树形存储结构是一种较为常用的存储形式,许多学者也将该存储结构应用到数据挖掘中。Schlüter等[19]提出利用2种树结构挖掘时间序列的关联规则,Rashid等[20]基于树结构,采用模式增长方法挖掘时态模式并给出关联规则,Pankaj等[21]也用到了FP-tree结构。另外,马慧等[22]利用FP-tree的优势并考虑项间具有不同的有效时间,提出一种基于FP-tree挖掘时态关联规则算法。
鉴于上述文献的理论研究及其所存在的问题,本文针对多条时间序列数据,通过数据降维并将符号化后的降维数据用趋势项−位置表示,再利用树结构找出频繁K项集,该过程通过求树的叶子节点与列表项间的信息交集,便可判断该项是否与该树枝中的所有结点构成频繁K项集,无需产生大量的候选频繁项集,此外,算法还能给出频繁项集的支持度和置信度。由于在某些情况下需要考虑多条时间序列在同时区内的关联关系,例如:在带有时间属性的零售商品销售数据中,顾客常会同时购买A和B等商品,若仅知道商品A的需求变化趋势但不知道商品B的变化趋势,此时可以通过挖掘商品间的销售量变化趋势的关联规则,进而预测商品B的需求变化趋势。因此,在同时区内,本文提出一种基于同步频繁树的时序数据关联规则算法(synchronize frequent tree, SFT)。
1 时间序列特征表示挖掘多条时间序列数据间的频繁项集,需要先对原数据进行特征表示。本文定义了2种表示法,即趋势项−位置表示法和事务集表示法。经典算法Apriori、FP-growth以及近些年提出的MapReduce、BM_Apriori和WV_Apriori算法都是基于事务集表示的数据,而SFT算法则是基于趋势项−位置表示的数据。
1.1 事务集表示法和趋势项−位置表示法Apriori、FP-growth、MapReduce、BM_Apriori和WV_Apriori等算法只能挖掘事务集数据的频繁项集,对于时间序列数据,需要将其转换为事务集才可以使用。本文将时间序列转换为事务集的方法定义为事务集表示法,其转换规则为:多条时间序列数据在同时区内的趋势项组合表示一个事务。例如:TA=(a1,a2,a3)、TB=(b1,b2,b3)和TC=(c1,c2,c3) 是3条符号化后的时间序列,其转换为事务集的结果为[(a1,b1,c1), (a2,b2,c2), (a3,b3,c3)]。
趋势项−位置表示法是为了提出SFT算法而定义的一种时间序列转换方法,其关键在于考虑到时间序列数据的时间属性具有一维性的特点,表示规则为趋势项+位置列表,其中趋势项是由时间序列进行线性分段后的斜率确定,共分上升、平稳和下降3种,用q1、q2 、q3表示,q表示时间序列名。例如:TA=(a2,a2,a1,a3,a1,a3,a1,a1) 是一条符号化后的时间序列数据,将其用趋势项−位置表示为list_A=[{a1:(2,4,6,7)},{a2:(0,1)},{a3:(3,5)}],其中,{a2:(0,1)}表示趋势项a2在第0和第1个时区内出现。
1.2 性能比较与分析显然事务集表示法并没有减少原数据量,而趋势项−位置表示法只保留每个趋势项,相同趋势项则用位置索引代替。由于特征表示数据是各类算法挖掘工作的基础,其对算法运行效率具有很大影响,因此有必要从转换时效和转换后数据的内存占用情况对上述2种表示法的性能进行比较和分析。实验采用python程序将后文使用的3条股票时间序列数据分别进行事务集表示和趋势项−位置表示,每条数据量为5343,共16029个数据。实验结果如表1所示。
| 表 1 2种表示法的性能比较 Tab.1 Performance comparison of two representations |
从转换时效方面,2种表示法处理的数据量相同,因而差异性不大;从内存占用方面,由趋势项−位置表示的数据要远低于事务集表示的数据,因为趋势项−位置表示法以数值型(int)数据记录趋势项的变化趋势,而事务集表示法则以字符型(str)数据记录,由于int占用的内存要低于str占用的内存,因此用前者表示的数据,内存占用情况要优于后者。
2 同步频繁树鉴于经典算法Apriori和FP-growth不能直接对时间序列数据进行关联规则挖掘,提出了一种可以解决上述问题的新算法,即SFT算法。新算法通过求叶子节点与列表项间的信息交集,便可判断该项是否与该树枝中的所有节点构成频繁项集。算法总体思路:先将时间序列用趋势项−位置表示,并去除非频繁项,再用首条时间序列构建一棵基础树,通过求叶子节点与列表项间的信息交集,便可以在树的生长过程中不断挖掘出频繁K项集。通过给出频繁K项集所有前缀项的信息量,便可以计算出频繁K项集的支持度与置信度。新方法除了适用于多条数时间序列数据外,在小数据和大数据中,其都能取得较优的时间效率,此外还能给出频繁项集的支持度和置信度。
X表示叶子节点所在的列表,x为树的叶子节点,也是列表的部分项,即X中的项需要满足某些条件后才能成为树的叶子节点。yi表示列表Y的项。loc_list表示叶子节点信息表与列表项位置表的信息交集,其信息量用loc_count表示,data表示仅包含频繁项的数据集,min_supc表示最小支持度计数。
算法 SFT算法
输入 data,min_supc;
输出 频繁K项集。
1)
2)
3)
①是,将loc_list作为yi的节点信息表,yi作为叶子节点,即xi。xi所在的树枝节点构成频繁项集,频繁项数即为xi所在的树层,项集个数即为loc_count。判断Y是否为最后一条时间序列:
是,输出频繁K项集;
否,输出频繁K项集,重复2)、3);
② 否,yi不是叶子节点,舍弃。
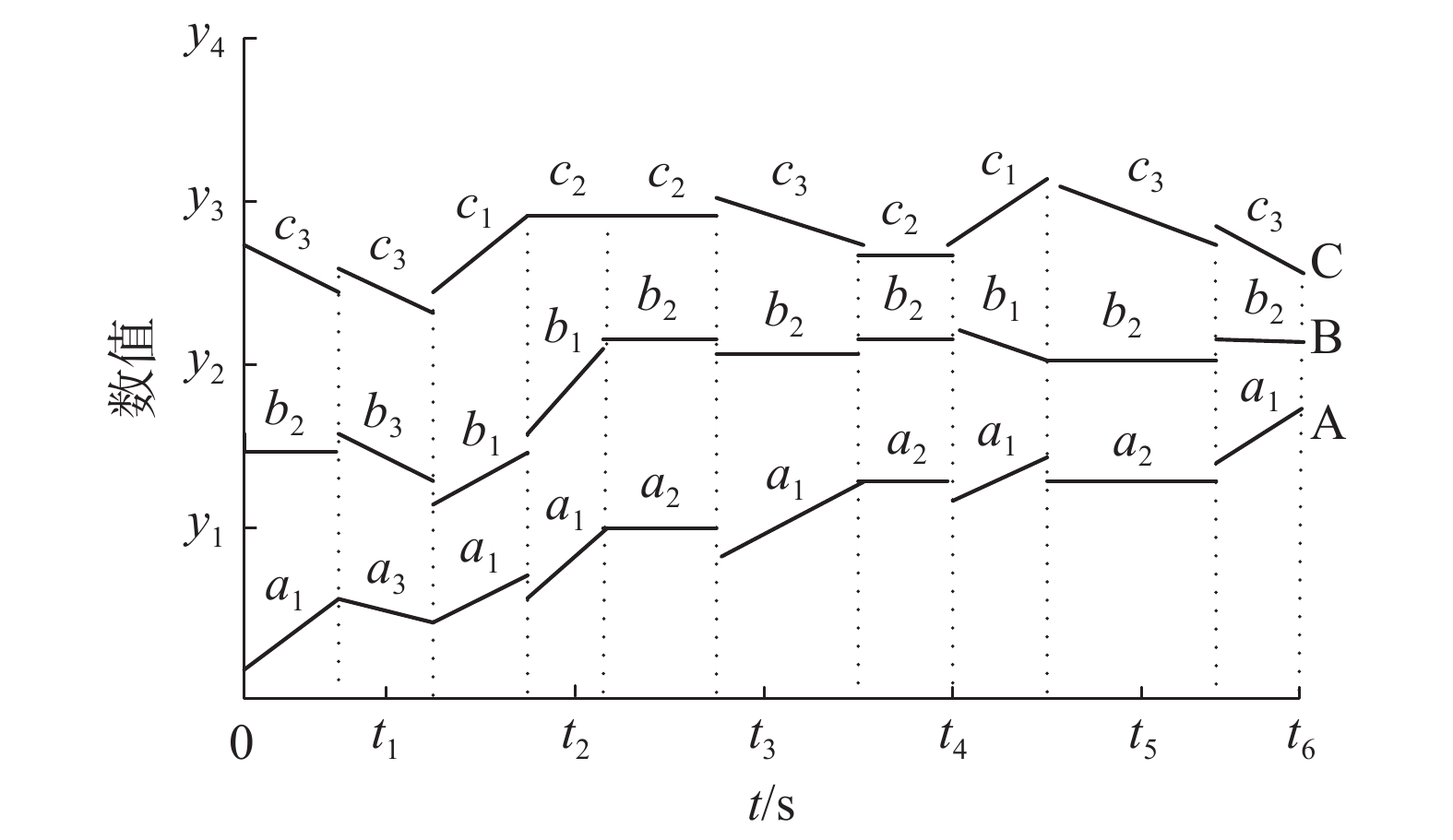
3 实例分析设最小支持度计数min_supc为2,用趋势项−位置表示的时间序列数据集data=[[{a1: (0, 2, 3, 5, 7, 9), a2: (4, 6, 8), a3: (1)}],[{b1: (2, 3), b2: (0, 4, 5, 6, 8, 9), b3: (1,7)}],[{ c1: (3, 4, 6), c2: (2, 7), c3: (0, 1, 5, 8, 9) }]], data可视化结果如图1所示,{b1: (2, 3)}表示趋势项b1在第2和第3个时区内出现过。在构建同步频繁树前,需要先去除data中的非频繁项。
|
Download:
|
| 图 1 实例数据可视化 Fig. 1 Visualization of an instance data | |
在data中,由于a3的数量仅为1,小于2,因此去掉此非频繁项。根据SFT算法的挖掘步骤,利用首条时间序列[{a1: (0, 2, 3, 5, 7, 9), a2: (4, 6, 8) }]中的a1和a2项构建一棵基础树,如图2所示。

|
Download:
|
| 图 2 基础树 Fig. 2 Base tree | |
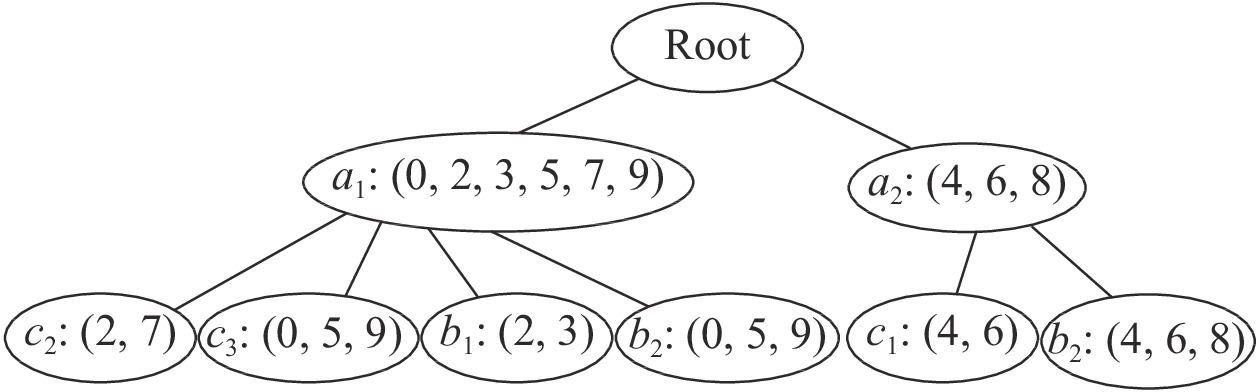
叶子节点a1、a2分别与时间序列B和C中的项进行匹配计算,即[{b1: (2, 3), b2: (0, 4, 5, 6, 8, 9), b3: (1,7) }]和[{ c1: (3, 4, 6), c2: (2, 7), c3: (0, 1, 5, 8, 9) }],结果如图3所示。例如a1与b2的loc_list为(0,5,9),即loc_count为3,因而b2成为叶子节点,其信息表为(0,5,9),信息量为3,由于b2位于第2层树,则a1b2是频繁2项集,项集个数为3。而a1与b3的loc_list为(7),即loc_count小于2,因此b3不是叶子节点。
|
Download:
|
| 图 3 同步频繁树的生长 Fig. 3 Growth process of synchronize frequent tree | |
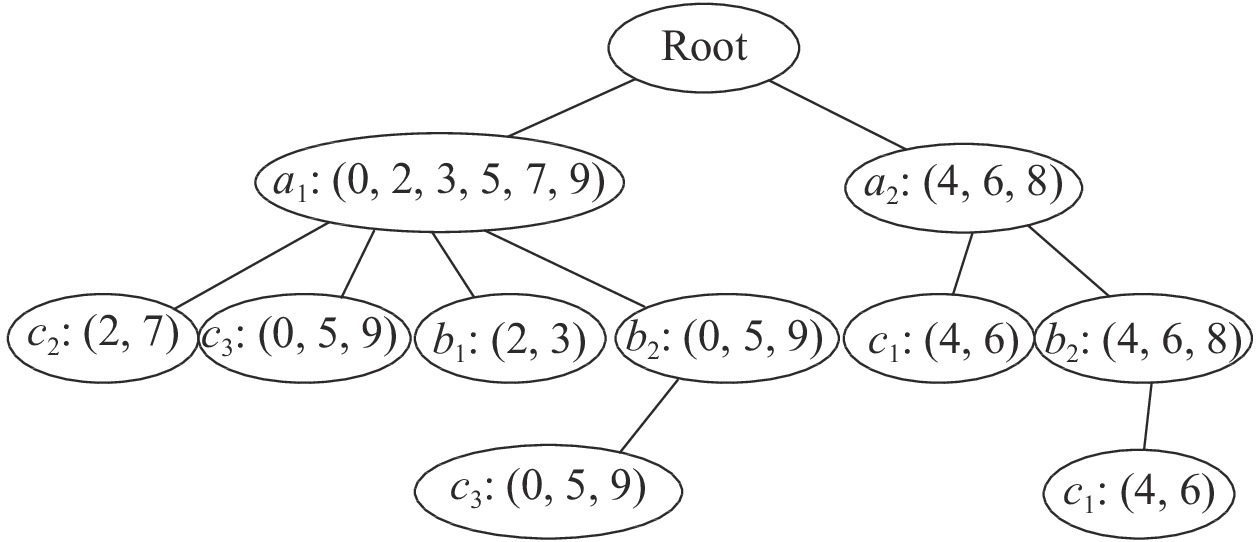
由于C是最后一条时间序列,因此输出图3中的所有频繁2项集:a1c2、a1c3、a2c1,其项集个数分别为2、3、2,但B并非最后一条时间序列,先输出频繁2项集a1b1、a1b2、a2 c1、a2b2,再以同样的思路将叶子节点b1、b2、b1与时间序列C中的项进行匹配计算,结果如图4所示,由于叶子结点是最后一条时间序列中的项,因此一棵完整的同步频繁树构建完成,并输出所有的频繁3项集,即a1b2c3、a2b2 c1。
|
Download:
|
| 图 4 完整的同步频繁树 Fig. 4 Complete synchronized frequent tree | |
为了验证SFT算法具有普适性,使用零售商品数据和股票数据分别进行实验。分别与基于时间序列事务集的Apriori[7]、FP-growth[14]、MapReduce[9-10]、BM_Apriori[9]以及WV_Apriori[13]算法的挖掘结果进行比较和分析,以检验SFT算法的有效性和性能。
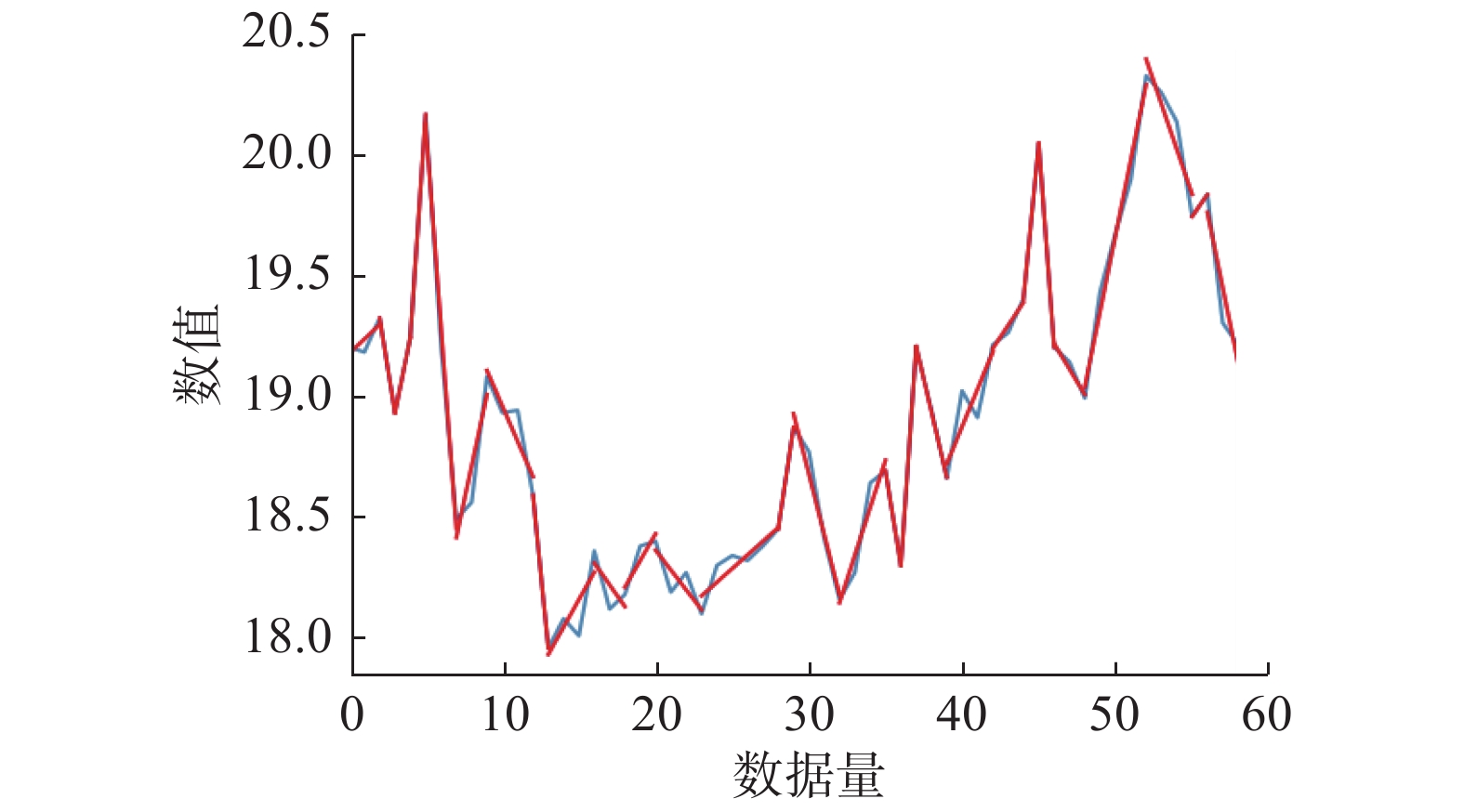
4.1 数据介绍零售商品数据是从UCI 网站下载的Online_Retail_II,取其中代号为20 725、20 727和20 728的销售量。每条数据的时间在2010年12月2日−2011年12月9日,共225天,675个数据量。股票数据是从预测者网中获取,冠城大通股票(600067)、中船科技股票(600072)和上汽集团股票(600104)的日收盘价,每支股票的时间在1997年12月25日−2021年3月4日,共5 343个工作日,16 029个数据量。为了获取多条时间序列间的变化趋势规则,需要先将每条时间序列分割成多个趋势项,然后再借鉴文献[23]的对齐思想将多条时间序列的趋势项对齐。例如,在时区[0, 3]内,时间序列A的趋势项是a1,而时间序列B在[0,1]和[1, 3]区间内的趋势项为b1和b2,为了与B对齐,序列A的[0, 3]时区被分成[0,1]和[1, 3],对应的趋势项是a1、a1。本文使用的分割策略为基于滑动窗口的线性回归,分割所得线段可以保留原数据的局部变化趋势。以上汽集团股票数据为例,图5是它的原始变化趋势,图6展示的是时间在2020年8月14日−2020年9月24日该支股票的数据分割过程,蓝色表示原始时间序列,红色表示分割后的局部拟合线段,表2则给出部分具体的原始数据。

|
Download:
|
| 图 5 上汽集团历年的股票数据 Fig. 5 Stock data of Shangqi group over the years | |
|
Download:
|
| 图 6 时间序列线性分段(上汽集团股票) Fig. 6 Linear segmentation of time series(Shangqi group) | |
| 表 2 原始数据(上汽集团股票) Tab.2 Raw data(Shangqi group) |
本次实验共分为2组,第1组使用商品销售数据集,第2组使用股票数据集。实验采用SFT算法,除了与经典算法Apriori和FP-growth进行比较外,实验还给出了近年来提出并且具有较好性能的MapReduce、BM_Apriori和WV_Apriori算法的挖掘结果进行比较。由于近年来从时间序列角度研究商品销售关联性成为热门方向[24-25],因此本文将给出详细的商品销售数据挖掘结果,并用股票数据的部分结果说明新方法具有普适性。第1组实验结果如图7所示,图7中展示了基于不同的min_supc,实验算法和对比算法的频繁2、3项集的个数。实验表明,无论min_supc取什么值,这些算法的挖掘结果都是相同的,进而说明SFT方法能够取得同样精度的效果。

|
Download:
|
| 图 7 频繁项集个数对比(商品数据) Fig. 7 Comparison of frequent itemsets(commodity data) | |
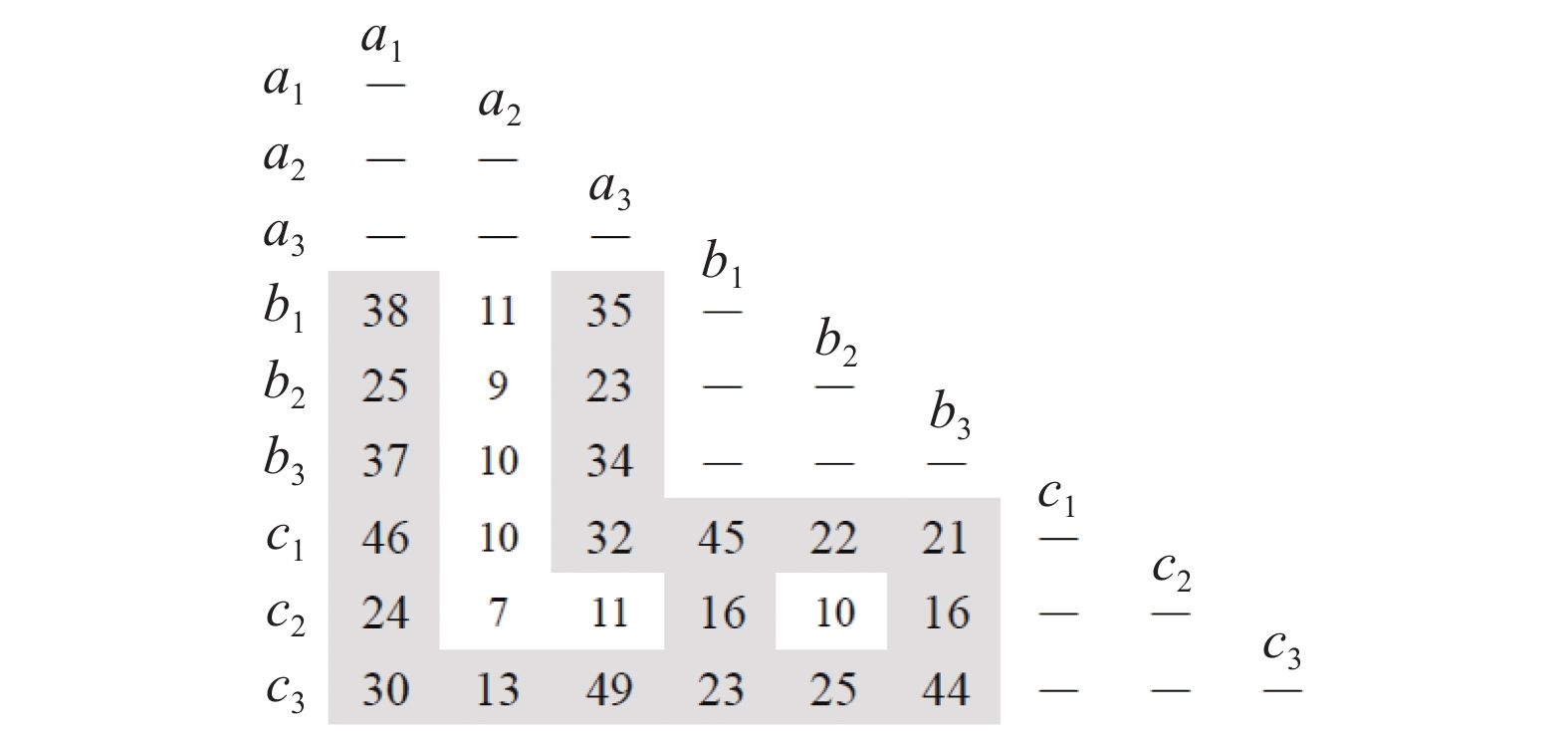
为说明实验结果的真实可靠性,图8给出了当min_supc =12时,频繁2项集的详细数据。其中,阴影部分的数字表示满足min_supc的频繁项集个数,例如频繁项集a1b1共有38个,非阴影部分的数字表示不满足min_supc的项集个数,‘—’则表示该频繁项集不存在,因为本文挖掘的是不同时间序列间的关联关系,所以a1a2等不是要找的频繁2项集。
|
Download:
|
| 图 8 频繁2项集及其个数 Fig. 8 Frequent 2 itemsets and their number | |
鉴于FP-growth算法不能给出频繁项集的支持度和置信度,而MapReduce、BM_Apriori和WV_Apriori是为挖掘频繁项集而提出的算法,故本文仅给出SFT和Apriori算法所挖掘频繁项集的支持度和置信度。当min_supc=12时,2个算法均给出如表3所示的结果,其中Rule表示规则,Sup表示支持度,Conf 表示置信度。以
| 表 3 SFT与Apriori算法挖掘关联规则 Tab.3 Association rules mined by SFT and Apriori |
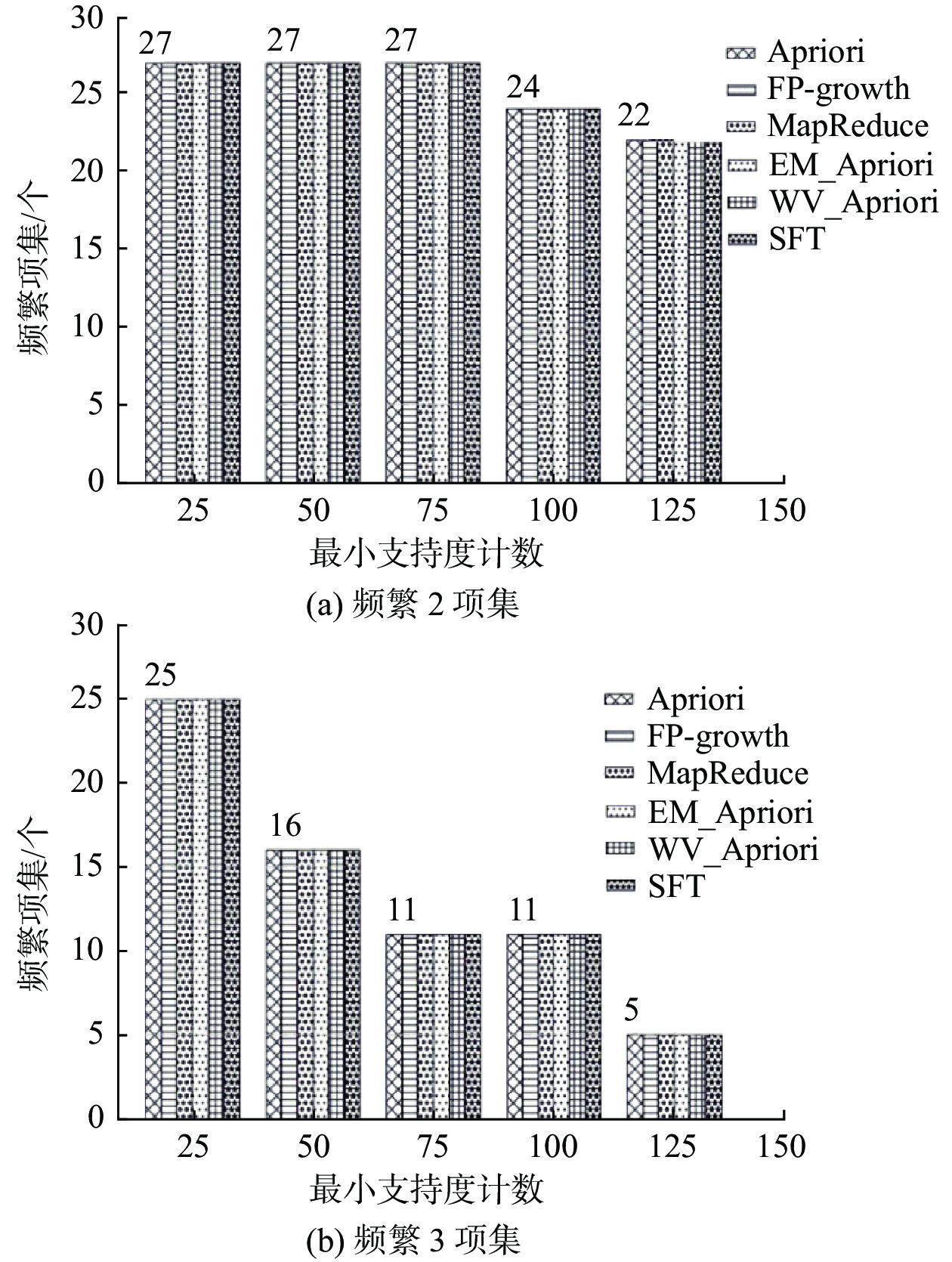
为了说明SFT算法具有普适性,第2组实验使用股票数据。由于挖掘步骤与第1组实验相同,因此图9直接给出挖掘结果,其表明6种算法的挖掘结果相同,因而说明SFT算法具有较强的普适性。
|
Download:
|
| 图 9 频繁项集个数对比(股票数据) Fig. 9 Comparison of frequent itemsets (stock data) | |
时间效率是衡量算法好坏的重要指标之一。由于挖掘频繁项集所耗时间占整个挖掘过程的多数时间,因此图10给出6种算法在挖掘商品数据和股票数据频繁项集时所消耗的时间可视化图,表4是具体的数值结果。实验表明,无论在数据量为675的商品数据,还是在数据量为16 029的股票数据,SFT算法的时间效率在不同最小支持计数的取值下都要优于其他算法,因而说明SFT算法具有较强的稳健性。

|
Download:
|
| 图 10 时间复杂度对比 Fig. 10 Comparison of time complexity-commodity data | |
| 表 4 6种算法挖掘频繁项集的时耗 Tab.4 Time consumption of six algorithms for mining frequent itemsets |
由图10和表4的定量结果分析可知,SFT算法要优于其他5种对比算法,因而有必要从定性角度进一步分析实验结果。本文认为影响SFT算法取得较好性能的主要因素有:1) 在生成频繁K项集的过程中,SFT算法不会产生候选频繁项集;2) SFT算法只需要对叶子节点和列表趋势项求一次信息交集,即可快速判断出频繁K项集;3) 由1.2节分析得出,由趋势项−位置表示的数据,其所占内存要远低于事务集表示的数据,因而导致在程序运行过程中,SFT算法的处理速度要快于其他算法。
限于篇幅有限并且考虑到各类因素对不同算法的影响程度不同,因而对于每个对比算法,仅给出必要的分析和解释:1) WV_Apriori算法在数据量较少的商品数据中,具有较好的时间效率,而在数据量较大的股票数据中,其时间效率明显降低,表现出很差的稳健性。导致这种结果的原因:①在创建0-1矩阵的过程中,每项表示一列,每个事务表示一行,当数据量越来越大时,其创建的矩阵会越来越大,因而将会消耗更多的时间;②由于频繁项集的挖掘是基于0-1矩阵,当矩阵很大时,除了遍历矩阵需要较多的时间外,矩阵占用较多内存也会影响程序的运行速率;③ 由于WV_Apriori算法只需要遍历一次数据库,并且在挖掘更高的频繁项集时,不断缩小矩阵,因此当数据量较小时,其效率要高于Apriori、FP-growth和MapReduce算法,正因为该算法需要遍历完整个矩阵后才能判断项间是否构成频繁项集,因此其运行速率不及BM_Apriori和SFT算法。2) 由于BM_Apriori算法直接求2个频繁K−1项之间的序号列表交集,即可快速找出它们之间的所有项集个数,但是该算法的基础数据用事务集表示,因而在数据量较少的商品数据中,其时间效率要优于除了SFT算法以外的其他算法,然而在数据量较大的股票数据中,该算法会产生候选频繁K项集,因而其时间效率略低于FP-growth算法。3) MapReduce算法通过合并具有相同键的频繁K−1项集,即可快速产生候选频繁K项集,因而其挖掘速率要快于Apriori算法,但是正因它还会产生较多的候选项集,因此导致其运行效率不及余下的其他算法。4) FP-growth算法只需要扫描2次数据库,并通过头指针可以快速找到其他树枝上的相同项,因而在数据量较大的股票数据中,其挖掘速率要优于除了SFT以外的其他算法,但是由于其挖掘的基础数据用事务集表示,此外,在重新对事务集进行排序、构建FP-tree、提取条件模式基以及构建条件FP-tree过程中,消耗了较多时间,因此导致其运行速率不及SFT算法。5) 当最大频繁项集是K时,Apriori算法需要扫描K次数据库,并从大量候选频繁项集中挖掘出频繁K项集,因而导致其具有较低的挖掘速率。
表5分别从6个层面,概括总结6种算法的区别与联系:除了SFT算法外,其他算法都是基于用事务集表示的数据;SFT和BM_Apriori算法分别用项的位置和事务的序号代替原数据,而其他算法仅仅是通过不同的方法表示保留原数据;SFT算法与FP-growth和WV_Apriori算法一样不会产生候选频繁项集;仅有SFT算法和BM_Apriori算法可以直接判断频繁K项集,而其他算法则需要遍历完整个数据库才能判断;SFT和Apriori算法能给出频繁项集的支持度与置信度,而其他算法不能;SFT算法与FP-growth、Mapreduce和BM_Apriori算法都能应用于大数据中。
| 表 5 6种算法对比 Tab.5 Comparison of six algorithms |
显然,无论在定量分析还是定性分析中,SFT算法都要优于其他算法。
5 结束语针对经典算法Apriori和FP-growth不适用于时间序列数据,提出了一种挖掘时间序列数据关联规则的新方法,即SFT算法,并给出了近些年来提出的,且具有较好性能的MapReduce、BM_Apriori和WV_Apriori算法挖掘结果作对比。SFT算法的总体思路是先将时间序列数据用趋势项−位置表示,再通过求叶子节点与列表项间的信息交集,进而可以快速挖掘出频繁K项集。
本文具的创新点:1) 新定义的事务集表示法可以将多条时间序列数据转换成事务集,该转换法让仅适用于挖掘无序数据的关联规则算法也可以挖掘时间序列数据,此外还定义了趋势项−位置表示法,用该方法表示的数据,其内存占用要低于原数据所占的内存,而内存占用情况会影响算法运行速率;2) SFT算法可以挖掘多条时间序列数据间的关联规则,弥补了Apriori、FP-growth等算法不适用于时间序列数据的缺点;3) 通过计算树叶子节点与列表项间的信息交集,便可快速判断频繁K项集,并且不会产生候选频繁项集,因而提高了算法的挖掘速率;4) SFT算法充分利用时间序列具有一维性特点,并采用了直观易懂的树型结构,这为时间序列数据关联分析的研究提供了一种新的研究思路和视角。实验表明:1) 基于趋势项−位置表示法表示的时间序列数据,其内存占用要远低于用事务集表示的时间序列数据;2) 利用SFT算法挖掘出的频繁项集与经典算法Apriori、FP-growth以及近些年来所提的,并且具有较好性能的MapReduce、BM_Apriori和WV_Apriori算法的挖掘结果相同;3) 无论在大数据还是小数据中,SFT算法的时间效率都要优于对比算法;4) 对于关联规则,SFT算法给出的结果与Apriori的结果相同。
SFT算法具有较高较优的时间性能,使其有较强的普适性。然而,SFT算法只考虑到同时区内不同时间序列间的关联关系,挖掘在不同时区内不同时间序列间的关联关系,将是进一步需要研究的工作。
| [1] |
陈海燕, 刘晨晖, 孙博. 时间序列数据挖掘的相似性度量综述[J]. 控制与决策, 2017, 32(1): 1-11. CHEN Haiyan, LIU Chenhui, SUN Bo. Survey on similarity measurement of time series data mining[J]. Control and decision, 2017, 32(1): 1-11. (  0) 0)
|
| [2] |
ACHEBAK H, DEVOLDER D, BALLESTER J. Trends in temperature-related age-specific and sex-specific mortality from cardiovascular diseases in Spain: a national time-series analysis[J]. The lancet planetary health, 2019, 3(7): e297–e306.
( 0) 0)
|
| [3] |
李海林, 梁叶. 基于关键形态特征的多元时间序列降维方法[J]. 控制与决策, 2020, 35(3): 629-636. LI Hailin, LIANG Ye. Dimension reduction for multivariate time series based on crucial shape features[J]. Control and decision, 2020, 35(3): 629-636. (  0) 0)
|
| [4] |
程小林, 郑兴, 李旭伟. 基于概率后缀树的股票时间序列预测方法研究[J]. 四川大学学报, 2018, 55(1): 61-66. CHENG Xiaolin, ZHENG Xing, LI Xuwei. Research of stock time based on probabilistic suffix tree[J]. Journal of Sichuan University, 2018, 55(1): 61-66. DOI:10.3969/j.issn.0490-6756.2018.01.011 (  0) 0)
|
| [5] |
王 玲, 徐培培, 彭开香. 基于因子模型和动态规划的多元时间序列分段方法[J]. 控制与决策, 2020, 35(1): 35-44. WANG Ling, XU Peipei, PENG Kaixiang. Segmentation of multivariate time series with factor model and dynamic programming[J]. Control and decision, 2020, 35(1): 35-44. (  0) 0)
|
| [6] |
AGRAWAL R, IMIELIŃSKI T, SWAMI A. Mining association rules between sets of items in large databases[C]//Proceedings of the 1993 ACM SIGMOD International Conference on Management of Data. Washington, USA, 1993: 207–216.
( 0) 0)
|
| [7] |
AGRAWAL R, SRIKANT R. Mining sequential patterns[C]//Proceedings of the 11th International Conference on Data Engineering. Taipei, China, 1995: 3–14.
( 0) 0)
|
| [8] |
魏玲, 魏永江, 高长元. 基于Bigtable与MapReduce的Apriori算法改进[J]. 计算机科学, 2015, 42(10): 208-210, 243. WEI Lin, WEI Yongjiang, GAO Changyuan. Improved Apriori algorithm based on bigtable and MapReduce[J]. Computer science, 2015, 42(10): 208-210, 243. (  0) 0)
|
| [9] |
KARIM R, HOSSAIN A, RASHID M, et al. A MapReduce framework for mining maximal contiguous frequent patterns in large DNA sequence datasets[J]. IETE technical review, 2012, 29(2): 162–168.
( 0) 0)
|
| [10] |
ZHANG Xiaolu. Pythagorean fuzzy clustering analysis: a hierarchical clustering algorithm with the ratio index-based ranking methods[J]. International journal of intelligent systems, 2018,33(9): 1798–1822.
( 0) 0)
|
| [11] |
TRAN T N, DRAB K, DASZYKOWSKI M. Revised DBSCAN algorithm to cluster data with dense adjacent clusters[J]. Chemometrics and intelligent laboratory systems. 2013,120(15): 92−96.
( 0) 0)
|
| [12] |
杨秋翔, 孙涵. 基于权值向量矩阵约简的Apriori算法[J]. 计算机工程与设计, 2018, 39(3): 690-693,762. YANG Qiuxiang, SUN Han. Apriori algorithm based on weight vector matrix reduction[J]. Computer engineering and design, 2018, 39(3): 690-693,762. (  0) 0)
|
| [13] |
HAN Jiawei, PEI Jian, YIN Yiwen. Mining frequent patterns without candidate generation[J]. ACM sigmod record, 2000, 29(2): 1–12.
( 0) 0)
|
| [14] |
DAS G, LIN K I, MANNILA H, et al. Rule discovery from time series[C]//Proceedings of the 4th International Conference on Knowledge Discovery and Data Mining. New York, USA, 1998: 16−22.
( 0) 0)
|
| [15] |
VELUMANI B, UMAJOTHY P. Mining temporal association rules from time series microarray using apriori algorithm[J]. Review of bioinformatics and biometrics, 2013, 2(2): 29−36.
( 0) 0)
|
| [16] |
赵益. 多时间序列上时序关联规则的挖掘[D]. 上海: 东华大学, 2018. ZHAO Yi. Discovery of tempopal assocition rules in multivariate time series[D], Shang Hai: Donghua University, 2018. (  0) 0)
|
| [17] |
CHEN Yicheng, PENG W C, LEE S Y. CEMiner—An efficient algorithm for mining closed patterns from time interval-based data[C]//Proceedings of the IEEE 11th International Conference on Data Mining. Vancouver, Canada, 2011: 121−130.
( 0) 0)
|
| [18] |
RUAN Guangchen, ZHANG Hui, PLALE B. Parallel and quantitative sequential pattern mining for large-scale interval-based temporal data[C]//Proceedings of 2014 IEEE International Conference on Big Data (Big Data). Washington, USA, 2014: 32−39.
( 0) 0)
|
| [19] |
SCHLÜTER T, CONRAD S. Mining several kinds of temporal association rules enhanced by tree structures[C]//Proceedings of the 2nd International Conference on Information, Process, and Knowledge Management. Saint Maarten, Netherland Antilles, 2010: 86−93.
( 0) 0)
|
| [20] |
RASHID M M, GONDAL I, KAMRUZZAMAN J. Mining associated patterns from wireless sensor networks[J]. IEEE transactions on computers, 2015, 64(7): 1998−2011.
( 0) 0)
|
| [21] |
PANKAJ G, SAGAR B B. Discovering weighted calendar-based temporal relationship rules using frequent pattern tree[J]. Indian journal of science and technology, 2016, 9(28): 1–6.
( 0) 0)
|
| [22] |
马慧, 汤庸, 潘炎. 一种基于FP-树的时态关联规则的分区挖掘方法[J]. 计算机工程, 2006, 32(17): 132−134. MA Hui, TANG Yong, PAN Yan. A FP-tree based partition mining approach to discovering temporal association rules[J]. Computer engineering, 2006, 32(17): 132−134. (  0) 0)
|
| [23] |
张建业, 潘泉, 张鹏等. 基于斜率表示的时间序列相似性度量方法[J]. 模式识别与人工智能, 2007, 20(2): 271−274. ZHANG Jianye, PAN Quan, ZHANG Peng, et al. Similarity measuring method in time series based on slope[J]. Pattern recognition and artificial intelligence, 2007, 20(2): 271−274. (  0) 0)
|
| [24] |
SALEM M Z. Effects of perfume packaging on Basque female consumers purchase decision in Spain[J]. Management decision, 2018, 56(8): 1748−1768.
( 0) 0)
|
| [25] |
LI Hailin, WU Y J, CHEN Yewang. Time is money: dynamic-model-based time series data-mining for correlation analysis of commodity sales[J]. Journal of computational and applied mathematics, 2020, 370: 112659.
( 0) 0)
|
 2021, Vol. 16
2021, Vol. 16


