2. 哈尔滨金融学院 计算机系,黑龙江 哈尔滨 150030;
3. 火箭军工程大学 导弹工程学院,陕西 西安 710025
2. Department of Computer Science, Harbin Finance University, Harbin 150030, China;
3. Missile Engineeting College, Rocket Force University of Engineering, Xi’an 710025, China
无线传感器网络(WSN)已广泛用于大型工业结构件的安全检测[1]、军事领域的实时信息采集[2]、生态环境监测[3]、辅助农业生产和复杂的机械控制等领域[4-5]。在实际应用中,传感器节点发生故障和通信信道受到干扰等因素会导致传感器节点采集数据不完整不准确,同时传感器节点工作环境的复杂性和WSN的无中心特性也会增加人工维护和故障排查的难度,所以对WSN节点进行实时准确地故障检测对无线传感器网络的应用和发展具有十分重要的意义。目前对WSN节点的故障检测方法主要分为2种:1) 基于数据驱动的WSN节点故障检测方法[6-15];2) 基于专家知识的WSN节点故障检测方法[16-17]。
方法1需要处理大量的传感器数据,且算法准确性依赖于传感器节点发送数据的完整性和准确性。典型的数据驱动方法又分为构建神经网络[6-8]及构建数据模型2种方式[9-15]。方法2基于专家知识,算法检测准确率较高,但检测准确率依赖于专家知识的准确性。如文献[16]提出一种基于可信度和邻居协作的WSN节点故障检测算法,依赖可信度模型以及邻居节点的诊断回复完成节点故障检测过程。目前大部分WSN故障检测方法无法准确地描述不确定、模糊以及未知信息,导致故障检测失去可靠性。为解决该问题,有学者使用证据推理规则描述不确定、模糊以及未知信息[18]。杨建波等[19]在证据推理基础上进一步提出置信规则库(belief rule base,BRB)模型。相比其他故障检测算法,置信规则库在具备数据样本可训练的优势上集成了专家知识,同时使用半定量信息描述数据不确定性和专家知识模糊性2个不确定信息,还具有过程可解释、结果可追溯等优点。因此,本文引入置信规则库开展故障检测算法的研究。同时,为了准确地描述传感器数据的变化趋势和节点间数据的相关程度,在置信规则库基础上加入时间相关性和空间相关性来描述故障检测过程。
1 问题描述 1.1 基本假设假设1 故障检测输出的结果包括正常故障、偏移故障、高噪声故障、离群点故障和固定值故障,用
假设2 数据处理中心接收到的传感器数据用矩阵
| ${{X}}_m^n(t) = \left[ {\begin{array}{*{20}{c}} {x_1^1(t)}& {x_2^1(t)}&\cdots &{x_m^1(t)} \\ \vdots &{}& \vdots \\ {x_1^n(t)}& {x_2^n(t)}&\cdots &{x_m^n(t)} \end{array}} \right]$ | (1) |
故障检测过程需要的数据特征(模型的前提属性)用矩阵
| ${{A}}_m^n(t) = \left[ {\begin{array}{*{20}{c}} {a_1^1(t)}& {a_2^1(t)}& \cdots &{a_m^1(t)} \\ \vdots &{}& \vdots \\ {a_1^n(t)}& {a_2^n(t)}& \cdots &{a_m^n(t)} \end{array}} \right]{\rm{ }}$ | (2) |
为检测故障需要依据式(3)提取数据特征:
| ${{A}}_m^n(t) = g({{X}}_m^n{\rm{(}}t{\rm{)}},\sigma )$ | (3) |
式中:
| $\widehat Y(t) = h({{A}}_m^n(t),\lambda )$ | (4) |
式中:
| $\widehat Y(t) = h(g({{X}}_m^n(t),\sigma ),\lambda ))$ | (5) |
由第1节可知本文的故障检测包括前提属性提取和传感器故障类型确定2个过程,可用图1直观表示出来。

|
Download:
|
| 图 1 故障检测模型工作流程 Fig. 1 Workflow of the fault detection model | |
在模型前提属性提取部分,数据处理中心采集汇聚节点发送的传感器数据后,由故障检测模型进行同属性数据筛选;将被检测传感器节点集群同属性数据构建成数据矩阵,然后以同属性矩阵为目标提取前提属性以构建前提属性矩阵
采用文献[20]提出的趋势相关性表述相邻节点在某一时间段内数据的趋势变化相似性:
| ${{X}}_m^i(t) = [x_m^i(t - k) \;\; x_m^i(t - k + 1)\; \cdots \;x_m^i(t)]$ |
式中
| $\begin{split} c(i,j) = \sum\limits_{k = 1}^{m + 1} \left[x_m^i(t - k + 1) - {{\overline {{X}}}}_m^i(t)\right] \times \\ \sum\limits_{k = 1}^{m + 1} \left[x_m^j(t - k + 1) - {{\overline {{X}}}}_m^j(t)\right] \times {m^{ - 1}}\quad \\ \end{split} $ |
进一步可得节点i、j在时刻t的趋势相关性系数定义为
| ${\chi _{i,j}}(t) = c(i,j)/\sqrt {v(i)v(j)} $ | (6) |
趋势相关性系数
本文用空间相关性表示相邻节点在某一时刻的数据相似程度,空间相关性使用残差计算获得:
| ${{X}}_m^i(t) = \left[x_m^i(t - k)\;\; x_m^i(t - k - 1)\; \cdots \;x_m^i(t)\right]$ |
式中
| ${\eta _i}(t) = x_m^i(t) - {\overline {{X}}_m}(t)$ | (7) |
式中
置信规则库(BRB)的建模依赖于一系列的置信规则,其中第k条置信规则可以描述为
| $\begin{split} {R_k}:&{\rm{if }}{x_1}\;{\rm{ is}}\;{A_1}, \cdots ,{x_M}\;{\rm{ is}}\;{A_M} \\ &{\rm{then}}\{ ({D_1},{\beta _{1,k}}), ({D_2},{\beta _{2,k}}),\cdots ,({D_N},{\beta _{N,k}})\} \\ &{\rm{with\;rule\;weight }}\;{\theta _k} \\ &{\rm{and \; attribute\; weight }}\;{\delta _1}, {\delta _2},\cdots ,{\rm{ }}{\delta _M}{\rm{ }} \\ \end{split} $ |
其中:
在置信规则库的构建过程中需要设定前提属性和与之对应的参考值,通过前提属性间的一一映射,初始置信表被构建出来。基于杨剑波等[19-22]提出的ER解析算法对置信规则进行规则融合,可得本文置信规则库模型的推理过程:
1) 计算规则匹配度
| ${F}_i^k = \left\{ {\begin{array}{*{20}{l}} {\left(R_i^{l + 1} - {x_i}\right) \times {{\left(R_i^{l + 1} - R_i^l\right)}^{{\rm{ - }}1}},}\quad k = 1\;{\text{且}}\; R_i^l \leqslant {x_i} \leqslant R_i^{l + 1}\\ {1 - {F}_i^k,}\quad{k = l + 1}\\ {0,}\quad{k = 1 ,\cdots, K;k \ne l;k\ne l + 1} \end{array}} \right.$ |
2) 计算激活规则的激活权重
| ${\omega _k} = {\theta _k}\mathop \Pi \limits_{i = 1}^M {\left({{F}}_i^k\right)^{{\delta _i}}} \times {\left[\sum\limits_{i = 1}^K {} {\theta _l}\mathop \Pi \limits_{i = 1}^M {\left({{F}}_i^k\right)^{{\delta _i}}}\right]^{ - 1}}$ |
3) ER解析算法进行规则融合
| $\begin{split} {\beta _n} = \left[ {\begin{array}{*{20}{c}} {\mu \times \mathop \Pi \limits_{l = 1}^L \left({\omega _l}{\beta _{n,l}} + 1 - {\omega _l}\displaystyle\sum\limits_{i = 1}^N {\beta _{i,l}}\right) - } {\mu \times \mathop \Pi \limits_{l = 1}^L \left(1 - {\omega _l}\displaystyle\sum\limits_{i = 1}^N {\beta _{i,l}}\right)} \end{array}} \right] \times \left[1 - \mu \times \left[\mathop \Pi \limits_{l = 1}^L (1 - {\omega _l})\right]\right]^{ - 1} \end{split} $ |
| $\mu {\rm{ = }}\left[ {\begin{array}{*{20}{c}} {\left[\displaystyle\sum\limits_{i = 1}^N \mathop \Pi \limits_{l = 1}^L \left({\omega _l}{\beta _{n,l}} + 1 - {\omega _l}\displaystyle\sum\limits_{i = 1}^N {\beta _{i,l}}\right)\right] - } {(N - 1)\mathop \Pi \limits_{l = 1}^L \left(1 - {\omega _l}\displaystyle\sum\limits_{i = 1}^N {\beta _{i,l}}\right)} \end{array}} \right]$ |
4) 效用计算得出结果
| $y = \displaystyle\sum\limits_{n = 1}^N \mu ({D_n}){\beta _n}$ |
在优化之前首先需要确定规则权重
1) 规则权重,在置信规则库模型构建时,对于每一条置信规则
2) 属性权重,在置信规则库模型构建时,需要确定M个前提属性对应的属性权重
3) 对于第k条规则,其对应的第N个结果
| $0 \leqslant {\beta _{n,k}} \leqslant 1,\quad n = 1,2, \cdots ,N;k = 1,2, \cdots ,L$ |
同时所有置信规则置信度总和可以表示为
| $\displaystyle\sum\limits_{n = 1}^N {\beta _{n,k}} \leqslant 1,\quad n = 1,2, \cdots ,N;k = 1,2, \cdots ,L$ |
其次,模型预测结果的精度表示为
| $\psi ({\hat Y_n}(t)) = \dfrac{1}{N}\displaystyle\sum\limits_{n = 1}^N {\left({\hat Y_n}(t) - {\hat \varphi _n}(t)\right)^2}$ | (8) |
式中:N为测试样本的数量;
在本节中,使用Intel Lab Data无线传感器数据集作为验证数据集,来检验本文所提故障检测方法的有效性。

|
Download:
|
| 图 2 BRB模型优化流程 Fig. 2 BRB model optimization flow | |
根据不同的实验要求生成的实验样本集描述如下:
1) 数据集1:选取3月1−7日内传感器所有节点的温度数据,采样完成后以10 min为间隔求解温度数据均值。经过上述处理得到数据集1,共包含1008个样本数据。
2) 数据集2:通过对传感器节点进行分簇,选择传感器1、2、3、4作为实验节点,节点1为故障节点,以6个样本点为步距将1008个温度数据分为168组,每组6个样本点。1~32组为正常样本,33~66组为偏移故障,67~100为高噪声故障,101~134为离群点故障,135~168为固定值故障。基于故障类型设置相应的故障类型标签0、1、2、3、4,并生成数据集2。
3.2 模型参数设置为构建基于BRB的WSN节点故障检测模型,需要事先确定模型的前提属性。通过分析前提属性
| ${A_1} = \left\{ {S,J,L,M,H,B,T} \right\}$ | (9) |
前提属性2参考点的选取方式与前提属性1保持一致,前提属性
| ${A_2} = \left\{ {S,J,L,M,H,B,T} \right\}$ | (10) |
对于BRB模型的输出结果,确定5个参考点,分别是正常(N)、偏移故障(O)、高噪声故障(G)、离群点故障(D)、固定值故障(F)。结果
| $\widehat Y = \left\{ {N,O,G,D,F} \right\}$ | (11) |
前提属性1、前提属性2和输出结果参考点及其对应参考值设置如表1、2所示。
| 表 1 前提属性1、2参考点及参考值 Tab.1 Referential points and values of the premise attributes 1 and 2 |
| 表 2 输出结果
|
前提属性和输出结果的参考点及参考值设置合理以后,即可进行置信表的设置,将前提属性1和前提属性2的所有参考点进行充分组合,组成置信规则。本文中置信表置信规则数目为2个前提属性参考点数量之积,置信规则数为49条,每条规则对应的5个结果的置信度由专家知识进行确定。
3.3 实验结果分析 3.3.1 实验结果为了使模型具有较强的泛化能力,在实验过程中将训练集设置为测试集的一半,在本实验中,将168组残差、趋势相关性以及结果标签组成测试集,则可确定模型训练所需的样本规模为84组。
为验证BRB模型进行传感器节点故障检测的有效性,重复了10轮实验,每轮最大迭代次数为2 000次;使用3个指标进行性能描述以准确地衡量故障检测方法的性能:均方误差(
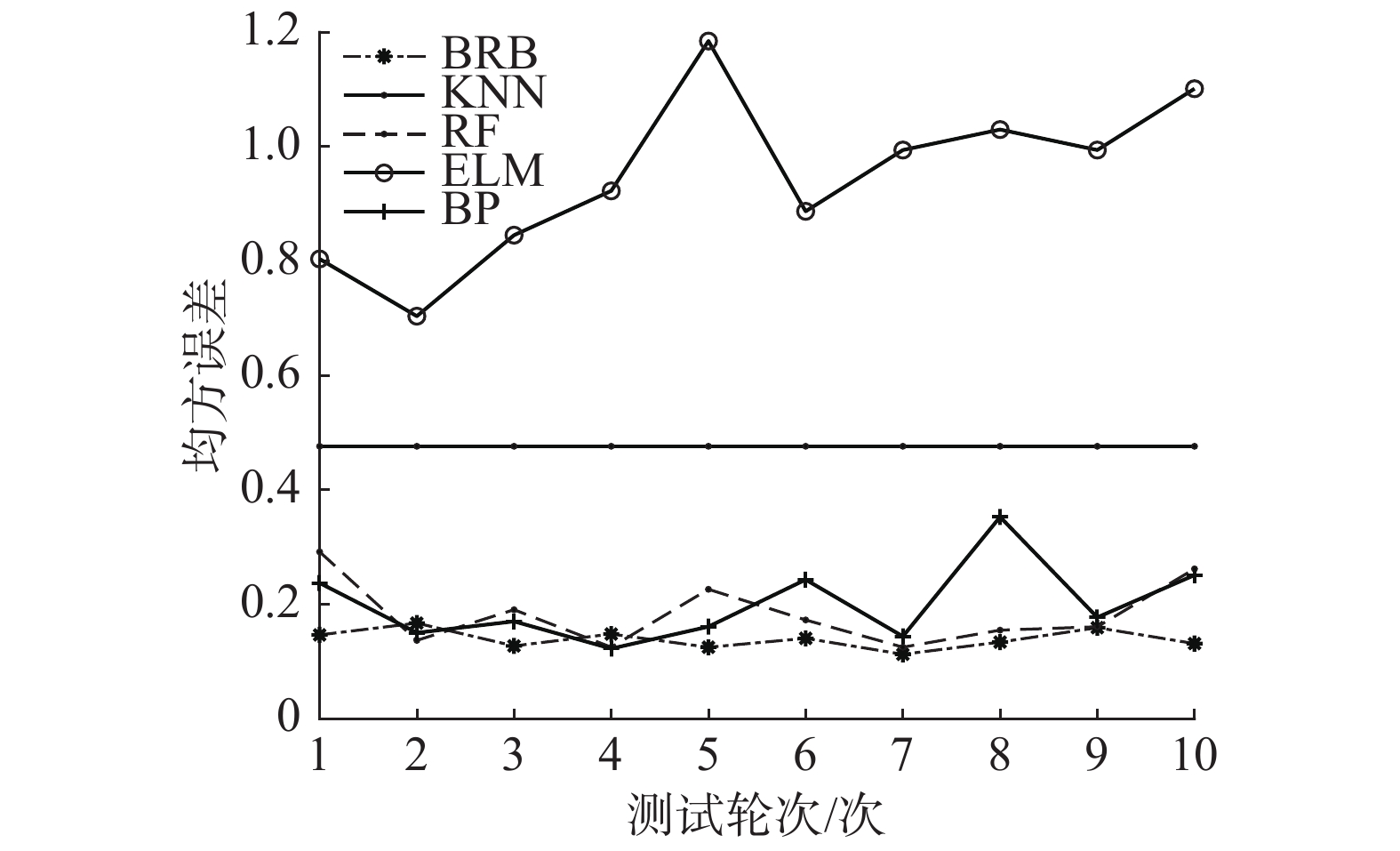
在本节设置对比实验验证置信规则库(BRB)在WSN传感器节点故障检测领域中的优越性。设置对比对象为KNN神经网络、随机森林(RF)神经网络、极限学习机(ELM)和BP神经网络。KNN神经网络、RF神经网络、ELM和BP神经网络是典型的数据驱动方法,每轮测试的迭代次数为2 000次,每种方法都进行了10轮测试。测试后计算不同方法的各项性能指标(均方误差、故障检测准确率、故障错检率)平均数值。其余性能指标MSE、检测准确率、错检率的均值对比如图3~5所示。
|
Download:
|
| 图 3 MSE值比较 Fig. 3 Comparison of MSE values | |
|
Download:
|
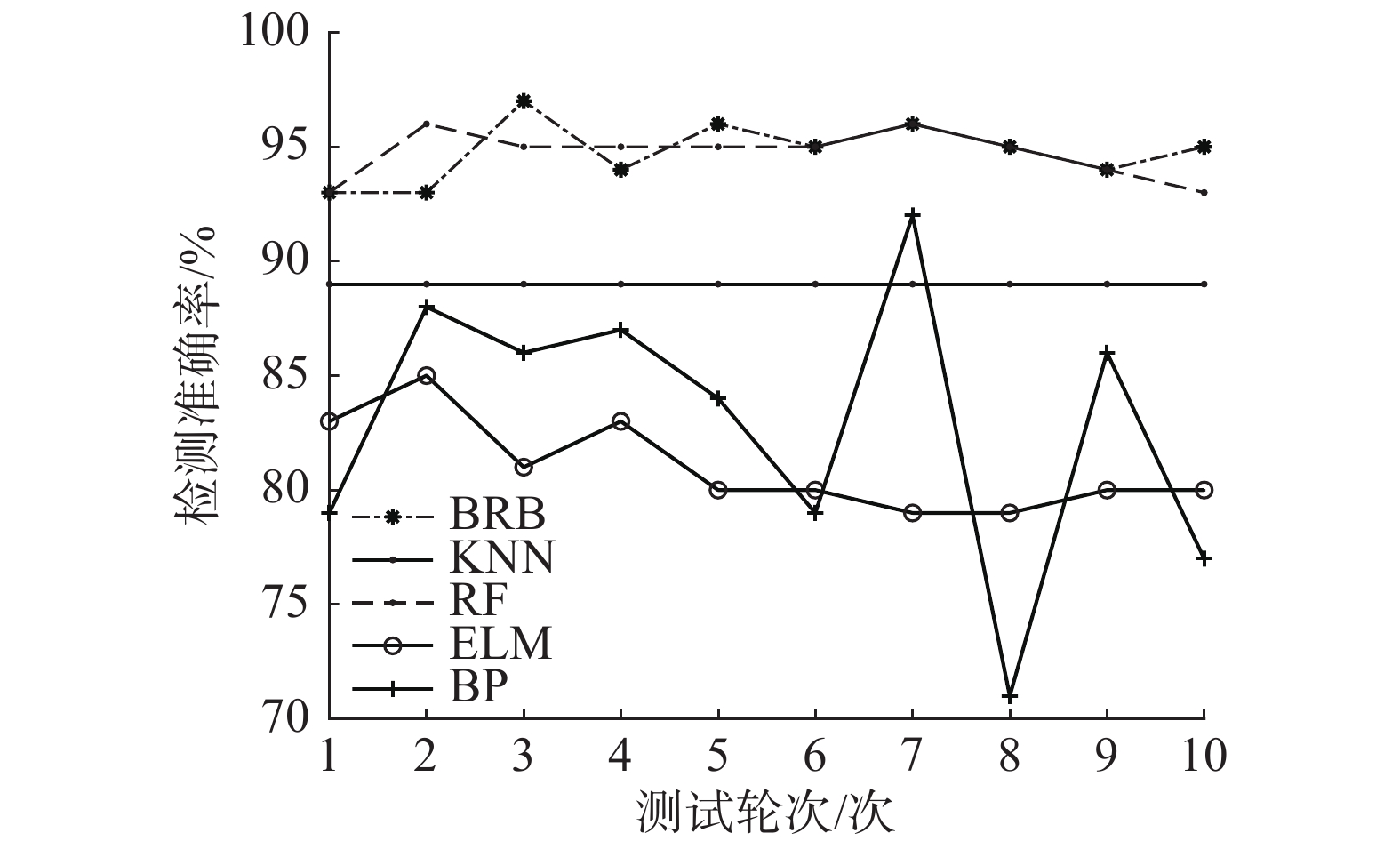
| 图 4 检测准确率比较 Fig. 4 Comparison of detection accuracies | |
|
Download:
|
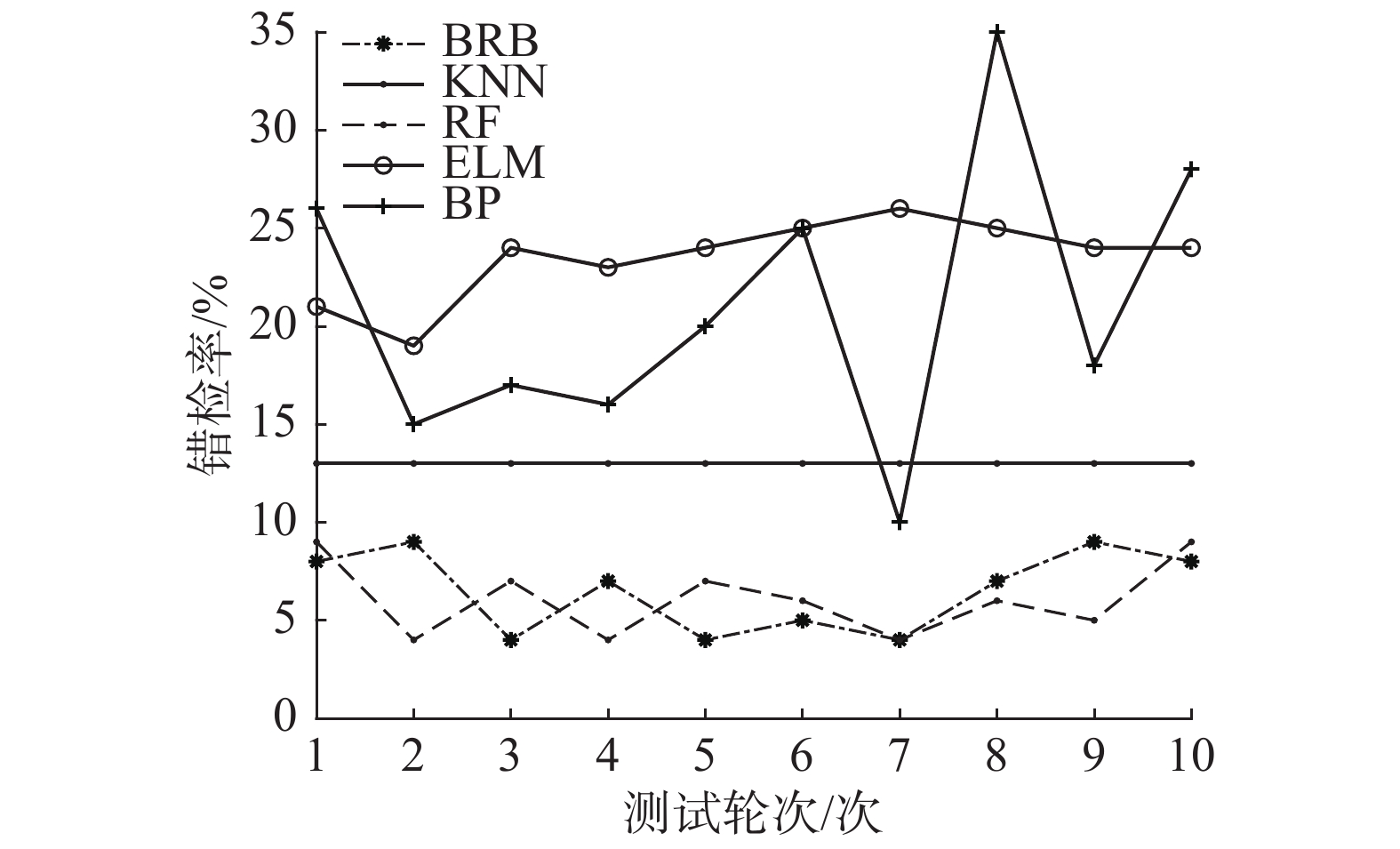
| 图 5 错检率比较 Fig. 5 Comparison of false detection rates | |
通过3个指标的比较,可以看出本文所提的基于BRB的WSN节点故障检测方法相比其他4种方法,具有最高的平均检测准确率、最低的平均MSE值和最低的平均错检率,主要指标10轮测试平均值如表3所示。通过表3和图3~5对5种方法的性能进行观察比较,发现本文所提方法相比较KNN、RF、ELM以及BP神经网络具有更高的故障检测精度。
| 表 3 性能指标平均值对比表 Tab.3 Comparison of average performance indicators |
本文提出的基于置信规则库的WSN传感器节点故障检测算法,用残差和趋势相关性描述传感器数据趋势变化和数值相似性,进行故障节点定位和故障类型确定;同时使用残差和趋势相关性并结合专家知识来确定模型的初始参数。实验结果证明,该方法减少了不确定性信息对故障检测准确率的影响,增强了BRB在WSN传感器节点故障检测中的有效性。但BRB在WSN中的应用仅仅处于开始阶段,日后的工作将从以下几方面进行:
1) 探索BRB在干扰环境下对WSN传感器节点故障检测的有效性;
2) 探索深度学习、大数据技术与BRB的融合应用,并运用到WSN传感器节点故障检测中;
3) 探索BRB在复杂网络拓扑WSN中故障检测的应用。
| [1] |
魏访, 郑朝霞. 基于无线传感器网络的工业环境温湿度监测系统[J]. 仪表技术与传感器, 2018(5): 55-57, 82. WEI Fang, ZHENG Zhaoxia. Industrial environment temperature and humidity monitoring system based on wireless sensor network[J]. Instrument technique and sensor, 2018(5): 55-57, 82. DOI:10.3969/j.issn.1002-1841.2018.05.014 (  0) 0)
|
| [2] |
宋航, 李建成, 张春华, 等. 军事物联网的关键技术[J]. 国防科技, 2015, 36(6): 24-34. SONG Hang, LI Jiangcheng, ZHANG Chunhua, et al. Overview of military IoT key technologies[J]. National defense science & technology, 2015, 36(6): 24-34. (  0) 0)
|
| [3] |
苗春雷. 无线传感器网络在环境监测中的应用[J]. 环境与发展, 2017, 29(10): 144, 148. MIAO Chunlei. Application of wireless sensor network in environmental monitoring[J]. Environment and development, 2017, 29(10): 144, 148. (  0) 0)
|
| [4] |
杨莺, 杨武德, 吴华瑞, 等. 基于移动sink的农田无线传感器网络数据收集策略[J]. 计算机科学, 2019, 46(4): 106-111. YANG Ying, YANG Wude, WU Ruihua, et al. Mobile sink based data collection strategy for farmland WSN[J]. Computer science, 2019, 46(4): 106-111. DOI:10.11896/j.issn.1002-137X.2019.04.017 (  0) 0)
|
| [5] |
向模军, 邹承俊. 无线传感器网络在农业应用中的特点和前景[J]. 中国沼气, 2018, 36(4): 54-60. XIANG Mojun, ZOU Chengjun. Characteristics and prospects of wireless sensor networks in agricultural applications[J]. China biogas, 2018, 36(4): 54-60. DOI:10.3969/j.issn.1000-1166.2018.04.011 (  0) 0)
|
| [6] |
周奚, 薛善良. 基于改进的粗糙集和神经网络的WSN故障诊断[J]. 计算机科学, 2016, 43(S2): 21-25. ZHOU Xi, XUE Shanliang. WSN fault diagnosis with improved rough set and neural network[J]. Computer science, 2016, 43(S2): 21-25. (  0) 0)
|
| [7] |
薛善良, 杨佩茹, 周奚. 基于模糊神经网络的WSN无线数据收发单元故障诊断[J]. 计算机科学, 2018, 45(5): 38-43. XUE Shanliang, YANG Peiru, ZHOU Xi. WSN wireless data transceiver unit fault diagnosis with fuzzy neural network[J]. Computer science, 2018, 45(5): 38-43. (  0) 0)
|
| [8] |
黄旭. MRNN: 一种新的基于改进型递归神经网络的WSN动态建模方法: 应用于故障检测[J]. 计算机工程与科学, 2015, 37(4): 711-718. HUANG Xu. MRNN: A novel wireless sensor network dynamic modeling method for fault detection using modified recurrent neural network[J]. Computer engineering & science, 2015, 37(4): 711-718. DOI:10.3969/j.issn.1007-130X.2015.04.014 (  0) 0)
|
| [9] |
常琳, 黄志清, 张严心. 基于数据驱动的WSN节点故障诊断算法[J]. 计算机工程, 2017, 43(9): 105-109. CHANG Lin, HUANG Zhiqing, ZHANG Yanxin. Node fault diagnosis algorithm in WSN based on data driven[J]. Computer engineering, 2017, 43(9): 105-109. DOI:10.3969/j.issn.1000-3428.2017.09.019 (  0) 0)
|
| [10] |
LU Siliang, ZHOU Peng, WANG Xiaoxian, et al. Condition monitoring and fault diagnosis of motor bearings using under sampled vibration signals from a wireless sensor network[J]. Journal of sound and vibration, 2018, 414: 81-96. DOI:10.1016/j.jsv.2017.11.007 ( 0) 0)
|
| [11] |
SUN Qiaoyan, SUN Yumei, LIU Xuejiao, et al. Study on fault diagnosis algorithm in WSN nodes based on RPCA model and SVDD for multi-class classification[J]. Cluster computing, 2019, 22(3): 6043-6057. ( 0) 0)
|
| [12] |
JIN Xiaohang, CHOW T W S, SUN Yi, et al. Kuiper test and autoregressive model-based approach for wireless sensor network fault diagnosis[J]. Wireless networks, 2015, 21(3): 829-839. DOI:10.1007/s11276-014-0820-0 ( 0) 0)
|
| [13] |
DARWISH S M, EL-DIRINI M N, ABD EL-MOGHITH I A. An adaptive cellular automata scheme for diagnosis of fault tolerance and connectivity preserving in wireless sensor networks[J]. Alexandria engineering journal, 2018, 57(4): 4267-4275. DOI:10.1016/j.aej.2018.11.012 ( 0) 0)
|
| [14] |
兰涯雯, 李强, 邓淑桃, 等. 基于多属性关联决策的WSN故障检测方法[J]. 计算机工程, 2019, 45(10): 84-89. LAN Yawen, LI Qiang, DENG Shutao, et al. WSN fault detection method based on correlative multi-attribute decision-making[J]. Computer engineering, 2019, 45(10): 84-89. (  0) 0)
|
| [15] |
周光海, 宁兆龙, 陈志奎, 等. 基于核偏最小二乘法的物联网无线传感网络故障分析与研究[J]. 通信学报, 2017, 38(S2): 94-98. ZHOU Guanghai, NING Zhaolong, CHEN Zhikui, et al. Fault analysis and research of wireless sensor network based on kernel partial least squares[J]. Journal on communications, 2017, 38(S2): 94-98. (  0) 0)
|
| [16] |
蔺艳斐, 邵苏杰, 钟成, 等. 基于可信度和邻居协作的传感器故障检测算法[J]. 通信学报, 2016, 37(9): 183-190. LIN Yanfei, SHAO Sujie, ZHONG Cheng, et al. Sensor fault detection algorithm based on credibility and neighbor-cooperation[J]. Journal on communications, 2016, 37(9): 183-190. DOI:10.11959/j.issn.1000-436x.2016170 (  0) 0)
|
| [17] |
徐晓斌, 张光卫, 王尚广, 等. 基于群体信任的WSN异常数据过滤方法[J]. 通信学报, 2014, 35(5): 108-117, 123. XU Xiaobin, ZHANG Guangwei, WANG Shangguang, et al. Abnormal data filtering approach based on collective trust for WSN[J]. Journal on communications, 2014, 35(5): 108-117, 123. DOI:10.3969/j.issn.1000-436x.2014.05.015 (  0) 0)
|
| [18] |
YANG Jianbo. Rule and utility based evidential reasoning approach for multiattribute decision analysis under uncertainties[J]. European journal of operational research, 2001, 13(1): 31-61. DOI:10.1016/S0377-2217(99)00441-5 ( 0) 0)
|
| [19] |
YANG Jianbo, LIU Jun, WANG Jin, et al. Belief rule-base inference methodology using the evidential reasoning approach-RIMER[J]. IEEE transactions on systems, man, and cybernetics-part A: systems and humans, 2006, 36(2): 266-285. DOI:10.1109/TSMCA.2005.851270 ( 0) 0)
|
| [20] |
符修文, 杨勇生, 姚海庆. 基于趋势相关性的传感器网络故障检测算法[J]. 华中科技大学学报(自然科学版), 2018, 46(10): 98-104. FU Xiuwen, YANG Yongsheng, YAO Haiqing. Fault detection algorithm for sensor network based on tendency-similarity[J]. Journal of Huazhong University of Science and Technology (natural science edition), 2018, 46(10): 98-104. (  0) 0)
|
| [21] |
YANG Jianbo, XU Dongling. Evidential reasoning rule for evidence combination[J]. Artificial intelligence, 2013, 205: 1-29. DOI:10.1016/j.artint.2013.09.003 ( 0) 0)
|
| [22] |
XU Dongling, LIU Jun, YANG Jianbo, et al. Inference and learning methodology of belief-rule-based expert system for pipeline leak detection[J]. Expert systems with applications, 2007, 32(1): 103-113. DOI:10.1016/j.eswa.2005.11.015 ( 0) 0)
|
| [23] |
HU Guanyu, ZHOU Zhijie, ZHANG Bangcheng, et al. A method for predicting the network security situation based on hidden BRB model and revised CMA-ES algorithm[J]. Applied soft computing, 2016, 48: 404-418. DOI:10.1016/j.asoc.2016.05.046 ( 0) 0)
|
| [24] |
ZHAO Fuqing, DU Songlin, ZHANG Yi, et al. Hybrid biogeography-based optimization with enhanced mutation and CMA-ES for global optimization problem[J]. Service oriented computing and applications, 2020, 14(1): 65-73. DOI:10.1007/s11761-019-00284-8 ( 0) 0)
|
| [25] |
HANSEN N, MÜLLER S D, KOUMOUTSAKOS P. Reducing the time complexity of the derandomized evolution strategy with covariance matrix adaptation (CMA-ES)[J]. Evolutionary computation, 2003, 11(1): 1-18. DOI:10.1162/106365603321828970 ( 0) 0)
|
 2021, Vol. 16
2021, Vol. 16


