标签分布学习(label distribution learning,LDL)是多标签学习(muti-label learning,MLL)的泛化[1-8]。MLL用标签集的部分标签来描述实例[9-11],LDL用标签集所有标签的表征程度构成的分布来描述实例[12-15]。文献[12]将年龄估计问题泛化到LDL中,降低了平均绝对误差(mean absolute deviation,MAE)。文献[13]将人群计数问题泛化到LDL中,提高了人群计数的准确率。
Geng等[1]提出了SA-IIS(specialized algorithm improithm lternative scaling)算法,将单个标签数据转换为分布数据,但未考虑标签的相关性。Jia等[16]提出了LDLLC(label distribution learning by exploiting label correlation)算法,使用皮尔逊相关系数描述了标签之间的相关性。Zheng等[17]提出了LDL-SCL(label distribution learning by exploiting sample correlation locally)算法,考虑实例之间的相关性。后2种方法显著提高了模型对标签分布的预测能力。
本文提出了一种三角距离相关性的标签分布学习算法(label distribution learning based on triangular distance correlation,T-LDL)。首先,令X和D分别表示特征矩阵和标签分布矩阵,构建距离映射矩阵θ描述X和D之间的映射关系。其次,设计新的相似度距离,以表征标签之间的相关性。最后,结合标签相关性,设计基于KL (kullback-leibler divergence)散度[18]的目标函数,利用从训练数据直接获取的X和D拟合θ以预测标签分布。
在8个真实数据集上,将本文提出算法与8种主流算法进行对比实验,利用Euclidean距离[19]、Sørensen距离[20]、Squardχ2距离[21]、KL散度[18]、Intersection相似度[22]和Fidelity相似度[23]共6种指标进行评价。结果表明,本文提出的算法在其中3个数据集上所有指标均为最优,在其余的数据集上部分指标占优。
1 相关工作首先提出LDL的问题描述与运行实例,然后讨论流行的LDL算法及其目标函数。表1列出了本文的符号系统。
| 表 1 符号系统 Tab.1 Notations |
标签分布学习相对于单标签和多标签学习而言,以一种更自然的方式去标记实例,并且为它的每个可能的标签分配一个数值。下面给出它的形式化定义[1]。令X = Rq为q维输入空间,表示特征矩阵;Y = {y1, y2, …, yc}为完整标签集,c为标签的数量;D表示实际标签分布矩阵;给定一个训练集S = {X, D} = {{x1, d1}, {x2, d2},…,{xn, dn}},其中xi = [xi1xi2… xiq]∈X为第i个实例,di = [di1di2… dic]∈[0,1]c为xi对应的实际标签分布,dij是标签yj对xi的实际表征度,且
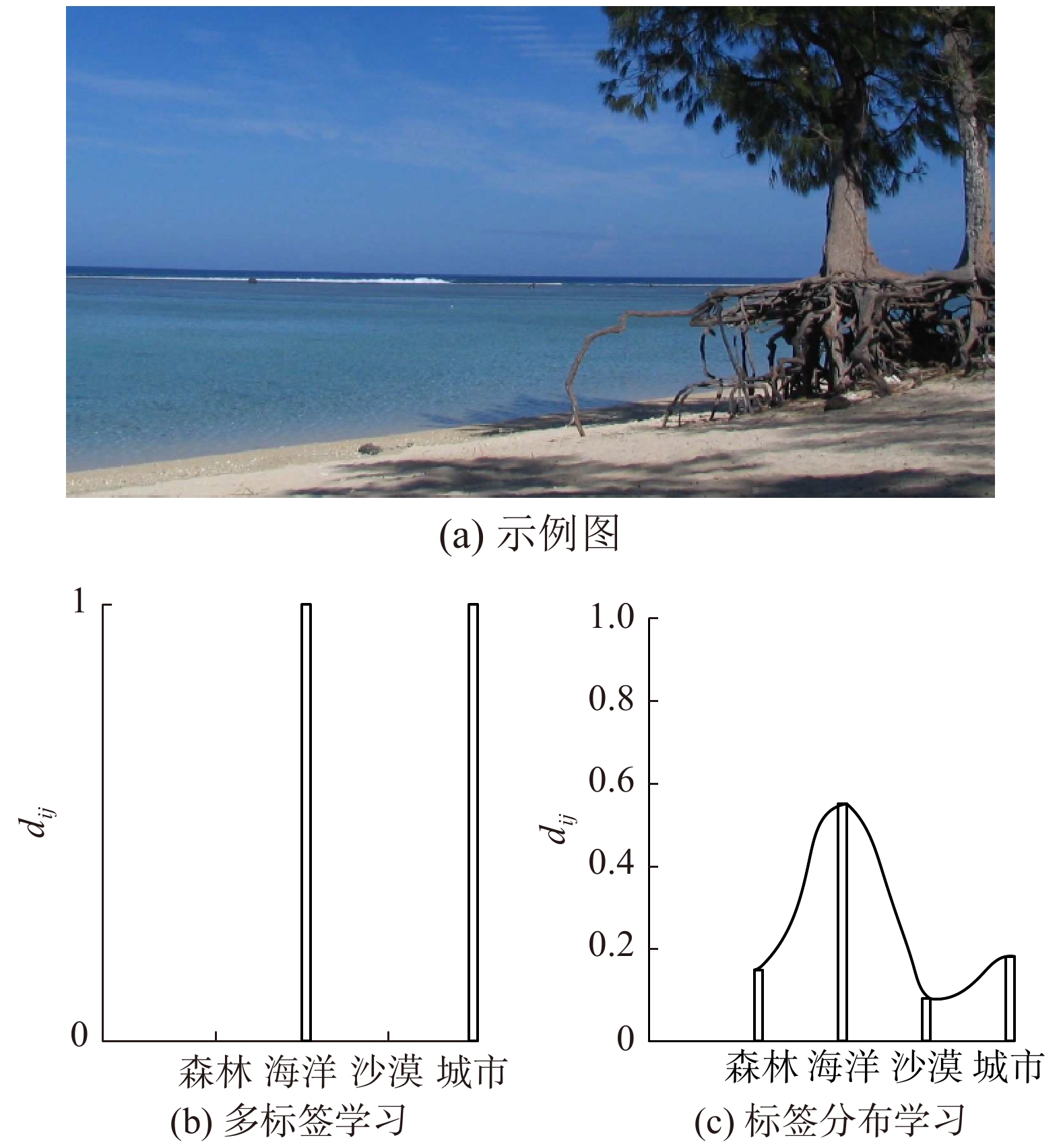
图1(a)为需要标记的一个示例图片[24],其完整标签集为{森林,海洋,沙漠,城市}。图1(b)表明MLL中仅有{海洋,城市}2个标签能够描述图1(a)。图1(c)说明LDL利用这4个标签构成的分布来描述该图片,且{海洋,城市}2个标签对图1(a)的表征度较高,{森林,沙漠}2个标签对图1(a)的表征度较低。
|
Download:
|
| 图 1 MLL与LDL的比较 Fig. 1 Differences between MLL and LDL | |
表2和表3为一个标签分布学习的运行实例,分别为特征矩阵X和实际标签分布矩阵D,这里S = {(x1,d1), (x2, d2), …, (x4, d4)},q = 5,c = 4。{天空,水,房屋,沙子,树木}5个特征表征了图1(a)中包含的信息。{森林,海洋,城市,沙漠}为完整标签集。以加粗行为例,x1 = [0.38, 0.35, 0.00, 0.12, 0.15],d1 = [0.16, 0.55, 0.10, 0.19],其中x11 = 0.38表示天空占图片面积的38%,d11 = 0.16表示森林描述该图片的程度为16%。
| 表 2 特征矩阵X Tab.2 Feature matrix X |
| 表 3 标签分布矩阵D Tab.3 Label distribution matrix D |
X和D之间的映射关系可以通过距离映射矩阵θ来描述。给定训练集后,LDL的目标为学习到该距离映射矩阵θ[16],再通过θ计算出预测标签分布矩阵P = {p1, p2, …, pi},其中pi = [pi1 pi2 … pic],pij为标签yj对xi的预测表征度,该表征度用最大熵模型[25]表示,如式(1)所示:
| $ p({y_j}|{x_i};{{\theta }}){\rm{ = }}\frac{{\exp \left(\displaystyle\sum\limits_{r = 1}^q {{{{\theta }}_{kr}}{x_{ir}}} \right)}}{{\displaystyle\sum\limits_{k = 1}^c {\exp \left(\displaystyle\sum\limits_{r = 1}^q {{{{\theta }}_{kr}}{x_{ir}}} \right)} }} $ | (1) |
为优化求解θ,LDL算法的目标函数需约束预测分布与真实分布之间的差异。文献[1]构建了以KL散度为基础的目标函数,通过求解式(2),可得到最优距离映射矩阵θ*,即
| $ {{{\theta }}^{\rm{*}}}{\rm{ = arg}}\mathop {{\rm{min}}}\limits_{{\theta }} \sum\limits_{i = 1}^n \sum\limits_{j = 1}^c \left({d_{ij}}\ln {\frac{d_{ij}}{p\left({y_j}|{x_i};{{\theta }}\right)}} \right) $ | (2) |
表4列出了4种流行的LDL算法及其目标函数,表中第一行的SA-IIS[1]和SA-BFGS(specialized algorithm effective quasi-newton)[1]两种算法使用相同的目标函数,它们均采用KL散度表征所有实例的真实分布与预测分布之间的差异。前者使用类似于改进迭代缩放的策略作为其优化方法,后者使用BFGS算法作为其优化方法。该目标函数缺少正则项,易导致欠拟合。
| 表 4 已有的4种流行的LDL算法及其目标函数 Tab.4 Objective functions of four popular LDL algorithms |
LDLLC[16]在IIS-LLD算法的目标函数基础上增加了正则项和标签相关性项。如表4中第2行所示,等号右边第2项为距离映射矩阵θ的F-范数,以防止过拟合。第3项为符号函数与不同距离共同决定的标签相关性项,其中符号函数由皮尔逊相关系数决定。但皮尔逊相关系数存在“2个输入向量间应有线性关系”的约束条件,而距离映射矩阵θ中的任意2个向量要满足该条件较为困难。
EDL(emotion distribution learning from texts)[26]通过采用新散度公式表征所有实例的真实分布与预测分布之间的差异,并增加2个约束项。如表4中第3行所示,等号右边第2项为距离映射矩阵θ的1-范数,以防止过拟合。第3项用不同标签的特征向量之差的2-范数,再乘以基于Plutchik的情绪轮得到的权重,表征不同标签之间的关系。该算法在情绪分类场景下表现较好。
2 本文工作常见的LDL算法的输入为特征矩阵X与实际标签分布矩阵D,输出为预测标签分布矩阵P,构建距离映射矩阵θ描述X和D之间的映射关系。为了得到更精准的预测标签分布矩阵P,设计目标函数是LDL算法工作的重点。本节重点介绍如何设计目标函数以及本文提出的T-LDL算法。
本文设计的目标函数为
| $ T({{\theta }}) = \sum\limits_{i{\rm{ = }}1}^n {\sum\limits_{j{\rm{ = }}1}^c {\left( {{d_{ij}}\ln \frac{{{d_{ij}}}}{{p\left( {{y_j}|{x_i};{{\theta }}} \right)}}} \right)} } + {\lambda _1}\sum\limits_{i{\rm{ = }}1}^c {\sum\limits_{j{\rm{ = }}1}^c {\eta \left( {{{{\theta }}_i},{{{\theta }}_j}} \right)} } $ | (3) |
式中:等号右侧第1项用KL散度表征所有实例的真实分布与预测分布之间的差异;等号右侧第二项为本文亮点,设计标签相关性项以获得更好的预测结果。
2.1 标签相关性本文的亮点为结合三元相关性和距离相关性来描述标签之间的相关性,如式(4)所示:
| $ \eta \left( {{{{\theta }}_i},{{{\theta }}_j}} \right) = {\rm{sgn}}({\rm{triangle}}\left( {{{{\theta }}_i},{{{\theta }}_j}} \right)) \cdot {\rm{Dis}}\left( {{{{\theta }}_i},{{{\theta }}_j}} \right) $ | (4) |
式中:sgn(triangle(θi, θj))表征三元相关性,Dis(θi, θj)表征距离相关性。sgn(triangle(θi, θj))用三角距离来表征标签之间存在何种相关性,即正相关、不相关或负相关;Dis(θi, θj)用Euclidean距离[19]表征标签之间的相关程度。
由于使用皮尔逊相关系数时需要考虑任意2个向量是否存在线性关系,故提出一种不考虑该约束条件的新三角距离来衡量2个向量是否相关。这里,仅考虑2个向量θi、θj以及2个向量之差θi − θj,设计该三角距离,且使得其取值范围为[−1,1],如式(5)所示:
| $ {\rm{triangle}}\left( {{{{\theta }}_i},{{{\theta }}_j}} \right) = 1 - \frac{{2\sqrt {\displaystyle\sum\limits_{k = 1}^m {{{({{{\theta }}_{ik}} - {{{\theta }}_{jk}})}^2}} } }}{{\sqrt {\displaystyle\sum\limits_{k = 1}^m {{{{\theta }}_{ik}}^2} } + \sqrt {\displaystyle\sum\limits_{k = 1}^m {{{{\theta }}_{jk}}^2} } }} $ | (5) |
将该三角距离代入符号函数,用于判断标签之间存在何种相关性:正相关、不相关或负相关。
| $ {\rm{sgn}}\left( {{\rm{triangle}}\left( {{{{\theta }}_i},{{{\theta }}_j}} \right)} \right) = \left\{ \begin{array}{l} 1,\;\;{\rm{ 0 < triangle}}\left( {{{{\theta }}_i},{{{\theta }}_j}} \right) \leqslant 1 \\ 0,\;\;{\rm{ triangle}}\left( {{{{\theta }}_i},{{{\theta }}_j}} \right) = 0 \\ {\rm{ - }}1,\;\;{\rm{ - 1}} \leqslant {\rm{triangle}}\left( {{{{\theta }}_i},{{{\theta }}_j}} \right) < 0 \\ \end{array} \right. $ | (6) |
式中,sgn(·)为1、0、−1分别表示标签之间为正相关、不相关或负相关。
由于上述部分只能判断标签之间存在何种相关性,并不能判断标签之间的相关程度,故引入Euclidean距离[19]表示标签之间的相关程度:
| $ {\rm{Dis}}\left( {{{{\theta }}_i},{{{\theta }}_j}} \right) = \sqrt {\sum\limits_{k = 1}^m {{{\left( {{{{\theta }}_{ik}} - {{{\theta }}_{jk}}} \right)}^2}} } $ | (7) |
T-LDL描述见算法1。首先将距离映射矩阵θ(0)和逆拟Hessian矩阵B(0)初始化为单位矩阵,再通过式(3)计算初次目标函数的梯度
算法1 T-LDL算法
输入 X, D, ξ;
输出 p(y|x;θ)。
1)初始化距离映射矩阵θ(0)和逆拟Hessian矩阵B(0);
2)通过式(3)计算梯度
3)如果||
4)end if;
5)l ← l + 1;
6)通过式(1)计算 p(yj|xi;θ)。
3 实验及结果分析本节首先介绍实验使用的8个数据集和6个评价指标,再将本文提出的T-LDL算法与LDLLC[16]、PT-Bayes[1]、PT-SVM[1, 17]、AA-kNN[1, 4]、AA-BP[1]、SA-IIS[1, 16]、SA-BFGS(specialized algorithm effective quasi-newton)[1, 2]和EDL[26]8种主流的LDL算法进行比较,最后对实验结果进行讨论。
3.1 数据集表5列出了从芽殖酵母的8个生物学实验中收集得到的8个真实数据集[28]。实例为2 465个酵母基因,特征是长度为24的系统发育谱,标签为不同生物实验中的离散时间点,数量范围为4~18。
| 表 5 数据集 Tab.5 Datasets |
Alpha数据集记录在α因子的影响下酵母在有丝分裂期间的基因表达情况;Cdc数据集记录酵母在细胞分裂期间停滞的cdc-15基因表达情况;Elu数据集记录酵母经离心淘洗后的基因表达情况;Diau数据集记录酵母在双峰转换过程中的基因表达情况;Heat数据集记录酵母在经过高温冲击后的基因表达情况;Spo数据集记录酵母在孢子形成过程中的基因表达情况;Cold数据集记录酵母经低温处理后的基因表达情况;Dtt数据集记录酵母经还原剂处理后的基因表达情况[28]。
3.2 评价指标表6列出了评估LDL算法的6个评价指标的名称和公式。其中,pij是标签yj对xi的预测表征度;dij是标签yj对xi的实际表征度;“↓”表示“越小越好”;“↑”表示“越大越好”。
| 表 6 LDL算法的评价指标 Tab.6 Evaluation measures for the LDL algorithms |
表7~14的第1~6列列出了10次实验的平均结果±标准差(当前方法性能的排名),末列为前6列平均性能排名。首先比较表7~14中的平均值,如果平均值相同,再比较标准差。
| 表 7 Alpha数据集上的实验结果 Tab.7 Experimental results on the Alpha dataset |
| 表 8 Cdc数据集上的实验结果 Tab.8 Experimental results on the Cdc dataset |
| 表 9 Elu数据集上的实验结果 Tab.9 Experimental results on the Elu dataset |
| 表 10 Diau数据集上的实验结果 Tab.10 Experimental results on the Diau dataset |
| 表 11 Heat数据集上的实验结果 Tab.11 Experimental results on the Heat dataset |
| 表 12 Spo数据集上的实验结果 Tab.12 Experimental results on the Spo dataset |
| 表 13 Cold数据集上的实验结果 Tab.13 Experimental results on the Cold dataset |
| 表 14 Dtt数据集上的实验结果 Tab.14 Experimental results on the Dtt dataset |
对于数据集Elu和Cold,本文提出的方法在所有评价指标上都比其他8种方法表现更好。对于数据集Alpha、Cdc和Heat,本文提出的方法在大多数评价指标上排名第一。对于其余3个数据集,本文提出的方法排在第二或者第三。
3.4 讨论各种算法通常在不同的数据集上具有不同的排名,表明每种算法都有其合适的应用场景,如EDL算法更适用于文本情绪分类场景。不同评价指标下同一算法的不同排名,反映了6项评价指标的多样性。在比较不同方法对新数据集的预测效果时,应综合考虑多个评价指标。
与同样考虑标签相关性的LDLLC算法相比,T-LDL算法在绝大多数数据集上的表现均优于LDLLC算法。LDLLC算法基于皮尔逊相关系数表征标签相关性,而T-LDL算法基于本文设计的三角距离。皮尔逊相关系数要求输入的2个向量满足线性相关,而本文设计的三角距离无该约束条件。实验证明在本文场景中,三角距离更加合适。
4 结束语为了进一步提高标签分布学习算法的预测性能,本文提出了三角距离相关性的标签分布学习算法。新的三角距离可以充分考虑向量本身和向量之差,能更好地描述标签之间的相关性。实验结果表明,本文的方法比大多数现有的方法表现更好。
未来的工作将尝试从以下几个方面提高标签分布学习方法的性能:1)采用属性约简以降低算法的时间复杂度;2)使用其他度量取代作为目标函数基础的KL散度;3)利用新的距离映射函数表示标签的相关性。
| [1] |
GENG Xin. Label distribution learning[J]. IEEE transactions on knowledge and data engineering, 2016, 28(7): 1734-1748. DOI:10.1109/TKDE.2016.2545658 ( 0) 0)
|
| [2] |
JIA Xiuyi, ZHENG Xiang, LI Weiwei, et al. Facial emotion distribution learning by exploiting low-rank label correlations locally[C]//Proceedings of 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Long Beach, USA, 2019: 9841−9850.
( 0) 0)
|
| [3] |
YANG Xu, GAO Binbin, XING Chao, et al. Deep label distribution learning for apparent age estimation[C]//Proceedings of 2015 IEEE International Conference on Computer Vision Workshops. Santiago, Chile, 2015: 102−108.
( 0) 0)
|
| [4] |
ZHANG Hengru, HUANG Yuting, XU Yuanyuan, et al. COS-LDL: label distribution learning by cosine-based distance-mapping correlation[J]. IEEE access, 2020, 8: 63961-63970. DOI:10.1109/ACCESS.2020.2984622 ( 0) 0)
|
| [5] |
邵东恒, 杨文元, 赵红. 应用k-means算法实现标记分布学习
[J]. 智能系统学报, 2017, 12(3): 325-332. SHAO Dongheng, YANG Wenyuan, ZHAO Hong. Label distribution learning based on k-means algorithm [J]. CAAI transactions on intelligent systems, 2017, 12(3): 325-332. (  0) 0)
|
| [6] |
刘玉杰, 唐顺静, 高永标, 等. 基于标签分布学习的视频摘要算法[J]. 计算机辅助设计与图形学学报, 2019, 31(1): 104-110. LIU Yujie, TANG Shunjing, GAO Yongbiao, et al. Label distribution learning for video summarization[J]. Journal of computer-aided design & computer graphics, 2019, 31(1): 104-110. (  0) 0)
|
| [7] |
王一宾, 田文泉, 程玉胜. 基于标记分布学习的异态集成学习算法[J]. 模式识别与人工智能, 2019, 32(10): 945-954. WANG Yibin, TIAN Wenquan, CHENG Yusheng. Heterogeneous ensemble learning algorithm based on label distribution learning[J]. Pattern recognition and artificial intelligence, 2019, 32(10): 945-954. (  0) 0)
|
| [8] |
耿新, 徐宁. 标记分布学习与标记增强[J]. 中国科学: 信息科学, 2018, 48(5): 521-530. GENG Xin, XU Ning. Label distribution learning and label enhancement[J]. Scientia sinica informationis, 2018, 48(5): 521-530. DOI:10.1360/N112018-00029 (  0) 0)
|
| [9] |
ZHANG Mingling, ZHANG Kun. Multi-label learning by exploiting label dependency[C]//Proceedings of the 16th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. Washington, USA, 2010: 999−1007.
( 0) 0)
|
| [10] |
BI Wei, KWOK J T. Multilabel classification with label correlations and missing labels[C]//Proceedings of the 28th AAAI Conference on Artificial Intelligence. Québec City, Canada, 2014: 1680−1686.
( 0) 0)
|
| [11] |
HUANG Shengjun, ZHOU Zhihua. Multi-label learning by exploiting label correlations locally[C]//Proceedings of the 26th AAAI Conference on Artificial Intelligence. Toronto, Canada, 2012: 949−955.
( 0) 0)
|
| [12] |
GENG Xin, WANG Qin, XIA Yu. Facial age estimation by adaptive label distribution learning[C]//Proceedings of the 22nd International Conference on Pattern Recognition. Stockholm, Sweden, 2014: 4465−4470.
( 0) 0)
|
| [13] |
ZHANG Zhaoxiang, WANG Mo, GENG Xin. Crowd counting in public video surveillance by label distribution learning[J]. Neurocomputing, 2015, 166: 151-163. DOI:10.1016/j.neucom.2015.03.083 ( 0) 0)
|
| [14] |
GENG Xin, YIN Chao, ZHOU Zhihua. Facial age estimation by learning from label distributions[J]. IEEE transactions on pattern analysis and machine intelligence, 2013, 35(10): 2401-2412. DOI:10.1109/TPAMI.2013.51 ( 0) 0)
|
| [15] |
GENG Xin, LING Miaogen. Soft video parsing by label distribution learning[C]. Proceedings of the 31th AAAI Conference on Artificial Intelligence. San Francisco, USA, 2017: 1331−1337.
( 0) 0)
|
| [16] |
JIA Xiuyi, LI Weiwei, LIU Junyu, et al. Label distribution learning by exploiting label correlations[C]//Proceedings of the 32nd AAAI Conference on Artificial Intelligence. New Orleans, USA, 2018: 3310−3317.
( 0) 0)
|
| [17] |
ZHENG Xiang, JIA Xiuyi, LI Weiwei. Label distribution learning by exploiting sample correlations locally[C]// Proceedings of the 32nd AAAI Conference on Artificial Intelligence. New Orleans, USA, 2018: 4556−4563.
( 0) 0)
|
| [18] |
KULLBACK S, LEIBLER R A. On information and sufficiency[J]. The annals of mathematical statistics, 1951, 22(1): 79-86. DOI:10.1214/aoms/1177729694 ( 0) 0)
|
| [19] |
DANIELSSON P E. Euclidean distance mapping[J]. Computer graphics and image processing, 1980, 14(3): 227-248. DOI:10.1016/0146-664X(80)90054-4 ( 0) 0)
|
| [20] |
SØRENSEN T. A method of establishing groups of equal amplitude in plant sociology based on similarity of species content, and its application to analyses of the vegetation on Danish commons[J]. Kongelige danske videnskabernes selskab biologiske skrifter, 1948, 5(4): 1-34. ( 0) 0)
|
| [21] |
GAVIN D G, OSWALD W W, WAHL E R, et al. A statistical approach to evaluating distance metrics and analog assignments for pollen records[J]. Quaternary research, 2003, 60(3): 356-367. DOI:10.1016/S0033-5894(03)00088-7 ( 0) 0)
|
| [22] |
DUDA R O, HART P E, STORK D G. Pattern classification[M]. 2nd ed. New York: Wiley, 2000.
( 0) 0)
|
| [23] |
DEZA E, DEZA M M. Dictionary of distances[M]. Amsterdam: Elsevier, 2006.
( 0) 0)
|
| [24] |
JEGOU H, DOUZE M, SCHMID C. Hamming embedding and weak geometric consistency for large scale image search[C]//Proceedings of the 10th European Conference on Computer Vision. Marseille, France, 2008: 304−317.
( 0) 0)
|
| [25] |
BERGER A L, PIETRA V J D, PIETRA S A D. A maximum entropy approach to natural language processing[J]. Computational linguistics, 1996, 22(1): 39-71. ( 0) 0)
|
| [26] |
ZHOU Deyu, ZHANG Xuan, ZHOU Yin, et al. Emotion distribution learning from texts[C]//Proceedings of the 2016 Conference on Empirical Methods in Natural Language Processing. Austin, Texas, 2016: 638−647.
( 0) 0)
|
| [27] |
YUAN Yaxiang. A modified BFGS algorithm for unconstrained optimization[J]. IMA journal of numerical analysis, 1991, 11(3): 325-332. DOI:10.1093/imanum/11.3.325 ( 0) 0)
|
| [28] |
EISEN M B, SPELLMAN P T, BROWN P O, et al. Cluster analysis and display of genome-wide expression patterns[J]. Proceedings of the national academy of sciences of the united states of America, 1998, 95(25): 14863-14868. DOI:10.1073/pnas.95.25.14863 ( 0) 0)
|
| [29] |
CHA Su H. Comprehensive survey on distance/similarity measures between probability density functions[J]. International journal of mathematical models and methods in applied sciences, 2007, 1(4): 300-307. ( 0) 0)
|
 2021, Vol. 16
2021, Vol. 16


