图像分割^[1]的目的是通过某种方法把图像划分为几块区域以进行后续的目标识别、目标测量等工作，是图像预处理的重要内容。模糊C均值算法(fuzzy C-means, FCM)是一种有效的无监督分类方法且已在遥感^[2]、医学^[3]、工件^[4]等方面被广泛地应用和研究。

由于图像数据本身拥有特定的结构与性质导致FCM算法分割时未考虑邻域信息而对噪声敏感，于是很多考虑邻域信息的改进版本被提出^[5-7]。这一类改进本质在于将邻域信息融入至FCM的隶属度和聚类中心表达式中，使得图像在进行去噪(滤波)的同时完成图像像素的划分^[8]。这类算法需要遍历像素，其时间复杂度随图像分辨率的提升而增大。诚然，也有加快迭代速度的改进算法，如在迭代中对隶属度进行奖惩^[9]，或者迭代中修改像素至聚类中心的相对距离^[10]等方法，但仍不能从根本上解决随图像分辨率提升导致的时间复杂度迅速增加问题。考虑到图像像素只有256个灰度级，利用灰度级进行模糊聚类可有效减小时间复杂度。遵循这一思路，研究者提出基于灰度级的FCM算法^[11-13]，这类算法需首先对图像进行去噪再进行图像分割，以免算法受噪声干扰。另外，该类算法的去噪过程可以预先处理，进一步降低分割的时间成本。

无损检测图像(non-destructive testing, NDT)通过涡流检测、红外检测、超声检测等方法对工件材料进行探伤或尺寸测量而得^[14]。由于工况条件复杂，图像清晰度较差，而且，图像中待测量目标一般占据图像很小的面积，导致目标与背景的面积差异很大，即呈现出类间差异较大的特点^[15]。这种特征的图像利用基于灰度级的FCM算法进行分割时经常得不到期望的目标，原因是这类方法趋于均分所有像素，导致部分背景区域划分至目标区域。文献[16-17]对这种情形进行了探讨，但未有严格的理论分析。

针对无损检测图像具有类间差异大的特点，希望减小较大类(背景)对目标函数的贡献以改善“趋于均分所有像素”的缺点，提出与类大小反向相关的“类贡献抑制因子”表达式并将该因子引入目标函数后再进行隶属度和聚类中心的理论推导，后续的无损检测图像分割测试验证了这一改进的有效性。

1 相关工作 1.1 有效的图像去噪方法

设图像像素集X={x₁,x₂,…,x_n}，N_j为x_j的邻域窗口。陆海青等提出了一种有效的图像去噪方法^[18]，首先计算局部灰度相似性测度C_j：

${{\boldsymbol{C}}_{\boldsymbol{j}}}=\left\| {{x_r} - {{\sum_{r \in {N_j}} {{x_r}} } / {{N_R}}}} \right\|$

(1)

式中:N_R表示N_j的势；r为N_j窗口像素的索引号。该表达式反映了局部邻域像素灰度分布的均匀程度。

邻域的灰度分布度量用 $\bar c$ 表示，有

$\bar c=\sum {{{{{\boldsymbol{C}}_{\boldsymbol{j}}}} / {{N_R}}}} $

(2)

对于N_j，邻域像素的权重用如下形式表示：

${{\boldsymbol{\omega }}_{{\boldsymbol{jr}}}}=\exp \left[ { - \left( {{{\boldsymbol{C}}_{\boldsymbol{j}}} - \bar c} \right)} \right]$

(3)

可以看出，当 ${{\boldsymbol{C}}_{\boldsymbol{j}}} - \bar c$ 内较小的值对应的像素为非边缘点或者非噪声点，应增加该点影响，否则减小该点影响。最后，将窗口N_j内权重与灰度值线性加权并归一化，得到含邻域信息的滤波图像 ${\tilde{\boldsymbol{X}}}=[{\tilde x_1}\;\;{\tilde x_2}\;\; \cdots \;\;{\tilde x_n}]$ ，有

${\tilde x_j}={{\sum_{r \in {N_j}} {{\omega _{jr}}{x_r}} } \Big/ {\sum_{r \in {N_j}} {{\omega _{jr}}} }}$

(4)

1.2 基于灰度级模糊C均值算法

基于灰度级FCM算法的目标函数如下^[12]：

$ \begin{split} & {J_s}=\sum_{i=1}^c {\sum_{l=0}^q {{\gamma _l}u_{il}^m{{\left\| {{\zeta _l} - {v_i}} \right\|}^2}} } ,\\& {\rm{s.t.}}\quad \sum_{i=1}^c {u_{il}^{}=1,\quad } \sum_{l=0}^q {{\gamma _l}=N\quad } \end{split} $

(5)

式中：v_i(i=1,2,…,c)为聚类中心；N表示图像总像素数；γ_l表示灰度级的像素数；m是模糊指数；u_il表示灰度级l属于第i类的隶属度；ζ_l和γ_l分别表示去噪(滤波)后图像 ${\tilde{\boldsymbol{X}}}$ 的灰度级和相应的像素数。最小化式(5)，可得

${u_{il}}=\left\| {{\zeta _l} - {v_i}} \right\|{{^{ - 2/(m - 1)}} \Big/ {\sum_{k=1}^c {{{\left\| {{\zeta _l} - {v_k}} \right\|}^{ - 2/(m - 1)}}} }}$

(6)

${v_i}={{\sum_{l=0}^q {{r_l}u_{il}^m{\zeta _l}} } \Big/ {\sum_{l=0}^q {{r_l}u_{il}^m} }}$

(7)

基于灰度级FCM算法的迭代步骤见文献[11-12]。

2 改进的快速模糊C均值算法 2.1 类贡献抑制因子

当图像类间差异较大时，由于较大类对目标函数的贡献较大导致较小类的聚类中心更容易受到较大类的作用，即使得较小类的聚类中心向较大类偏移，进而导致分割效果较差。因此，需要针对这种状况进行调整，设计了类贡献抑制因子(restrain factor of cluster contribution，RFC)表达式减弱较大类对目标函数作用，增大较小类作用，表达式为

${{\rm{RFC}}_i}=\sum_{s=0}^q {{\gamma _s}\left( {1 - u_{is}^b} \right)} $

(8)

式中：RFC_i为第i类贡献抑制因子；b为贡献指数。显然地， ${\gamma _s}\left( {1 - u_{is}^b} \right)$ 表示灰度级s的像素对应的第i类的抑制值，其中b值越小，抑制作用越强。如果u_is>u_ps(p=1,2,…,c；i≠p)，那么该灰度级对应的像素属于第i类，产生的抑制值 ${\gamma _s}\left( {1 - u_{is}^b} \right)$ 较小，否则，抑制值较大。当绝大多数(灰度级)像素属于第i类时，有

$\sum_{s=0}^q {{\gamma _s}\left( {1 - u_{is}^b} \right)} <\sum_{s=0}^q {{\gamma _s}\left( {1 - u_{ps}^b} \right)} $

(9)

由式(9)可得，RFC_i的值与类大小反向相关，能够调整类大小对目标函数的影响。

2.2 目标函数改进及求解

将式(9)融入式(5)所示的目标函数，有

${J_s}=\sum_{i=1}^c {\sum_{l=0}^q {{{\rm{RFC}}_i}{\gamma _l}u_{il}^m{{\left\| {{\zeta _l} - {v_i}} \right\|}^2}} } $

(10)

采用拉格朗日乘子法最小化式(10)，构造如下拉格朗日辅助函数：

$ \begin{split} & L=\sum_{i=1}^c {\sum_{l=0}^q {{\rm{RF}}{{\rm C}_i}{\gamma _l}u_{il}^m{{\left\| {{\zeta _l} - {v_i}} \right\|}^2}} }- \\& \quad \quad \sum_{l=0}^q {{\lambda _l}\left( {\sum_{i=1}^c {{u_{il}}} - 1} \right)} \end{split} $

(11)

令 ${{\partial L} / {\partial {v_i}}}=0$ ，整理可得聚类中心表达式：

${v_i}={{\sum_{l=0}^q {{r_l}u_{il}^m{\zeta _l}} } \Big/ {\sum_{l=0}^q {{r_l}u_{il}^m} }}$

(12)

令 $ {{\partial L} / {\partial {u_{il}}}}=0$ ，可得：

${u_{il}}={\left( {{\lambda _l}} \right)^{\frac{1}{{m - 1}}}} \cdot {\left[ {\frac{1}{{\left[ {m{{\rm{RFC}}_i} - b{\gamma _l}u_{il}^b} \right]{\gamma _l}{{\left\| {{\zeta _l} - {v_i}} \right\|}^2}}}} \right]^{{1 / {\left( {m - 1} \right)}}}}$

(13)

由 $\displaystyle \sum_{i=1}^c {{u_{il}}=1}$ 再结合式(13)可得：

$ {\left( {{\lambda _l}} \right)^{\frac{1}{{m - 1}}}}={1 \Big/ {\sum\limits_{k=1}^c {{{\left[ {\frac{1}{{\left[ {m{{\rm{RFC}}_k} - b{\gamma _l}u_{kl}^b} \right]{\gamma _l}{{\left\| {{\zeta _l} - {v_k}} \right\|}^2}}}} \right]}^{\frac{1}{{m{\rm{ - 1}}}}}}} }} $

(14)

将式(14)代入式(13)，有

${u_{il}}=\frac{{{{\left[ {{1 / {\left\{ {\left[ {m{{\rm{RFC}}_i} - b{\gamma _l}u_{il}^b} \right]{{\left\| {{\zeta _l} - {v_i}} \right\|}^2}} \right\}}}} \right]}^{{1 / {\left( {m - 1} \right)}}}}}}{{\displaystyle \sum\limits_{k=1}^c {{{\left[ {{1 / {\left\{ {\left[ {m{{\rm{RFC}}_k} - b{\gamma _l}u_{kl}^b} \right]{{\left\| {{\zeta _l} - {v_k}} \right\|}^2}} \right\}}}} \right]}^{{1 / {\left( {m - 1} \right)}}}}} }}$

(15)

其中，式(15)和式(14)中的k表示第k类的索引号，以求取分母表达式的累加和。

则式(12)和式(15)为新的聚类中心和隶属度表达式。为了简单起见，后续将本文所提的算法简称为FCMRFC算法。

2.3 FCMRFC算法流程

所提算法的执行流程描述如下：

输入　模糊指数m，聚类中心个数c，贡献指数b，最大迭代次数T，终止条件ε；

输出　由最终的隶属度得到分割结果。

1)利用式(4)得到去噪后的图像 ${\tilde{\boldsymbol{X}}}=[{\tilde x_1},{\tilde x_2}, \cdots ,{\tilde x_n}]$ ；

2)利用去噪后的图像得到灰度级ζ_l和相应的像素数γ_l；

3)随机初始化聚类中心 $V^{(0) }$ ；

4) For t=1: T do

5)利用 $V^{(t-1)}$ 由式(6)计算隶属度 $U^{(t)} $ ；

6)将类贡献抑制因子参与隶属度更新，如式(15)所示，得到更新后的 $U^{(t)} $ ；

7)利用式(2)更新 $V^{(t)} $ ；

8) If || $U^{(t)} -U^{(t-1)} $ ||<ε或q>T，then执行步骤5)；

9) End if

10) End for

3 实验与结果 3.1 实验参数设置及说明

与本文算法(FCMRFC)进行对比的算法皆为基于灰度级的模糊C均值算法，包括基于自适应滤波的广义模糊C均值算法^[5](fast generalized FCM based on adaptive filtering，FFCMAF)、噪声检测的模糊C均值算法^[7](noise detecting FCM，NDFCM)、增强型模糊C均值算法^[11](enhanced FCM，EnFCM)、快速广义模糊C均值算法^[12](fast generalized FCM，FGFCM)和加入后处理的快速模糊C均值算法^[13](fast noise detecting FCM and post-processing，FNDFCM_P)。需要说明的是，NDFCM算法并未给出基于灰度级形式的表达式，但是文献[8]指出，该算法遵循先去噪再分割的流程，可归结为基于灰度级的模糊C均值算法这一类。算法所涉及的参数设定如表1所示，参数的取值均为算法所在文献的建议值。

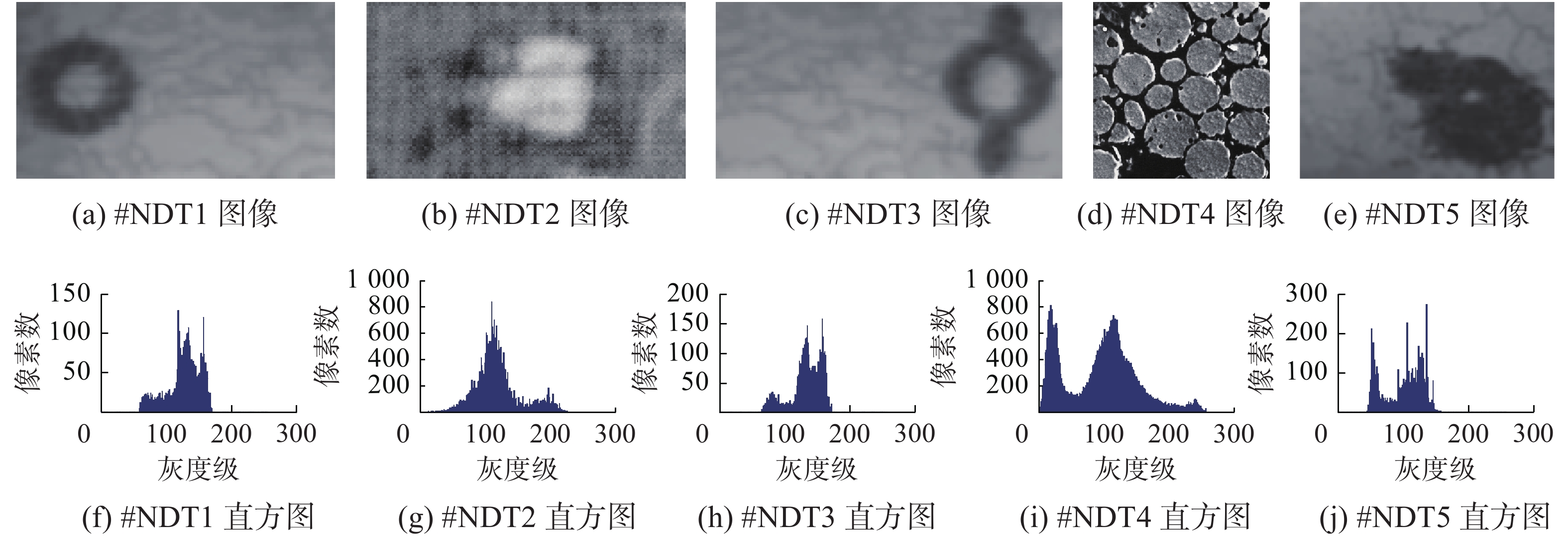
所选择的评价指标为G_mean^[19]，该指标能够有效评价类间差异较大图像的分割结果，分割效果与该值的大小成正比。选择无损检测图像(分别命名为#NDT1- #NDT5)如图1(a)~(e)所示，其对应的灰度直方图如图1(f)~(j)所示，通过灰度直方图可以看出，所选图像类间差异较大，满足我们对测试图像的要求。

3.2 参数(贡献指数)b的讨论

由式(8)或式(9)可以看出，参数b对算法的抑制程度有较大影响，b值越大，抑制程度越低。当b=0时，算法没有意义。为验证参数b对算法的影响，选取图1(a)~(e)进行测试，图2给出由本文算法(FCMRFC)得到的G_mean值随参数b的变化情况，其中b从0.1取值至2.0，步长为0.1。可以看出，对于#NDT1和#NDT2，大趋势是随b增加指标减小；对于#NDT3，指标变化不大(在0.995附近浮动)；对于#NDT4，大趋势是随b增加指标大致是先增后减；对于#NDT5，指标不变。出于均衡考虑，在后续的实验中，参数b取值为0.5。

3.3 分割结果

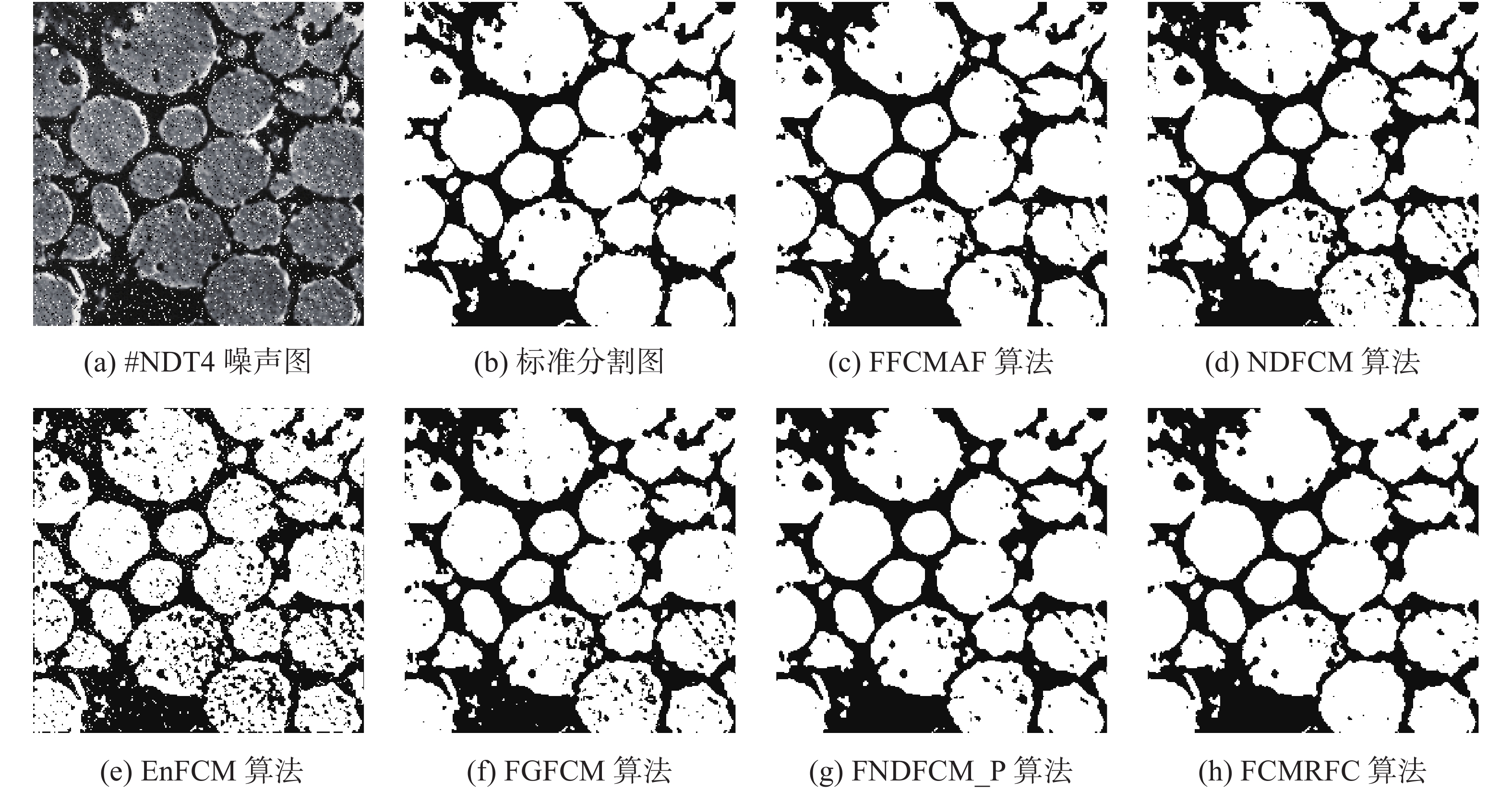
为测试FCMRFC算法的鲁棒性，对所选图像添加高斯白噪声(white Gaussian noise，WGN)，强度均值为0，归一化方差为0.01或0.02；或添加椒盐噪声(salt & pepper noise，SPN)，噪声比例为10%或20%，表2给出了各算法得到的指标G_mean值。同时，为显示分割的视觉效果，图3~7给出了在SPN(10%)噪声下各算法的分割结果。

将图2~7所示的图像分割结果与对应的标准分割图对比，可以看出，FCMRFC算法的分割结果更接近标准分割图，这为后续的目标识别和测量奠定基础。另外，可以看出，FFCMAF算法和FNDFCM_P算法去噪能力较强，其原因在于前者考虑了像素的非邻域信息，后者增加了后处理步骤。由表2指标结果可以看出，FCMRFC算法在绝大多数情形下取得了最优的分割效果，显示出算法的有效性和适应性，充分说明了算法能够有效分割类间差异较大的图像，扩展了基于灰度级模糊C均值算法的应用范围。

4 结束语

为了改善基于灰度级模糊C均值算法不能有效分割类间差异较大图像的缺点，在该算法基础上提出一种改进版本。改进的算法主要是通过引入一种新颖的类贡献抑制因子至目标函数中，减弱较大类对目标函数的作用，避免较小类的聚类中心向较大类偏移。基于新的目标函数对图像进行迭代聚类分割，结果显示新算法的有效性和鲁棒性。需指出，改进算法如果在图像去噪阶段能够得到更好的待分割图像，那么算法的指标值和视觉效果会进一步改善，故研究图像去噪算法仍具有较大意义。