特征选择是数据挖掘、机器学习和模式识别中的一项重要技术,是当前信息领域的研究热点之一[1-3]。它在数据分析和预处理过程中起着非常重要的作用。特征选择在不改变特征原始表达的基础上,仅从特征集中筛选最能代表数据特点的最优特征子集。因此,不仅可以去除不相关和冗余信息,降低训练样本的维度和分类样本的复杂度,而且能很好地保持原始特征包含的信息,对于人们理解和判断观测来说更加容易。特征选择根据其是否与后续学习算法独立可以分为过滤式和封装式两种。过滤式特征选择方法独立于后续的学习算法,通过数据的本质属性对所有特征进行评分,在此评价过程中不会借用分类模型来完成[4-5]。其中具有代表性的方法有T检验(T-test)[6]、Fisher score[7]、信息增益(information gain,IG)[8]等。但是,过滤式特征选择方法往往会忽略特征之间的相关性。封装式特征选择算法与后续学习算法相关,利用学习算法的性能评价所选特征子集的好坏,因此在精度方面要优于过滤式特征选择[8-12]。基于特征选择的目的,已经有部分学者做了相关研究。例如,传统的基于空间搜索的最大相关最小冗余(minimal redundancy maximal relevance,MRMR)[13]算法,使用互信息来度量特征之间的冗余度以及与类别之间的相关度,并且利用信息熵和信息差两个函数来选取最优特征子集。但是,由于冗余度和相关度的评价准则单一,所以使得该特征选择算法的使用范围较窄。2018年,郭凯文等[14]提出了基于特征选择和聚类的分类算法,特征选择标准采用的是传统的基于空间搜索的最大相关最小冗余准则,将信息差作为目标函数来求解最优特征子集。虽然该算法在目标函数中增加了相关度和冗余度的权重因子,但是,在求解最优特征子集的过程中需要对权重因子不断地赋值以寻求最优子集,计算量较大;2020年,李纯果等[15]提出的基于排序互信息的无监督特征选择,是基于排序互信息反应的两属性之间的单调关系,用每个属性与其他属性之间的平均互信息,来衡量每个属性与排序学习的相关度,平均互信息最高的视为排序最相关的属性。但是,该算法忽略了特征与特征之间的冗余度,只在低维度且样本量较少的模拟数据集上进行了有效性验证,对真实数据集的特征选择效果不明了;2020年,刘云等[16]提出了混合蒙特卡罗搜索的特征选择算法的优化,根据蒙特卡罗树搜索方法生成了一个初始特征子集,然后利用ReliefF算法选择前k个特征组成候选特征集,最后,用KNN分类器的分类精度评估候选特征, 选择高精度的候选特征作为最佳特征子集。然而,ReliefF算法是从同类和不同类中各选取k个近邻样本,求平均值得到各个特性权值,即特征与类别之间的相关性,并没有考虑特征与特征之间的冗余度。2020年,周传华等[17]提出的最大相关与独立分类信息最大化特征选择算法,用互信息度量特征与类别之间的相关性,用独立分类信息综合衡量新分类信息和特征冗余,尽管在特征选择过程中综合考虑了特征与类别的相关性、特征之间的冗余性,以及特征包含的新分类信息,并结合最大最小准则对特征的重要性进行了非线性评价,但其目标函数与传统的MRMR算法的目标函数类似,依然不能根据客户的实际需求进行特征选择。
针对上述特征选择算法中存在的冗余度和相关度的度量准则单一以及评价函数问题,提出了新方案。在冗余度度量准则方面引入了2种不同的方法,在相关度度量准则方面引入了4种不同的方法,从而组合衍生出8种特征选择算法,提出了新的目标函数。
1 新的特征选择算法MRMR算法是最常用、最典型的基于空间搜索的特征选择算法。其中,最大相关即特征与类别间的相关度要最大,最小冗余即特征与特征之间的相关度要最小[18-19],该算法中,冗余度和相关度均是利用互信息作为度量准则,就效能而言,比只考虑特征与类别之间的相关度,或者只考虑特征之间冗余度的特征选择算法要好。但是,在现实生活中,我们面临的数据往往纷繁复杂,面对不同的数据,MRMR算法呈现出的效果有较大差异,从而降低了该算法的适用范围。
针对MRMR算法存在的问题,提出一种新的最大相关最小冗余特征选择算法(new algorithm for feature selection with maximum relation and minimum redundancy,New-MRMR)。这里New-MRMR算法仅是新提出的一个特征选择的框架,在度量特征与特征之间冗余度时选用了2种评价准则,在度量特征与特征之间相似度时选用了4种评价准则,从而衍生出8种特征选择算法,当面对不同的用户需求时,选用不同特征选择算法,使得新提算法的适用范围更广。具体的特征选择流程见图1。
图1可以看出,特征选择算法的基本流程为:先对原始数据集进行预处理,将原始数据集分为测试集和训练集,然后,在训练集上选择不同的冗余度和相关度评价准则来训练模型,进行特征选择,得到最优特征子集,最后,利用测试集来验证模型的有效性。

|
Download:
|
| 图 1 New-MRMR特征选择流程 Fig. 1 New-MRMR feature selection flow | |
特征选择是为了去除原始特征集中的冗余特征,达到降维目的。因此,利用冗余度评价可以作为New-MRMR特征选择算法的一部分,其基本思想是:两个特征的相关度越大,则这两个特征冗余度也越高。但是,由于评价特征之间冗余度以及特征与类别之间相关度的准则众多,且目前缺乏相关研究给出具体哪种方法更适用于哪种数据类型。所以,本文新提出的算法仅采用了Pearson相关系数[14]以及互信息[14]两种准则来度量特征之间的冗余度。
1.2 相关度评价准则在特征选择过程中,通常优先选择与类别相关度较大的特征,而特征的重要度在一定程度上反映了与类别的相关度大小,因此,相关度的度量准则就转化成了特征重要度的衡量。衡量特征重要度的评价准则有很多,例如:Fisher score[7]、信息增益(information gain,IG)[8]、Laplacian Score[20]、Chi-squar Test[21-22]等。Fisher score 主要是按照类内距离小,类间距离大的原则,选出包含鉴别信息比较多的特征,其值越大,说明该特征越重要,与类别的相关度越大;信息增益是通过计算某特征被使用前后的信息熵来为该特征进行打分,信息增益越大,说明该特征越重要,与类别的相关度越大;Laplacian Score是根据拉普拉斯特征映射等对单个特征评分,然后选出方差和局部几何结构保持能力较强的特征,其分值越高,特征越重要。New-MRMR算法也采用这4种评价准则作为相关度的度量准则。
1.3 目标函数基于特征选择和聚类的众多分类算法中,目标函数常采用加权的信息差方式,并且通过对权重信息不断赋值来求解最优特征子集,不能根据不同用户实际需求的维度求解最优特征子集。因此,本文提出了一种新的目标函数,引入了一个指示向量
| $ \mathop {\max }\limits_{\boldsymbol{\lambda }} \left( {\frac{{{{\boldsymbol{\lambda }}^{\rm{T}}}{\boldsymbol{D}}}}{k} - \frac{{{{\boldsymbol{\lambda }}^{\rm{T}}}{\boldsymbol{C\lambda }}}}{{k(k - 1)}}} \right)\;\;, {\rm{s.t.}}\;\sum {{{\boldsymbol{\lambda }}_i}} = k,\;{{\boldsymbol{\lambda }}_{\boldsymbol{i}}} \in \left[ {0,1} \right] $ |
式中:k为用户需求的实际数据维度;D为冗余度矩阵;C为特征与类别之间的相关性矩阵。
对于该目标函数的求解,与最优化标准二次规划问题[23]相似,本文采用成对更新方法[24]来求解以上目标函数的最优解。
2 实验结果与分析 2.1 数据集信息及评价指标为验证New-MRMR算法的有效性,本文使用了4个真实的UCI数据集。先利用新提出的算法处理原始特征,进而使用支持向量机对所得到的特征子集进行分类实验,最后比较各种算法在测试集上的分类准确率(classification precision,CP)。相关定义如下:
| ${\rm{CP}} = \dfrac{{{\rm{CC}}}}{{\rm{Num}}} \times 100{\text{%}} $ |
式中:CC(correct classification,CC)为正确分类的样本数量;Num为样本数量总数。
| 表 1 实验数据集 Tab.1 Experimental data set |
实验中,与新提算法进行对比的特征选择算法分别是:Fisher Score、基于Information Gain的方法、基于Laplacian Score的方法、基于Chi-squar Test的方法、基于MRMR的方法。表2列出了以上方法。
2.2 实验结果对比分析特征选择过程是剔除原始数据集中的不相关以及冗余特征,达到数据降维目的。为验证以上各种算法在数据降维和用支持向量机分类后的分类准确率,表3给出了以上各种算法在数据集isolet上的实验结果,即经支持向量机分类后,计算得到的分类准确率达到最大时所选择的特征数。
| 表 2 新提出的8种特征选择算法与其他算法对比 Tab.2 Comparison of 8 newly proposed feature selection algorithms with other algorithms |
| 表 3 分类准确率最大时,数据集isolet上各种算法分别所选择的特征数 Tab.3 Number of features selected by various algorithms when the Classification precision is maximum on the isolet dataset |
由表3可以看出,由以上各种算法对数据集isolet进行特征选择后,利用支持向量机对所选特征子集进行分类,本文新提出的8种特征选择算法的分类准确率,均高于传统的5种特征选择算法,尤其是新提出的算法New-MRMR-IG-P,其分类准确率达到了0.9635,远高于传统的5种特征选择算法。在保证准确率的情况下,其所选的特征数也均小于传统的5种特征选择算法。可见,本文新提出的特征选择算法在数据降维方面效果更佳。
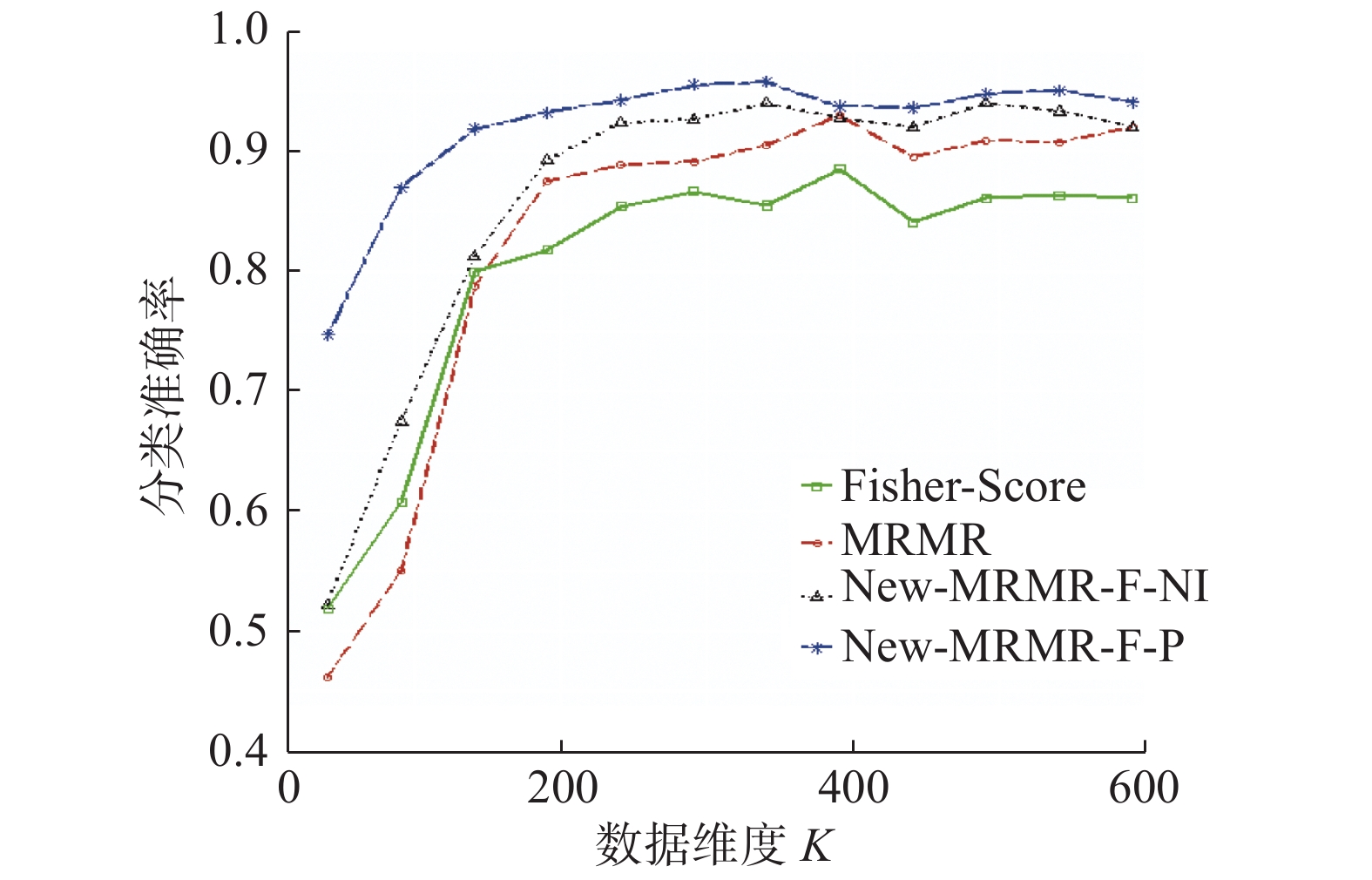
图2是在数据集isolet上,本文新提出的特征选择算法New-MRMR-F-NI、New-MRMR-F-P,传统特征选择算法MRMR、Fisher Score在不同维度下的分类准确率变化趋势。
|
Download:
|
| 图 2 New-MRMR-F-NI、New-MRMR-F-P、Fisher-Score、MRMR在数据集isolet上分类准确率的变化趋势 Fig. 2 Correct classification trend of New-MRMR- F-NI, New-MRMR-F-P, Fisher-Score, MRMR on the dataset isolet | |
从图2可以看出,对于在不同维度下的分类准确率,新提出的特征选择算法New-MRMR-F-NI、New-MRMR-F-P明显高于传统算法Fisher Score、MRMR。所以,对于减少原始特征集中的冗余和不相关特征,New-MRMR-F-NI、New-MRMR-F-P有更好的优势。
不同维度下,本文新提算法New-MRMR-K-NI、New-MRMR-K-P,传统算法MRMR、Chi-Square-Test在数据集isolet上的分类准确率变化趋势见图3。

|
Download:
|
| 图 3 New-MRMR-K-NI、New-MRMR-K-P、Chi-Square-Test、MRMR在数据集isolet上分类准确率的变化趋势 Fig. 3 Correct classification trend of New-MRMR-K-NI、New-MRMR-K-P、Chi-Square-Test、MRMR on the dataset isolet | |
图3显示,不同维度下,New-MRMR-K-P的分类准确率曲线明显高于传统特征选择算法,并且,在所选特征子集数为289时,其分类准确率达到了最高,既很好地去除了原始特征集中的冗余和不相关特征,又保证了分类准确率。此外,算法New-MRMR-K-P除了在维度为195时的分类准确率与传统算法MRMR相近之外,在其他维度上的分类准确率均高于Chi-Square-Test、MRMR。可见,本文新提出的特征选择算法效果更佳。
不同维度下,新提出的特征选择算法New-MRMR-L-NI、New-MRMR-L-P,传统特征选择算法MRMR、Laplacian-Score的分类准确率变化趋势见图4。

|
Download:
|
| 图 4 New-MRMR-L-NI、New-MRMR-L-P、Laplacian-Score、MRMR在数据集isolet上,分类正确的变化趋势 Fig. 4 Correct classification trend of New-MRMR-L-NI、New-MRMR-L-P, Laplacian-Score, MRMR on the dataset isolet | |
图4显示,在特征维度为342的时候,算法New-MRMR-L-P的分类准确率就已经达到了最高,并且大于传统算法Laplacian-Score、MRMR的最大分类准确率。此外,在分类准确率达到最高时,算法New-MRMR-L-NI所选的特征子集数仅为288,远小于传统算法Laplacian-Score、MRMR所选的特征子集数。因此,新提出的算法New-MRMR-L-NI、New-MRMR-L-P对于特征选择效果更好。
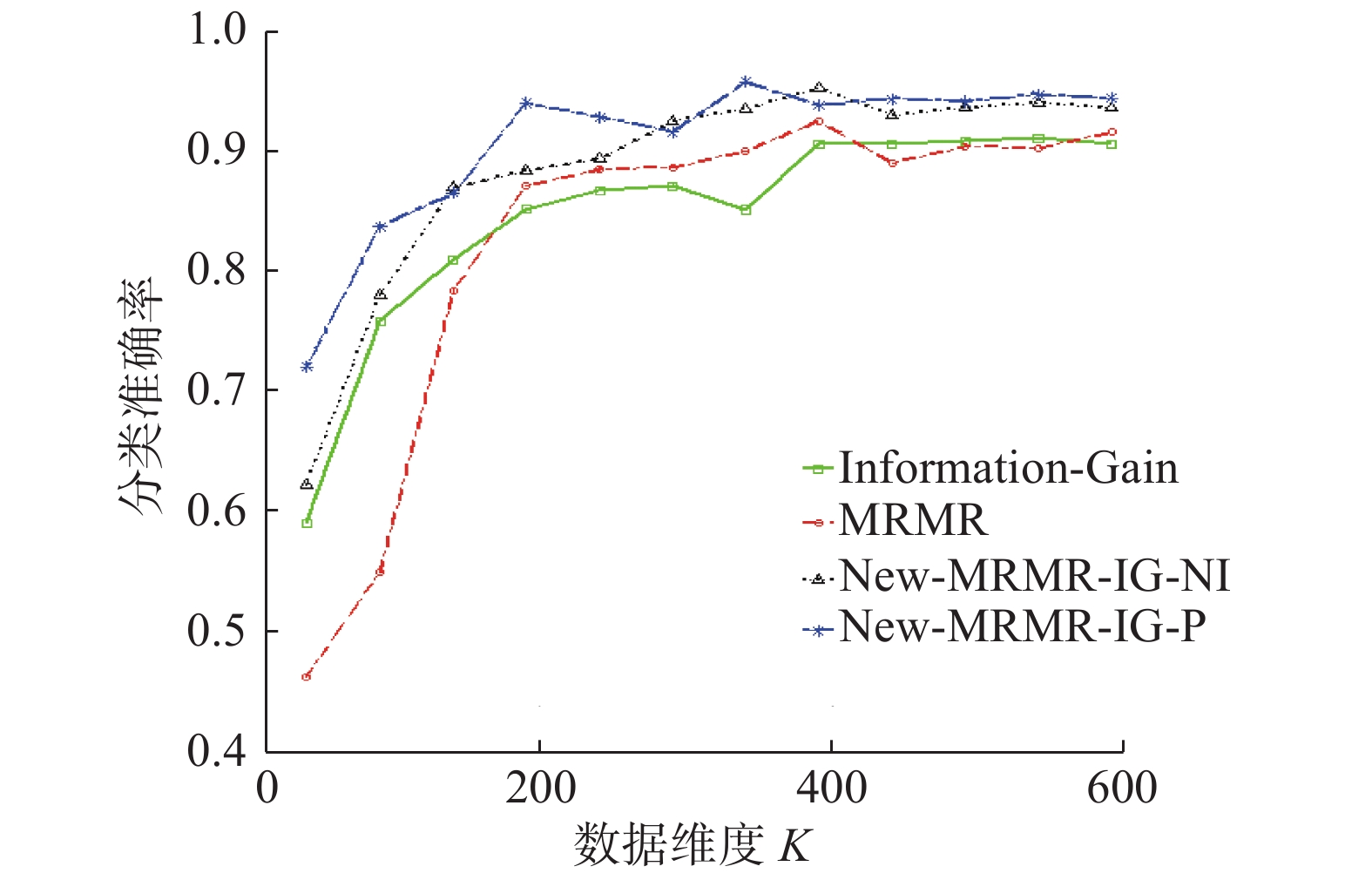
不同维度下,新提出的特征选择算法New-MRMR-IG-NI、New-MRMR-IG-P,传统特征选择算法MRMR、Laplacian-Score的分类准确率变化趋势见图5。
由图5可以看出,在不同维度下,算法New-MRMR-IG-NI、New-MRMR-IG-P分类准确率的曲线,均高于传统的两种特征选择算法Information- Gain、MRMR所代表的曲线。分类准确率越高,表明所选特征子集越好。可见,新出的算法New-MRMR-IG-NI 以及New-MRMR-IG-P在特征选择方面更加有效。
|
Download:
|
| 图 5 New-MRMR-IG-NI、New-MRMR-IG-P、Information-Gain、MRMR在数据集isolet上,分类准确率的变化趋势 Fig. 5 Correct classification trend of New-MRMR-IG-NI, New-MRMR-IG-P, Information-Gain, MRMR on the dataset isolet | |
表4给出了以上各种算法在数据集waveform上的实验结果,即经支持向量机分类后计算得到的分类准确率达到最大时所选择的特征数。
表4显示,在数据集waveform上,本文新提出的算法New-MRMR-F-P的最大分类准确率达到了0.9534,远大于传统特征选择算法的分类准确率;并且New-MRMR-F-P在分类准确率达到最大时,所选的特征子集数仅为17,小于传统的5种特征选择算法在分类准确率达到最大时所选的特征子集数。除此之外,本文新提出的其余特征选择算法的分类准确率,也均大于传统的特征选择算法的分类准确率,且所选特征子集数相对来说较小。因此,综合考虑分类准确率以及所选特征子集维度两个方面,本文新提算法特征选择效果更加明显。
| 表 4 分类准确率最大时数据集waveform上各种算法分别所选择的特征数 Tab.4 Number of features selected by various algorithms when the Classification precision is maximum on the waveform dataset |
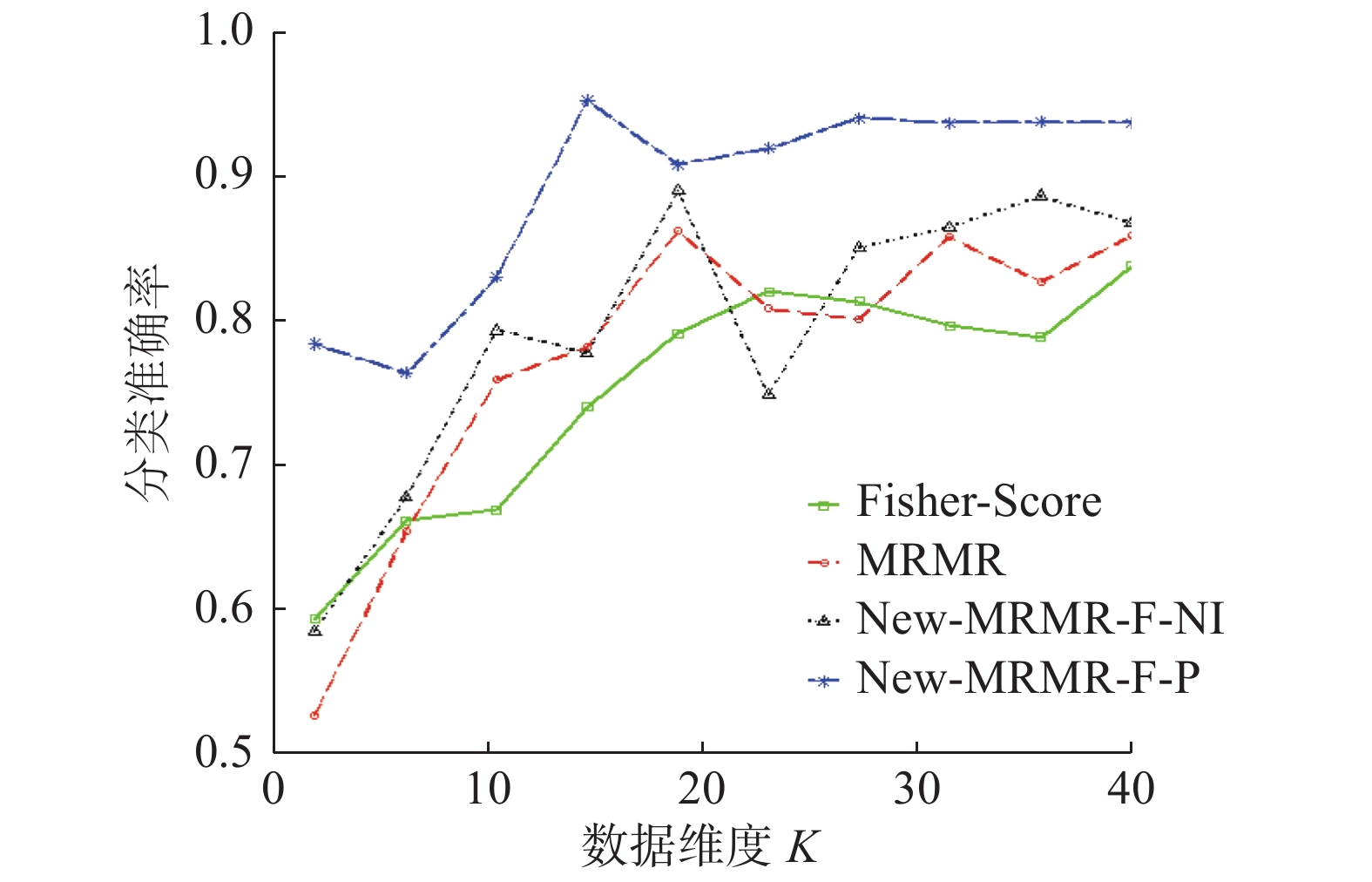
不同维度下,本文新提出的特征选择算法New-MRMR-F-NI、New-MRMR- F-P,传统特征选择算法MRMR、Fisher Score在数据集waveform上的分类准确率变化趋势见图6。
由图6看出,在数据集waveform上,New-MRMR-F-P的表现最好,其所代表的曲线远高于传统的特征选择算法MRMR、Fisher-Score所代表的曲线。此外,虽然在维度为24时,算法New-MRMR-F-NI的分类准确率低于传统算法MRMR、Fisher-Score。但是,在其余维度上,New-MRMR-F-NI的分类准确率均高于MRMR、Fisher-Score。综合分析,本文新提算法New-MRMR-F-NI、New-MRMR-F-P的特征选择效果更好。
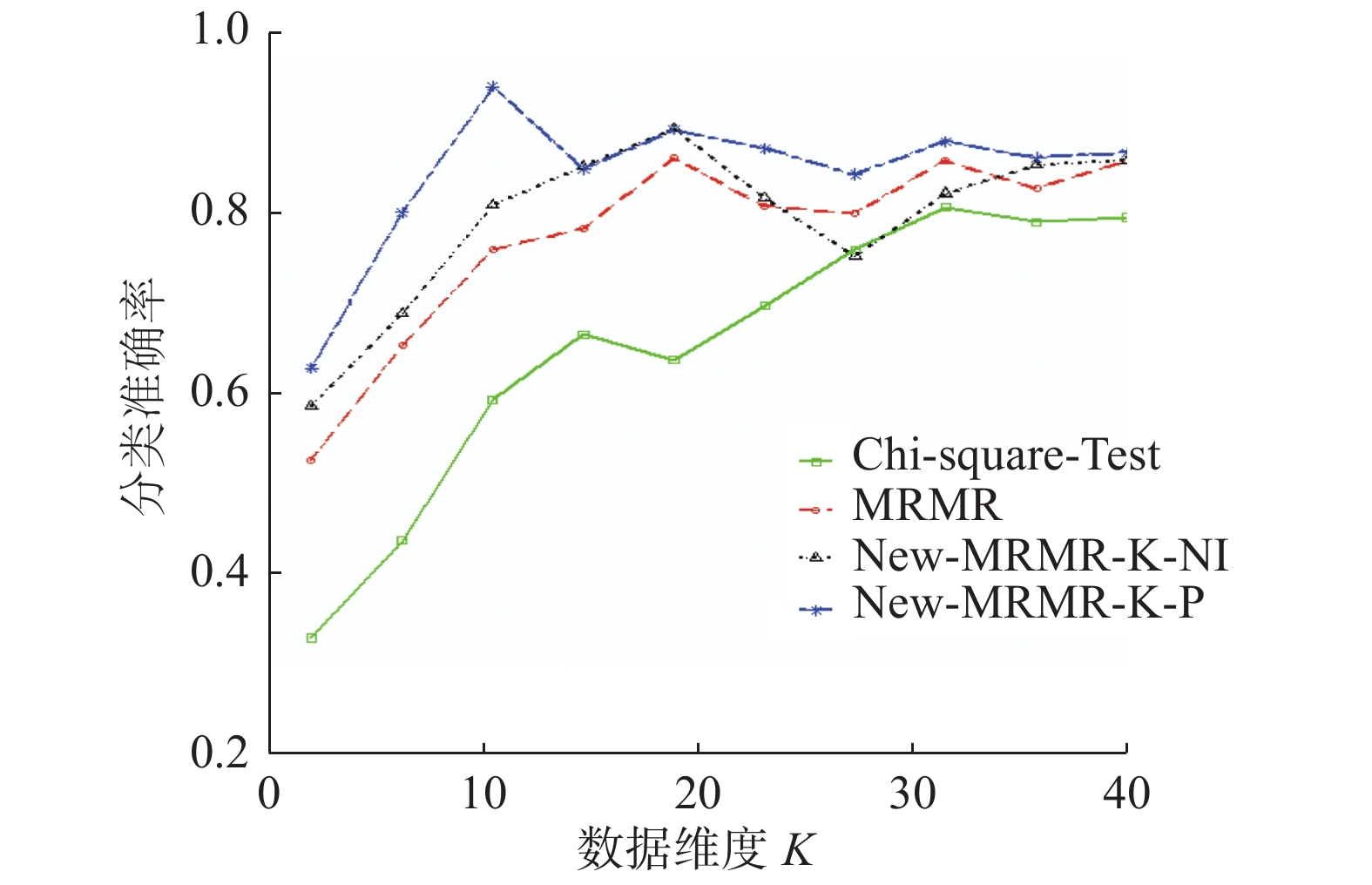
不同维度下,算法New-MRMR-K-NI、New-MRMR-K-P以及传统特征选择算法MRMR以及Chi-Square-Test在数据集waveform上的分类准确率变化趋势见图7。
图7显示,维度为20时,New-MRMR-K-NI的分类准确率就达到了最大,大于MRMR、Chi-Square-Test的最大分类准确率。并且其所选特征子集数小于MRMR、Chi-Square-Test的最优特征子集数。此外,算法New-MRMR-K-P的分类准确率曲线高于MRMR、Chi-Square-Test的分类准确率曲线。所以,在waveform数据集上,本文新提出的算法New-MRMR-K-NI、New-MRMR-K-P的特征选择效果更好。
|
Download:
|
| 图 6 New-MRMR-F-NI、New-MRMR-F-P、Fisher-Score、MRMR在数据集waveform上,分类准确率的变化趋势 Fig. 6 Correct classification trend of New-MRMR-F-NI New-MRMR-F-P, Fisher-Score, MRMR on the dataset waveform | |
|
Download:
|
| 图 7 New-MRMR-K-NI、New-MRMR-K-P、Chi-Square-Test、MRMR在数据集waveform上,分类准确率的变化趋势 Fig. 7 Correct classification trend of New-MRMR-K-NI, New-MRMR-K-P, Chi-Square-Test, MRMR on the dataset waveform | |
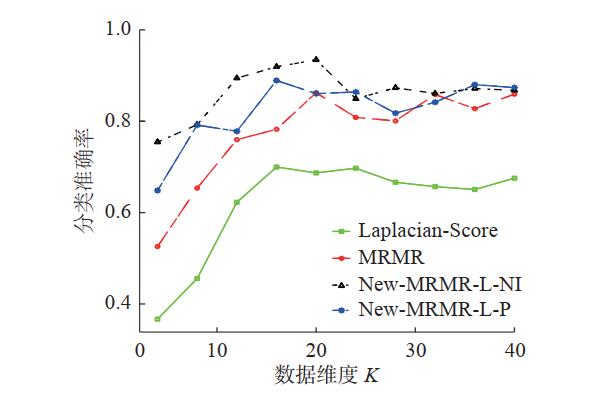
不同维度下,算法New-MRMR-L-NI、New-MRMR-L-P,传统特征选择算法MRMR、Laplacian-Score在数据集waveform上的分类准确率变化趋势见图8。
图8显示,New-MRMR-L-NI的分类准确率高于传统算法MRMR、Laplacian-Score。在分类准确率达到最大时,New-MRMR-L-NI所选特征子集数仅为20,小于MRMR、Laplacian-Score的最优特征子集数。另外,新提算法在多数维度上均大于传统算法MRMR、Laplacian-Score的分类准确率。由于分类准确率越高,特征选择效果越好,所以,在数据集waveform上,New-MRMR-L-NI、New-MRMR-L-P的特征选择效果更好。
|
Download:
|
| 图 8 New-MRMR-L-NI、New-MRMR-L-P、Laplacian-Score、MRMR在数据集waveform上,分类准确率的变化趋势 Fig. 8 Correct classification trend of New-MRMR-L-NI, New-MRMR-L-P, Laplacian-Score, MRMR on the dataset waveform | |
不同维度下,New-MRMR-IG-NI、New-MRMR-IG-P、传统算法MRMR、Information-Gain在数据集waveform上分类准确率变化趋势见图9。

|
Download:
|
| 图 9 New-MRMR-IG-NI、New-MRMR-IG-P、Information-Gain、MRMR在数据集waveform上,分类准确率的变化趋势 Fig. 9 Correct classification trend of New-MRMR-IG-NI, New-MRMR-IG-P, Information-Gain, MRMR on the dataset waveform | |
图9显示,在数据集waveform上,算法New-MRMR-IG-NI的分类准确率的曲线高于传统的算法MRMR、Information-Gain的分类准确率。且算法New-MRMR-IG-P的分类准确率在维度为24时达到最大。维度为11时,New-MRMR-IG-P的分类准确率略低于MRMR、Information-Gain,但是,在其余维度上均大于MRMR、Information-Gain。综上分析,在数据集waveform上,本文新提出的特征选择算法效果明显。
表5给出了以上各种算法在数据集clean上的实验结果,即经支持向量机分类后,得到的分类准确率达到最大时所选择的特征数。
| 表 5 分类准确率最大时数据集clean上各种算法分别所选择的特征数 Tab.5 Number of features selected by various algorithms when the Classification precision is maximum on the clean dataset |
由表5可以看出,在分类准确率方面,本文新提出的算法的最大分类准确率均高于5种传统的特征选择算法。在分类准确率达到最优时所选的特征子集数方面,尤其是算法New-MRMR-K-NI,其所选的特征子集数仅20,远小于原始的特征子集数。所以,对于数据集clean而言,本文新提出的特征选择算法更加有效。
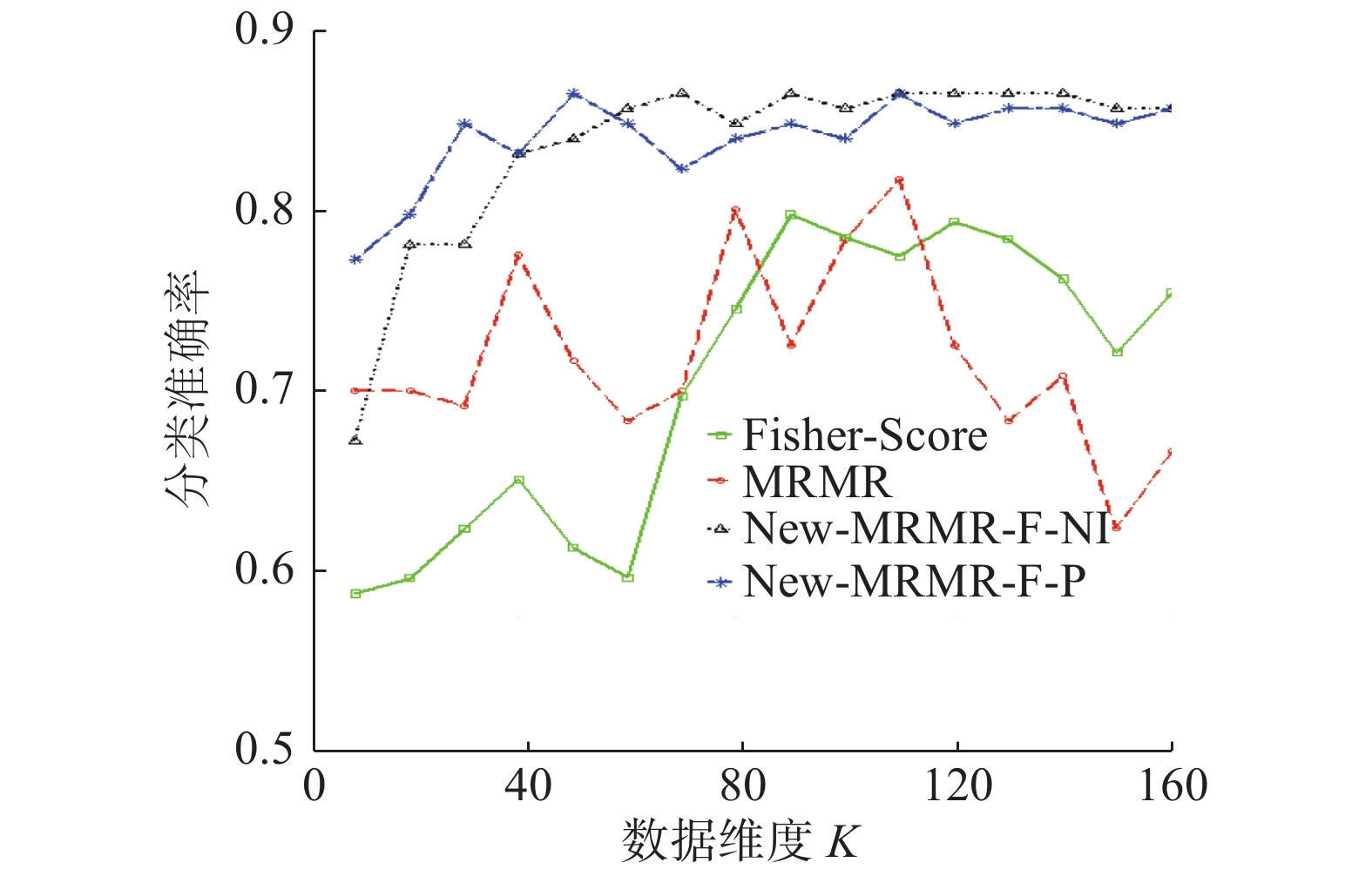
不同维度下,算法New-MRMR-F-NI、New-MRMR-F-P、传统特征选择算法MRMR、Fisher Score在数据集clean上的分类准确率变化趋势见图10。
|
Download:
|
| 图 10 New-MRMR-F-NI、New-MRMR-F-P、Fisher-Score、MRMR在数据集clean上分类准确率的变化趋势 Fig. 10 Correct classification trend of New-MRMR-F-NI, New-MRMR-F-P, Fisher-Score, MRMR on the dataset clean | |
由图10可以看出,本文新提算法New-MRMR-F-NI、New-MRMR-F-P的分类准确率曲线均MRMR、Fisher-Score的分类准确率的曲线之上。由此可见,在数据集claen上,算法New-MRMR-F-NI、New-MRMR-F-P的特征选择结果更优。
不同维度下,算法New-MRMR-K-NI、New-MRMR-K-P、传统特征选择算法MRMR、Chi-Square-Test在数据集clean上的分类准确率变化趋势见图11。

|
Download:
|
| 图 11 New-MRMR-K-NI、New-MRMR-K-P、Chi-Square-Test、MRMR在数据集clean上,分类准确率的变化趋势 Fig. 11 Correct classification trend of New-MRMR-K-NI, New-MRMR-K-P, Chi-Square-Test, MRMR on the dataset clean | |
图11中,New-MRMR-K-NI、New-MRMR-K-P的分类准确率的曲线均在传统的特征选择算法MRMR、Chi-quare-Test之上,尤其是New-MRMR-K-NI,当分类准确率达到最大时,所选的特征子集数为20,远小于两种传统算法所选择的最优特征子集数。可见,在数据集clean上,算法New-MRMR-K-NI、New-MRMR-K-P的特征选择效果更优。
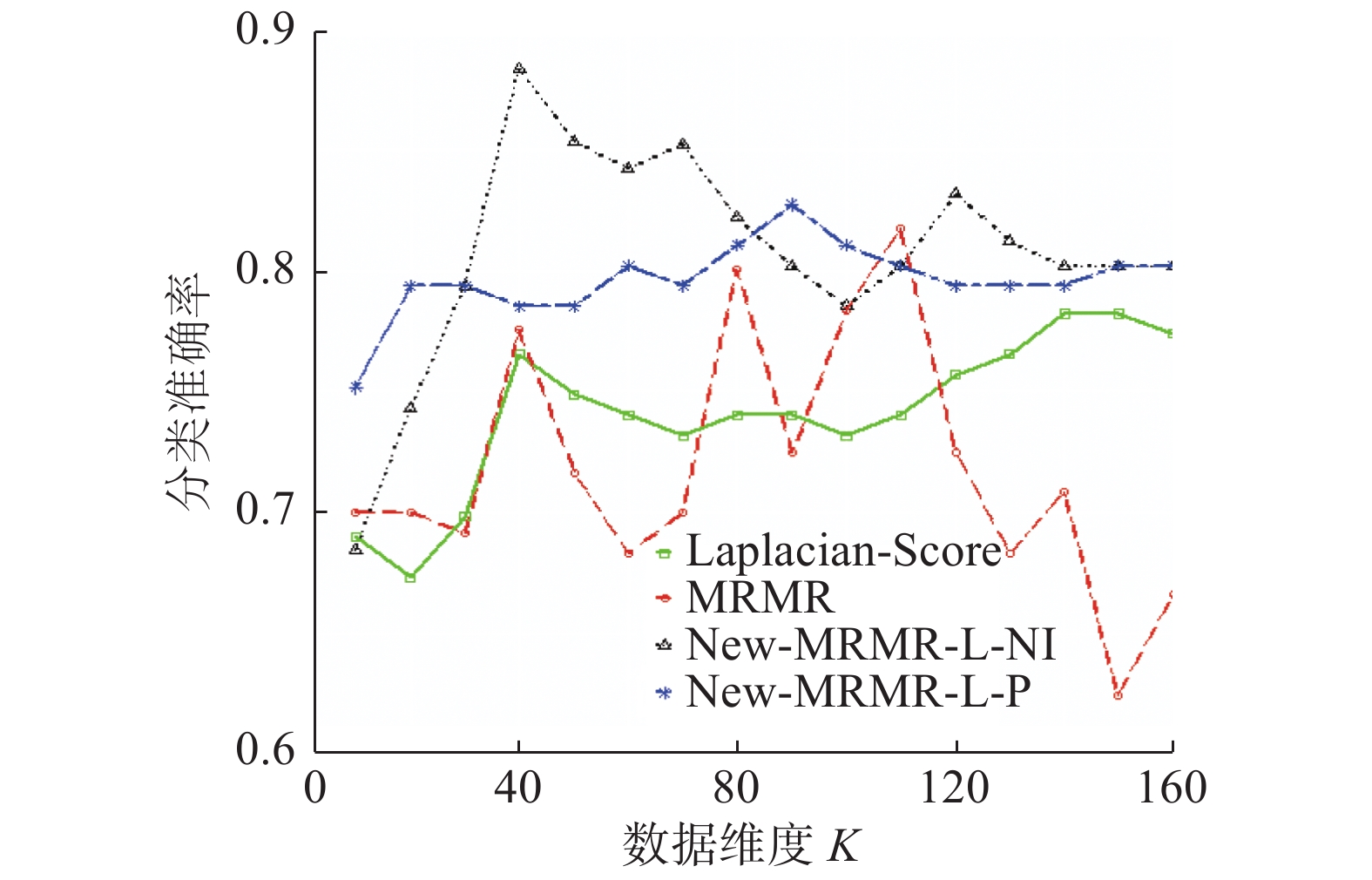
不同维度下,算法New-MRMR-L-NI、New-MRMR-L-P、传统特征选择算法MRMR、Fisher Score在数据集clean上的分类准确率变化趋势见图12。
|
Download:
|
| 图 12 New-MRMR-L-NI、New-MRMR-L-P、Laplacian-Score、MRMR在数据集clean上分类准确率的变化趋势 Fig. 12 Correct classification trend of New-MRMR-L-NI, New-MRMR-L-P, Laplacian-Score, MRMR on the dataset clean | |
图12可以看出,维度为40时,算法New-MRMR-L-NI就达到了最大分类准确率,且高于传统算法MRMR、Laplacian-Score的分类准确率。此外,虽然在维度为110时,New-MRMR-L-P的分类准确率略低于MRMR,但在其余维度上的分类准确率均高于MRMR、Laplacian-Score的分类准确率。
可见,在数据集clean上,新提算法New- MRMR-L-NI、New-MRMR-L-P的特征选择效果更好。
不同维度下,算法New-MRMR-IG-NI、New-MRMR-IG-P、传统特征选择算法MRMR、Fisher Score在数据集clean上的分类准确率变化趋势见图13。

|
Download:
|
| 图 13 New-MRMR-IG-NI、New-MRMR-IG-P、Information-Gain、MRMR在数据集clean上分类准确率的变化趋势 Fig. 13 Correct classification trend of New-MRMR-IG-NI, New-MRMR-IG-P, Information-Gain, MRMR on the dataset clean | |
图13显示,本文新提算法New-MRMR-IG-NI、New-MRMR-IG-P的分类准确率曲线均在传统算法的分类准确率曲线之上。所以,对于数据集clean,本文新提出的两种特征选择算法New-MRMR-IG-NI、New-MRMR-IG-P所选择的特征子集更加有效。
表6给出了以上各种算法在数据集Parkinson’s Disease上的实验结果,即经支持向量机分类后,得到的分类准确率达到最大时所选择的特征数。
| 表 6 分类准确率最大时,数据集Parkinson’s Disease上各种算法分别所选择的特征数 Tab.6 Number of features selected by various algorithms when the Classification precision is maximum on the Parkinson’s Disease dataset |
表6显示,算法New-MRMR-F-P的分类准确率高达0.9124,且此时所选择的特征子集数仅为150,远小于传统的5种算法的最优特征子集数。另外,除了New-MRMR-K-P的分类准确率略低于传统算法MRMR的分类准确率之外,新提出的其余算法均大于传统特征选择算法。由此可见,本文新提出的特征选择算法在数据集Parkinson’s Disease上的特征选择效果更好。
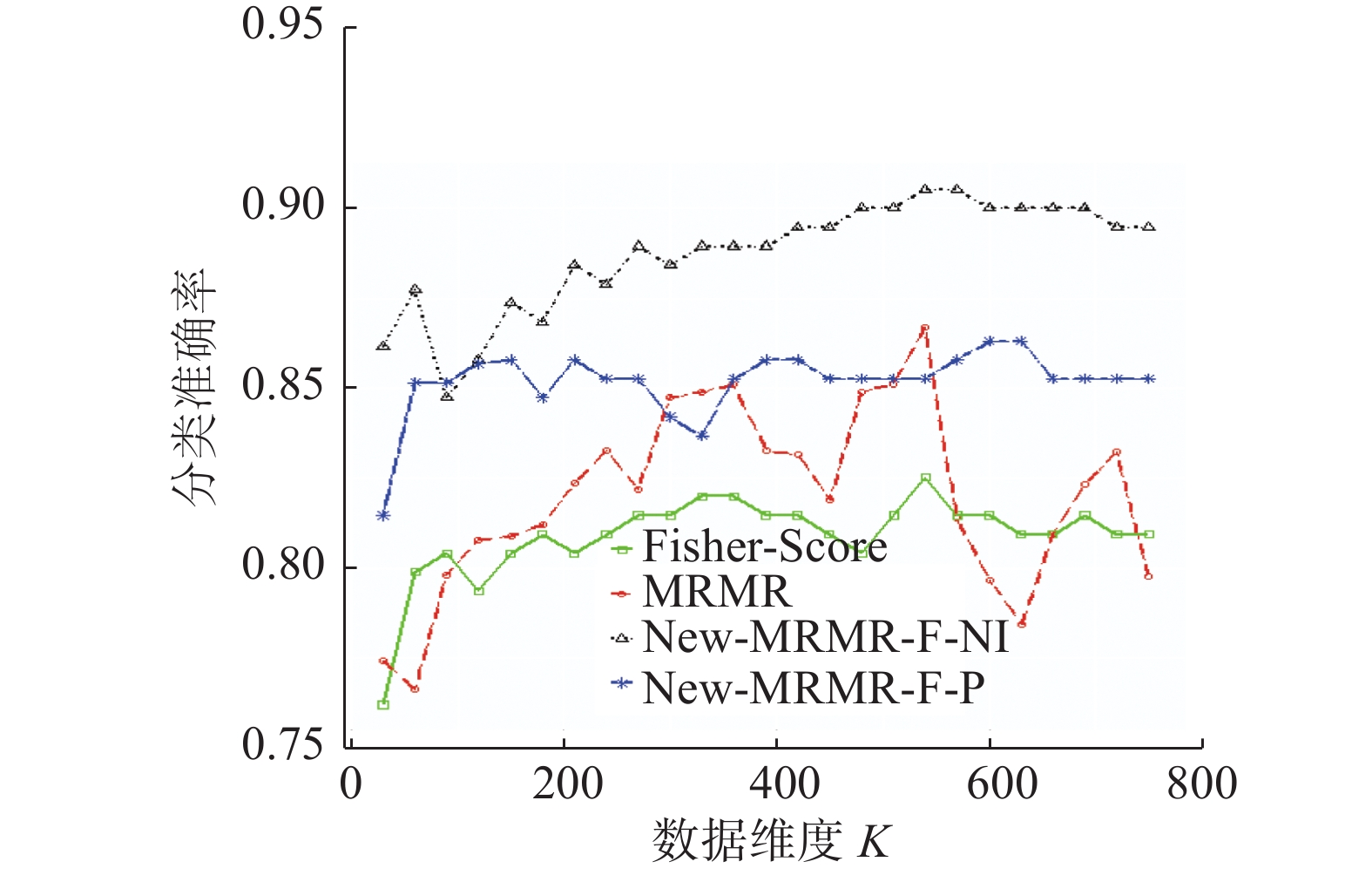
不同维度下,算法New-MRMR-F-NI、New-MRMR-F-P,传统特征选择算法MRMR、Fisher-Score在数据集Parkinson’s Disease上的分类准确率变化趋势见图14。
|
Download:
|
| 图 14 New-MRMR-F-NI、New-MRMR-F-P、Fisher-Score、MRMR在数据集Parkinson’s Disease上分类准确率的变化趋势 Fig. 14 Correct classification trend of New-MRMR-F-NI, New-MRMR-F-P, Fisher-Score, MRMR on the Parkinson’s Disease dataset | |
图14显示,算法New-MRMR-F-NI的分类准确率曲线在传统算法MRMR、Fisher-Score的分类准确率曲线之上。在维度为540时,New-MRMR-F-P的分类准确率略低于MRMR的分类准确率。但是,在其余维度上,New-MRMR-F-P的分类准确率均高于传统算法MRMR、Fisher-Score的分类准确率。更重要的是,在达到最大分类准确率时,New-MRMR-F-NI所选的特征子集数仅为210,远低于MRMR、Fisher-Score的最优特征子集数。所以,在数据集Parkinson’s Disease上,本文新提出的算法特征选择效果更好。
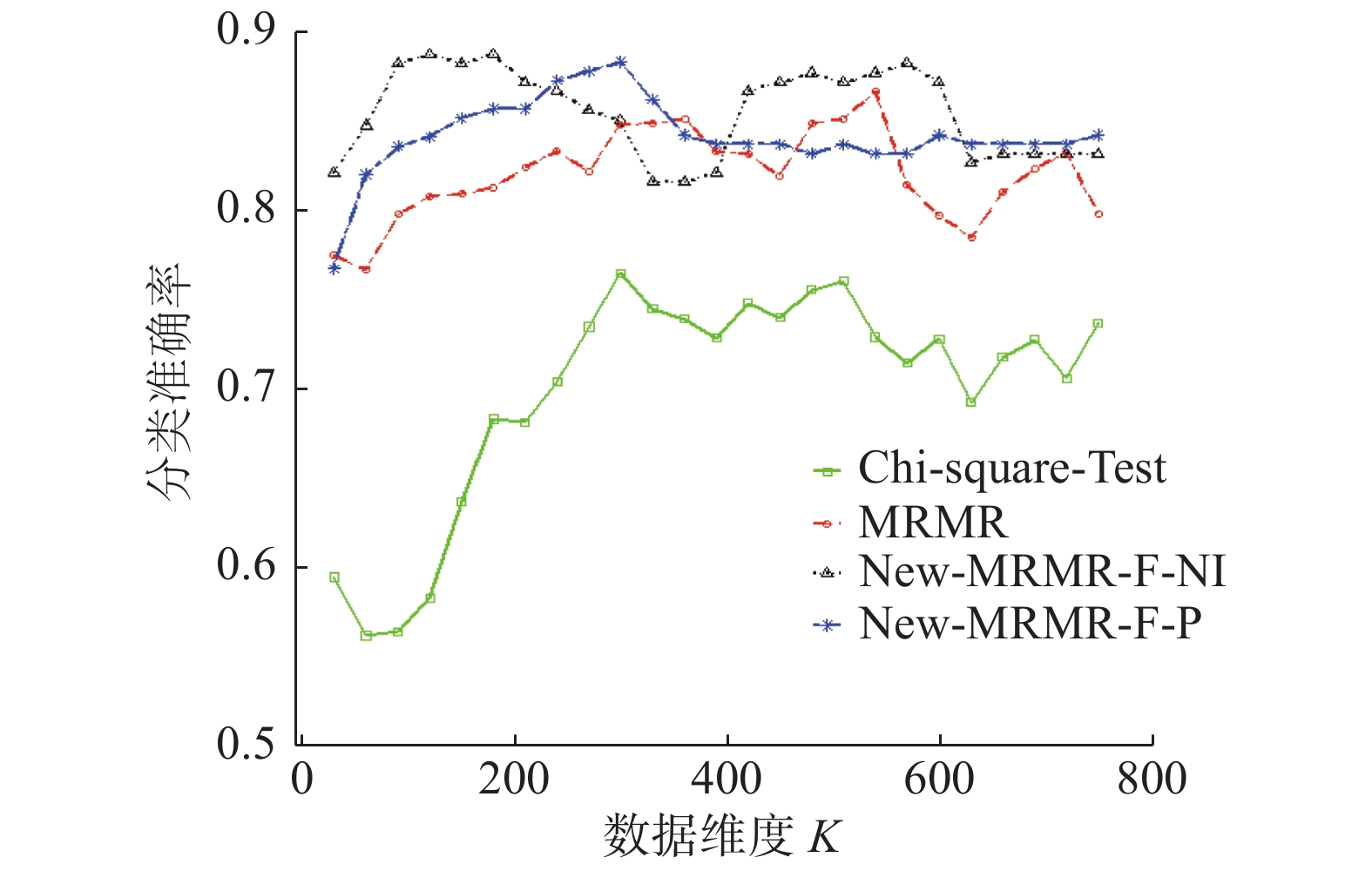
不同维度下,本文新提算法New-MRMR-F-NI、New-MRMR-F-P、传统算法MRMR、Fisher-Score在数据集Parkinson’s Disease上的分类准确率变化趋势见图15。
|
Download:
|
| 图 15 New-MRMR-K-NI、New-MRMR-K-P、Chi-Square-Test、MRMR在数据集Parkinson’s Disease上分类准确率的变化趋势 Fig. 15 Correct classification trend of New-MRMR-K-NI, New-MRMR-K-P, Chi-Square-Test, MRMR on the Parkinson’s Disease dataset | |
由图15可见,在绝大多数维度上,New-MRMR-F-NI、New-MRMR-F-P的分类准确率均高于MRMR、Chi-Square-Test的分类准确率。在维度为120时,New-MRMR-F-NI就已然达到了最大分类准确率,大于MRMR、Chi-Square-Test的最大分类准确率。由此可见,在数据集Parkinson’s Disease上,本文新提算法特征选择效果更好。
不同维度下,本文新提出的特征选择算法New-MRMR-F-NI、New-MRMR-F-P以及传统特征选择算法MRMR以及Fisher Score在数据集Parkinson's Disease上的分类准确率变化趋势见图16。
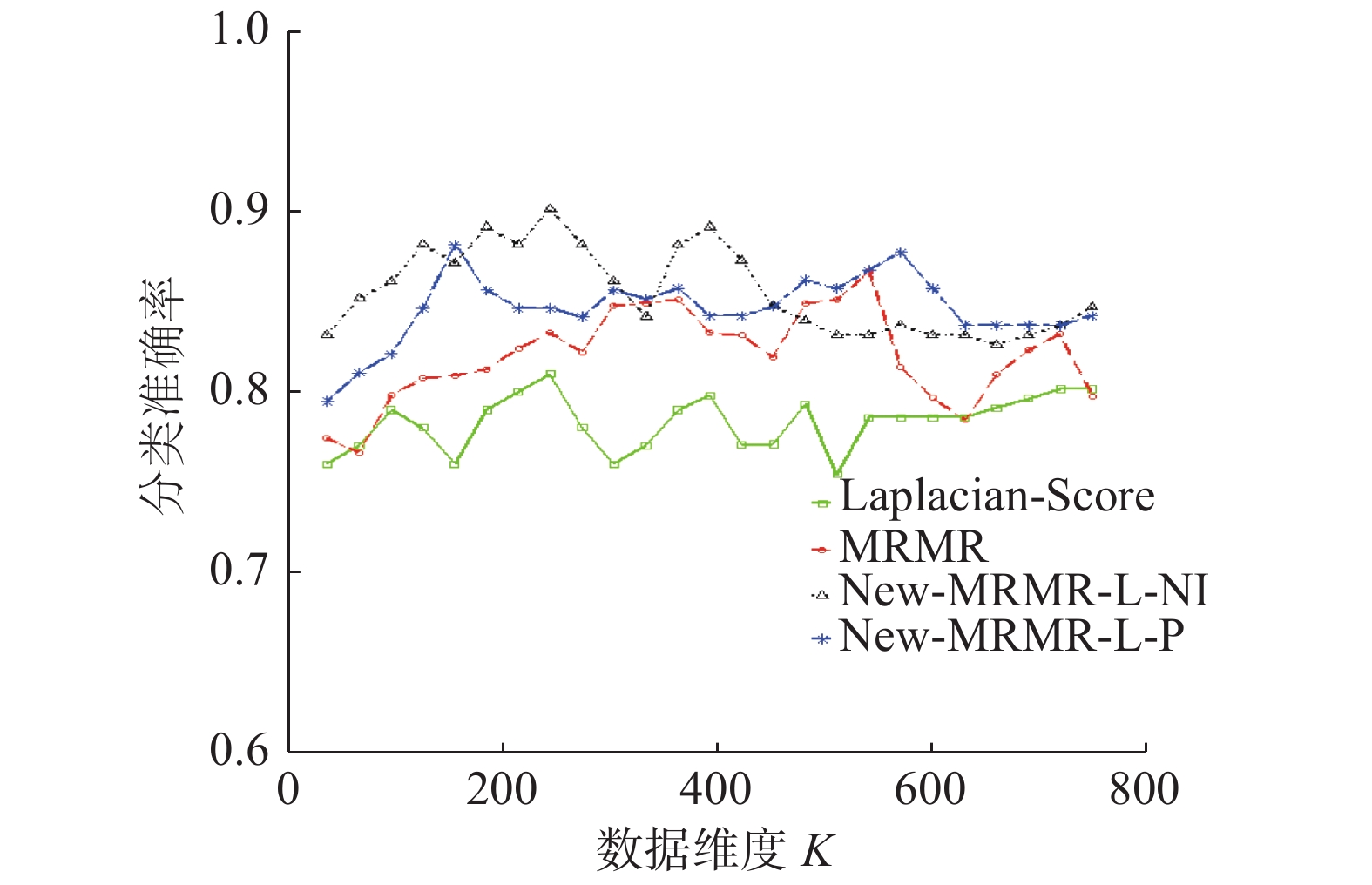
由图16可以看出,算法New-MRMR-L-P的分类准确率的曲线高于传统算法MRMR、Laplacian-Score的分类准确率曲线,并且,在维度为240时,New-MRMR-L-NI就已经达到了最大分类准确率,远小于MRMR达到最大分类准确率时所选择的特征子集数(540)。由此可见,在数据集Parkinson’s Disease上,本文新提算法特征选择效果更好。
不同维度下,本文新提算法New-MRMR-F-NI、New-MRMR-F-P以及传统算法MRMR、Fisher Score在数据集Parkinson’s Disease上的分类准确率变化趋势见图17。
|
Download:
|
| 图 16 New-MRMR-L-NI、New-MRMR-L-P、Laplacian-Score、MRMR在数据集Parkinson’s Disease上分类准确率的变化趋势 Fig. 16 Correct classification trend of New-MRMR-L-NI, New-MRMR-L-P, Laplacian-Score, MRMR on the Parkinson’s Disease dataset | |
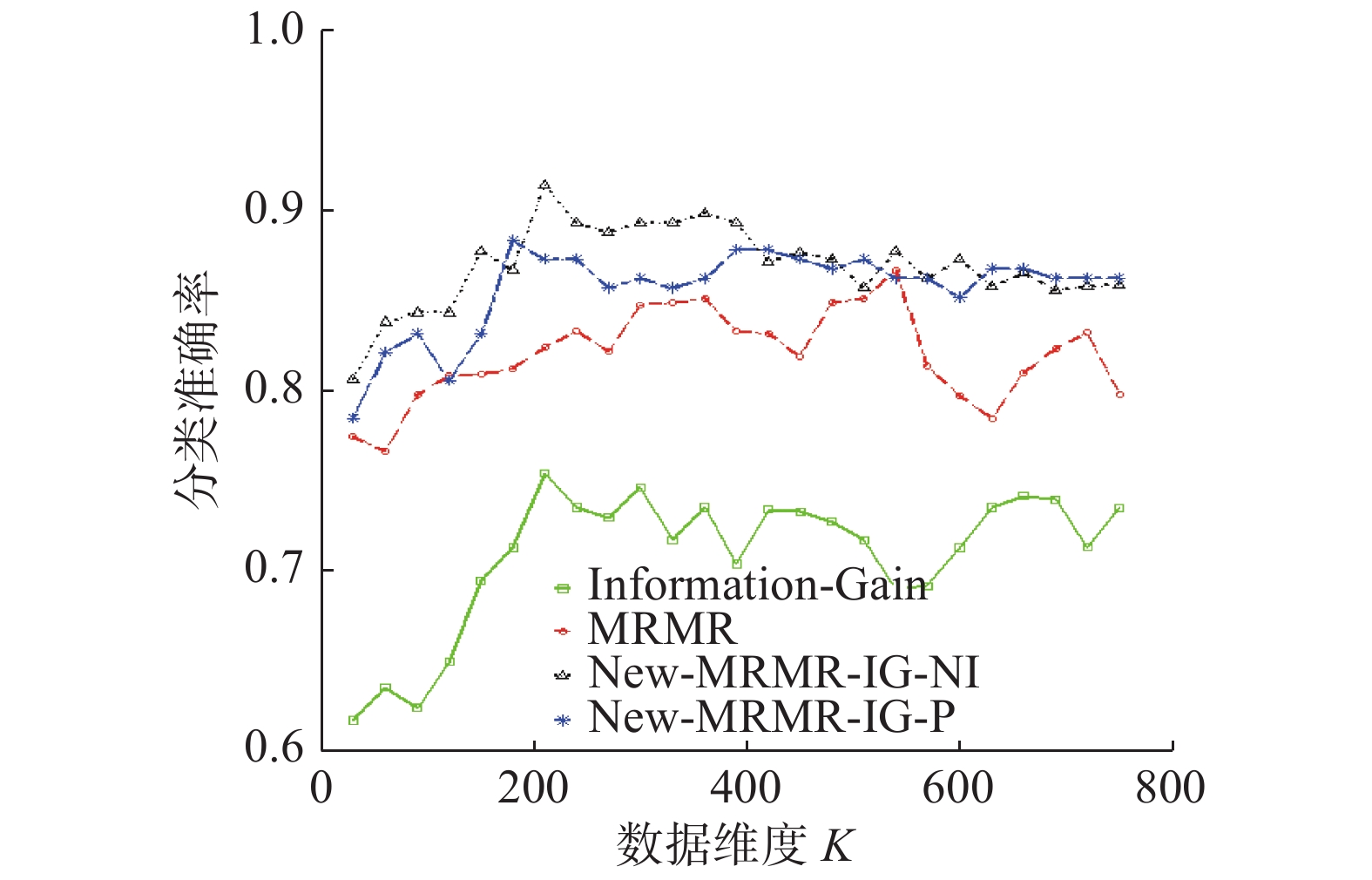
由图17可以看出,在维度为120和540时,New-MRMR-IG-P的分类准确率与算法MRMR的分类准确率较为接近,但在其余维度上,其分类准确率均大于MRMR的分类准确率。而且,在分类准确率达到最大时,New-MRMR-IG-P所选择的特征子集数仅为180,远小于MRMR的最优特征子集数。此外,New-MRMR-IG-NI的分类准确率的曲线高于算法MRMR、Information-Gain的分类准确率曲线。由上述分析可知,针对数据集Parkinson’s Disease而言,本文提出算法在整体上比传统算法选择结果更好。
|
Download:
|
| 图 17 New-MRMR-IG-NI、New-MRMR-IG-P、Information- Gain、MRMR在数据集Parkinson’s Disease上分类准确率的变化趋势 Fig. 17 Correct classification trend of New-MRMR-IG-NI, New-MRMR-IG-P, Information-Gain, MRMR on the Parkinson’s Disease dataset | |
为更加有效地证明本文新提的8种特征选择算法的有效性,以下采用成对单边T检验来证明其有效性。原假设为:本文新提算法与传统算法的特征选择效果相同;备择假设为:本文新提算法的特征选择效果优于传统特征选择算法。表7为假设检验结果,其中包含了检验的统计量,置信区间以及P值。
| 表 7 新提算法与传统算法的成对单边T检验的检验结果 Tab.7 Test results of paired unilateral T-test between the new algorithm and the traditional algorithm |
由表7可以看出,成对单边T检验的P值均小于0.05,所以拒绝原假设,故认为本文新提出的8种特征选择算法的特征选择结果优于传统特征选择算法的特征选择结果。
综上分析,从分类准确率以及假设检验的结果可以看出,本文新提出的8种特征选择算法所选择的特征子集更优,特征选择效果更好。
3 结束语虽然传统的基于特征选择的分类算法的理念已较为新颖,但是还是存在一定的提升空间。一方面,传统的基于特征选择的分类算法在特征选择过程中采用的度量特征之间冗余度以及与类别的相关度的评价准则单一;另一方面,它只考虑了特征与类别之间的相关度而忽略了冗余度;最后,其目标函数也存在缺陷,不能根据用户实际的维度需求来选择特征子集。本文针对这些问题引入了4种不同的相关度评价准则以及两种不同的冗余度评价准则,目标函数中引入了指示向量
最后需要指出,评价特征冗余度和相关度的方法有多种,本文仅用了2种评价冗余度的方法和4种评价相关度的方法,但是其他评价冗余度和相关度的方法也可以适用于New-MRMR框架,此外,新提特征选择算法在不同数据集上表现性能不同。因此,后续研究中,会更深入地研究和挖掘数据本质,尝试利用足够多的数据集以及评价相关度和冗余度的方法来深入探索具体哪种算法更适合哪种领域。
| [1] |
王娟, 慈林林, 姚康泽. 特征选择方法综述[J]. 计算机工程与科学, 2005, 27(12): 68-71. WANG Juan, CI Linlin, YAO Kangze. A survey of feature selection[J]. Computer engineering and science, 2005, 27(12): 68-71. DOI:10.3969/j.issn.1007-130X.2005.12.024 (  0) 0)
|
| [2] |
周红标, 乔俊飞. 基于高维k-近邻互信息的特征选择方法
[J]. 智能系统学报, 2017, 12(5): 595-600. ZHOU Hongbiao, QIAO Junfei. Feature selection method based on high dimensional k-nearest neighbors mutual information [J]. CAAI transactions on intelligent systems, 2017, 12(5): 595-600. (  0) 0)
|
| [3] |
徐洪峰, 孙振强. 多标签学习中基于互信息的快速特征选择方法[J]. 计算机应用, 2019, 39(10): 2815-2821. XU Hongfeng, SUN Zhenqiang. Fast feature selection method based on mutual information in multi-label learning[J]. Journal of computer applications, 2019, 39(10): 2815-2821. (  0) 0)
|
| [4] |
计智伟, 胡珉. 一种双重过滤式特征选择算法[J]. 计算机工程与应用, 2011, 47(19): 190-193, 206. JI Zhiwei, HU Min. A double-filtered feature selection algorithm[J]. Computer engineering and applications, 2011, 47(19): 190-193, 206. DOI:10.3778/j.issn.1002-8331.2011.19.053 (  0) 0)
|
| [5] |
吴红霞, 吴悦, 刘宗田, 等. 基于Relief和SVM-RFE的组合式SNP特征选择[J]. 计算机应用研究, 2012, 29(6): 2074-2077. WU Hongxia, WU Yue, LIU Zongtian, et al. Combined SNP feature selection based on Relief and SVM-RFE[J]. Application research of computers, 2012, 29(6): 2074-2077. DOI:10.3969/j.issn.1001-3695.2012.06.018 (  0) 0)
|
| [6] |
肖忆南, 谢榕, 杜娟. 基于t检验和弹性网的数据分类特征选择方法
[J]. 小型微型计算机系统, 2015, 36(10): 2213-2217. XIAO Yinan, XIE Rong, DU Juan. Feature selection method for data classification based on t-test and elastic net [J]. Journal of Chinese computer systems, 2015, 36(10): 2213-2217. DOI:10.3969/j.issn.1000-1220.2015.10.007 (  0) 0)
|
| [7] |
SRIVIDHYA S, MALLIKA R. Feature selection for high dimensional imbalanced datasets using game theory and fisher score[J]. Journal of advanced research in dynamical and control systems, 2017, 9(8): 195-202. ( 0) 0)
|
| [8] |
SAINZ L V, SAINZ J S, LÁZARO M. Oscillatory brain activity in morphological parsing of complex words[J]. Information gain from stems and suffixes, 2018, 9(5): 271. ( 0) 0)
|
| [9] |
MALDONADO S, WEBER R. A wrapper method for feature selection using support vector machines[J]. Information sciences, 2009, 179(13): 2208-2217. DOI:10.1016/j.ins.2009.02.014 ( 0) 0)
|
| [10] |
林棋, 张宏, 李千目. 一种基于MA-LSSVM的封装式特征选择算法[J]. 南京理工大学学报, 2016, 40(1): 10-16. LIN Qi, ZHANG Hong, LI Qianmu. Wrapper feature selection algorithm based on MA-LSSVM[J]. Journal of Nanjing University of Science and Technology, 2016, 40(1): 10-16. (  0) 0)
|
| [11] |
胡峰, 杨梦. 基于特征聚类的封装特征选择算法[J]. 计算机工程与设计, 2018, 39(1): 230-237. HU Feng, YANG Meng. Algorithm for wrapper feature selection based on feature clustering[J]. Computer engineering and design, 2018, 39(1): 230-237. (  0) 0)
|
| [12] |
王晓初, 王士同, 包芳, 等. 最小化类内距离和分类算法[J]. 电子与信息学报, 2016, 38(3): 532-540. WANG Xiaochu, WANG Shitong, BAO Fang, et al. Minimize intra-class distance and classification algorithm[J]. Journal of electronics & information technology, 2016, 38(3): 532-540. (  0) 0)
|
| [13] |
PENG Hanchuan, LONG Fuhui, DING C. Feature selection based on mutual information criteria of max-dependency, max-relevance, and min-redundancy[J]. IEEE transactions on pattern analysis and machine intelligence, 2005, 27(8): 1226-1238. DOI:10.1109/TPAMI.2005.159 ( 0) 0)
|
| [14] |
郭凯文, 潘宏亮, 侯阿临. 基于特征选择和聚类的分类算法[J]. 吉林大学学报(理学版), 2018, 56(2): 395-398. GUO Kaiwen, PAN Hongliang, HOU Alin. Classification algorithm based on feature selection and clustering[J]. Journal of Jilin University (science edition), 2018, 56(2): 395-398. (  0) 0)
|
| [15] |
李纯果, 张春琴, 李海峰. 基于排序互信息的无监督特征选择[J]. 河北大学学报(自然科学版), 2020, 40(2): 200-204. LI Chunguo, ZHANG Chunqin, LI Haifeng. Unsupervised feature selection based on ranking mutual information[J]. Journal of Hebei University (natural science edition), 2020, 40(2): 200-204. DOI:10.3969/j.issn.1000-1565.2020.02.013 (  0) 0)
|
| [16] |
刘云, 肖雪, 黄荣乘. 混合蒙特卡罗搜索的特征选择算法的优化[J]. 信息技术, 2020, 44(5): 28-31, 36. LIU Yun, XIAO Xue, HUANG Rongcheng. Optimization of feature selection based on hybrid Monte Carlo Tree[J]. Information technology, 2020, 44(5): 28-31, 36. (  0) 0)
|
| [17] |
周传华, 李鸣, 吴幸运. 最大相关与独立分类信息最大化特征选择算法[J]. 计算机技术与发展, 2020, 30(8): 46-52. ZHOU Chuanhua, LI Ming, WU Xingyun. Feature selection algorithm for maximizing maximum correlation and independent classification information[J]. Computer technology and development, 2020, 30(8): 46-52. DOI:10.3969/j.issn.1673-629X.2020.08.008 (  0) 0)
|
| [18] |
张俐, 王枞. 基于最大相关最小冗余联合互信息的多标签特征选择算法[J]. 通信学报, 2018, 39(5): 111-122. ZHANG Li, WANG Cong. Multi-label feature selection algorithm based on joint mutual information of max-relevance and min-redundancy[J]. Journal on communications, 2018, 39(5): 111-122. DOI:10.11959/j.issn.1000-436x.2018082 (  0) 0)
|
| [19] |
李扬, 顾雪平. 基于改进最大相关最小冗余判据的暂态稳定评估特征选择[J]. 中国电机工程学报, 2013, 33(34): 179-186. LI Yang, GU Xueping. Feature selection for transient stability assessment based on improved maximal relevance and minimal redundancy criterion[J]. Proceedings of the CSEE, 2013, 33(34): 179-186. (  0) 0)
|
| [20] |
胡敏杰, 林耀进, 王晨曦, 等. 基于拉普拉斯评分的多标记特征选择算法[J]. 计算机应用, 2018, 38(11): 3167-3174. HU Minjie, LIN Yaojin, WANG Chenxi, et al. Multi-label feature selection algorithm based on Laplace score[J]. Journal of computer applications, 2018, 38(11): 3167-3174. DOI:10.11772/j.issn.1001-9081.2018041354 (  0) 0)
|
| [21] |
陈谌, 梁雪春. 基于基尼指标和卡方检验的特征选择方法[J]. 计算机工程与设计, 2019, 40(8): 2342-2345, 2360. CHEN Chen, LIANG Xuechun. Feature selection method based on Gini index and chi-square test[J]. Computer engineering and design, 2019, 40(8): 2342-2345, 2360. (  0) 0)
|
| [22] |
徐明, 高翔, 许志刚, 等. 基于改进卡方统计的微博特征提取方法[J]. 计算机工程与应用, 2014, 50(19): 113-117, 142. XU Ming, GAO Xiang, XU Zhigang, et al. Microblog feature extraction method based on improved chi-square statistics[J]. Computer engineering and applications, 2014, 50(19): 113-117, 142. DOI:10.3778/j.issn.1002-8331.1312-0375 (  0) 0)
|
| [23] |
BOMZE I M, DE KLERK E. Solving standard quadratic optimization problems via linear, semidefinite and copositive programming[J]. Journal of global optimization, 2002, 24(2): 163-185. DOI:10.1023/A:1020209017701 ( 0) 0)
|
| [24] |
LIU Hairong, YANG Xingwei, LATECKI L J, et al. Dense neighborhoods on affinity graph[J]. International journal of computer vision, 2012, 98(1): 65-82. DOI:10.1007/s11263-011-0496-1 ( 0) 0)
|
| [25] |
DORA S, SUBRAMANIAN K, SURESH S, et al. Development of a self-regulating evolving spiking neural network for classification problem[J]. Neurocomputing, 2016, 171: 1216-1229. DOI:10.1016/j.neucom.2015.07.086 ( 0) 0)
|
 2021, Vol. 16
2021, Vol. 16


