2. 江南大学 物联网工程学院,江苏 无锡 214122
2. School of the Internet of Things Engineering, Jiangnan University, Wuxi 214122, China
随着新型传感器、数据采集设备和系统的迅速发展,一些先进工业过程积累了丰富的过程数据,使得多元统计过程监控(multivariate statistical process monitoring, MSPM)技术不断进步[1-3]。其中的主成分分析(principal component analysis, PCA)和k近邻方法(k-nearest neighbor, kNN)是较为基础的方法,得到了大量的研究和应用[4-7]。
作为一种降维技术,PCA通过将数据投影到低维空间以有效地处理高维和线性相关的数据,通过建立主元子空间和残差子空间的统计量进行过程监控。但是,对于具有非线性和非高斯特性的过程数据,PCA方法可能无法进行有效的监测。He等[8]提出基于k近邻规则的故障监测算法,该算法不局限于线性和高斯数据,使用局部近邻距离度量样本相似度,根据故障样本和正常样本的相似度不同实现故障监测。但是由于每一个样本都需要计算与其他样本的距离,计算量明显增大。为此,学者们提出了许多改进的kNN故障监测算法。例如:文献[9]利用改进K-means聚类将原始建模数据分成多个类,对每个类分别建立kNN监测模型,大大缩短故障检测时间;文献[10]提出将动态PCA和kNN相结合的故障诊断方法,先建立主元模型,再利用kNN获取样本的k个近邻,明显提高了故障的报警率;文献[11]针对kNN模型不能及时更新的问题,提出了一种特征空间自适应k近邻故障检测方法,有效提高模型实时监测的能力;文献[12]考虑到多模态过程数据具有多中心、方差差异大等特点,通过构造标准距离,实现了kNN方法对多模态数据的有效监测。
由于现代工业过程具有多个操作单元、变量关系复杂等特点,全局建模策略无法更加准确地对过程建模,多块建模策略成为有效的解决方案。Macgrego等[13]首次提出了多块投影方法,为每个子块以及整个过程建立监测模型。文献[14]采用Jarque-Bera(J-B)检测方法并利用变量间的Hellinger距离获得高斯和非高斯子块,然后分别采用不同的方法进行建模,并对每个子块的统计量进行加权得到总的联合指标实现在线监控;文献[15]将整个过程划分成多个子块单元,然后在每个子块单元内分别进行相对变换独立主元分析处理,实现故障排查和识别;Ge等[16]提出分布式PCA的全流程过程监控方法,利用过程变量在主元方向上的贡献度划分子块,有效地提高了监控效果。
在信息论领域里,互信息(mutual information, MI)是一种相对成熟的统计分析技术,可以通过信息熵度量两个随机变量之间的依赖性,并且这种度量不局限于数据线性关系的假设条件[17-19],已经在数据分析与建模领域得到了比较多的应用。文献[20]利用变量间的互信息定义数据的相关性矩阵,为过程数据建立更为精确的描述模型。文献[21]利用互信息矩阵之和替代传统主成分分析中的协方差矩阵,计算其特征向量与特征值,得到较主成分分析更好的降维效果。文献[22]利用高维k近邻互信息方法,有效解决建模过程中的特征选择问题。
综上所述,为了更加充分地对复杂过程变量之间的关系进行描述,并提取过程的局部特征,利用多块建模策略,提出一种基于互信息的k近邻故障监测算法。该算法在计算训练集样本间的互信息基础上,根据互信息值的大小将变量分成多个子块,对每个子块建立相应的kNN模型,并利用核密度估计方法求出控制限,最后利用贝叶斯推断将各子块的监测结果融合,使得整体的监测效果更为直观。本文进一步采用基于马氏距离的故障诊断方法,通过计算样本中各变量与其均值的马氏距离,找出引发故障的源变量并对其隔离。利用田纳西−斯曼(Tennessee Eastmann, TE)和实际高炉炼铁过程数据,对所提方法进行了仿真,并与几种传统监测方法进行了对比,验证了本文方法的性能。
1 相关算法介绍 1.1 kNN算法k近邻算法是数据挖掘和数据分类中最常用的方法之一,传统kNN算法通过寻找k个近邻样本,采用投票的方法确定待测样本的类别。基于kNN的故障监测,其基本思想是通过计算近邻距离度量样本间的相似度,若样本点与训练集中前k个近邻样本距离的平方和大于正常样本的相应距离平方和,则该样本点被定义为故障点。监测过程包括模型建立和故障检测两步,具体描述如下:
1)建立模型
首先在训练集中,寻找每个样本
| $ D_i^2 = \sum\limits_{j = 1}^k {d_{ij}^2} ,\;d_{ij}^2 = {\left\| {{x_i} - x_i^j} \right\|^2} $ | (1) |
式中:
2)在线故障检测
首先,在训练集中寻找待测样本
在概率论和信息论领域,互信息是一种非常实用的信息度量方法。它可以度量两个随机变量相互依赖的程度,表示出两个变量共享的信息,反映两个变量的相关性[21],这种度量同样适用于非线性相关的变量。对于密切相关的变量,它们拥有较大的互信息。令随机变量
| $H(X) = - \sum\limits_{x \in X} {p(x)\log } p(x)$ | (2) |
联合熵为
| $H(X,Y) = - \sum\limits_{x \in X} {\sum\limits_{y \in Y} {p(x,y)\log p(x,y)} } $ | (3) |
则变量
| $I(X;Y) = \sum\limits_{y \in Y} {\sum\limits_{x \in X} p } (x,y)\log \frac{{p(x,y)}}{{p(x)p(y)}}$ | (4) |
若
在实际的工业过程中,变量之间大多是线性、非线性共存,高斯、非高斯混合分布,传统的PCA与kNN方法往往从全局的角度出发,系统的本质特征无法得到充分的展示。因此,首先对变量进行MI计算,将互信息大的多个变量放在一起组成子块,使得子块内的变量拥有更多相同的信息,最大化地反映变量的一个或者多个局部特征,同时也大大降低了监控过程的复杂度,从而有效地提高系统的监控效果。
对于训练集
| ${I_{ij}} = I({x_i},{x_j})(i = 1,2, \cdots, m;j = 1,2, \cdots, m)$ | (5) |
若

|
Download:
|
| 图 1 本文所采用的多块建模方法 Fig. 1 Multi-block modeling method in this paper | |
针对划分好的子块,建立kNN监测模型。寻找各子块中样本的k近邻样本集,记做
| $T({x_{ib}},k) = \{ x_{ib}^1,x_{ib}^2, \cdots ,x_{ib}^k\} (b = 1,2, \cdots ,B)$ | (6) |
其中
然后计算每个子块中样本与其k近邻样本的欧式距离平方和作为子块统计量,即
通过核密度估计法(kernel density estimation, KDE)估计每个统计量的概率密度,再绘制累加概率密度图,根据置信度确定每个块中统计量的控制限。由于子块数目较多且产生多个监测结果,无法得到一个直观的最终决策,因此,采用贝叶斯融合策略[23],将正常事件和故障事件与贝叶斯推断相结合,从概率的角度将所有子块的统计量组合成一个新的统计量来得到最终的监测结果。
在贝叶斯推断(bayesian inference, BI)中,测试样本
| ${P_{{D^2}}}({\rm{F}}|{x_{{\rm{test}}}},b) = \frac{{{P_{{D^2}}}({x_{{\rm{test}},b}}|{\rm{F}}){P_{{D^2}}}({\rm{F}})}}{{{P_{{D^2}}}({x_{{\rm{test}},b}})}}$ | (7) |
| $\begin{array}{c} {P_{{D^2}}}({x_{{\rm{test}},b}}) = {P_{{D^2}}}({x_{{\rm{test}},b}}|{\rm{N}}){P_{{D^2}}}({\rm{N}}) + {P_{{D^2}}}({x_{{\rm{test}},b}}|{\rm{F}}){P_{{D^2}}}({\rm{F}}) \end{array} $ | (8) |
式中:
| $\begin{array}{l} {P_{{D^2}}}({x_{{\rm{test}},b}}|{\rm{N}}) = {{\rm{e}}^{ - D_{b,{\rm{new}}}^2/D_{b,\lim }^2}} \\ {P_{{D^2}}}({x_{{\rm{test}},b}}|{\rm{F}}) = {{\rm{e}}^{ - D_{b,\lim }^2/D_{b,{\rm{new}}}^2}} \end{array} $ | (9) |
其中,“N”和“F”分别代表“normal”和“fault”,即正常样本和故障样本。
| ${{\rm{BIC}}_{{D^2}}} = \sum\limits_{b = 1}^B {\left\{ {\left. {\frac{{{P_{{D^2}}}({x_{{\rm{test}},b}}|{\rm{F}}){P_{{D^2}}}({\rm{F}}|{x_{{\rm{test}},b}})}}{{\displaystyle\sum\limits_{j = 1}^B {{P_{{D^2}}}({x_{{\rm{test}},j}}|{\rm{F}})} }}} \right\}} \right.} $ | (10) |
BIC统计量的控制限由
当检测到故障后,需要找出引发故障的源变量并对其进行分离。计算数据样本中各变量与其均值的马氏距离[17],即加权计算数据样本中各变量相较于其均值的偏移量,偏移量越大,说明该变量对于故障贡献越大。该方法可以有效辨识引发故障的源变量,即发生故障的根本原因。
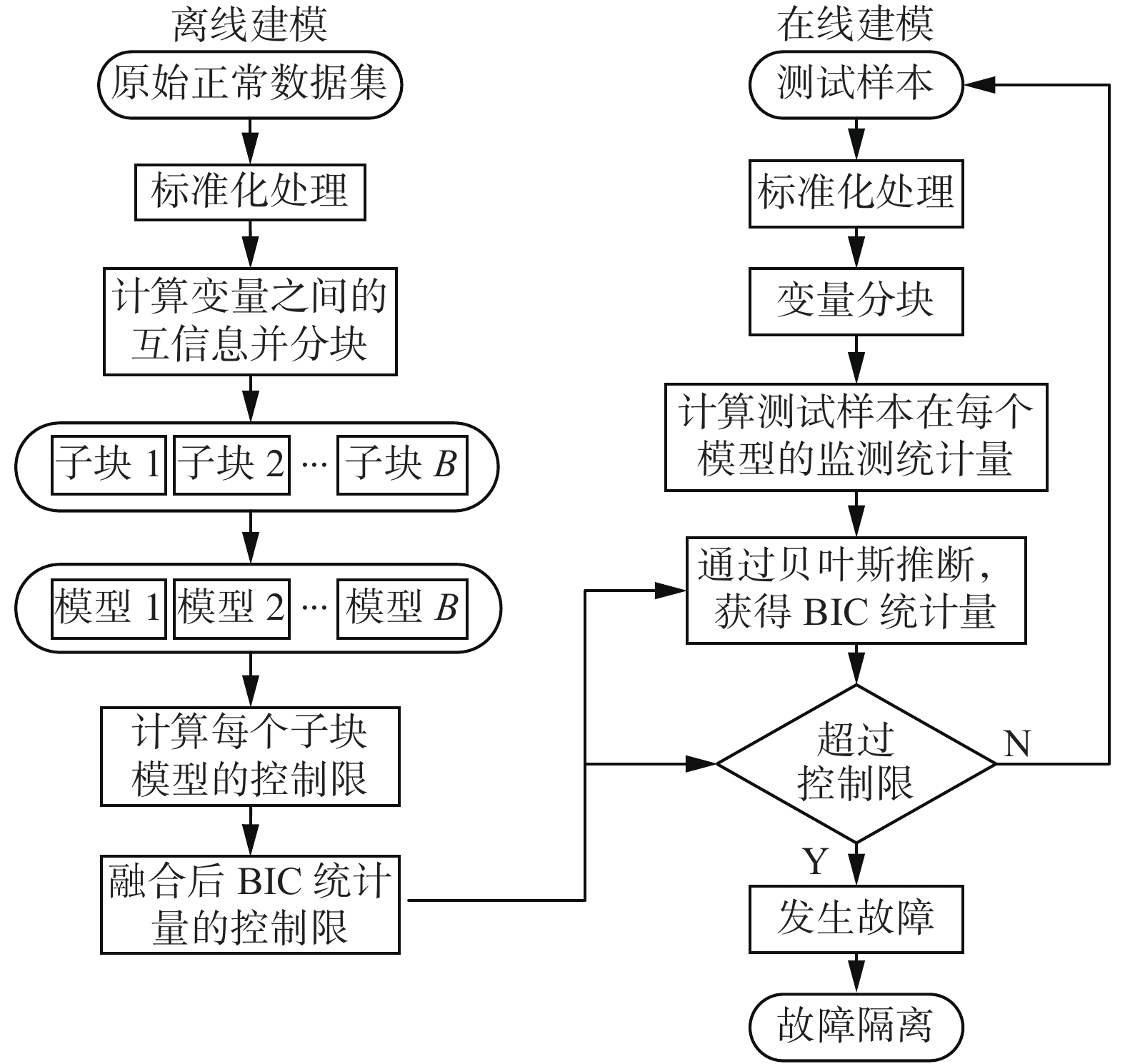
2.3 基于MI-MBkNN故障监测算法流程基于互信息的多块kNN故障监测算法流程如图2所示,具体步骤描述如下。
|
Download:
|
| 图 2 基于MI-MBkNN的故障监测流程 Fig. 2 Fault monitoring flowchart based on MI-MBkNN | |
1) 获取正常训练数据,并对其进行标准化处理;
2) 计算两两变量间互信息,根据2.1节所述方法对变量进行分块,得到各个子块;
3) 对每个子块分别建立kNN模型,利用核密度估计方法确定各自的故障控制限;
4) 对于新来的测试样本,同样对其进行标准化处理和分块处理;
5) 对每个子块进行kNN故障监测,获得每个子块的监测结果;
6) 通过贝叶斯推断方法,利用式(10)将各个子块的统计量组合成为一个新的BIC统计量,并根据置信度确定控制限,当BIC超过控制限时则判断发生了故障,否则正常;
7) 监测到故障后计算数据样本中各变量与其均值的马氏距离,确定故障变量及故障块,分离出对故障影响最大的变量。
3 仿真实验 3.1 TE过程仿真TE仿真平台是基于实际工业过程的仿真平台,它由反应器、冷凝器、压缩机、分离器和汽提塔5个主要操作单元组成[24-25]。该过程包含的变量数目多,且变量与变量之间的关系复杂。主要分为12个操作变量,41个测量变量,21个预设定的故障。本文选取22个过程测量变量和11个操作变量(不包括搅动速度)用于监测方法建模和监测性能测试,具体变量描述见文献[16]。对于每种故障,训练集用于训练建立模型,测试集用来检验模型监测性能。训练集和测试集均采用960个样本,测试集中故障从第161个样本点引入。
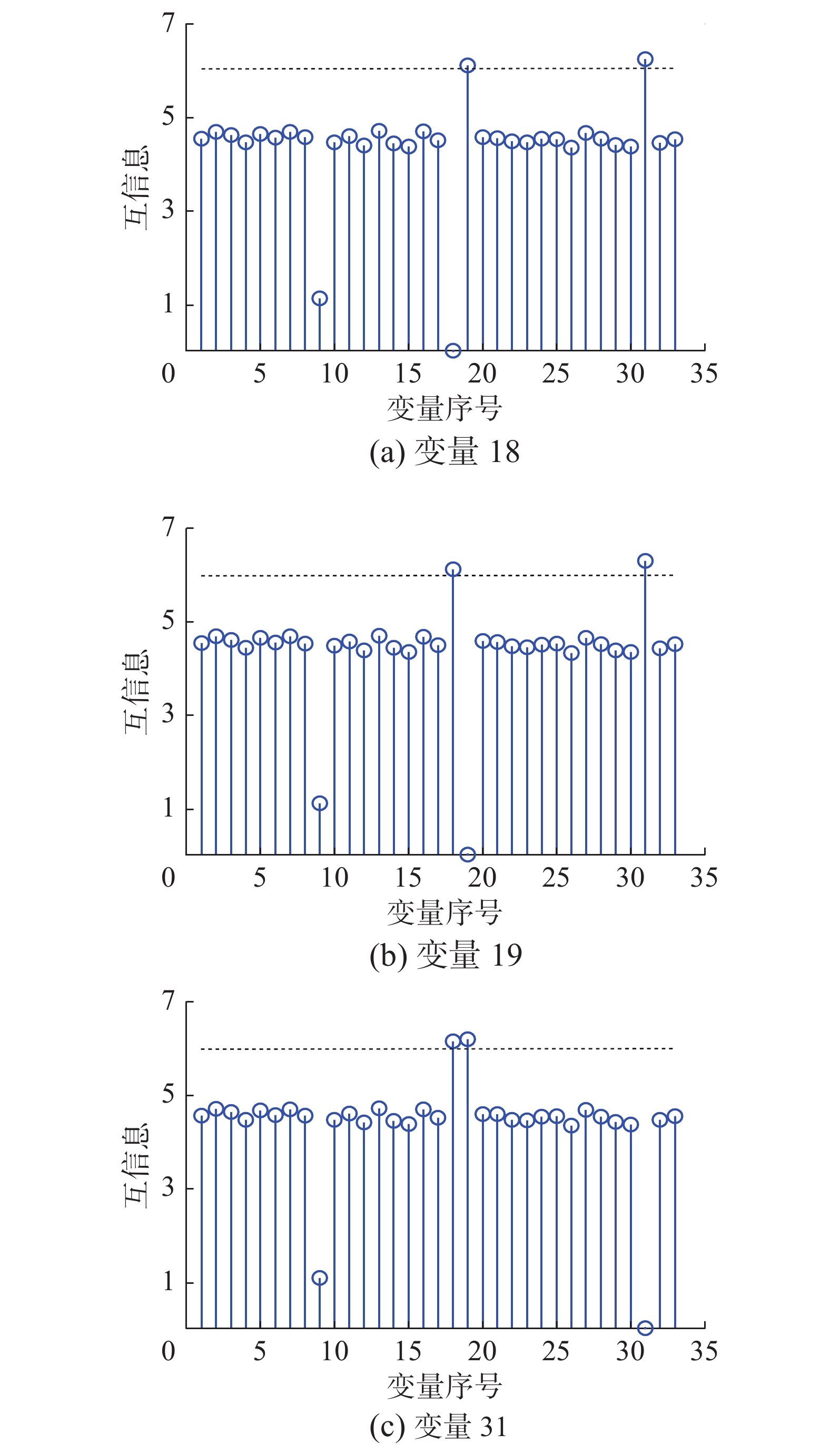
为了建立多块模型,对选取的过程变量和操作变量进行互信息的计算并进行分块,分块结果如表1所示。图3分别展示了变量18、变量19、变量31与其他32个变量间的互信息,图中的虚线表示为1.3倍互信息中值,互信息超过虚线的变量即为与该变量具有较大互信息的变量。因此将变量18、变量19和变量31放到相同的子块中。图4分别展示了变量10、变量17、变量28、变量33与其他32个变量间的互信息,因此将它们组成一个子块。
| 表 1 TE过程子块的划分 Tab.1 Blocks division in the TE process |
|
Download:
|
| 图 3 子块4中各变量间的互信息 Fig. 3 Mutual information between variables in block 4 | |

|
Download:
|
| 图 4 子块5中各变量间的互信息 Fig. 4 Mutual information between variables in block 5 | |
表2给出了7个子块对21种故障的报警率、平均报警率和平均误报率。从报警率来看,对于大多数故障类型,子块7的监测结果要优于其他6个子块。子块5的平均报警率很低,但是对于某些故障(如故障5),子块5的报警率达96%,对整个的监测起到了关键的作用。对于不同的故障,由于某些子块拥有较高的报警率和较低的误报率,使得最终融合的BIC统计量表现了良好的监测性能。从对21种故障的监测结果来看,对于大部分故障,融合后的监测性能有了明显的提高。
| 表 2 TE过程各故障报警率 Tab.2 Alarm rates of TE process |
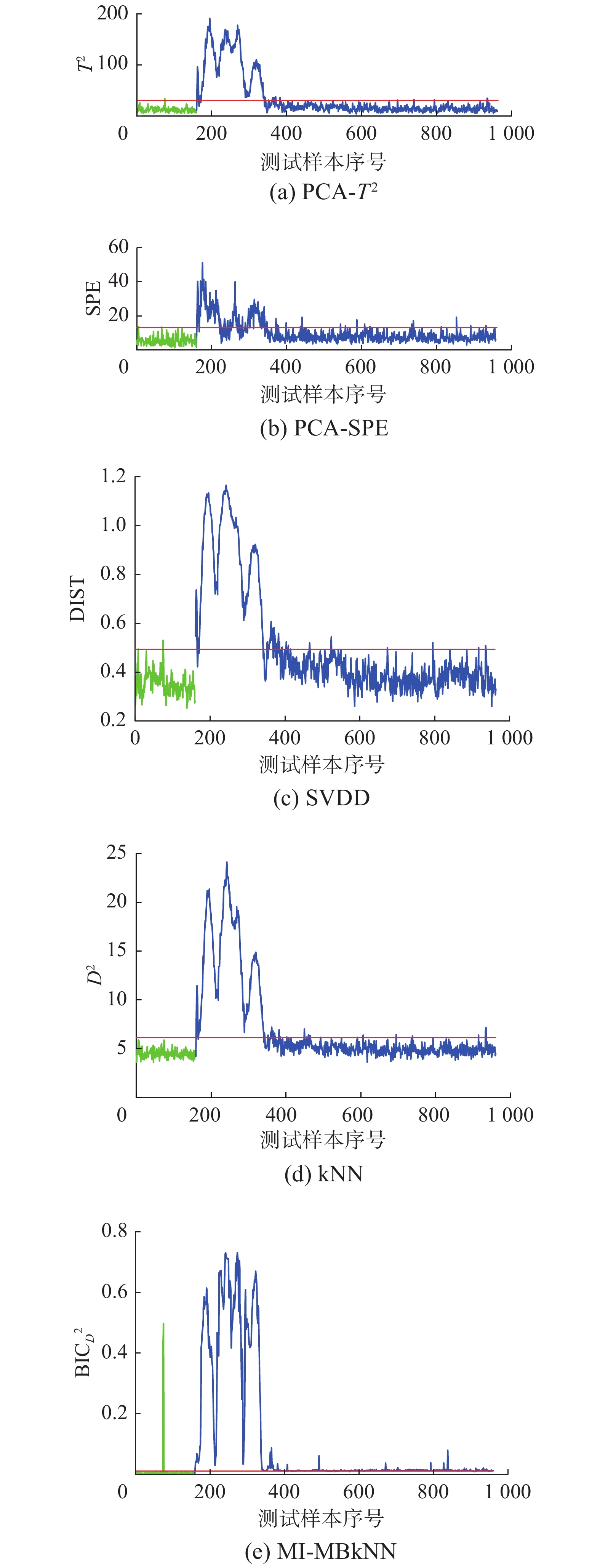
表3给出了TE过程21种故障在不同监测方法下的报警率和误报率,主要方法包括传统PCA、SVDD、kNN和本文提出的MI-MBkNN。从仿真结果可以看出,对于绝大多数故障类型,MI-MBkNN能取得优越于其他3种方法的监测结果,尤其是对故障5、故障10、故障 16、故障 19的监测。图5以故障5为例展示了详细的监测过程与结果。
| 表 3 几种现有的监测方法性能比较 Tab.3 Comparison of some state of monitoring methods |
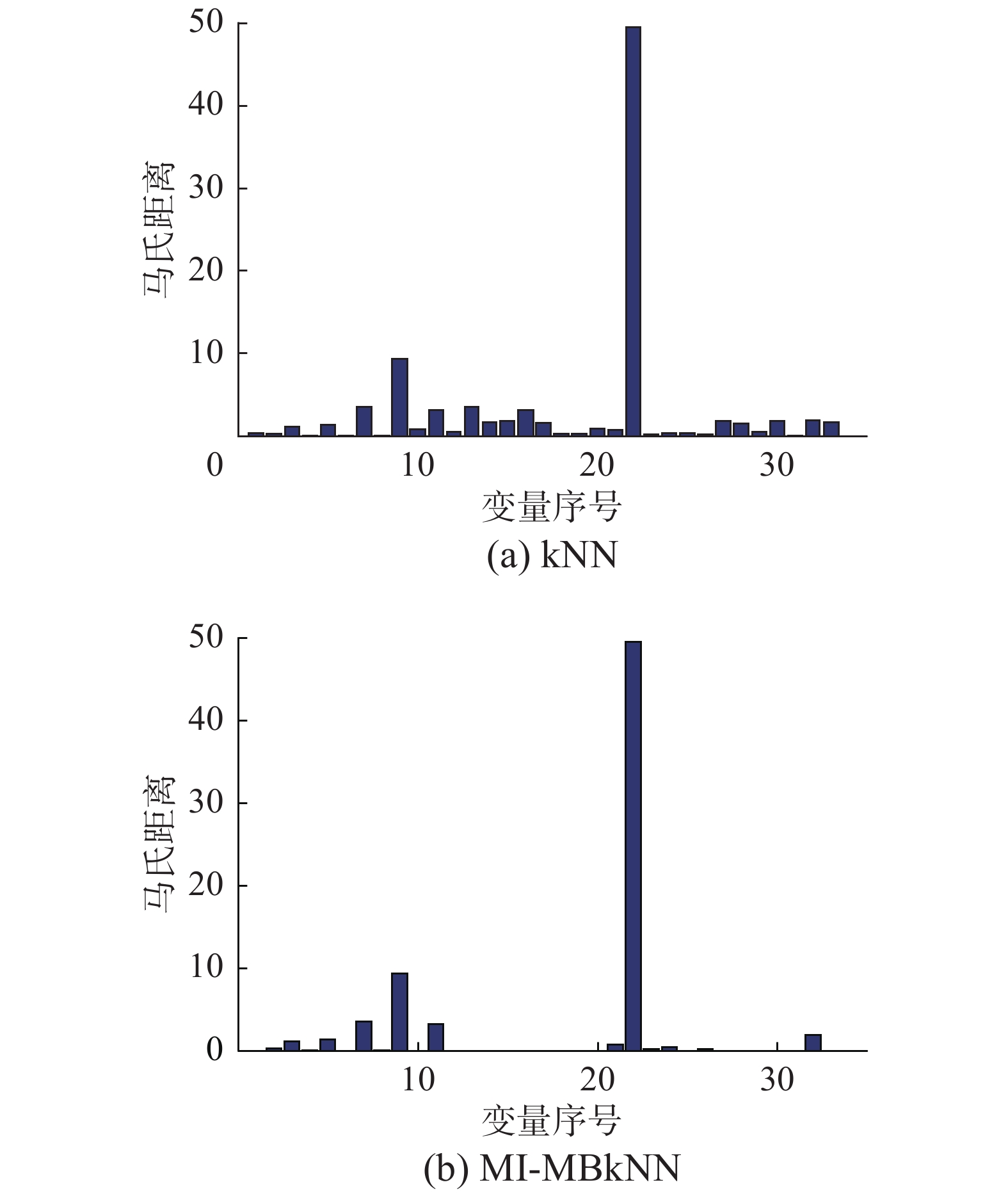
TE过程中的故障5涉及冷凝器冷却水入口温度的变化,当故障发生时,从冷凝器到气/液分离器的出口流量增加,使温度升高。使用传统PCA、kNN、SVDD方法和本文提出的MI-MBkNN的监测结果如图5所示。从图5(a)~(d)可以发现,在故障开始时就可以检测出故障,但是在大约350个样本的时候,统计量出现低于控制限的情况,导致故障的漏报。由于该故障是局部故障,因此很难在全局模型中检测到,为了更好地找出故障的原因,图6给出了数据样本在第161个样本点(故障最开始处)的各变量与其均值中心的马氏距离。
|
Download:
|
| 图 5 故障5监测结果 Fig. 5 Monitoring result of fault 5 | |
|
Download:
|
| 图 6 第161样本点故障5的变量识别结果 Fig. 6 Variables identification results of fault 5 on the 161th point | |
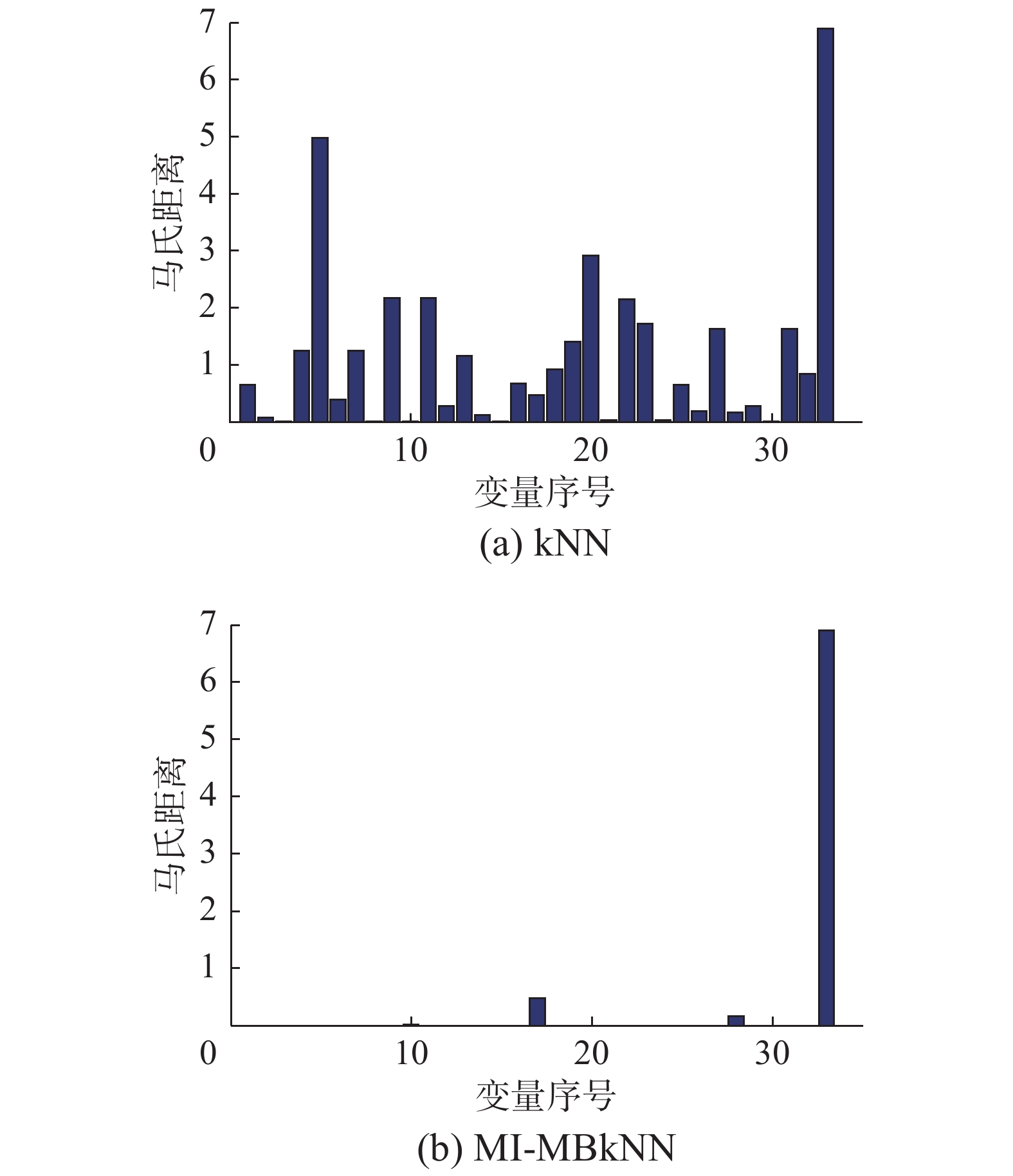
可以看出这两个模型都能正确识别变量在过程中的变化,如分离器冷却水出口温度的变化(变量22),反应器温度(变量9),产品分离器温度(变量11)和反应器冷却水流量(变量32)。但是在350个样本点后,从图7(第400个样本点)可以看出,kNN无法识别出冷凝器冷却水流量的变化(变量33),但是MI-MBkNN模型可以成功识别,因此MI-MBkNN对故障5表现出了优越的监测效果。
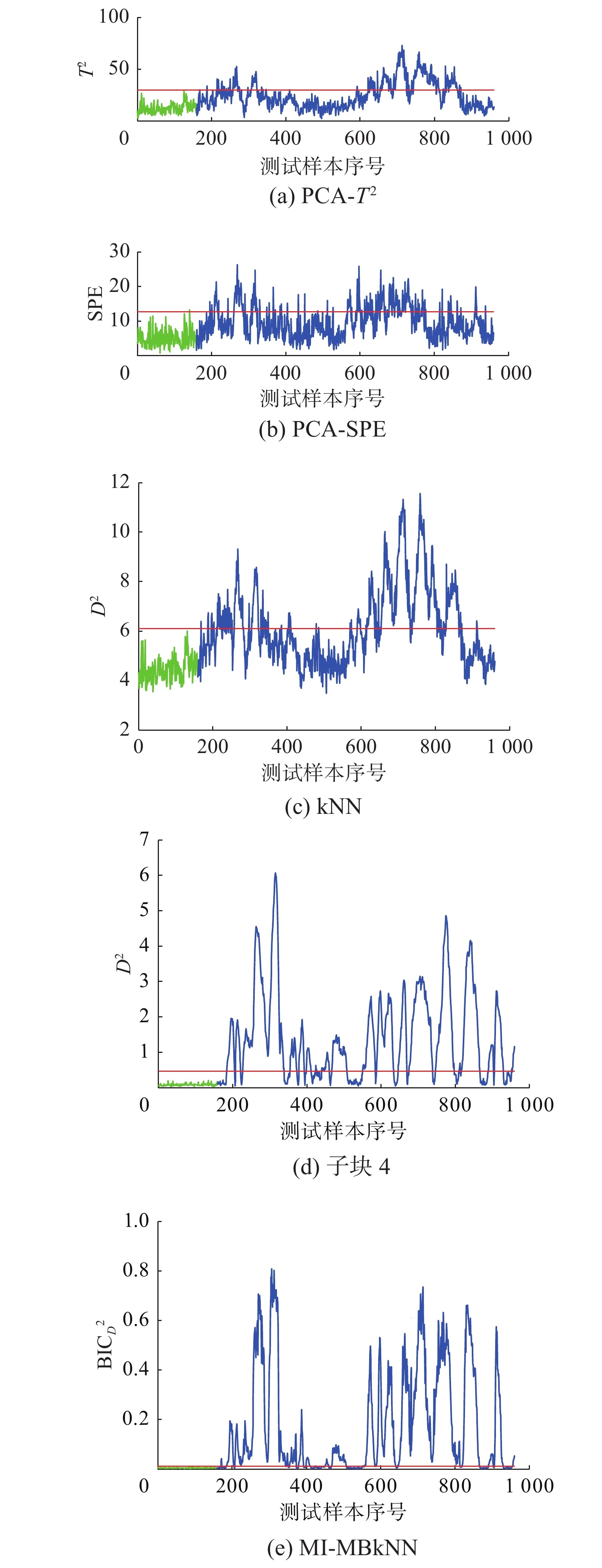
故障10是流2(C进料)中温度的随机变化,从图8中可以看出350~650样本,传统的监测方法很难监测到故障,但是MI-MBkNN却能很好地检测出来。
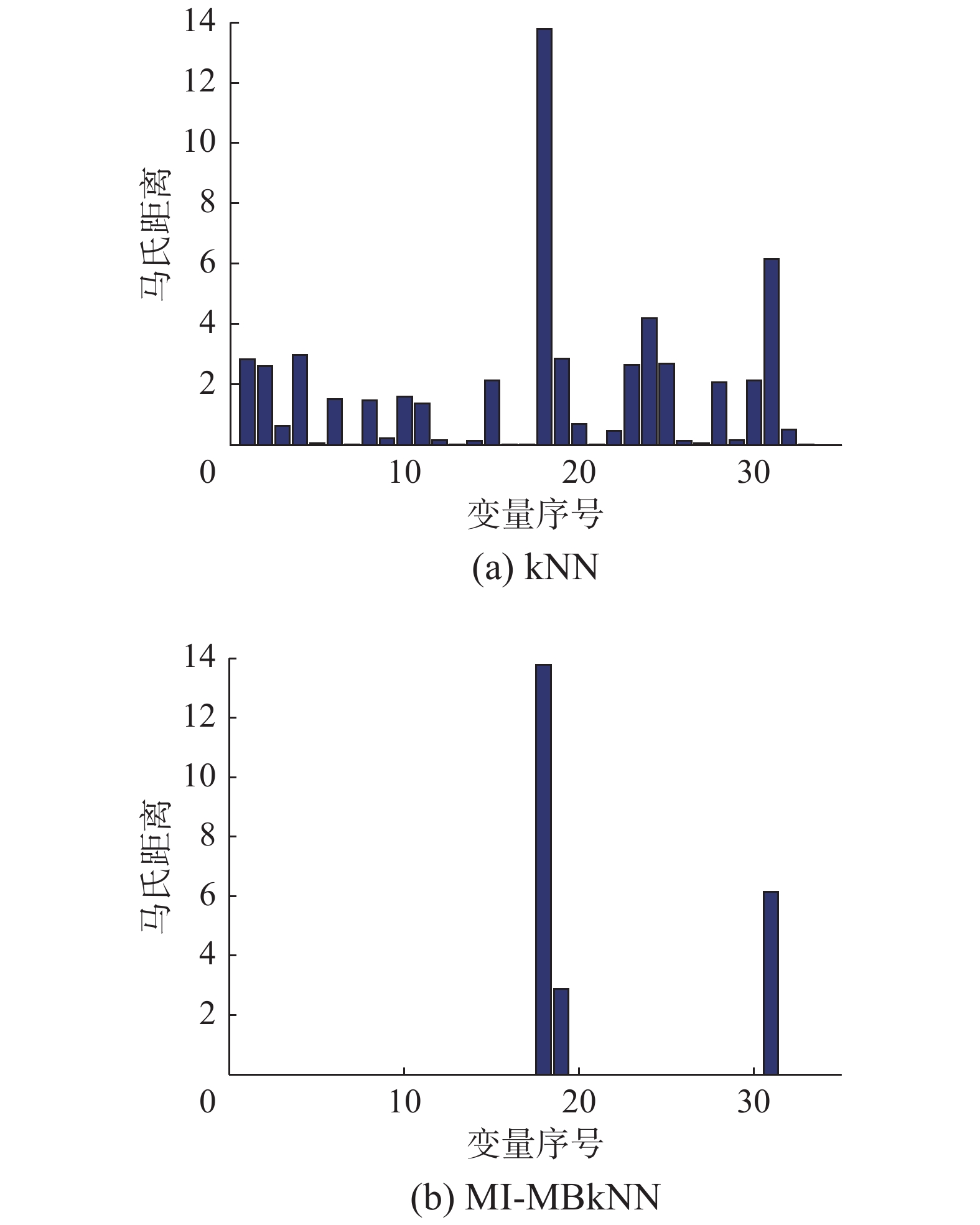
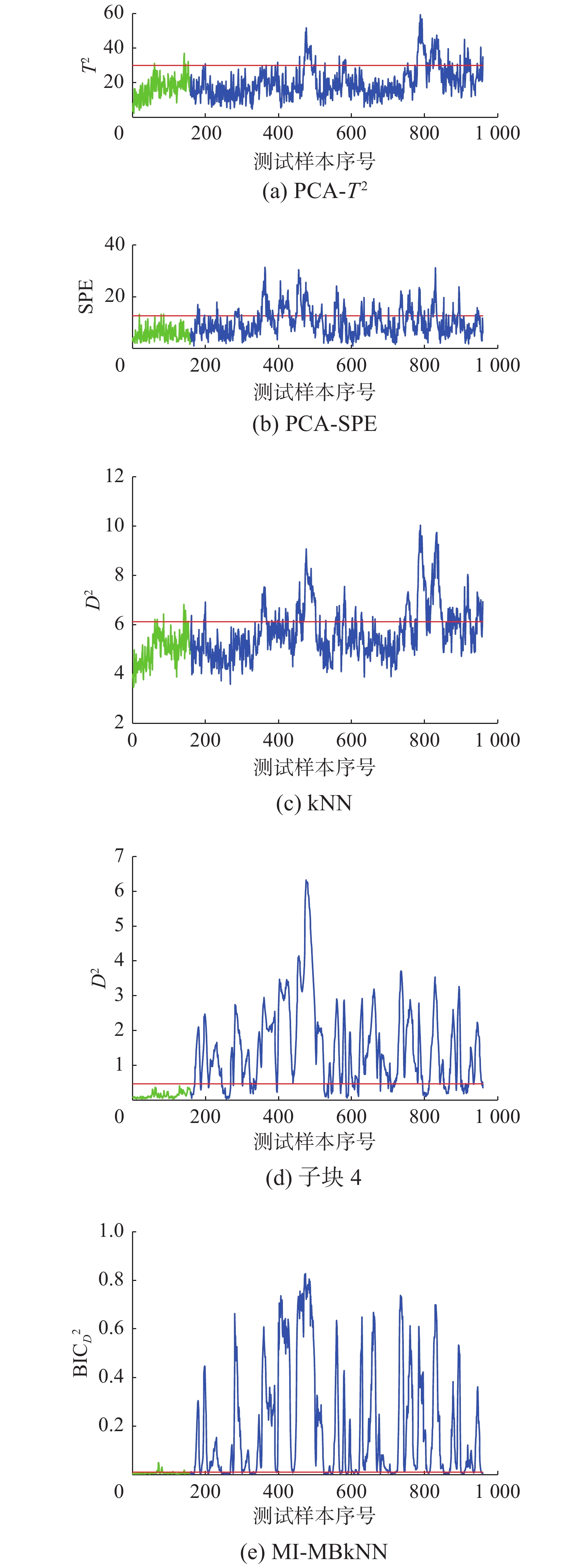
为了更好地找出引发故障的源变量,图9(a)和(b)分别给出了使用kNN和MI-MBkNN方法时数据样本在第400样本点处的各变量与其均值中心的马氏距离,可以发现MI-MBkNN在寻找故障源变量方面提供更重要的指导,即汽提塔温度(变量18),汽提塔蒸汽流量(变量19),汽提塔蒸汽阀的变量(变量31)是引起故障10的原因,因此子块4的监测效果明显优于其他子块。通过贝叶斯融合后,使得整体的监测效果得到了很高的提升。因此本文提出的方法对故障10的监测效果优于其他几种传统的监测方法。图10对比了PCA、kNN、本文方法的子块4和MI-MBkNN的对故障16的监测结果,传统kNN方法在统计量上只能从450~500样本和790~840样本之间做到相对持续的报警,而本文监测方法从故障引入点处开始就能做到大范围的持续报警。
|
Download:
|
| 图 7 第400样本点故障5的变量识别结果 Fig. 7 Variables identification results of fault 5 on the 400th point | |
|
Download:
|
| 图 8 故障10监测结果 Fig. 8 Monitoring result of fault 10 | |
|
Download:
|
| 图 9 变量识别结果 Fig. 9 Variables identification results | |
图11给出了对故障16的诊断结果,可以看出,相比于kNN,本文方法对故障提供更清晰的识别结果,即引起该故障的源变量是变量
|
Download:
|
| 图 10 故障16监测结果 Fig. 10 Monitoring result of fault 16 | |

|
Download:
|
| 图 11 变量识别结果 Fig. 11 Variables identification results | |
为了达到高炉炼铁过程节能降耗的目的,必须保证铁水的生产质量和产量。当气体流动不稳定时会影响碳的燃烧,最终导致炉腹架空,产生悬挂故障。若没有及时检测出悬挂故障,将会导致热应力和内部的气体压力过大,使得顶部结构受到严重的破损。本节考虑了实际情况中悬挂故障的存在,采集正常工况下的8个过程变量的2 000个样本作为训练样本,同时采集了悬挂故障下的1 900个样本作为测试样本。在悬挂故障下,炉内的温度和压力增加,炉顶的一氧化碳和二氧化碳浓度上升,氢气的浓度下降。为了更好地表现变量的特性,表4给出了8个过程变量的描述,图12给出了8个变量的变化曲线图,其中前2 000个样本为正常样本,后1 900个样本为故障样本。
| 表 4 悬挂故障监测中选择的过程变量 Tab.4 Process variables selected for monitoring of the hanging fault |

|
Download:
|
| 图 12 高炉过程各变量曲线图 Fig. 12 Curves of Blast furnace process variable | |
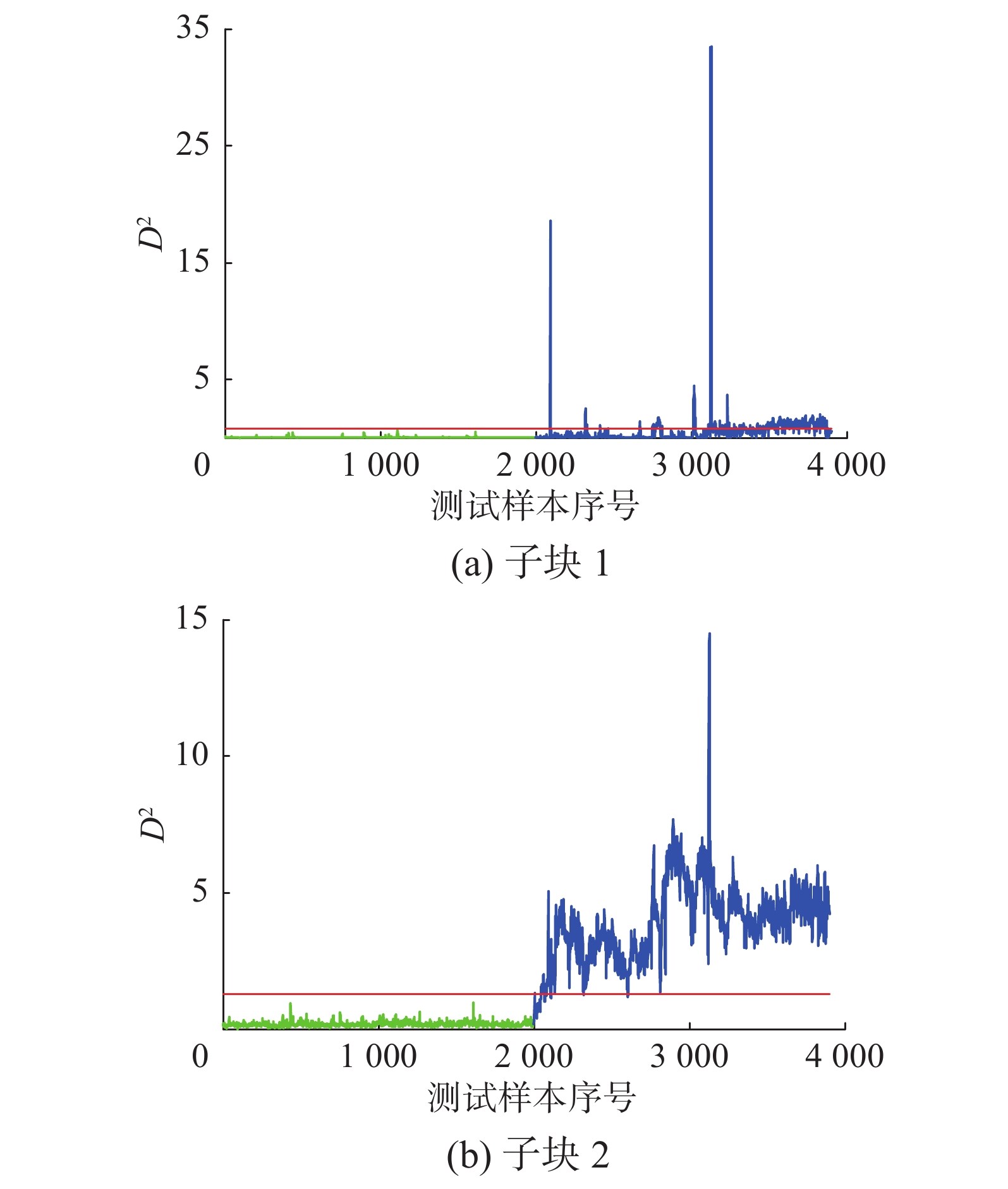
利用上述所提分块方法将8个变量分成两个子块,子块1为

|
Download:
|
| 图 13 高炉过程子块1变量间的互信息 Fig. 13 Mutual information between variables in blast furnace process block 1 | |
| 表 5 不同方法的监测性能比较 Tab.5 Comparison of monitoring performance of two methods in blast furnace process |
|
Download:
|
| 图 14 高炉过程子块1和子块2的监测性能比较 Fig. 14 Comparison of monitoring performance of block1 and block2 in blast furnace process | |
|
Download:
|
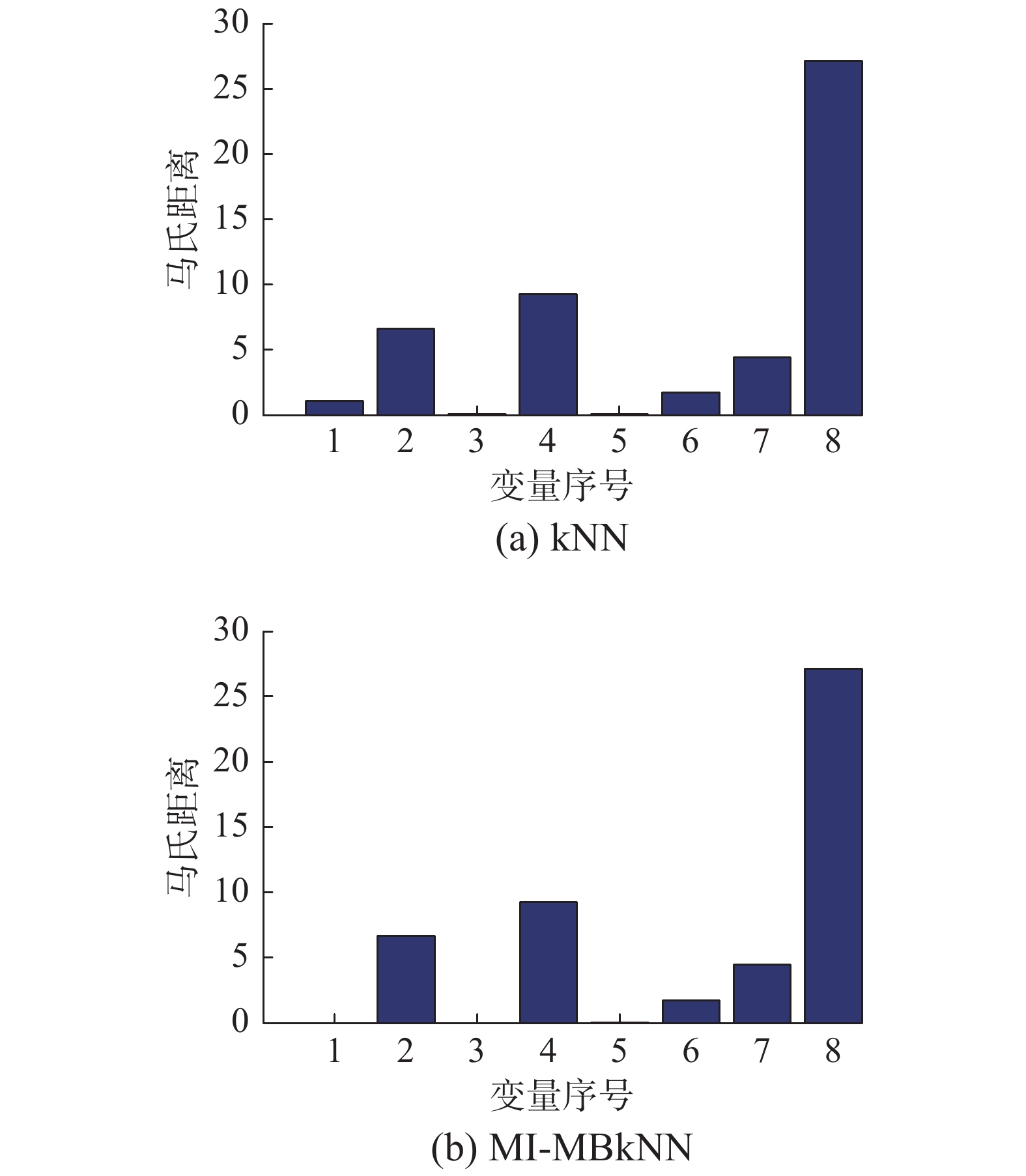
| 图 15 高炉过程变量识别结果 Fig. 15 Variables identification results of the blast furnace process | |
本文提出了一种基于互信息的多块k近邻故障监测方法,使用互信息对过程变量进行划分,并在每个子块中建立基于kNN的故障监测模型,所提方法反映了过程的更多局部特征,所以更易于故障的监测和诊断。将所提方法应用于TE过程和实际高炉炼铁过程中,均取得了比较好的监测效果。本文所提方法是一种完全基于数据驱动的监测方法,可以考虑将其与先验知识或专家经验相结合,并且可以考虑变量间关系的更多细节,提出其他分块方法,是本文进一步研究的工作之一。
| [1] |
CHIANG L H, RUSSELL E L, BRAATZ R D. Fault detection and diagnosis in industrial systems[J]. Measurement science and technology, 2001, 12(10): 1745. ( 0) 0)
|
| [2] |
GE Zhiqiang, SONG Zhihuan, GAO Furong. Review of recent research on data-based process monitoring[J]. Industrial & engineering chemistry research, 2013, 52(10): 3534-3562. ( 0) 0)
|
| [3] |
QIN S J. Statistical process monitoring: basics and beyond[J]. Journal of chemometrics, 2003, 17(8/9): 480-502. ( 0) 0)
|
| [4] |
JIANG Qingchao, YAN Xuefeng, ZHAO Weixiang. Fault detection and diagnosis in chemical processes using sensitive principal component analysis[J]. Industrial & engineering chemistry research, 2013, 52(4): 1635-1644. ( 0) 0)
|
| [5] |
KRESTA J V, MACGREGOR J F, MARLIN T E. Multivariate statistical monitoring of process operating performance[J]. The Canadian journal of chemical engineering, 1991, 69(1): 35-47. DOI:10.1002/cjce.5450690105 ( 0) 0)
|
| [6] |
NOMIKOS P, MACGREGOR J F. Multivariate SPC charts for monitoring batch processes[J]. Technometrics, 1995, 37(1): 41-59. DOI:10.1080/00401706.1995.10485888 ( 0) 0)
|
| [7] |
HE Q P, WANG Jin. Principal component based k-nearest-neighbor rule for semiconductor process fault detection[C]//Proceedings of 2018 American Control Conference. Seattle, USA, 2008: 1606−1611.
( 0) 0)
|
| [8] |
HE Q P, WANG Jin. Fault detection using the k-Nearest neighbor rule for semiconductor manufacturing processes[J]. IEEE transactions on semiconductor manufacturing, 2007, 20(4): 345-354. DOI:10.1109/TSM.2007.907607 ( 0) 0)
|
| [9] |
陈海彬, 郭金玉, 谢彦红. 基于改进K-means聚类的kNN故障检测研究[J]. 沈阳化工大学学报, 2013, 27(1): 69-73. CHEN Haibin, GUO Jinyu, XIE Yanhong. kNN fault detection based on improved K-means clustering[J]. Journal of Shenyang University of Chemical Technology, 2013, 27(1): 69-73. DOI:10.3969/j.issn.2095-2198.2013.01.015 (  0) 0)
|
| [10] |
魏域琴, 宋丹丹, 翁正新. 基于DPCA-KNN的工业过程故障诊断方法研究[C]//第三十八届中国控制会议论文集(7). 广州, 2019: 14−19. WEI Yuqin, SONG Dandan, WENG Zhengxin. Research on fault diagnosis method of industrial process based on DPCA-KNN[C]//Proceedings of the 38th China Control Conference. Guangzhou, 2019: 14−19. (  0) 0)
|
| [11] |
郭小萍, 徐月, 李元. 基于特征空间自适应k近邻工业过程故障检测[J]. 高校化学工程学报, 2019, 33(2): 453-461. GUO Xiaoping, XU Yue, LI Yuan. A feature space adaptive k-nearest neighbor method for industrial fault detection[J]. Journal of chemical engineering of Chinese universities, 2019, 33(2): 453-461. DOI:10.3969/j.issn.1003-9015.2019.02.025 (  0) 0)
|
| [12] |
冯立伟, 张成, 李元, 等. 基于标准距离k近邻的多模态过程故障检测策略[J]. 控制理论与应用, 2019, 36(4): 553-560. FENG Liwei, ZHANG Cheng, LI Yuan, et al. Fault detection strategy of standard-distance-based k nearest neighbor rule in multimode processes[J]. Control theory & applications, 2019, 36(4): 553-560. DOI:10.7641/CTA.2018.70806 (  0) 0)
|
| [13] |
MACGREGOR J F, JAECKLE C, KIPARISSIDES C, et al. Process monitoring and diagnosis by multiblock PLS methods[J]. AIChE journal, 1994, 40(5): 826-838. DOI:10.1002/aic.690400509 ( 0) 0)
|
| [14] |
王振雷, 江伟, 王昕. 基于多块MICA-PCA的全流程过程监控方法[J]. 控制与决策, 2018, 33(2): 269-274. WANG Zhenlei, JIANG Wei, WANG Xin. Plant-wide process monitoring based on multiblock MICA-PCA[J]. Control and decision, 2018, 33(2): 269-274. (  0) 0)
|
| [15] |
石怀涛, 王雨桐, 李颂华, 等. 基于多块相对变换独立主元分析的故障诊断方法[J]. 控制与决策, 2018, 33(11): 2009-2014. SHI Huaitao, WANG Yutong, LI Songhua, et al. Fault diagnosis approach based on relative transformation ICA of multiblock[J]. Control and decision, 2018, 33(11): 2009-2014. (  0) 0)
|
| [16] |
GE Zhiqiang, SONG Zhihuan. Distributed PCA model for plant-wide process monitoring[J]. Industrial & engineering chemistry research, 2013, 52(5): 1947-1957. ( 0) 0)
|
| [17] |
JIANG Qingchao, YAN Xuefeng. Plant-wide process monitoring based on mutual information–multiblock principal component analysis[J]. ISA transactions, 2014, 53(5): 1516-1527. DOI:10.1016/j.isatra.2014.05.031 ( 0) 0)
|
| [18] |
HUANG Junping, YAN Xuefeng. Quality relevant and independent two block monitoring based on mutual information and KPCA[J]. IEEE transactions on industrial electronics, 2017, 64(8): 6518-6527. DOI:10.1109/TIE.2017.2682012 ( 0) 0)
|
| [19] |
JIANG Qingchao, YAN Xuefeng. Nonlinear plant-wide process monitoring using MI-spectral clustering and Bayesian inference-based multiblock KPCA[J]. Journal of process control, 2015, 32: 38-50. DOI:10.1016/j.jprocont.2015.04.014 ( 0) 0)
|
| [20] |
童楚东, 史旭华. 基于互信息的PCA方法及其在过程监测中的应用[J]. 化工学报, 2015, 66(10): 4101-4106. TONG Chudong, SHI Xuhua. Mutual information based PCA algorithm with application in process monitoring[J]. CIESC journal, 2015, 66(10): 4101-4106. (  0) 0)
|
| [21] |
范雪莉, 冯海泓, 原猛. 基于互信息的主成分分析用于声场景分类[J]. 声学技术, 2013, 32(3): 222-227. FAN Xueli, FENG Haihong, YUAN Meng. Mutual information based principal component analysis for acoustic environment classification[J]. Technical acoustics, 2013, 32(3): 222-227. (  0) 0)
|
| [22] |
周红标, 乔俊飞. 基于高维k-近邻互信息的特征选择方法
[J]. 智能系统学报, 2017, 12(5): 595-600. ZHOU Hongbiao, QIAO Junfei. Feature selection method based on high dimensional k-nearest neighbors mutual information [J]. CAAI transactions on intelligent systems, 2017, 12(5): 595-600. (  0) 0)
|
| [23] |
GE Zhiqiang, SONG Zhihuan. Multimode process monitoring based on Bayesian method[J]. Journal of chemometrics, 2009, 23(12): 636-650. ( 0) 0)
|
| [24] |
YIN Shen, DING S X, HAGHANI A, et al. A comparison study of basic data-driven fault diagnosis and process monitoring methods on the benchmark Tennessee Eastman process[J]. Journal of process control, 2012, 22(9): 1567-1581. DOI:10.1016/j.jprocont.2012.06.009 ( 0) 0)
|
| [25] |
CHIANG L H, RUSSELL E L, BRAATZ R D. Tennessee Eastman process[M]//CHIANG L H, RUSSELL E L, BRAATZ R D. Fault Detection and Diagnosis in Industrial Systems. London: Springer, 2001: 103−112.
( 0) 0)
|
 2021, Vol. 16
2021, Vol. 16


