中国的书法艺术已有几千年的历史，无数书法名家留下大量墨宝。时至今日，随着手机电脑普及，人们对于书法艺术不甚了解。应用现代技术进行书法创作，可以使更多人重新认识书法的魅力^[1]。同时，机器人书法的研究成果可以为解决其他问题提供思路，推进机器人发展^[2]。

目前国内外很多研究者都提出了书法机器人系统，机器人书法的研究重点是生成一条机器人书写字符轨迹。其中，Li等^[3]使用编码器提取笔画的特征，由解码器获得笔画轨迹序列；Wu等^[4]提出了一种基于深度强化学习算法的书法机器人模型，使机器人能够直接从笔画图像中获得包括画笔的压力信息在内的三维位置信息。Li等^[5]将书法机器人分为笔画分离、汉字特征建模、汉字轨迹规划三部分，成功复现了颜体汉字。但是，绝大多数书法机器人都假定笔画宽度只与压力有关。当毛笔保持竖直状态移动的情况下是成立的，但是实际书法过程中，毛笔会发生倾斜。因此，有必要分析笔画宽度与倾斜角度之间的关系，使机器人从笔画图像中获得更加准确轨迹信息。

书法评价对产生高质量书写结果起着促进作用，但一些常规的机器人书法系统通常使用单一的评估指标。Mueller等^[6]仅考虑书写结果及其参考笔画的轮廓匹配，并以此评价结果更新书写轨迹。Xu等^[7]将书写结果与知名书法家的示例模板进行比较，以产生笔画质量得分。Wang等^[8]提出了一种使用圆盘B样条曲线对字符进行矢量化，通过迭代最近点(iterative closest point，ICP)算法进行相似性评估。Zhou等^[9]使用可能性−概率分布方法对汉字提取的特征，从而计算字符的评估值。本文提出3种评价指标，不仅从外形进行对比，较直观地显示笔画差异，又包含了笔画的骨架特征和起笔收笔特征，获得更全面的评价。

本文提出了一种基于毛笔建模的机器人书法系统，该系统不仅控制机器人进行实际书写，而且结合评价指标提高书写质量。这项工作的主要贡献有两个方面：1)考虑倾斜状态对毛笔足迹形状的影响，并使机器人复现了这一状态；2)针对笔画设计评价指标，多角度评价书写结果。

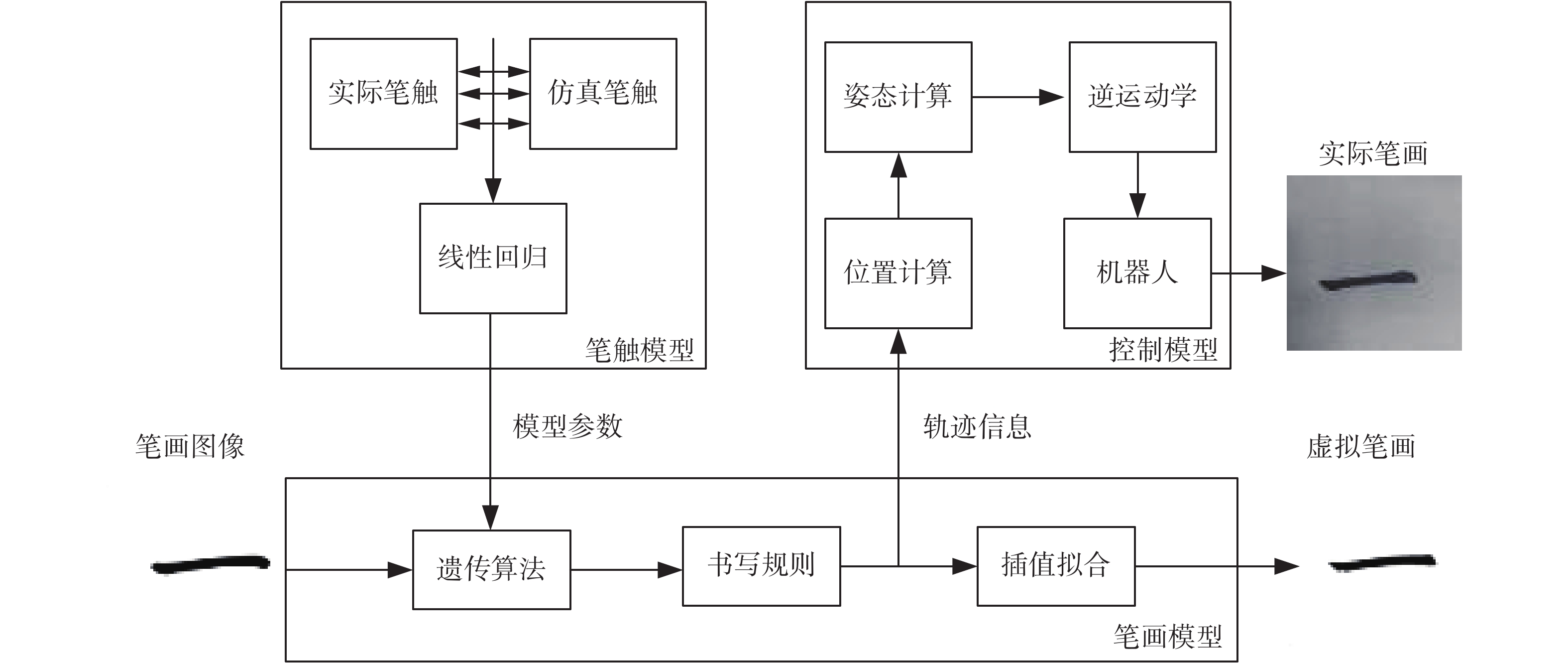
1 机器人毛笔模型 1.1 模型概述

本文拟议的机器人毛笔模型框架如图1所示，该模型由笔触模型、笔画模型和控制模型组成。笔触模型分析毛笔足迹，为笔画模型提供足迹形状与机器人位姿的函数关系。基于遗传算法的笔画模型从笔画图像中获得轨迹信息，并加入了起笔、行笔、收笔规则，结合插值算法叠加笔触形成笔画图像。控制模型根据笔画模型提供的轨迹信息进行轨迹规划，控制机器人进行实际书写。

1.2 笔触模型

本文笔触模型采用经验模拟，着重观察分析毛笔和纸张交互产生的毛笔足迹，避免对毛笔位置的实时计算^[10]。参考张俊松等的笔触模型^[11]，在考虑毛笔倾斜情况下，机器人使用示教方式采集实际足迹，使用线性回归算法计算笔触模型参数。

1.2.1 采集实际足迹

机器人向下运动在纸面留下毛笔足迹，如图2所示。这个过程中需要控制的机器人位姿参数包括毛笔下降高度和毛笔倾斜角度。其中，当毛笔沿着Z轴向下移动到笔尖恰好接触纸张时，设为初始位置， $h$ 值随着毛笔下降而增加。足迹水平中心线为X轴，毛笔从垂直纸面的竖直状态绕Y轴顺时针旋转 $\alpha $ 度， $\alpha $ 即毛笔倾斜角度。实验规定毛笔下降高度值为8~20 mm，毛笔倾斜角度 $ {\rm{\alpha }} $ 为0°~10°。

采集笔触过程如图3所示，描述如下，首先机器人以末端垂直纸面的姿态运行至起始点，进行姿态变化调整到指定倾斜度。然后，机器人沿纵向缓慢下降到指定高度，到达指定高度后迅速提笔。

1.2.2 计算模型参数

笔触模型用2条3次Bézier曲线进行拟合，如图4。定义仿真足迹 ${S_t} = \left( {{L_t}{\rm{}},{L_h}{\rm{}},{L_r}} \right)$ ，其中 ${L_t}$ 为笔锋长度， ${L_h}$ 为笔根长度， ${L_r}$ 为笔肚长度。

3次Bézier曲线如式(1)所示：

$\begin{aligned}B({{t}}) = {P_0}{(1 - t)^3} + 3{P_1}t{(1 - t)^2} + 3{P_2}{t^2}(1 - t) + {P_3}{t^3} \\ \;t \in [0,1]\quad\quad\quad\quad\quad\quad\quad\quad \end{aligned}$

(1)

式中： ${P_0}$ 和 ${P_3}$ 为曲线起止点， ${P_1}$ 和 ${P_2}$ 坐标 $({P_{1x}},{P_{1y}})$ 、 $({P_{2x}},{P_{2y}}) $ ，如式(2)：

$\left\{ {\begin{aligned} &{{P_{1x}} = \frac{{{L_t} - 4{L_h}}}{3}} \\ &{{P_{2x}} = {L_h}} \\ &{{P_{1y}} = {P_{2y}} = \frac{{4{L_r}}}{3}} \end{aligned}} \right.$

(2)

式中： ${L_t}$ 为笔锋长度； ${L_h}$ 为笔根长度； ${L_r}$ 为笔肚长度。

将一幅机器人参数为 $\left( {h,\alpha } \right)$ 的实际笔触图像转换成二值图像，并提取轮廓信息。随机设置仿真笔触参数 $ ({L}_{t}{ ,}{L}_{h}{ ,}{L}_{r})$ ，拟合形成仿真笔触图像，将该笔触的轮廓与实际笔触轮廓进行匹配，调整仿真笔触参数令两者基本重合，如图5所示，记录模型参数 $ ({L}_{t}{ ,}{L}_{h}{ ,}{L}_{r})$ 。

对模型参数和机器人参数采用逐步分析法，分析模型参数 $ ({L}_{t}{ ,}{L}_{h}{ ,}{L}_{r})$ 与 $\left( {{h^2},{\alpha ^2},h,a} \right)$ 函数关系，并进行线性回归，笔触模型参数描述如式(3)：

$\left\{ {\begin{array}{*{20}{c}} {{L_{{t}}} = 0.205\;5h + 0.040\;5\alpha + 0.481\;4} \\ {{L_{{h}}} = 0.001\;1{h^2} + 0.004\;8\alpha + 0.240\;7} \\ {{L_{{r}}} = 0.057\;5h + 0.009\;7\alpha + 0.413\;4} \end{array}} \right.$

(3)

式中： ${L_t}$ 为笔锋长度； ${L_h}$ 为笔根长度； ${L_r}$ 为笔肚长度； $h$ 为毛笔下降高度值； $\alpha $ 为倾斜角度。

1.3 笔画模型

${S_{{n}}}\! =\! \left\{ {\left( {{x_1},{y_1},{h_1},{\alpha _1}} \right), \left( {{x_2},{y_2},{h_2},{\alpha _2}} \right), \cdots \left( {{x_n},{y_n},{h_n},{\alpha _n}} \right)} \right\}$ 表示笔画模型中毛笔运动轨迹，其中 $x$ 和 $y$ 是笔触模型原点在纸面坐标系上坐标值， $h$ 值表示毛笔所受压力，而 $\alpha $ 值的改变反应毛笔倾斜情况。位置信息和高度信息是通过遗传算法从笔画图像中提取，遗传算法得到的初步轨迹信息需要根据起笔、行笔、收笔规则进行修改，并添加倾斜信息。

1.3.1 遗传算法提取信息

遗传算法是模仿自然界生物进化机制发展起来的随机全局搜索和优化方法，不断向搜索空间中适应度越高的区域移动以求得最优解。遗传算法流程如图6所示，染色体是多个基因的集合，而基因决定了个体的外部表现。笔画模型设计两条染色体，第一条染色体包含位置信息，决定了笔画的骨架特征。第二条染色体包含位置信息和高度信息，即轨迹信息，决定了笔画的外型特征。

对参考笔画图像(图7(a))进行形态学处理，提取骨架如图7(b)，图中所有灰度值为0的像素点位置是初始数据，染色体 ${S_{{m}}} = \left\{ \left( {{x_1},{y_1}} \right),\left( {{x_2},{y_2}} \right), \cdots, \right. $ $ \left.\left( {{x_m},{y_m}} \right) \right\}$ 。根据笔画垂直水平两个方向端点差值大小确定笔画趋向，笔画“橫”为水平趋向，数据按趋向进行排序并分为 $k$ 组。

将初始数据拟合成目标曲线，通过计算对比多种拟合函数拟合误差平方和，选择使用5次多项式进行拟合的，如式(4)所示：

${f_1} = {p_1}{x^5} + {p_2}{x^4} + {p_3}{x^3} + {p_4}{x^2} + {p_5}{x^1} + {p_6}$

(4)

式中 ${p_1},\;{p_2},\; \cdots, \;{p_6}$ 为多项式系数。

遗传算法随机生成一个原始的种群，种群中每个个体含有 $k$ 个基因，将基因对应的数据通过拉格朗日插值法拟合成一条曲线，拟合曲线描述如式(5)：

$\left\{ \begin{aligned} &{f_2} = \sum_{i = 0}^k {{y_i}} \cdot{l_i}(x) \\ &{l_i}(x) = \frac{{\left( {x - {x_0}} \right) \cdots \left( {x - {x_{i - 1}}} \right)\left( {x - {x_{i + 1}}} \right) \cdots \left( {x - {x_k}} \right)}}{{\left( {{x_i} - {x_0}} \right) \cdots \left( {{x_i} - {x_{i - 1}}} \right)\left( {{x_i} - {x_{i + 1}}} \right) \cdots \left( {{x_i} - {x_k}} \right)}} \end{aligned} \right.$

(5)

因此，最优个体的拟合曲线应该与目标曲线尽可能地重合，目标函数要最小化，如式(6)所示：

$\min {\rm{ObjV}} = \left| {{f_1} - {f_2}} \right|$

(6)

更加适应于环境的个体应该拥有更高的适应度，第i个体适应度如式(7)所示：

$F(i) = \frac{1}{{{\rm{ObjV}}(i)}}$

(7)

在每个种群50个个体，染色体含有10个基因，80%交叉概率，20%变异概率下，经过20代进化最佳个体骨架图像与目标图像骨架对比结果，如图8所示。结果说明两条曲线较为重合，证明遗传算法选取的坐标信息是具有代表性。

将位置信息作为输入信息，对种群初始化，染色体 ${S_{{k}}} = \left\{ {\left( {{x_1},{y_1},{h_1},{\alpha _1}} \right),\left( {{x_2},{y_2},{h_2},{\alpha _2}} \right), \cdots ,\left( {{x_k},{y_k},{h_k},{\alpha _{\rm{k}}}} \right)} \right\}$ ，其中高度信息取值范围8~20 mm，倾斜信息均设为0°

对于每一个体，已知每个轨迹点的位置、高度信息、倾斜信息，根据笔触模型可计算得到每个轨迹点的笔肚长度 ${L_r}$ ，从而计算得到2 $k$ 个笔画轮廓点位置，通过闭合B样条将这些轮廓点光滑连接形成笔画图像。由于目标函数取最大值，目标函数和适应度函数相等，描述如式(8)：

$\left\{ {\begin{aligned} & {{F^{'}} = {{\rm{ObjV}}^{'}} = 1 - \frac{{\displaystyle\sum\limits_{i = 1}^M {\displaystyle\sum\limits_{j = 1}^N {\left| {{X_{i,j}} - X_{i,j}^{'}} \right|} } }}{{\displaystyle\sum\limits_{i = 1}^M {\displaystyle\sum\limits_{j = 1}^N {\left({X_{i,j}}\cdot X_{i,j}^{'} + \left| {{X_{i,j}} - X_{i,j}^{'}} \right|\right)} } }}} \\ &{{X_{i,j}} = \left\{ {\begin{array}{*{20}{c}} {1,\quad {\rm{ pixel}}\;{{(i, j)}}\;{\rm{is}}\;{\rm{white}}} \\ {0,\quad {\rm{pixel}}\;{{ (i, j)}}\;{\rm{ is }}\;{\rm{black}}} \end{array}} \right.} \end{aligned}} \right.$

(8)

式中： ${X_{i,j}}$ 为参考笔画图像像素点； $X_{i,j}^{'}$ 为仿真笔画图像像素点。

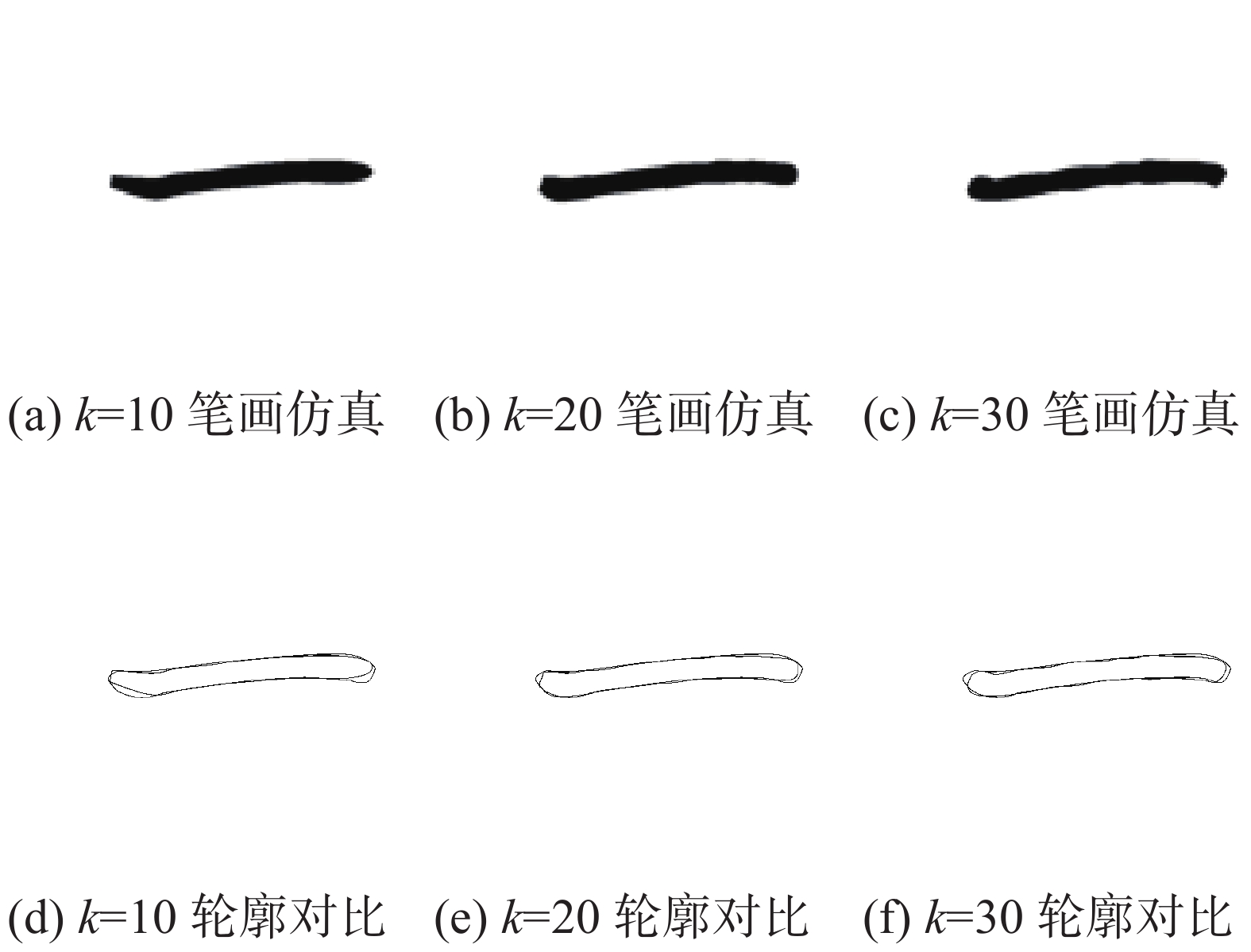
图9显示了在每个种群50个个体，80%交叉概率，20%变异概率下，基因数 $k$ 取不同值，经过100代进化后笔画仿真以及与目标图像轮廓对比结果。

当 $k = 10$ 时，两者存在较大差异；当 $k = 20$ 和 $k = 30$ 的仿真效果较好，但是 $k = 30$ 时，虚拟笔画轮廓不光滑，说明需要增加迭代次数进行优化，但这会增加运算成本。因此合理选择基因数 $k$ ，既可以较好复现目标图像，又降低运算量。

1.3.2 书写规则修改轨迹

笔画仿真图像在笔画开始和结束阶段与目标图像存在较大差距，这是由于中国书法在这两个阶段充满变化，轨迹信息需要根据书写规则进行调整。

在起笔阶段，书法家握住毛笔，使笔尖刚好达到纸面。此时，手在身体的左前方，而肘部朝右后方。然后将毛笔持续下压，形成杏仁点。然后，根据不同笔画毛笔向不同方向运动。对于“橫”，毛笔向右运动，扩大墨迹。最后，书法家逆时针转动毛笔，带动笔锋作逆时针调锋，使原来的笔锋指向由向左前变成向左，起笔结束。

在起笔阶段，根据毛笔运动方向调整位置信息；对毛笔的压力逐渐加大，逐步增大高度信息，毛笔保持竖直状态，倾斜信息设为零。

在行笔阶段，毛笔在纸上运行时，笔画模型根据毛笔运行轨迹结合笔触模型不断进行累加笔触，模拟汉字书写。在实际书写中为了突出层次，书法家往往会将毛笔前倾加重痕迹，故行笔阶段，倾斜角 $\alpha $ 会发生变化。

在行笔阶段，遗传算法计算的轨迹点数量较多，实际机器人进行书写会出现卡顿现象。在不影响笔画光滑的前提下，删减轨迹点；对毛笔的压力变化不大，适当调整高度信息；同时根据书写的笔画类别对倾斜信息进行修改。

行笔结束后，接下来就要收笔，毛笔收笔有两种方法：藏锋收笔、露峰收笔。

藏锋收笔以橫为例，藏峰收笔在笔画末端形成棱角，需要连续变化毛笔方向，最后将笔尖轻轻收回，藏在已有足迹中。“横”的仿真过程如图10所示。

露峰收笔以撇为例，露峰收笔强调写出笔锋，需要慢慢提高毛笔，使笔毛渐渐收拢，最后毛笔快速从纸面移开，形成笔锋。“撇”的仿真过程如图11所示。

在收笔阶段，藏锋收笔要求位置信息连续变化形成棱角；对毛笔的压力变化逐渐减小，高度信息缓慢减小；倾斜信息设为零。露锋收笔仅需要一两个轨迹点；高度信息迅速减小；倾斜信息设为零。

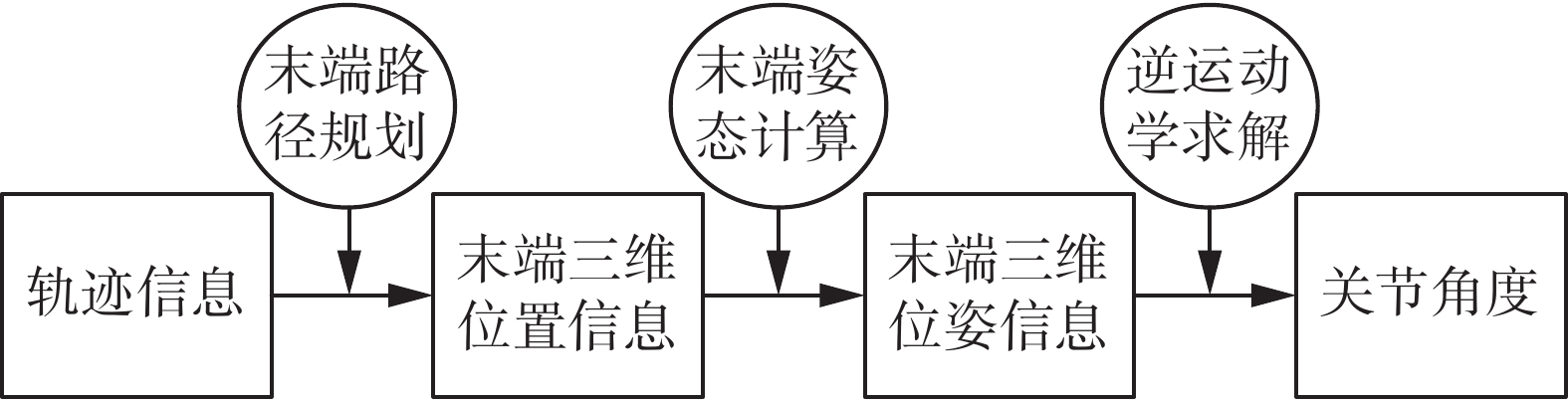
1.4 控制模型

控制模型根据笔画模型的数据进行轨迹规划，控制机器人书写汉字。控制模型框图如图12所示，采用B样条进行路径规划，获得连续光滑的机器人末端位置，通过姿态计算获得机器人末端位姿信息，运用逆运动学转换为关节参数。其中，本文采用的AUBO-i5协作机械臂符合Pieper准则^[12]，由于其自带的逆解算法在姿态计算方面存在不连续的问题，根据文献[13]采用基于球面几何的解析法求机器人运动学的逆解。

1.4.1 路径规划

轨迹信息 ${S_{{n}}} = \left\{ \left( {{x_1},{y_1},{h_1},{\alpha _1}} \right),\left( {{x_2},{y_2},{h_2},{\alpha _2}} \right), \cdots , \right.$ $\left. \left( {{x_n},{y_n},{h_n},{\alpha _n}} \right) \right\}$ 是不连续的，控制模型采用3次B样条作为插值函数进行路径规划。

对于 $n$ 个轨迹点，存在 $n - 1$ 条曲线。其中第 $i$ 条曲线的三维坐标为 ${p_i}\left( {{t}} \right)$ 描述如式(9)：

$\left\{ \begin{aligned} &{p_i}(t) = \displaystyle\sum\limits_{k = 0}^3 {{P_{i + k}}} \cdot {F_k}(t),\quad 0 \leqslant t \leqslant 1 \\ & {F_k}(t) = \frac{1}{6}\displaystyle\sum\limits_{j = 0}^{3 - k} {{{( - 1)}^j}C_4^j{{(t + 3 - k - j)}^3}} \end{aligned} \right.$

(9)

式中 ${P_{i + k}}$ 为样条控制点。显然， $n - 1$ 条曲线需要 $n + 2$ 个控制点，设 ${P_0}$ 、 ${P_{n + 1}} $ 控制点分别与 ${P_2}$ 、 ${P_{n - 1}} $ 重合，所有控制点计算如式(10)所示：

$\left( {\begin{array}{*{20}{c}} {{{{P}}_{{0}}}} \\ {{{{P}}_{{1}}}} \\ {{{{P}}_{{2}}}} \\ \vdots \\ {{{{P}}_{{{n - 1}}}}} \\ {{{{P}}_{{n}}}} \\ {{{{P}}_{{{n + 1}}}}} \end{array}} \right){{ = 6}}{\left( {\begin{array}{*{20}{c}} {{{ - 3}}}&{{0}}&{{3}}&{}&{}&{}&{} \\ {{1}}&{{4}}&{{1}}&{}&{}&{}&{} \\ {}&{{1}}&{{4}}&{{1}}&{}&{}&{} \\ {}&{}&{}& \vdots &{}&{} \\ {}&{}&{}&{{1}}&{{4}}&{{1}}&{} \\ {}&{}&{}&{}&{{1}}&{{4}}&{{1}} \\ {}&{}&{}&{}&{{{ - 3}}}&{{0}}&{{3}} \end{array}} \right)^{{{ - 1}}}}\left( {\begin{array}{*{20}{c}} {\left( {{{0,0,0}}} \right)} \\ {\left( {{{{x}}_{{1}}}{{,}}{{{y}}_{{1}}}{{,}}{{{h}}_{{1}}}} \right)} \\ {\left( {{{{x}}_{{2}}}{{,}}{{{y}}_{{2}}}{{,}}{{{h}}_{{2}}}} \right)} \\ \vdots \\ {\left( {{{{x}}_{{{n - 1}}}}{{,}}{{{y}}_{{{n - 1}}}}{{,}}{{{h}}_{{{n - 1}}}}} \right)} \\ {\left( {{{{x}}_{{n}}}{{,}}{{{y}}_{{n}}}{{,}}{{{h}}_{{n}}}} \right)} \\ {\left( {{{0,0,0}}} \right)} \end{array}} \right)$

(10)

式中： ${P_1},{P_2}, \cdots, {P_{n + 1}}$ 是控制点坐标， $\left( {{x_1},{y_1},{h_1}} \right), $ $ \left( {{x_2},{y_2},{h_2}} \right), \cdots, \left( {{x_n},{y_n},{h_n}} \right)$ 是轨迹点坐标。

将所有控制点代入B样条计算公式，拟合出机械臂的运动路径。

1.4.2 姿态计算

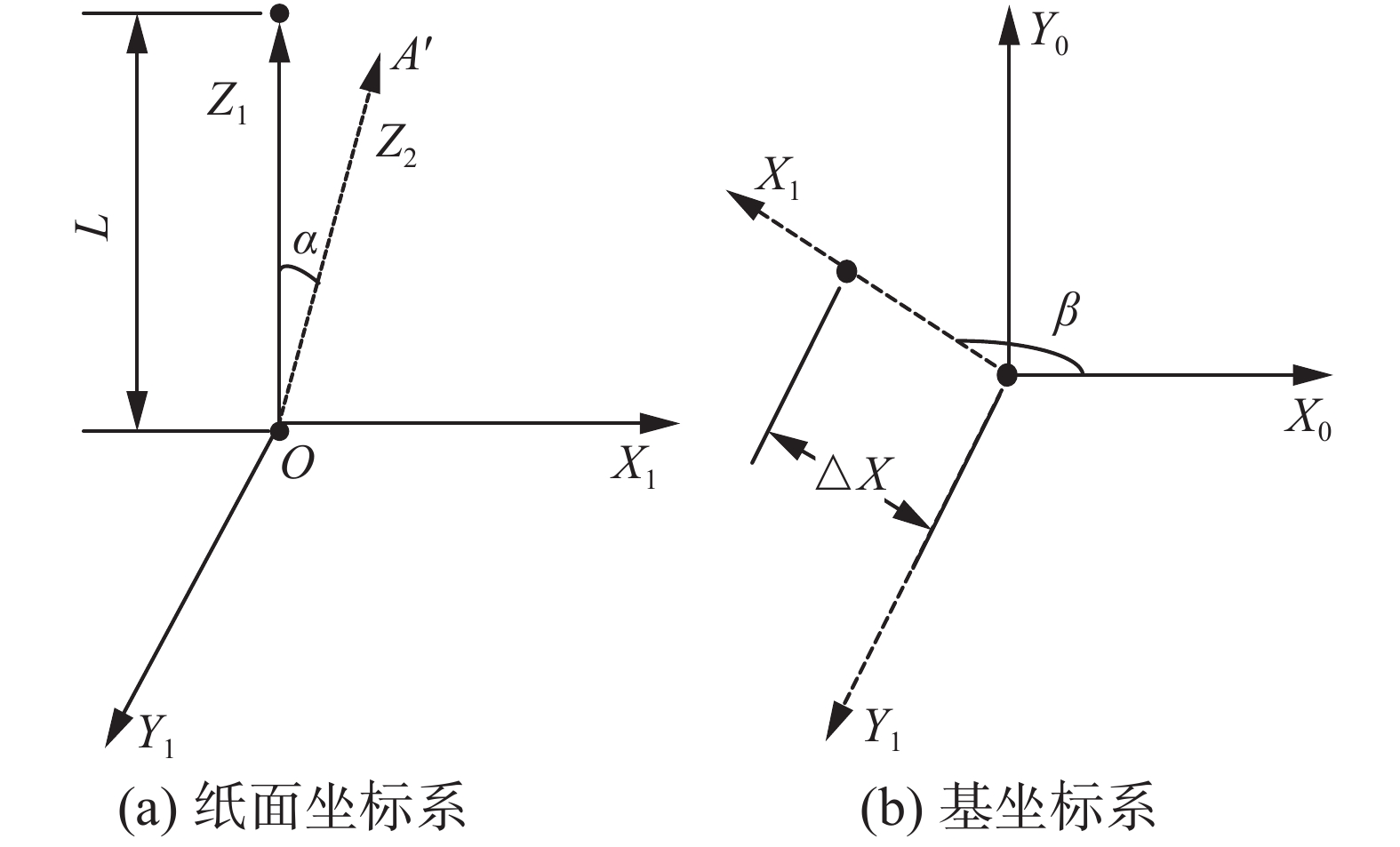
在笔画模型中，起笔和收笔阶段毛笔垂直纸面，设该姿态为机器人末端初始姿态。在行笔阶段，毛笔可能处于倾斜的状态，根据 $\alpha $ 进行姿态求解。

毛笔垂直纸面，与Z₁轴重合，O点为笔尖，A点为笔帽。绕Y₁轴顺时针旋转 $\alpha $ 度，点A移动到点A′。点A′相对点A在坐标轴上投影 $\Delta {{X}}$ 、 $\Delta {{Z}} $ 如式(11)所示：

$\left\{ \begin{array}{l} \Delta {{X = L \cdot}}\sin \alpha \\ \Delta Z{{ = L\cdot (1 - \cos}}\;\alpha ) \end{array} \right.$

(11)

式中：L为毛笔长度； $ \alpha $ 为倾斜角度。

在机器人基坐标系X₀Y₀Z₀中，如图13(b),毛笔旋转 $ {\rm{\alpha }} $ 度后姿态P描述如式(12)：

$ \left\{ \begin{aligned} &{\boldsymbol{P = M}}\times{{\boldsymbol{P}}_{{0}}} \\ &{\boldsymbol{M = }}\left[ {\begin{array}{*{20}{c}} {{{{a}}^{{2}}}{{ + (1 - }}{{{a}}^{{2}}}{{)c}}}&{{{ab(1 - c)}}}&{{{ - bd}}}&{{{\Delta X'}}} \\ {{{ab(1 - c)}}}&{{{{b}}^{{2}}}{{ + (1 - }}{{{b}}^{{2}}}{{)c}}}&{{{ad}}}&{{{\Delta Y'}}} \\ {{{bc}}}&{{{ - ad}}}&{{c}}&{{{\Delta Z'}}} \\ {{0}}&{{0}}&{{0}}&{{1}} \end{array}} \right] \\ &{a = - 1\cdot \cos (\beta - \frac{{\text{π}} }{2} + \theta ),b = - 1\cdot \sin (\beta - \frac{{\text{π}} }{2} + \theta ),c = \cos (\alpha ),d = \sin (\alpha )} \\ & \Delta X' = L\cdot \sin \alpha \cdot \sin (\beta + \theta ),\Delta Y' = L\cdot \sin \alpha \cdot \sin (\beta + \theta ),\Delta Z' = L\cdot(1 - \cos \alpha ) \end{aligned} \right. $

(12)

式中： ${{\boldsymbol{P}}_0}$ 为机器人末端初始姿态； ${\rm{\alpha }}$ 为毛笔倾斜角度； ${\rm{\beta }}$ 为纸面坐标系与机器人基坐标系夹角，本文设定为2.391 1 rad。 ${\rm{\theta }}$ 为笔画与X₁轴夹角，例如“横”， ${\rm{\theta }}$ 约为0.7188 rad，“竖” ${\rm{\theta }}$ 约为−1.570 8 rad； $L$ 为毛笔长度。

2 笔画评价指标

书法评价可以促进机器人产生高质量书写结果，如果书写结果评价值较低，说明笔画模型轨迹信息修改存在问题，需要对笔画进行进一步修改。本文首先对机器人书写图像和仿真图像提取骨架特征，利用一致性点漂移(coherent point drift，CPD)和ICP进行骨架匹配，获得骨架相似度；根据骨架匹配结果对书写结果图像进行旋转平移，处理后的图像与参考图像对比计算外形相似度；根据书写规则，提取书写特征，利用余弦相似度计算起笔收笔相似度，取平均值代表整个笔画的书写质量。

2.1 骨架相似度

使用细化算法获得骨架信息，从图像中提取获得的特征 ${N_n} = (({{{x}}_1},{y_1}),({{{x}}_2},{y_2}) ,\cdots, ({{{x}}_n},{y_n}))$ 。需要找到书写图像和参考图像两个特征点集之间的关系，然后将书写图像点集(下文称原始点集)进行转换映射到参考图像点集上(下文称目标点集)，从而计算两者相似度。

CPD算法将点集配准问题转换为概率密度估计问题，其将原始点集的分布表示成混合高斯模型，迭代修改高斯模型的参数，当原始点集与目标点集对应的似然函数达到最大时，配准完成。

ICP算法要求两个点集成员个数一致，计算出从原始点集上的每个点到目标点集的每个点的距离，使其和目标点集的最近点匹配，计算均方差误差，如直到均方差误差满足要求时，配准完成。

通过CPD匹配计算两者尺度信息 $S$ 、旋转矩阵 ${\boldsymbol{R}}$ 、平移矩阵 ${\boldsymbol{T}}$ ，根据尺度 $S$ ，将参考图像进行缩放，更新原始点集，使两个点集个数相同，将CPD所得旋转矩阵 ${\boldsymbol{R}}$ 、平移矩阵 ${\boldsymbol{T}}$ 作为初始矩阵，进行ICP匹配，骨架相似度描述如式(13)：

${S_1} = \frac{m}{n}$

(13)

式中：若存在映射后原始点集中的数据点与目标点集中的数据点的距离小于阈值，则认为匹配成功，统计匹配成功的数据点个数为 $m$ ， $n$ 为目标点集总个数。

2.2 外形相似度

书写图像通过相机采集获得的，其笔画位置、大小、方向与参考图像存在差异，通过CPD计算得到的尺度信息，将参考图像进行缩放，ICP匹配计算得到旋转矩阵 ${\boldsymbol{R}}$ 、平移矩阵 ${\boldsymbol{T}}$ 对其进行旋转平移。对经过处理后的参考图像和书写图像进行二值化，获得光栅图像，外形相似度描述如式(14)：

$\left\{ {\begin{aligned} & {{S_2} = 1 - \frac{{\displaystyle\sum\limits_{i = 1}^M {\displaystyle\sum\limits_{j = 1}^N {\left| {{X_{i,j}} - X_{i,j}^{'}} \right|} } }}{{\displaystyle\sum\limits_{i = 1}^M {\displaystyle\sum\limits_{j = 1}^N {\left({X_{i,j}} \cdot X_{i,j}^{'} + \left| {{X_{i,j}} - X_{i,j}^{'}} \right|\right)} } }}} \\ & {{X_{i,j}} = \left\{ {\begin{aligned} {1,\quad{\rm{ pixel}}\;{{ (i, j)}}\;{\rm{ is}}\;{\rm{ white}}} \\ {0,\quad{\rm{ pixel}}\;{{ (i, j)}}\;{\rm{ is }}\;{\rm{black}}} \end{aligned}} \right.} \end{aligned}} \right.$

(14)

式中： ${X_{i,j}}$ 为书写笔画图像像素点； $X_{i,j}^{'}$ 为变换后的仿真笔画图像像素点。

2.3 起笔收笔相似度

将栅格图片提取轮廓，见图14，设书写特征 $X = [{x_1}\;\;{x_2}\;\; \cdots\;\; {x_n}\;\;{x_{n + 1}}]$ ，以字符端点为圆心，半径r画圆，记录在圆内的所有灰度值为1的像素点。将圆分为 $n$ 份，每个像素点根据其与点A所形成角度值分配至不同区域，统计每个区域内像素点的个数 ${X_i}$ 和总数 ${X_{n + 1}}$ 。

余弦相似度表示起笔相似度，如式(15)所示：

${S_3} = \frac{{X \cdot {X'}}}{{\sqrt {\displaystyle\sum\nolimits_i {{x_i}} } \times \sqrt {\displaystyle\sum\nolimits_i {{x'}_i} } }}$

(15)

式中： $X$ 为参考图像书写特征； ${X'}$ 为实际书写图像书写特征。

同理，取字符末端端点，计算收笔相似度，两者平均值为起笔收笔相似度。

3 实际机器人书写实验

本文拟议的书法机器人系统由硬件和软件两部分组成，研究中使用的机器人是六自由度机械臂，毛笔安装在机械臂的末端执行器上，宣纸位于机械臂正前方，如图15。除此之外，模型的硬件还包括一台计算机，该计算机用于实现模型的软件部分。

书法机器人从参考笔画图像提取轨迹信息，机器人进行实际书写，根据评价结果修改轨迹信息。然后，我们优化了现有的笔画分离算法,将颜体字笔画分离的正确率提高到90%^[7]，进行了基本笔画书写和汉字仿真，写作结果证明了系统的性能。

3.1 评价指标验证

图16显示了3次机器人实际书写结果，其中笔画1的位置信息来自第一阶段遗传算法，高度信息设置为10 ${\rm{mm}}$ ，笔画2是第二阶段遗传算法结果，笔画3是轨迹信息根据书写规则修改后的结果，图17为机器人实际书写的实验照片。

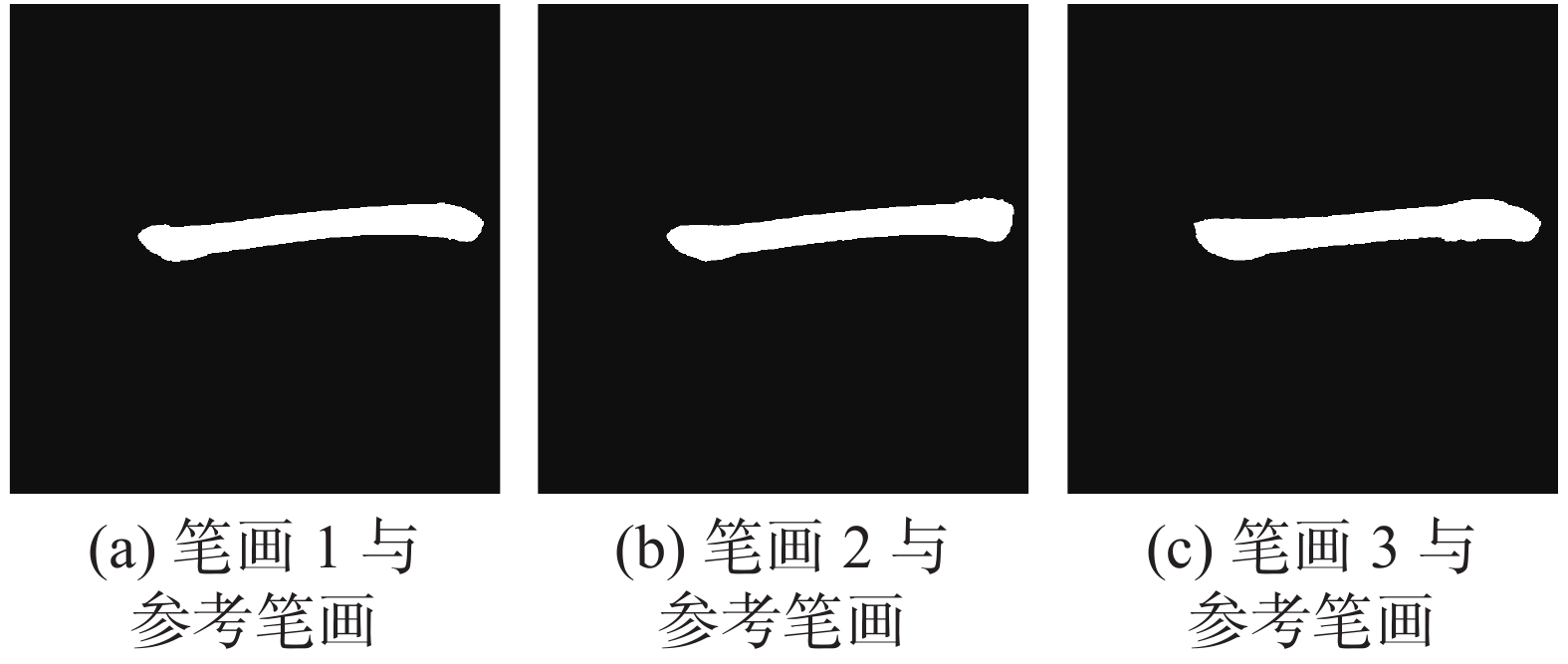
图18显示了笔画骨架对比结果，其中蓝色曲线是参考笔画骨架，红色是实际笔画骨架。图19显示了实际笔画与参考笔画轮廓对比结果。

实际书写笔画评价结果如表1所示。从评价结果可以看出，笔画1骨架相似度很高，这符合事实，因为第一阶段遗传算法只计算位置信息。同时，由于高度信息较小，图19(a)显示笔画被参考笔画包括在内，所以外形相似度较低。第二阶段遗传算法综合考虑了位置信息和高度信息，外形相似度有了明显提高，但是骨架相似度降低了，从图18(e)说明笔画2骨架开始和结束与参考图像存在较大偏差。第3次书写效果最好，说明进行书写规则修改后轨迹信息能很好地反映笔画特征，评价指标可以为提高书写质量提出改进意见。

3.2 基本笔画书写

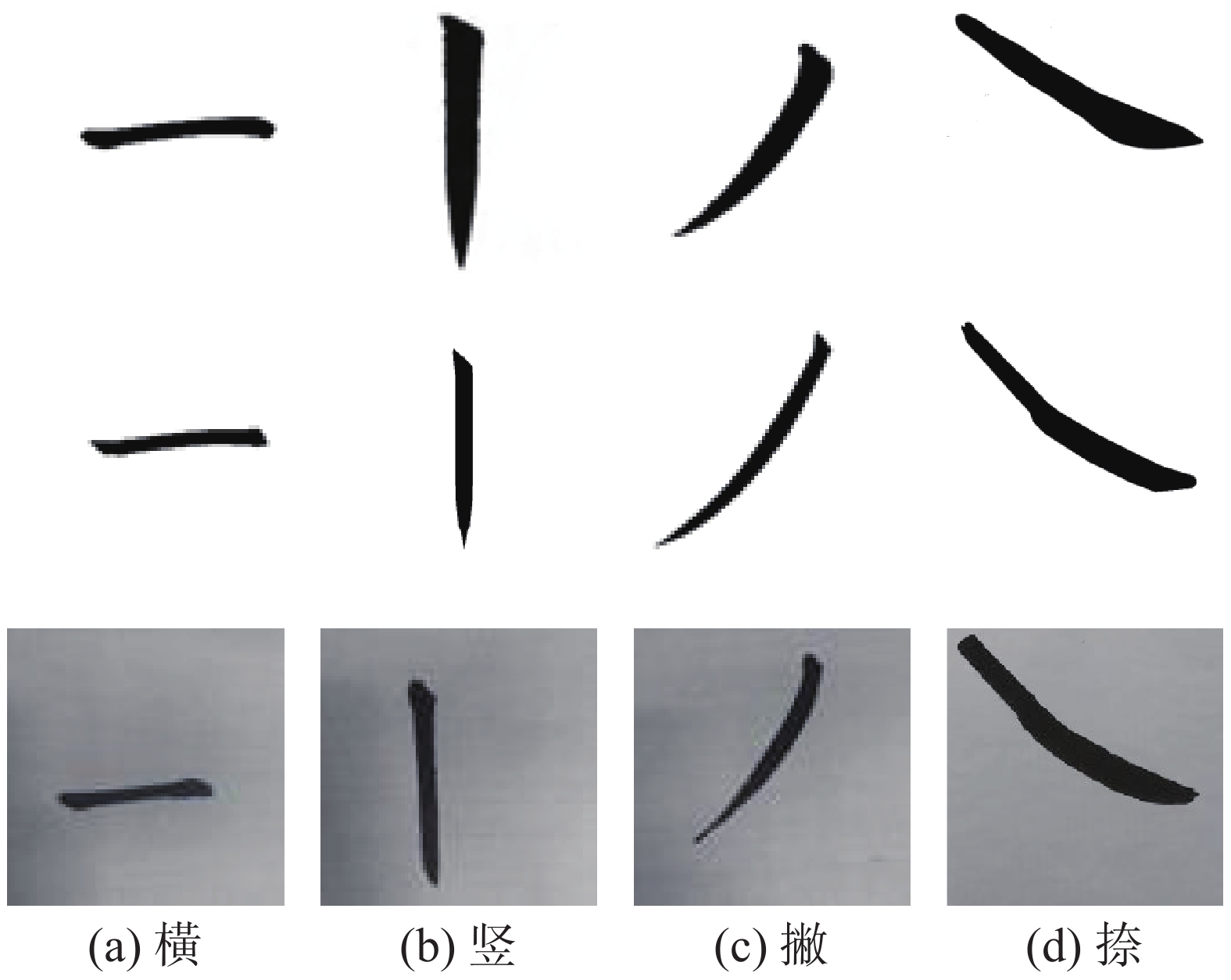
楷书由基本笔画和其他复杂笔画组成，而复杂笔画可以通过基本笔画经过变形、叠加获得。实验将参考笔画图像输入计算机，并用机械臂写下相应笔画。书写效果如图20所示。

在该图中，第1行是参考笔画图像；第2行是仿真图像；第3行是机器人的书写结果。这些书写结果具有很高的质量，证明本文提出书写模型的有效性。

3.3 汉字仿真

笔画按书写顺序进行排序形成汉字，实验采用最基本的书法规则：从上到下，从左到右的方式排列基本笔画和复杂笔画，图21显示“不忘初心”的实验结果。

结果表明，机器人书写结果与参考书法相似。

4 结束语

针对机器人毛笔书法，本文提出了一种基于毛笔建模的机器人书法系统，通过观察毛笔足迹建立笔触模型，采用遗传算法计算书写轨迹建立笔画模型，结合B样条轨迹规划建立控制模型。对笔画和汉字进行书写测试，并提出了骨架、外形、起笔收笔3种评价指标。评价结果表明，本文的机器人毛笔书法系统可以得到较好的书写效果。

这项工作仍有改进的空间。特别是，本文采用遗传算法结合书写规则计算汉字轨迹信息，而人工神经网络具有自学习能力，因此下一步计划将神经网络纳入笔画模型。另外，我们计划通过观察、模仿大师书写视频获取汉字书写信息，将其与图像获得汉字轨迹信息对比筛选提高书写质量。