模糊逻辑和模糊推理被用来描述知识和表达的不确定性。而模糊系统就是由模糊逻辑和模糊推理发展而来的。相比于传统的机器学习模型，模糊系统能够更准确地描述和估计现实中不确定的复杂非线性系统模型^[1-4]。近年来，学者们提出了众多的模糊系统建模方法，其中TSK模糊系统因其能够将非线性系统转化为多个局部线性结构的逼近，而成为最受欢迎的模型之一^[5-7]。

TSK模糊系统由若干条模糊规则构成，每条模糊规则由前件和后件组成。传统的模糊规则构建依靠专家经验。近年来，数据驱动的模糊规则构建方法受到了充分的研究。通常可以划分为两个步骤：一是使用某种划分规则将训练数据分为若干子体来提取规则前件参数，在实际建模中，通常使用聚类来实现；二是学习优化后件参数，从机器学习的角度，可以视为一个线性回归问题^[8-11]。

TSK模糊系统建模是重要的有监督学习的过程，因此需要充分的训练数据。然而，在很多实际应用中，样本数据经常是有限的高维数据，这就不可避免导致了模型的过拟合问题。而多任务学习可以从其他任务中获取相关信息，一定程度弥补训练数据不足的问题，进而提高模型的学习性能^[12-17]。在多任务建模中，任务之间往往具有明显的相关性，并存在着共享信息，因此充分利用多个任务间的共享信息进行多任务模糊系统建模，有助于提高每个任务的泛化性能。例如，Jiang等^[18]提出了一种利用潜在任务间关系信息的多任务模糊系统，该方法为多个任务学习了一个共享的后件参数来表示任务间的共享信息。然而，这些方法都只着重于任务间后件参数的共享结构，而忽视了如何利用各任务的自身特点。

鉴于此，本文提出了一种新型多任务TSK模糊系统建模方法，在挖掘多任务间共享信息的同时，保留单个任务的特殊性。该方法将多任务的后件参数矩阵分解为共享参数矩阵和特有参数矩阵两个部分：共享参数矩阵表示了任务之间共享的结构信息，而特有参数矩阵保留了每个任务的不同于其他任务的差异信息。本文通过为共享参数矩阵和特有参数矩阵分别引入低秩和稀疏约束来实现这一目标。

1 多任务TSK模糊模型的基本原理

经典的单任务TSK模糊系统利用多个局部线性子模型来近似非线性模型。而多任务模糊系统就是多个单任务模糊系统的联合优化。在多任务设置中， $ T $ 、 $N=\displaystyle\sum_{t=1}^{T}{N}_{t}$ 和 $ D $ 分别表示任务、样本和特征的数量，其中 $ {N}_{t} $ 表示任务 $ t $ 的样本数量。对于任意输入向量 ${\boldsymbol{x}}_{t}=({x}_{t}^{1},{x}_{t}^{2}, \cdots ,{x}_{t}^{D})^{\rm T}\in {\bf{R}}^{D}$ ，其表示任务 $ t $ 的一个样本的特征向量，其中 $ {x}_{t}^{d} $ , $d=1,2,\cdots ,D$ 是向量 $ {\boldsymbol{x}}_{t} $ 的第 $ d $ 变量。

因此，任务 $ t $ 的第 $ m $ 个规则可以表示为：

$ \begin{split} & {{\rm{IF}}\;{x}_{t}^{1}\;{\rm{is}}\;{\boldsymbol{A}}_{t}^{m,1}\wedge {x}_{t}^{2}\;{\rm{is}}\;{\boldsymbol{A}}_{t}^{m,2}\wedge \; \cdots \;\wedge {x}_{t}^{D}\;{\rm{is}}\;{\boldsymbol{A}}_{t}^{m,D}, }\\&\qquad {{\rm{THEN}}\;{\boldsymbol{f}}_{t}^{m}\left({\boldsymbol{x}}_{t}\right)={w}_{t}^{m,0}+{w}_{t}^{m,1}{x}_{t}^{1}+ }\\&\qquad\qquad {{w}_{t}^{m,2}{x}_{t}^{2}+ \cdots +{w}_{t}^{m,D}{x}_{t}^{D} } \end{split} $

(1)

式中： $ {\boldsymbol{A}}_{t}^{m,d} $ 表示输入变量 $ {x}_{t}^{d} $ 对应于任务t的第m个规则的模糊子集， $m=1,2, \cdots ,M$ , $d= 1, 2,\cdots ,D$ ， $ M $ 表示模糊规则数， $ \wedge $ 表示合取操作。本文选择式(2)的Gaussian函数作为模糊隶属度函数。

$ {\mu }_{{\boldsymbol{A}}_{t}^{m,d}}\left({x}_{t}^{d}\right)=\exp\left(-\frac{{\left({x}_{t}^{d}-{c}^{m,d}\right)}^{2}}{2{\sigma }^{m,d}}\right) $

(2)

$ {c}^{m,d}=\frac{\displaystyle \sum _{t=1}^{T}\displaystyle \sum _{i=1}^{{N}_{t}}{\mu }_{t,i}^{m}{x}_{t,i}^{d}}{\displaystyle \sum _{t=1}^{T}\displaystyle \sum _{i=1}^{{N}_{t}}{\mu }_{t,i}^{m}} $

(3)

$ {\sigma ^{m,d}} = h\displaystyle \sum\limits_{t = 1}^T {\displaystyle \sum\limits_{i = 1}^{{N_t}} {\mu _{t,i}^m} } \left( {x_{t,i}^d - {c^{m,d}}} \right) \cdot {\left( {\displaystyle \sum\limits_{t = 1}^T {\displaystyle \sum\limits_{i = 1}^{{N_t}} {\mu _{t,i}^m} } } \right)^{ - 1}} $

(4)

式中 $ {c}^{m,d} $ 和 $ {\sigma }^{m,d} $ 分别表示均值与方差。本文使用FCM聚类方法进行模糊划分，获得样本的模糊隶属度，其中 $ {\mu }_{t,i}^{m} $ 表示任务 $ t $ 所属的第 $ i $ 个样本对于第 $ m $ 个聚类的模糊隶属度。式(4)中， $ h $ 是可调节参数。

定义 $\left({\boldsymbol{x}}_{t,i},{y}_{t,i}\right)$ 表示任务 $ t $ 中的第 $ i $ 个样本和其对应的标签， $i=1,2,\cdots ,{N}_{t}$ ， $t=1,2,\cdots ,T$ ， ${\boldsymbol{X}}_{t}= \left(\begin{array}{c}{\boldsymbol{x}}_{t,1}^{\rm T}\\ {\boldsymbol{x}}_{t,2}^{\rm T}\\ \vdots \\ {\boldsymbol{x}}_{t,{N}_{t}}^{\rm T}\end{array}\right)\in $ $ {\bf{R}}^{{N}_{t}\times D}$ ， ${\boldsymbol{y}}_{t}=[{y}_{t,1},{y}_{t,2}, \cdots ,{y}_{t,{N}_{t}}]^{\rm T}\in {\bf{R}}^{{N}_{t}}$ 。对于任务 $ t $ ，其模糊系统的输出可以表示为

$ \widehat{{\boldsymbol{y}}_{t}}={\boldsymbol{\varPhi }}_{t}{\boldsymbol{w}}_{t} $

(5)

式中： $ {\boldsymbol{\varPhi }}_{t}=\left({\boldsymbol{\varPhi }}_{t}^{1},{\boldsymbol{\varPhi }}_{t}^{2}, \cdots ,{\boldsymbol{\varPhi }}_{t}^{M}\right) $ 称为模糊系统的字典， ${\boldsymbol{\varPhi }}_{t}^{m}= $ $ {\rm{diag}}\left({\varphi }^{m}\left({\boldsymbol{x}}_{t,1}\right),{\varphi }^{m}\left({\boldsymbol{x}}_{t,2}\right), \cdots ,{\varphi }^{m}\left({\boldsymbol{x}}_{t,{N}_{t}}\right)\right)\cdot (1,{\boldsymbol{X}}_{t})\in {\bf{R}}^{{N}_{t}\times D}$ ， ${\boldsymbol{y}}_{t}= $ $ [{y}_{t,1},{y}_{t,2}, \cdots ,{y}_{t,{N}_{t}}]^{\rm T}\in {\bf{R}}^{{N}_{t}}$ ， $ {\varphi }^{m}\left({\boldsymbol{x}}_{t,i}\right) $ 表示输入 $ {\boldsymbol{x}}_{t,i} $ 对于第 $ m $ 条模糊规则的触发强度，可由式(6)获得。 ${\boldsymbol{w}}_{t}= $ $ \left(\left({\boldsymbol{w}}_{t}^{1}\right)^{\rm T},\left({\boldsymbol{w}}_{t}^{2}\right)^{\rm T}, \cdots ,\left({\boldsymbol{w}}_{t}^{M}\right)^{\rm T}\right)^{\rm T}\in {\bf{R}}^{\left(D+1\right)M}$ 是任务 $ t $ 的后件参数向量； $ {\boldsymbol{w}}_{t}^{m} $ 是对应于 $ {\boldsymbol{\varPhi }}_{t}^{m} $ 的后件参数向量。

$ {\varphi }^m({\boldsymbol x}_t)=\frac{\mu^m({\boldsymbol x}_t)}{\displaystyle\sum^M_{k=1}\mu^k({\boldsymbol x}_t)} $

(6)

$ \mu^m({\boldsymbol x}_t)=\prod^D_{d=1}\mu_{{\boldsymbol A}^{m,d}_t}\left(x^d_t\right) $

(7)

为方便计算，本文为多任务TSK模糊模型进一步定义 ${\boldsymbol{W}}=\left({\boldsymbol{w}}_{1},{\boldsymbol{w}}_{2}, \cdots ,{\boldsymbol{w}}_{T}\right)\in {\bf{R}}^{(D+1)M\times T}$ ，表示多任务模糊模型的后件参数联合矩阵。所以，基本多任务模糊系统的目标函数可以表示为

$ \underset{{\boldsymbol{W}}}{{\rm{min}}}\mathop \sum \limits_{t = 1}^T {||{\boldsymbol{y}}_{t}-{\boldsymbol{\varPhi }}_{t}{\boldsymbol{w}}_{t}||}_{2}^{2}+R\left({\boldsymbol{W}}\right) $

(8)

2 任务间共享和特有结构分解的多任务TSK模糊系统建模新方法

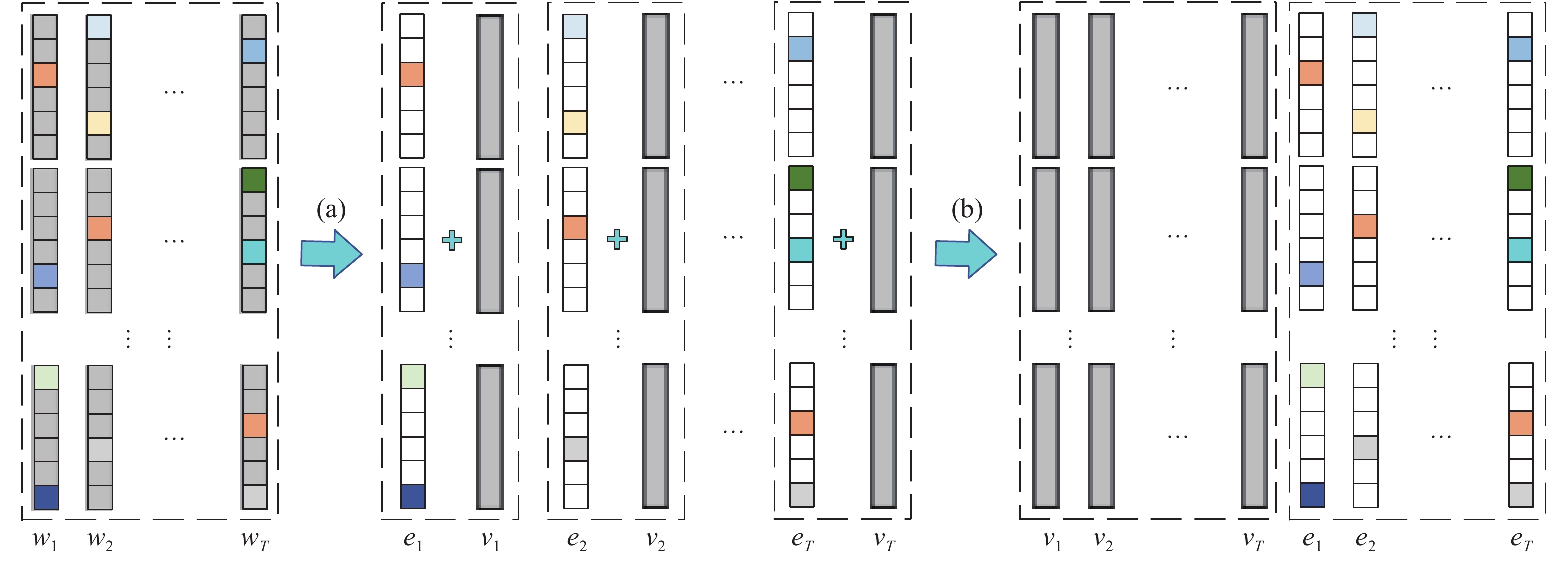
本节在基本多任务模糊系统的基础上，进一步提出新型多任务模糊系统建模方法。考虑到多任务之间是相互关联的，因此可以认为多个任务的模型参数包含着潜在的共享信息；另一方面，各任务的模型参数中都包含了自身不同于其他任务的特有信息。如图1所示，本文将各后件参数联合矩阵 $ {\boldsymbol{W}} $ 分解为共享参数矩阵 $ {\boldsymbol{V}} $ 和特有参数矩阵 $ {\boldsymbol{E}} $ ，即：

$ {\boldsymbol{W}}={\boldsymbol{V}}+{\boldsymbol{E}} $

(9)

共享参数矩阵 $ {\boldsymbol{V}} $ 包含了任务之间的共享参数信息，这种共享信息是指同一个特征在不同的任务中发挥相似的作用。具体表现在，如果某个特征在任务 $ i $ 中被赋予了一个较高的权重值，那么它在相关任务 $ j $ 中也将被赋予较高的权重，反之亦然，即对应于任务 $ i $ 和任务 $ j $ 的共享参数 $ {\boldsymbol{v}}_{i} $ 和 $ {\boldsymbol{v}}_{j} $ 是相似的。因此，共享参数矩阵 $ {\boldsymbol{V}} $ 具有低秩性，本文通过引入核范数 $ {||\cdot ||}_{*} $ 来实现对共享参数矩阵 $ {\boldsymbol{V}} $ 的低秩约束 $ {||{\boldsymbol{V}}||}_{*} $ 。特有参数矩阵 $ {\boldsymbol{E}} $ 表示各项任务不同于其他任务的特有信息，这种特有信息体现在某一特征在不同任务中发挥不同的作用，即特有参数矩阵 $ {\boldsymbol{E}} $ 是行稀疏的，本文通过引入 $ {||{\boldsymbol{E}}||}_{{1,2}} $ 正则化项实现行稀疏。

所以，通过对后件参数联合矩阵的分解，再分别施加低秩和行稀疏约束，在多任务建模中兼顾多任务之间共享信息和特有信息的作用，提出了任务间共享和特有结构划分的多任务TSK模糊系统的目标函数，表示如下：

$ \begin{split} & { \underset{{\boldsymbol{W}}}{\rm{min}}\displaystyle \sum \limits_{t=1}^{T}{||{\boldsymbol{y}}_{t}-{\boldsymbol{\varPhi }}_{t}{\boldsymbol{w}}_{t}||}_{2}^{2}+\alpha {||{\boldsymbol{V}}||}_{*}+\beta {||{\boldsymbol{E}}||}_{{1,2}} }\\&\qquad\qquad\quad { {\rm{s}}.{\rm{t}}.{\boldsymbol{W}}={\boldsymbol{V}}+{\boldsymbol{E}} } \end{split} $

(10)

式中： $ \alpha $ 和 $ \beta $ 是正则化参数，用于调节共享参数和特有参数在模型训练中发挥的作用，参数越大，惩罚力度越大。

3 目标函数优化

本文使用增广拉格朗日乘子法^[19-20]求解式(10)提出的最优化问题，其增广拉格朗日目标函数为

$ \begin{split} & \qquad\quad{ \underset{{\boldsymbol{W}},{\boldsymbol{V}},{\boldsymbol{E}},{\boldsymbol{Y}}}{\rm{min}}\displaystyle \sum \limits_{t=1}^{T}{||{\boldsymbol{y}}_{t}-{\boldsymbol{\varPhi }}_{t}{\boldsymbol{w}}_{t}||}_{2}^{2}+\alpha {||{\boldsymbol{V}}||}_{*}+ }\\&\;\;\; { \beta {||{\boldsymbol{E}}||}_{{1,2}}+<{\boldsymbol{Y}},{\boldsymbol{W}}-{\boldsymbol{V}}-{\boldsymbol{E}}>+ } {\dfrac{\mu }{2}||{\boldsymbol{W}}-{\boldsymbol{V}}-{\boldsymbol{E}}||_{2}^{2}} \end{split} $

(11)

式中： $ {\boldsymbol{Y}}\in {\bf{R}}^{\left(D+1\right)\times T} $ 是拉格朗日乘子矩阵， $ \left\langle {\cdot ,\cdot } \right\rangle $ 表示两个矩阵的内积运算。为便于计算，使用LADMAP方法^[21]将目标函数重新表示为

$ \begin{split} & { \underset{{\boldsymbol{W}},{\boldsymbol{V}},{\boldsymbol{E}},{\boldsymbol{Y}}}{\rm{min}}\displaystyle \sum \limits_{t=1}^{T}{||{\boldsymbol{y}}_{t}-{\boldsymbol{\varPhi }}_{t}{\boldsymbol{w}}_{t}||}_{2}^{2}+\alpha {||{\boldsymbol{V}}||}_{*}+ }\\&\;\; {\beta {||{\boldsymbol{E}}||}_{{1,2}}+\dfrac{\mu }{2}||{\boldsymbol{W}}-{\boldsymbol{V}}-{\boldsymbol{E}}+\frac{{\boldsymbol{Y}}}{\boldsymbol{\mu }}||_{2}^{2} } \end{split} $

(12)

这是一个包含 $ {\boldsymbol{W}}$ 、 ${\boldsymbol{V}}$ 、 ${\boldsymbol{E}} $ 、 ${\boldsymbol{Y}} $ 4个优化变量的最优化问题，所以本文交替使用其他变量的固定值迭代优化每个变量，原问题被转化为下面若干个子问题：

1) 固定 $ {\boldsymbol{V}}$ 、 ${\boldsymbol{E}} $ 、 ${\boldsymbol{Y}} $ ，式(12)化为如下目标函数：

$ \begin{split} & \underset{{\boldsymbol{W}},{\boldsymbol{V}},{\boldsymbol{E}}}{\rm{min}}\frac{{\bf{1}}}{\boldsymbol{N}}\sum\limits _{{\boldsymbol{t}}={\bf{1}}}^{\boldsymbol{T}}{||{\boldsymbol{y}}_{{\boldsymbol{t}}}-{\boldsymbol{\varPhi }}_{{\boldsymbol{t}}}{\boldsymbol{w}}_{{\boldsymbol{t}}}||}_{\bf{2}}^{\bf{2}}+\\&\quad \frac{\boldsymbol{\mu }}{\bf{2}}||{\boldsymbol{W}}-{\boldsymbol{V}}-{\boldsymbol{E}}+\frac{{\boldsymbol{Y}}}{\boldsymbol{\mu }}||_{\bf{2}}^{\bf{2}} \end{split} $

(13)

对 $ {\boldsymbol{w}}_{t} $ 求导，并令其等于 ${{0}}$ ，整理之后，可以通过式(14)获得 $ {\boldsymbol{w}}_{t} $ 的解：

$ \begin{split} & \quad{{\boldsymbol{w}}_{t}={\left(\mu {\boldsymbol{I}}+2{\left({\boldsymbol{\varPhi }}_{t}\right)}^{\rm T}{\boldsymbol{\varPhi }}_{t}\right)}^{-1}\cdot }\\& {[2{\left({\boldsymbol{\varPhi }}_{t}\right)}^{\rm T}{\boldsymbol{y}}_{t}+\mu \left({\boldsymbol{v}}_{t}+{\boldsymbol{e}}_{t}-{\boldsymbol{y}}_{t}/\mu \right)]} \end{split} $

(14)

因此，可以进一步得到 $ {\boldsymbol{W}} $ 的解：

$ {\boldsymbol{W}}=\left({\boldsymbol{w}}_{1},{\boldsymbol{w}}_{2}, \cdots ,{\boldsymbol{w}}_{T}\right) $

(15)

2) 固定 $ {\boldsymbol{W}} $ 、 ${\boldsymbol{E}} $ 、 ${\boldsymbol{Y}} $ ，式(12)转化为目标函数：

$ \underset{{\boldsymbol{V}}}{\rm{min}}\alpha {||{\boldsymbol{V}}||}_{*}+\frac{\mu }{2}||{\boldsymbol{W}}-{\boldsymbol{V}}-{\boldsymbol{E}}+\frac{{\boldsymbol{Y}}}{\mu }||_{2}^{2} $

(16)

使用奇异值阈值算子^[22]求解式(16)的低秩问题， $ {\boldsymbol{V}} $ 的最优解可以写成如下形式：

$ {\boldsymbol{V}}={\mathcal{D}}_{\frac{\alpha }{\mu }}\left({\boldsymbol{W}}-{\boldsymbol{E}}+\left(\frac{1}{\mu }\right){\boldsymbol{Y}}\right) $

(17)

3) 固定 $ {\boldsymbol{W}}$ 、 ${\boldsymbol{V}}$ 、 ${\boldsymbol{Y}} $ ，式(11)变成如下目标函数：

$ \underset{{\boldsymbol{E}}}{\rm{min}}{\boldsymbol{\beta }}{||{\boldsymbol{E}}||}_{{\bf{1}},{\bf{2}}}+{\frac{\boldsymbol{\mu }}{\bf{2}}\left\|{\boldsymbol{W}}-{\boldsymbol{V}}-{\boldsymbol{E}}+\frac{{\boldsymbol{Y}}}{\boldsymbol{\mu }}\right\|}_{\bf{2}}^{\bf{2}} $

(18)

式(18)等同于求解如下问题：

$ \underset{{\boldsymbol{E}}}{\rm{min}}\frac{\beta }{\mu }{||{\boldsymbol{E}}||}_{{1,2}}+\frac{1}{2}||{\boldsymbol{V}}-{\boldsymbol{Q}}||_{2}^{2} $

(19)

其中 $ {\boldsymbol{Q}}={\boldsymbol{W}}-{\boldsymbol{V}}+{\boldsymbol{Y}}/\mu $ ，可以使用文献[23]中的方法求解式(19)的最优化问题，得到 $ {\boldsymbol{E}} $ 的最优解。

4) 更新拉格朗日乘子矩阵 $ {\boldsymbol{Y}} $ 和正则化参数 $ \mu $ ：

$ {\boldsymbol{Y}}={\boldsymbol{Y}}+\mu \left({\boldsymbol{W}}-{\boldsymbol{V}}-{\boldsymbol{E}}\right) $

(20)

$ \mu ={\rm{min}}(\rho \mu ,{\mu }_{\rm{max}}) $

(21)

式中： $ \;\rho $ 是一个大于1的正数。

最终，本文提出多任务TSK模糊系统建模方法具体描述如下：

算法　MTTSKFS-CS

输入　多任务数据集 ${\boldsymbol{X}}_{1}, {\boldsymbol{X}}_{2}, \cdots ,{\boldsymbol{X}}_{T}$ 和对应的标签 ${\boldsymbol{y}}_{1},{\boldsymbol{y}}_{2}, \cdots ,{\boldsymbol{y}}_{T}$ ；模糊规则数量 $ M $ ；正则化参数 $ \alpha $ , $ \beta $ , $ \mu $ ；可调节参数 $ h $ ；正整数 $ \rho >1 $ ， ${\mu }_{\rm{max}}={10}^{3}$ ；

输出　多任务的模糊前件和多任务后件参数联合矩阵。

训练过程

1) 生成模糊字典：首先对全部任务的样本使用FCM聚类，获得 $ M $ 个聚类中心。然后计算每个样本的模糊隶属度，生成每个任务的模糊字典。

2) 联合学习多任务的后件参数：求解式(12)，得到 $ {\boldsymbol{W}} $ 、 ${\boldsymbol{V}}$ 、 ${\boldsymbol{E}} $ 最优解：

①初始化: 设定 $ {\boldsymbol{W}} $ 是一个随机矩阵， $ {\boldsymbol{V}}={\boldsymbol{W}} $ ， $ {\boldsymbol{E}}={\boldsymbol{W}}-{\boldsymbol{V}} $ 。拉格朗日乘子矩阵 $ {\boldsymbol{Y}}=\dfrac{{\boldsymbol{W}}}{{||{\boldsymbol{W}}||}_{\bf{2}}} $ 。

②当式(12)不收敛

　　使用式(15)更新 $ {\boldsymbol{W}} $ ;

　　使用式(17)更新 $ {\boldsymbol{V}} $ ;

　　使用式(19)更新 $ {\boldsymbol{E}} $ ;

　　使用式(20)更新 $ {\boldsymbol{Y}} $ ;

　　使用式(21)更新 $ \mu $ ;

　end while

　return $ {\boldsymbol{W}} $

3) 输出多任务的模糊前件和多任务后件参数联合矩阵。

4 结果与分析 4.1 实验设置

为了验证本文提出的多任务建模方法的有效性，在多个真实数据集上进行泛化性能实验。实验中用到的数据集包含2种类型：一种是相同输入不同输出的SIDO数据集，将数据集的每一个输出作为一个回归任务构成一个多任务数据集，数据集的多个任务共享同一个输入数据，但每个任务拥有不同的输入空间到输出空间的映射函数；另一种是不同输入不同输出的DIDO数据集，同样将每一个输出作为一个回归任务，每个任务拥有不同的输入数据和不同的输入空间到输出空间的映射函数。

本节选择的Slump、Parkinsons Telemonitoring、Winequality、House数据集来自UCI Machine Learning Repository数据集网站。Slump数据集用来模拟混凝土的坍落度，涉及到坍落度、流动性和抗压强度3个输出，是一个SIDO数据集。Parkinsons Telemonitoring数据集由来自42名早期帕金森氏症患者的生物医学声音测量组成，用来测量motor和total UPDRS scores，也是一个SIDO数据集。Winequality数据集是一个利用基于理化测试数据来划分葡萄酒质量等级的数据集，包括红葡萄酒和白葡萄酒两个子集，本节分别将每个子集视为一个任务，这是一个DIDO数据集。House数据集被用于波士顿房价预测，在本节根据特征变量“RAD”的值将数据集划分为(Task 1: RAD<5; Task 2: 5<=RAD <7.5; Task 3: RAD>=7.5)3个子集，作为一个DIDO数据集。Multivalued (MV) Data Modeling数据集可以从KEEL Datasets Repository获得，是一个具有特征间依赖关系的人工数据集，本节中根据第8个特征变量可以将数据集划分为两个任务，作为DIDO数据集。表1中列出来了上述所选用的数据集的特征维数、样本数量等具体细节。

我们在实验中比较了几种经典的回归算法，包括多任务和单任务回归算法。算法中涉及到的参数的设置通过5折交叉验证来进行寻优，这些算法的详细介绍以及参数的寻优范围如表2所示。

本文选用RRSE来评价各对比算法的泛化性能，定义如下：

$ {J}_{\rm{RRSE}}=\sqrt{\sum \limits_{i=1}^{N}{(\widehat{{y}_{i}}-{y}_{i})}^{2}\Bigg/\sum \limits_{i=1}^{N}{(\overline{{y}_{i}}-{y}_{i})}^{2}} $

(22)

式中： $ \widehat{{y}_{i}} $ 是模型的预测输出； $ \overline{{y}_{i}} $ 是真实标签的均值。 $ {J}_{\rm{RRSE}} $ 越小表示模型的泛化能力越好。

4.2 泛化性能实验

我们分别在每个数据集上验证了MTTSKFS-CS及对比算法。

分别计算各模型在每个数据集的每个子任务上的泛化性能，其中“Average”表示算法在每个数据集的所有任务中的平均表现。若算法为单任务算法时，分别对每个子任务进行建模，来评价算法性能。本文提出的MTTSKFS-CS建模方法与对比方法在真实数据集上的实验结果如表3所示。

4.3 后件参数划分的可视化分析

为了进一步说明本文提出的对于后件参数矩阵的低秩和稀疏划分的重要作用，我们将模型在Parkinsons Telemonitoring数据集上训练出的后件参数 $ {\boldsymbol{W}}$ 、 ${\boldsymbol{V}} $ 、 ${\boldsymbol{E}} $ 进行可视化。图2展示了后件参数的可视化结果，从中可以看到，训练出的参数结果，基本符合图1中的假设， $ {\boldsymbol{W}} $ 被划分为了低秩部分 $ {\boldsymbol{V}} $ 和稀疏部分 $ {\boldsymbol{E}} $ 。

4.4 算法收敛性分析

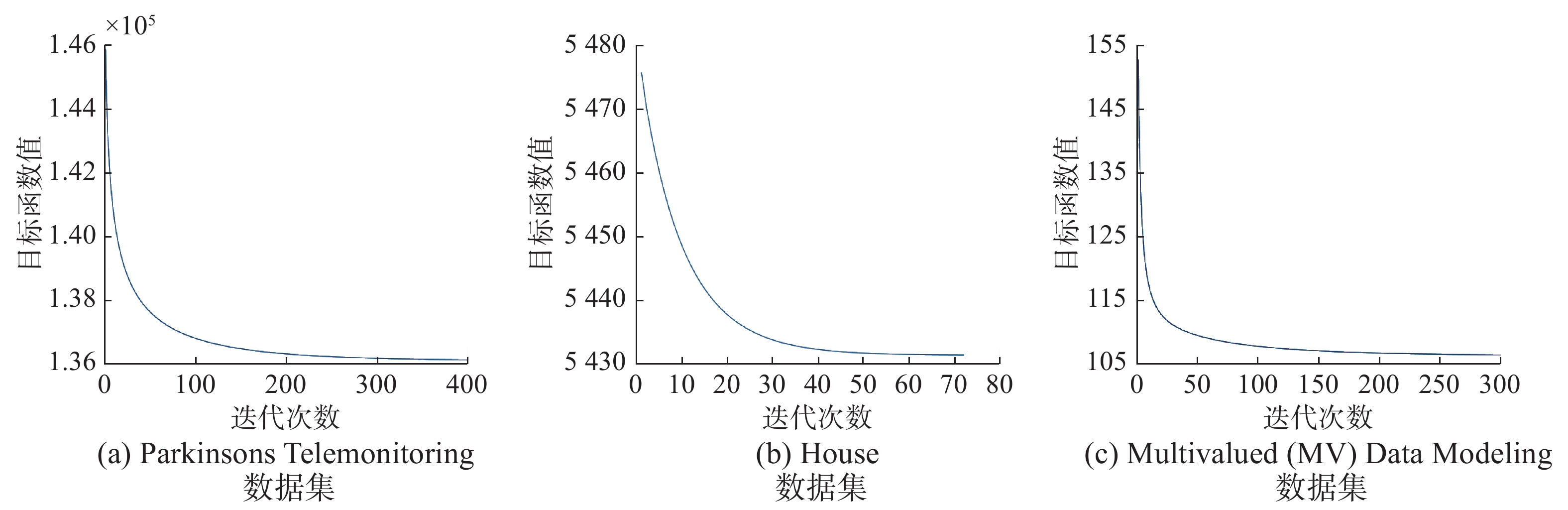
为了进一步研究本文提出的MTTSKFS-CS建模方法的收敛性，我们选取了Multivalued (MV) Data Modeling、Parkinsons Telemonitoring和House 3个数据集，通过交叉验证寻优得到最优参数，并在最优参数的基础上进行收敛性实验。算法在3个数据集上的收敛曲线如图3所示。从收敛曲线中可以看到，算法在前期可以快速收敛，并迅速进入稳定状态。实验结果说明，本文第3节提出的优化方法具有良好的收敛性能，能够真正达到模型最优化的目的，从而使模型获得较高的实用性。

4.5 实验结果分析

表3的实验结果证明MTTSKFS-CS方法在大多数任务上获得了比对比算法更好的性能表现。与单任务方法相比，多任务建模方法明显提升了每个任务的预测表现，拥有更好的泛化性能。与多任务算法的对比结果说明，本文提出的方法在利用了多任务之间的的共享信息的同时有效利用了单个任务自身的特有信息，从而获得了更好的表现。对于图2 的可视化结果，我们可以看到，后件参数联合矩阵 $ {\boldsymbol{W}} $ 被划分为了低秩部分 $ {\boldsymbol{V}} $ 和稀疏部分 $ {\boldsymbol{E}} $ ，实现了本文提出的模型设想，也间接验证了MTTSKFS-CS模型的有效性。

5 结束语

本文提出了一种新型多任务模糊系统建模方法，首先使用模糊聚类方法获得多任务的模糊前件，然后通过合理划分后件参数联合矩阵为共享参数矩阵和特有参数矩阵，同时兼顾多任务之间的共享信息和各任务的特有信息。最后通过ALM方法求解最优化问题，获得模型的最优解。在多个真实多任务数据集上的实验结果说明了，本文提出的MTTSKFS-CS建模方法能够有效解决传统多任务模型只着重于多任务共享信息的问题。在今后的工作中，如何更好地在建模中平衡共享信息和特有信息将是我们研究的重点。