2. 烟台大学 计算机与控制工程学院,山东 烟台 264005;
3. 德拉萨大学达斯玛里纳斯校区 科学与计算机学院,甲米地 达斯玛里纳斯 999005
2. College of Computer and Control Engineering, Yantai University, Yantai 264005, China;
3. College of Science and Computer Studies, DE la Salle University-Dasmarinas, Dasmarinas 999005, Philippines
随着移动互联网的飞速发展,众包任务[1]开始出现时间上和空间上的约束,一种新型的众包模式——时空众包应运而生。VRP(vehicle route planning)路径规划是一个经典问题,其目的是寻找一条从起点到目标终点能满足各种时间、空间约束的行驶路线,与时空众包中的任务分配问题具有很多相似性,因此本文考虑将两者结合起来,以解决任务分配问题。
在现有的时空众包研究中,任务分配是最核心的研究问题之一[2-3]。在当前的时空众包问题中,大部分问题场景都是基于动态场景,众包任务[4-5]和众包工人是动态出现的[6],随着时间推移,不断有新的对象出现和旧的对象消失。相比于传统的静态场景下的时空众包问题[7],动态场景更符合实际情况,在实际生活中更有应用价值。但是,现有的在线任务分配大多只考虑到众包任务和工人,研究的重点主要集中在工人完成任务的质量上,对于空间中的位置和工人执行任务时的路径规划研究得比较少,而三类对象的研究,通常只考虑距离范围,未考虑路径规划和移动成本的问题,对距离和时间的转换问题也研究较少。为将任务推荐给合适的工人[8],本文将众包任务、众包工人和它们所对应的时空属性结合起来,提出了基于自适应阈值的禁忌搜索算法,在满足时间约束和地理位置约束的条件下使得任务分配数最大化,同时保证众包工人能获得更多的收益。
1 相关工作 1.1 时空众包众包指的是一个公司或机构把过去由员工执行的工作任务,以自由自愿的形式外包给非特定的(而且通常是大型的)大众志愿者的做法[1]。随着众包应用的不断发展,众包形式由传统众包转变为了如今的时空众包,研究的内容也更加多样化。Boutsis等[9]首次提出了动态场景下的三类对象的在线任务分配问题,面向众包任务、众包工人以及任务执行地点的合理匹配。可以看出目前研究更多的是三类对象条件下的问题[10]。刘辉等[11]提出了一种能够对任务分配的当前情况自动调整阈值的算法,但分配总效用不高;Hassan等[12]提出一种基于统计预测的自适应阈值算法,进一步提高了分配总效用。不难看出,自适应阈值的应用能使问题解决方案得到优化。
1.2 车辆路径规划问题(VRP)随着科技的迅速发展,路径规划在众多领域内发挥着关键作用。比如:无人机驾驶、机器人避障行驶、GPS卫星导航等。
旅行商问题[13]是车辆路径规划问题的典型案例,Gaery[14]已经证明旅行商问题是NP难问题,因此可以推出车辆路径规划问题也属于NP难问题。
在真实环境中,通常VRP问题[15]的优化目标不是要求整个行车路程最短(费用最少),而是要求最长的子线路距离最短(时间最短),也就是VRP问题中经典的最小最大车辆路径问题。苏畅等[16]提出了一种改进模型,通过自适应地改进状态转移规则、权系数等条件使得解决方案效果得到了提升。Bai等[17]和Yu 等[18]分别提出车辆路径问题的模型与算法,通过在仿真数据的实验对该问题进行了理论分析。Ren[19]对于MMRVP问题,通过对问题模型的分析提出优化效果更好的混合算法。
由于车辆路径问题是NP难问题,通过算法得到精确的结果是十分困难的,需通过寻找近似算法来获得近似最优解,因此目前学者们在构造高质量的启发式算法上做了大量的工作。
2 问题描述本节给出形式化的问题描述,首先对问题以及对象进行定义,然后介绍一下问题模型,并进行动态场景下的复杂性分析。
2.1 基本定义定义1 众包任务。众包任务定义为
定义2 众包工人。众包工人定义为
定义3 任务对应地点。任务对应地点定义为
定义4 任务分配问题。给定任务集
| $ {\rm{Minavg}}(R) = \frac{{\displaystyle\sum\limits_{i = 1}^n {{\rm{W}}{{\rm{T}}_i}} }}{n} $ | (1) |
| $ {\rm{Max}}C = \sum\limits_{i = 1}^n {{\rm{Coupl}}{{\rm{e}}_{{\rm{WT}}_{i}}}} $ | (2) |
| $ {\rm{Coupl}}{{\rm{e}}_{{{wt}}}}=\left\{ \begin{array}{l} 0 \\ 1,\;\quad{\kern 1pt} {\rm{ a}}{{\rm{l}}_{wt}} < {d_t},{\rm{dist}}(w,t) <{\rm{min}}\left( { {r_w}\;{\rm{, }}\;{r_t}} \right) \\ \end{array} \right. $ | (3) |
| $ {\rm{Arriv}}{{\rm{e}}_{{{wt}}}} < {\rm{Arriv}}{{\rm{e}}_{{\rm{wc}}}} $ | (4) |
| $ \sum\limits_{i = 1}^{|w|} {{\rm{Coupl}}{{\rm{e}}_{{\rm{wt}}_i}} \approx \frac{{|T|}}{{|W|}}} $ | (5) |
式中:
1)每个任务都有最后的结束时间,要求工人必须在任务结束前将任务带到任务执行地点并完成任务,假设工人们的技术水平相同,并且任务到达任务执行地点便视为任务完成,如式(3)所示。
2)任务完成具有先后顺序,必须先领取任务,才能将任务带到执行地点,未领取任务之前便到达任务执行地点则不能视为任务完成,即式(4)中工人领取任务的时间必须早于工人到达任务
3)同一个工人执行的任务数不可过多,为保证总体的执行时间较少,在保证时间约束和总路程最小化的前提下,将任务平均地分配给工人,使得每个工人都能凭劳动力获得报酬。如式(5)所示,等号左边为工人
4)众包任务、工人以及任务执行地点要求在一定的区域范围内,距离过远的对象将不能进行任务分配,如式(3)所示。
例1描述了任务分配的执行过程。
例1 假设众包工作环境中有3个众包任务

|
Download:
|
| 图 1 任务、工人和任务执行地点位置示意 Fig. 1 Locations of tasks,workers, and customers | |
| 表 1 任务、工人和任务执行地点信息表 Tab.1 Information of tasks,workers, and customers |
由于问题的背景为动态情景,为了避免出现局部最优的情况,设置了时间窗,即在一定的时间段内,该时间段出现的3类对象的所有信息都是可知的。众包工人和众包任务随机散落在各个位置,当有任务出现的时候,其所对应的执行地点也会相应地出现,此时首先出现的任务就会分配给符合条件的工人。
假设工人
禁忌搜索算法被广泛地用来解决组合优化问题,如调度问题、TSP问题等。在此用组合优化的思想来简单介绍禁忌搜索算法的计算复杂度。对于
本文提出禁忌搜索算法与自适应阈值算法相结合的方法来解决基于路径规划的时空众包任务分配问题,首先分别对两种算法进行简单的介绍。
3.1 禁忌搜索算法禁忌搜索算法是在局部邻域搜索算法的基础上发展而来的,它的特点是采用了“禁忌表”的概念,利用了人类短时记忆的特点,从而避免重复性搜索,所谓禁忌[20]就是防止重复之前已经进行的工作,避免算法陷入局部最优,将搜索过程中出现的局部最优点记录在禁忌表中,在之后的搜索过程中,禁忌表中存在的信息便不再搜索,这样便可以跳出局部最优点。
禁忌搜索算法在最大车辆路径问题中应用较多。刘霞等[21]对禁忌搜索算法进行了改进,并通过一些典型的算法对最大最小车辆路径问题进行了研究;对车辆路径静态子问题,提出了蚁群算法[22]。为求解带时间窗和多配送人员的车辆路径问题,苏欣欣等[23]对该问题进行了数学建模,并用禁忌搜索算法来求解。
对于组合优化问题
算法输入迭代次数、禁忌搜索次数、禁忌表长度、循环次数以及工人集、任务集和地点集。为了提高搜索效率,采用贪婪的策略获取初始解,将总体迭代次数设置为100次,禁忌表的长度设置为10,输入任务集、工人集和地点集合。得到初始解后,进行下一步移动,迭代次数用来控制邻域搜索的次数,当所有任务都被分配后,迭代结束。将获取的局部最优解与禁忌表中的解进行对比,如果表中不存在,则填入禁忌表中,当禁忌表的长度达到10时,将表中的第一个解去掉,反复进行上述过程,在算法迭代100次后输出最优候选集,输出的结果为三类对象的顺序集合以及最小的总时间耗费。
对于众包工人的任务完成质量以及众包任务的预计等待时间,我们希望通过在线学习的方式训练出最理想的数值,在本小节借鉴自适应阈值的算法思想,来对工人服务质量进行设计。
质量控制是众包中的一个核心问题[24],众包工人初始都具有自己的服务质量属性,但是这个属性不是一成不变的,工人在完成任务过程中的表现,将会影响他们的服务质量:在规定的时间内更快地完成任务,工人的服务质量将获得提升,而不能在规定的时间内完成任务将受到差评,工人的服务质量将会相应地降低,虽然工人服务质量不会影响单个任务的报酬,但在任务分配过程中,在相似距离的条件下,系统将会优先把任务分配给服务质量更高的工人。
| $ {q_w} = {q_w} + \Bigg(1 - \frac{{{\rm{AW}}{{\rm{T}}_{{t}}}}}{{{\rm{EW}}{{\rm{T}}_{{t}}}}}\Bigg) \times \varepsilon $ | (6) |
式(6)用来计算每次完成任务后,工人
| $ \sigma = \frac{{\displaystyle\sum\limits_{i = 1}^{|W|} {{q_i}} }}{{|W|}} - \theta $ | (7) |
通过式(7)计算出一个阈值,每个工人必须大于该阈值才能参与任务分配。式(7)中的
| $ {P_i} = {P_i} \times {(1 + \tau )^{({\rm{cos}}{{\rm{t}}_{{\rm{max}}}} - {\rm{cost}})/{\rm{cos}}{{\rm{t}}_{{\rm{max}}}}}} $ | (8) |
阈值的自适应变化过程具体如下:
不同的任务由于与所分配工人的距离不同,所以预计等待完成的时间也不相同,每个任务在分配的时候都要计算出一个预计等待时间,工人要求在这个预计等待时间内完成任务。预计等待时间过长,则工人的效率就会降低,总体所耗费的时间便会增加,并影响到最终的优化目标;如果预计等待时间过短,那么工人便无法在短时间内同时执行多个任务,工人不能顺路接取任务,也会造成一定的时间浪费,同样无法达到优化平均任务完成时间的目的,所以预计等待时间的选取需要经过认真考虑。
| $ {\rm{EW}}{{\rm{T}}_{\rm{i}}} = \frac{{|T|}}{{|W|}} \times \alpha + [{\rm{dist}}({l_t},{l_c}) + {\rm{dist}}({l_t},{l_w})] \times \beta $ | (9) |
预计等待时间的计算式(9)所示,影响预计等待时间的因素包括任务与地点之间的距离以及任务与工人之间的距离,当这两个距离过长时,意味着工人耗费在路程上的时间更多,需要更多的时间来执行该任务。另一个影响因素是当前区域工人密度,本文使用任务数与工人数的比值来表示。当工人数量较多的时候,每个工人分配到的任务数较少,任务可以更早完成;当工人数量较少时,每个工人将分配更多任务,导致一定数量的任务较迟执行。其中
实验环境:处理器为AMD Athlon(tm) Quad-Core Processor 2.79 GHz,内存容量为8 GB,Windows 7操作系统,编程语言 为 Python3.7。
为验证本文算法的有效性,从时空众包平台gMission[25]获取了8000条记录,并在此数据的基础上进行了模拟数据的实验。该数据集包括工人、任务和任务对应地点3部分数据组成,每一个对象用一列数据表示,所包含的属性包括该对象出现的时间、截止的时间、对象所在的地理坐标、可匹配的半径范围以及每个对象所特有的属性,例如:任务有其所对应的报酬,而工人具有服务质量的属性。将任务、工人以及任务对应的执行地点映射在100×100的网格中,对象的位置以二维坐标表示。
本实验从多方面与基于统计预测的自适应阈值算法(ASPT)[11]、自适应随机阈值算法(Adaptive RT)[10]进行比较。
4.2 实验结果 4.2.1 改变工人数、任务数在本组实验中,通过改变工人和任务的数量,对比3个算法在任务的行驶的总路程、平均耗费的时间以及匹配数3个方面的对比情况,设置工人数分别为10、20、30,实验结果分别如表2~4所示。
表2为3个算法的任务总行驶距离的对比结果。从表中可以看出,随着任务数的增加,3个算法的总行驶距离都在不断增加。随着工人数量的增加,总行驶距离随之增加,当工人数量为30人时,3个算法的行驶总距离趋于稳定或者有所下降,这是因为当工人数较多时,本文所提算法能够进行更广泛的候选项搜索,并得出行驶总路径较少的结果,而Adaptive RT算法和ASPT算法较多地考虑匹配对象之间的距离和效用是否满足阈值,因此匹配约束较多。
表3和表4分别为算法的平均耗费时间和匹配数的对比结果。从表中可以看出:随着任务数增加,3个算法的平均耗费时间和匹配数都是不断增加的;随着工人数量的增加,平均耗费的时间是不断减少的。
| 表 2 3种算法在行驶总距离的对比结果 Tab.2 Comparison results of the three algorithms in terms of the total distance traveled |
| 表 3 3种算法在平均耗费时间的对比结果 Tab.3 Comparison results of the three algorithms in terms of the average time consumption |
| 表 4 3种算法在匹配数的对比结果 Tab.4 Comparison results of the three algorithms in terms of the number of allocations |
由于本文算法目标是优化平均任务执行时间,因此希望更多的工人参与,为此本文设定了工作质量阈值,目的是使略微低于平均工作质量的工人能够在保证整体任务完成质量的前提下也能参与进来,从而增加工人数量。因此本文算法在匹配数和平均耗时方面取得了较好的效果。
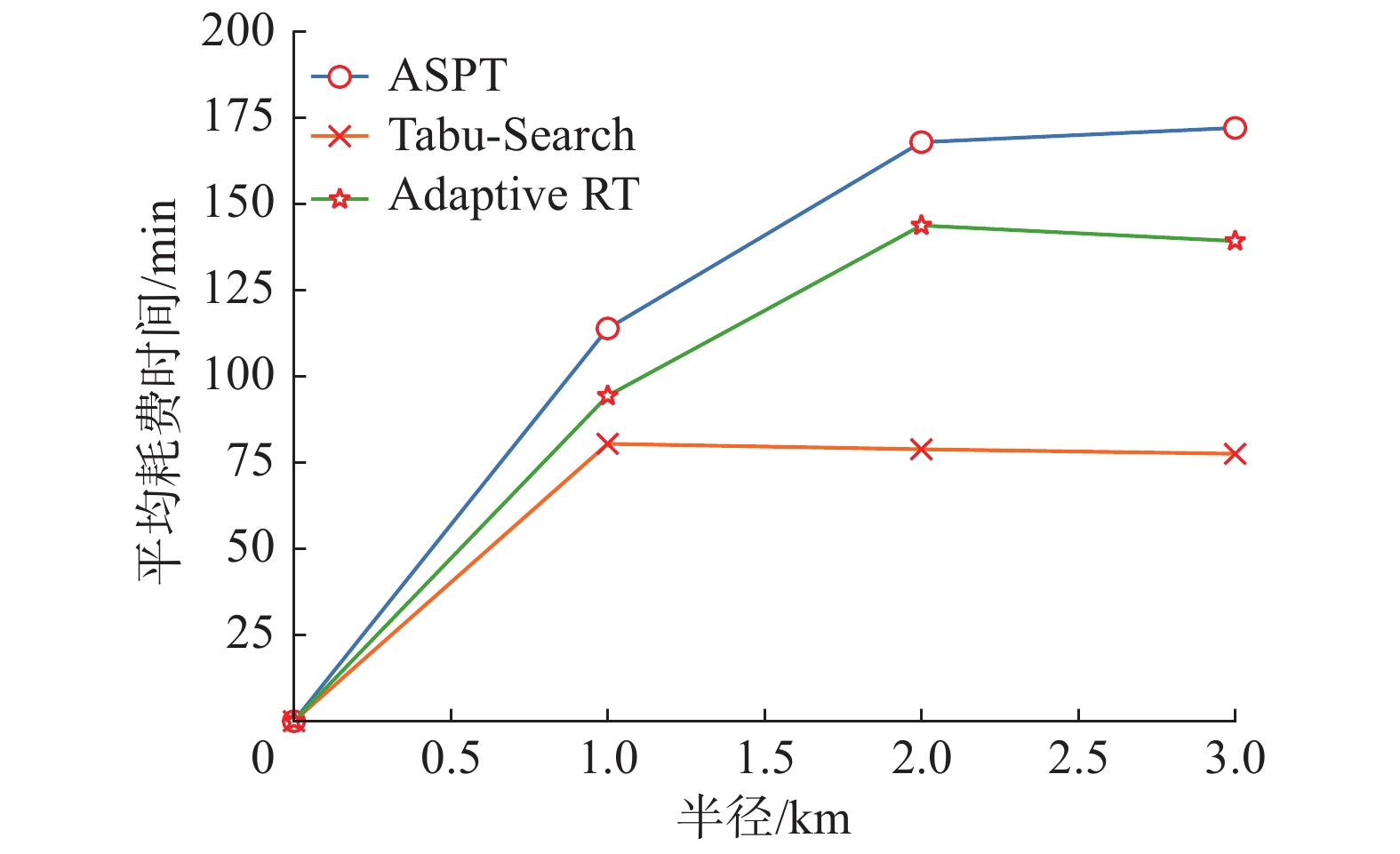
4.2.2 半径对比设置工人数量为20,任务数量为50,通过改变任务和工人的有效半径,对比3种算法在任务的分配数、耗费的总时间以及行驶的总路程几个方面的情况,实验结果如图2~4所示。
|
Download:
|
| 图 2 3种算法在半径变化时平均耗费时间的对比结果 Fig. 2 Comparison of the average calculation time-consuming results of the three algorithms when the radius changes | |
|
Download:
|
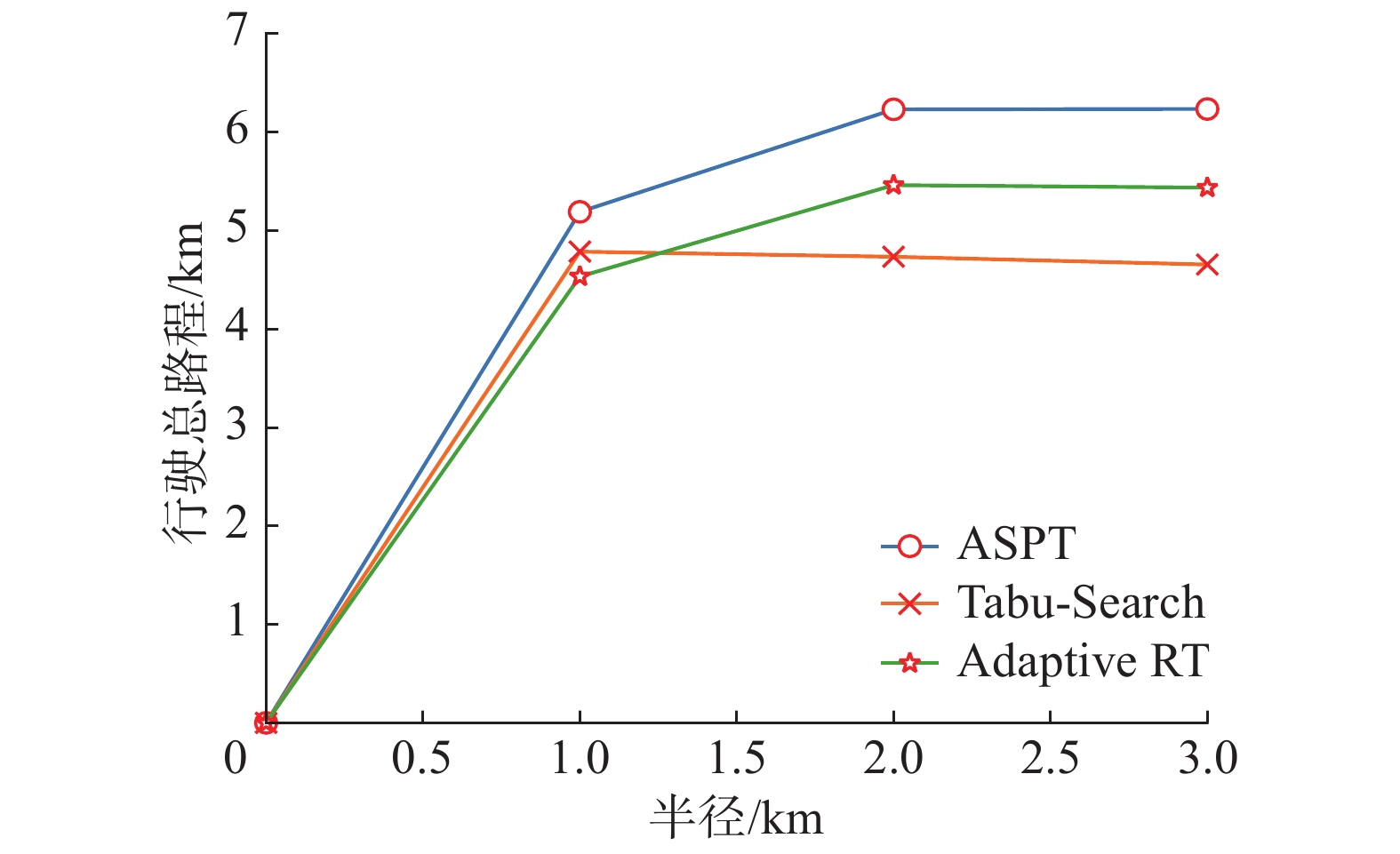
| 图 3 3种算法在半径变化时总行驶路程的对比结果 Fig. 3 Comparison of the total distance of the three algorithms when the radius changes | |

|
Download:
|
| 图 4 3种算法在半径变化时分配数的对比结果 Fig. 4 Comparison results of the allocation numbers of the three algorithms when the radius changes | |
从图2和图4可以看出,ASPT算法的平均耗费时间是在不断增加的,在半径为2 km时达到最佳匹配数。Adaptive RT算法同样在半径为2 km时达到最佳匹配数,由于工人数量充足,在半径为3 km时得到了更少的平均时间耗费。从图3和图4可以看出由于工人数量增加,在半径为1 km时ASPT和Adaptive RT算法的匹配数都更多一些,因此在总行驶路程上有了一定的增加。而本文所提算法由于已达到最大任务数,并且工人数量增加提高了算法邻域搜索的多样性,总行驶距离有小幅度减少。
从上述实验可以看出,工人和任务有效半径的大小对ASPT算法和Adaptive RT算法具有较大的影响,对本文所提算法的影响较小,原因是本文算法更多地考虑时间约束,并且追求匹配数量的优化,同时禁忌搜索算法本身的搜索优化能力较强,能够在相同条件下产生更多的有效匹配。
4.2.3 参数设置在计算预计等待时间时,设置
通过对比试验可以看出,改进后的禁忌搜索算法在行驶的总距离、耗费的平均时间以及对象的匹配数等方面都取得了相比于ASPT和Adaptive RT算法更理想的效果:本文所提算法在任务耗费时间上平均比Adaptive RT算法降低13%,比ASPT算法降低23.3%。在移动成本上比Adaptive RT算法降低了6.99%,比ASPT算法降低了25.9%。但是在算法的运行时间方面,本文所提算法具有较高的复杂度,运行时间较长,需要进行改进。

|
Download:
|
|
图 5 |
|
本文提出了众包工人需要携带任务到指定地点完成的工作模式,首次考虑了三类对象条件下众包工人的路径规划问题和移动成本问题;将空间上的距离成本换算成时间成本,分析了时间约束对任务分配过程的影响,提出了基于自适应阈值的禁忌搜索算法,并通过在线学习的方式,计算出每个任务合理的预估等待时间,通过合理的匹配使得区域内的众包任务能在最短的时间内得到分配。最后通过在真实数据集实验,验证了该算法在降低任务分配时间、提高匹配效率上具有高效性。在未来工作中,还要进行更多研究来降低算法的复杂度。同时,我们将继续研究路径规划中其他的经典算法,并将之应用到众包领域。
| [1] |
LAW E, VON AHN L. Human computation[J]. Synthesis lectures on artificial intelligence and machine learning, 2011, 5(3): 1-121. ( 0) 0)
|
| [2] |
童咏昕, 袁野, 成雨蓉, 等. 时空众包数据管理技术研究综述[J]. 软件学报, 2017, 28(1): 35-58. TONG Yongxin, YUAN Ye, CHENG Yurong, et al. Survey on spatiotemporal crowdsourced data management techniques[J]. Journal of software, 2017, 28(1): 35-58. (  0) 0)
|
| [3] |
刘辉. 时空众包环境下在线任务分配策略的研究[D]. 济南: 山东建筑大学, 2018. LIU Hui. Research of online task allocation strategy in spatio-temporal crowdsourcing environment[D]. Jinan: Shandong Jianzhu University, 2018. (  0) 0)
|
| [4] |
KAZEMI L, SHAHABI C. Geocrowd: enabling query answering with spatial crowdsourcing[C]//Proceedings of the 20th International Conference on Advances in Geographic Information Systems. Redondo Beach, USA, 2012: 189−199.
( 0) 0)
|
| [5] |
TONG Yongxin, SHE Jieying, DING Bolin, et al. Online mobile micro-task allocation in spatial crowdsourcing[C]//2016 IEEE 32nd International Conference on Data Engineering (ICDE). Helsinki, Finland, 2016: 49−60.
( 0) 0)
|
| [6] |
LI Yu, YIU M L, XU Wenjian. Oriented online route recommendation for spatial crowdsourcing task workers[C]//Proceedings of the 14th International Symposium on Spatial and Temporal Databases. Hong Kong, China, 2015: 137−156.
( 0) 0)
|
| [7] |
LI Guoliang, WANG Jiannan, ZHENG Yudian, et al. Crowdsourced data management: a survey[J]. IEEE transactions on knowledge and data engineering, 2016, 28(9): 2296-2319. DOI:10.1109/TKDE.2016.2535242 ( 0) 0)
|
| [8] |
PAN Qingxian, DONG Hongbin, WANG Yingjie, et al. Recommendation of crowdsourcing tasks based on word2vec semantic tags[J]. Wireless communications and mobile computing, 2019, 2019: 2121850. ( 0) 0)
|
| [9] |
BOUTSIS I, KALOGERAKI V. On task assignment for real-time reliable crowdsourcing[C]//2014 IEEE 34th International Conference on Distributed Computing Systems (ICDCS). Madrid, Spain, 2014: 1−10.
( 0) 0)
|
| [10] |
宋天舒, 童咏昕, 王立斌, 等. 空间众包环境下的3类对象在线任务分配[J]. 软件学报, 2017, 28(3): 611-630. SONG Tianshu, TONG Yongxin, WANG Libin, et al. Online task assignment for three types of objects under spatial crowdsourcing environment[J]. Journal of software, 2017, 28(3): 611-630. (  0) 0)
|
| [11] |
刘辉, 李盛恩. 时空众包环境下基于统计预测的自适应阈值算法[J]. 计算机应用, 2018, 38(2): 415-420. LIU Hui, LI Shengen. Adaptive threshold algorithm based on statistical prediction under spatial crowdsourcing environment[J]. Journal of computer applications, 2018, 38(2): 415-420. (  0) 0)
|
| [12] |
HASSAN U U, CURRY E. Efficient task assignment for spatial crowdsourcing: a combinatorial fractional optimization approach with semi-bandit learning[J]. Expert systems with applications, 2016, 58: 36-56. DOI:10.1016/j.eswa.2016.03.022 ( 0) 0)
|
| [13] |
GAREY M R, JOHNSON D S. Computers and intractability: a guide to the theory of NP-completeness[M]. New York: W. H. Freeman & Co., 1979: 79−87.
( 0) 0)
|
| [14] |
DANTZIG G B, RAMSER J H. The truck dispatching problem[J]. Management science, 1959, 6(1): 80-91. DOI:10.1287/mnsc.6.1.80 ( 0) 0)
|
| [15] |
毕国通. 车辆路径问题及其优化算法研究综述[J]. 物流科技, 2016, 39(6): 95-97. BI Guotong. The review of vehicle routing problem and its optimization algorithm[J]. Logistics sci-tech, 2016, 39(6): 95-97. DOI:10.3969/j.issn.1002-3100.2016.06.028 (  0) 0)
|
| [16] |
苏畅, 徒君. 一种自适应最大最小蚁群算法[J]. 模式识别与人工智能, 2007, 20(5): 688-691. SU Chang, TU Jun. An adaptive max-min ant colony algorithm[J]. Pattern recognition and artificial intelligence, 2007, 20(5): 688-691. DOI:10.3969/j.issn.1003-6059.2007.05.017 (  0) 0)
|
| [17] |
BAI Jie, YANG Genke, CHEN Yuwang, et al. A model induced max-min ant colony optimization for asymmetric traveling salesman problem[J]. Applied soft computing, 2013, 13(3): 1365-1375. DOI:10.1016/j.asoc.2012.04.008 ( 0) 0)
|
| [18] |
YU Jiapeng, WANG Chengen. A max-min ant colony system for assembly sequence planning[J]. The international journal of advanced manufacturing technology, 2013, 67(9/10/11/12): 2819-2835. ( 0) 0)
|
| [19] |
REN Chunyu. Solving min-max vehicle routing problem[J]. Journal of software, 2011, 6(9): 1851-1856. ( 0) 0)
|
| [20] |
李阳, 李文芳, 马骊, 等. 混合退火算法求解旅行商问题[J]. 计算机应用, 2014, 34(S1): 110-113. LI Yang, LI Wenfang, MA Li, et al. Hybrid annealing algorithm for solving travellling salesman problem[J]. Journal of computer applications, 2014, 34(S1): 110-113. (  0) 0)
|
| [21] |
刘霞, 齐欢. 最小−最大车辆路径问题的禁忌搜索算法[J]. 系统工程, 2007, 25(1): 49-52. LIU Xia, QI Huan. Tabu search algorithm of min-max vehicle routing problems[J]. Systems engineering, 2007, 25(1): 49-52. DOI:10.3969/j.issn.1001-4098.2007.01.009 (  0) 0)
|
| [22] |
刘霞, 杨超. 最小−最大车辆路径问题的蚁群算法[J]. 解放军理工大学学报(自然科学版), 2012, 13(3): 336-341. LIU Xia, YANG Chao. Min-max vehicle routing problem based on ant colony algorithm[J]. Journal of PLA University of Science and Technology (Natural Science Edition), 2012, 13(3): 336-341. (  0) 0)
|
| [23] |
苏欣欣, 秦虎, 王恺. 禁忌搜索算法求解带时间窗和多配送人员的车辆路径问题[J]. 重庆师范大学学报 (自然科学版), 2020, 37(1): 22-30. SU Xinxin, QIN Hu, WANG Kai. Tabu search algorithm for the vehicle routing problem with time windows and multiple deliverymen[J]. Journal of Chongqing Normal University (Natural Science Edition), 2020, 37(1): 22-30. (  0) 0)
|
| [24] |
PAN Qingxian, PAN Tingwei, DONG Hongbin, et al. An online task assignment based on quality constraint for spatio-temporal crowdsourcing[J]. IEEE access, 2019, 7: 170292-170303. DOI:10.1109/ACCESS.2019.2942155 ( 0) 0)
|
| [25] |
CHEN Zhao, FU Rui, ZHAO Ziyuan, et al. gMission: a general spatial crowdsourcing platform[J]. Proceedings of the VLDB endowment, 2014, 7(13): 1629-1632. DOI:10.14778/2733004.2733047 ( 0) 0)
|
 2020, Vol. 15
2020, Vol. 15


