相机标定与畸变校正是计算机视觉技术的基础,视觉测量、三维重建、增强现实等机器视觉研究,均基于对所使用的视觉传感器内外部参数的精确标定和有效的畸变校正,以确定二维像平面上的点与三维空间点的映射关系。对于精度要求较高的视觉测量工程应用领域,大广角相机常有的大范围非线性畸变、制造工艺以及应用场景(基于摄像机的汽车增强现实[1])造成的非规则的特殊畸变校正问题十分关键。目前相机标定的方法一般分为两类:传统方法和自标定方法[2-3]。传统方法需要精确的参照物,通过参照物三维空间的坐标与图像中的对应点,求取内外参数和畸变校正,通过标定物的不同又细分为基于3D和基于2D平面靶标的标定,主要代表算法有张正友标定算法[4]和Tsai两步法[5-6]。Chang等[7]根据霍夫变换峰值的特点,以现有畸变模型为基础,提出了一种透镜畸变参数辨识方法,该方法只需要场景中存在直线即可进行辨识,更加灵活;自标定方法则通过图像自身的信息来对视觉传感器进行标定,它分为3类,即基于主动视觉[8]、利用矩估计[9]和本质矩阵[10]、利用绝对二次曲线[11]和极线变换性质。自标定虽然有着无需标定物的优势,但主动视觉方法需要昂贵的系统成本。也有一些特殊的标定方法,例如基于消失点的单张图片标定[12],使用二元三次多项式与三角插值的方法[13]实现短焦距大广角的非线性畸变校正等。
现有的棋盘检测方法仍然只能检测规则的棋盘格。广角相机相对于一般相机,视野更加开阔,能够从图像中获取更多的信息,但是传统二维标定方法在复杂畸变(透镜有凹陷或突出、透镜不规则等情况)和广角相机广角方向的畸变校正,受限于畸变模型,仍然存在一定的误差,影响成像的有效信息区域,以及应用的测量精度。
针对上述2种情况,本文改进了棋盘格检测方法,使其能够检测不规则的棋盘格。基于传统二维标定物,提出了使用插值算法来进行相机畸变校正。通过本文方法进行畸变校正后,再求取内外参数。在应用时,可以根据需要选择将畸变校正部分转换成插值映射表,特殊情况下也可以将拟合曲面以及内外参数合并转换成插值映射表,提高使用时的速度。
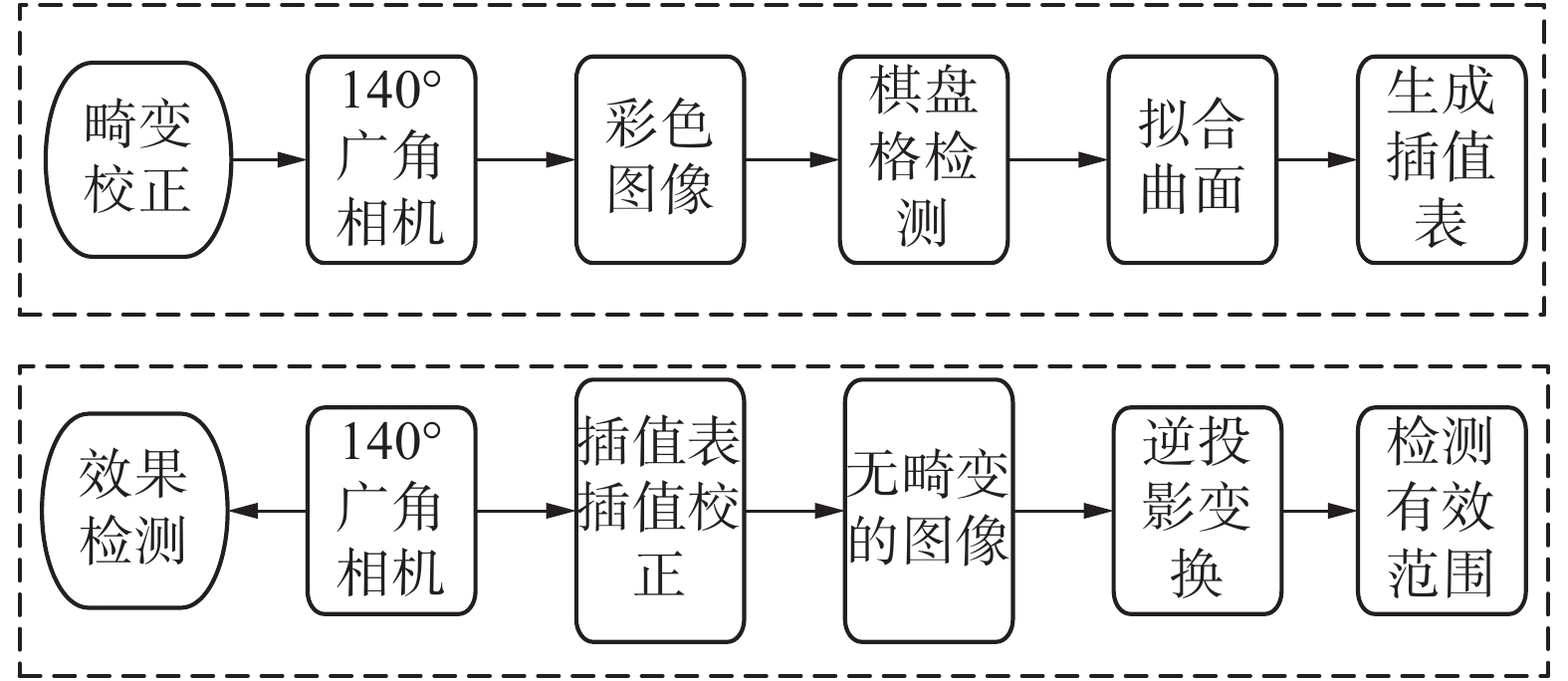
1 基于插值算法的广角相机畸变校正基本原理 1.1 系统流程本文提出的基于插值算法的广角畸变校正的流程如图1所示,分为畸变校正与效果检测两部分内容。
|
Download:
|
| 图 1 系统流程 Fig. 1 System flow | |
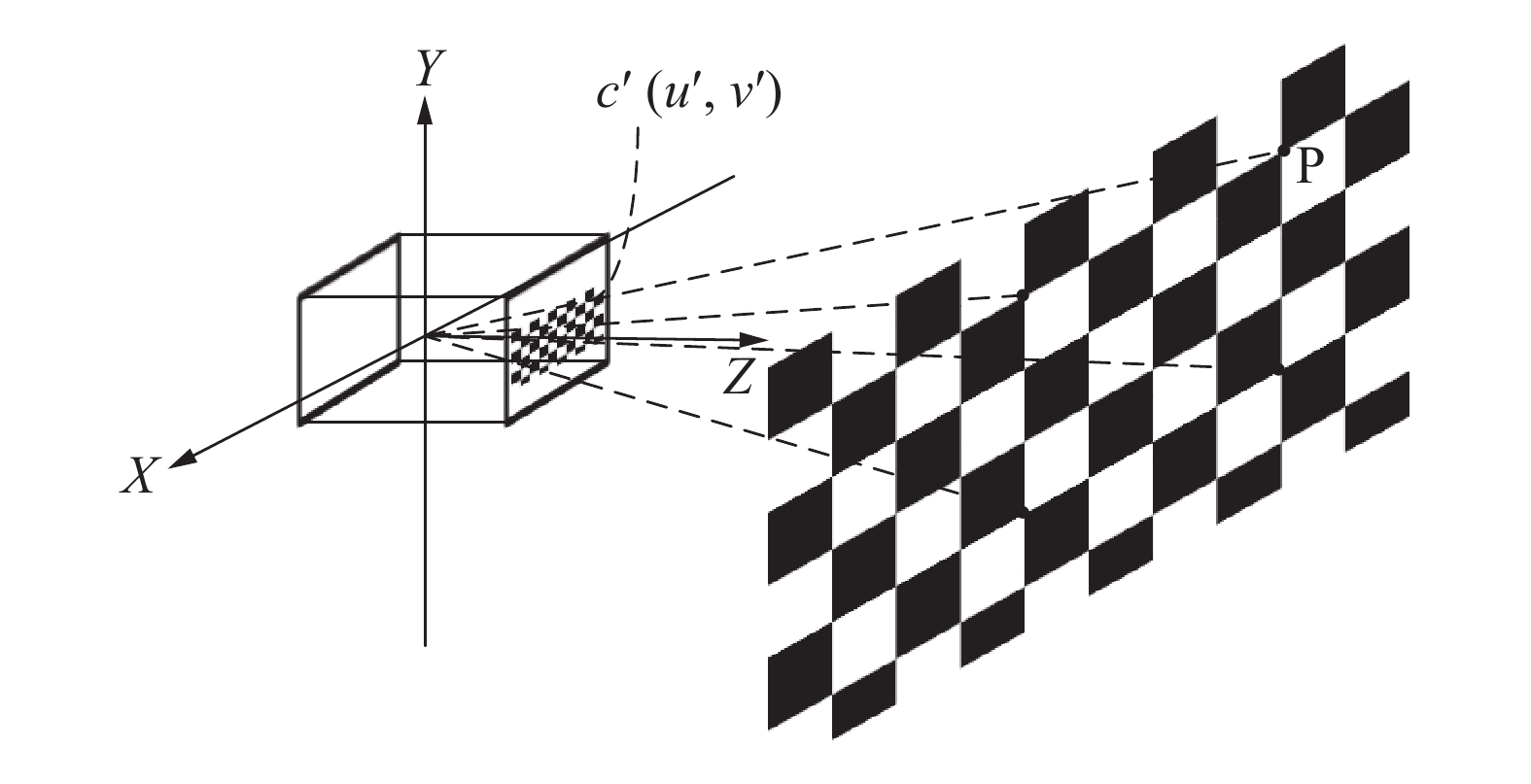
畸变校正部分:如图2所示拍摄的一张包含棋盘格的图像,通过在成像平面内画出对称的点、线 ,来作为实时检测成像窗口的辅助线,使棋盘平面与像平面平行;通过特征点检测和棋盘格检测,得到棋盘格内角点数据,并初始化期望角点数据。通过检测和期望角点进行曲面拟合,得到两个畸变插值曲面。最后使用反向双线性插值,得到插值表格。检测部分,首先对同一张图片,使用不同方法进行畸变校正,然后逆投影变换到同一个平面和尺度,计算其真实角点(检测到的棋盘格内角点)与期望角点(根据中心附近的点生成)的误差,最后拟合成误差曲面,转换为误差范围内的正视图,比较有效范围。
|
Download:
|
| 图 2 拍摄位姿 Fig. 2 Shooting pose | |
相机校正方法涉及两方面的问题:一方面是数据的获取,另一方面是标定的模型。数据获取的关键在于棋盘格检测。
现有的棋盘格检测大致分为形态匹配和特征匹配[14]:一种是通过腐蚀膨胀检测正方形,来寻找棋盘格内角点,然后根据棋盘格特征得到棋盘格;另一种是通过匹配角点特征寻找内角点,然后通过棋盘格特征得到棋盘格。而对于畸变较严重的部分,是无法检测出棋盘格黑色部分为正方形的,故采用后一种基于生长法的角点特征匹配方法。该方法的主要步骤如下:
1)角点检测。设置基础模版,并进行角点匹配。
2)筛选角点。极大值抑制,去除边沿点,去除评分较低的点。
3)寻找棋盘。以棋盘能量作为生长的依据,当4个方向上的总能量都大于零时结束。
1.3 改进棋盘检测方法由于拍摄到的图像不是规则的棋盘格(有一部分棋盘格未在图像中出现)且棋盘格离像平面较近,现有的检测方法无法满足需要。
1)改进筛选角点步骤,改进图像中间区域。由于距离较近且灰度变换后,在中间区域的梯度值下降,影响到角点的打分,会在剔除低评分角点的时候误删除。通过一定的膨胀,使比例范围的中间区域内的评分增加。
2)改进寻找棋盘步骤,新增匹配部分。将生长出来的且满足棋盘格能量阈值的棋盘格进行拼接,达到增加棋盘内角点的目的。首先进行棋盘格方向校正:
| $\begin{aligned} & {\rm{acha}}(i) = {P_a}(i + 1) - {P_a}(i),i = 1 ,2,\cdots, n - 1\\ & {\rm{direction}}{\rm{.}}ab = {\rm{direction}}{\rm{.}}a - {\rm{direction}}{\rm{.}}b\\ & C_b^a = {\rm{rot}}90({C_b},{\rm{direction}}{\rm{.}}ab)\\ \end{aligned}$ |
式中:
| 表 1 相对角度查值表 Tab.1 Relative angle checklist |
然后,通过匹配进行棋盘格的扩张:
| $\begin{array}{l} C\left( {m + \max ({a_1},{b_1}) - {a_1},n + \max ({a_2},{b_2}) - {a_2}} \right) = a\left( {m,n} \right)\\ C\left( {m + \max ({a_1},{b_1}) - {b_1},n + \max ({a_2},{b_2}) - {b_2}} \right) = b\left( {m,n} \right) \end{array}$ |
改进前后的棋盘格如图3所示,可以看到原有的检测方法只能检测出5个棋盘格,且棋盘格未联通,改进之后的棋盘格扩大了检测到的棋盘格,增加了数据点的数量。

|
Download:
|
| 图 3 改进前后棋盘格检测 Fig. 3 Chess board detection before and after improvement | |
拟合曲面的方法大致可以分为整体拟合和局部拟合两类,在这两类中同时存在确定性和非确定性两个类别。常见的有趋势面、回归、泰森、密度估算、反距离权重[15]、薄板样条[16](TPS)、克里金、双简谐(Biharmonic)。其中的TPS和Biharmonic方法都是以最小曲率曲面拟合数据点,具有数据点限制(个数和位置)较小,实现容易等优点。
TPS是一种最小曲率插值方法,该函数分为2部分:基函数和趋势函数。基函数作为离散部分,通过对每个数据点附近的曲面进行弯曲拉伸,使其通过数据点,并使能量函数最小;趋势函数作为仿射部分,根据所有数据点拟合的一个平面,反映数据点外的薄板的曲面趋势。通过对函数中的参数计算,得到拟合后的曲面:
| $f\left( {x,y} \right) = \underbrace {{a_0} + {a_x}x + {a_y}y}_{\text{趋势函数}} + \underbrace {\sum\limits_{i = 1}^n {{w_i}U(\left| {{P_i}} \right| - (x,y))} }_{\text{基函数}}$ |
式中:
Biharmonic是基于双谐波算子的Green函数的插值算法,适合一维和多维数据。通过寻找一组非均匀间距数据点的最小曲率曲面,调整每个数据点为中心的Green函数的幅值对曲面进行拉伸,使曲面能通过这些数据点,其曲面函数如下:
| $\left\{ {\begin{aligned} & {{\nabla ^4}w(x) = \sum\limits_{j = 1}^N {{\alpha _j}} \delta (x - {x_j})} \\ & {w({x_i}) = {w_i}} \end{aligned}} \right.$ |
式中:x是在m维空间中的位置;
| 表 2 Biharmonic Green函数 Tab.2 Biharmonic Green function |
传统的畸变校正方法,是由切向畸变(一般不考虑)和径向畸变共同构成:
| $\begin{array}{*{20}{c}} {u = {u^*}[1 + {k_1} \cdot ({u^{*2}} + {v^{*2}}) + {k_2} \cdot {{({u^{*2}} + {v^{*2}})}^2}]} \\ {v = {v^*}[1 + {k_2} \cdot ({u^{*2}} + {v^{*2}}) + {k_2} \cdot {{({u^{*2}} + {v^{*2}})}^2}]} \\ \end{array}$ |
式中:
但是在计算畸变参数的时候,是将内外参数、畸变参数以及主点(光心偏移)、焦距等参数同时求解,构造最大似然估计函数,转换成多参数非线性系统优化问题。存在的误差主要来自3个方面:1)畸变函数并不能完全代表畸变曲面,其得到的畸变结果存在误差;2)在求解内外参数以及畸变参数的最优解时,其内外参数不准确,导致求出的畸变参数也会产生误差;3)对于广角相机的广角方向有效区间并不大,失去了广角相机的优势。
1.6 本文畸变校正方法本文将畸变校正从相机整体标定中分离出来。使用TPS和Biharmonic插值算法,对映射关系数据点进行曲面拟合,再进一步得到畸变校正插值表,然后对图像去畸变。在后续使用的时候,可以直接载入畸变校正插值表,实时对相机采集到的图像去畸变。
映射数据的映射关系为
| $\begin{array}{*{20}{c}} {u = {f_u}({u^*},{v^*})} \\ {v = {f_v}({u^*},{v^*})} \\ \end{array}$ |
式中:
通过遍历无畸变图像坐标得到畸变校正的插值表,使用反向双线性映射对畸变图像进行畸变校正来获得无畸变图像 。
2 实验结果及分析实验使用了摄像头(锐尔威视 140°)、A4纸打印的棋盘格、win7(x64)、MATLAB2015、opencv3.2、visual studio2015等器材和软件。
在实验中,使摄像头的成像平面尽可能地平行于A4纸上的棋盘格,通过实时显示成像窗口,拍摄一张图像,如图4(a)所示。

|
Download:
|
| 图 4 实时成像窗口与映射数据 Fig. 4 Real-time imaging window and mapping data | |
检测棋盘格,提取到广角相机659个数据点(在21×43的棋盘中内角点),初始化期望点,得到如图4(b)所示的由期望点到检测棋盘点的映射数据,仅展示了棋盘格右半部分。
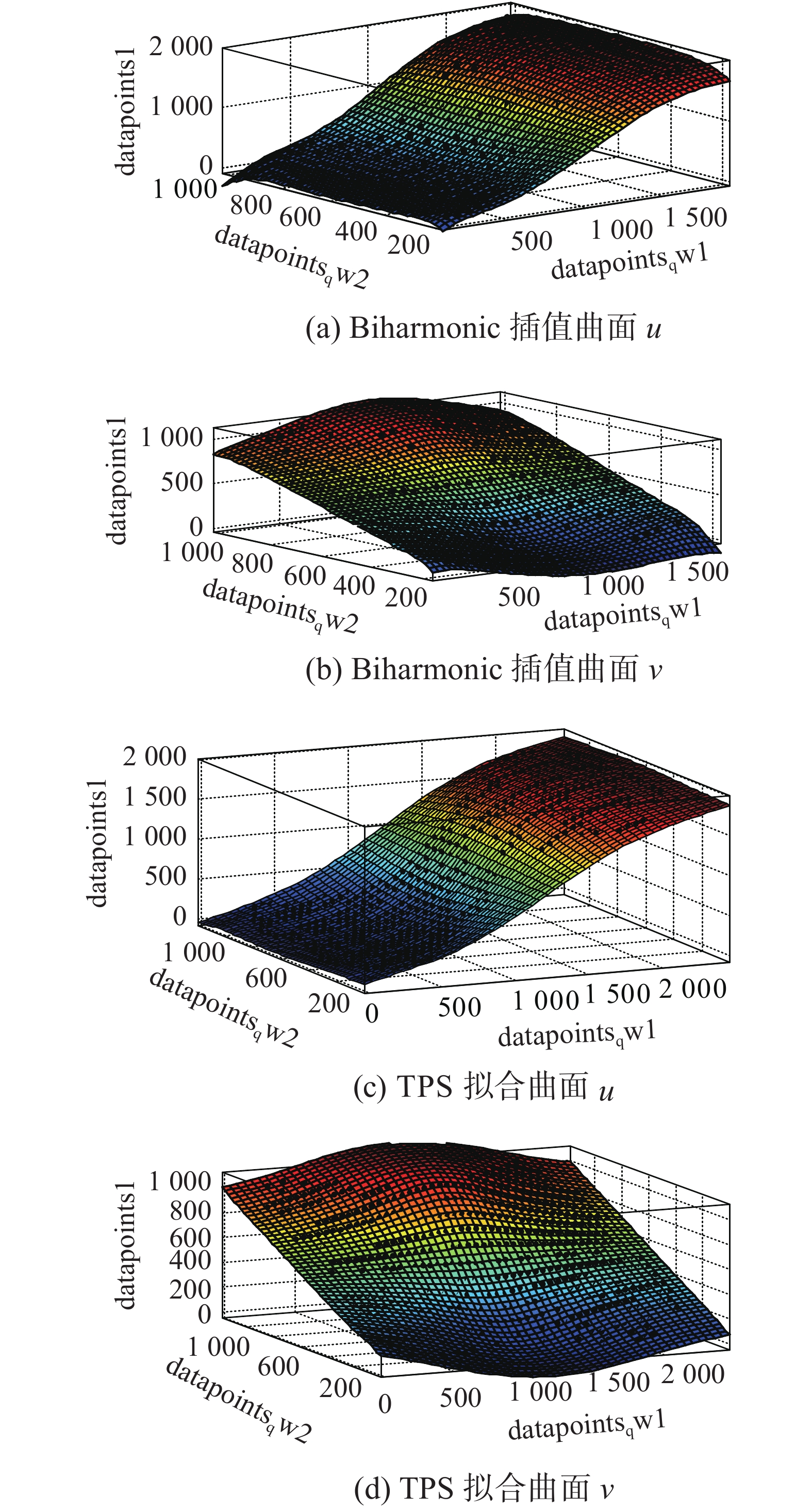
使用TPS和Biharmonic算法分别拟合曲面,如图5(单位:像素),其中横纵坐标(datapointsqw1, datapointsqw2) 表示原图像坐标(u, v), datapointsqwl 表示原图像坐标在u方向的映射值。生成插值表格后,就能够进行反向二插值映射得到去畸变后的图片。使用相机拍摄到的另一张图片(非拟合曲面的畸变图片),得到畸变校正后图像棋盘内角点和期望棋盘内角点曲面,然后通过图片中间区域(横向8个内角点×纵向3个内角点),进行正投影变换。检测正投影变换后的棋盘格内角点,根据中间区域的内角点,生成期望角点的坐标数据。
|
Download:
|
| 图 5 拟合曲面(TPS Biharmonic) Fig. 5 Fitting surface (TPS Biharmonic) | |
表3中的数据均来自标定的图片,曲面点误差为拟合曲面的数据点误差,即标定过程中实际坐标点与期望点的平均二范数。
| 表 3 畸变校正误差 Tab.3 Distortion correction error (pixels) |
综合表3与图6,Opencv的特征点误差为重投影误差,与插值方式的特征点误差可比性较差;畸变校正图中,Opencv校正后的图像,边沿区域偏差越靠近边沿区域误差越大,插值方法校正结果在边沿区域的误差更小,更精确。但插值法的角落区域存在更大的误差。
1)中间部分不平滑:主要由于去畸变后图像的角点检测,不是很精确,其生成的期望坐标不准确。
2)曲面点误差极小:由于其最小曲面拟合的特殊性,其边沿点并不能达到该精度。且对于边沿区域的效果,误差从最边缘向内的第2个数据点开始出现,并随着靠近边缘而增大,如图6所示。

|
Download:
|
| 图 6 畸变校正图 Fig. 6 Distortion correction and re-projection error surface | |
3)边沿区域的畸变:①对于TPS插值方法,主要是由于趋势函数引起的。在数据点外,距离中心点越远,偏移量在无穷远处会趋于零(平面),表现在离中心点越远的区域越接近原图像。②对于Biharmonic方法,主要是因为Green函数引起的。在数据点外,距离中心点越远,偏移量会在无穷远处趋于无穷大,表现在离中心点越远的区域,向
本文针对TPS方法进行了实时视觉定位的实验。该系统的硬件部分主要是由3部分组成:实验主体单元(长安逸动改装版)、视觉传感单元(锐尔威视140°)、处理单元(华硕K550JX)。
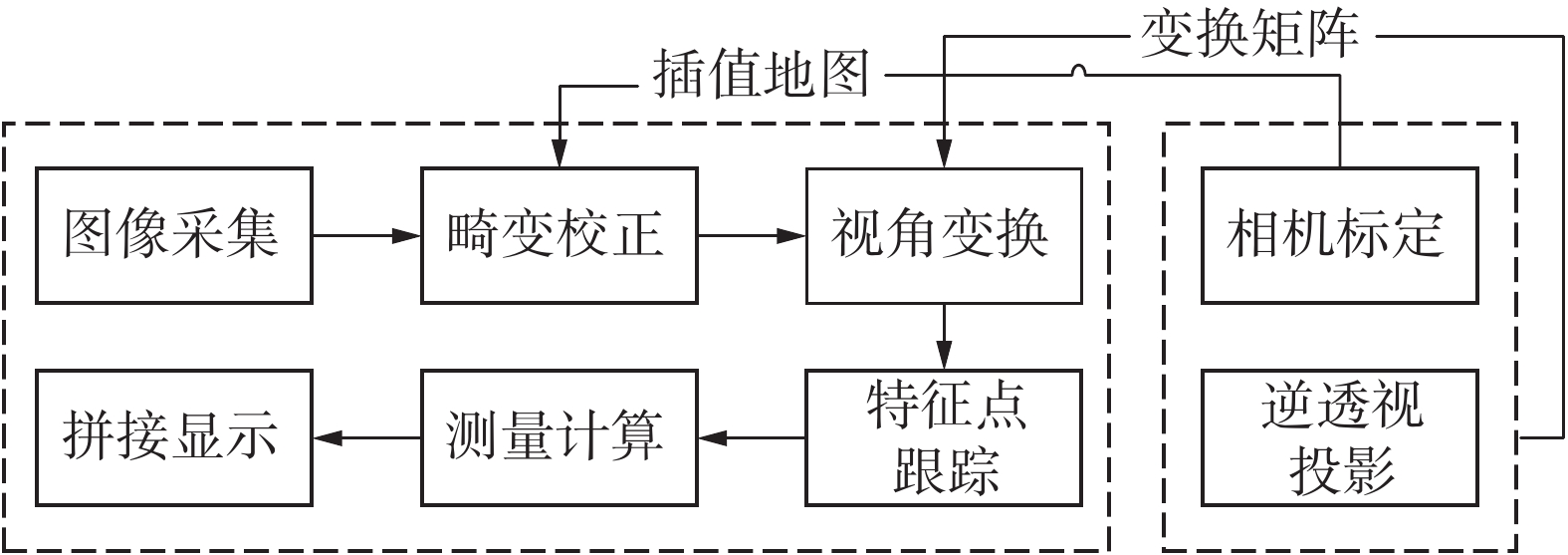
离线部分,图7右侧虚线内部分。标定了相机的外部参数以及成像的有效区域,为后文视觉定位的后台处理部分做准备。同时离线部分还能够标定出图像中的像素物理比例和车辆位置信息,直接测量出目标物体距离车辆的距离。其离线过程如图8所示。
|
Download:
|
| 图 7 软件系统构架 Fig. 7 Software architecture | |

|
Download:
|
| 图 8 汽车环境下相机标定 Fig. 8 Calibration under automotive | |
在线部分,如图7左侧虚线内部分。在线部分包含了后台处理部分,如图9(a)~(d)所示,还包含一个大地图(视觉惯导作用),在实际运行中并不显示。
在图9(e)的显示系统中,将车辆显示在地图中,得到车辆周围的环境,并在车辆尾部显示当前车辆的相对位置和相对姿态(相对于启动位置),若后向倒车则可将相机经过的地图保存下来,提供更宽的固定物体的参考,实现实时视觉定位的目的。
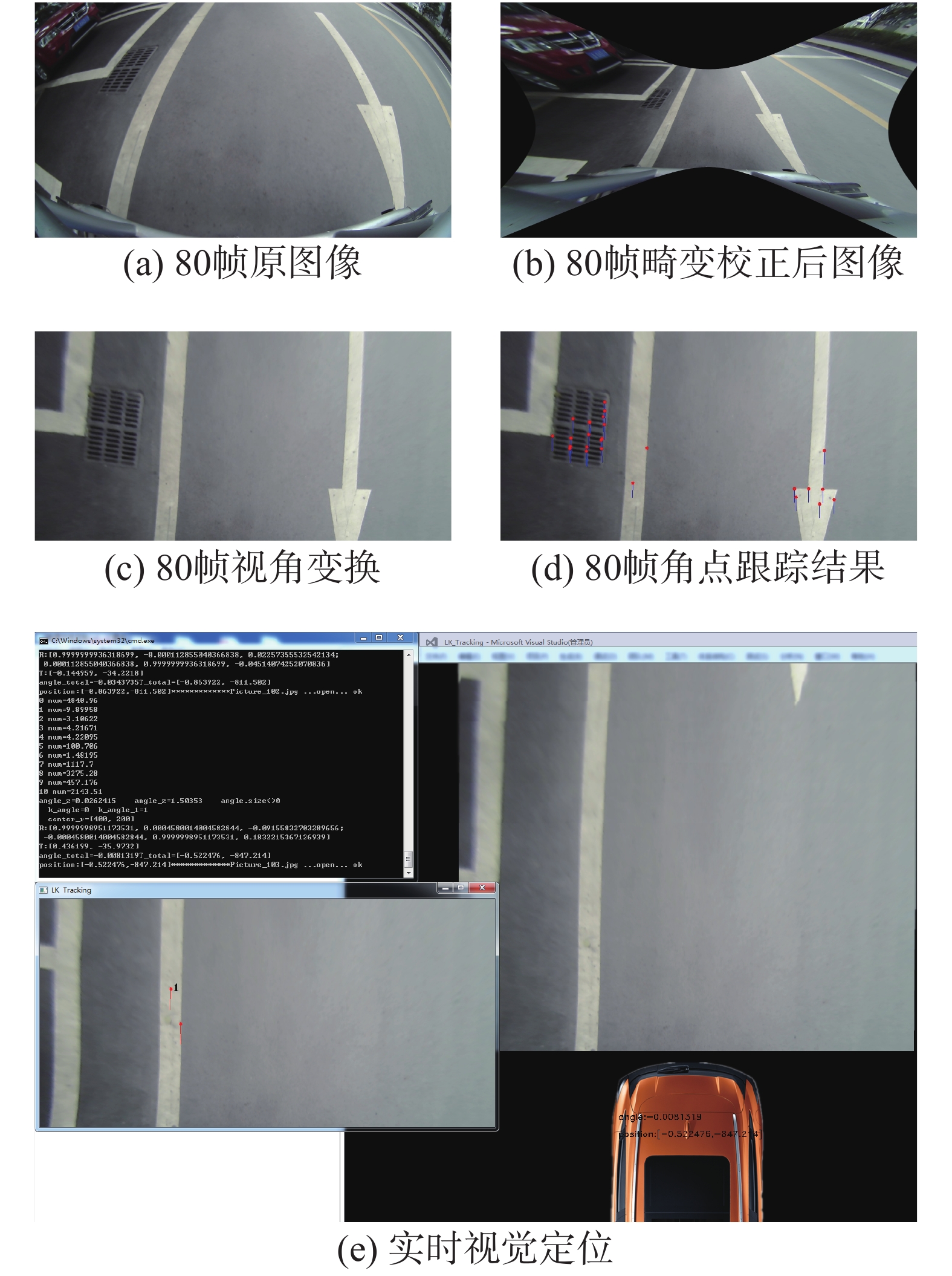
|
Download:
|
| 图 9 实车实验 Fig. 9 Experiment of real-vehicle | |
本文使用两种插值方法(双谐波、薄板样条),对广角相机的畸变和一些不规则畸变,均能够较好地校正。本文能够应用于一些需要广角精度较高的场合,节约了安装多个摄像头的成本。
改进的棋盘格检测方法,提高了棋盘格内角点检测的数量,丰富了数据。由于该畸变校正插值方法的特殊性,能实现某些特殊的镜头畸变校正,还能够对精度要求较高的环境,进行二次畸变校正;由于该插值方法依赖每个数据点,所以对于棋盘格中的每一个内角点精度都需要较高的精确度,即对标定物的精度和棋盘角点检测精度有较高要求,可能会增加一定的成本。
在实验中,对于畸变较大的边沿部分,仍然无法获取其棋盘格角点。对于边沿部分的畸变校正存在较大的误差。进一步研究方向:1)改进棋盘格角点检测,增加数据点的检测精度和数量;2)改进TPS趋势函数,提高边沿校正效果。
| [1] |
WIENTAPPER F, WUEST H, ROJTBERG P, et al. A camera-based calibration for automotive augmented reality Head-Up-Displays[C]// 2013 IEEE International Symposium on Mixed and Augmented Reality (ISMAR), Adelaide, Australia, 2013: 10−21.
( 0) 0)
|
| [2] |
彭亚丽, 刘侍刚, 裴炤, 等. 基于非刚体轨迹基的线性自标定方法[J]. 电子学报, 2017, 45(1): 135-139. PENG Yali, LIU Shigang, PEI Zhao, et al. WANG Xi-li. Linear camera self-calibration method based on non-rigid trajectory basis[J]. Acta electronica sinica, 2017, 45(1): 135-139. DOI:10.3969/j.issn.0372-2112.2017.01.019 (  0) 0)
|
| [3] |
石恬. 车载鱼眼相机自标定研究[D]. 西安, 西安电子科技大学, 2015: 1−21. SHI Tian. Self-calibration of a vehicle-mounted fish-eye camera[D]. Xian: Xidian University, 2015: 1−21. (  0) 0)
|
| [4] |
ZHANG Z. A flexible new technique for camera calibration[J]. IEEE transactions on pattern analysis and machine intelligence, 2000, 22(11): 1330-1334. DOI:10.1109/34.888718 ( 0) 0)
|
| [5] |
徐杰. 机器视觉中摄像机标定Tsai两步法的分析与改进[J]. 计算机工程与科学, 2010, 32(4): 45-48. XU Jie. Analyzing and improving the Tsai camera calibration m ethod in machine vision[J]. Computer engineering & science, 2010, 32(4): 45-48. (  0) 0)
|
| [6] |
李文涛, 马钺. 基于两步法的摄像机标定[J]. 控制工程, 2011, 18(S1): 48-51. LI Wentao, MA Yue. Camera calibration based on two-stage method[J]. Control engnieering of China, 2011, 18(S1): 48-51. (  0) 0)
|
| [7] |
CHANG Y, BAILEY D, Le MOAN S. Lens distortion correction by analysing peak shape in Hough transform space[C]// IEEE 2017 International Conference on Image and Vision Computing New Zealand (IVCNZ), Christchurch, New Zealand, 2017: 1−6.
( 0) 0)
|
| [8] |
曲学军, 张璐. 基于空间平行直线束的CCD摄像机内外参数标定[J]. 计算机工程与设计, 2010, 31(19): 4320-4323. QU Xuejun, ZHANG Lu. Camera calibration technique for computer vision detection[J]. Computer engineering and design, 2010, 31(19): 4320-4323. (  0) 0)
|
| [9] |
黄春燕, 韩燮, 韩慧妍, 等. 一种改进的基础矩阵估计算法[J]. 小型微型计算机系统, 2014, 35(11): 2578-2581. HUANG Chunyan, HAN Xie, HAN Huiyan, et al. Improved fundamental matrix estimation algorithm[J]. Journal of Chinese mini-micro computer systems, 2014, 35(11): 2578-2581. DOI:10.3969/j.issn.1000-1220.2014.11.039 (  0) 0)
|
| [10] |
张迪. 基于本质矩阵的摄像机自标定研究[D]. 安徽: 中国科学技术大学, 2014: 1−60. ZHANG Di. A high accuracy camera self-calibration method based on the essential matrix[D]. Anhui: university of science and technology of China, 2014: 1−60. (  0) 0)
|
| [11] |
王刃, 朱东兴, 蒋渤. 逆向仿真工程中的一种相机自标定技术[J]. 武汉大学学报(信息科学版), 2006, 31(4): 336-339. WANG Ren, ZHU Dongxing, JIANG Bo. Self-calibration applied in converting simulation surveying[J]. Geomatics and information science of Wuhan University, 2006, 31(4): 336-339. (  0) 0)
|
| [12] |
李竹良, 赵宇明. 基于单幅图片的相机完全标定[J]. 计算机工程, 2013, 39(11): 5-8. LI Zhuliang, ZHAO Yuming. Full calibration of camera based on single image[J]. Computer engineering, 2013, 39(11): 5-8. DOI:10.3969/j.issn.1000-3428.2013.11.002 (  0) 0)
|
| [13] |
WANG X, LI M, CUI Y. An improved method of nonlinear distortion correction for wide-angle lens[C]// IEEE International Conference on Signal & Image Processing. Singapore, 2017: 10−17.
( 0) 0)
|
| [14] |
GEIGER A, MOOSMANN F, CAR O, et al. Automatic camera and range sensor calibration using a single shot[C]// IEEE International Conference on Robotics and Automation. St. Paul, USA, 2012: 1−8.
( 0) 0)
|
| [15] |
WATSON D F P G M. A refinement of inverse distance weighted interpolation[J]. Geoprocessing, 1985, 2(4): 315-327. ( 0) 0)
|
| [16] |
彭延军, 乔羽, 王元红. 基于薄板样条的快速插值人脸变形算法[J]. 软件导刊, 2016, 15(2): 52-54. ( 0) 0)
|
 2020, Vol. 15
2020, Vol. 15


