2. 中国矿业大学 机电与信息工程学院,北京 100083
2. School of Mechanical Electronic & Information Engineering, China University of Mining and Technology, Beijing 100083, China
地铁轨道交通车站作为地铁轨道交通网络的链接点与交叉点,相较于地铁轨道交通普通停靠站台而言,其人流通道、设施设备布局、安全紧急疏散通道以及其他服务措施与输运组织、疏散能力等复杂性与多元化的特点,对地铁轨道交通车站的规划设计与安全运营提出了更高的要求[1]。此外,地铁轨道交通车站的乘客行为具有主观性,即高集中性、多方向与多路径性、方向不均衡性和时间不均衡性等特点,为满足乘客行为的大众化、多样化的出行需求,地铁轨道交通车站站台的科学合理设计与运营具有重要的理论与现实意义。
目前国内外众多学者进行了相关研究。文献[2-3]建立了基于元胞自动机模型的复杂形势下乘客行为仿真模型,研究了在势能场的影响下,具有不同出行目的的乘客在地铁站台内进行方向选择和制定进出站决策问题。文献[4]针对地铁车站行人拥堵和瓶颈处,以北京西直门地铁站为例,建立了地铁车站M/G/C/C排队网络模型,计算分析出地铁通道内疏散瓶颈并对其进行优化,提高了疏散能力。文献[5]进一步提出了将数学模型和社会力模型进行耦合的行人疏散模型,并且仿真模拟了灾难突发状况下地铁车站的行人疏散过程。文献[6]首先对几种行人运动仿真模型进行归纳总结,并通过研究当前行人运动的发展现状,提出研究行人运动,改善行人通行能力的必要性。文献[7]构建了基于社会力的行人交通微观仿真模型,以目标点局部极小化为准则并对其模型进行优化,验证了优化方案的可行性与优越性。文献[8]设计了一种列车驾驶模拟器,其中通过层级递进结构可实现虚拟乘客的乘车意图、环境感知、目标决策等行为。文献[9-10]应用Anylogic仿真软件分别对北京市南站地铁通道宽度和北京玄武门车站不同时刻乘客流向以及乘客密度进行仿真模拟,提出了不同的改进优化方案。文献[11]对不同运行时段地铁车站内乘客疏散能力进行Pathfinder仿真建模,并从疏散用时、拥堵点、人员疏散路径和出口利用率等方面进行结果分析,提出了相应的建议。文献[12]为了解决地铁换乘过程中人流拥堵问题,构建了人流流动路径拉普拉斯方程,通过计算人流流动势能场完成人流交互导向,提高了地铁车站通行效率。文献[13]对地铁换乘站内设施布局以及乘客换乘路径进行仿真,对于乘客在地铁车站内行走的流畅性、舒适性和逗留性进行分析,地铁车站内部设施布局进行优化。文献[14]为了提高船舶疏散效率,增强疏散人员的安全性,建立了一种社会力模型与智能体建模技术相结合的船舶疏散仿真模型,仿真结果表明了该模型的合理性和有效性。
通过上述研究可知,客流组织是一项复杂的动态时空排队服务系统,地铁轨道交通车站作为客流组织的载体,两者之间相互影响而又相互作用,关于两者之间作用机理与耦合现象的相关研究较少。然而基于社会力模型算法的Anylogic动态仿真软件能够实现离散、连续和混合行为的复杂系统仿真,同时其灵活的人机交互仿真功能可以从宏观与微观双层面快速构建客流组织与地铁轨道交通车站之间的动态交互仿真模型,为研究两者之间的相互作用与影响关系提供了平台。因此,本文针对乘客流的多样性与多元化特点,分析了地铁轨道交通车站站台乘客行为的特殊性,以某市地铁轨道交通车站站台为例,构建了面向复杂交织乘客行人流的地铁轨道交通车站站台场景模型,通过实例仿真对其进行了校核与验证,科学合理地阐述了客流组织与地铁轨道交通车站之间的动态关系,为地铁轨道交通车站的规划设计与运营提供了理论基础和分析手段。
1 地铁轨道交通车站站台乘客行为特殊性分析相较于其他城市交通工具而言,由于地铁轨道交通车站的乘车时间以及乘客群社会关系、乘客社会层次等因素的影响,地铁轨道交通车站站台的乘客流具有如下特殊性:
1)乘客行为的制约性。由于地铁车站内设备设施、乘客行走通道以及其他服务设施的限制,乘客在地铁车站内行走、寻路等行为具有一定的规范性,行走空间有限且主要行动方向由地铁内线路引导。
2)乘客的动态时空排队性。地铁通道内站台层的行人流主要聚集在进出站楼梯扶梯、换乘设施出入口以及狭窄的通道等处;此外,地铁列车到站时乘客会大量涌入列车内,也会产生拥堵现象。随着时间的推进,地铁通道内流量增多,也会影响到整个地铁通道内站台系统的通行能力。
3)乘客流线的不确定性。乘客的行走路径不仅由其出行目的决定,还需考虑站内环境及拥堵条件的影响,特别是地铁车站内站台空间和设施能力相对有限,因此乘客的行走方向、步行速度等行为特征可能因周围其他乘客的行为发生突变或波动。
由于地铁轨道交通站台乘客行为的特殊性,为了更好地了解地铁车站内行人交通组织与空间换乘情况,本文将整个地铁车站看作一个完整的动态系统对地铁车站内部站点平面布局、设施设备能力、乘客的动向安排和紧急疏散通道进行评价。
2 地铁轨道交通车站站台行人流场景模型基于Anylogic的地铁轨道交通车站站台复杂交织乘客行人流场景模型[15-16]构建流程如图1所示,其具体步骤见1)~5)。

|
Download:
|
| 图 1 仿真模拟流程 Fig. 1 Flowchart of the simulation | |
1)资料收集与整理。根据地铁轨道交通车站站台与乘客行为特性,所需收集的资料包括基础资料和乘客特性资料,其中基础资料以地铁车站站内部设计资料为主,即平面布局图;而乘客特性资料主要以客流及乘客行为特征的资料为主,即地铁轨道交通车站站台中各出入口行人行走路径及行人数量等调研数据。
2)建立仿真实验模型。首先通过所收集的资料数据,结合地铁车站内具体内部布局,绘制地铁车站站台地下出站厅的CAD平面图,确认地下空间的边界与建筑内障碍物尺寸,在Anylogic仿真软件中建立地铁车站平面布局图,定位各种设施设备之间的相关关系;其次将建立的仿真模型与实地调查情况相比对,确定所建立模型的真实性与正确性。
3)参数设置调整。通过实地调研与访谈等形式,对地铁轨道交通车站站台不同时段内的行人数量、行人通行路径等进行调查与统计,计算入口、出口、安检设施、闸机等模块的参数,并对车站内某个时间段内的行人走行过程进行观察与统计,所调查与统计的数据类型主要以行人类型(男性和女性)、数量、步速等为主,得到地铁车站站内各设施设备的通过能力,然后将数据录入仿真模拟系统,并观察仿真模拟结果与实际情况的吻合程度,如果仿真结果与实际情况有出入,需要根据实际情况对模型参数进行适当的调整,直到建立的仿真模型与观察到的地铁站实际运行情况相符为止。
4)仿真实验。运行建立的二维、三维仿真模型,观察模型运行情况,输出各种模拟对象指标,如人流密度、平均走行时间等各项评价指标。
5)分析输出结果,提出方案优化建议。依据仿真输出的各项指标的数据,对模拟对象的空间使用情况进行评估,找出容易发生拥堵瓶颈点或安全隐患,提出优化建议,再次进行仿真模拟,最后将优化前、后的结果进行对比,验证了优化后方案能更好地提高地铁车站内空间使用率,为提高地铁车站的运行效率提出相应的建议。
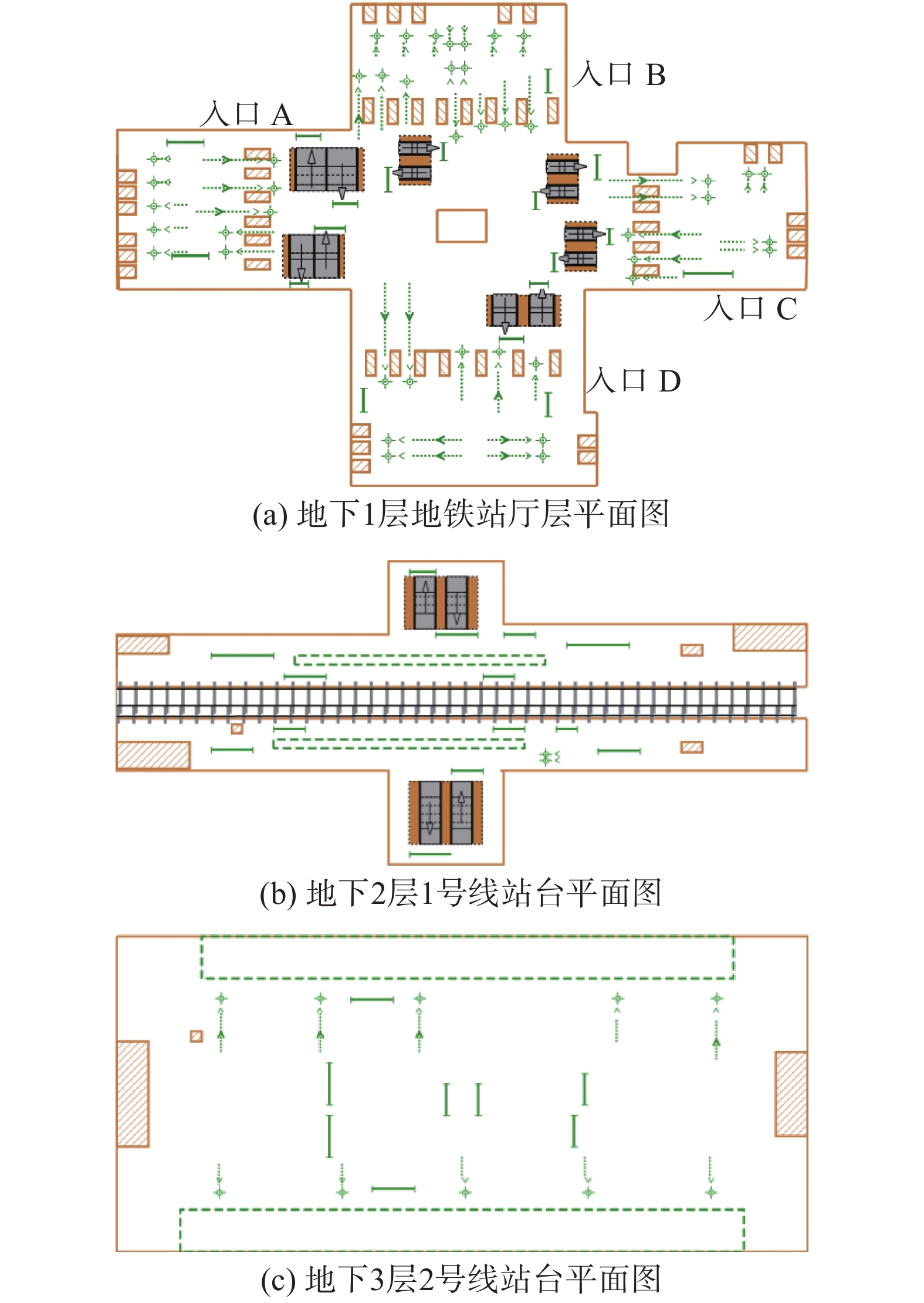
3 仿真实验 3.1 某市地铁轨道交通车站站台场景构建某市地铁轨道交通车站站台的平面形状近似为长方形,共有3层,其中地下1层为地铁站站厅层,地下2层为地铁1号线站台层,地下3层为地铁2号线站台层。地铁站厅层与地下1层之间共有6个出入口且均通过楼梯和自动扶梯相连接,而地下1层站厅层、地下2层1号线站台层与地下3层2号线站台层通过自动扶梯和电梯相连接。
1)三层站台平面模型绘制
首先在Anylogic仿真软件中绘制出三层车站模型,如图2所示,其中字母表示该地铁车站站厅层的6个出入口,绿色的虚线箭头表示进站乘客流线和出站乘客流线,橙色正方形表示出站、进站,灰色正方形和绿色的目标线表示换乘的扶梯和电梯。
|
Download:
|
| 图 2 地铁通道站台平面图 Fig. 2 Subway platform plan | |
2)乘客进出站逻辑关系与换乘关系
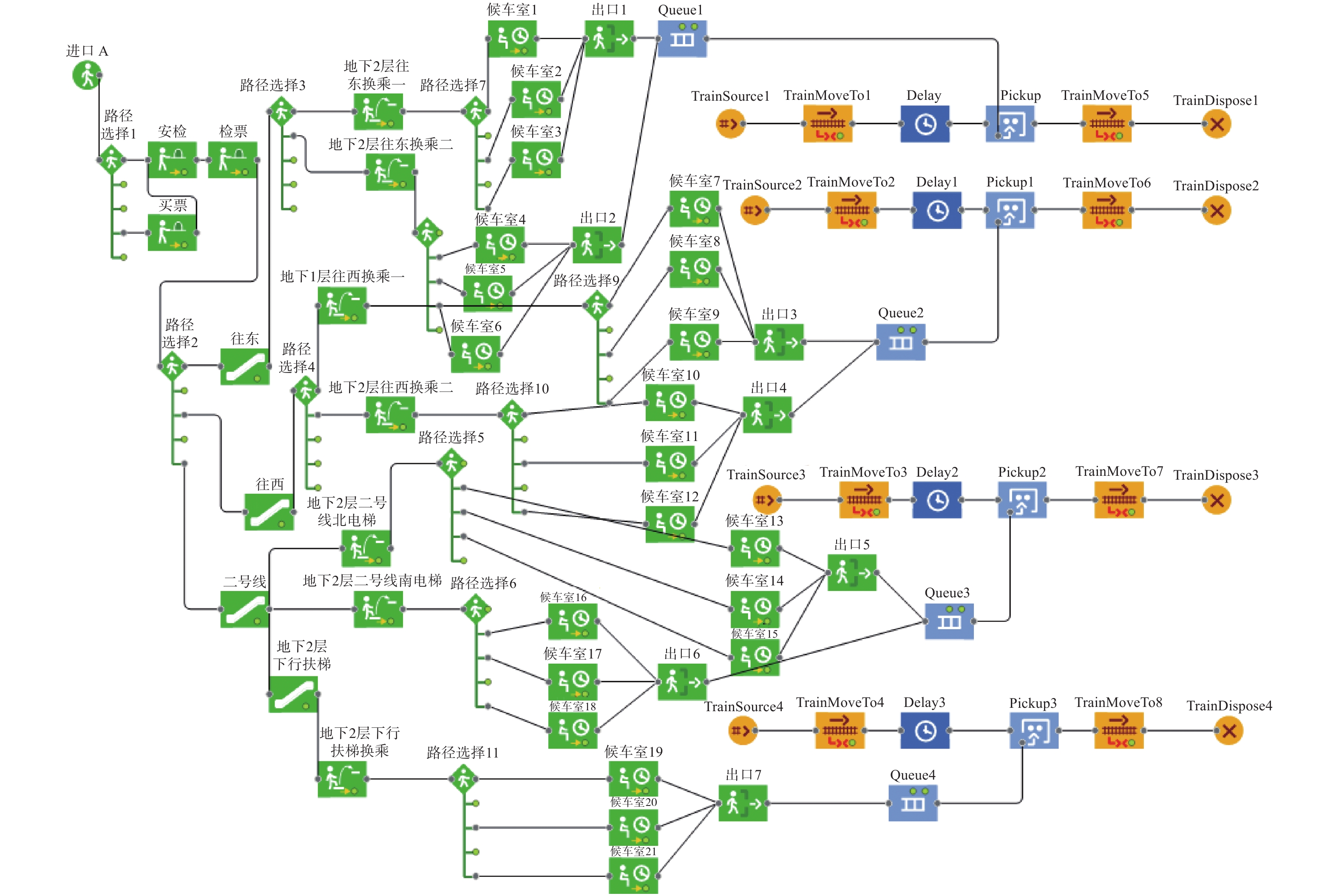
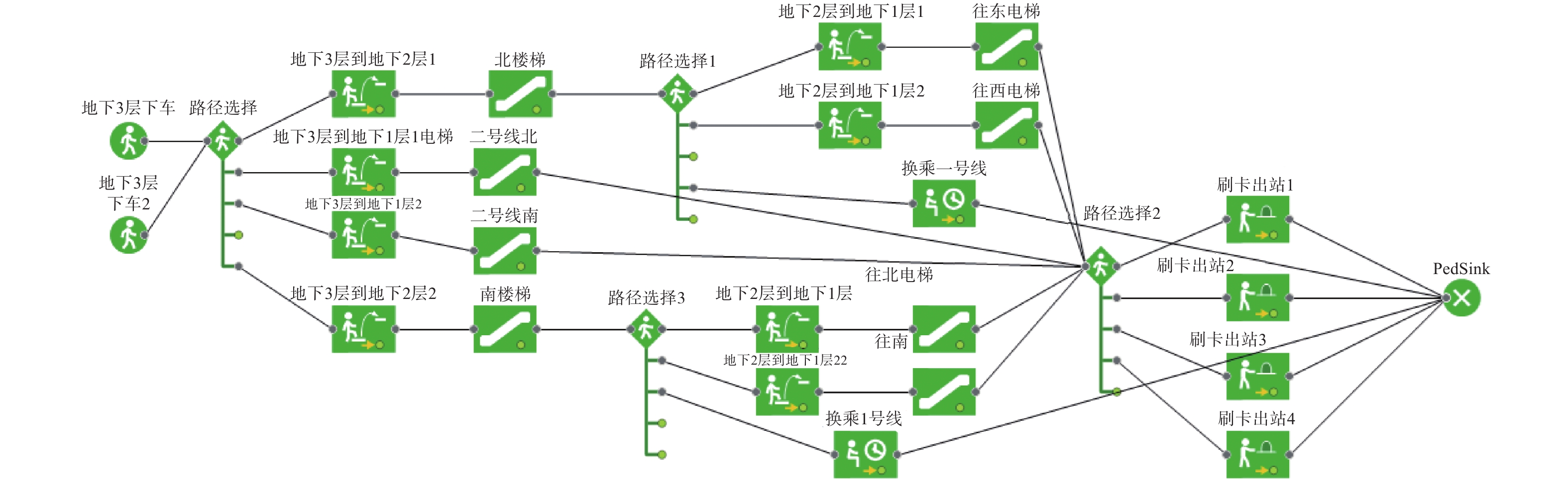
根据上述绘制的三层站台平面模型,对每一层中乘客行走路径以及设备设施之间的逻辑关系进行分析,分别根据每层的逻辑关系将设备设施进行连接,最后考虑三层之间的逻辑联系,建立出该地铁车站完整的逻辑框架图,乘客进出站逻辑框架图与换乘站逻辑框架图分别如图3和4所示。
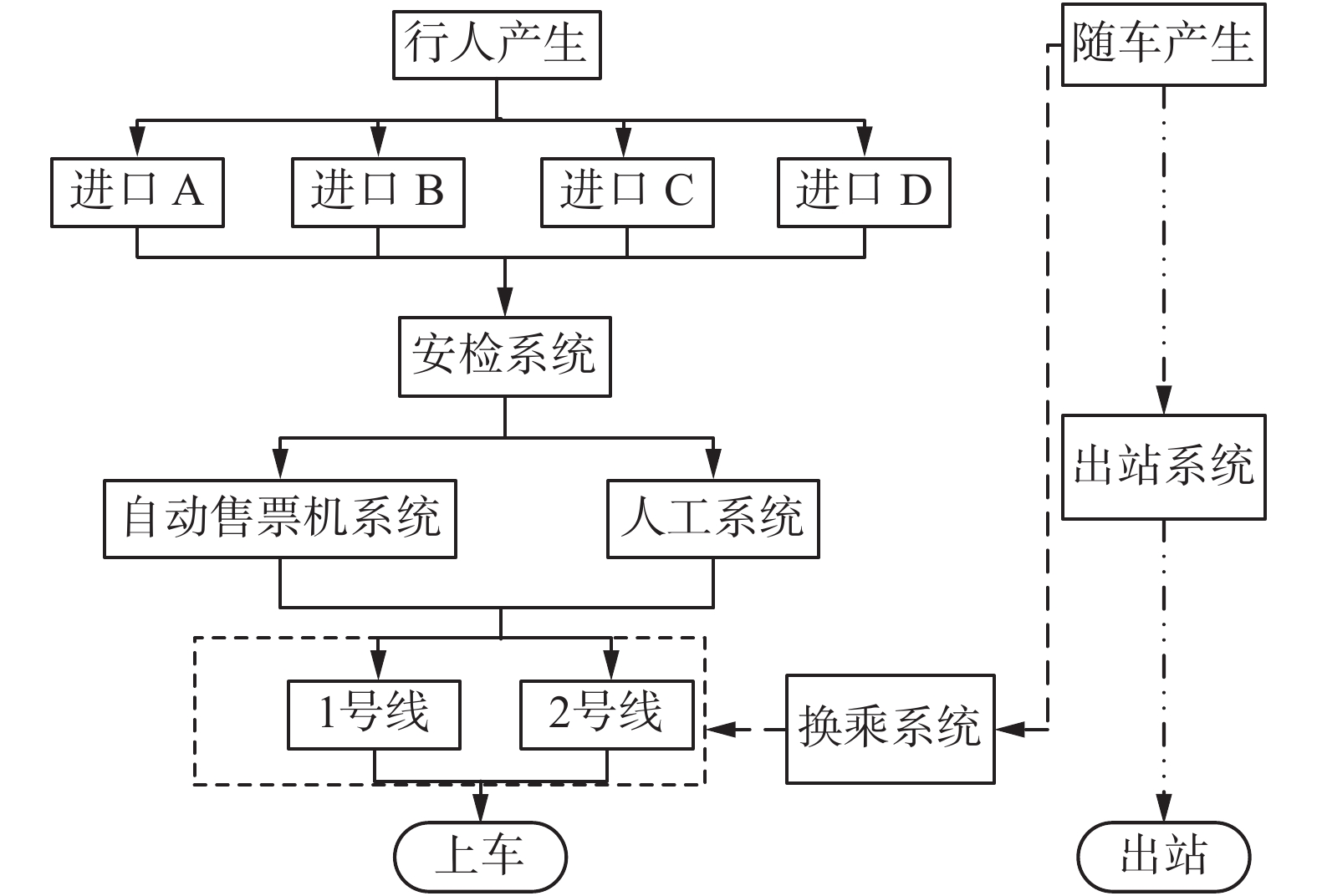
3.2 某市地铁轨道交通车站站台乘客流线路径设定地铁换乘站内乘客流线可以分为3类:进站流线、出站流线和换乘流线,如图5所示。进站流线中乘客行走流程为:乘客从6个入口进入地下1层站厅层,购票后进行安检,到达地铁的检票口,经地下2层的扶梯到1号线站台上车,或经地下3层的扶梯到1号线站台上车,通过地铁进入城市其他区域。出站及换乘流线中乘客行走流程为:乘客从地铁下来,经过扶梯进行换乘或者经过扶梯直接出站。
|
Download:
|
| 图 3 乘客进出站逻辑框架 Fig. 3 Logical framework for passenger entry and exit stations | |
|
Download:
|
| 图 4 换乘站逻辑框架 Fig. 4 Schematic of the transfer station logic frame | |
|
Download:
|
| 图 5 地铁换乘站内乘客流线 Fig. 5 Passenger flow line in a subway transfer station | |
根据上述构建的场景模型,此处需设定的参数主要以模型参数和行人参数为主,其中模型参数是地铁车站设备设施的具体参数以及地铁列车达到参数,分别见表1和2。
而行人参数是地铁轨道交通车站站台内运动的行人描述,其包括行人数量、行人速度和行人空间等参数。为分析行人数量对地铁轨道交通车站站台的影响,本文选择早、中、晚3个时段内站台的行人数量为研究对象,对某市地铁轨道交通车站站台的行人数量进行了为期一个月的调查与统计,取其平均值作为行人数量的参数,具体见表3。
| 表 1 地铁车站设备通行能力 Tab.1 Capacity of the subway station equipment |
| 表 2 列车到达情况调查表 Tab.2 Train arrival questionnaire |
| 表 3 某市地铁轨道交通车站站台行人流量平均值 Tab.3 Average pedestrian flow at a subway station |
行人速度是表征行人交通特性的主要参数,行人的步幅和步频是行走过程的基本特性,两者构成行人速度,具体参数见表4。
| 表 4 某市地铁轨道交通车站站台行人速度 Tab.4 Pedestrian speed at a subway station platform |
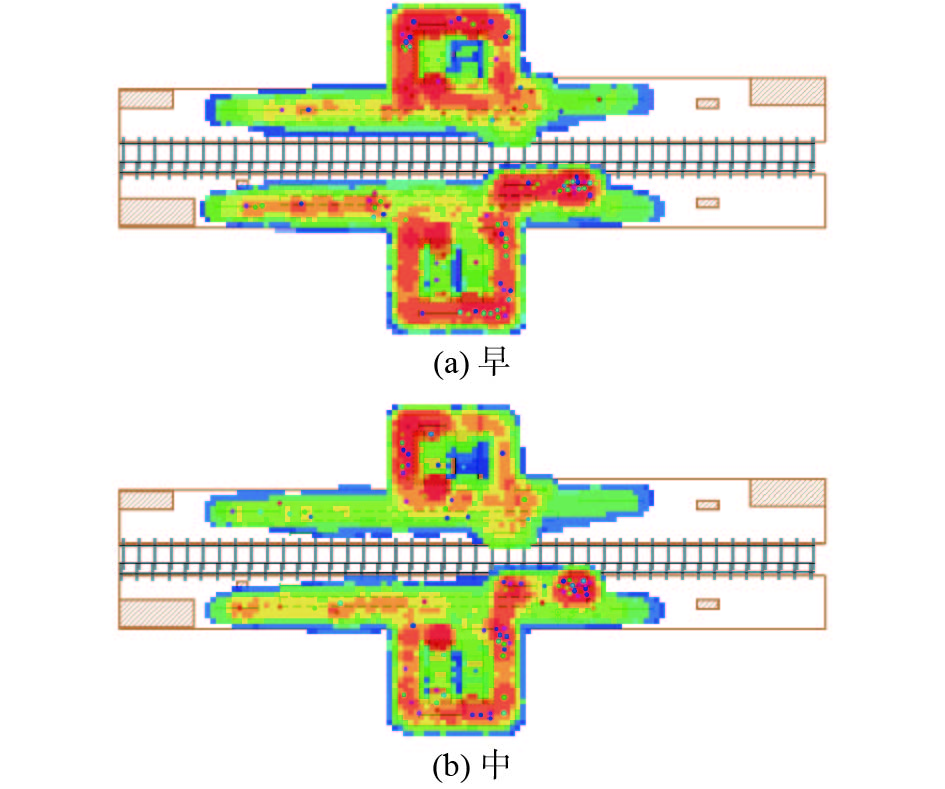
图6~8分别表示地下不同层站台在早、中、晚3个时间段的行人密度,图中圆点表示单个行人,不同颜色代表行人密度的高低,密度越高则色彩偏红色,反之则偏蓝色。

|
Download:
|
| 图 6 地下1层不同时间段对比 Fig. 6 Comparison of different time periods of the first level of the underground station | |
|
Download:
|
| 图 7 | |
|
Download:
|
| 图 7 地下2层不同时间段对比 Fig. 7 Comparison of different time periods of the second level of the underground station | |

|
Download:
|
| 图 8 地下3层不同时间段对比 Fig. 8 Comparison of different time periods of the third level of the underground station | |
通过对地下不同层站台早、中、晚3个时间段的行人密度分析,可得出以下结论:
1)对比图6~8发现,在早、中、晚3个时间段内,地下1层站厅的行人密度最大,地下2层次之,地下3层行人密度最低,相较于其他两层,其中地下1层站厅的行人密度以红色为主,部分区域存在严重拥堵现状。分析其原因可知,地下1层站厅为乘客进站乘车和所有出站乘客的汇集点,行人数量约为其他层站台的行人数量之和,是导致其行人密度较大的原因之一。其次,由图6可知,地下1层站厅的主要拥堵点和瓶颈点是在楼梯扶梯处和进站闸机口处,特别是进站闸机口A和C,分析其原因发现,楼梯扶梯与进站闸机口的设备通行能力决定着行人的通行速度,而地下1层站厅属于各种行人汇集点且行人数量较大,受到设备通行能力的限制,导致了地下1层站厅出现拥堵的情况。
2)由图7可知,地下2层站台的南、北扶梯处人流密度较大,存在较为严重的拥堵现象,分析其原因发现,地下2层站台的南、北两侧各有一台扶梯,该扶梯的行人通行能力已无法满足大流量行人的使用需求,与地下1层站厅的楼梯扶梯处发生拥堵现象的原因相似。
3)观察不同层站台在早、中、晚3个时间段的行人密度发现,与中午时间段相比,在早、晚两个时间段内3个站台的行人密度均较大,其中在该两个时间段内,3个站台的部分区域均出现了严重拥堵情况,分析其原因发现,早、晚时间段属于上下班、上学高峰期,3个站台的设备服务能力有限,特别是不同站台之间的楼梯扶梯、进出站楼梯扶梯以及闸机口等设备的通行能力。
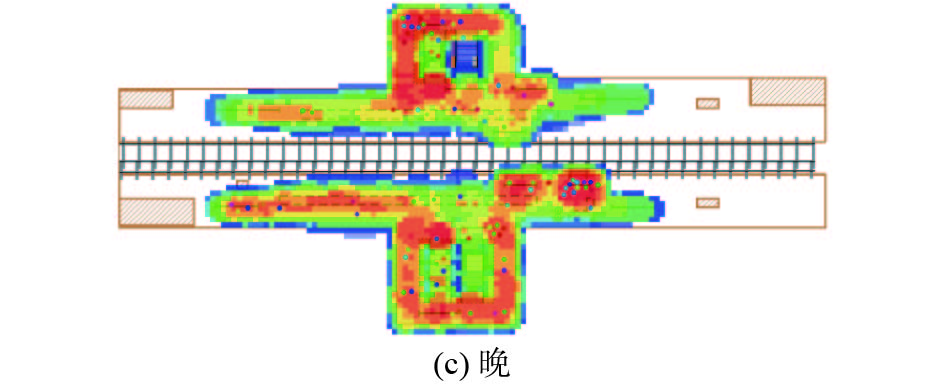
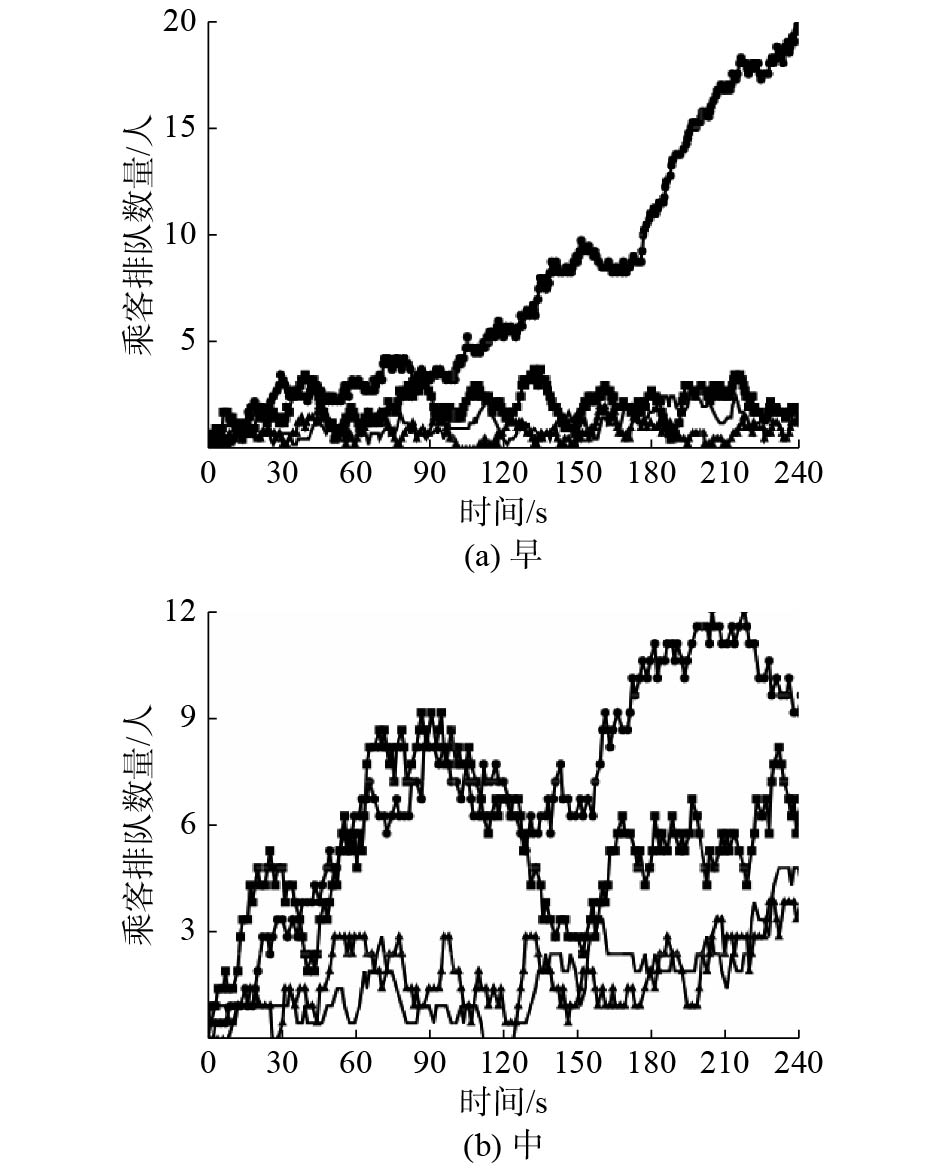
4.1.2 不同时间段进出口闸机乘客排队数量分析如图9所示为不同时间段内进出口闸机A、B、C和D处乘客排队数量。由图9的(a)和(c)可知,在早、晚时间段内,进出口闸机A处乘客排队数量呈线性增长趋势,而进出口闸机B、C和D处乘客排队数量略有增加但总体趋于稳定,在中午时间段内,进出口闸机A和C处乘客排队数量略高于其他两处。
|
Download:
|
| 图 9 | |

|
Download:
|
| 图 9 各入口不同时间段闸机乘客排队数量分析 Fig. 9 Analysis of the number of passengers queuing at each entrance at different time periods | |
分析其原因发现,早、晚时间段属于行人高峰期,在4个进出口闸机数量与通行能力相同的前提下,可能受出行方便与否的影响,行人选择进出口A和C的概率较其他两个进出口的概率大,进而导致进出口A和C处出现了拥堵现象,其根本原因为闸机数量不足和闸机通行能力不够。
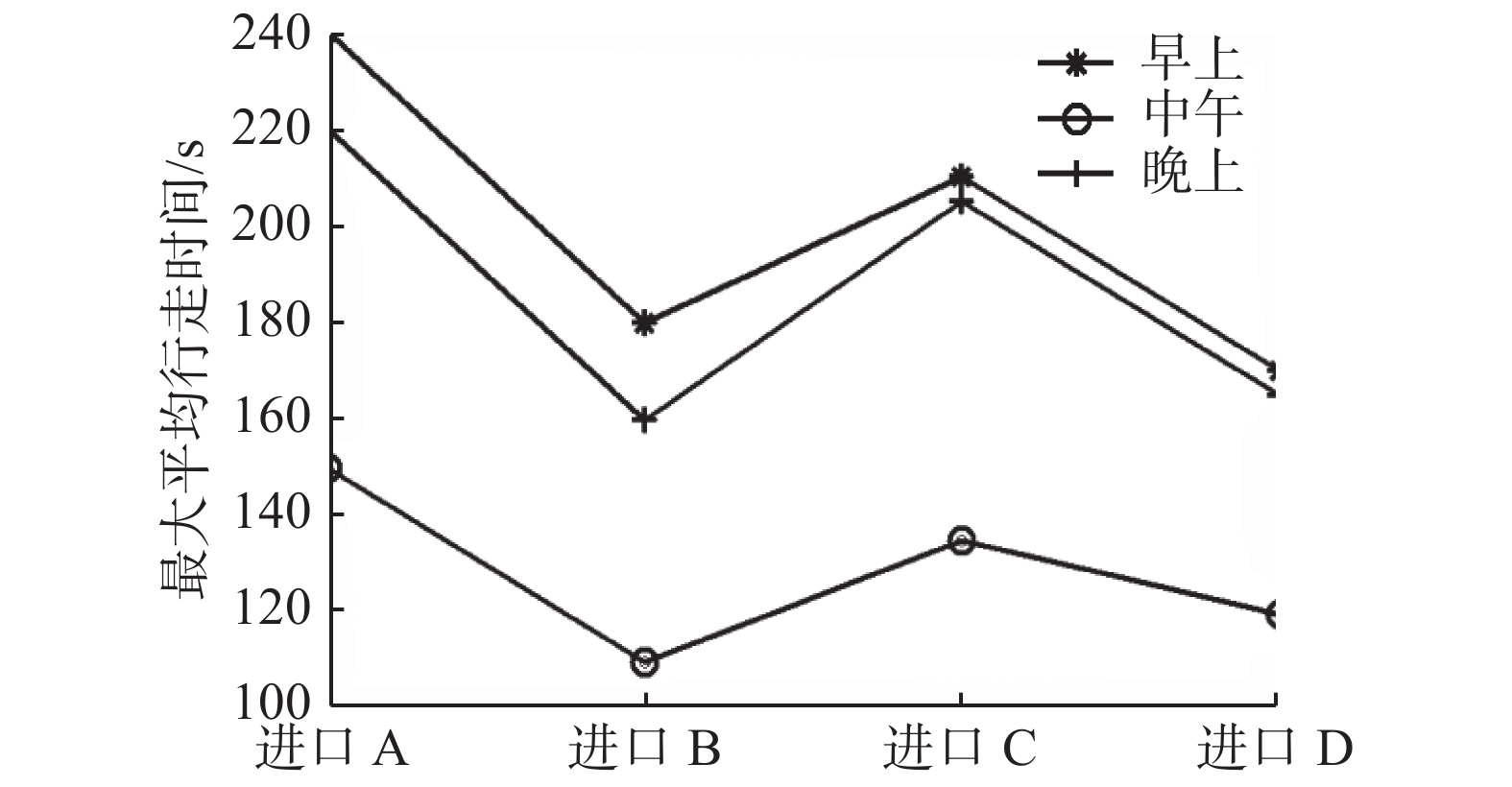
4.1.3 不同时间段行人平均行走时间分析平均走行时间是指乘客在站厅层中从各入口到进入站台层的候车系统所花费的平均时间。在不同时间段内,由于各个站台层乘客数量的不同,乘客到达目的站台的走行时间有所不同。本文以进站口到地下3层站台的乘客走行时间为研究对象,对早、中、晚3个时间段内的乘客平均走行时间进行分析,如图10所示。
|
Download:
|
| 图 10 不同时间段平均走行时间对比 Fig. 10 Comparison of the average travel time in different time periods | |
1)由图10可知,乘客在早高峰的平均走行时间最长,晚高峰次之,中午时间段内乘客的平均走行时间最短。其原因在于,早晚高峰期时间段内,乘客数量较多,而设备通行能力有限,导致在某些处存在排队现象,是早晚高峰时间段内乘客平均走行时间的增多的原因之一;另一方面,在各个站台内区域面积一定的情况下,由于乘客数量的增多,导致行人拥挤,进而增加了乘客的平均走行时间。
2)由图10可知,相较于从进站闸机口B和D进入的乘客平均走行时间,乘客从进站闸机口A和C进入地下3层站台候车区域的平均走行时间较长。由上述的不同时间段进出口闸机乘客排队数量分析结果可知,该两处的人流密度较大,导致行人拥挤,延长了乘客的平均走行时间;此外,该两处缺乏合理的导向服务措施,致使乘客因某些原因在某区域停滞,进而增加了乘客自身和其他乘客的平均走行时间。
4.2 优化前后结果对比针对该市地铁轨道交通车站站台存在的问题,拟提出以下两点优化方案:
1)增加地下1层站厅和地下2层站台的楼梯与扶梯数量。根据地下1层站厅和地下2层站台在不同时间段内行人密度和乘客平均走行时间,预估在地下1层站厅和地下2层站台各两部楼梯或直梯以提高通行效率。
2)增加进出口A和C处闸机数量。根据不同时间段进出口A和C处乘客排队数量与乘客平均走行时间,在两处各增加1台闸机可有效缓解拥挤程度。
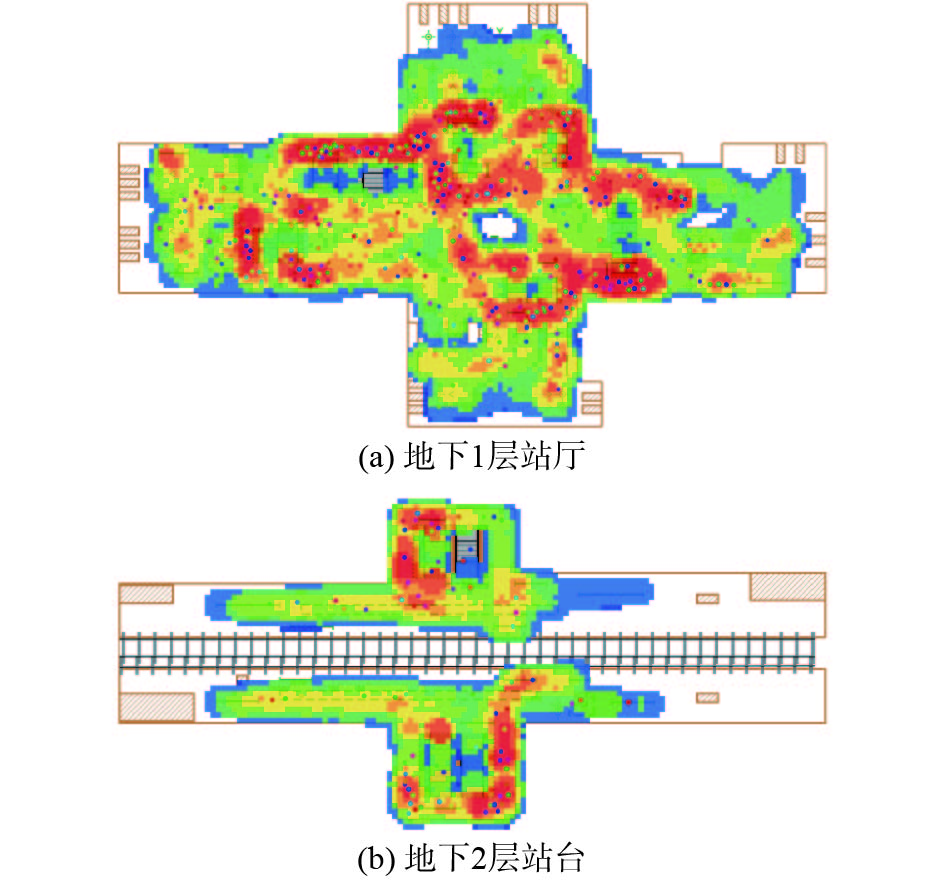
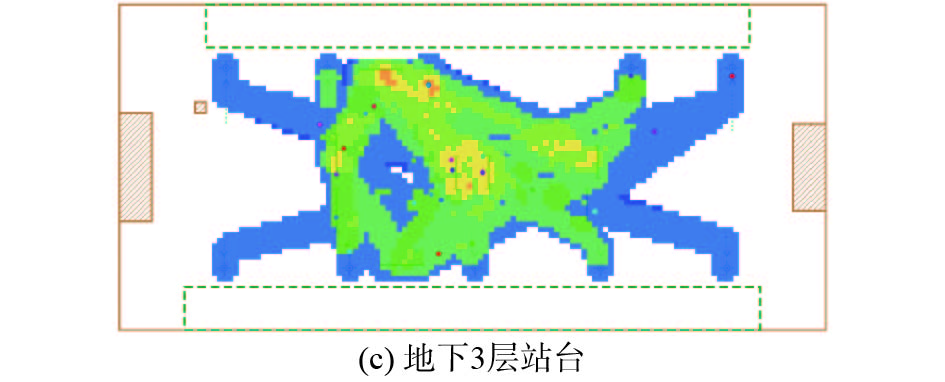
根据上述优化方案,重新构建该市的地铁轨道交通车站站台复杂交织乘客行人流场景模型,在其他参数均不变的情况下,增加地下1层站厅、地下2层站台的楼梯与扶梯数量和进出口A、C处闸机数量,进而对乘客走行流线进行优化设计。仅以早高峰时间段为模拟仿真对象,优化后不同站台层行人密度图、进出口闸机乘客排队数量和乘客平均走行时间分别如图11和12所示。
|
Download:
|
| 图 11 | |
|
Download:
|
| 图 11 优化后行人密度 Fig. 11 Pedestrian density map after optimization | |
|
Download:
|
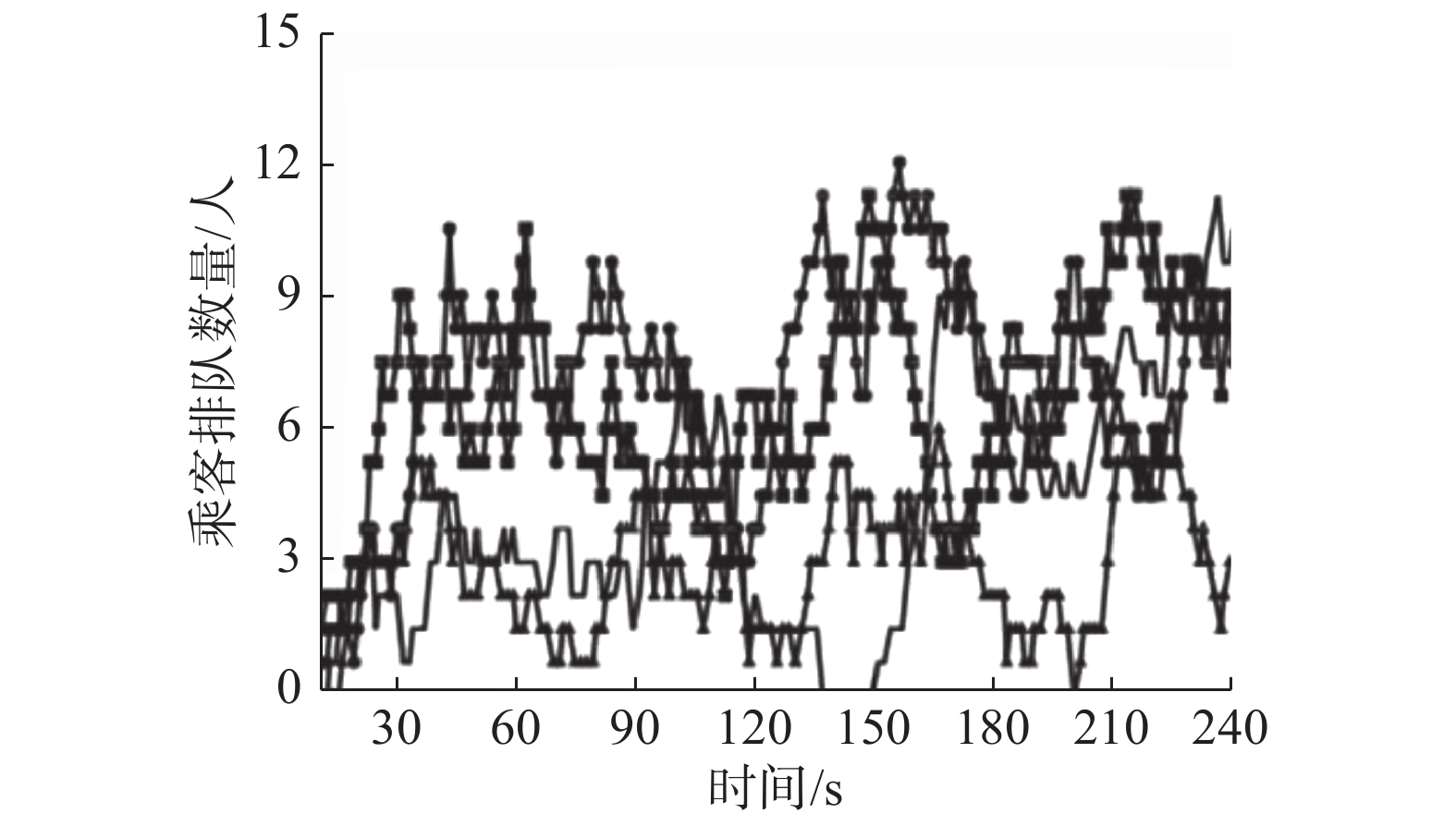
| 图 12 优化后乘客排队数量 Fig. 12 Number of passengers queuing after optimization | |
对比图6~8中的(a)图和图11,地下1层站厅的整体行人密度显著降低,且各进出站闸机口处和楼梯扶梯处行人密度均有所下降,同时表明该优化方案合理有效,但优化后地下1层站厅部分区域仍存在区域拥挤现象,说明为更加科学合理地优化站厅层需同时对多种地铁服务设施进行优化设计,制定更加完善的优化方案。
对比图9(a)和图12,优化后不同进出口闸机处乘客排队数量趋于稳定,优化前进出口闸机A处乘客排队数量呈线性增长趋势消失。
由表5可知,优化后早高峰时间段内乘客平均走行时间显著降低,其中进出口闸机A处的乘客平均走行时间降低了33.4%,进出口闸机C处的乘客平均走行时间降低了28.6%,极大地缓解了站台内拥挤现象。
| 表 5 优化后平均走行时间表 Tab.5 Average travel schedule after optimization |
以某市地铁轨道交通车站站台为例,构建了面向复杂交织乘客行人流的地铁轨道交通车站站台场景模型,以不同时间段站台行人密度、不同时间段进出口闸机乘客排队数量和不同时间段乘客平均走行时间为评价指标,提出了该市地铁轨道交通车站站台的优化改进方案,并通过优化前后结果对比分析,验证了优化方案的可行性与科学性,同时对其他地铁轨道交通车站的规划设计与运营具有重要的借鉴与指导意义。
| [1] |
ZHONG Maohua, SHI Congling, TU Xuwei, et al. Study of the human evacuation simulation of metro fire safety analysis in China[J]. Journal of loss prevention in the process industries, 2008, 21(3): 287-298. DOI:10.1016/j.jlp.2007.08.001 ( 0) 0)
|
| [2] |
ZHANG Qi, HAN Baoming, LI Dewei. Modeling and simulation of passenger alighting and boarding movement in Beijing metro stations[J]. Transportation research part C: emerging technologies, 2008, 16(5): 635-649. DOI:10.1016/j.trc.2007.12.001 ( 0) 0)
|
| [3] |
张琦, 韩宝明, 李得伟, 等. 地铁枢纽站台的乘客行为仿真模型[J]. 系统仿真学报, 2007, 19(22): 5120-5124. ZHANG Qi, HAN Baoming, LI Dewei, et al. Modeling and simulation of passenger behavior in platform of MTR stations[J]. Journal of system simulation, 2007, 19(22): 5120-5124. DOI:10.3969/j.issn.1004-731X.2007.22.006 (  0) 0)
|
| [4] |
陈绍宽, 刘爽, 肖雄, 等. 基于M/G/c/c模型的地铁车站楼梯通道疏散能力瓶颈分析[J]. 铁道学报, 2012, 34(1): 7-12. CHEN Shaokuan, LIU Shuang, XIAO Xiong, et al. M/G/c/c-based model of passenger evacuation capacity of stairs and corridors in metro stations[J]. Journal of the china railway society, 2012, 34(1): 7-12. DOI:10.3969/j.issn.1001-8360.2012.01.002 (  0) 0)
|
| [5] |
LI Fang, CHEN Shaokuan, WANG Xiudan, et al. Pedestrian evacuation modeling and simulation on metro platforms considering panic impacts[J]. Procedia-social and behavioral sciences, 2014, 138: 314-322. DOI:10.1016/j.sbspro.2014.07.209 ( 0) 0)
|
| [6] |
郭谨一, 刘爽, 陈绍宽, 等. 行人运动仿真研究综述[J]. 系统仿真学报, 2008, 20(9): 2237-2242. GUO Jinyi, LIU Shuang, CHEN Shaokuan, et al. Review of pedestrian movement simulation studies[J]. Journal of system simulation, 2008, 20(9): 2237-2242. (  0) 0)
|
| [7] |
王爱丽, 董宝田, 王泽胜. 基于社会力的行人交通微观仿真模型研究[J]. 系统仿真学报, 2014, 26(3): 662-669. WANG Aili, DONG Baotian, WANG Zesheng. Modeling and simulation of microscopic pedestrian based on social force[J]. Journal of system simulation, 2014, 26(3): 662-669. (  0) 0)
|
| [8] |
唐春林, 苏虎, 金炜东. 一种地铁列车乘客仿真模型[J]. 系统仿真学报, 2014, 26(10): 2470-2475. TANG Chunlin, SU Hu, JIN Weidong. Metro passenger simulation model[J]. Journal of system simulation, 2014, 26(10): 2470-2475. (  0) 0)
|
| [9] |
聂广渊, 袁振洲, 吴昊灵. 基于AnyLogic仿真的城市轨道交通枢纽通道宽度研究[J]. 城市轨道交通研究, 2016, 19(6): 34-38. NIE Guangyuan, YUAN Zhenzhou, WU Haoling. Research on passageway width at urban rail transit hub based on AnyLogic simulation[J]. Urban mass transit, 2016, 19(6): 34-38. (  0) 0)
|
| [10] |
李洪旭, 李海鹰, 樊校, 等. 基于Anylogic的地铁车站集散能力仿真分析评估[J]. 铁路计算机应用, 2012, 21(8): 48-50. LI Hongxu, LI Haiying, FAN Xiao, et al. Anylogic-based simulation analysis and evaluation of subway stations assemble capacity[J]. Railway computer application, 2012, 21(8): 48-50. DOI:10.3969/j.issn.1005-8451.2012.08.013 (  0) 0)
|
| [11] |
吴桂庆. 基于Pathfinder的地铁车站行人疏散仿真研究[J]. 交通科技与经济, 2014, 16(3): 80-83. WU Guiqing. Study on evacuation simulation of Pedestrian in subway station based on pathfinder[J]. Technology & economy in areas of communications, 2014, 16(3): 80-83. DOI:10.3969/j.issn.1008-5696.2014.03.021 (  0) 0)
|
| [12] |
李莹, 苏也惠. 地铁换乘过程人流避免拥堵路径规划仿真[J]. 计算机仿真, 2018, 35(6): 146-150. LI Ying, SU Yehui. Simulation of traffic congestion avoidance path planning in subway transfer process[J]. Computer simulation, 2018, 35(6): 146-150. DOI:10.3969/j.issn.1006-9348.2018.06.032 (  0) 0)
|
| [13] |
陈伟, 李宗平. 地铁换乘站设施布局优化仿真研究[J]. 交通运输工程与信息学报, 2016, 14(2): 110-115. CHEN Wei, LI Zongping. Simulation of layout optimization of metro transfer station[J]. Journal of transportation engineering and information, 2016, 14(2): 110-115. DOI:10.3969/j.issn.1672-4747.2016.02.15 (  0) 0)
|
| [14] |
倪宝成, 林壮, 李平. 考虑逆行避让行为的客船疏散仿真模型[J]. 哈尔滨工程大学学报, 2020, 41(1): 44-51. NI Baocheng, LIN Zhuang, LI Ping. Passenger ship evacuation simulation model considering retrograde avoidance behavior[J]. Journal of Harbin Engineering University, 2020, 41(1): 44-51. (  0) 0)
|
| [15] |
王亚娜, 赵永翔. 基于社会力模型的地铁站乘客上下车行为影响因素分析[J]. 交通信息与安全, 2017, 35(1): 105-111. WANG Ya’na, ZHAO Yongxiang. An analysis of impact factors of boarding and alighting behaviors of passengers based on a social force model[J]. Journal of transport information and safety, 2017, 35(1): 105-111. DOI:10.3963/j.issn.1674-4861.2017.01.014 (  0) 0)
|
| [16] |
Helbing D, Molnár P. Social force model for pedestrian dynamics[J]. Physical review E, 1995, 51(5): 4282-4286. DOI:10.1103/PhysRevE.51.4282 ( 0) 0)
|
 2020, Vol. 15
2020, Vol. 15


