民航飞机油箱中存在大量的诸如油管、隔板、桁条等障碍物，并且有大量易燃易爆气体，是一个结构复杂、空间狭窄的环境，在其中进行人工作业难度高、劳动强度大，并且存在安全隐患，因此需要一种能够替代人工检查的装置^[1-3]。相比于传统的刚性连杆机器人，连续型机器人具有多冗余自由度、驱动器和控制器分离的特点，理论上可以达到空间上的任一点^[4-6]，因此更加灵活、安全，更加适用于飞机油箱检查任务^[7]。目前，很多研究者对连续型机器人在人体手术^[8-9]、燃气涡轮发动机维修^[10]、核电厂检修^[11]等领域的应用进行了探索。

由于连续型机器人各个关节之间具有耦合性，不能将其每一个关节看作一个操作关节，其操作方法也是一项具有挑战的任务^[12-13]。钱文欢等^[14-15]设计了一种仿象鼻混合关节的连续型机器人，对机器人的机械结构、运动学等进行了分析，并搭建了两关节的混合关节机器人。该机器人由离散关节和连续关节串联而成，其各个关节之间并非为连续的，所以其本质仍然是多关节串联机械臂。Li等^[16]提出了一种新型的连续体机器人，它由两个模块和一个由螺旋弹簧构成的柔性骨架构成。每个模块由4个平行排列的肌腱驱动，实现冗余驱动系统，保证机器人的灵活运动。在此基础上，设计了连续体机器人的位置反馈控制器，并在控制器中加入二次规划算法，实现了机器人的平滑配置。Dong等^[17]设计了一款双枢轴关节结构的连续型机器人，可最大程度地减少绕其轴的扭曲，该连续型机器人由导向盘、驱动绳索以及连接导向盘的双枢轴组成，驱动绳索穿过导向盘实现关节姿态控制，相邻两个双枢轴之间相互交错90°，这样的结构能够得到较好的刚度又能保证连续型机器人一定的弯曲能力。曹燕飞等^[18-19]设计了变刚度微创介入手术的连续体机器人，该机器人由导向盘、芯柱、绳索、连接盘、硅胶壁组成，每个关节由3根绳索驱动关节运动，并深入研究了SMA的相变机理，并且设计其控制模式为点位控制模式和关节控制模式。赵智远等^[20-22]仿照章鱼触手的结构和运动机理，设计了一款线驱动的连续型机器人，对连续型机器人的运动学进行了分析，并在三关节样机平台上进行了关节弯曲和旋转实验；该机器人由远程驱动机构和机械臂部分组成，驱动部分采用步进电机带动卷轴进而改变驱动绳长的方式，各个关节之间采用球铰链连接，增加其灵活性。

目前，课题组针对飞机油箱检查的问题，提出了使用连续型机器人辅助进行飞机油箱泄漏点检查的构想^[23]，并在连续型机器人运动学、路径规划^[24]、路径跟随^[25]等方面都进行了研究。本文设计了一种仿蛇脊椎骨的线驱动连续型机器人，机器人由直线模组、导向圆盘，钢丝绳、导向滑轮、支撑杆等组成，机器人以镍钛合金杆作为支撑轴，各导向圆盘球铰连接，用以保证关节的灵活性和关节的等曲率弯曲，以钢丝绳作为驱动线穿过导向圆盘驱动关节运动，保证关节韧性，以直线模组组成驱动机构，降低绳长变化误差的影响；并且分析连续型机器人的关节映射模型，设计手柄控制方式，实现样机平台手柄操作控制，搭建三关节样机平台，在样机平台进行关节实验。

1 连续型机器人的结构设计和运动学分析 1.1 结构设计

课题组模仿蛇脊椎骨的构造设计了基于球铰链连接的连续型机器人结构，连续型机器人由驱动机构和柔性机械臂组成，如图1所示。柔性机械臂由多个关节段和柔性支撑杆组成，各个关节段穿过中间的柔性支撑杆组成整个柔性机械臂；其中每个关节段由多个导线圆盘连接而成，导线圆盘分为底端圆盘、受力圆盘、中间引线圆盘和顶端圆盘，各圆盘都是以中间引线圆盘为基础改型的，中间导线圆盘含有球头、球壳、导线孔、支撑杆孔以及预留孔，如图2所示，图中D表示圆盘直径，d表示导线孔所在圆直径，α表示相邻导线孔角度，h表示导线圆盘厚度，l表示相邻圆盘距离。各个导线圆盘穿过中间的弹性支撑杆，相邻两个导线圆盘的球头和球壳相连，球头球壳相接于同心圆，这种结构既能方便各个导线圆盘的连接又能给柔性机械臂提供轴向支撑力，使关节弯曲更趋于等曲率圆弧。

连续型机器人的驱动机构由直线模组、上下连接板、导线滑轮以及钢丝绳等组成。以直线模组作为连续型机器人的驱动器，直线模组将步进电机的旋转运动转换为直线模组中滑台的直线运动，这样可以有效减少转轴驱动带来的误差，导向滑轮改变钢丝绳的受力方向，避免钢丝绳的摩擦，每个关节由三根钢丝绳驱动，钢丝绳连接直线模组的滑台和连续型机器人柔性机械臂的各个关节末端，以驱动各关节的运动。

1.2 运动学分析

在进行连续型机器人的操作控制之前需建立连续型机器人从操作空间到驱动信号空间的映射关系，其空间转换图如图3所示。这里假设连续型机器人柔性机械臂为等曲率圆弧模型，且各个关节长度恒定。

图3中操作空间 $(x,y,z)$ 表示连续型机器人操作空间的坐标，关节空间 $\{ \varTheta ,\varPhi \}$ 表示连续型机器人的姿态参数，即弯曲角度和旋转角度，绳长空间 $\Delta {L_{ij}}$ 表示连续型机器人第i关节第j根钢丝绳的绳长变化量，驱动信号空间 $\{ F,M\} $ 表示步进电机的所需的驱动信号的频率和脉冲个数。

1.2.1 运动学建模

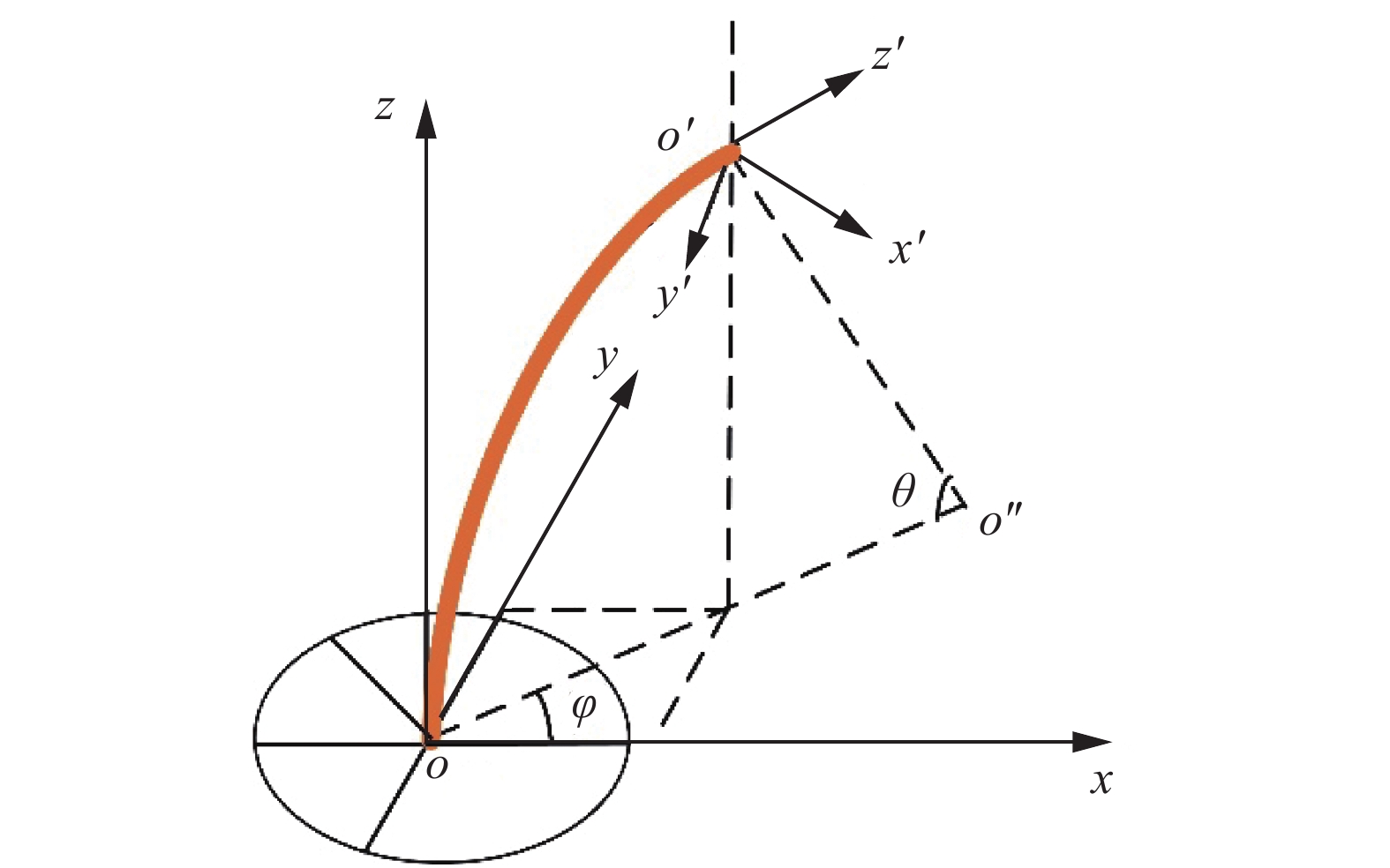
连续型机器人单关节运动学模型如图4所示。将其简化为等曲率连续光滑曲线，定义连续型机器人的三个变量，单关节长度 $L$ ，弯曲角度 $\theta $ 和旋转角度 $\varphi $ ，弯曲角度 $\theta $ 为圆弧的圆心角，旋转角度 $\varphi $ 为平面 $oo'o''$ 和平面 $xoz$ 的夹角。

由几何关系可以知道，连续型机器人单关节首端坐标系到末端坐标系的齐次变换矩阵可用式(1)表示，它是一个4×4的矩阵。

$ \begin{gathered} {{T}} = {{P}}({{L}},{{\theta}} ,{{\varphi }}){{{R}}_{{Z}}}({{\varphi}} ){{{R}}_{{Y}}}({{\theta}} ){{{R}}_{{Z}}}( - {{\varphi}} ) = \left[ {\begin{array}{*{20}{c}} {{R}}&{{P}} \\ 0&1 \end{array}} \right] =\\ \left(\!\! {\begin{array}{*{20}{c}} {c\theta {c^2}\varphi + {s^2}\varphi }&{c\theta s\varphi c\varphi - c\varphi s\varphi }&{s\theta c\varphi }&{\dfrac{L}{\theta }c\varphi (1 - c\theta )} \\ {c\theta c\varphi s\varphi - c\varphi s\varphi }&{{c^2}\varphi + {s^2}\varphi c\theta }&{s\theta s\varphi }&{\dfrac{L}{\theta }s\varphi (1 - c\theta )} \\ { - s\theta c\varphi }&{ - s\theta s\varphi }&{c\theta }&{\dfrac{L}{\theta }s\theta } \\ 0&0&0&1 \!\! \end{array}} \right) \end{gathered} $

(1)

为了方便，记 $c\theta = \cos \theta $ ， $s\theta = \sin \theta $ ， ${s^2}\theta = {\sin ^2}\theta $ ， ${c^2}\theta = {\cos ^2}\theta $ ，其中 $\theta \in (0,{\rm{{\text{π}} }}]$ ， $\varphi \in [0,2{\rm{{\text{π}} }}]$ ， ${{P}}({{L}},{{\theta}} ,{{\varphi}} )$ 表示平移矩阵， ${{{R}}_{{Z}}}({{\varphi}} )$ 、 ${{{R}}_{{Y}}}({{\theta}} )$ 和 ${{{R}}_{{Z}}}( - {{\varphi}} )$ 分别表示绕+Z、+Y和+Z的坐标转换矩阵， ${{R}}$ 表示旋转矩阵，它是一个3×3的矩阵， ${{P}}$ 表示位置向量，它是一个3×1的矩阵。

各个关节都为等曲率圆弧模型，则根据坐标转换公式可得第 $n$ 关节段坐标系 $\{ n\} $ 到第1关节段坐标系 $\{ 1\} $ 之间的齐次变换矩阵如式(2)所示：

${}_{{{n}} + 1}^1{{T}} = {}_2^1{{T}} \times {}_3^2{{T}} \times {{L}} \times {}_{{{n}} + 1}^{{n}}{{T}}$

(2)

1.2.2 关节空间到绳长空间的转换

由连续型机器人的结构分析可知，机器人的每个关节的姿态变化依赖于穿过该关节绳长的变化，为了实现连续型机器人的操作运动，建立了从关节空间到绳长空间的映射关系。

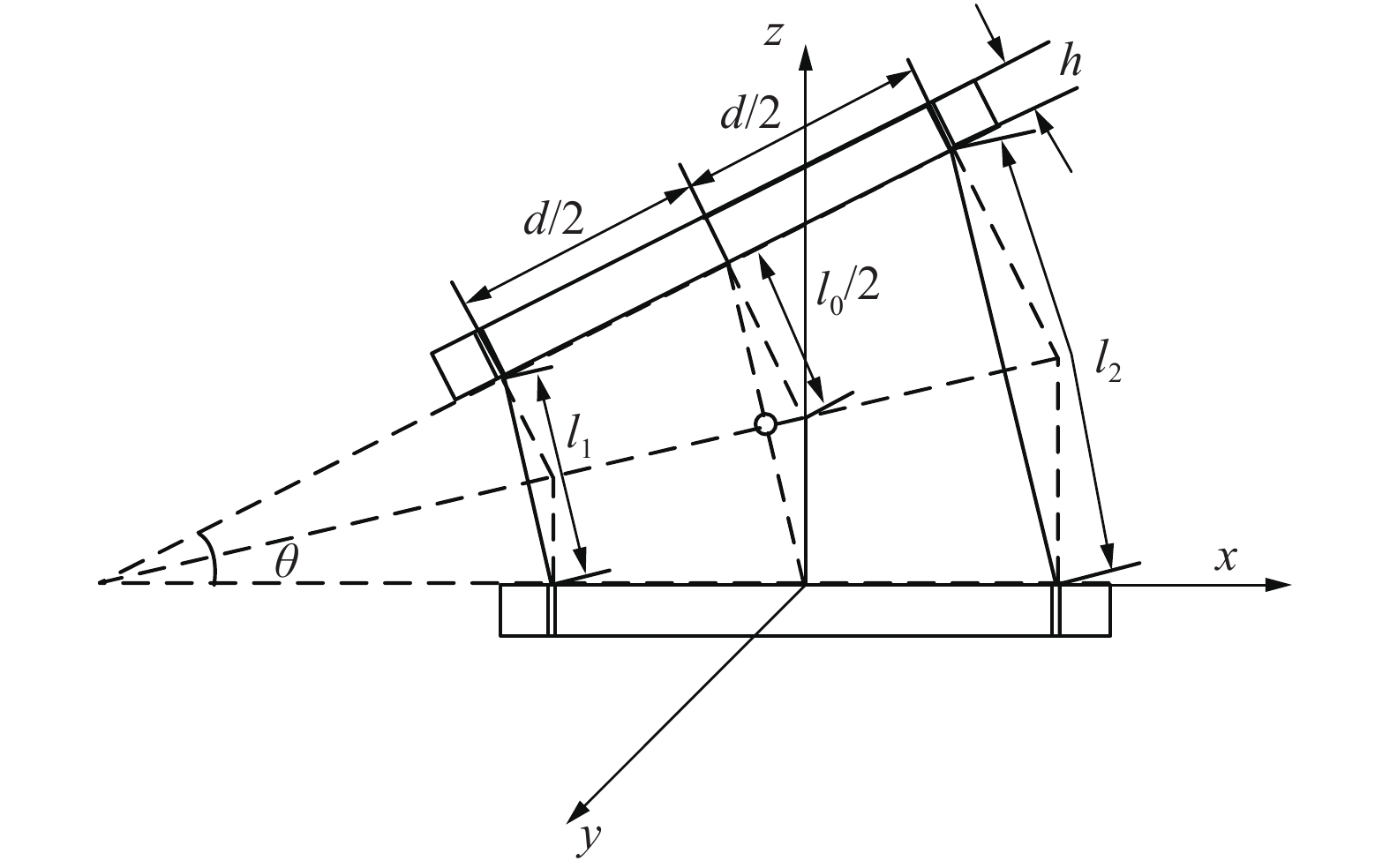
根据关节等曲率模型，可知每个关节的相邻导线圆盘之间的夹角相同，为了便于分析建立连续型机器人的关节空间到绳长空间的映射关系，对其进行简化（如图5所示），上下两个矩形表示导线圆盘截面，圆点表示关节的旋转中心。把用来完成驱动功能的钢丝绳分成两部分，在驱动线孔中的部分，长度为 $h$ ，处于两个导线圆盘之间的部分，长度分别为 ${l_1}$ 和 ${l_2}$ 。假设连续型机器人有 $n$ 个关节，则其直立状态时驱动线长度为 $L = n \cdot $ $ (h + {l_0})$ 。

假设导线圆盘导线孔按逆时针进行编号，由于每个关节由3根钢丝绳驱动，则相邻两孔夹角为 $\alpha = {\dfrac{2{\text{π}}} {3n}}$ 。在连续型机器人机械臂弯曲时，存在导线孔无线的情况，在该情况下，线长变化量为零，设第i关节段的关节变量为 $({\theta _i},{\varphi _i})$ ，由几何分析即可得到第i关节，第j个孔的驱动线在该关节范围内的线长为

$ {L_{ij}} \!=\! n \left[H \!+ \!{l_0} \cos \dfrac{{{\theta _i}}}{{2n}} - d \sin \dfrac{{{\theta _i}}}{{2n}} \cos ({\varphi _i} + (j - 1) \alpha )\right] \!\!\!$

(3)

则线长变化量为

$\Delta {L_{ij}} = n\left\{ {{l_0} - \left[ {{l_0}\cos \frac{{{\theta _i}}}{{2n}} - d\sin \frac{{{\theta _i}}}{{2n}}\cos ({\varphi _i} + (j - 1)\alpha )} \right]} \right\}$

(4)

由于连续型机器人在进行关节运动时，越靠近连续型机器人基座，穿过该关节的驱动线数量越多，所有穿过该关节的驱动线线长都将随之改变。在进行实际计算时，需要的是整体机械臂一个驱动线的变化量，则第j导线孔驱动线总线长变化量 $\Delta {l_j}$ 为

$\Delta {L_j} = \mathop \sum \limits_{i = 1}^n \Delta {L_{ij}}$

(5)

1.2.3 ZYZ欧拉角求解

为了测量连续型机器人的姿态，这里采用姿态传感器采集连续型机器人的姿态信息。由连续型机器人单关节段建模可知，其坐标旋转变换按照Z-Y-Z次序，分别为 $(\varphi ,\theta , - \varphi )$ ，而姿态传感器测量的姿态角的旋转变换按照Z-Y-X次序，假设分别为 $(\alpha ,\beta ,\gamma )$ ，因此无法直接将姿态传感器的输出角度应用到连续型机器人的姿态测量上，需要进行角度转换，建立从 $(\alpha ,\beta ,\gamma )$ 到 $(\varphi ,\theta , - \varphi )$ 的转换关系。

根据旋转公式可求得旋转顺序为Z-Y-X的旋转变换矩阵为

$\begin{gathered} {{R}}({{\alpha}} ,{{\beta }},{{\gamma}} ) = {{{R}}_{{Z}}}({{\alpha}} ){{{R}}_{{Y}}}({{\beta}} ){{{R}}_{{Z}}}({{\gamma}} ) = \left( {\begin{array}{*{20}{c}} {{a_{11}}}&{{a_{12}}}&{{a_{13}}} \\ {{a_{21}}}&{{a_{22}}}&{{a_{23}}} \\ {{a_{31}}}&{{a_{32}}}&{{a_{33}}} \end{array}} \right) =\\ \left( {\begin{array}{*{20}{c}} {c\beta c\alpha }&{s\beta s\gamma c\alpha - c\gamma s\alpha }&{s\beta c\gamma c\alpha + s\gamma s\alpha } \\ {c\beta s\alpha }&{s\beta s\gamma s\alpha + c\gamma c\alpha }&{s\beta c\gamma s\alpha - s\gamma c\alpha } \\ { - s\beta }&{s\gamma c\beta }&{c\gamma c\beta } \end{array}} \right) \\ \end{gathered} \!\!\!\!\!\!$

(6)

由于姿态传感器测量Z轴旋转角度易受环境磁场等因素的影响，所以这里避免使用角度 $\alpha $ ，联合式(6)和式(1)中的旋转变换矩阵 ${{R}}$ ，则可以得到从姿态传感器角度到关节姿态的转换式(7)、式(8)：

$\theta = \left\{ {\begin{array}{*{20}{l}} {A\tan 2(\sqrt {a_{31}^2 + a_{32}^2} ,{a_{33}}),}\;\;{s\theta \ne 0}\\ {{0^ \circ }}\\ {{{180}^ \circ }} \end{array}} \right.$

(7)

$\varphi = \left\{ {\begin{array}{*{20}{l}} { - A\tan 2({a_{32}}, - {a_{31}}),}\;\;{s\theta \ne 0}\\ {{0^ \circ }{\rm{,}}}\;\;{\theta = {0^ \circ }}\\ {{0^ \circ }{\rm{,}}}\;\;{\theta = {{180}^ \circ }} \end{array}} \right.$

(8)

1.2.4 绳长空间到驱动信号空间的映射

连续型机器人绳长的变化控制最终将反映到电机的驱动信号控制上，通过式(5)可以计算出连续型机器人从一个姿态转换到另一个姿态绳长的变化量，这里选择直线模组驱动连续型机器人的线长变化，直线模组导程为 $c$ ，单位mm，设置直线模组驱动器电机每转的脉冲个数为 $s$ ，根据式(5)可计算出各个驱动绳长的变化值 $\Delta l$ ，设直线模组速度为 $v$ ，单位为mm/s，则可以得到绳长变化量和步进电机驱动信号频率和脉冲的映射关系，如式(9)所示：

$\left\{ \begin{gathered} m = \dfrac{s}{c} \cdot \Delta l \\ f = \dfrac{s}{c} \cdot v \\ \end{gathered} \right.$

(9)

式中： $m$ 表示脉冲数目； $f$ 表示在设定速度 $v$ 下的频率，单位为Hz。

2 操作方法研究 2.1 系统设计

为了验证连续型机器人的运动学，搭建了三关节的连续型机器人控制系统，如图6所示，连续型机器人平台由PC、MCU、电源、步进电机驱动器、姿态传感器、直线模组、连续型机器人机械臂等组成。连续型机器人柔性机械臂由3个关节组成，单关节长度220 mm，驱动部分由9个直线模组构成。

由式(7)和式(8)可知，能够由姿态传感器得到连续型机器人姿态，且连续型机器人的姿态计算与绕Z轴的旋转角度无关，因此只需要保证X轴和Y轴与关节末端坐标系的对应轴的平行关系即可，如图6所示，在每一关节末端安装一个姿态传感器。

连续型机器人操控系统主要由PC、MCU、连续型机器人、操控手柄和姿态传感器5个部分组成。图7为各个模块之间的控制框图。

其中，PC为主控程序的载体，负责姿态传感器、操控手柄的信息采集、解析；与MCU模块进行信息交互，发送控制命令实现连续型机器人的手柄控制；实现连续型机器人各个关节姿态的实时显示。姿态传感器负责采集连续型机器人各个关节的姿态信息，并将姿态信息传输到PC。操控手柄负责手动控制的人机交互，将手柄信息传输到PC。MCU为驱动程序的载体，与PC实现信息交互，接受PC的控制命令，并进行控制命令的解析，根据解析结构产生驱动信号直接驱动连续型机器人。连续型机器人平台搭载姿态传感器，受MCU的直接驱动，根据直线模组的运动，实现不同的关节姿态。

2.2 末端跟随控制

连续型机器人具有多个关节，对每个关节都进行直接控制必然会加大控制难度，这里设计末端跟随控制方法实现手柄控制连续型机器人多关节达到设定姿态，即只控制连续型机器人的末端关节姿态，其余关节都跟随末端关节的姿态进行逐步改变。连续型机器人的关节为等曲率模型，各关节之间具有连续性，不能突然弯折，且各关节姿态改变需要依靠多根钢丝绳的协同运动，如果钢丝绳的运动不同步，将会造成连续型机器人偏离预期姿态，甚至造成机械结构的损坏。

为了防止连续型机器人单次姿态变化过大，造成结构破坏，将连续型机器人的姿态变化离散化小角度变化，步长为0.05 rad；同时也为了使所有的直线模组在相同的时间内完成线长变化，这里选取单次线长变化最大的直线模组作为基准，通过改变其他直线模组的驱动信号频率，从而达到直线模组的同步。这样既便于实现连续型机器人的姿态控制，又能够有效避免驱动绳长变化不均匀造成的潜在危险。

3 实验验证 3.1 工作空间仿真

由连续型机器人的结构设计可知，其单关节长度为220 mm，根据连续型机器人的运动学模型，可以得到连续型机器人关节末端点位置，遍历连续型机器人的末端点进行连续型机器人的工作空间仿真。设置连续型机器人各个关节弯曲角度范围[0,180°]，关节旋转角度范围为[0,360°]，分别进行连续型机器人单关节、两关节和三关节的工作空间仿真，仿真结果分别如图8(a)、(c)、(e)所示；由于连续型机器人工作空间的对称性，对其工作空间在XoZ平面的剖视图进行仿真，仿真结果分别如图8(b)、(d)、(f)所示。

根据仿真结果可知随着关节的增加，其可达空间越来越大，且在XoZ平面正方向包围空间的盲区越来越小，与只有一个自由度的单关节传统连杆机器人对比，连续型机器人单关节具有旋转和弯曲两个自由度，证明连续型机器人优越的空间可达性。

3.2 绳长变化仿真

连续型机器人在初始状态下，处于直立状态，以首关节底端为坐标系原点，可得到连续型机器人末端点坐标为{0,0,660}。根据连续型机器人的结构可知关节驱动之间存在耦合关系，对连续型机器人弯曲和旋转对绳长的影响进行仿真。

设置初始关节状态弯曲角度为 $\varTheta = \{ 0,0,0\} $ ，旋转角度为 $\varPhi = \{ 0,0,0\} $ ，然后分别将关节1(#1)、关节2(#2)和关节3(#3)从0°弯曲到180°，进行关节弯曲和绳长变化的仿真实验；3个关节(#1#2#3)整体同时从0°弯曲到180°，进行关节弯曲和绳长变化的仿真实验，仿真结果如图9(a)~(d)所示，纵坐标为220、440、660 mm附近的红、绿、蓝三线分别代表3个关节的3根绳长变化。

分别设置初始状态弯曲角度为 ${\varTheta _1} = \{ 0,0,90\}$ ， ${\varTheta _2} = \{ 0,90,0\}$ ， ${\varTheta _3} = \{ 90,0,0\}$ ，旋转角度为 $\varPhi = \{ 0,0,0\}$ ，然后使相应的弯曲关节从0°旋转到360°，进行关节旋转对绳长变化的仿真实验；设置初始状态弯曲角度为 ${\varTheta _4} = \{ 90,90,90\}$ ，3个关节同时从0°旋转到360°，进行关节旋转对绳长变化仿真实验，仿真结果如图9(e)~(h)所示，纵坐标为220、440、660 mm附近的红、绿、蓝三线分别代表3个关节的3根绳长变化。

根据仿真结果可以验证连续型机器人关节驱动之间的耦合性，低层关节姿态改变时，高层关节穿过该层的驱动线绳长也会改变，由关节旋转仿真图9(e)~(h)可知每个关节的每根绳长变化仿真图波峰波谷相隔120°，对应于连续型机器人结构中单关节驱动绳相隔120°。

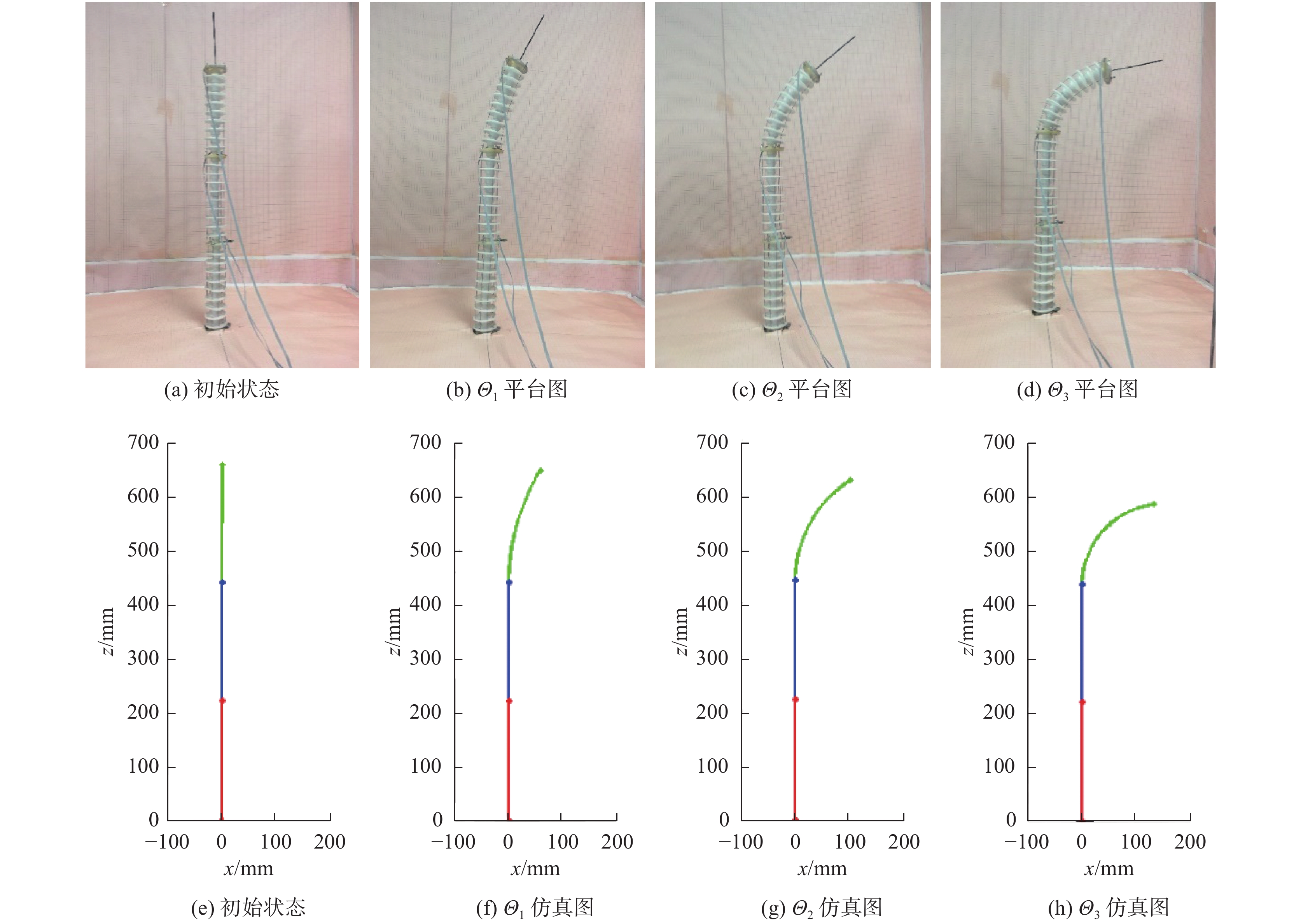
3.3 单关节弯曲实验

通过控制手柄，进行连续型机器人单关节弯曲实验和三关节的末端跟随实验。进行程序初始化，连续型机器人初始状态为：弯曲角度 $\varTheta = $ $ \{ 0,0,0\}$ ，旋转角度为 $\varPhi = \{ 0,0,0\}$ ，设置关节角度每次改变为0.05 rad，遥控手柄设置连续型机器人第三关节的弯曲角度分别为 ${\varTheta _1} = \{ 0,0,31.52\}$ ， ${\varTheta _2} = \{ 0,0, $ $ 57.30\}$ ， ${\varTheta _3} = \{ 0,0,83.08\}$ ，则可得到仿真姿态和实际姿态，如图10所示。并记录连续型机器人第三关节从0°弯曲到90°的过程中理论弯曲角度和姿态传感器采集到的角度，进行误差仿真，如图11所示。

根据实验结果可知姿态传感器角度变化结果、连续型的仿真结果以及连续型机器人的实际结果具有一致性，验证了姿态传感器解算连续型机器人姿态的合理性以及连续型机器人手柄控制方式的可行性。

姿态传感器的角度测量与连续型机器人样机平台操控的理论弯曲角度存在偏差，且误差积累主要发生在弯曲角度较小时，是由于连续型机器人初始状态下钢丝绳不能处于绝对紧绷状态所致，在第五个采样点之后，误差趋于稳定，此时连续型机器人样机平台姿态控制趋于正常。

3.4 三关节操作实验

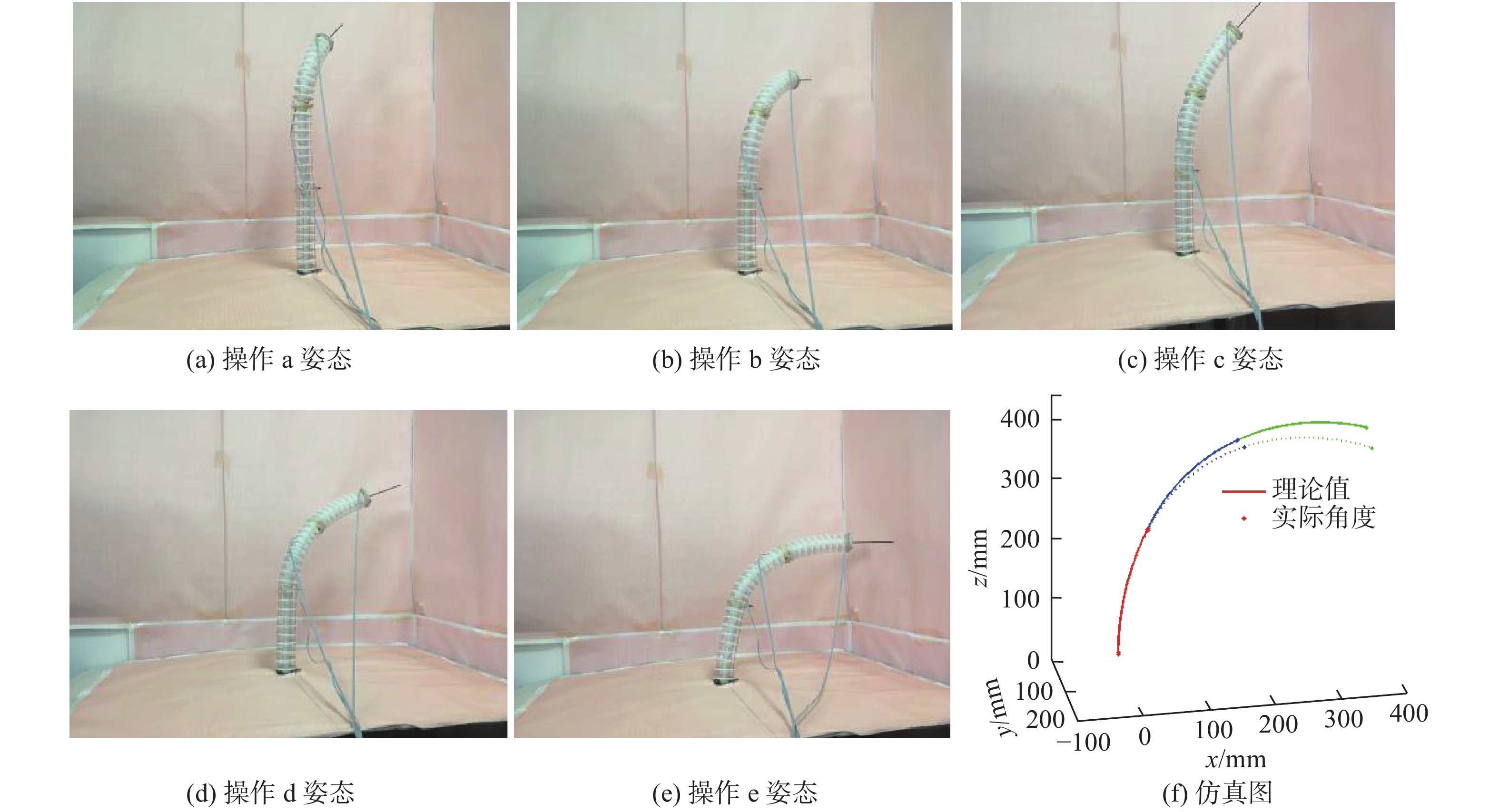
为了验证末端跟随手柄操控方法的正确性，设置连续型机器人初始状态弯曲角度为 $\varTheta = \{ 0,0,0\}$ ，旋转角度为 $\varPhi = \{ 0,0,0\}$ 。

1)操控手柄使第一关节弯曲角度为57.32°，旋转角度为37.83°，结果如图12(a)所示；

2)点击前进按钮实现第一关节的姿态跟随，图12(b)为姿态跟随的中间过程图；

3)操作第一关节弯曲角度为34.39°，结果如图12(c)所示；

4)继续点击前进按钮，完成第二关节姿态跟随，此时连续型机器人姿态为弯曲角度 $\varTheta = $ $ \{ 0,57.32,34.39\}$ ，旋转角度 $\varPhi = \{ 0,37.83,37.83\} $ ，结果如图12(d)所示；

5)继续点击前进按钮，直到关节姿态参数为 $\varTheta = \{ 22.93,34.39,34.39\}$ ， $\varPhi = \{ 15.13,37.83,37.83\}$ ，其姿态传感器的结果为 $\varTheta = \{ 22.93,34.39,34.39\}$ ， $\varPhi = $ $ \{ 17.19,37.83,36.69\}$ ，样机平台图如图12(e)所示，仿真图如图12(f)所示。

根据图12(a)~(e)可知，可以通过手柄进行连续型机器人末端姿态的控制，并可以实现在控制过程中实现末端关节的操作，验证了连续型机器人手柄控制策略的可行性和正确性。根据图12(f)可知，连续型机器人理论姿态和实际姿态之间存在误差，可知在进行多关节弯曲时，随着弯曲角度变大，连续型机器人柔性机械臂易受到重力的影响，这是由于无法保证各关节初始时刻钢丝绳处于绝对紧绷状态和关节处于绝对直立状态。

4 结束语

本文主要模仿蛇脊椎骨的构造设计了基于球铰链连接的连续型机器人柔性机械臂结构，柔性机械臂由各关节段穿过柔性支撑杆构成，相邻导线圆盘的球头球壳同心连接，这种结构较大程度地保证了柔性机械臂的韧性和等曲性；使用直线模组作为驱动机构，减小卷轴驱动过程中缠绕不均带来的线长误差。

针对样机平台建立连续型机器人运动学模型，进行空间可达仿真实验，验证连续型机器人优越的空间可达性，建立从工作空间到姿态空间再到绳长变化空间、驱动空间的映射关系，并进行仿真验证，验证了运动学模型和驱动映射关系的正确性和合理性。

搭建了三关节连续型机器人样机平台整体系统，分析了姿态传感器测量姿态到连续型机器人姿态的转换关系，并根据连续型机器人多自由度的特点，选择多自由度手柄，设计手柄末端跟随控制模式，通过实际平台实验，验证了姿态转换关系的正确性以及手柄控制连续型机器人多关节实现设置姿态方法的正确性和可行性。