Decision costs of the similarity three-way decision-theoretic fuzzy rough set model
模糊集用隶属函数描述对象的隶属程度来刻画模糊边界的不分明性。粗糙集用上、下近似刻画对象间的不可区分关系来对对象进行分类。模糊集和粗糙集都是处理不完全、不确定性信息的重要数学工具,同时都推广了经典集合论处理不确定性和不精确性问题。两者既有相似性又有区别,因此不能互相包含、互相取代,很多人就试图将粗糙集和模糊集进行融合。20世纪90年代,Dubois 等[1-2]将粗糙集和模糊集结合在一起,提出了描述不确定性的模糊粗糙集模型。在概率近似空间上,Sun等[3]提出了粗糙近似模糊概念。Yao等[4]基于贝叶斯决策近似概念的含义提出了模糊粗糙集。Zhao等[5]在模糊概率近似空间和区间值模糊概率近似空间的框架下研究了决策粗糙集。
基于决策粗糙集,Yao[6]提出了三支决策。通过推广贝叶斯决策理论得到了三支决策粗糙集,其考虑的是粗糙集三个成对互不相交的区域,即正域、负域和边界域。之后,Liang等[7]提出了一系列新的三支决策模型,比如区间值粗糙集三支决策、双重犹豫模糊粗糙集三支决策[8],基于点算子的直觉模糊粗糙集的三支决策[9]等。最近,Feng等[10]基于多粒度模糊近似空间和隶属度算子,将三支决策和变精度粗糙集结合在一起,提出了1型变精度多粒度决策模糊粗糙集模型。随着研究的深入,Deng等[11]推广了三支近似模糊集决策模型,提出可变的决策理论公式,通过最小化决策代价计算阈值对
$\left( {\alpha ,\beta } \right)$
。杨雯琳等[12]建立了基于相似度的三支决策模糊粗糙集最优模型来计算阈值对
$\left( {\alpha ,\beta } \right)$
。衷锦仪等[13]基于区间值决策粗糙集模型,从模糊数学的角度得出了更为紧凑的阈值对
$\left( {\alpha ,\beta } \right)$
的上、下近似。对于多重集值,Zhao等[14]提出了多重集决策粗糙集模型和多重集模糊决策粗糙集模型来计算损失函数的期望代价。Liang等[15]将精确值的损失函数概念推广到三角模糊决策粗糙集上来计算决策损失。Lin[16]基于约束满意度提出了一种解决模糊线性关系的方法,该方法被其他学者用于研究阈值对
$\left( {\alpha ,\beta } \right)$
。
目前,三支决策已经得到了广泛的应用,而且决策粗糙集理论[17]是求解三支分类的经典理论之一。因此,三支决策相关的研究成果包括了不同数据模型的决策粗糙集推广,例如:基于代价敏感度量的概率粗糙集三支决策[18-19]、模糊集三支决策[8]、区间集三支决策[20]、邻域三支决策[21]等。不同模型阈值对确定的方法可能是不同的。邢航[22]提出的基于构造性覆盖算法的三支决策模型可以根据样本的分布特征自动形成三个域,相比于基于决策粗糙集的三支决策模型,基于构造性覆盖算法的三支决策模型不必人为决定关键参数,能自动形成三个域,使得如何获得决策粗糙集理论模型中损失函数、阈值的取值问题得以解决。徐健锋等[23]提出了一种基于三支决策代价目标函数间逻辑关系的新型阈值计算方法。Liu等[24]为决策理论粗糙集中的阈值参数优化建立了理论和系统的框架,并且提出了一种基于优化的通用方法来确定具有各种语义的决策理论粗糙集的阈值对。
在模糊决策粗糙集模型中,大多数研究是以总体决策代价最小化为目标,得出计算最优阈值对
$\left( {\alpha ,\beta } \right)$
的方法,其中决策代价是专家给出的,并没有进行进一步的研究。而衷锦仪等[13]基于区间值模糊决策粗糙集模型,得出了计算决策代价的方法。本文采用了属性值来描述决策代价,用对象间的曼哈顿距离表示决策代价函数,得出最优阈值对
$\left( {\alpha ,\beta } \right)$
。
1 决策粗糙集模型
本节介绍了多重集的相关概念和基于模糊数的决策粗糙集模型,该模型用区间值来刻画损失代价得到更为紧凑的阈值对
$\left( {\alpha ,\beta } \right)$
的上、下近似。
1.1 多重集
定义1[18] 设一个非空论域
$U$
,在
$U$
上的一个多重集
$M$
上定义函数
${C_M}:U \to N$
,其中
$N$
是自然数集,
${C_M}\left( x \right)$
是
$x$
的重数,
$\forall x \in U$
。
函数
${C_M}$
称为有限函数,表示每个元素出现的次数。
$\mu \left( U \right)$
表示
$U$
上的所有多重集族。如果
$\forall x \in U,{C_M}\left( x \right) = 0$
,则
$M$
是一个空的多重集,记为
${\text{Ø}}$
。多重集有多种表示方式,
$M = \left( {x,x,x,y,y, \cdot \cdot \cdot } \right)$
,
$M = $
$ \left\{ {\left( {x,{C_M}\left( x \right)} \right)\left| {x \in U,{C_M}\left( x \right) \in N} \right.} \right\}$
,
$M = \displaystyle\sum\limits_{x \in U} {\dfrac{{{C_M}\left( x \right)}}{x}} $
(
$U$
是有限集)或
$M = \displaystyle\int\limits_{x \in U} {\dfrac{{{C_M}\left( x \right)}}{x}} $
(
$U$
是无限集)。
定义2[14] 在
${\mu _F}\left( {\left[ {0,1} \right]} \right)$
上,多重集
$M = \{ ( x, $
$ {C_M}\left( x \right) )\left| {x \in \left[ {0,1} \right],{C_M}\left( x \right) \in N} \right. \}$
,
$M$
的长度定义为:
${\left\| M \right\|_p} = $
$ {\left( {\displaystyle\sum\limits_x {{C_M}\left( x \right) \cdot {x^p}} } \right)^{\frac{1}{p}}},p \geqslant 1$
。
常用的长度有:曼哈顿长度,即
${\left\| M \right\|_1} = \displaystyle\sum\limits_x {{C_M}\left( x \right) \cdot x} $
;欧几里得长度,即
${\left\| M \right\|_2} = {\left( {\displaystyle\sum\limits_x {{C_M}\left( x \right) \cdot {x^2}} } \right)^{\frac{1}{2}}}$
;无限长度,即
${\left\| M \right\|_\wp } = {\max _x}\left\{ {{C_M}\left( x \right) \cdot x} \right\}$
。
1.2 基于模糊数的决策粗糙集模型
Yao等[4]基于贝叶斯决策过程,提出决策理论粗糙集模型,该模型利用状态集
$O = \left\{ {A,{A^C}} \right\}$
和动作集
$a = \left\{ {{a_e},{a_b},{a_r}} \right\}$
来描述决策过程,其中状态集
$O = \left\{ {A,{A^C}} \right\}$
中的元素分别表示某事件属于
$A$
和不属于
$A$
,动作集
$a = \left\{ {{a_e},{a_b},{a_r}} \right\}$
中的元素分别表示将对象
$x$
划分到正域、边界域和负域。
对象
$x$
采取3个行动之一引起的实际代价
$R\left( {{a_e}\left| {\left[ x \right]} \right.} \right),R\left( {{a_b}\left| {\left[ x \right]} \right.} \right),R\left( {{a_r}\left| {\left[ x \right]} \right.} \right)$
分别为
|
$\begin{array}{l} \left. 1 \right)R\left( {{a_e}\left| {\left[ x \right]} \right.} \right) = {\lambda _{ep}} \cdot P\left( {A\left| {\left[ x \right]} \right.} \right) + {\lambda _{en}} \cdot P\left( {{A^C}\left| {\left[ x \right]} \right.} \right) \\ \left. 2 \right)R\left( {{a_b}\left| {\left[ x \right]} \right.} \right) = {\lambda _{bp}} \cdot P\left( {A\left| {\left[ x \right]} \right.} \right) + {\lambda _{bn}} \cdot P\left( {{A^C}\left| {\left[ x \right]} \right.} \right) \\ \left. 3 \right)R\left( {{a_r}\left| {\left[ x \right]} \right.} \right) = {\lambda _{rp}} \cdot P\left( {A\left| {\left[ x \right]} \right.} \right) + {\lambda _{rn}} \cdot P\left( {{A^C}\left| {\left[ x \right]} \right.} \right) \\ \end{array} $
|
式中:
${\lambda _{ep}}{\text{、}}{\lambda _{bp}}{\text{、}}{\lambda _{rp}}$
分别表示当
$x$
$ \in $
$A$
采取行动
${a_e}{\text{、}}{a_b}{\text{、}}{a_r}$
时的决策代价;
${\lambda _{en}}{\text{、}}{\lambda _{bn}}{\text{、}}{\lambda _{rn}}$
分别表示当
$x$
$ \notin $
$A$
采取行动
${a}_{e}{\text{、}}{a}_{b}{\text{、}}{a}_{r}$
时的决策代价;
$P\left( {A\left| {\left[ x \right]} \right.} \right)$
表示
$x$
$\in $
$A$
的条件概率,
$P\left( {{A^C}\left| {\left[ x \right]} \right.} \right) $
表示
$x$
$ \notin $
$A$
的条件概率。
所以,总体决策代价为
$R = \displaystyle\sum\limits_{x \in U} {R\left( {a\left| x \right.} \right)} = \displaystyle\sum\limits_{x \in U} {{\lambda _{ap}}} \cdot $
$ { P\left( {A\left| {\left[ x \right]} \right.} \right) + {\lambda _{an}} \cdot P\left( {{A^C}\left| {\left[ x \right]} \right.} \right)}$
。
根据贝叶斯决策准则,要使总体决策代价达到最小,则需要采取行动的实际代价最小,即决策规则为:
1)如果
$R\left( {{a_e}\left| {\left[ x \right]} \right.} \right) \leqslant R\left( {{a_b}\left| {\left[ x \right]} \right.} \right)$
且
$R\left( {{a_e}\left| {\left[ x \right]} \right.} \right) \leqslant R( {a_r}| $
$ {\left[ x \right]} )$
,则采取接受决策;
2)如果
$R\left( {{a_b}\left| {\left[ x \right]} \right.} \right) \leqslant R\left( {{a_e}\left| {\left[ x \right]} \right.} \right)$
且
$R\left( {{a_b}\left| {\left[ x \right]} \right.} \right) \leqslant R( {a_r}| $
$ {\left[ x \right]} )$
,则采取延迟决策;
3)如果
$R\left( {{a_r}\left| {\left[ x \right]} \right.} \right) \leqslant R\left( {{a_e}\left| {\left[ x \right]} \right.} \right)$
且
$R\left( {{a_r}\left| {\left[ x \right]} \right.} \right) \leqslant R( {a_b}| $
$ {\left[ x \right]} ) $
,则采取拒绝决策。
可以计算出阈值对
$\left( {\alpha ,\beta } \right)$
为
$\Bigg( \dfrac{{{\lambda _{an}} - {\lambda _{bn}}}}{{\left( {{\lambda _{an}} - {\lambda _{bn}}} \right) + \left( {{\lambda _{bp}} - {\lambda _{ap}}} \right)}}, $
$ \dfrac{{{\lambda _{bn}} - {\lambda _{rn}}}}{{\left( {{\lambda _{bn}} - {\lambda _{rn}}} \right) + \left( {{\lambda _{rp}} - {\lambda _{bp}}} \right)}} \Bigg)$
。
定义3[13] 设论域
$U$
上的模糊数为
$F$
,如果
$F$
的隶属度函数
${\mu _F}:U \to \left[ {0,1} \right]$
表示为
|
${\mu _F}\left\{ \begin{array}{l} 0,\quad x < {r_1} \\ \dfrac{{x - {r_1}}}{{{r_2} - {r_1}}},\quad {r_1} \leqslant x < {r_2} \\ 1,\quad {r_2} \leqslant x < {r_3} \\ \dfrac{{{r_4} - x}}{{{r_4} - {r_3}}},\quad {r_3} \leqslant x < {r_4} \\ 0,\quad x \geqslant {r_4} \end{array} \right.$
|
则称
$M = \left( {{r_1},{r_2},{r_3},{r_4}} \right)$
为梯形模糊数。
设一组决策代价
${\lambda _{ep}} = \left[ {\lambda _{ep}^L,\lambda _{ep}^U} \right],{\lambda _{bp}}$
$= \left[ {\lambda _{bp}^L,\lambda _{bp}^U} \right], {\lambda _{rp}} = $
$ \left[ {\lambda _{rp}^L,\lambda _{rp}^U} \right], {\lambda _{en}} = \left[ {\lambda _{en}^L,\lambda _{en}^U} \right],{\lambda _{bn}} =$
$\left[ {\lambda _{bn}^L,\lambda _{bn}^U} \right],{\lambda _{rn}} = \left[ {\lambda _{rn}^L,\lambda _{rn}^U} \right]$
。设
${\lambda _{ * * }}$
为某个状态决策动作的决策代价,模糊统计方法如下:
1)设在一次统计中,
$n$
位专家给出了
$n$
个区间值
${\lambda _{ * * }} = \left[ {\lambda _{ * * }^L,\lambda _{ * * }^U} \right]$
;
2)找出
$n$
个区间值中的最小值
${\lambda _{\min }}$
和最大值
${\lambda _{\max }}$
,以
${\lambda _{\min }}$
为起点,
${\lambda _{\max }}$
为终点,
$\dfrac{{{\lambda _{\max }} - {\lambda _{\min }}}}{k}$
为长度(
$k \in {N^ * }$
),作
$k$
个区间的划分;
3)计算每个区间的隶属频率
$f = \dfrac{m}{n}$
,其中
$n$
为随机选择的样本总数,
$m$
为区间样本覆盖
${\lambda _{ * * }}$
的频数;
4)以实数
$x$
为横坐标,隶属频率为纵坐标,绘出
${\lambda _{ * * }}$
的模糊分布曲线。
5)对该模糊分布左右两边的曲线进行直线拟合,得到一个梯形分布函数。
设决策代价
${\lambda _{ * * }}$
的梯形模糊数为
${M_{ * * }}$
,即
|
${M_{ep}} = \left( {{r_{11}},{r_{12}},{r_{13}},{r_{14}}} \right)$
|
|
${M_{bp}} = \left( {{r_{21}},{r_{22}},{r_{23}},{r_{24}}} \right)$
|
|
${M_{rp}} = \left( {{r_{31}},{r_{32}},{r_{33}},{r_{34}}} \right)$
|
|
${M_{en}} = \left( {{s_{11}},{s_{12}},{s_{13}},{s_{14}}} \right)$
|
|
${M_{bn}} = \left( {{s_{21}},{s_{22}},{s_{23}},{s_{24}}} \right)$
|
|
${M_{rn}} = \left( {{s_{31}},{s_{32}},{s_{33}},{s_{34}}} \right)$
|
可以得到
$\alpha {\text{、}}\beta $
的模糊分布为
|
$ \begin{split}& \;\alpha \!=\! \left( {\dfrac{1}{{1 \!+\! \dfrac{{{r_{24}} - {r_{11}}}}{{{s_{31}} - {s_{24}}}}}},\dfrac{1}{{1 \!+\! \dfrac{{{r_{23}} - {r_{12}}}}{{{s_{32}} - {s_{23}}}}}},\dfrac{1}{{1 \!+\! \dfrac{{{r_{22}} - {r_{13}}}}{{{s_{33}} - {s_{22}}}}}},\dfrac{1}{{1 \!+\! \dfrac{{{r_{21}} - {r_{14}}}}{{{s_{34}} - {s_{21}}}}}}} \right)\\ &\;\beta \!=\! \left( {\dfrac{1}{{1 \!+\! \dfrac{{{r_{34}} - {r_{21}}}}{{{s_{21}} - {s_{14}}}}}},\dfrac{1}{{1 \!+\! \dfrac{{{r_{33}} - {r_{22}}}}{{{s_{22}} - {s_{13}}}}}},\dfrac{1}{{1 \!+\! \dfrac{{{r_{32}} - {r_{23}}}}{{{s_{23}} - {s_{12}}}}}},\dfrac{1}{{1 \!+\! \dfrac{{{r_{31}} - {r_{24}}}}{{{s_{24}} - {s_{11}}}}}}} \right) \end{split} $
|
设
$M = \left( {{r_1},{r_2},{r_3},{r_4}} \right)$
是梯形模糊数,
$\alpha = ( {a_1},{a_2}, $
$ {a_3},{a_4} ),\beta = \left( {{b_1},{b_2},{b_3},{b_4}} \right)$
,用模糊满意度[16]来比较两个模糊数的大小,
$\eta $
-水平截集的左右断点分别记为
$\alpha _\eta ^L{\text{、}}\alpha _\eta ^U{\text{、}}\beta _\eta ^L{\text{、}}\beta _\eta ^U$
,则
$\alpha _\eta ^L = {a_2}\eta + {a_1}\left( {1 - \eta } \right),$
$\alpha _\eta ^U = {a_3}\eta + $
$ {a_4}\left( {1 - \eta } \right),\beta _\eta ^L = {b_2}\eta + {b_1}\left( {1 - \eta } \right), \beta _\eta ^U = {b_3}\eta +$
${b_4}\left( {1 - \eta } \right)$
。
2 基于三支决策模糊粗糙集模型的决策代价
在文献[12]中只是给出了最优阈值对
$\left( {\alpha ,\beta } \right)$
关于决策代价的表示,并没有讨论决策代价的问题。文献[14]在多重集中用了重数刻画决策代价,那么在三支决策的模糊粗糙集模型中也可以用属性值来刻画决策代价。对比文献[13]计算决策代价的方法,本文用对象间的曼哈顿距离表示决策代价函数,再进行模糊统计,提出了一种基于相似度三支决策模糊粗糙集模型的计算决策代价的方法。
定义4 设模糊信息系统
$\varOmega = \left( {U,A,V,f} \right)$
,
$A = $
$ \left\{ {{a_1},{a_2}, \cdot \cdot \cdot ,{a_m}} \right\}$
是属性集,
$U = \left\{ {{x_1},{x_2}, \cdot \cdot \cdot ,{x_n}} \right\}$
是对象集,
$V = \left\{ {{V_a}\left| {a \in A} \right.} \right\} = {\left( {{v_{ij}}} \right)_{n \times m}}$
是属性值集,
${V_a}$
是一个隶属函数值,则每个对象在每个属性下相对于其他对象的距离为
${{\rm{dis}}_{ij}} = {\left[ {\dfrac{{\displaystyle\sum\limits_{k = 1}^n {{{\left| {{v_{ij}} - {v_{kj}}} \right|}^p}} }}{n}} \right]^{1/p}}$
,其中
$i = 1, 2, \cdots , n,j = $
$ 1,2, \cdot \cdot \cdot ,m$
,则对象对相应属性的距离
$D = {\left( {\rm{di}}{{\rm{s}}_{ij}^{p}}\right)_{n \times m}}$
。
常用的距离有:
曼哈顿距离:
${\rm{di}}{{\rm{s}}_{ij}^{1}} = \dfrac{{\displaystyle\sum\limits_{k = 1}^n {\left| {{v_{ij}} - {v_{kj}}} \right|} }}{n}$
欧氏距离:
${\rm{di}}{{\rm{s}}_{ij}^{2}} = \sqrt {\dfrac{{\displaystyle\sum\limits_{k = 1}^n {{{\left| {{v_{ij}} - {v_{kj}}} \right|}^2}} }}{n}}$
切比雪夫距离:
${\rm{di}}{{\rm{s}}_{ij}^{m}} = {\max _{1 \leqslant k \leqslant n}}\left\{ {\left| {{v_{ij}} - {v_{kj}}} \right|} \right\}$
定义5 在
$\varOmega = \left( {U,A,V,f} \right)$
中,决策代价函数
${\lambda _ * }:D \to {\lambda _ * }\left( D \right)$
,
${\lambda _ * }$
为决策动作的决策代价:
1)接受决策:
${\lambda _e}\left( D \right) = 1 - D$
。
2)延迟决策:
${\lambda _b}\left( D \right) = \left| {0.5 - D} \right|$
。
3)拒绝决策:
${\lambda _r}\left( D \right) =D$
。
当采取接受决策时,需要付出的决策代价为产生错误决策的决策代价,
${\lambda _e}\left(D\right) = 1 - D$
;当采取延迟决策时,未做任何决策,保留了对象的不确定性,
${\lambda _b}\left(D \right) = \left| {0.5 - D} \right|$
;当采取拒绝决策时,需要付出的决策代价为
${\lambda _r}\left(D \right) = D$
。
模糊统计方法如下:
设某个决策动作的决策代价组
${\lambda _ * } = \left( {\lambda _ * ^1,\lambda _ * ^2, \cdot \cdot \cdot ,\lambda _ * ^m} \right)$
,
$\lambda _ * ^l$
表示第
$l$
个属性的决策代价。
1)在一个模糊信息系统
$\varOmega = \left( {U,A,V,f} \right)$
中,计算每个对象在每个属性下相对于其他对象的距离(此处用曼哈顿距离
${\rm{di}}{{\rm{s}}_{ij}^{1}} = \dfrac{{\displaystyle\sum\limits_{k = 1}^n {\left| {{v_{ij}} - {v_{kj}}} \right|} }}{n}$
),得到关于决策代价的曼哈顿距离
$D = {\left( {{\rm{di}}{{\rm{s}}_{ij}^{1}}} \right)_{n \times m}}$
,其中
$i = $
$ 1,2, \cdot \cdot \cdot ,n{\text{;}}j = 1,2, \cdot \cdot \cdot ,m$
;
2)计算决策代价函数
${\lambda }_{*}\left(D\right)$
;
3)找出
$n$
个值中的最小值
${\lambda _{\min }}$
和最大值
${\lambda _{\max }}$
,以
${\lambda _{\min }} - \delta - \dfrac{{{\lambda _{\max }} - {\lambda _{\min }}}}{{2k}}$
为起点,
${\lambda _{\max }} + \delta + \dfrac{{{\lambda _{\max }} - {\lambda _{\min }}}}{{2k}}$
为终点,
$\dfrac{{{\lambda _{\max }} - {\lambda _{\min }}}}{k}$
为区间长度(
$k \in {N^ * }$
),划分为
$k + 1$
个区间,其中
$\delta $
为邻域值;
4)计算每个动作在不同属性下的隶属频率
$f = \dfrac{m}{n}$
,其中
$n$
为随机选择的样本总数,
$m$
为区间样本覆盖某个值的
$\delta $
邻域的频数;
5)以实数
$x$
为横坐标,隶属频率为纵坐标,对点进行曲线拟合,取决策动作在每个属性下曲线最高点的横坐标,得到一个不同属性下的决策代价组;
6)某个决策动作的决策代价即为
|
$ {\lambda _ * } = \sqrt {\dfrac{{\displaystyle\sum\limits_{l = 1}^m {\lambda {{_ * ^l}^2}} }}{m}} $
|
3 实例分析
实验采用的配置如下:CPU为Intel(R) Celeron(R) CPU 1007U @ 1.5 GHz,4.0 GB内存,软件是64位MATLAB R2014a。
基于文献[12]的模糊信息系统实例来分析本文基于三支决策模糊粗糙集模型的决策代价。
例1
$\varOmega = \left( {U,A,V,f} \right)$
是一个模糊信息系统,如表1所示。其中,对象集合
$U = \left\{ {{x_1},{x_2}, \cdot \cdot \cdot ,{x_8}} \right\}$
,属性集合
$A = \left\{ {{a_1},{a_2}, \cdot \cdot \cdot ,{a_4}} \right\}$
,
$\forall a \in A,\forall x \in U$
,对象的隶属度为
${\mu _a}\left( x \right) \in \left[ {0,1} \right]$
。
表 1(Tab. 1
表 1 模糊信息系统
Tab. 1 Fuzzy information system
| U\A
|
${a_1} $
|
${a_2}$
|
${a_3}$
|
${a_4}$
|
|
${x_1}$
|
0.1 |
0.8 |
0.9 |
0.8 |
|
${x_2}$
|
1.0 |
0.1 |
0.3 |
0.2 |
|
${x_3}$
|
0.6 |
0.3 |
0.8 |
0.4 |
|
${x_4}$
|
0.1 |
0.6 |
0.9 |
0.6 |
|
${x_5}$
|
0.2 |
0.9 |
0.9 |
0.5 |
|
${x_6}$
|
0.5 |
0.2 |
0.7 |
0.3 |
|
${x_7}$
|
0.3 |
0.9 |
0.5 |
0.7 |
|
${x_8}$
|
1.0 |
0.6 |
0.2 |
0.1 |
|
表 1 模糊信息系统
Tab.1 Fuzzy information system |
计算每个对象在每个属性下相对于其他对象的曼哈顿距离
${\rm{di}}{{\rm{s}}_{ij}^{1}} = \dfrac{{\displaystyle\sum\limits_{k = 1}^8 {\left| {{v_{ij}} - {v_{kj}}} \right|} }}{8}$
,其中,
$i = 1,2, \cdot \cdot \cdot , $
$ 8{\text{;}}j = 1, 2, \cdot \cdot \cdot ,4$
,得到的关于决策代价的曼哈顿距离
$D= {\left( {{\rm{di}}{{\rm{s}}_{ij}^{1}}} \right)_{8 \times 4}}$
如表2所示。
表 2(Tab. 2

表 2 曼哈顿距离
Tab. 2 Manhattan distance
| 对象 |
${a_1}$
|
${a_2}$
|
${a_3}$
|
${a_4}$
|
|
${x_1}$
|
0.3750 |
0.3000 |
0.2500 |
0.3500 |
|
${x_2}$
|
0.5250 |
0.4500 |
0.3750 |
0.2750 |
|
${x_3}$
|
0.3250 |
0.3250 |
0.2250 |
0.2000 |
|
${x_4}$
|
0.3750 |
0.2500 |
0.2500 |
0.2250 |
|
${x_5}$
|
0.3250 |
0.3500 |
0.2500 |
0.2000 |
|
${x_6}$
|
0.3000 |
0.3750 |
0.2250 |
0.2250 |
|
${x_7}$
|
0.3000 |
0.3500 |
0.2750 |
0.2750 |
|
${x_8}$
|
0.5250 |
0.2500 |
0.4500 |
0.3500 |
|
表 2 曼哈顿距离
Tab.2 Manhattan distance |
计算当采取接受决策时的决策代价
${\lambda _e}\left( D\right) = $
$ 1 - D$
,则得到接受决策的决策代价如表3所示。
表 3(Tab. 3

表 3 接受决策的决策代价
Tab. 3 Decision costs of accepting the decision
| 对象 |
${a_1}$
|
${a_2}$
|
${a_3}$
|
${a_4}$
|
|
${x_1}$
|
0.6250 |
0.7000 |
0.7500 |
0.6500 |
|
${x_2}$
|
0.4750 |
0.5500 |
0.6250 |
0.7250 |
|
${x_3}$
|
0.6750 |
0.6750 |
0.7750 |
0.8000 |
|
${x_4}$
|
0.6250 |
0.7500 |
07500 |
0.7750 |
|
${x_5}$
|
0.6750 |
0.6500 |
0.7500 |
0.8000 |
|
${x_6}$
|
0.7000 |
0.6250 |
0.7750 |
0.7750 |
|
${x_7}$
|
0.7000 |
0.6500 |
0.7250 |
0.7250 |
|
${x_8}$
|
0.4750 |
0.7500 |
0.5500 |
0.6500 |
|
表 3 接受决策的决策代价
Tab.3 Decision costs of accepting the decision |
接受决策的决策代价在属性
${a_1}$
下的最小值为0.475,最大值为0.7,取
$\delta = 0.15$
,以0.3125为起点,0.8625为终点,0.025为区间长度,划分为22个区间。接受决策属性
${a_1}$
的决策代价频率分布如表4所示。
表 4(Tab. 4

表 4 属性
${a_1}$
决策代价频率分布
Tab. 4 Attribute
${a_1}$
decision costs frequency distribution
| 序号 |
区间 |
频数 |
频率 |
| 1 |
$\left[ {0.312\;5,0.337\;5} \right]$
|
2 |
0.2500 |
| 2 |
$\left[ {0.337\;5,0.362\;5} \right]$
|
2 |
0.2500 |
| 3 |
$\left[ {0.362\;5,0.387\;5} \right]$
|
2 |
0.2500 |
| 4 |
$\left[ {0.387\;5,0.412\;5} \right]$
|
2 |
0.2500 |
| 5 |
$\left[ {0.412\;5,0.437\;5} \right]$
|
2 |
0.2500 |
| 6 |
$\left[ {0.437\;5,0.462\;5} \right]$
|
2 |
0.2500 |
| 7 |
$\left[ {0.462\;5,0.487\;5} \right]$
|
4 |
0. 5000 |
| 8 |
$\left[ {0.487\;5,0.512\;5} \right]$
|
4 |
0.5000 |
| 9 |
$\left[ {0.512\;5,0.537\;5} \right]$
|
6 |
0.7500 |
| 10 |
$\left[ {0.537\;5,0.562\;5} \right]$
|
8 |
1.0000 |
| 11 |
$\left[ {0.562\;5,0.587\;5} \right]$
|
8 |
1.0000 |
| 12 |
$\left[ {0.587\;5,0.612\;5} \right]$
|
8 |
1.0000 |
| 13 |
$\left[ {0.612\;5,0.637\;5} \right]$
|
8 |
1.0000 |
| 14 |
$\left[ {0.637\;5,0.662\;5} \right]$
|
6 |
0.7500 |
| 15 |
$\left[ {0.662\;5,0.687\;5} \right]$
|
6 |
0.7500 |
| 16 |
$\left[ {0.687\;5,0.712\;5} \right]$
|
6 |
0.7500 |
| 17 |
$\left[ {0.712\;5,0.737\;5} \right]$
|
6 |
0.7500 |
| 18 |
$\left[ {0.737\;5,0.762\;5} \right]$
|
6 |
0.7500 |
| 19 |
$\left[ {0.762\;5,0.787\;5} \right]$
|
6 |
0.7500 |
| 20 |
$\left[ {0.787\;5,0.812\;5} \right]$
|
4 |
0.5000 |
| 21 |
$\left[ {0.812\;5,0.837\;5} \right]$
|
4 |
0.5000 |
| 22 |
$\left[ {0.837\;5,0.862\;5} \right]$
|
2 |
0.2500 |
|
表 4 属性
${a_1}$
决策代价频率分布
Tab.4 Attribute
${a_1}$
decision costs frequency distribution |
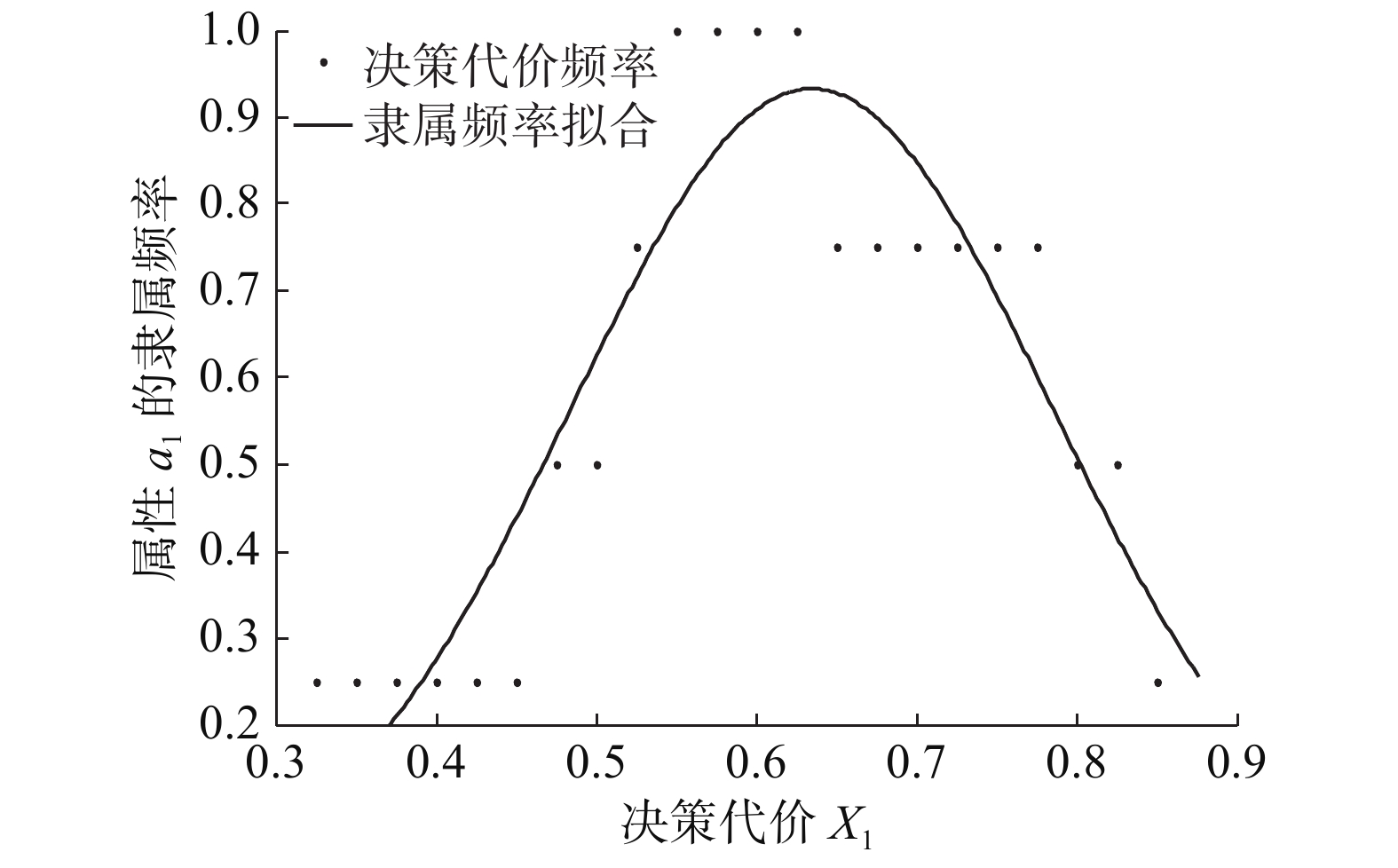
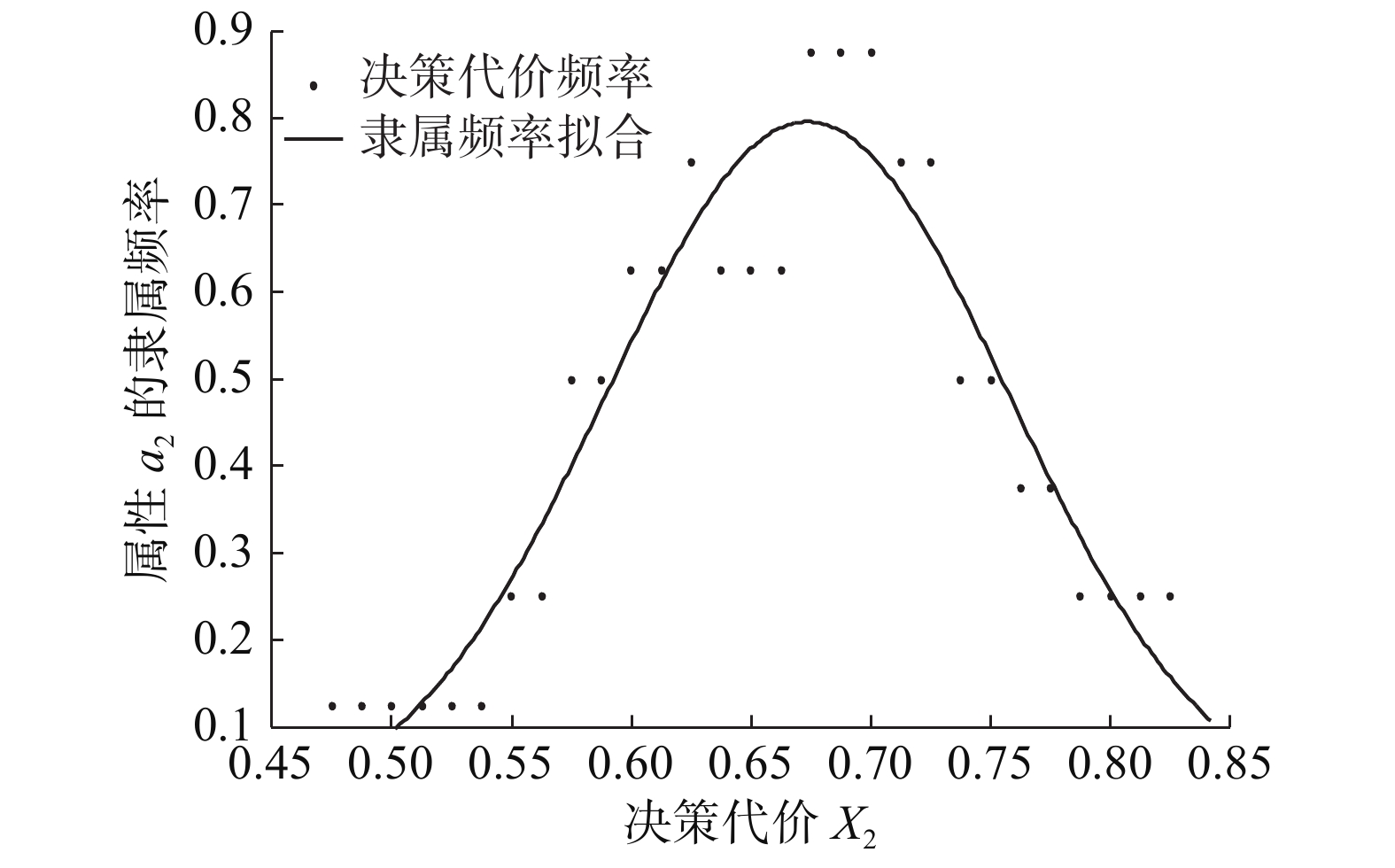
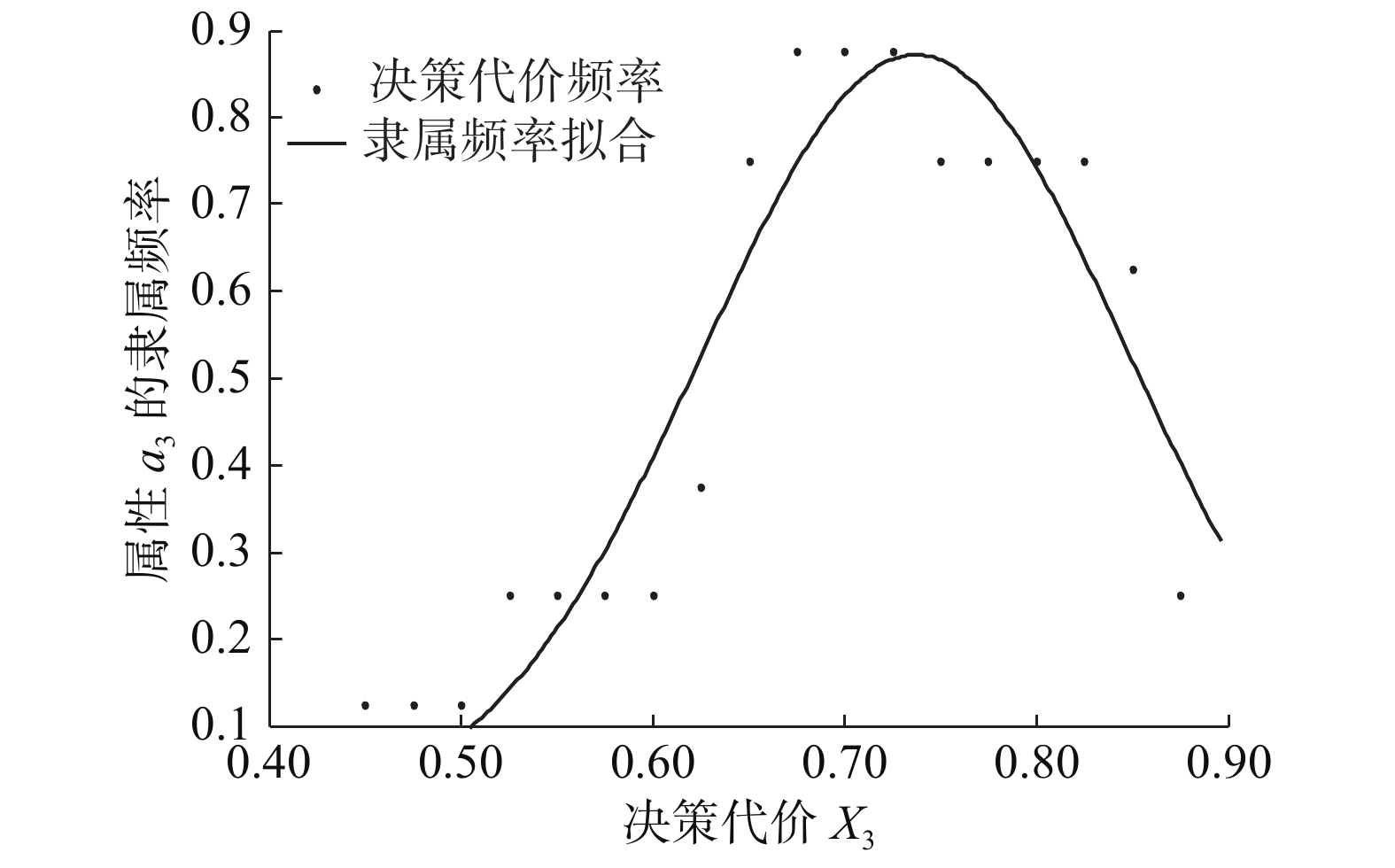
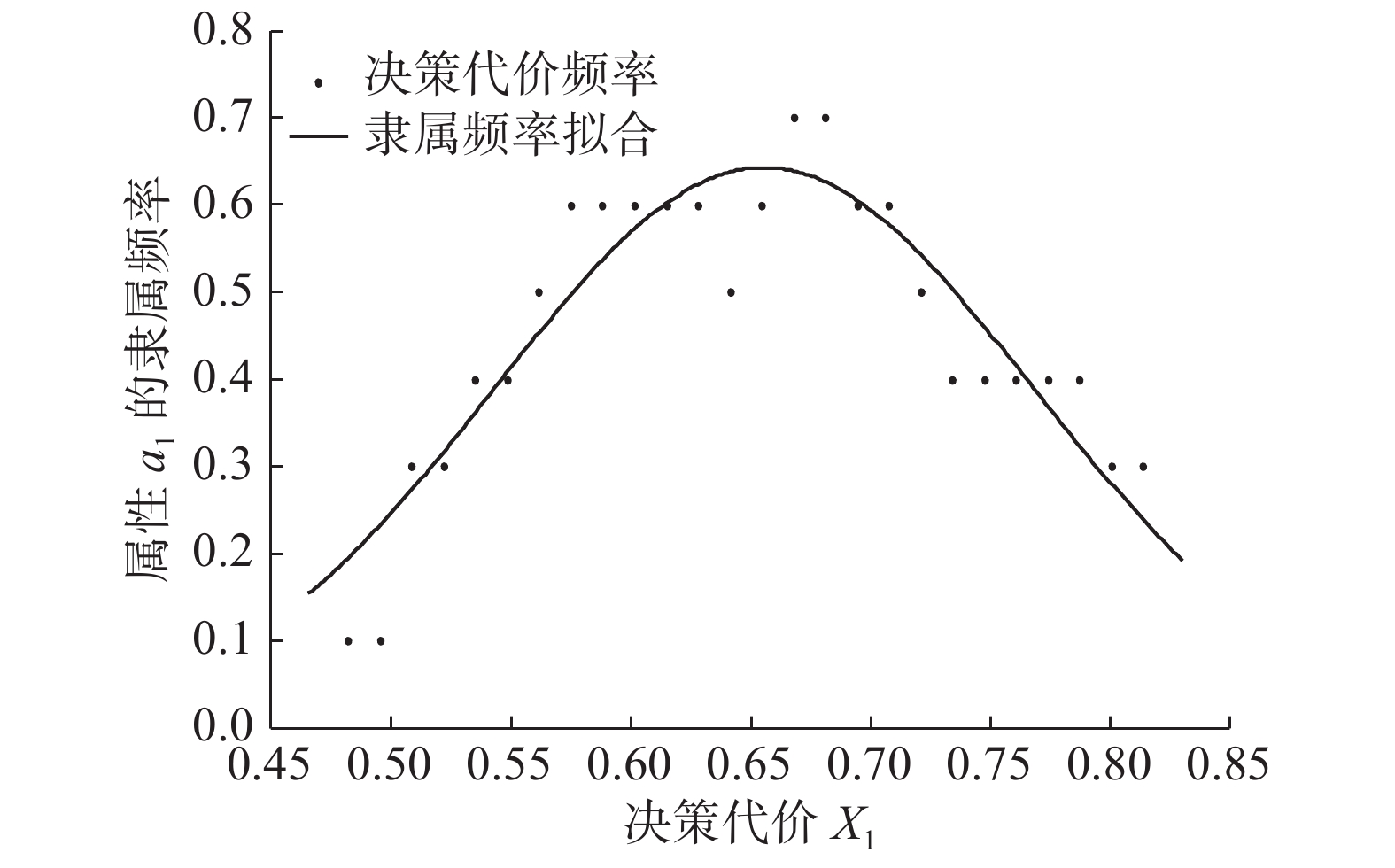
以决策代价
$x_1$
为横坐标,隶属频率为纵坐标,对点进行曲线拟合,接受决策的决策代价在属性
${a_1}$
下的隶属频率拟合曲线如图1所示。图2~4分别是接受决策在属性
${a_2}{\text{、}}{a_3}{\text{、}}{a_4}$
下的隶属频率拟合曲线。
以上各个拟合曲线取最高点的横坐标作为该决策动作不同属性下的决策代价,得到接受决策在属性
${a_1}{\text{、}}{a_2}{\text{、}}{a_3}{\text{、}}{a_4}$
下的决策代价分别为0.6347、0.6738、0.737、0.7465,因此接受决策的决策代价组为
${\lambda _e} = \left( {0.634\;7,0.673\;8,0.737\;0,0.746\;5} \right)$
。同理,对延迟决策和拒绝决策按照以上步骤处理,得到延迟决策的决策代价组为
${\lambda _b} = ( 0.145\;9,0.174\;1,0.237\;8, $
$ 0.246\;5 )$
,拒绝决策的决策代价组为
${\lambda _r} = ( 0.365\;3, $
$ 0.326\;2, 0.263\;0,0.253\;5)$
。
对3个决策代价组分别求欧氏距离
${\lambda _ * } = $
$ \sqrt {\dfrac{{\displaystyle\sum\limits_{l = 1}^4 {\lambda {{_ * ^l}^2}} }}{4}} $
,得到3个决策动作的决策代价分别为
${\lambda _e} = $
$ 0.699\;5,{\lambda _b} \!=\! 0.205\;5,{\lambda _r} = 0.305\;5$
。所以,
$\alpha \!= \!\dfrac{{{\lambda _e} + 0.5{\lambda _b}}}{{{\lambda _e} + {\lambda _b}}} = $
$ 0.886, \beta = \dfrac{{0.5{\lambda _b}}}{{{\lambda _b} + {\lambda _r}}} = 0.201$
。
通过比较文献[12]与本文的结果,可以看出本文计算得出的阈值对是合理的。表5给出了文献[12]与本文计算得出的阈值对。
表 5(Tab. 5

表 5 文献[12]与本文的阈值对比
Tab. 5 Comparision of the threshold pair between Ref. [12] and this study
| 阈值 |
文献[12]
|
本文 |
|
$\alpha $
|
0.829 |
0.886 |
|
$\beta $
|
0.219 |
0.201 |
|
表 5 文献[12]与本文的阈值对比
Tab.5 Comparision of the threshold pair between Ref. [12] and this study
|
例2
$\varOmega = \left( {U,A,V,f} \right)$
是一个模糊信息系统,如表6所示。其中,对象集合
$U = \left\{ {{x_1},{x_2}, \cdot \cdot \cdot ,{x_{10}}} \right\}$
,属性集合
$A = \left\{ {{a_1},{a_2},{a_3},{a_4}} \right\}$
,
$\forall a \in A,\forall x \in U$
,对象的隶属度为
${\mu _a}\left( x \right) \in \left[ {0,1} \right]$
(数据来源UCI:Connectionist Bench(Sonar, Mines vs. Rocks))。
表 6(Tab. 6

表 6 联结主义数据
Tab. 6 Connectionist date
| U\A
|
${a_1}$
|
${a_2}$
|
${a_3}$
|
${a_4}$
|
|
${x_1}$
|
0.2086 |
1.0000 |
0.9212 |
0.8703 |
|
${x_2}$
|
1.0000 |
0.0864 |
0.3724 |
0.2863 |
|
${x_3}$
|
0.5946 |
0.2314 |
0.1036 |
0.3894 |
|
${x_4}$
|
0.2484 |
0.7440 |
0.8169 |
0.6942 |
|
${x_5}$
|
0.1348 |
0.8626 |
0.8547 |
0.6627 |
|
${x_6}$
|
0.5268 |
0.2969 |
0.5163 |
0.1873 |
|
${x_7}$
|
0.5100 |
0.7310 |
0.4134 |
0.6898 |
|
${x_8}$
|
0.7115 |
0.1757 |
0.1428 |
0.1436 |
|
${x_9}$
|
0.8878 |
0.1331 |
0.0440 |
0.3204 |
|
${x_{10}}$
|
1.0000 |
0.5356 |
0.5271 |
0.5308 |
|
表 6 联结主义数据
Tab.6 Connectionist date |
计算每个对象在每个属性下相对于其他对象的曼哈顿距离
${\rm{di}}{{\rm{s}}_{ij}^{1}} = \dfrac{{\displaystyle\sum\limits_{k = 1}^{10} {\left| {{v_{ij}} - {v_{kj}}} \right|} }}{{10}}$
,
$i = 1,2, \cdots ,10,j = 1, $
$ 2, \cdots ,4$
,得到的关于决策代价的曼哈顿距离
$D = $
$ {\left( {{\rm{di}}{{\rm{s}}_{ij}^{1}}} \right)_{10 \times 4}}$
如表7所示。
计算接受决策的决策代价
${\lambda _e}\left( D \right) = 1 -D$
,得到接受决策的决策代价如表8所示。
表 7(Tab. 7

表 7 曼哈顿距离
Tab. 7 Manhattan distance
| 对象 |
${a_1}$
|
${a_2}$
|
${a_3}$
|
${a_4}$
|
|
${x_1}$
|
0.3884 |
0.5203 |
0.4500 |
0.3928 |
|
${x_2}$
|
0.4177 |
0.3933 |
0.2642 |
0.2395 |
|
${x_3}$
|
0.2565 |
0.3081 |
0.3796 |
0.2121 |
|
${x_4}$
|
0.3645 |
0.3393 |
0.3741 |
0.2519 |
|
${x_5}$
|
0.4475 |
0.4104 |
0.3968 |
0.2385 |
|
${x_6}$
|
0.2565 |
0.2950 |
0.2560 |
0.2989 |
|
${x_7}$
|
0.2599 |
0.3341 |
0.2560 |
0.2493 |
|
${x_8}$
|
0.2799 |
0.3304 |
0.3560 |
0.3339 |
|
${x_9}$
|
0.3504 |
0.3559 |
0.4272 |
0.2259 |
|
${x_{10}}$
|
0.4177 |
0.2950 |
0.2582 |
0.2121 |
|
表 7 曼哈顿距离
Tab.7 Manhattan distance |
表 8(Tab. 8

表 8 接受决策的决策代价
Tab. 8 Decision costs of accepting the decision
| 对象 |
${a_1}$
|
${a_2}$
|
${a_3}$
|
${a_4}$
|
|
${x_1}$
|
0.6116 |
0.4797 |
0.5500 |
0.6072 |
|
${x_2}$
|
0.5823 |
0.6067 |
0.7358 |
0.7605 |
|
${x_3}$
|
0.7435 |
0.6919 |
0.6204 |
0.7879 |
|
${x_4}$
|
0.6355 |
0.6607 |
0.6259 |
0.7481 |
|
${x_5}$
|
0.5525 |
0.5896 |
0.6032 |
0.7615 |
|
${x_6}$
|
0.7435 |
0.7050 |
0.7440 |
0.7011 |
|
${x_7}$
|
0.7401 |
0.6659 |
0.7440 |
0.7507 |
|
${x_8}$
|
0.7201 |
0.6696 |
0.6440 |
0.6661 |
|
${x_9}$
|
0.6496 |
0.6441 |
0.5728 |
0.7741 |
|
${x_{10}}$
|
0.5823 |
0.7050 |
0.7418 |
0.7879 |
|
表 8 接受决策的决策代价
Tab.8 Decision costs of accepting the decision |
接受决策的决策代价在属性
${a_1}$
下的最小值为0.5525,最大值为0.7435,取
$\delta = 0.070\;5$
,以0.47536为起点,0.82064为终点,0.01328为区间长度,划分为26个区间。其频率分布如表9所示。
表 9(Tab. 9

表 9 属性
${a_1}$
决策代价频率分布
Tab. 9 Attribute
${a_1}$
decision costs frequency distribution
| 序号 |
区间 |
频数 |
频率 |
| 1 |
$\left[ {0.475\;36,0.488\;64} \right]$
|
1 |
0.1 |
| 2 |
$\left[ {0.488\;64,0.501\;92} \right]$
|
1 |
0.1 |
| 3 |
$\left[ {0.501\;92,0.51\;52} \right]$
|
3 |
0.3 |
| 4 |
$\left[ {0.515\;2,0.528\;48} \right]$
|
3 |
0.3 |
| 5 |
$\left[ {0.528\;48,0.541\;76} \right]$
|
4 |
0.4 |
| 6 |
$\left[ {0.541\;76,0.555\;04} \right]$
|
4 |
0.4 |
| 7 |
$\left[ {0.555\;04,0.568\;32} \right]$
|
5 |
0.5 |
| 8 |
$\left[ {0.568\;32,0.581\;6} \right]$
|
6 |
0.6 |
| 9 |
$\left[ {0.581\;6,0.594\;88} \right]$
|
6 |
0.6 |
| 10 |
$\left[ {0.594\;88,0.608\;16} \right]$
|
6 |
0.6 |
| 11 |
$\left[ {0.608\;16,0.621\;44} \right]$
|
6 |
0.6 |
| 12 |
$\left[ {0.621\;44,0.634\;72} \right]$
|
6 |
0.6 |
| 13 |
$\left[ {0.634\;72,0.648} \right]$
|
5 |
0.5 |
| 14 |
$\left[ {0.648,0.661\;28} \right]$
|
6 |
0.6 |
| 15 |
$\left[ {0.661\;28,0.674\;56} \right]$
|
7 |
0.7 |
| 16 |
$\left[ {0.674\;56,0.687\;84} \right]$
|
7 |
0.7 |
| 17 |
$\left[ {0.687\;84,0.701\;12} \right]$
|
6 |
0.6 |
| 18 |
$\left[ {0.701\;12,0.714\;4} \right]$
|
6 |
0.6 |
| 19 |
$\left[ {0.714\;4,0.727\;68} \right]$
|
5 |
0.5 |
| 20 |
$\left[ {0.727\;68,0.740\;96} \right]$
|
4 |
0.4 |
| 21 |
$\left[ {0.740\;96,0.754\;24} \right]$
|
4 |
0.4 |
| 22 |
$\left[ {0.754\;24,0.767\;52} \right]$
|
4 |
0.4 |
| 23 |
$\left[ {0.767\;52,0.780\;8} \right]$
|
4 |
0.4 |
| 24 |
$\left[ {0.780\;8,0.794\;08} \right]$
|
4 |
0.4 |
| 25 |
$\left[ {0.794\;08,0.807\;36} \right]$
|
3 |
0.3 |
| 26 |
$\left[ {0.807\;36,0.820\;64} \right]$
|
3 |
0.3 |
|
表 9 属性
${a_1}$
决策代价频率分布
Tab.9 Attribute
${a_1}$
decision costs frequency distribution |
以决策代价
$x_1$
为横坐标,隶属频率为纵坐标,对点进行曲线拟合,接受决策的决策代价在属性
${a_1}$
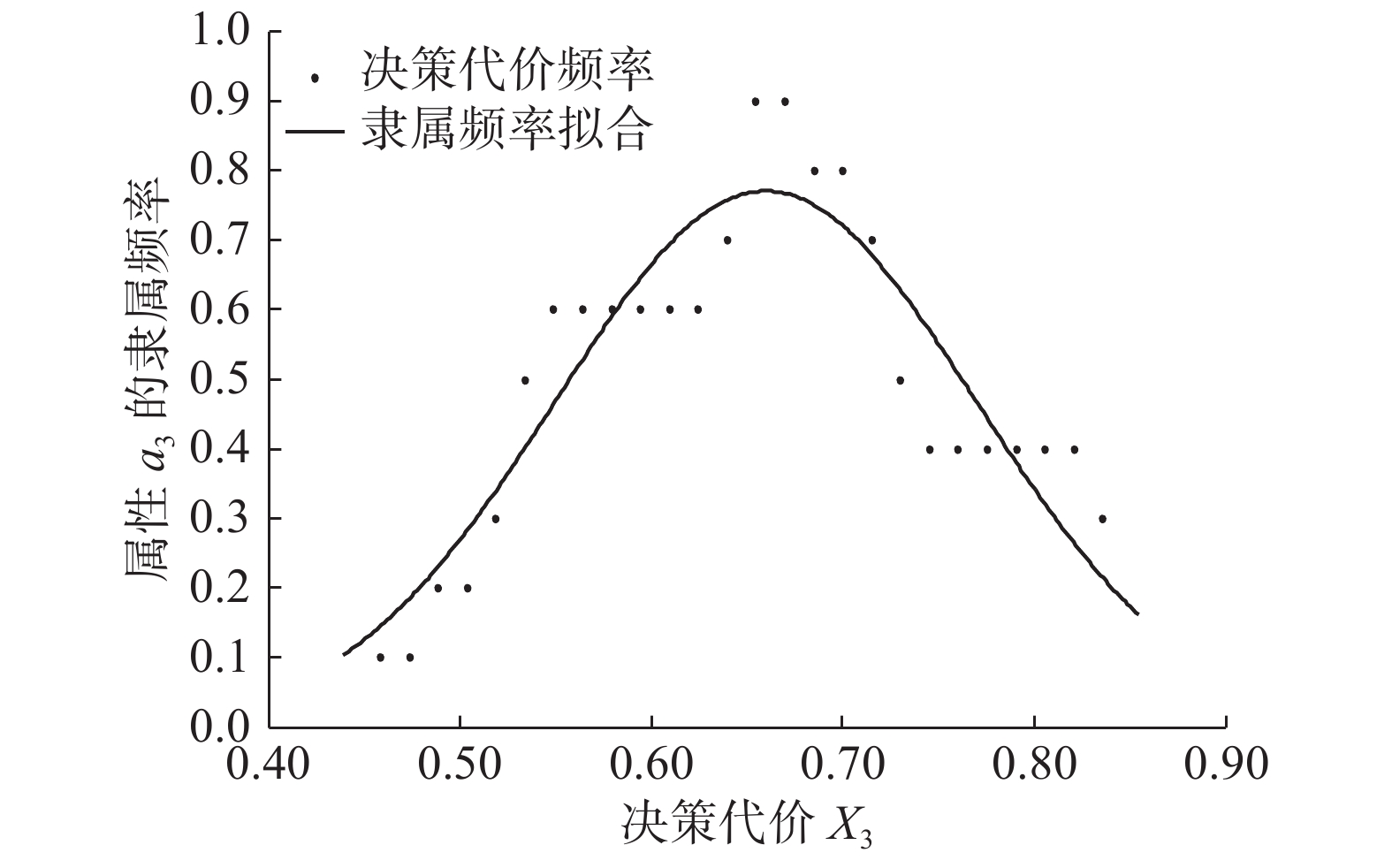
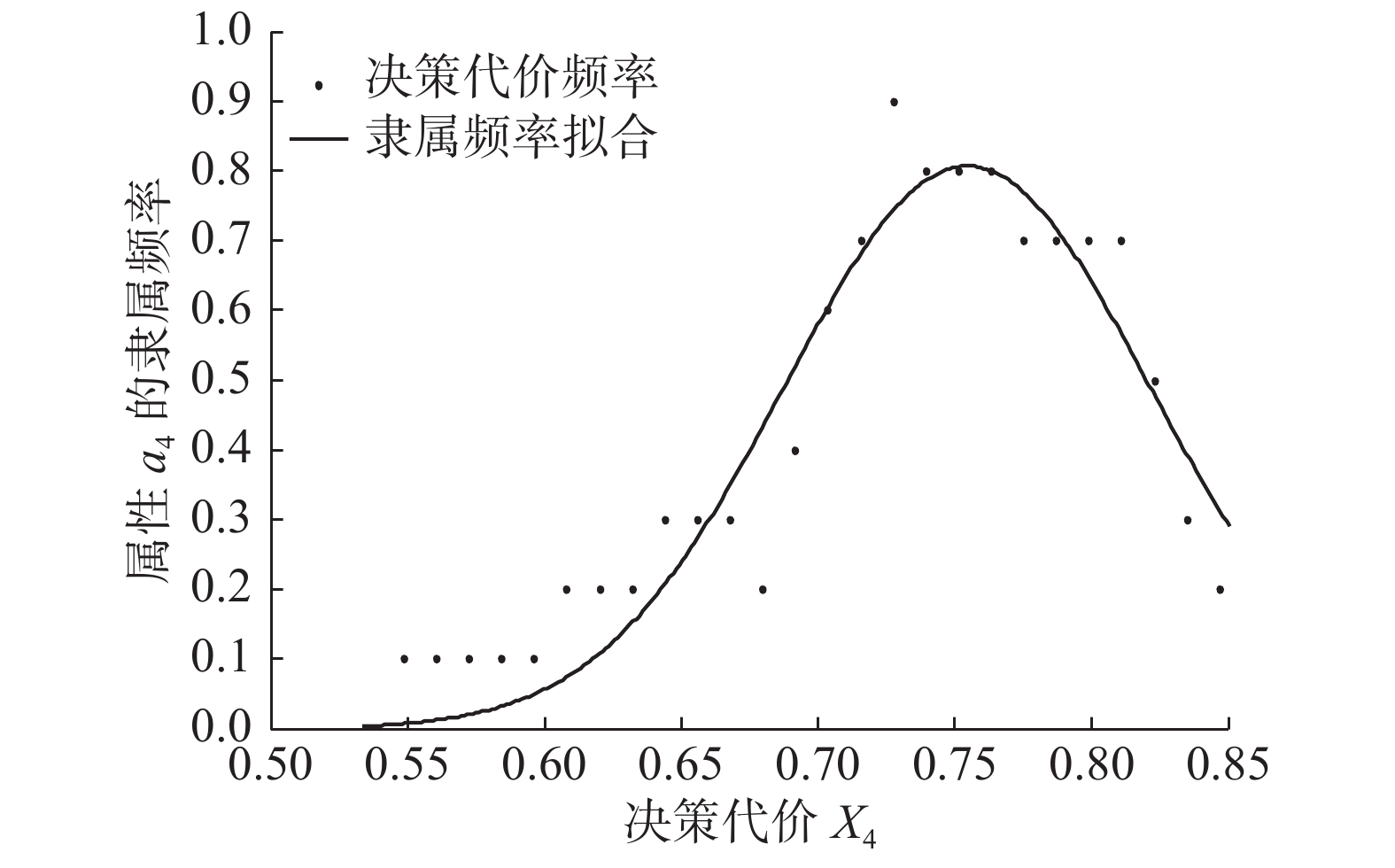
下的隶属频率拟合曲线如图5所示。图6~8分别是接受决策在属性
${a_2}{\text{、}}{a_3}{\text{、}}{a_4}$
下的隶属频率拟合曲线。
以上各个拟合曲线取最高点的横坐标作为该决策动作不同属性下的决策代价,得到接受决策在属性
${a_1}{\text{、}}{a_2}{\text{、}}{a_3}{\text{、}}{a_4}$
下的决策代价分别为0.6557、0.6568、0.6599、0.7546,因此接受决策的决策代价组为
${\lambda _e} = \left( {0.655\;7,0.656\;8,0.659\;9,0.754\;6} \right)$
。同理,对延迟决策和拒绝决策按照以上步骤处理,得到延迟决策的决策代价组为
${\lambda _b} = ( 0.154\;9, 0.157\;5, 0.159\;2, $
$ 0.254\;6)$
,拒绝决策的决策代价组为
${\lambda _r} = ( 0.344\;3, $
$ 0.343\;3,0.340\;1, $
$ 0.245\;4)$
。
对3个决策代价组分别求欧氏距离
${\lambda _ * } = $
$ \sqrt {\dfrac{{\displaystyle\sum\limits_{l = 1}^4 {\lambda {{_ * ^l}^2}} }}{4}} $
,得到3个决策动作的决策代价分别为
${\lambda _e}\! =\! $
$ 0.683\;0,{\lambda _b} \!=v 0.186\;4,{\lambda _r} \!=\! 0.321\;0$
。所以 ,
$\alpha\! =\! \dfrac{{{\lambda _e}\! +\! 0.5{\lambda _b}}}{{{\lambda _e} + {\lambda _b}}} = $
$ 0.892\;8,\beta = \dfrac{{0.5{\lambda _b}}}{{{\lambda _b} + {\lambda _r}}}$
$ = 0.183\;7$
。
例3
$\varOmega = \left( {U,A,V,f} \right)$
是一个模糊信息系统,如表10所示。其中,对象集合
$U = \left\{ {{x_1},{x_2}, \cdot \cdot \cdot ,{x_{10}}} \right\}$
,属性集合
$A = \left\{ {{a_1},{a_2},{a_3},{a_4},{a_5}} \right\}$
,
$\forall a \in A,\forall x \in U$
,对象的隶属度为
${\mu _a}\left( x \right) \in \left[ {0,1} \right]$
(数据来源UCI:Ionosphere)。
表 10(Tab. 10

表 10 逸散层数据
Tab. 10 Lonosphere data
|
$\Omega $
|
${a_1}$
|
${a_2}$
|
${a_3}$
|
${a_4}$
|
${a_5}$
|
|
${x_1}$
|
0.10135 |
0 |
0.54730 |
0.31081 |
0.37162 |
|
${x_2}$
|
0.28409 |
0.68182 |
0.30682 |
0.64394 |
0.59091 |
|
${x_3}$
|
1.0000 |
0.92106 |
0.77152 |
0.52798 |
0.52940 |
|
${x_4}$
|
0.47368 |
0.83155 |
0.68421 |
0.68421 |
0.84211 |
|
${x_5}$
|
0.39394 |
0.45455 |
0.63636 |
0.21212 |
0.56156 |
|
${x_6}$
|
0.68198 |
0.46643 |
0.25795 |
1.0000 |
0.18681 |
|
${x_7}$
|
0.35346 |
0.68195 |
0.55717 |
0.61836 |
0.42271 |
|
${x_8}$
|
0.97513 |
1.0000 |
0.99290 |
0.95737 |
0.97869 |
|
${x_9}$
|
0.74468 |
0.88542 |
0.87234 |
0.73050 |
0.95745 |
|
${x_{10}}$
|
0.43636 |
0.18182 |
0.34545 |
0.29091 |
0.20000 |
|
表 10 逸散层数据
Tab.10 Lonosphere data |
计算每个对象在每个属性下相对于其他对象的曼哈顿距离
${\rm{di}}{{\rm{s}}_{ij}^{1}} = \dfrac{{\displaystyle\sum\limits_{k = 1}^{10} {\left| {{v_{ij}} - {v_{kj}}} \right|} }}{{10}}$
,
$i = 1,2, \cdots ,10,j = 1, $
$ 2, \cdots ,5$
,得到的关于决策代价的曼哈顿距离
$D = $
$ {\left( {{\rm{di}}{{\rm{s}}_{ij}^{1}}} \right)_{10 \times 5}}$
,如表11所示。
表 11(Tab. 11

表 11 曼哈顿距离
Tab. 11 Manhattan distance
| U\S
|
${a_1}$
|
${a_2}$
|
${a_3}$
|
${a_4}$
|
${a_5}$
|
|
${x_1}$
|
0.4431 |
0.6105 |
0.1962 |
0.3105 |
0.2638 |
|
${x_2}$
|
0.2969 |
0.2535 |
0.3002 |
0.2056 |
0.2279 |
|
${x_3}$
|
0.4555 |
0.3264 |
0.2388 |
0.2237 |
0.2220 |
|
${x_4}$
|
0.2306 |
0.2835 |
0.2038 |
0.2136 |
0.3284 |
|
${x_5}$
|
0.2391 |
0.3014 |
0.1943 |
0.3855 |
0.2220 |
|
${x_6}$
|
0.2723 |
0.2966 |
0.3393 |
0.4024 |
0.3773 |
|
${x_7}$
|
0.2553 |
0.2535 |
0.1943 |
0.2056 |
0.2434 |
|
${x_8}$
|
0.4356 |
0.3895 |
0.3957 |
0.3683 |
0.4146 |
|
${x_9}$
|
0.2974 |
0.3050 |
0.2993 |
0.2322 |
0.3976 |
|
${x_{10}}$
|
0.2306 |
0.4650 |
0.2770 |
0.3225 |
0.3668 |
|
表 11 曼哈顿距离
Tab.11 Manhattan distance |
计算接受决策的决策代价
${\lambda _e}\left(D \right) = 1 - D$
,得到接受决策的决策代价如表12所示。
表 12(Tab. 12

表 12 接受决策的决策代价
Tab. 12 Decision costs of accepting the decision
| 对象 |
${a_1}$
|
${a_2}$
|
${a_3}$
|
${a_4}$
|
${a_5}$
|
|
${x_1}$
|
0.5569 |
0.3895 |
0.8038 |
0.6895 |
0.7362 |
|
${x_2}$
|
0.7031 |
0.7465 |
0.6998 |
0.7944 |
0.7721 |
|
${x_3}$
|
0.5445 |
0.6736 |
0.7612 |
0.7763 |
0.7780 |
|
${x_4}$
|
0.7694 |
0.7165 |
0.7962 |
0.7864 |
0.6716 |
|
${x_5}$
|
0.7609 |
0.6986 |
0.8057 |
0.6145 |
0.7780 |
|
${x_6}$
|
0.7277 |
0.7034 |
0.6607 |
0.5976 |
0.6227 |
|
${x_7}$
|
0.7447 |
0.7465 |
0.8057 |
0.7944 |
0.7566 |
|
${x_8}$
|
0.5644 |
0.6105 |
0.6043 |
0.6317 |
0.5854 |
|
${x_9}$
|
0.7026 |
0.6950 |
0.7007 |
0.7678 |
0.6024 |
|
${x_{10}}$
|
0.7694 |
0.5350 |
0.7230 |
0.6775 |
0.6332 |
|
表 12 接受决策的决策代价
Tab.12 Decision costs of accepting the decision |
接受决策的决策代价在属性
${a_1}$
下的最小值为0.5445,最大值为0.7694,取
$\delta = 0.138\;3$
,以0.393665为起点,0.920135为终点,0.02507为区间长度,划分21个区间。其频率分布如表13所示。
表 13(Tab. 13

表 13 属性
${a_1}$
决策代价频率分布
Tab. 13 Attribute
${a_1}$
decision costs frequency distribution
| 序号 |
区间 |
频数 |
频率 |
| 1 |
$\left[ {0.393\;665,0.418\;735} \right]$
|
2 |
0.2 |
| 2 |
$\left[ {0.418\;735,0.443\;805} \right]$
|
3 |
0.3 |
| 3 |
$\left[ {0.443\;805,0.468\;875} \right]$
|
3 |
0.3 |
| 4 |
$\left[ {0.468\;875,0.493\;945} \right]$
|
3 |
0.3 |
| 5 |
$\left[ {0.493\;945,0.519\;015} \right]$
|
3 |
0.3 |
| 6 |
$\left[ {0.519\;015,0.544\;085} \right]$
|
3 |
0.3 |
| 7 |
$\left[ {0.544\;085,0.569\;155} \right]$
|
5 |
0.5 |
| 8 |
$\left[ {0.569\;155,0.594\;225} \right]$
|
6 |
0.6 |
| 9 |
$\left[ {0.594\;225,0.619\;295} \right]$
|
7 |
0.7 |
| 10 |
$\left[ {0.619\;295,0.644\;365} \right]$
|
10 |
1.0 |
| 11 |
$\left[ {0.644\;365,0.669\;435} \right]$
|
10 |
1.0 |
| 12 |
$\left[ {0.669\;435,0.694\;505} \right]$
|
10 |
1.0 |
| 13 |
$\left[ {0.694\;505,0.719\;575} \right]$
|
9 |
0.9 |
| 14 |
$\left[ {0.719\;575,0.744\;645} \right]$
|
7 |
0.7 |
| 15 |
$\left[ {0.744\;645,0.769\;715} \right]$
|
7 |
0.7 |
| 16 |
$\left[ {0.769\;715,0.794\;785} \right]$
|
7 |
0.7 |
| 17 |
$\left[ {0.794\;785,0.819\;855} \right]$
|
7 |
0.7 |
| 18 |
$\left[ {0.819\;855,0.844\;925} \right]$
|
7 |
0.7 |
| 19 |
$\left[ {0.844\;925,0.869\;995} \right]$
|
5 |
0.5 |
| 20 |
$\left[ {0.869\;995,0.895\;065} \right]$
|
4 |
0.4 |
| 21 |
$\left[ {0.895\;065,0.920\;135} \right]$
|
3 |
0.3 |
|
表 13 属性
${a_1}$
决策代价频率分布
Tab.13 Attribute
${a_1}$
decision costs frequency distribution |
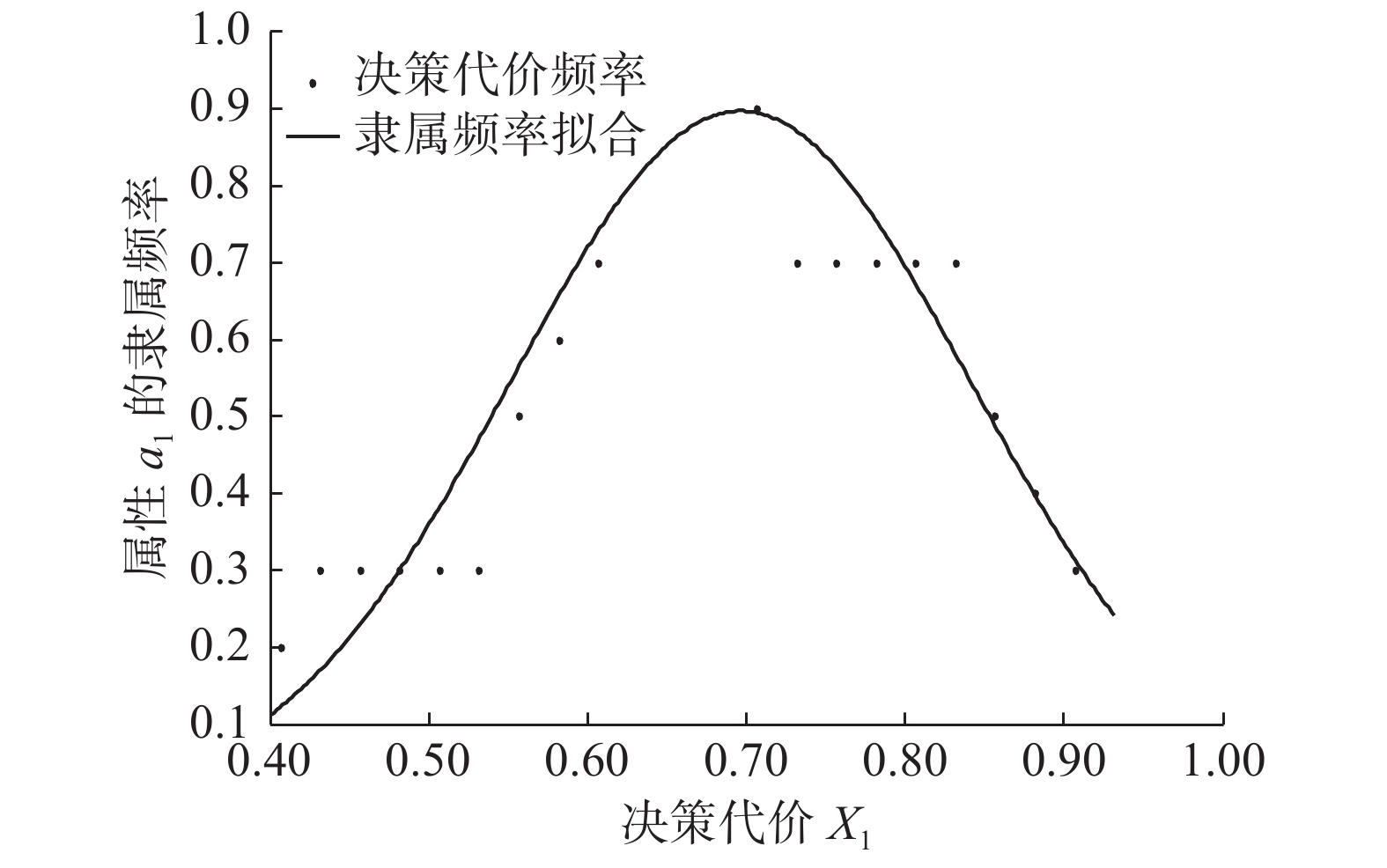
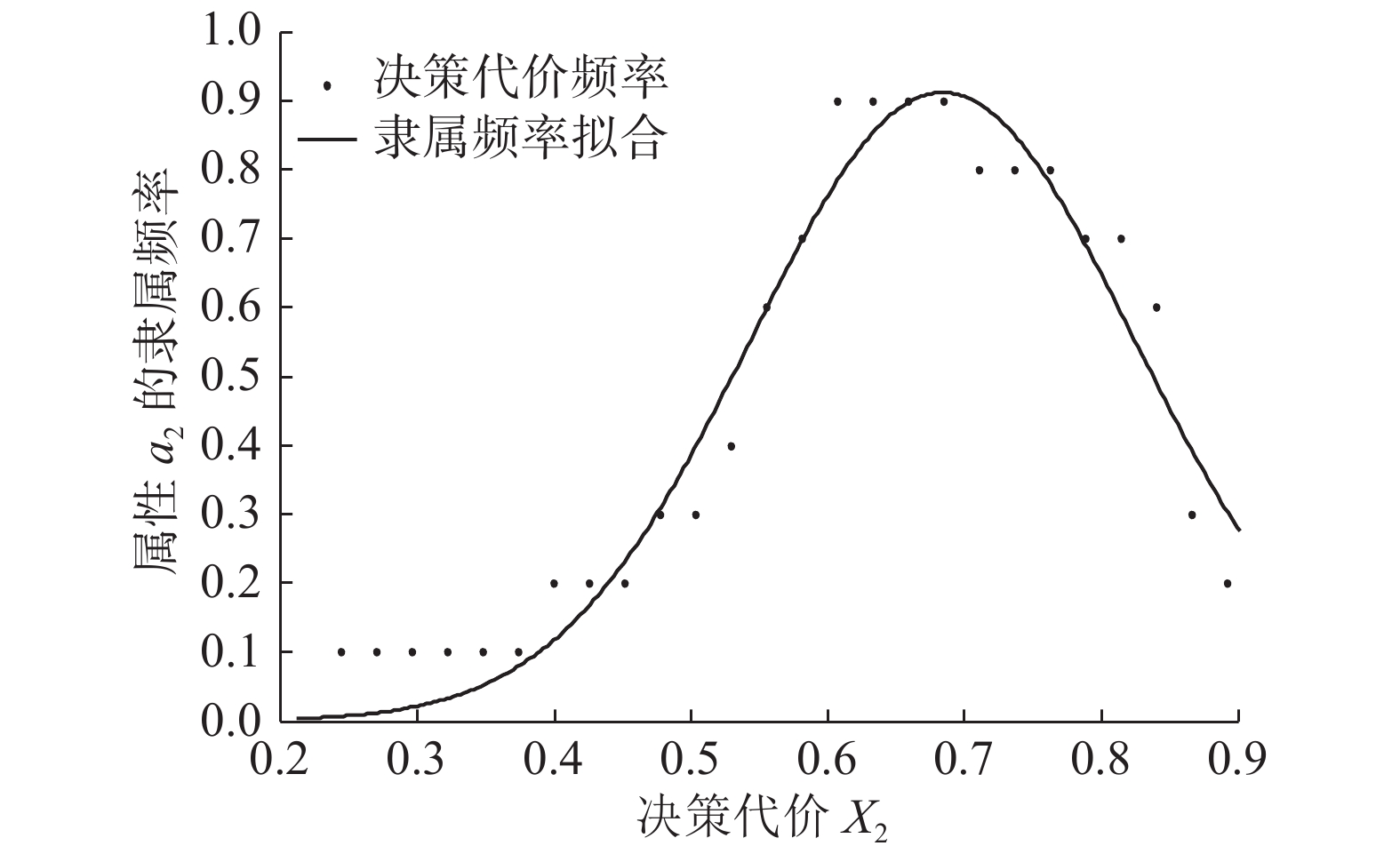
以决策代价
$x$
为横坐标,隶属频率为纵坐标,对点进行曲线拟合,接受决策的决策代价在属性
${a_1}$
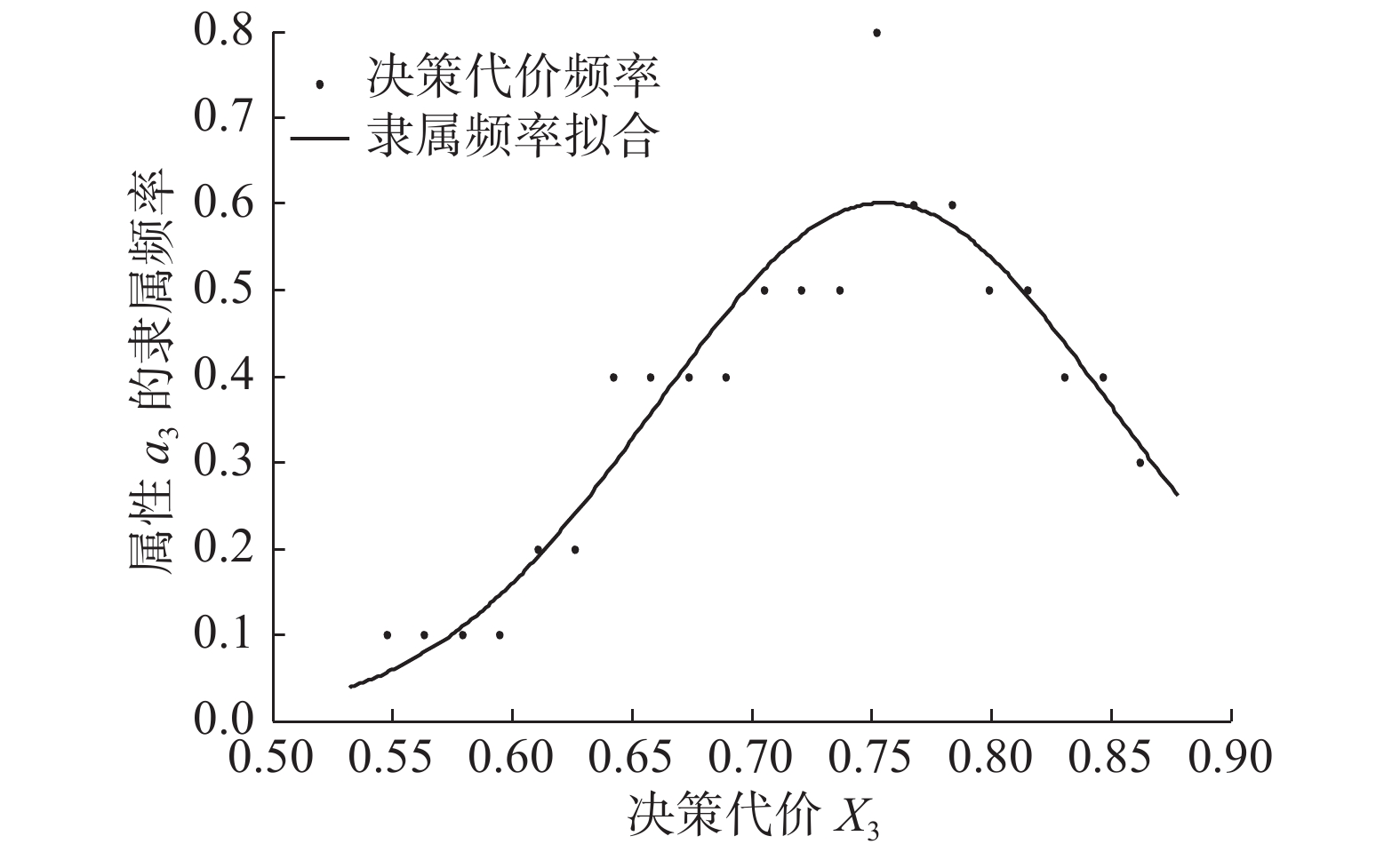
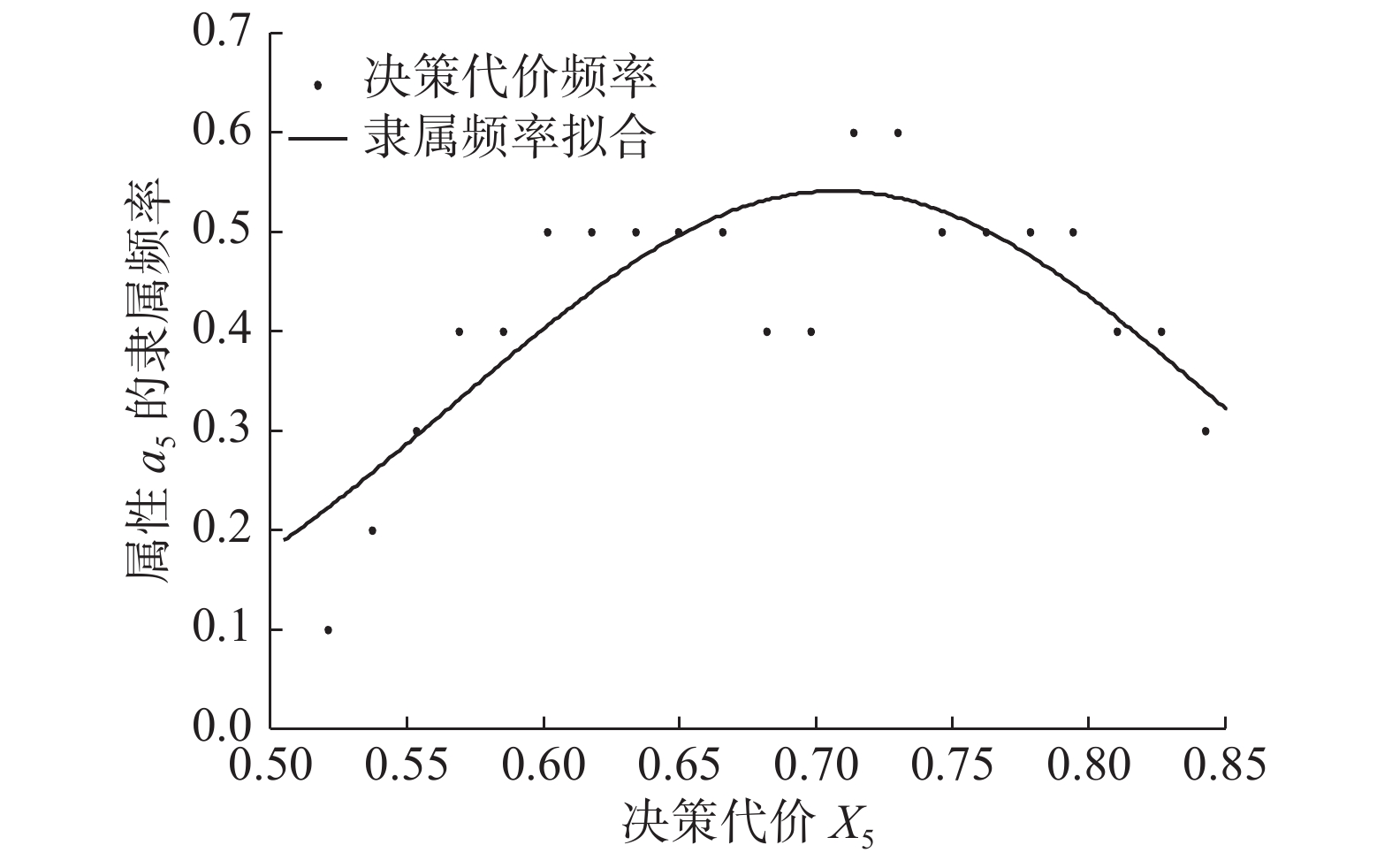
下的隶属频率拟合曲线如图9所示。图10~13分别是接受决策在属性
${a_2}{\text{、}}{a_3}{\text{、}} $
$ {a_4}{\text{、}}{a_5}$
下的隶属频率拟合曲线。
以上各个拟合曲线取最高点的横坐标作为该决策动作不同属性下的决策代价,得到接受决策在属性
${a_1}{\text{、}}{a_2}{\text{、}}{a_3}{\text{、}}{a_4}{\text{、}}{a_5}$
下的决策代价分别为0.6966、0.6840、0.7552、0.7272、0.7077,因此接受决策的决策代价组为
${\lambda _e} = ( 0.696\;6,0.684\;0,0.755\;2, $
$ 0.727\;2, 0.707\;7)$
。同理,对延迟决策和拒绝决策按照以上步骤处理,得到延迟决策的决策代价组为
${\lambda _b} = \left( {0.202\;5,0.187\;2,0.255\;2,0.227\;2,0.207\;7} \right)$
,拒绝决策的决策代价组为
${\lambda _r} =( 0.303\;3,0.316\;0,0.244\;7, 0.272\;9, $
$ 0.292\;3)$
。
对3个决策代价组分别求欧氏距离
${\lambda _ * } = $
$ \sqrt {\dfrac{{\displaystyle\sum\limits_{l = 1}^5 {\lambda {{_ * ^l}^2}} }}{5}} $
,得到3个决策动作的决策代价分别为
${\lambda _e} \!=\! $
$ 0.714\;6,{\lambda _b} \!=\! 0.217\;2,{\lambda _r} \!=\! 0.286\;9$
。所以,
$\alpha = \dfrac{{{\lambda _e} + 0.5{\lambda _b}}}{{{\lambda _e} + {\lambda _b}}} = $
$ 0.883\;5,\beta = \dfrac{{0.5{\lambda _b}}}{{{\lambda _b} + {\lambda _r}}}$
$= 0.215\;4$
。
4 结束语
决策粗糙集模型是粗糙集模型的概率拓展,其通过使用损失函数和贝叶斯决策过程计算阈值对。在区间值决策粗糙集的框架下,已经研究了最优阈值对
$\left( {\alpha ,\beta } \right)$
的上、下近似。本文在基于相似度的三支决策模糊粗糙集模型中讨论决策代价,通过定义函数将模糊信息系统中的模糊数与三支决策的决策代价联系在一起,通过对隶属频率拟合的过程,得到不同决策动作在不同属性下的决策代价,再计算其欧氏距离,得到不同决策动作的决策代价,代入文献[12]得到的阈值对表达式来计算
$\left( {\alpha ,\beta } \right)$
。本文只是在基于相似度的三支决策模糊粗糙集模型中讨论决策代价,还有许多其他的模糊粗糙集模型中的决策代价有待研究。



 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 2020, Vol. 15
2020, Vol. 15


