粗糙集理论^[1-2]是一种有效的数据分析方法，主要用于处理不确定、不一致和模糊的数据^[3-4]，已被广泛地应用于知识发现、数据挖掘和机器学习等领域。属性约简是粗糙集理论的重要研究内容之一，它旨在保持原属性集区分能力不变的情况下，剔除不重要或冗余的属性^[5-6]。由于属性约简的结果往往不是唯一的，找到数据所有约简的结果，已经被证明是一个NP-hard问题。因此在实际应用中通常采用启发式算法处理大规模数据，获取满足知识发现要求的属性约简结果^[7-9]。

然而，在众多现实应用领域中存在大量的高维复杂数据。并且在数据采集阶段，由于采集成本和技术的限制，导致这些高维数据往往存在缺失。同时，给这些数据进行类别标注，需要耗费大量的人力资源，并且利用经典粗糙集无法直接处理不完备数据。针对上述问题研究人员引入容差关系和限制容差关系等，拓展了经典粗糙集的应用^[10-12]，但这些扩展的关系模型难以直接处理含有连续型的不完备混合数据。同时，由于在实际应用中，这些高维数据通常仅包含少量已标注的数据。若仅利用带标记的数据进行属性约简，约简结果不能有效反映数据的分布，且分类性能较弱。

弱监督属性约简旨在有效利用无标记数据来增强属性约简的有效性，从而提高学习模型的分类性能。近年来，弱监督属性约简引起了许多研究人员的关注和研究。文献[13]针对弱标记的符号型数据，在区分对的基础上，利用有监督学习框架和无监督学习框架，构造相对应的启发式半监督属性约简算法。文献[14]基于粗糙集理论和信息熵的概念，在对无标记数据进行部分标注后，设计了一种基于信息熵的半监督特征选择算法。文献[15]将粗糙集理论和集成学习框架相结合，利用有标记的数据训练基分类器对无标记的数据进行标注，扩充有标记的数据。文献[16]提出了一种基于流形正则化的半监督特征选择算法，通过最大化不同类别之间的间距对特征的重要性进行度量分析。文献[17]提出了一种半监督特征选择算法，算法通过组合半监督散点，有效利用大量未标记的视频数据中的信息来区分目标类别。上述这些方法为弱标记数据的属性约简，提供了有效的解决方案。

另外，在大数据时代，许多数据随着时间的推移而动态变化。在这种复杂应用场景中，传统的属性约简算法在处理这些动态数据时，将会产生大量重复计算，无法快速更新属性约简结果。近年来，许多学者对动态属性约简算法进行了大量的研究。文献[18]提出了一种基于信息熵的组增量式属性约简算法，在动态增加一组实例后，快速更新属性约简结果。文献[19]采用一种复合粗糙集模型，处理动态的不完备数据，在数据动态变化后快速更新近似集合。文献[20]提出了一种基于知识粒度模型的动态属性约简算法，在实例变化后动态更新属性约简集。文献[21]提出了一种不完备动态属性约简算法，该算法在不完备决策系统中单个实例变化后动态获取新的属性约简结果集。上述研究都是针对所有实例均有标记的数据，目前对弱标记数据的增量式属性约简研究较少。为此，有效地利用无标记数据来增强属性约简结果，并在保证分类精度前提下动态更新属性约简结果，已成为了当前亟待解决的问题。

针对上述问题，本文提出了弱标记不完备数据的区分对概念，给出了属性的相对重要度的度量方法。并以此为基础，设计了启发式的半监督属性约简算法，算法在每次迭代过程中能剔除相对冗余的属性和当前属性约简集已能够区分的区分对，算法的搜索空间显著缩减。同时，根据数据中实例的动态变化情况，给出属性约简集的动态更新机制，并通过实例分析详细说明动态属性约简算法的计算过程。最后，采用来自UCI的真实数据集，进一步验证了算法的高效性和可行性。

1 基本知识

定义1　四元组 ${\rm{IS}} = < U,A,V,f > $ 是一个信息系统，其中 $U$ 表示实例的非空有限集合，称为论域； $A$ 表示属性的非空有限集合 $V = \bigcup\limits_{a \in A} {{V_a}} $ ， ${V_a}$ 是属性 $a \in A$ 所有可能值的集合； $f$ 表示 $U \times A \to V$ ，是一个信息函数，它为每个实例的每一个属性赋予一个值，即 $\forall a \in A$ ， $x \in U$ ， $f(x,a) \in {V_a}$ 。

给定信息系统，如果至少有一个属性 $a \in A$ 使得 ${V_a}$ 含有缺失值，其中缺失值用 $ "\ast "$ 表示，此时该系统称为不完备信息系统，用 ${\rm{IIS}} = < U,A,V,f > $ 表示。

定义2　在不完备信息系统 ${\rm{IIS}} = < U,A,V,f > $ 中，有 $A = {A_d} \cup {A_r}$ ，其中 ${A_d}$ 表示离散型属性集， ${A_r}$ 表示连续型属性集，对于任意 $B \subseteq A$ ，关于属性子集 $B$ 的区分对定义为 ${\rm{Di}}{{\rm{s}}_{{\rm{UL}}}}(B,{U^2}) = {\rm{\{ }} < {x_i},{x_j} > {\rm{\} }}$ 。 $\forall p \in $ $ B,$ 对 $\forall < {x_i},{x_j} > $ 有

$ \left\{ \begin{array}{l} \exists p \in {A_r},{\rm{|}}\;f({x_i},p) - f({x_j},p)\;{\rm{|}} > \delta \\ \vee \exists p \in {A_d},f({x_i},p) \ne f({x_j},p) \\ \wedge f({x_i},p) \ne * \wedge f({x_j},p) \ne * \end{array} \right. $

给定的不完备信息系统 ${\rm{IIS}} = < U,A,V,f > $ ，对 $\forall B \subseteq A$ ， $|{\rm{Di}}{{\rm{s}}_{{\rm{UL}}}}(B,U{}^2)|$ 表示属性集 $B$ 重要度，其物理含义为属性集 $B$ 的区分度。属性集区分的实例对的数量越多，该属性集越重要。由定义可知 $ < {x_i},{x_j} > \in {\rm{Di}}{{\rm{s}}_{{\rm{UL}}}}(B,{U^2})$ 满足自反性、对称性，因此在考虑实例之间的区分对 $ < {x_i},{x_j} > $ 后，则不再重复考虑区分对 $ < {x_j},{x_i} > $ 。

定义3　对于给定信息系统 ${\rm{IS}} = < U,A,V,f > $ ，令 $A = C \cup D$ ，其中子集 $C$ 是条件属性集合， $D$ 是决策属性集合，又称四元组为决策系统，用 ${\rm{DS}} = < U, $ $ C \cup D,V,f > $ 表示。

对于给定决策系统 ${\rm{DS}} = < U,C \cup D,V,f > $ ，如果至少有一个属性 $c \in C$ 使得 ${V_c}$ 含有缺失值，其中缺失值用 $ "\ast "$ 表示。此时，该系统称为不完备决策系统，用 ${\rm{IDS}} = < U,C \cup D,V,f > $ 表示。

定义4　给定不完备决策系统 ${\rm{IDS}} = < U, $ $ C \cup D,V,f > $ ，有 ${C_d},{C_r} \subseteq B$ ，其中 ${C_d}$ 表示离散型属性， ${C_r}$ 表示连续型属性，设 $ < {x_i},{x_j} > \in {U^2}$ ，对 $\forall p \in $ $ B$ 、 $B \subseteq C$ ， $D$ 关于 $B$ 的区分对定义为 ${\rm{Di}}{{\rm{s}}_L}(B,{U^2}) = $ $ < {x_i},{x_j} >$ (其中 $L$ 表示有标记)，对 $\forall < {x_i},{x_j} > $ 有

$ \left\{ \begin{array}{l} \left\{ \begin{array}{l} (\exists p \in {C_r},|f({x_i},p) - f({x_j},p)| > \delta ) \\ \vee \exists p \in {C_d},f({x_i},p) \ne f({x_j},p)\\ f({x_i},p) \ne * \wedge f({x_j},p) \ne * \end{array} \right\} \wedge \\ f({x_i},D) \ne f({x_j},D) \end{array} \right. $

给定的不完备决策系统 ${\rm{IDS}} = < U,C \cup D,V,f > $ ，对 $\forall B \subseteq C$ ， $|{\rm{Di}}{{\rm{s}}_L}(B,U{}^2)|$ 表示属性集 $B$ 的重要度，其物理含义为属性集 $B$ 的区分度。属性集能区分的实例对的数量越多，则表明该属性集越重要。

由于在现实应用中，在大量不完备数据中只有少部分实例存在标记，若仅利用带标记的实例获取属性约简结果，由于无标记的实例未得到有效的利用，使得属性约简结果较难反映数据的整体信息，分类算法难以学习有效的知识规则，导致分类模型的分类性能较弱。为此，针对弱标记不完备决策系统，设计有效的属性重性度量方法显得尤为重要。本文在文献[8,13]的基础上，构造了面向弱标记不完备数据的属性重要性度量方法。

给定的不完备决策系统 ${\rm{IDS}} = < U,C \cup D,V,f > $ ，若决策属性 $d$ 存在缺失值。此时该系统称为弱标记不完备决策系统，用 ${\rm{WIDS}} = < U,C \cup D,V,f > $ 表示。

定义5　给定弱标记不完备决策系统 ${\rm{WIDS}} = $ $ < U,C \cup D,V,f > $ ，设 $U = L \cup M$ ，其中 $L$ 表示有标记实例的集合， $M$ 表示无标记实例的集合，属性集 $B \subseteq C$ 的重要度定义为

${\rm{Dis}}(B,{U^2}) \!=\! \left\{ \begin{array}{l} \!\!\! {\rm{Di}}{{\rm{s}}_L}(B,{L^2}) + {\rm{Di}}{{\rm{s}}_{M}}(B,U{L^2}),\quad L \ne { \text{Ø}} , M \ne {\text{Ø}} \\ \!\!\!{\rm{Di}}{{\rm{s}}_L}(B,{L^2}),\quad L \ne { \text{Ø}} ,M = {\text{Ø}} \\ \!\!\! {\rm{Di}}{{\rm{s}}_{M}}(B,U{L^2}),\quad L = { \text{Ø}} ,M \ne { \text{Ø}} \\ \end{array} \right.$

性质1　给定弱标记不完备决策系统 ${\rm{WIDS}} = $ $ < U,C \cup D,V,f > $ ，设 $U = L \cup M$ ，其中 $L$ 表示有标记实例的集合， $M$ 表示无标记实例的集合，对 $\forall a \in C - B$ 满足：

${\rm{Dis}}(B \cup a,{U^2}) \geqslant {\rm{Dis}}(B,{U^2})。$

证明　根据定义2可得 ${\rm{Di}}{{\rm{s}}_{M}}(B \cup a,{U^2}) \geqslant {\rm{Di}}{{\rm{s}}_{M}} (B, $ $ {U^2})$ ，根据定义4有 ${\rm{Di}}{{\rm{s}}_L}(B \cup a,{U^2}) \geqslant {\rm{Di}}{{\rm{s}}_L}(B,{U^2})$ 。从而可证 ${\rm{Di}}{{\rm{s}}_L}(B \cup a,{U^2}){\rm{ + Di}}{{\rm{s}}_{M}}(B \cup a,{U^2}) \geqslant {\rm{Di}}{{\rm{s}}_L}(B, {U^2}) + $ $ {\rm{Di}}{{\rm{s}}_{M}}(B,{U^2})$ ，即 ${\rm{Dis}}(B \cup a,{U^2}) \geqslant {\rm{Dis}}(B,{U^2})$ 。

定义6　给定弱标记不完备决策系统 ${\rm{WIDS}} = $ $ \; < U,C \cup D,V,f > $ ，设 $U = L \cup M$ ，其中 $L$ 表示有标记实例的集合， $M$ 表示无标记实例的集合， $R \subseteq C$ 是一个属性约简，当且仅当 $R$ 满足：

1) ${\rm{Dis}}(R,{U^2}){\rm{ = Dis}}(C,{U^2})$ ；

2) $\forall c \in R$ ， ${\rm{Dis}}(R - c,{U^2}) \ne {\rm{Dis}}(C,{U^2})$ 。

定义7　给定弱标记不完备系统 ${\rm{WIDS}} = $ $ \; < U,C \cup D,V,f > $ ，设 $U = L \cup M$ ，其中 $L$ 表示有标记实例的集合， $M$ 表示无标记实例的集合，并且 $B \subseteq C$ ，对 $\forall c \in C - B$ ，则

1)属性 $c$ 相对于属性集合 $B$ 的区分度:

${\rm{RSig}}(c,B,{U^2}) = \left\{ \begin{array}{l} |{\rm{Dis}}(B \cup c,{U^2}){\rm{| - }}|{\rm{Dis}}(c,{U^2})\;{\rm{|}},\quad B \ne \text{Ø} \\ |{\rm{Dis}}(c,{U^2})|,\quad B = \text{Ø} \\ \end{array} \right.$

2)当 ${\rm{RSig}}(c,B,{U^2}) = 0$ 时，则称属性 $c$ 相对于 $B$ 是不必要的(相对冗余的)。

如图1所示，利用 $|{\rm{Dis}}(B \cup c,{U^2}){\rm{| - }}|{\rm{Dis}}(c,{U^2})\;|= $ $ {\rm{ RSig}}(c,B,{U^2})$ 计算属性 $c$ 相对于属性集 $B$ 的重要度时，仅需要在属性集 $B$ 无法区分的区分对中，搜索属性 $c$ 能够区分的实例对。由于相对重要度的引入，在算法的迭代过程中，可不断地剔除当前属性约简集已能够区分的实例对和相对冗余的属性，使得算法的搜索空间不断缩减，避免了大量的重复计算，从而有效地减少算法的计算时间。

性质2　给定弱标记不完备决策系统 ${\rm{WIDS}} = $ $ < U,C \cup D,V,f > $ ，设 $U = L \cup M$ ，其中 $L$ 表示有标记实例的集合， $M$ 表示无标记实例的集合，并且 $R \subseteq C$ 是 $C$ 的一个属性约简集有

1) ${\rm{RSig}}(c,R,{U^2}) = 0$ ，　 $\forall c \in C - R$ ；

2) ${\rm{RSig}}(c,R - c,{U^2}) \ne 0$ ，　 $\forall c \in R$ 。

证明　因为 $R \subseteq C$ 是 $C$ 的一个属性约简集，根据定义6有 ${{{\rm{Dis}}}}(R,{U^2}){{ = {\rm{Dis}}}}(C,{U^2})$ ，对 $\forall c \in C - R$ 有： ${{{\rm{RSig}}}}(c,R,{{{U}}^2}{{) = }}\left| {{{{\rm{Dis}}(c,}}{{{U}}^2}{{) - {\rm{Dis}}(c,}}{{{U}}^2}{{)}} \cap {{{\rm{Dis}}(R,}}{{{U}}^2}{{)}}} \right| = $ $ \left| {{{{\rm{Dis}}(c,}}{{{U}}^2}{{) - {\rm{Dis}}(c,}}{{{U}}^2}{{)}} \cap {{{\rm{Dis}}(c,}}{{{U}}^2}{{)}}} \right| = 0 $

证明了1)的充分性。

若 $R \subseteq C$ 是 $C$ 的一个属性约简集，对 $\forall c \in $ $ C -R$ ，假设 ${\rm{RSig}}(c,R, $ $ {U^2}) \ne 0$ ，根据定义6有 ${\rm{Dis}}(R, $ $ {U^2}) = {\rm{Dis}}(C,{U^2})$ ，根据定义7可知：

$ \begin{array}{c} {\rm{RSig}}(c,R,{U^2}){\rm{ = |Dis}}(c,{U^2}) - {\rm{Dis}}(c,{U^2}) \cap {\rm{Dis}}(R,{U^2})| \\ {\rm{ = |Dis}}(c,{U^2}) - {\rm{Dis}}(c,{U^2}) \cap {\rm{Dis}}(C,{U^2})| = {\rm{0}} \end{array} $

与假设矛盾。证明了1)的必要性，同理可证2)。

2 弱标记不完备决策系统的属性约简

基于属性重要度设计启发式属性约简算法，被广泛地用于粗糙集理论的属性约简，传统的启发式算法每次迭代时，每次将最重要的属性增加到属性约简集中，但是在迭代过程中无法剔除相对冗余的属性。本文提出一种基于区分对的向前启发式属性约简算法，在每次迭代中，将相对于当前属性约简集最重要的属性加入属性约简集中，并剔除相对冗余属性和当前属性集已经能够区分的实例对，快速缩减算法的搜索空间。

2.1 属性约简算法

算法1　弱标记不完备决策系统属性约简算法(WIDAR算法)

输入　弱标记不完备决策系统 ${\rm{WIDS}} = < U, $ $ C,V,f > $ ；

输出　属性约简集red。

1) $j = 0$ ， ${\rm{Pai}}{{\rm{r}}_j} = \text{Ø}$ ， ${C_j} = C$ ， $C' = \text{Ø}$ ， ${\rm{Pair'}} = \text{Ø}$ ， ${\rm{red}} = \text{Ø}$ ；

2) 计算属性集 $C$ 的区分对 ${\rm{Pai}}{{\rm{r}}_j} = {\rm{Dis}}(C,{U^2})$ ;

3) ${\rm{while}}(|{\rm{Pai}}{{\rm{r}}_j}| \ne 0)$

{对 $\;{c_k} \in {C_j}$ ,计算 ${\rm{RSig}}({c_k},{\rm{red,Pai}}{{\rm{r}}_j})$ :

当 $R{\rm{Sig}}({c_k},{\rm{red,Pai}}{{\rm{r}}_j}) = 0$ ， ${c_k}$ 相对 ${\rm{red}}$ 为冗余属性， $C'{\rm{ = }}C' \cup {c_k}$ ;

${c_k}{\rm{ = argmax\{ RSig}}({c_k},{\rm{red,Pai}}{{\rm{r}}_{_j}})|{c_k} \in {C_j} - C'\} ;$

${\rm{red}} = {\rm{red}} \cup {c_k}$ , ${\rm{Pair'}} = {\rm{Dis}}({c_k},{\rm{Pai}}{{\rm{r}}_{_j}})$ ;

$C' = C' \cup {c_k};$

${\rm{Pai}}{{\rm{r}}_{j + 1}} = {\rm{Pai}}{{\rm{r}}_{_j}} - {\rm{Pair'}}$ //剔除当前属性集已经能区分的区分对

${C_{j + 1}} = {C_j} - C'$ //剔除已加入属性约简集的属性和相对冗余的属性

$j = j + 1$ ;}

4) 对可能存在的冗余属性进行逆向剔除

计算 ${\rm{Pair}} = {\rm{Dis}}({\rm{red}},{U^2})$

对于 $\forall {c_k} \in {\rm{red}}$ ,如果 ${\rm{RSig}}({c_k},{\rm{red}} - {c_k},{\rm{Pair}}) = 0$ ， ${\rm{red}} = {\rm{red}} - {c_k}$ ;

5) 输出属性约简集 ${\rm{red}}$

2.2 时间复杂度分析

算法1的1)初始化变量；2)根据定义2和定义4计算实例在属性集 $C$ 上的区分对，其时间复杂度为 $O(|U{|^2}|C|)$ ；3)是在性质2的基础上，采用相对重要度为标准设计启发式算法，在迭代过程中不断缩减算法的搜索空间，其时间复杂度为 $O\Bigg(\displaystyle\sum\limits_{j{\rm{ = }}0}^{|{\rm{red}}|} {|{\rm{Pai}}{{\rm{r}}_j}||{C_j}{\rm{|}}} \Bigg)$ ；4)对可能存在的冗余属性进行剔除，时间复杂度为 $O(|{\rm{Pair}}||{\rm{red|}}{}^2{\rm{)}}$ 。

3 弱标记不完备决策系统的增量式属性约简

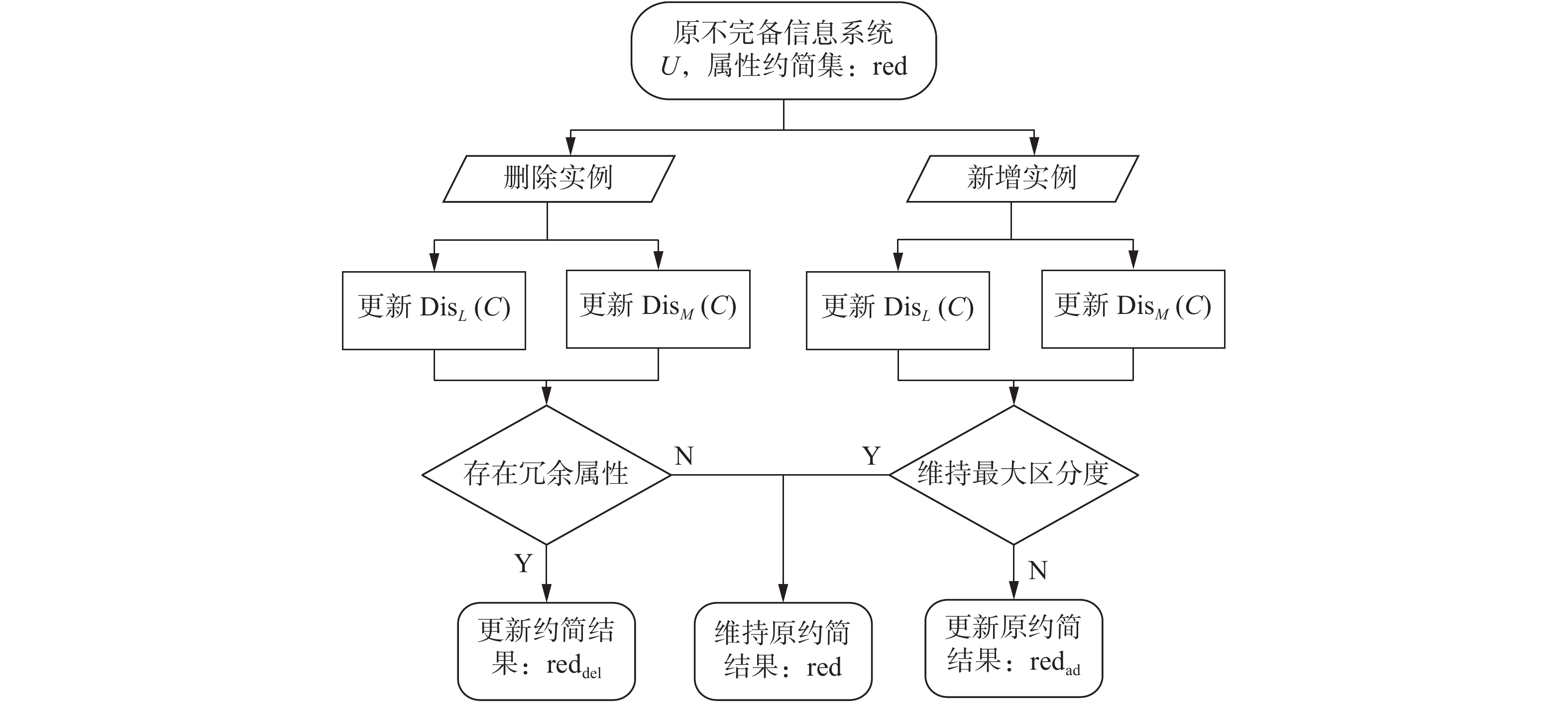
在动态数据中使用传统的属性约简方法，往往无法快速获取约简结果，而增量式属性约简算法能有效地利用原约简结果，避免大量的重复计算。针对数据动态变化的情况，本节分析了数据动态变化对实例区分对的影响，图2给出了属性约简的增量式更新机制，并针对动态数据中的实例变化情况，算法2设计了属性约简增量式更新算法。

3.1 增量式属性约简算法

算法2　弱标记不完备决策系统的增量式约简算法(WIDIAR算法)

输入　弱标记不完备决策系统 ${\rm{WIDS}} = < U, $ $ C \cup D,V,f > $ ， $U = L \cup M$ ，删除的实例 $\Delta {U_{{\rm{de}}}} = \Delta {M_{{\rm{de}}}} \cup $ $ \Delta {L_{{\rm{de}}}}$ ，增加的实例 $\Delta {U_{{\rm{ad}}}} = \Delta {M_{{\rm{ad}}}} \cup \Delta {L_{{\rm{ad}}}}$ ，原属性约简结果 ${\rm{red}}$ ；

输出　属性约简结果 ${\rm{red'}}$ 。

1) 计算删除实例 $\Delta {U_{{\rm{de}}}}$ 后存在的区分对 ${\rm{Pai}}{{\rm{r}}_{{\rm{de}}}}$ ；

2) 对于 $\forall {c_k} \in {\rm{red'}}$ ， ${\rm{red'}} = {\rm{red}}$ ，如果满足条件： ${\rm{RSig}}({c_k},{\rm{red'}} - {c_k},{\rm{Pai}}{{\rm{r}}_{{\rm{de}}}}) = 0$ ，则根据定义7逆向剔除冗余属性， ${\rm{red'}} = {\rm{red'}} - {c_k}$ ;

3) 计算增加的区分对 $\Delta {\rm{Pai}}{{\rm{r}}_{{\rm{ad}}}}$ ;

4) $j = 0$ , $C' = {\rm{red'}}$ , ${C_j} = C - C'$ ;

$\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! \Delta {\rm{Pair}}_{{\rm{ad}}}^j = \Delta {\rm{Pai}}{{\rm{r}}_{{\rm{ad}}}};$

$ \!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! {\rm{while}}(\Delta {\rm{Pair}}_{{\rm{ad}}}^j \ne {\rm{0)}}:$

{ $\forall {c_k} \in {C_j}$ ， ${\rm{if}} ({\rm{RSig}}({c_k},{\rm{red,Pai}}{{\rm{r}}_j}) = 0)$ ， $C'{\rm{ = }}C' \cup {c_k}$ ；

$ \begin{array}{l} {c_k}{\rm{ = argmax\{ RSig}}({c_k},{\rm{red'}},\Delta {\rm{Pair}}_{{\rm{ad}}}^j)|{c_k} \in {C_j} - C'\} ;\\ {\rm{red'}} = {\rm{red'}} \cup {c_k},C' = C' \cup {c_k};\\ {\rm{Pair'}} = {\rm{Dis}}({c_k},\Delta {\rm{Pair}}_{{\rm{ad}}}^j);\\ {C_{j{\rm{ + }}1}} = C - C',\Delta {\rm{Pair}}_{{\rm{ad}}}^{j + 1} = \Delta {\rm{Pair}} _{{\rm{ad}}}^j - {\rm{Pair'}}; \end{array} $

$j = j + 1$ ;}

5) 对可能存在的冗余属性进行逆向剔除，计算 ${\rm{Pair}} = {\rm{Dis}}({\rm{red'}},{{\rm{((}}U - \Delta {U_{{\rm{de}}}}) \cup \Delta {U_{{\rm{ad}}}})^2})$ ; $\forall {c_k} \in {\rm{red'}}$ ,如果 ${\rm{RSig}}({c_k},{\rm{red'}} - {c_k},{\rm{Pair}}) = 0$ ， ${\rm{red'}} = {\rm{red'}} - {c_k}$ ;

6) 输出新的属性约简结果 ${\rm{red'}}$ 。

3.2 时间复杂度分析

算法2中：1)计算删除实例后属性集 ${\rm{red}}$ 的区分对，其时间复杂度为 $O({(U - \Delta {U_{{\rm{de}}}})^2}|{\rm{red}}|)$ ；2)对可能存在的冗余属性逆向删除，其时间复杂度为 $O({(U - \Delta {U_{{\rm{de}}}})^2}|{\rm{red}}{|^2})$ ；3)计算由于增加实例 $\Delta {U_{{\rm{de}}}}$ 而增加的区分对，其时间复杂度为 $O({\rm{|}}U - \Delta {U_{{\rm{de}}}}{\rm{||}}\Delta {{{U}}_{{\rm{ad}}}}{\rm{|}} $ $ |C|)$ ；4) 若原属性约简集 ${\rm{red'}}$ 无法维持最大区分度，则需要在属性集 $C - {C'}$ 中筛选属性加入属性约简集，其时间复杂度为 $O\Bigg(\displaystyle\sum\limits_{i = 0}^j {|\Delta {\rm{Pair}}_{{\rm{ad}}}^i||{C_i}{\rm{|}}} \Bigg)$ ；5)对可能存在的冗余属性进行剔除，时间复杂度为 $O(|{\rm{Pair}}||{\rm{red'}}{{\rm{|}}^2}{\rm{)}}$ 。

4 实例分析

为进一步详细说明算法的流程。以表1中的弱标记不完备数据为例，进行分析说明。其中共有6个实例和4个属性， $U = \{ {x_1},{x_2},{x_3},{x_4}{x_5},{x_6},{x_7}\} $ 为实例集， $C = \{ {c_1},{c_2},{c_3},{c_4}\} $ 为条件属性集， $D$ 为决策属性，“*”表示缺失值，阈值 $\delta = 0.1$ 。

根据表1详细描述算法1属性约简的具体步骤：算法1中的1)变量初始化；2)计算关于属性集 $C$ 的区分对，确定算法的搜索空间 ${\rm{Pai}}{{\rm{r}}_0} = $ $ \{ < {x_1},{x_2} > , < {x_2},{x_3} > , < {x_4},{x_7} > , < {x_5},{x_7} > , < {x_6},{x_7} > \} $ ；在算法1的3)中第一次迭代时 ${\rm{red}} = \text{Ø}$ 、 ${\rm{RSig}}({c_1},{\rm{red}}, $ $ {\rm{Pai}}{{\rm{r}}_0}) = 3$ 、 ${\rm{RSig}}({c_2},{\rm{red}},{\rm{Pai}}{{\rm{r}}_0}) = {\rm{2}}$ 、 ${\rm{RSig}}({c_3},{\rm{red}},{\rm{Pai}}{{\rm{r}}_0}) = $ $ {\rm{2}}$ 、 ${\rm{RSig}}({c_4},{\rm{red}},{\rm{Pai}}{{\rm{r}}_0}) = {\rm{2}}$ ，第一次迭代结束后， ${\rm{Pai}}{{\rm{r}}_1} = $ $ {\rm{\{ }} < {x_1},{x_2} > , < {x_2},{x_3} > {\rm{\} }}$ ， ${\rm{red}} = {\rm{\{ }}{c_1}{\rm{\} }}$ 。由于此时 $|{\rm{Pai}}{{\rm{r}}_1}| \ne 0$ ，因此需进行第二次迭代， ${\rm{red}} = \{ {c_1}\} $ ， ${\rm{RSig}}({c_2},{\rm{red}}, $ $ {\rm{Pai}}{{\rm{r}}_1}) = 0$ 、 ${\rm{RSig}}({c_3},{\rm{red}},{\rm{Pai}}{{\rm{r}}_1}) = 0$ 、 ${\rm{RSig}}({c_4},{\rm{red}},{\rm{Pai}}{{\rm{r}}_1}) = 2$ ，第2轮迭代结束后， ${\rm{Pai}}{{\rm{r}}_2} = \text{Ø}$ 、 ${\rm{red}} = \{ {c_1},{c_4}\} $ 循环结束；算法1在4)中未发现冗余属性，最后输出属性约简结果 $ {\rm{red}} = \{ {c_1},{c_4}\} $ 。

为进一步详细说明算法2针对不同实例变化后对原属性约简结果产生的影响，下面首先分析算法2的2)中实例动态删除情况。在数据中删除实例将存在6种情况：1)只删除有标记的实例 $\{ {x_{\rm{1}}}\} $ ，对于 $\forall {c_k} \in {\rm{red}} = \{ {c_1},{c_4}\} $ 有 ${\rm{RSig}}({c_k},{\rm{red}} - {c_k}, $ $ {\rm{Pair}}) \ne 0$ ，属性约简集保持不变 ${\rm{red'}} = \{ {c_1},{c_4}\} $ ；2)只删除有标记的实例 $\{ {x_2}\} $ ，有 ${\rm{RSig}}({c_4},{\rm{red}} - {c_4},{\rm{Pair}}) = 0$ ，此时 ${c_4}$ 相对于 ${c_1}$ 为冗余属性，属性约简集更新为 ${\rm{red'}} = \{ {c_1}\} $ ；3)只删除无标记的实例 $\{ {x_4}\} $ ，对 $\forall {c_k} \in $ $ {\rm{red}} = \{ {c_1},{c_4}\} $ ， ${\rm{RSig}}({c_k},{\rm{red}} - {c_k},{\rm{Pair}}) \ne 0$ ，属性约简集保持不变 ${\rm{red'}} = \{ {c_1},{c_4}\} $ ；4)只删除无标记的实例 $\{ {x_7}\} $ ，有 ${\rm{RSig}}({c_4},{\rm{red}} - {c_4}, {\rm{Pair}}) = 0$ ，此时 ${c_4}$ 相对于 ${c_1}$ 为冗余属性，属性约简集更新为 ${\rm{red'}} = \{ {c_1}\} $ ；5)同时删除有标记的实例 $\{ {x_1}\} $ 和无标记的实例 $\{ {x_4}\} $ ，对 $\forall {c_k} \in {\rm{red}} = \{ {c_1},{c_4}\} $ ， ${\rm{RSig}}({c_k},{\rm{red}} - {c_k},{\rm{Pair}}) \ne 0$ ，属性约简集维持不变 ${\rm{red'}} = \{ {c_1},{c_4}\} $ ；6)同时删除有标记的实例 ${\rm{\{ }}{x_1}{\rm{\} }}$ 和无标记的实例 ${\rm{\{ }}{x_7}{\rm{\} }}$ ，有 ${\rm{RSig}}({c_1},{\rm{red}} - {c_1}, $ $ {\rm{Pair}}) = 0$ ，此时 ${c_1}$ 相对于 ${c_4}$ 为冗余属性，属性约简集更新为 ${\rm{red'}} = \{ {c_4}\} $ 。

由于在许多现实动态场景中不仅存在数据删除还有数据动态增加的情况，为了进一步分析算法2的3)和4)的计算流程，在上述实例中若在原始数据集中删除实例 ${U_{{\rm{de}}}} = \{ {x_1},{x_7}\}$ ，删除实例后属性约简集为 ${\rm{red'}} = \{ {c_4}\} $ ，在此基础上，在数据中增加实例将存在如下6种情况：1)只增加有标记实例 $\{ {x_7}\} = \{ [a,b,*,0.62,0]\} $ ，原属性约简能够维持最大区分度，根据性质2属性约简集维持不变， ${\rm{red}}' = $ $ \{ {c_4}\} $ ；2)只增加有标记实例 $\{ {x_7}\} = \{ [a,a,*,0.62,0]\} $ ，原属性约简无法维持最大区分度， $\exists c \in C - {\rm{red'}}$ 使得 ${\rm{RSig}}(c,C - c,\Delta {\rm{Pai}}{{\rm{r}}_{{\rm{ad}}}}) \ne 0$ ，根据性质2可知 ${\rm{red'}} = $ $ \{ {c_2}\} $ 不满足约简条件，在算法2的4)中属性约简更新为 ${\rm{red'}} = \{ {c_4},{c_2}\} $ ；3)只增加无标记的实例 $\{ {x_7}\} = \{ [b,a,b,0.68,*]\} $ ，同理根据性质2属性约简集维持不变， ${\rm{red'}} = \{ {c_4}\} $ ；4)只增加无标记的实例 $\{ {x_7}\} = \{ [b,a,*,0.62,0]\} $ ，原属性约简集无法维持最大区分度，同理属性约简更新为 ${\rm{red'}} = \{ {c_4},{c_1}\} $ ；5)同时增加有标记的实例 $\{ {x_7}\} = \{ [a,b,*,0.77,1]\} $ 和无标记的实例 ${\rm{\{ }}{x_8}{\rm{\} }} = \{ [b,a,a,0.65,*]\} $ ，同理属性约简集维持不变， ${\rm{red'}} = \{ {c_4}\} $ ；6)同时增加有标记的实例 $\{ {x_7}\} = \{ [a,b,*,0.77,1]\} $ 和无标记的实例 $\{ {x_8}\} = \{ [b,a,a, $ $ 0.65,*]\} $ ，原属性约简无法维持最大区分度，同理可得属性约简集更新为 ${\rm{red'}} = \{ {c_4},{c_3}{\rm{\} }}$ 。

通过上述实例分析可知，本文算法1采用相对重要度为属性重要度的度量标准，在迭代过程中不断剔除当前属性集已能够区分的区分对和相对冗余的属性，使得每次迭代的搜索空间不断缩减，避免了大量的重复计算。算法2通过分析实例动态变化对原属性约简集的影响，在实例变化后动态获取属性约简集，无需重新计算属性约简集。在删除实例后，对可能存在的冗余属性逆向剔除；增加实例后，通过搜索原属性约简集无法辨识的区分对，确定算法的搜索空间。为弱标记混合数据的属性约简提供了一种可借鉴的处理方法。

5 实验分析

为进一步验证本文算法的有效性，从UCI数据集中选取了6个真实数据集进行测试和分析，数据的详细信息如表2所示。实验的运行环境为：CPU Intel(R)Core(TM)i5-6500(3.20 Hz),内存8.0 GB，操作系统为Windows 10，采用Python编程语言，开发工具为Pycharm 2018.2.4。

本节详细讨论标记缺失对算法1的影响，首先以数据集的40%为基础数据，数据集大小的10%为梯度递增，对数据集的标记进行随机缺失处理。然后分别对弱标记的数据(weak labeled data)采用算法1(WIDAR)、Semi_D算法^[13]、Semi_P算法^[10]进行属性约简，并和算法1对有标记数据(Labeled data)的约简结果进行比较分析。对属性约简结果的分类性能评估，将采用KNN、CART、Naive Bayes三个分类器的精度作为约简结果的评价指标，将Automobile、Soybean、Dermatology、Cylinder Bands数据集随机分为两部分，一部分作为训练集，另一部分作为测试集，获取分类精度；Mushroom和Letter Recognition数据集采用10倍交叉验证，获取分类精度。针对数据中的连续型属性，本文的 $\delta $ 计算方式为 $\delta = ({{S}}{_i}/n)/\lambda$ ，其中， ${{S}}{_i}$ 为每个连续型属性的标准差， ${{S}}{_i}/n$ 为连续型属性标准差的平均值，由于每个数据集的连续型属性的平均标准差为固定值， $\delta $ 的取值由 $\lambda $ 决定^[22]。在本文中先对连续型的属性采用Min-Max Normalization归一化方法处理， $\lambda $ 取0.6。由于Semi_P和Semi_D算法的属性约简结果的分类精度基本相同，本节以Semi_D算法为例进行比较分析，实验结果如图3~5所示。

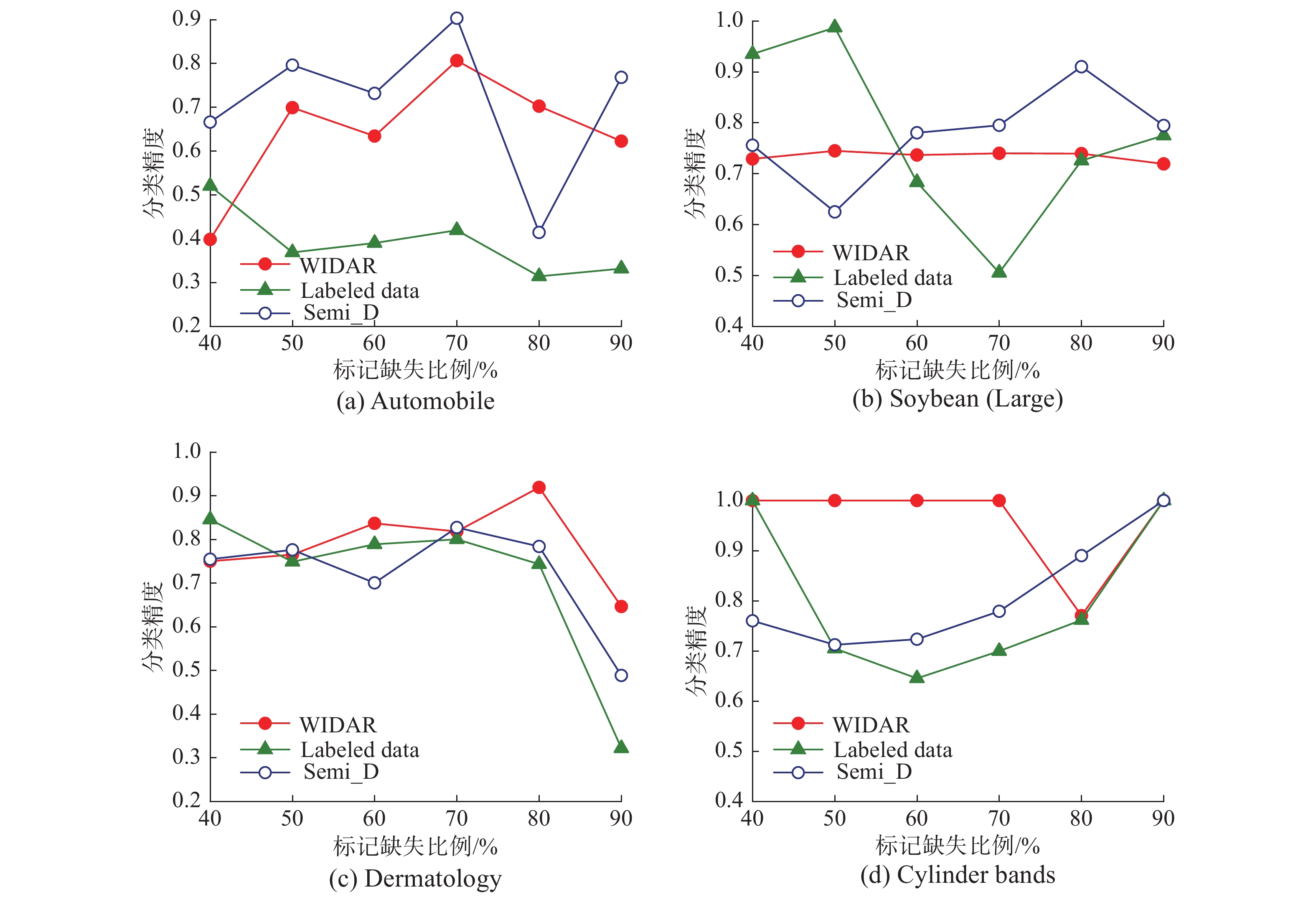
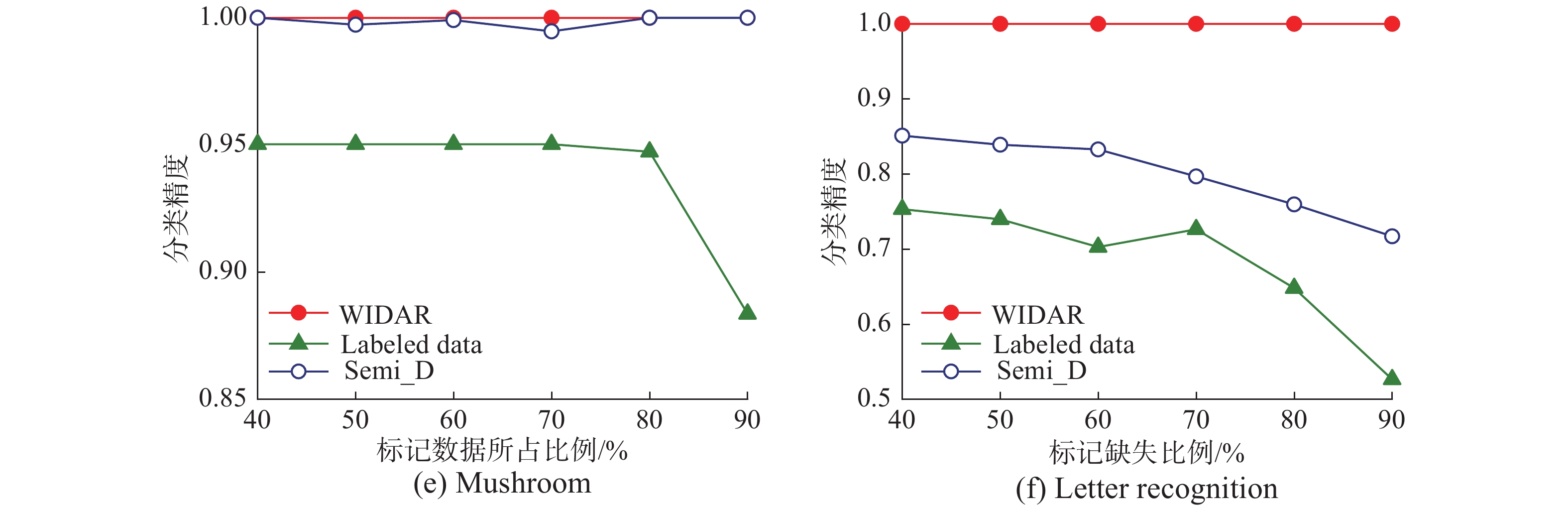
由图3~5可知，WIDAR算法能够有效利用有标记和无标记的数据，获取分类性能较优的属性约简集。特别地，随着标记缺失比例的增加，若采用WIDAR算法仅处理有标记数据(Labeled data)获取的属性约简结果，由于信息利用率的下降，分类器难以学习到较好的分类模型，在3个分类器中分类性能总体偏低，分类精度较低并且不稳定。相反，充分利用弱标记数据获取的属性约简结果，能够较好地利用原数据集的信息。分类模型的分类精度较高且稳定，分类性能较优。在前4个数据集中，由于数据的规模较小，使得分类器较难准确学习到其内在规则或模式，且对小数据集的标记进行随机缺失，对分类效果产生了一定影响。因此不同分类器在同一属性约简结果上的分类表现差异较大，但仅利用有标记的数据获取属性约简结果的分类性能显著偏弱。随着数据规模增大，在Mushroom、Letter Recognition数据集中，随着标记缺失比例的增加，WIDAR算法在有标记的数据中和Semi_D算法在弱标记数据中获取的属性约简结果分类精度出现较大的波动，但采用WIDAR算法利用弱标记的数据获取的属性约简结果分类精度稳定且对比Semi_D算法有较明显的优势。以数据集Letter Recognition为例，在图(3)的(f)中随着标记缺失比例的增加，WIDAR算法使用弱标记的数据获取的属性约简结果在KNN分类器上的分类精度仅出现了较小的波动，在标记缺失比例为40%时分类精度为99.0%，在标记缺失比例为90%时，分类精度仍有92.4%，与Semi_D算法相比分类精度从83.7%下降到58.4%。而在CART和Naive Bayes分类器中，WIDAR算法的表现更加稳定，CART分类器的分类精度稳定在100%，Naive Bayes分类器的分类精度则在73.6%~76.3%，与Semi_D算法相比具有较明显的优势。

为了进一步详细分析属性约简结果，本文以数据标记缺失比率为50%的情况为例，在表3中列举出了详细的属性约简结果,属性 ${C_i}$ 简写为 $i$ 。在同一数据集上，不同的算法属性结果存在一定的差异，结合图5和表3中的信息可知，仅利用有标记的数据获取的属性约简结果会丢失部分有效的分类信息。Semi_D算法和Semi_P算法中Automobile和Cylinder Bands数据集的约简结果完全相同，而这两个算法在其他数据集中属性约简结果大致相同，分类精度相近，为此在讨论属性约简结果的分类性能时，本文以Semi_D算法为例。与Semi_D算法和WIDAR算法仅利用有标记数据(Labeled data)相比较，本文提出的WIDAR算法能够获取一个分类性相对较优的属性约简结果。在实验过程中发现，本文的WIDAR算法在规模较小的数据集上对比Semi_D算法，其分类性能有时存在效果偏弱的情况，但随着数据规模的增大，WIDAR算法的性能表现趋于稳定，并且对比Semi_D算法存在较明显的优势。综上可得，本文的算法在大数据集中能够有效利用无标记的数据，增强属性约简结果的分类性能，显著提升了算法的鲁棒性。

综上可知，无标记数据也内含丰富的分类信息，仅利用有标记的数据获取属性约简集，往往会丢失部分信息，导致分类器的分类性能偏低。充分利用有标记数据和无标记数据，获取的属性约简结果，在分类器中的表现较优。WIDAR算法在对大数据进行属性约简时，能够快速获取分类性能较优的属性约简结果，且算法具有良好的鲁棒性。另外，为了进一步说明算法2 (WIDIAR算法)的有效性，在数据集的标记随机缺失50%后，将6组数据集划分为基准数据集和候选数据集两部分，取原数据集的前50%作为基准数据集。为应对现实应用领域中常见的复杂应用场景，每次实验剔除基准数据集中5%的数据后增加数据，并且增加的数据以候选数据集的10%为梯度增加，与WIDAR算法、Semi_P算法和Semi_D算法进行对比分析，实验结果如图6所示。

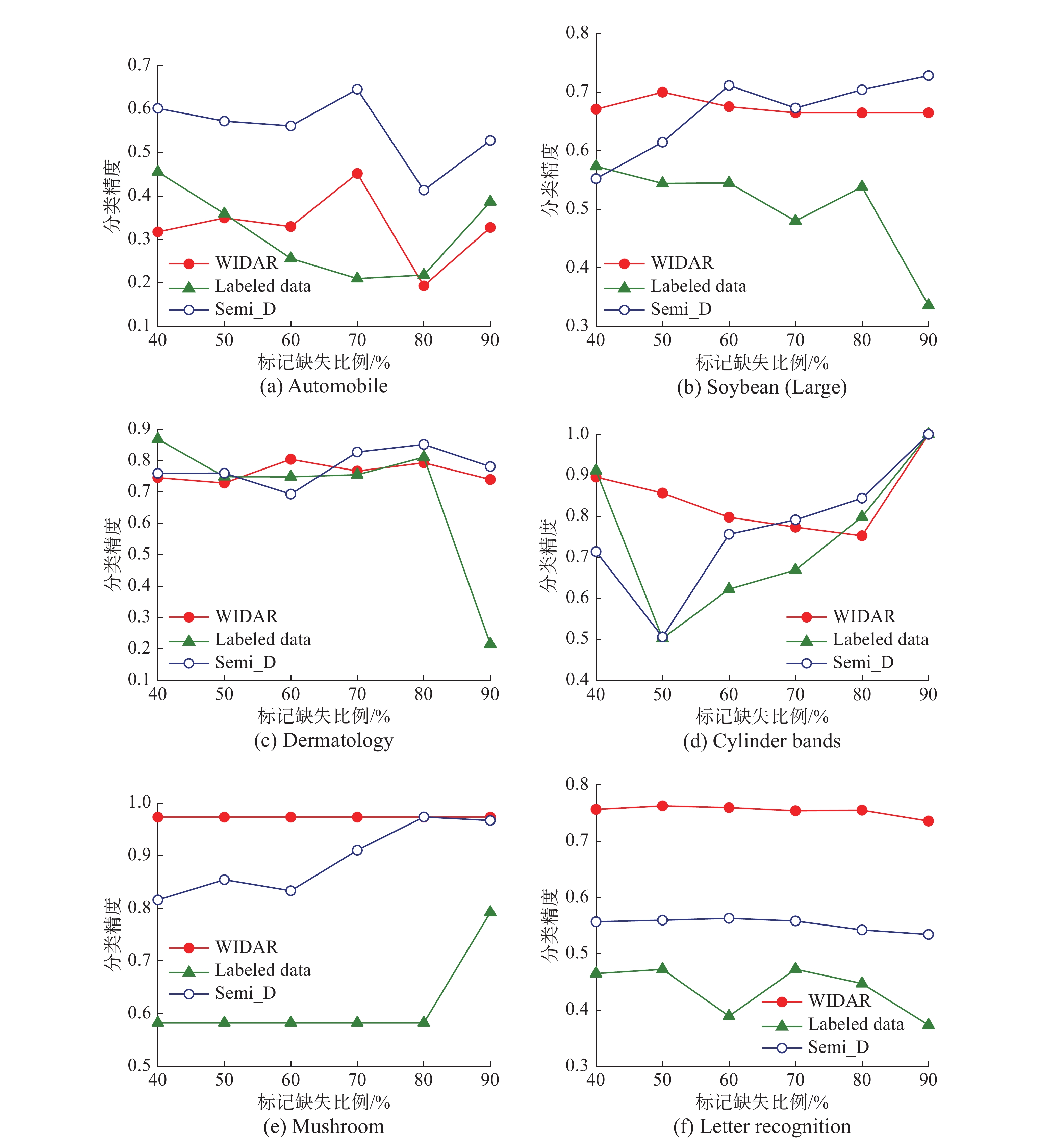
由图6(a)~(c)可知，WIDAR算法引入了相对重要度作为属性重要度的度量标准，在迭代中不断缩减算法搜索空间。因此在处理数据规模较小的数据集时，WIDIAR算法与WIDAR算法计算效率相近，但相比Semi_P算法和Semi_D算法有较明显的优势。但随着数据规模的增大，WIDAR算法在动态数据中更新属性约简结果需要进行大量的重复计算。采用WIDIAR算法，对属性约简集进行增量式更新，能够有效减少重复的计算，相比WIDAR算法，能够节约大量的时间。当增加的数据集的大小为100%时，在Mushroom数据集中，采用动态属性约简算法动态更新属性约简结果需要的时间仅为210.156 s，而采用静态属性约简算法，获取属性约简需要花费423.521 s，与静态属性约简算法相比较能够节约50.38%的时间。在Letter Recognition数据集中，采用动态属性约简算法动态更新属性约简结果需要的时间仅为356.823 s，而采用WIDAR算法获取属性约简需要花费2776.922 s，与WIDAR算法相比较能够节约87.15%的时间。

表4为增加的数据达到100%时，WIDIAR算法和WIDAR算法的属性约简结果的对比,属性 ${C_i}$ 简写为 $i$ 。从表4中可以看到，WIDIAR算法的属性约简结果与WIDAR算法相比，在较小的数据集中存在一定差异，但随着数据规模的增加，算法的属性约简结果差异逐步缩减，在Mushroom和Letter Recognition数据集中两者的属性约简结果完全相同。由此可知，本文提出的WIDIAR算法能够有效节约大量计算时间，同时能获取分类性能较优的属性约简结果。为大规模复杂数据的属性约简问题，提供了一个可行的增量式属性约简方法。

6 结束语

在众多的现实应用领域中，由于数据采集技术和成本的限制，存在大量的不完备高维数据，且通常只有少量的数据存在标记信息。若仅利用有标记的数据获取属性约简结果，将会丢失部分有效的信息。为了有效地利用弱标记不完备的高维数据，从中获取分类效果更优的属性约简集，本文基于实例的区分对，提出属性相对重要度的概念，设计了启发式属性约简算法。针对动态变化场景，详细分析了数据的动态变化对属性约简的影响和更新机制。并在此基础上，提出了增量式的属性约简算法。实验结果表明，该算法在处理大规模数据时，相比静态属性约简算法，在保证分类性能的同时，能够高效地获取属性约简结果。下一步工作将拓展增量式属性约简算法应用场景，考虑属性集变化后，属性约简集的更新问题。