随着互联网和移动技术的飞速发展,现在越来越多的人拥有智能手机、平板电脑和其他的智能终端,这使得生产信息的速度呈爆炸式增长,导致了信息超载问题。当用户搜索其感兴趣的信息时,会花费大量的时间和精力去过滤掉无用的信息,然而结果往往得不到用户的满意,于是个性化推荐技术应时而生。个性化推荐技术是指利用用户某种兴趣点和购买特点,向用户推荐感兴趣的内容,是缓和信息超载问题的有效途径。在个性化推荐技术[1]中协同过滤推荐(collaborative filtering, CF)技术是最成熟也是应用最广泛的一种技术,简单来说,协同过滤是根据某兴趣相投、拥有相似用户群体的喜好来预测用户感兴趣的信息,并将其推荐给目标用户。但是由于对象和商品数的快速增长,协同过滤推荐技术出现了冷启动、可扩展性、数据稀疏性问题[2]。
为了改善协同过滤推荐算法,一些研究者基于上述问题从不同角度出发对其进行研究,针对数据稀疏性问题,文献[3]提出了一种数据挖掘算法对稀疏矩阵进行填充,并引入相似性计算因子计算用户相似性。文献[4]利用降维技术,对高维稀疏数据在分布式平台下采用矩阵分解算法进行预处理,降低数据稀疏性。
针对传统协同过滤推荐技术的冷启动问题,文献[5]提出了扩展的基于概率论分类的朴素贝叶斯的混合推荐算法,文献[6-8]提出了基于用户本身特有的信息进行聚类的CF算法,这些算法的提出都有效缓解了用户冷启动问题,从而提升了推荐的响应速度。
针对传统协同过滤推荐技术的可扩展性问题,面对日益增多的用户,数据量的急剧增加,算法的可扩展性问题成为制约推荐系统的重要因素。文献[9]提出了基于传统的SVD协同过滤算法,但是这种矩阵分解算法有一定的代价。
在上述方法的启发下,本文提出了一种新颖的相似度模型(PCEDS),PCEDS是将用户属性特征和用户偏好相融合的一种相似度模型。首先根据用户属性特征进行聚类,聚类采用优化的K-means算法,即CF-act(u)对用户进行聚类,然后根据聚类后的目标用户采用一种新颖的PCEDS推荐模型为目标用户产生推荐。
1 基于用户活跃度(CF-act)聚类聚类[10-11]是指在物理或抽象对象的集合里,将相类似的对象分类成多个类的过程,这些对象在同一类中彼此相似,在不同类中相异。但是,传统的CF算法经常是基于用户对商品的评分数据进行聚类,而忽视了用户特有的一些特征属性,从而会出现一种对目标用户推荐一些完全不感兴趣的信息的尴尬情况,这在很大程度上影响了推荐的准确性。在现实中,每个用户都有其个人特征,本文将依据用户的性别、年龄、职业等属性特征进行聚类,认为拥有相似年龄、性别、职业的用户其偏好和消费行为也可能相似。
K-means是聚类方法[12-13]中最常用的一种算法。在K-means算法中,初始聚类中心的选取对聚类结果有一定的影响。为了降低初始聚类中心对聚类结果的影响,本文在使用K-means聚类算法时,对初始聚类中心的选取进行了优化。年龄、性别、职业作为用户特有的特征,本文在对用户属性特征进行K-means聚类时,初始聚类中心即K值的选取,依据用户特有特征(年龄、性别、职业)进行K的选取,本文根据年龄段的划分,可以分为7个阶段,即K值为7。
首先将出现次数最多的,即具有高活跃度的属性特征的用户群作为选取对象,因为选取聚类中心时是根据年龄段进行划分选取的,本文将划分的7个年龄段分别用数字0、1、2、3、4、5、6来表示,然后在每个年龄段中选取活跃度高的性别属性(男、女,本文用数字0、1代表),根据年龄、性别再选取每个年龄段中职业活跃度高的用户,本文将21种职业归属为4大类,分别用数字0、1、2、3来表示,这样在每个年龄段中依次选取,结果如表1所示。
| 表 1 初始聚类中心 Tab.1 Initial clustering center |
处理数据的算法如下:
输入 用户特征信息表CUser
输出 用数字代表的用户特征信息表NCUser
CUser表中选取n个用户,记为U={p1,p2,…,pn}
对所有的pi∈U
q=0,i=0,j=0;
if q<3;
if pi[j]∈{0−17||18−24||25−34||35−44||45−49||50−55||56−}
then int sign:={0||1||2||3||4||5||6}
else if pi[j+1]∈{男|女}
then int sign:={0||1}
else if pi[j+2]∈{某一职业类}
then int sign:={0||1||2||3}
q++;i++;j++;
end if
end if
end
根据表1选取的基于属性特征活跃度的初始聚类中心,再根据用户偏好活跃度选取属于每行聚类中心的用户ID集合,然后基于用户偏好活跃度的用户ID集合再选取评分活跃度高的用户作为初始聚类中心,最终K值的选取如图1所示。

|
Download:
|
| 图 1 基于用户活跃度的K值 Fig. 1 K value based on user activity | |
根据图1选取的初始聚类中心,利用用户特征属性数据集对用户进行K-means聚类,算法具体步骤如下:
输入 NCUser(用户特征信息表)、Rating(评分表)、K;
输出 k个聚类簇。
从NCUser表中选取n个用户,记为U={u1,u2,…,un}
initialize K, flag A={a1, a2, …, ak}
选取活跃度高的用户特征向量作为K个初始聚类中心,flag B={b1,b2,…bk}
Repeat
For all ui∈U
For all bj∈B
bj∈max sim(ui,bj)
For all ai∈A
For all uj∈U
Until K no change
back
因此,在聚类簇中搜索最近邻居为目标用户产生推荐,降低了推荐时间的复杂度。
2 融合的相似度模型 2.1 基于加权用户属性特征和用户偏好的相似度模型在计算用户之间的相似性时,如果仅参考用户的评分数据通常具有片面性,例如当用户第一次登录时,因为没有评分数据,而导致推荐不准确或无法为新用户产生推荐的现象,即冷启动问题。对于冷启动问题,本文在计算用户之间属性特征相似度时,采用欧几里德相似度算法[14],其公式如下:
| $\mathop {{\rm{sim}}\left( {u,v} \right)}\nolimits^{{\rm{EDS}}} = \frac{1}{{1 + \sqrt {\displaystyle\sum\nolimits_{} {{{\left( {r_u - r_v} \right)}^2}} } }}$ |
式中ru、rv分别表示用户u和用户v的属性特征向量。欧几里德相似度值越大说明d越小,即距离越相近,则用户之间的相似度越大。但是在计算用户之间的相似度时是大范围的相似性,这样计算出来的相似度具有一定的误差,所以本文提出了加权的欧几里德相似度模型。如果2个用户之间性别特征相同、在同一年龄段及职业相似,则这2个用户的偏好也相似,即用户之间的信任度。信任度是指用户之间相同个数的属性特征与属性特征总和之间的比例。公式如下:
| ${\rm{CD}}(u,v) = \frac{{\mathop {{\rm{ct}}}\nolimits_i }}{{\mathop {{\rm{ct}}}\nolimits_t }}$ |
式中:相同属性特征个数用cti表示;属性特征个数总和用ctt表示。加权用户之间的属性特征信任度与欧几里德相似度,新的相似度模型即CEDS模型如下:
| $\mathop {{\rm{sim}}\left( {u,v} \right)}\nolimits^{\rm CEDS} = \frac{{\mathop {{\rm{ct}}}\nolimits_i }}{{\mathop {{\rm{ct}}}\nolimits_t }} \frac{1}{{1 + \sqrt {\displaystyle\sum\nolimits_{} {{{\left( {r_u - r_v} \right)}^2}} } }}$ |
用户偏好相似度模型(PCC),本文在依据用户评分数据计算偏好相似性时,是在目标用户所在的聚类中计算相似度,这样很大程度上减少了计算的时间复杂度,能更好地实现实时推荐。用户偏好相似度模型(PCC)为
| $\mathop {{\rm{sim}}\left( {u,v} \right)}\nolimits^{{\rm{PCC}}} = \frac{{\displaystyle\sum\limits_{i \in I_{uv}} {\left( {r_{ui} - {\overline {r}}_{u} } \right)\left( {r_{vi} -{ \overline {r}}_{v} } \right)} }}{{\sqrt {\displaystyle\sum\limits_{i \in I_{uv}} {{{\left( {r_{ui} - {\overline {r}} _{u}} \right)}^2}{{\left( {r_{vi} - {\overline {r}}_{v} } \right)}^2}} } }}$ |
基于用户属性特征的加权相似度模型是根据用户特征数据集采用加权后的EDS算法计算用户相似度,当用户评分少或有新用户登录时,使用该模型可以缓解用户冷启动的问题。本文在计算用户相似度时是在目标用户所在的聚类簇中进行的,减少了目标用户最近邻的搜索时间,协同过滤的可扩展性问题有所改善。将2种相似度模型进行加权提出了PCEDS模型。公式为
| $\mathop {{\rm{sim}}\left( {u,v} \right)}\nolimits^{{\rm{PCEDS}}} = \lambda \times {\rm{PCC}} + (1 - \lambda )\times {\rm{CD}}\times {\rm{EDS}}$ |
线性加权后的模型简称为PCEDS模型,综合考虑了用户本身的特征属性和用户偏好相似性,实验表明,提出的PCEDS模型在推荐质量上有所提高。
3 实验结果与分析 3.1 PCEDS模型的RMSE结果MovieLens数据集是做推荐系统最有权威的数据集,是一个涉及电影评分的真实数据集,由美国Minnesota大学提供。本文实验采用的是MovieLens 100 K数据集,评分数据的最高分为5,最低分为1,评分的高低代表用户的喜欢程度。在对用户进行聚类和CEDS模型计算相似度时采用的都是用户属性特征数据集,属性特征信息包括4个组:用户ID、年龄、性别、职业,其中职业包括21种职业类型。PCC模型计算相似度时采用的是Rating数据集,其信息包括用户ID、项目ID、评分。
在计算用户偏好相似度时,将用户−项目评分数据集分为训练集和测试集,其中80%为训练集,20%为测试集。衡量协同过滤推荐质量的指标有均方根误差(mean absolute error,RMSE)、准确率、召回率等。
均方根误差(RMSE)为
| ${\rm{RMSE}}{\rm{ = }}\sqrt {\frac{{ \displaystyle\sum \limits_{i = 1}^N {{({p_i} - {q_i})}^2}}}{N}} $ |
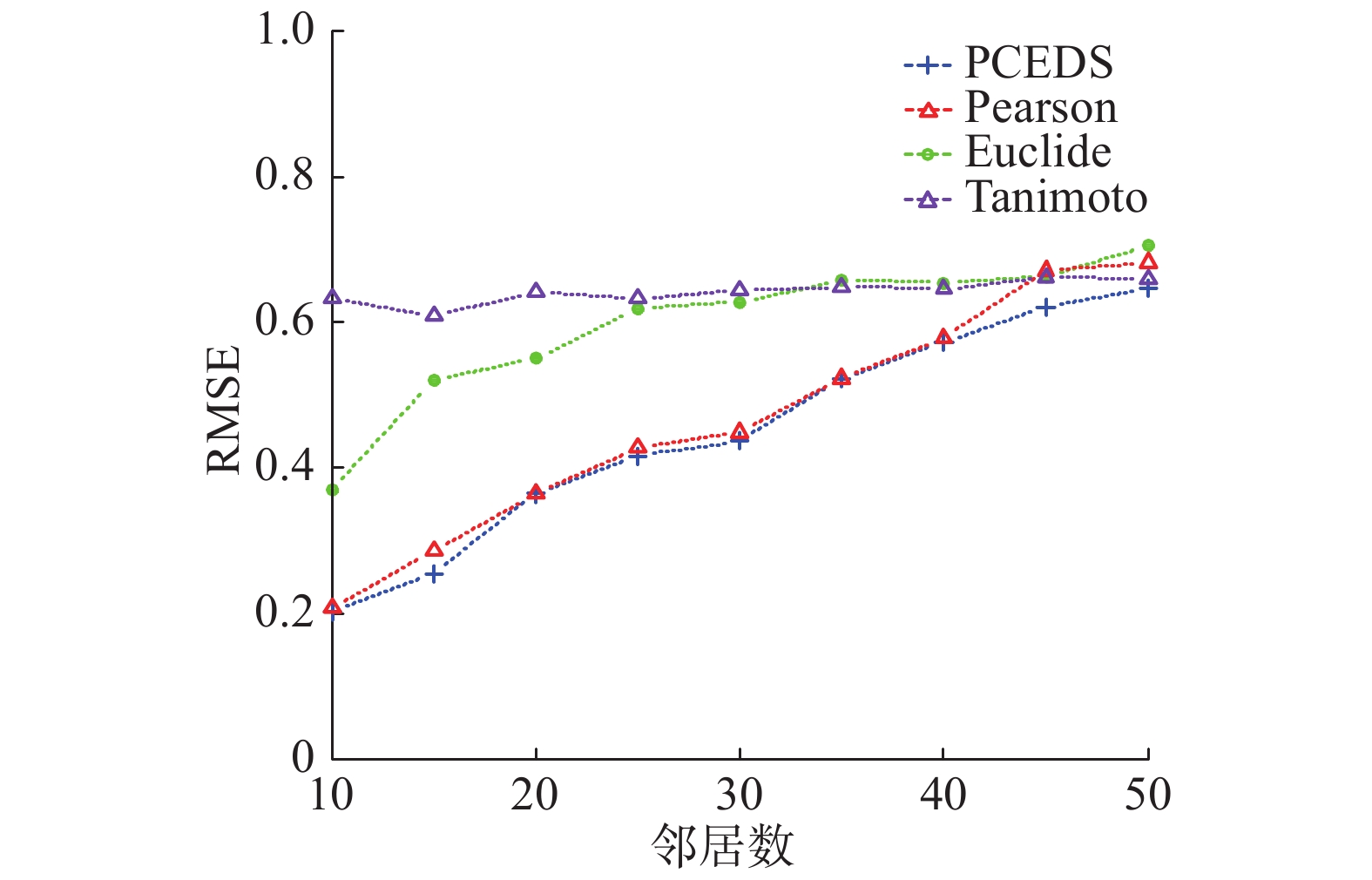
式中:pi表示预测的用户评分集合,qi表示用户评分集合。本文实验将PCEDS模型与传统的Pearson模型、Tanimoto模型以及Euclide模型进行了RMSE比较。4种模型在RMSE评价标准上的效果如图2所示。
|
Download:
|
| 图 2 PCEDS模型与Pearson、Euclide模型以及Tanimoto模型的RMSE Fig. 2 RMSE comparison between PCEDS、Pearson、Euclide and Tanimoto model | |
从图2分析得出,本文提出的PCEDS模型比传统的Pearson、Euclide以及Tanimoto模型的RMSE都要低,所以本文提出的PCEDS模型不仅缓解了用户冷启动问题,对用户产生的推荐质量也有所提高。
3.2 参数λ对PCEDS模型的影响为了检验权重参数对PCEDS模型的影响,选取λ的最佳值,将50作为本实验用户的邻居数量,观察随着λ的增长,融合后的相似度模型的均方根误差的变化,如图3所示。
由图3可知,当均方根误差最小时,λ取0.9,所以参数λ取0.9时PCEDS模型产生的推荐质量最好。

|
Download:
|
| 图 3 λ变化对PCEDS模型的RMSE影响 Fig. 3 Effect of change on RMSE of PCEDS model | |
用户−物品评分记录在最终的推荐列表中出现的比例用准确率表示,最终的推荐列表中包含用户−物品评分记录的比例用召回率描述。实验通过准确率/召回率评测推荐算法的精度:
| $ \begin{array}{*{20}{l}} {{\rm{Precision}} = \frac{{\displaystyle\sum\limits_u {|R(u) \cap T(u)|} }}{{\displaystyle\sum\limits_u {|R(u)|} }}}\\ {{\rm{Recall}} = \frac{{\displaystyle\sum\limits_u {|R(u) \cap T(u)|} }}{{\displaystyle\sum\limits_u {|T(u)|} }}} \end{array} $ |
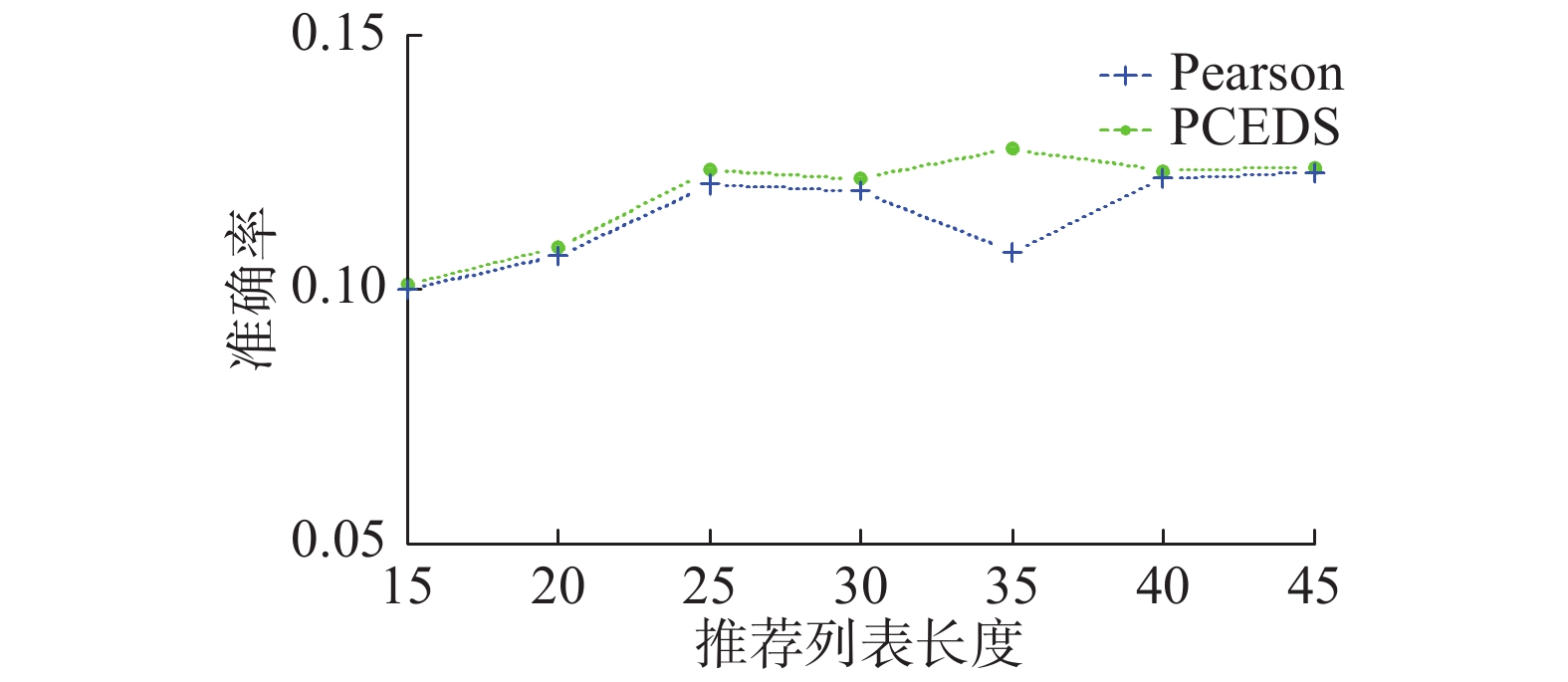
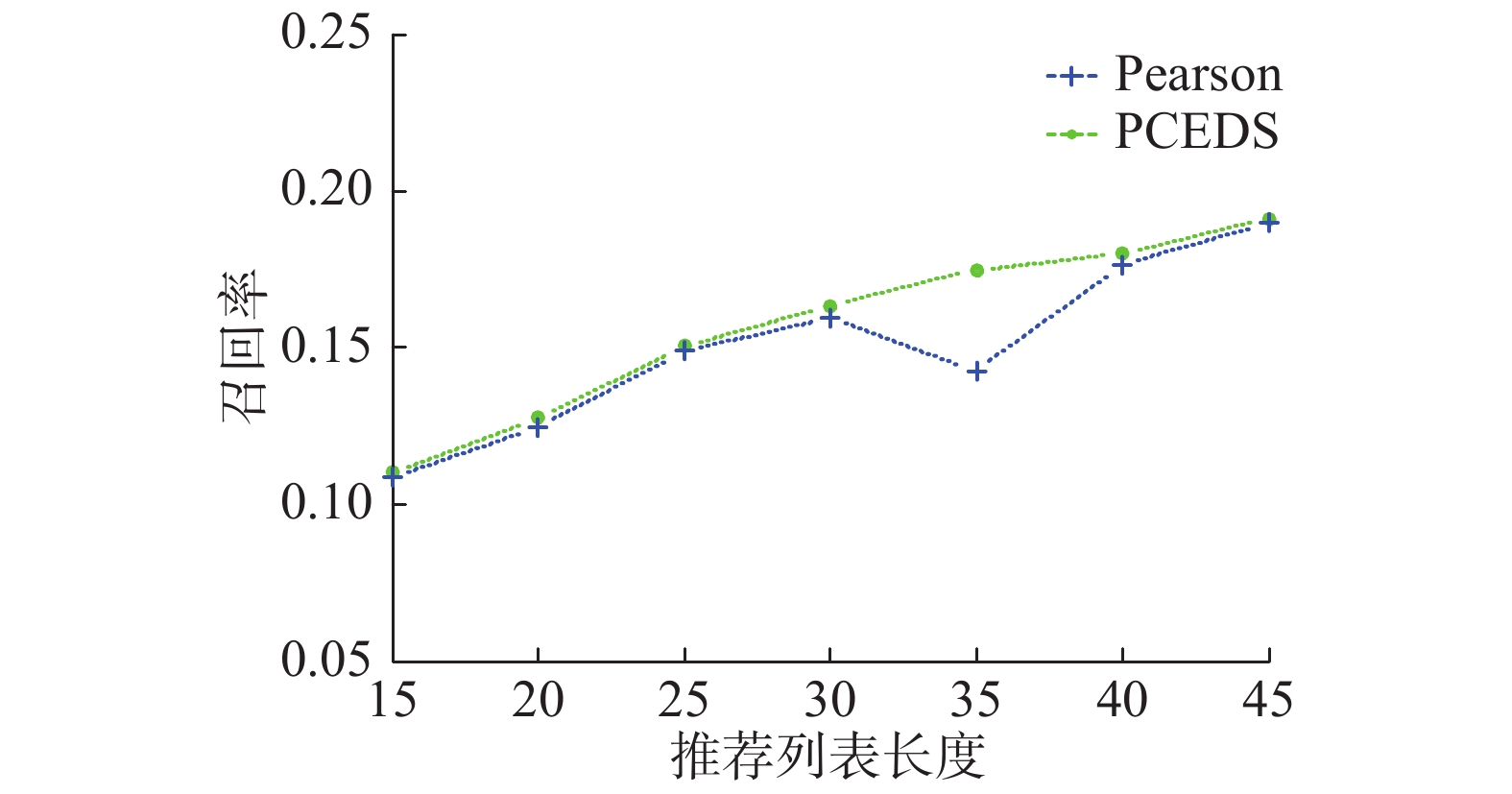
式中:Precision表示准确率;Recall表示召回率。对用户u推荐N个物品(记为R(u)),T(u)表示用户u在测试集上喜欢的物品集合。PCEDS模型与Pearson模型准确率/召回率的比较如图4、5所示。
|
Download:
|
| 图 4 准确率比较 Fig. 4 Comparison of precision | |
|
Download:
|
| 图 5 召回率比较 Fig. 5 Comparison of recall | |
由图4和图5可知,随着横坐标的变换,PCEDS模型的准确率、召回率与PCC模型相比均有提高。
4 结束语本文根据用户的属性特征采用优化的K-means算法首先对用户进行聚类,聚类中心是基于用户活跃度选取的,比传统的随机选取的聚类中心更有代表性,聚类的结果会更合理,并且缓解了协同过滤推荐系统的可扩展性问题。PCEDS模型具有融合了用户本身的属性特征信息和用户偏好信息的相似度计算的优点,在计算用户属性特征相似度时是基于属性特征信任度的相似度,提高了传统的相似度算法,根据相似度选取的目标用户最近邻居更准确。PCEDS相似度算法缓解了因用户评分数据少或新用户登录时导致的用户冷启动问题。

|
Download:
|
| 图 1 | |
| [1] |
王国霞, 刘贺平. 个性化推荐系统综述[J]. 计算机工程与应用, 2012, 48(7): 66-76. WANG Guoxia, LIU Heping. Survey of personalized recommendation system[J]. Computer engineering and applications, 2012, 48(7): 66-76. DOI:10.3778/j.issn.1002-8331.2012.07.018 (  0) 0)
|
| [2] |
Jamali M, Ester M. A transitivity aware matrix factorization model for recommendation in social networks[C]//Proceedings of the Twenty-Second International Joint Conference on Artificial Intelligence. Barcelona, Spain,2011:2644–2649.
( 0) 0)
|
| [3] |
WEI Jian, HE Jianhua, CHEN Kai, et al. Collaborative filtering and deep learning based recommendation system for cold start items[J]. Expert systems with applications, 2017, 69: 29-39. DOI:10.1016/j.eswa.2016.09.040 ( 0) 0)
|
| [4] |
AGGARWAL C C. An introduction to data mining[M]//AGGARWAL C C. Data Mining: the Textbook. Cham: Springer, 2015: 1–26.
( 0) 0)
|
| [5] |
孙天昊, 黎安能, 李明, 等. 基于Hadoop分布式改进聚类协同过滤推荐算法研究[J]. 计算机工程与应用, 2015, 51(15): 124-128. SUN Tianhao, LI Anneng, LI Ming, et al. Study on distributed improved clustering collaborative filtering algorithm based on Hadoop[J]. Computer engineering and applications, 2015, 51(15): 124-128. DOI:10.3778/j.issn.1002-8331.1405-0415 (  0) 0)
|
| [6] |
胡勋, 孟祥武, 张玉洁, 等. 一种融合项目特征和移动用户信任关系的推荐算法[J]. 软件学报, 2014, 25(8): 1817-1830. HU Xun, MENG Xiangwu, ZHANG Yujie, et al. Recommendation algorithm combing item features and trust relationship of mobile users[J]. Journal of software, 2014, 25(8): 1817-1830. (  0) 0)
|
| [7] |
LIU Haifeng, HU Zheng, MIAN A, et al. A new user similarity model to improve the accuracy of collaborative filtering[J]. Knowledge-based systems, 2014, 56: 156-166. DOI:10.1016/j.knosys.2013.11.006 ( 0) 0)
|
| [8] |
韦素云, 肖静静, 业宁. 基于联合聚类平滑的协同过滤算法[J]. 计算机研究与发展, 2013, 50(S2): 163-169. WEI Suyun, XIAO Jingjing, YE Ning. Collaborative filtering algorithm based on co-clustering smoothing[J]. Journal of computer research and development, 2013, 50(S2): 163-169. (  0) 0)
|
| [9] |
LEE D D, SEUNG H S. Learning the parts of objects by non-negative matrix factorization[J]. Nature, 1999, 401(6755): 788-791. DOI:10.1038/44565 ( 0) 0)
|
| [10] |
ELKAHKY A M, SONG Yang, HE Xiaodong. A multi-view deep learning approach for cross domain user modeling in recommendation systems[C]//Proceedings of the 24th International Conference on World Wide Web. Florence, Italy, 2015: 278-288.
( 0) 0)
|
| [11] |
陈克寒, 韩盼盼, 吴健. 基于用户聚类的异构社交网络推荐算法[J]. 计算机学报, 2013, 36(2): 349-359. CHEN Kehan, HAN Panpan, WU Jian. User clustering based social network recommendation[J]. Chinese journal of computers, 2013, 36(2): 349-359. (  0) 0)
|
| [12] |
张顺龙, 库涛, 周浩. 针对多聚类中心大数据集的加速K-means聚类算法[J]. 计算机应用研究, 2016, 33(2): 413-416. ZHANG Shunlong, KU Tao, ZHOU Hao. Accelerate K-means for multi-center clustering of big datasets[J]. Application research of computers, 2016, 33(2): 413-416. DOI:10.3969/j.issn.1001-3695.2016.02.021 (  0) 0)
|
| [13] |
贾洪杰, 丁世飞, 史忠植. 求解大规模谱聚类的近似加权核K-means算法[J]. 软件学报, 2015, 26(11): 2836-2846. JIA Hongjie, DING Shifei, SHI Zhongzhi. Approximate weighted kernel K-means for large-scale spectral clustering[J]. Journal of software, 2015, 26(11): 2836-2846. (  0) 0)
|
| [14] |
DRAISMA J, HOROBET E, OTTAVIANI G, et al. The Euclidean distance degree of an algebraic variety[J]. Foundations of computational mathematics, 2016, 16(1): 99-149. DOI:10.1007/s10208-014-9240-x ( 0) 0)
|
 2020, Vol. 15
2020, Vol. 15


