Adam是目前深度学习中广泛采用的一种优化算法^[1]。与经典梯度下降不同的是，Adam同时使用了自适应步长和动量两种技巧。其中自适应步长技巧使算法对超参数不敏感，动量技巧可以加速算法在处理凸优化问题时的收敛速率，在处理非凸问题时帮助算法避开鞍点甚至局部极值点。与仅使用单一技巧的方法相比，Adam在典型卷积深度学习的实验中具有一定的优势^[1]。

在梯度下降方法的基础上，首先使用基于梯度的自适应步长方法是AdaGrad，其主要的思路是通过对过往所有梯度的外积进行累加的方式进行步长自适应的调整^[2]。虽然AdaGrad在求解非光滑凸问题时具有和投影次梯度方法一样 $O\left( {\sqrt t } \right)$ 的regret界，其中 $t$ 是算法的迭代步数^[3]。AdaGrad算法最初主要用于正则化学习问题求解，但在深度学习应用中的效果却很不理想。出现这一问题的主要原因是算法对过去梯度的外积单纯做和，导致累加项变大得过快。为了克服这一缺陷，Hinton等^[4]采用EMA (exponential moving average)的形式修改AdaGrad算法累加项的计算方式，提出了RMSProp算法。RMSProp算法丢弃了相对遥远的历史梯度信息，保证了若干次迭代后学习能继续进行，较好地适应了目标函数平滑性的局部变化。在RMSProp算法的基础上，自适应步长算法又有了进一步的发展，典型的算法有AdaDelta^[5]等。

动量法是在经典梯度下降法基础上通过添加动量项演变而来的，广泛用于提高一阶梯度算法的收敛速率。根据动量表示方式的不同以及动量项中计算梯度位置的不同可以分成两类：一类是Polyak^[6]于1964年提出的Heavy-ball型动量法；另一类是Nesterov^[7]于1983年提出的NAG (nesterov accelerated gradient)型动量法。其中，Heavy-ball直接在当前点计算梯度；而NAG会根据当前动量预判下次迭代可能抵达的位置，并在预判的位置计算梯度。动量方法的加速性能主要体现在求解凸光滑目标函数时NAG取得的突破，将梯度下降法的收敛速率 $O\left( {{1 \mathord{\left/ {\vphantom {1 t}} \right. } t}} \right)$ 加速至最优的 $O\left( {{1 \mathord{\left/ {\vphantom {1 {{t^2}}}} \right. } {{t^2}}}} \right)$ ^[7]。当目标函数光滑且强凸时，虽然动量方法和梯度下降法都能达到线性收敛，但动量法由于具有小的收敛因子仍然具有加速性^[8]。

对于非光滑凸优化问题，投影次梯度方法目前获得的最好的个体收敛速率只是 $O\left( {{{\log \left( t \right)} /\!\!{\sqrt t }}} \right)$ ^[9]。2018年，陶蔚等^[10-11]将NAG步长策略引入到投影次梯度中，得到了最优个体收敛速率 $O\left( {{1 /\!\! {\sqrt t }}} \right)$ ，同时保证了良好的稀疏性。2019年，程禹嘉等^[12]证明了Heavy-ball型动量法具有 $O\left( {{1/\!\! {\sqrt t }}} \right)$ 的最优个体收敛速率。由此可以看出，动量方法对非光滑凸问题同样具有加速作用，只不过体现在个体收敛速率上。从Heavy-ball型动量法加速个体速率的证明过程来看，主要是借鉴了Ghadimi等^[8]在光滑条件下Heavy-ball算法收敛速率的证明。

Adam的最初形式是在梯度下降的基础上使用了EMA策略修正步长和Heavy-ball型动量法修正梯度方向^[1]。尽管Adam在深度学习中有着不错的表现^[13-14]，但自从Kingma等于2015年提出Adam后，其收敛性一直是一个具有挑战性的问题。对于非光滑凸问题，尽管Kingma等声称证明了Adam取得了 $O\left( {\sqrt t } \right)$ 的regret界，但Reddi等却对Adam的收敛性提出了质疑，他们通过理论和实验证明，即使是对简单的一维凸函数，Adam也会出现无法收敛到最优解甚至收敛到最差局部极值点的现象^[15]。出现这一问题的原因在于：采用EMA方式处理梯度时，在迭代后期步长会出现不降反升的现象，从而会导致目标函数值剧烈波动。为了克服这一问题，Reddi等提出了AMSGrad和AdamNC两个修改版本。其中，AMSGrad在Adam自适应矩阵上添加了一个确保步长衰减的操作，从而使得在线AMSGrad在一般凸的情况下能获得 $O\left( {\sqrt t } \right)$ 的regret界。2019年，Wang等^[16]通过对Adam进行适当的变形，得到了强凸情形下 $O\left( {\log \left( t \right)} \right)$ 的regret界。

从目前Adam的各种发展趋势来看，我们更愿意将Adam视为一种利用过去梯度信息同时更新下降方向和步长的一阶梯度算法框架^[17]。本文主要研究非光滑凸情形Adam型方法AMSGrad的个体收敛速率问题。为了避免叙述上的复杂性，直接简称为Adam算法。

本文的主要工作有以下3个方面：

1)证明了Adam具有 $O\left( {{1 /\!\! {\sqrt t }}} \right)$ 的最优个体收敛速率。据我们所知，这一理论结果填补了Adam算法在非光滑条件下个体最优收敛性方面研究的缺失，同时也说明了Adam继承了Heavy-ball型动量法的优点，体现了动量技巧的特性，可以将个体收敛加速至最优。

2)本文的收敛性分析思路具有一定的一般性，本文首先借鉴了Ghadimi等^[8]在光滑条件下Heavy-ball算法收敛速率的证明方法，得到与梯度下降法相似的迭代公式。为了进一步得到非光滑条件下的最优个体收敛速率，与文献[12]类似，本文巧妙设计了时变的步长和动量权重参数，同时使用Zinkevich在处理在线优化问题收敛性时使用的技巧，处理变步长与权重导致的递归问题^[3]。

3)本文选择了典型的 ${l_1}$ 范数约束下的hinge损失函数优化问题，通过与几种具有最优收敛速率算法的比较，验证了理论的正确性和算法在保持稀疏性方面的良好性能。

1 典型自适应及动量算法的收敛性

考虑有约束优化问题：

$\mathop {\min }\limits_{{{w}} \in Q} f\left( {{w}} \right)$

(1)

式中： $f\left( {{w}} \right)$ 为凸函数； $Q \subseteq {{\bf{R}}^n}$ 为有界闭凸集。记 ${{{w}}^*}$ 是式(1)的一个最优解。

梯度下降法是解决问题式(1)的经典方法，基于梯度反方向总是指向目标函数下降的方向这一事实，具体迭代步骤为

$ {{{w}}_{t + 1}} = {\pi _Q}\left( {{{{w}}_t} - {\alpha _t}{{{g}}_t}} \right) = {\rm{ }} \mathop {\arg \min }\limits_{{{w}} \in Q} \left\| {{{w}} - \left( {{{{w}}_t} - {\alpha _t}{{{g}}_t}} \right)} \right\|_2^2 $

(2)

式中： ${\pi _Q}$ 为集合 $Q$ 上的投影算子^[18]； ${\alpha _t} = {\alpha /\!\! {\sqrt t }}$ ， $\alpha $ 为大于0的常数； ${{{g}}_t}$ 是函数 $f\left( {{w}} \right)$ 在点 ${{{w}}_t}$ 处的次梯度。

平均收敛速率指的是 $f\left( {{{\overline {{w}} }_t} - {{{w}}^*}} \right)$ 的收敛速率，其中 ${\overline {{w}} _t} = {{\left( {\displaystyle\sum\limits_{j = 1}^t {{{{w}}_j}} } \right)} \Bigg/ t}$ 。与之对应，个体收敛速率指的是 $f\left( {{{{w}}_t}} \right) - f\left( {{{{w}}^*}} \right)$ 的收敛速率。通常来说，对于非光滑问题，个体收敛更难获得最优速率。

Agarwal等^[19]证明非光滑一般凸情形下投影次梯度式(2)能获得 $O\left( {{1 /\!\! {\sqrt t }}} \right)$ 的最优平均收敛速率，即

$E\left[ {f\left( {{{\overline {{w}} }_t}} \right) - f\left( {{{{w}}^*}} \right)} \right] \leqslant O\left( {{1/\!\! {\sqrt t }}} \right)$

AdaGrad的具体迭代步骤为

${{{w}}_{t + 1}} = {{{w}}_t} - \alpha {{V}}_t^{ - 1/2}{{{g}}_t}$

式中： ${{{V}}_t}$ 为 $d \times d$ 维对角矩阵，将矩阵第 $i$ 维上的元素表示为 ${{{V}}_{t,i}}$ ， ${{{V}}_{t,i}}{\rm{ = }}\displaystyle\sum\limits_{{{j}} = 1}^t {{{g}}_{j,i}^2}$ 为过去所有梯度第 $i$ 个元素的算数平方和, ${{V}}_t^{ - 1/2}$ 矩阵中对角元素 ${{V}}_{t,i}^{ - 1/2} = $ $ {\left( {\displaystyle\sum\limits_{{{j}} = 1}^t {{{g}}_{j,i}^2} } \right)^{ - 1/2}}$ 。显然，可以将AdaGrad算法的步长理解为 $\alpha {{V}}_t^{ - 1/2}$ ，因为梯度累积的影响，算法会自动增加稀疏维度的步长，减小其他维度的步长。对于凸的目标函数，AdaGrad能取得 $O\left( {\displaystyle\sum\limits_{i = 1}^d {{{\left\| {{{{g}}_{1:t,i}}} \right\|}_2}} } \right)$ 的regret界，其中 ${{{g}}_{1:t}}$ 为 $\left\{ {{{{g}}_1},{{{g}}_2}, \cdots ,{{{g}}_t}} \right\}$ 构成的 $d \times t$ 维矩阵， ${{{g}}_{1:t,i}}$ 表示由矩阵 ${{{g}}_{1:t}}$ 第 $i$ 行组成的向量。由此可以看出，AdaGrad在最坏情况下能取得 $O\left( {\sqrt t } \right)$ 的regret界，当梯度是稀疏时该regret界会变得更紧^[2]。

RMSProp算法采用EMA的形式改变AdaGrad算法中矩阵项算数平方和的计算方式，克服了当梯度较稠密时步长衰减过快的问题。RMSProp算法中矩阵的计算方式可以表示为

${{{V}}_t} = \beta {{{V}}_{t - 1}} + \left( {1 - \beta } \right){\rm{diag}}\left( {{{{g}}_t}{{g}}_t^{\rm{T}}} \right)$

式中： $\;\beta \in [0,1);\;{\rm{diag}}( \cdot )$ 表示只保留矩阵对角元素，其余元素置0。通过设置不同的 $\;\beta $ ，分配给过去梯度的权重会以指数方式衰减，起到主要作用的仅限于最近的几个梯度，实际应用中一般取 $\;\beta {\rm{ = }}0.9$ 。

相较于梯度下降法，Heavy-ball型动量法使用动量作为迭代的方向，EMA形式Heavy-ball型动量法可以表示为

${{{m}}_t} = {\beta _t}{{{m}}_t} + \left( {1 - {\beta _t}} \right){{{g}}_t}\\ {{{w}}_{t + 1}} = {{{w}}_t} - {\alpha _t}{{{m}}_t}$

(3)

式中 $\;{\beta _t} \in [0,1)$ 。通过巧妙设置步长和动量参数，Heavy-ball型动量法具有 $O\left( {{1 /\!\! {\sqrt t }}} \right)$ 的最优个体收敛速率^[12]。

Adam是在RMSProp基础上结合Heavy-ball型动量技巧发展而来的。具体迭代步骤为

${{{m}}_t} = {\beta _{1,t}}{{{m}}_t} + \left( {1 - {\beta _{1,t}}} \right){{{g}}_t}$

${{{V}}_t} = {\beta _2}{{{V}}_{t - 1}} + \left( {1 - {\beta _2}} \right){\rm{diag}}\left( {{{{g}}_t}{{g}}_t^{\rm{T}}} \right)$

${{{w}}_{t + 1}} = {{{w}}_t} - {\alpha _t}{{V}}_t^{ - 1/2}{{{m}}_t}$

(4)

式中： $ {\alpha }_{t}=\dfrac{\alpha}{\sqrt{t}{\beta }_{1,t}} {\text{；}}{\beta }_{2}\in [0,1)$ 。实际应用中一般取 $\;{\beta _{1,t}}{\rm{ = }}0.9,\;{\beta _2}{\rm{ = }}0.99$ 。

为了解决Adam的收敛性问题，AMSGrad在Adam自适应矩阵上添加一个使步长衰减的操作，具体形式为

${{{\hat V}}_t} = \max \left\{ {{{{{\hat V}}}_{t - 1}},{{{V}}_t}} \right\}$

${{{w}}_{t + 1}} = {{{w}}_t} - {\alpha _t}{{\hat V}}_t^{ - 1/2}{{{m}}_t}$

(5)

改进后的Adam算法在 $\;{\beta _{1,t}} = {\beta _1}/t$ 时能取得 $O\left( {\sqrt t } \right)$ 的regret界。

比较Heavy-ball型动量法的式(3)、Adam的式(4)和AMSGrad的式(5)可以看出：除了多了一个自适应步长的矩阵 ${{V}}_t^{ - 1/2}$ 外，Adam、AMSGrad的关键迭代步骤和Heavy-ball型动量法式(3)并无区别。既然自适应步长策略并不影响算法的收敛速率，这就启发我们：Adam型算法应该和Heavy-ball型动量法一样具有最优的个体收敛速率 $O\left( {{1 /\!\! {\sqrt t }}} \right)$ 。

2 个体收敛速率分析

本节给出非光滑条件下Adam算法在个体最优收敛速率的证明。

为了进行个体收敛性分析，首先借鉴Ghadimi等^[8]在光滑条件下Heavy-ball算法收敛速率的证明，引入加权动量项 ${p_t} = t\left( {{{{w}}_t} - {{{w}}_{t - 1}}} \right)$ 。通常情况下，Adam动量项的 $\;{\beta _{1,t}}$ 参数在实际应用中一般设定为常数，但对于非光滑问题，这种方式无法获得个体收敛速率。因此本文改变Adam动量项的计算方式为

${{{m}}_t} = {\beta _{1,t}}{{{m}}_t} + \beta' _{1,t}{{{g}}_t}$

通过巧妙地选取 $\beta _{1,t} $ 和 $\beta' _{1,t} $ 时变参数(见定理1)，可以将Adam算法的迭代步骤转化为

${{{w}}_{t + 1}} + {p_{t + 1}} = {{{w}}_t} + {p_t} - {\alpha _t}{{\hat V}}_t^{ - 1/2}{{{g}}_t}$

这个关系式和梯度下降法的关键迭代相似，也和Heavy-ball型动量法的关键迭代十分类似。正是基于这个关系式，梯度下降法的收敛分析思路可以用于Heavy-ball型动量法。受文献[12]的启发，巧妙设计了时变步长和动量项参数，得到了个体收敛速率的递归公式，为了得到递归后个体收敛速率的界，这里同样要使用Zinkevich在线优化时使用的迭代技巧。与文献[12]不同的是，本文需要处理自适应步长矩阵，而不是人为指定的步长，这里我们又借鉴Kingma在证明在线Adam的regret界时使用的技巧。

引理 1　令 ${D_\infty } = \mathop {\max }\limits_{{{w}},{{u}} \in Q} {\left\| {{{w}} - {{u}}} \right\|_\infty }$ ， ${G_\infty } = \mathop {\max }\limits_t {\left\| {{{{g}}_t}} \right\|_\infty }$ ，设 ${{{w}}_t}$ 由式(5)生成，则

$\begin{gathered} \sum\limits_{j = 1}^t {\sqrt j } \left\{ {\left\| {{{{w}}_j} - {{{w}}^*}} \right\|_{{{\hat V}}_j^{1/2}}^2 - \left\| {{{{w}}_{j + 1}} - {{{w}}^*}} \right\|_{{{\hat V}}_j^{1/2}}^2} \right\} + \\ \sum\limits_{j = 1}^t {\frac{1}{{\sqrt j }}} \left\| {{{{g}}_j}} \right\|_{{{\hat V}}_j^{ - 1/2}}^2 \leqslant \\ D_\infty ^2\sqrt t \sum\limits_{i = 1}^d {{{\hat V}}_{t,i}^{1/2}} + \frac{{2{G_\infty }}}{{\sqrt {1 - {\beta _2}} }}\sum\limits_{i = 1}^d {{{\left\| {{{{g}}_{1:t,i}}} \right\|}_2}} \\ \end{gathered} $

定理 1　设 $f\left( {{w}} \right)$ 是凸函数， ${\alpha _t} = {\alpha /{\sqrt t }}$ ，取 $\;{\beta _{1,t}} = \dfrac{{t\sqrt t }}{{\left( {t + 2} \right)\sqrt {t - 1} }}{{\hat V}}_t^{1/2}{{\hat V}}_{t - 1}^{ - 1/2}$ ， $\; \beta' _{1,t}{\rm{ = }}\dfrac{1}{{t + 2}}$ ， ${{{w}}_t}$ 由式(5)生成，则

$\begin{gathered} f\left( {{{{w}}_t}} \right) - f\left( {{{{w}}^*}} \right) \leqslant \frac{{f\left( {{{{w}}_0}} \right) - f\left( {{{{w}}^*}} \right)}}{{1 + t}} + \\ \frac{{D_\infty ^2\sqrt t }}{{2\alpha \left( {1 + t} \right)}}\sum\limits_{i = 1}^d {{{\hat V}}_{t,i}^{1/2}} + \frac{{\alpha {G_\infty }}}{{\left( {1 + t} \right)\sqrt {1 - {\beta _2}} }}\sum\limits_{i = 1}^d {{{\left\| {{{{g}}_{1:t,i}}} \right\|}_2}} \\ \end{gathered} $

至此，我们成功得到了Adam算法在非光滑情况下的最优个体收敛速率，然而，批处理形式的Adam算法每次迭代都使用全部样本计算次梯度 ${{{g}}_t}$ ，该操作对大规模机器学习问题显然是不可行的。为了解决该问题，将Adam算法推广至随机形式。

本文仅考虑二分类问题，假设训练样本集 $ S=\left\{\left({x}_{1},{y}_{1}\right),\left({x}_{2},{y}_{2}\right),\cdots ,\left({x}_{m},{y}_{m}\right)\right\}\in {R}^{d}\times \left\{+1, -1\right\}$ ，其中 ${{x}} $ 和 ${{y}}$ 分别对应样本的特征向量和监督值,同时 $\left( {{{{x}}_i},{y_i}} \right)$ 之间满足独立同分布。并且只考虑最简单的非光滑稀疏学习问题“hinge损失”，即 ${f_i}\left( {{w}} \right) = \max \left( {0,1 - {y_i}\left( {{{w}},{{{x}}_i}} \right)} \right)$ 的目标函数为

$\mathop {\min }\limits_{{{w}} \in Q} f\left( {{w}} \right) = \frac{1}{m}\sum\limits_{i = 1}^m {{f_i}\left( {{w}} \right)} $

约束情况下随机形式的Adam算法迭代步骤可以表示为

${{{w}}_{t + 1}} = {\pi _Q}\left( {{{{w}}_t} - {\alpha _t}{{\hat V}}_t^{ - 1/2}{{{m}}_t}} \right)$

(6)

相对于批处理形式的次梯度 ${{{g}}_t}$ ，随机优化每次只选择一个样本计算随机次梯度 $\nabla {f_i}\left( {{w}} \right)$ 。由于“hinge损失”次梯度的计算方式有很多种，这里选择文献[20]的方式：

$\nabla {f_i}\left( {{w}} \right){\rm{ = }}\frac{1}{m}\sum\limits_{\left( {{{{x}}_i},{y_i}} \right) \in A_t^ + } {{y_i}{{{x}}_i}} $

(7)

其中 $A_t^ + \subseteq S$ ， $A_t^ + {\rm{ = }}\left\{ {\left( {{{{x}}_i},{y_i}} \right) \subseteq {A_t};{y_i}\left\langle {{{w}},{{{x}}_i}} \right\rangle < 1} \right\}$ ，实验中选取 $\left| {{A_t}} \right|{\rm{ = }}1 $ 。

随机Adam算法：

1)初始化 ${{{w}}_1} \in Q$ ，定义步长为 ${\alpha _t}$ 且 $\left\{ {{\alpha _t} > 0} \right\}_{t = 1}^T$ ；

2) for t=1 to T；

3)等可能性选取 $i$ ；

4)根据式(7)计算随机次梯度 $\nabla {f_i}\left( {{{{w}}_t}} \right)$ ；

5)取 $\;{\beta _{1,t}} = \dfrac{{t\sqrt t }}{{\left( {t + 2} \right)\sqrt {t - 1} }}{{\hat V}}_t^{1/2}{{\hat V}}_{t - 1}^{ - 1/2}$ ， $\;\beta' _{1,t}{\rm{ = }}\dfrac{1}{{t + 2}}$ ；

6)由式(5)计算 ${{{w}}_{t + 1}} $ ；

7) end for；

8)输出 $ {{{w}}_T}$ 。

因为样本点间满足独立同分布，所以计算得到的随机次梯度 $\nabla {f_i}\left( {{{{w}}_t}} \right)$ 是损失函数在点 ${{{w}}_t}$ 处次梯度 ${{{g}}_t}$ 的无偏估计。应用文献[21]中将批处理算法收速率转化为随机算法收敛速率的技巧，可以得到定理2。

定理 2　设 $f\left( {{w}} \right)$ 是凸函数， ${\alpha _t} = {\alpha /\!\! {\sqrt t }}$ ，取 $\;{\beta _{1,t}} = \dfrac{{t\sqrt t }}{{\left( {t + 2} \right)\sqrt {t - 1} }}{{\hat V}}_t^{1/2}{{\hat V}}_{t - 1}^{ - 1/2}$ ， $\; \beta' _{1,t}{\rm{ = }}\dfrac{1}{{t + 2}}$ ， ${{{w}}_t}$ 由随机Adam算法生成，则

$ \begin{gathered} E\left[ {f\left( {{{{w}}_t}} \right) - f\left( {{{{w}}^*}} \right)} \right] \leqslant \frac{{f\left( {{{{w}}_0}} \right) - f\left( {{{{w}}^*}} \right)}}{{1 + t}} +\\ \frac{{D_\infty ^2\sqrt t }}{{2\alpha \left( {1 + t} \right)}}\sum\limits_{i = 1}^d {{{\hat V}}_{t,i}^{1/2}} + \frac{{\alpha {G_\infty }}}{{\left( {1 + t} \right)\sqrt {1 - {\beta _2}} }}\sum\limits_{i = 1}^d {{{\left\| {{{{g}}_{1:t,i}}} \right\|}_2}} \\ \end{gathered} $

由定理2可知，得到了随机Adam算法在非光滑条件下的最优个体收敛速率。

3 实验

本节主要对随机Adam算法的个体收敛速率的理论分析和稀疏性进行实验验证。

3.1 实验数据和比较算法

实验采用6个标准数据集，分别是ijcnn1、covtype、a9a、w8a、CCAT和astro-physic。这些数据均来自于LIBSVM网站，具体描述可见表1。

实验对5种随机优化方法进行比较，分别是平均形式输出的SGD方法、个体形式输出的Heavy-ball型动量法、NAG型动量法、平均形式输出的Adam算法及个体形式输出的Adam算法。从理论分析的角度来说，上述5种算法的收敛界均达到了最优。

3.2 实验方法及结论

为了算法比较的公平，各个算法在对应数据集上运行10次，每次迭代10 000步，最后取平均值作为输出。SGD算法的计算方式为式(2)，其中步长 ${\alpha _t} = {1 /\!\! {\sqrt t }}$ 。Heavy-ball型动量法的计算方式及步长选取同文献[11]。NAG型动量法的计算方式及步长选取同文献[10]。根据文献[15]，平均形式输出的Adam算法步长 $ {\alpha }_{t}=0.1/ \sqrt{t}，{\beta }_{1}= $ $ 0.9,\;{\beta }_{2}=0.99$ 。个体形式输出的Adam算法步长设置与迭代次数有关，其中 $ {\alpha }_{t}=0.1/\sqrt{t}，{\beta }_{2}=0.99$ 。本次实验我们调用SLEP工具箱来实现投影计算，集合 $Q$ 为 ${l_1}$ 范数球 $\left\{ {{{w}}:{{\left\| {{w}} \right\|}_1} < z} \right\}$ ，根据数据集的不同， $z$ 的取值也会有相应变化。

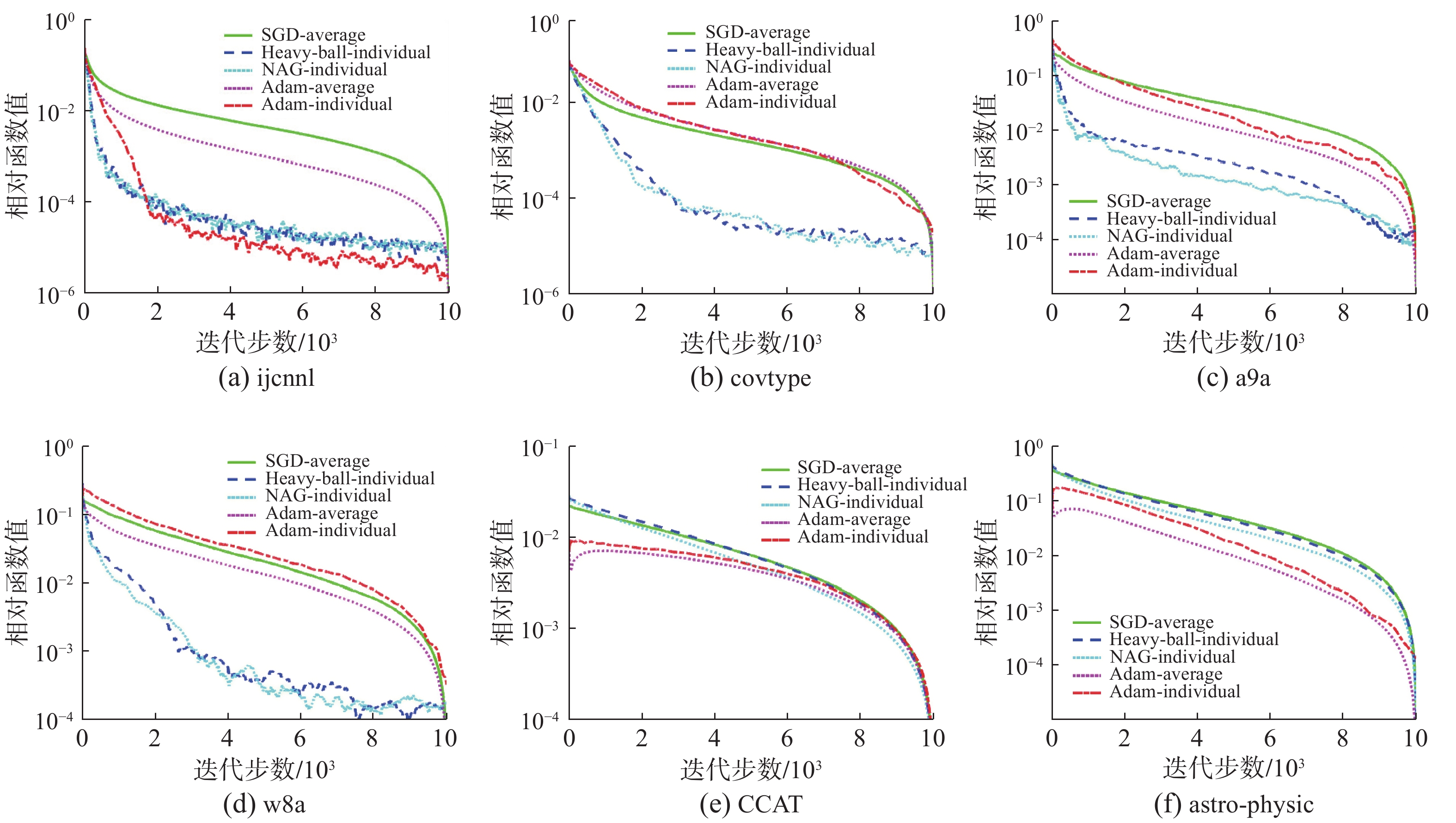
图1为5种算法的收敛速率对比图，纵坐标表示当前目标函数值与最优目标函数值之差。其中绿色、蓝色、青色、粉色、红色分别代表平均形式输出的SGD算法、个体形式输出的Heavy-ball型动量法、个体形式输出的NAG型动量法、平均形式输出的Adam算法、个体形式输出的Adam算法。可以看到，在5000步迭代之后，5种算法在6个标准数据集上都达到了 ${10^{ - 2}}$ 的精度，在迭代10000步后，5种算法在6个标准数据集上都达到了 ${10^{ - 4}}$ 的精度。5种算法的收敛趋势基本相同，这与理论分析基本吻合。

图2为5种算法的稀疏性对比，纵坐标表示各算法对应输出的稀疏度，稀疏度越低，变量中非零向量所占比例越小。可以看到，个体形式输出的Heavy-ball型动量法、NAG型动量法和Adam算法明显比平均形式输出的SGD算法和Adam算法拥有更低的稀疏度，同时，数据集越稀疏，算法获得的稀疏度也越低。这一结论充分说明，个体解输出比平均解输出能更好地描述样本的稀疏性。同时我们观察到在稀疏度一般的前4个数据集上有震荡的现象，这是算法的随机性导致的，在维度较大、稀疏度较低的后两个数据集上该震荡现象消失。

4 结束语

本文对非光滑条件下Adam算法的收敛性进行了初步的研究，证明了Adam算法可以获得最优的个体收敛速率。本文的结论表明，在最坏情况下Adam算法的个体收敛速率和Heavy-ball型动量法的个体收敛速率类似。但Adam算法保留了AdaGrad算法的优点，个体收敛速率界比Heavy-ball型动量法更紧。下一步将继续研究强凸情况下Adam算法最优的个体收敛速率问题以及基于NAG型动量的Adam算法的最优个体收敛速率问题。