2. 高端装备先进感知与智能控制教育部重点实验室,安徽 芜湖 241000;
3. 安徽工程大学 安徽省电气传动与控制重点实验室,安徽 芜湖 241000
2. Key Laboratory of Advanced Perception and Intelligent Control of High-End Equipment, Ministry of Education, Wuhu 241000, China;
3. Anhui Provincial Key Laboratory of Electric Transmission and Control, Anhui Polytechnic University, Wuhu 241000, China
在移动机器人领域,路径规划技术一直都是重要研究内容,其任务是在地图环境中为移动机器人从起点至终点避开障碍物而规划出的最优路径。目前国内外学者针对路径规划技术做了诸多研究,并取得相应成果,常用的传统路径规划算法有遗传算法、模拟退火算法、人工势场法、A*算法[1]等。随着人工智能技术的高速发展,群智能算法在路径规划技术中得到广泛应用和发展,如人工鱼群算法、蜂群算法、蚁群算法[2-4]、蛙跳算法等,人工鱼群算法是一种擅长随机搜索的算法,其算法原理简单,对初始值要求较低,但在算法后期存在收敛速率缓慢、计算结果不够精确。蜂群算法作为模仿蜜蜂行为提出的启发式算法,通过对单一的蜜蜂进行局部寻优,突出全局最优值,容易陷入局部最优,其算法鲁棒性不强。传统的群智能算法已经无法满足移动机器人在复杂环境下进行路径规划,因此,大量学者通过对传统的群智能算法进行改进,如多策略人工鱼群算法[5-7]、双层蚁群算法[8]、启发机制下的蚁群算法[9]等。改进的群智能算法已经明显提高复杂环境下移动机器人的路径规划[10-15]能力。
蚁群算法作为启发式全局优化算法是由意大利学者Dorigo在1992年提出,该算法得益于采用正反馈机制,收敛性能大幅提升,通过分布式计算方式进行搜索以及不同个体同时并行计算,提高了该算法的运算效率以及计算能力,但仍存在收敛速度慢以及死锁问题。因此,文献[9]对蚁群算法进行改进,提出了基于启发式机制的蚁群算法,该算法通过当前节点到终点的距离动态的调整启发函数,当算法处于局部最优时,引入惩罚函数机制,降低最优路径的信息素,减少蚁群算法的正反馈影响而跳出局部最优。文献[14]主要针对于蚁群算法收敛速度慢进行改进,合理分配信息素初始浓度,动态调整信息素挥发因子,进行二次路径规划,有效缩短了移动机器人的路径长度。文献[8]设计了双层蚁群算法,对移动机器人二维栅格环境进行凸化处理,同时用外层蚁群探索出一条路径作为一个小环境,内层蚁群在该环境下重新探索,两条路径择优筛选,提高蚁群算法路径搜索质量。
为了提高蚁群算法收敛速度以及缩短路径长度,本文提出变步长蚁群算法,寻找移动机器人可以达到的跳点,得到不同长度的路径,根据路径长度的不同,不均匀分配初始信息素浓度,以降低边缘障碍物对移动机器人的影响,从而提高算法的计算能力。改进启发式信息矩阵,提高蚁群避障能力,增强蚁群全局路径搜索能力,快速找到最优路径。
1 蚁群算法原理 1.1 环境表示移动机器人需要在二维空间环境下进行路径规划,因此,需要对移动机器人工作环境进行建模,常规环境建模方法如栅格图法[16-18]、可视图空间法、自由空间法、几何信息法等。本文选取栅格图法对移动机器人二维空间进行建模,将栅格分为黑色区域和白色区域,其中黑色区域为障碍物栅格,白色区域为自由栅格,机器人可以在白色区域自由移动,如图1所示,假设每个栅格为边长为1 m的正方形,不考虑机器人自身身高和体积的影响,机器人始终处于正方形的正中心位置。

|
Download:
|
| 图 1 栅格地图 Fig. 1 Raster map | |
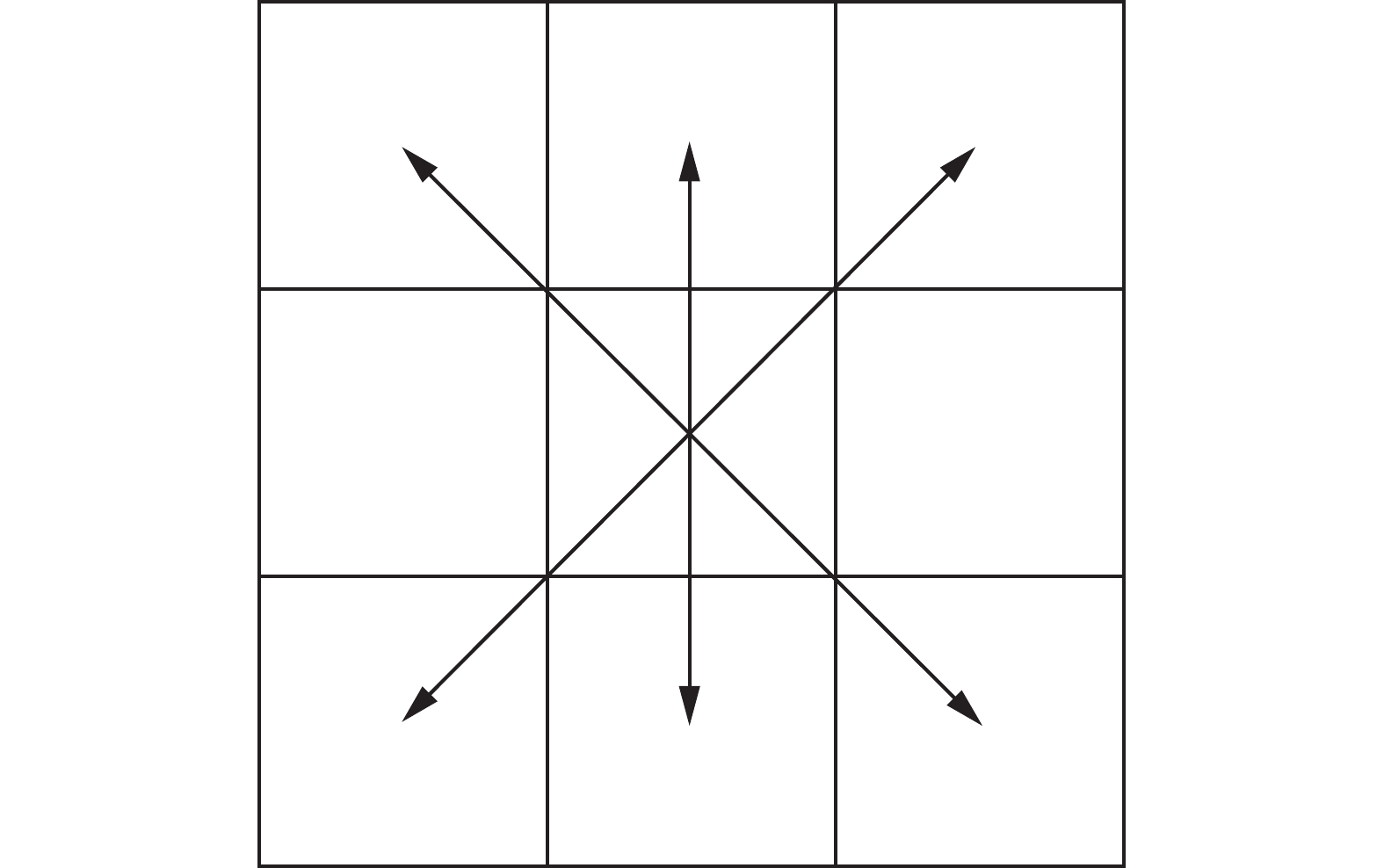
传统蚁群算法中蚁群为单步长[19-20]移动方式,每步移动距离为1或
|
Download:
|
| 图 2 移动方式 Fig. 2 Moving method | |
蚁群在寻路过程中,利用信息素相互通信,在经过的路径上释放信息素,当某一条路径通过的蚂蚁越来越多时,该路径的信息素浓度就越高,其他蚂蚁选择该路径的概率就越大,起到正反馈作用,同时也容易陷入局部最优及存在死锁现象。信息素会随着时间的增长而挥发,动态的调整各路径的信息素浓度,蚂蚁在选择路径时,会对信息素浓度、启发因子、路径方向等因素进行综合判断选择下一步移动位置,并利用轮盘算法计算当前节点到下一到达节点的概率:
| $p_{ij}^k(t) = \left\{ {\begin{array}{*{20}{l}} {\dfrac{{{{[{\tau _{ij}}(t)]}^\alpha } \cdot {{[{\eta _{ij}}(t)]}^\beta }}}{{\displaystyle\sum \limits_{s \in {a_{_k}}} {{[{\tau _{is}}(t)]}^\alpha } \cdot {{[{\eta _{{\rm{is}}}}(t)]}^\beta }}},}\quad{j \in {a_k}}\\ {0,}\quad{\text{其他}} \end{array}} \right.$ | (1) |
| ${\eta _{ij}} = \frac{1}{{{d_{ij}}}}$ | (2) |
式中:
为了避免蚂蚁选择已经达到过的节点,采用禁忌表记录蚂蚁
| ${\tau _{ij}} = (1 - \rho ){\tau _{ij}}$ | (3) |
式中:
| ${\tau _{ij}} = {\tau _{ij}} + \sum\limits_{k = 1}^m {\Delta \tau _{ij}^k} $ | (4) |
式中:
| $\Delta \tau _{ij}^k = \left\{ {\begin{array}{*{20}{l}} {1/{d_{ij}},}\quad{{\text{边}}(i,j){\text{在路径}}{T^{{k}}}{\text{上}}}\\ {{\rm{0,}}}\quad{\text{其他}} \end{array}} \right.$ | (5) |
由式(5)可知,蚂蚁所构建的路径长度
传统蚁群算法步长选择为单步长,蚁群仅能向相邻栅格位置移动,不能满足移动机器人实际需求,且搜索效率低及路径长度无法满足最优,因此,本文提出变步长选择策略,在避开障碍物的条件下,移动机器人可以从当前位置向全局地图的任何位置移动,大幅提高移动机器人搜索效率。
2.1 步长选择策略跳点的选择即步长的选择,所谓跳点就是移动机器人在搜索过程中从当前节点可以到达下一步的节点。如图3所示。移动机器人从起点到终点有4条路径可供选择,方案1为当前节点1跳跃至节点2再到终点3,节点1到节点2步长为3.16 m,节点2至节点3路径长度为2 m,因此,方案1路径总长度为5.16 m,方案2为节点1变步长跳跃至节点4再到节点5,最后由节点5单步移动至终点3,方案2路径总长度为4.65 m,方案3为传统蚁群算法的单步长移动方式,从当前节点1到节点6,再移动到节点7,再移动到节点8,最后再到终点3,该方案路径总长度为4.83 m,方案4为节点1跳跃至节点9,从节点9单步长移动到节点8,最后移动到终点3,该方案路径总长度为5.16 m,显然,方案2作为变步长移动方式优于其他方案,变步长蚁群算法在寻路过程中,对每种方案的路径长度进行评估,最终挑选出路径最短的方案。

|
Download:
|
| 图 3 步长选择 Fig. 3 Step size selection | |
在图3中,节点1为起始点,节点3为终点,移动机器人进行路径规划时,将节点1作为父节点,通过变步长选择策略,将下一步移动机器人要到达的节点4作为子节点,再将节点4作为父节点确定下一子节点,以此方法进行迭代,最终确定了本轮迭代后的最优路径{1,4,5,3},结合变步长蚁群算法的优点,移动机器人对于下一步所选择的节点越接近于终点,则可以减少节点转折的次数,同时,转折点越接近于障碍物,则可以减少无效路径,因此,为了缩短移动机器人路径长度,引入终点诱导因子
| $p_{ij}^k(t) = \left\{ {\begin{array}{*{20}{l}} {k \cdot \phi \cdot \mu \cdot \dfrac{{{{[{\tau _{ij}}(t)]}^\alpha } \cdot {{[{\eta _{ij}}(t)]}^\beta }}}{{\displaystyle\sum\limits_{s \in {a_k}} {{{[{\tau _{is}}(t)]}^\alpha }{{[{\eta _{is}}(t)]}^\beta }} }},}\quad{j \in {a_k}}\\ {{\rm{0,}}}\quad{\text{其他}} \end{array}} \right.$ | (6) |
| $\phi {\rm{ = }}\dfrac{{\displaystyle\sum\limits_{{{s}} \in {a_k}} {{{[{\gamma _{is}}(t)]}^\varepsilon }} }}{{{\sigma ^\varepsilon }}}$ | (7) |
| $\mu = \dfrac{{\displaystyle\sum\limits_{s \in {a_k}} {{{[{\gamma _{is}}(t)]}^\omega }} }}{{{\lambda ^\omega }}}$ | (8) |
式中:
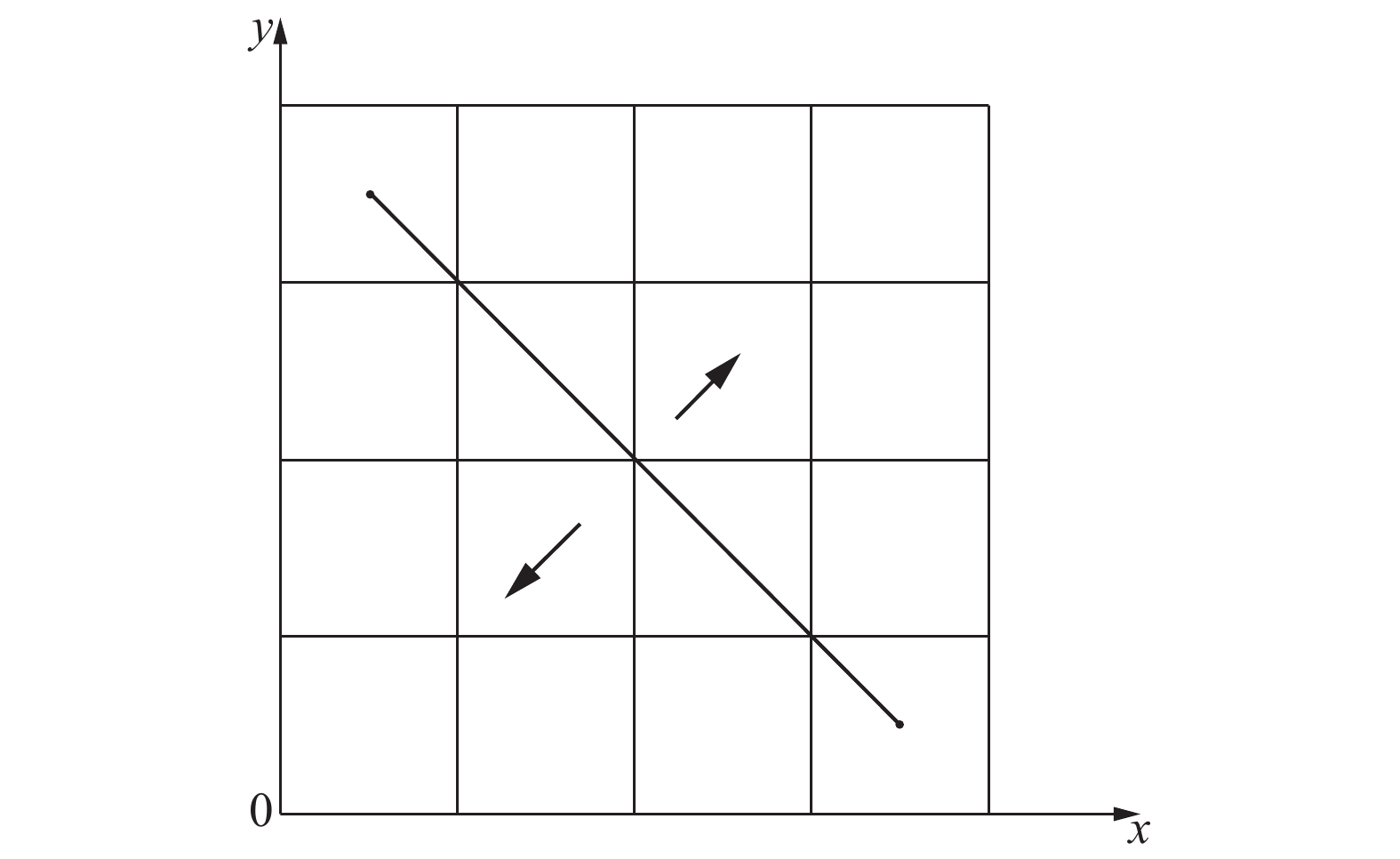
在移动机器人路径规划之前,需要给栅格地图环境的信息素进行初始化,初始化信息素采用不均匀分布,障碍物栅格的信息素设置为0,加强起点至终点直线所涉及到栅格的信息素浓度,平行的向外衰减,将栅格地图建立直角坐标系,如图4所示。
|
Download:
|
| 图 4 信息素分布策略 Fig. 4 Pheromone distribution strategy | |
连接移动机器人的起始点及终点,则该直线方程为
| $y = - x + C,\quad C \in {N^ * }$ | (9) |
在本文中,C取值为20或30,分别对应简单栅格环境和复杂栅格环境,令
| ${\tau _0} = \left\{ {\begin{array}{*{20}{l}} {T,}\quad{y = - x + C}\\ {\dfrac{{C - 1}}{C} \cdot T,}\quad{y = - x + C \pm 1}\\ {\dfrac{{C - 2}}{C} \cdot T,}\quad{y = - x + C \pm 2}\\ \cdots &{}\\ {\dfrac{1}{C} \cdot T,}\quad{y = - x + 1{\text{或}}y = - x + 2C - 1} \end{array}} \right.$ | (10) |
式中:
为了防止某条路径的信息素过高或过低,避免蚂蚁集中在某条路径上,将每条路径的信息素设置上下限为
| ${\tau _{ij}}(t + 1) = (1 - \rho ) \cdot {\tau _{ij}}(t) + \Delta \tau _{_{ij}}^{{\rm{best}}}(t),\quad\rho \in (0,1)$ | (11) |
| $\Delta \tau _{ij}^{{\rm{best}}} = \left\{ {\begin{array}{*{20}{l}} {\dfrac{1}{{{L^{{\rm{best}}}}}},}\quad{{\text{边}}(i,j){\text{包含在最优路径内}}}\\ {{\rm{0}},}\quad{\text{其他}} \end{array}} \right.$ | (12) |
为了提高搜索效率,一只蚂蚁在一轮迭代中走过的完整路径将不被以后的蚂蚁所选择,对于需要更新信息素的路径,可以是本轮迭代的最优解,也可以是全局最优解。
2.3 改进启发函数结合变步长蚁群算法的优点,在直角坐标系中,利用蚁群下一步到达的节点距离起点至终点连线的长短,对启发函数进行改进,传统蚁群算法的启发函数为蚁群下一步所选择的节点到终点之间距离的倒数,如式(2)所示,该函数收敛性不强,且容易使蚁群寻优路径冗长,改进后的启发函数如下:
| ${\eta _{{{ij}}}} = \frac{1}{{{d_{ij}}}} \cdot \frac{{\sqrt 2 }}{{|{x_i} + {y_j} - C|}}$ | (13) |
式中,
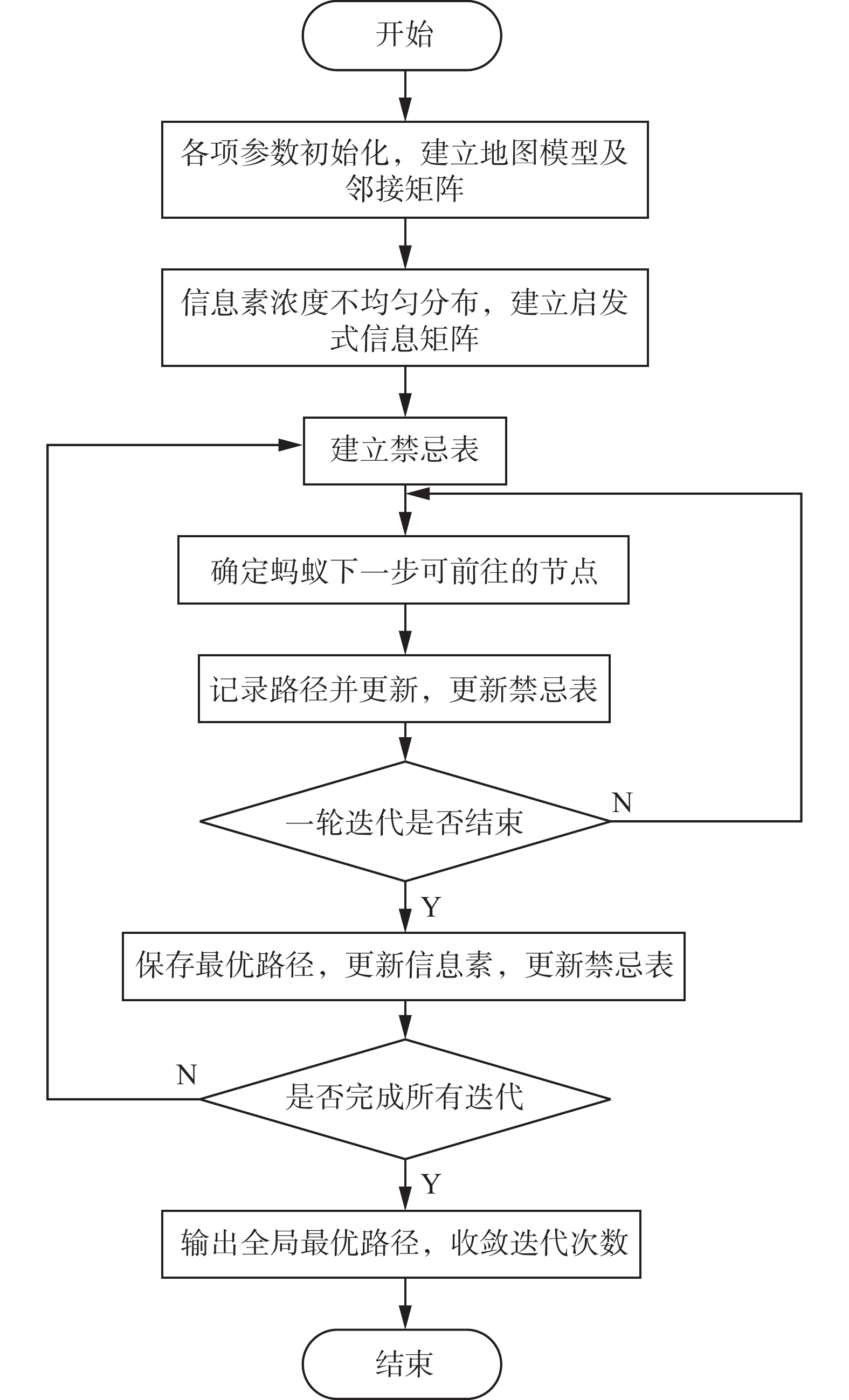
图5为变步长蚁群算法的流程图,算法的具体步骤如下:
1) 针对各项相关参数进行初始化:路径规划的起始点及终点、信息素重要程度参数
2) 初始化信息素采用不均匀分布,加强起点至终点直线所涉及栅格的信息素浓度,平行的向外衰减;改进启发式信息矩阵,调整移动机器人当前位置到终点位置的启发函数计算方法,建立启发式信息矩阵。
3) 建立禁忌表以及对禁忌表初始化,将起点、障碍物节点、引起死锁的节点均加入禁忌表中。
4) 计算启发信息,根据信息素浓度以及概率公式确定蚂蚁下一步可以到达的节点,记录路径并更新,更新禁忌表。
5) 当所有蚂蚁完成一次迭代后,保存最优路径,更新信息素及禁忌表,如果没有完成一次迭代,则继续开始下一只蚂蚁路径寻优。
6) 如果蚂蚁完成所有迭代次数,则输出最优路径及收敛迭代次数,如果没有完成所有迭代次数,则继续开始下一次迭代。
|
Download:
|
| 图 5 变步长蚁群算法流程 Fig. 5 Flow chart of variable step size ant colony algorithm | |
为了验证变步长蚁群算法的有效性,本文分别在简易环境和复杂环境下进行仿真对比,简易环境为
在

|
Download:
|
| 图 6 传统蚁群算法路径规划(20×20) Fig. 6 Path planning of traditional ant colony algorithm | |

|
Download:
|
| 图 7 本文算法路径规划(20×20) Fig. 7 Algorithm path planning in this paper | |
| 表 1 各算法实验结果对比 Tab.1 Comparison of experimental results of various algorithms |
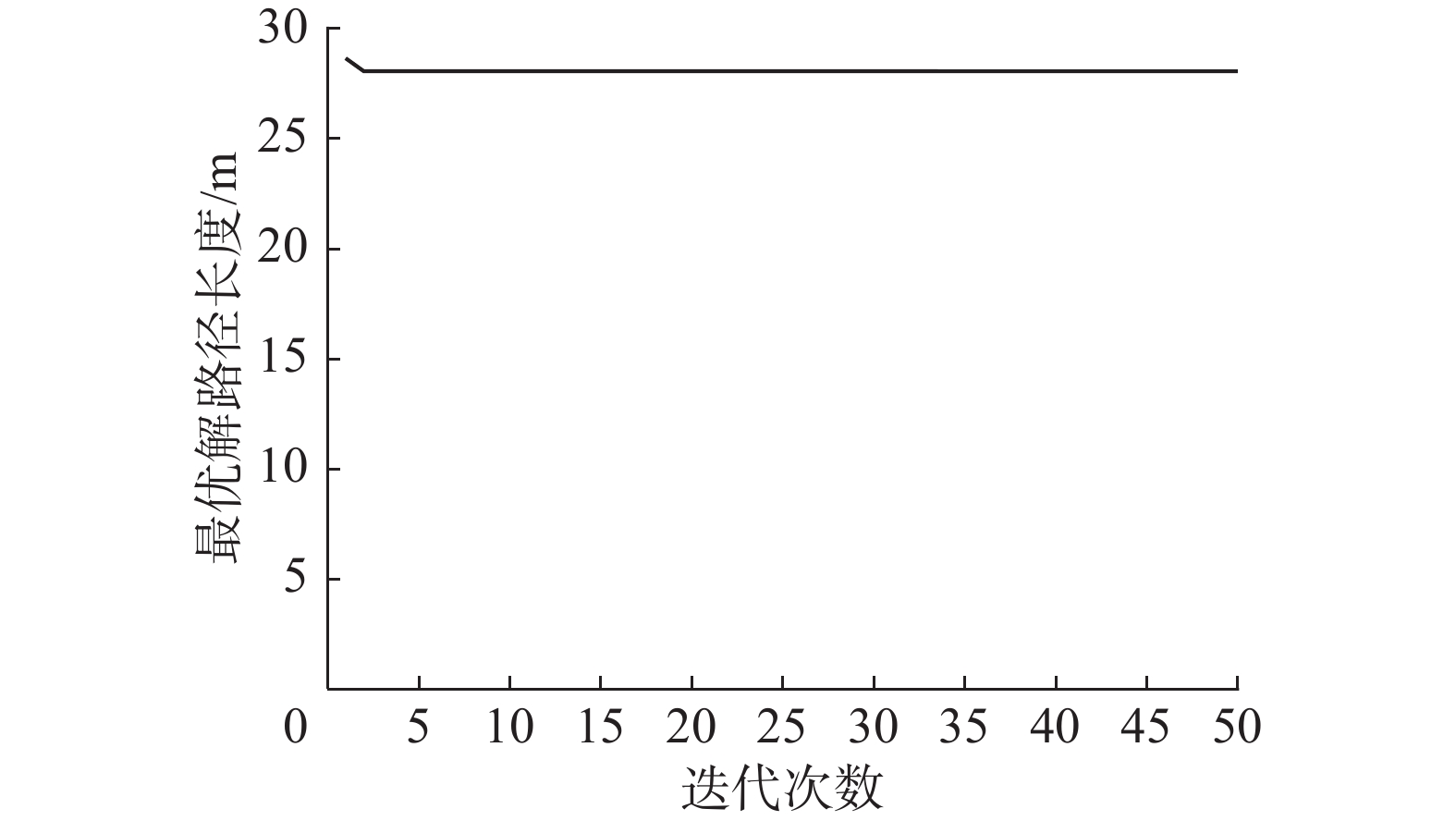
收敛迭代仿真分别如图8、9所示,传统蚁群算法收敛迭代次数为25次,文献[8]算法收敛迭代次数为4次,本文算法收敛迭代次数为2次,显然,本文算法在收敛速度方面优于文献[8]算法及传统蚁群算法,本文算法较文献[8]算法、传统蚁群算法的收敛迭代次数分别减少了50%及92%。图10为本文算法在该环境下各代蚂蚁最优路径规划路线,各代路线集中于起点至终点的连线处,表明信息素不均匀分布的有效作用,在

|
Download:
|
| 图 8 传统蚁群算法收敛曲线 Fig. 8 Convergence curve of traditional ant colony algorithm | |
|
Download:
|
| 图 9 本文算法收敛曲线 Fig. 9 Convergence curve of the algorithm presented in this paper | |

|
Download:
|
| 图 10 本文算法各代蚁群最优路径规划(20×20) Fig. 10 Optimal path planning of each generation of ant colony in this algorithm (20×20) | |
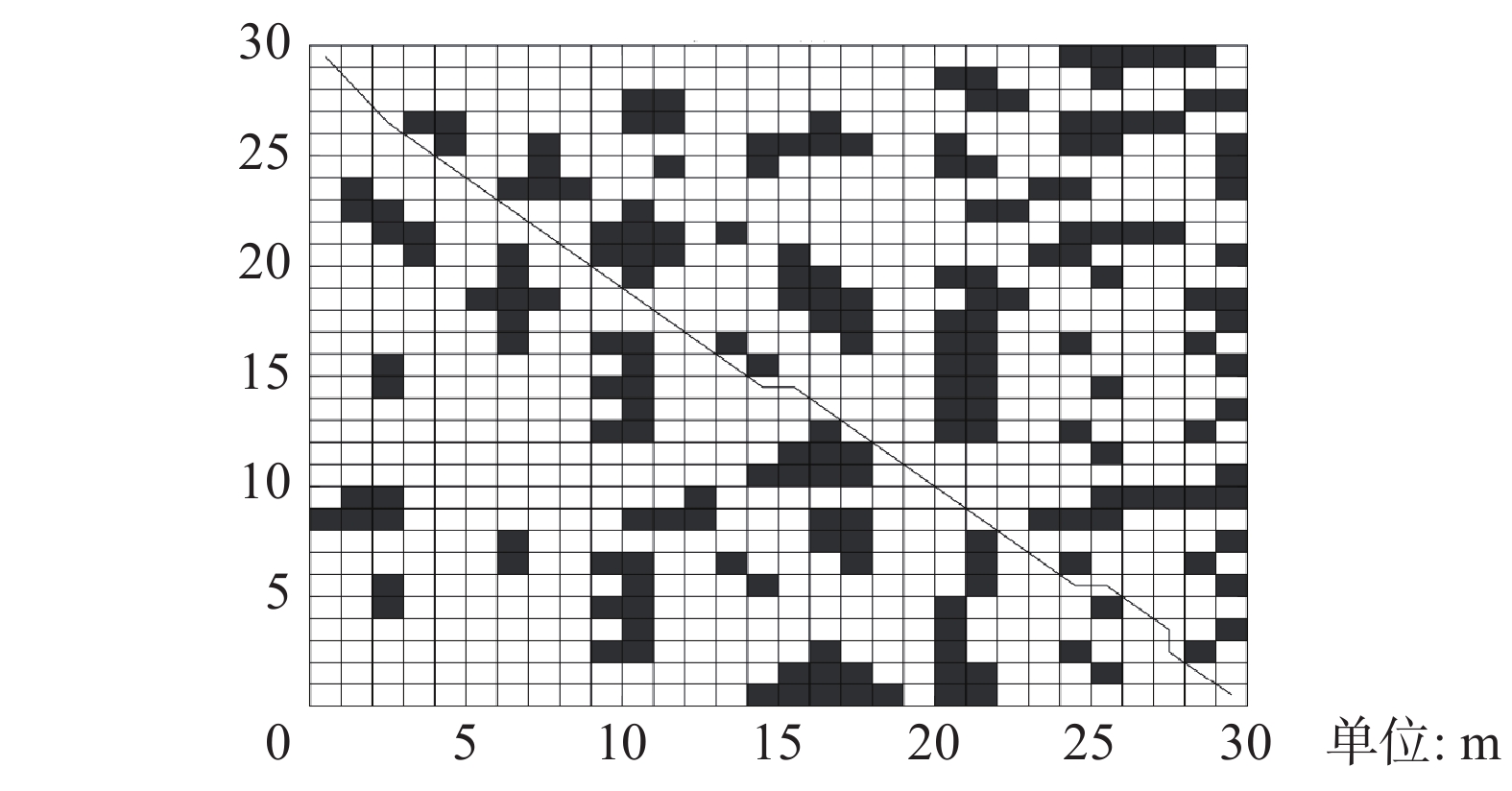
在
| 表 2 两种算法实验结果对比 Tab.2 Comparison of experimental results of various algorithms |
|
Download:
|
| 图 11 本文算法路径规划(30×30) Fig. 11 Algorithm path planning in this paper (30×30) | |
|
Download:
|
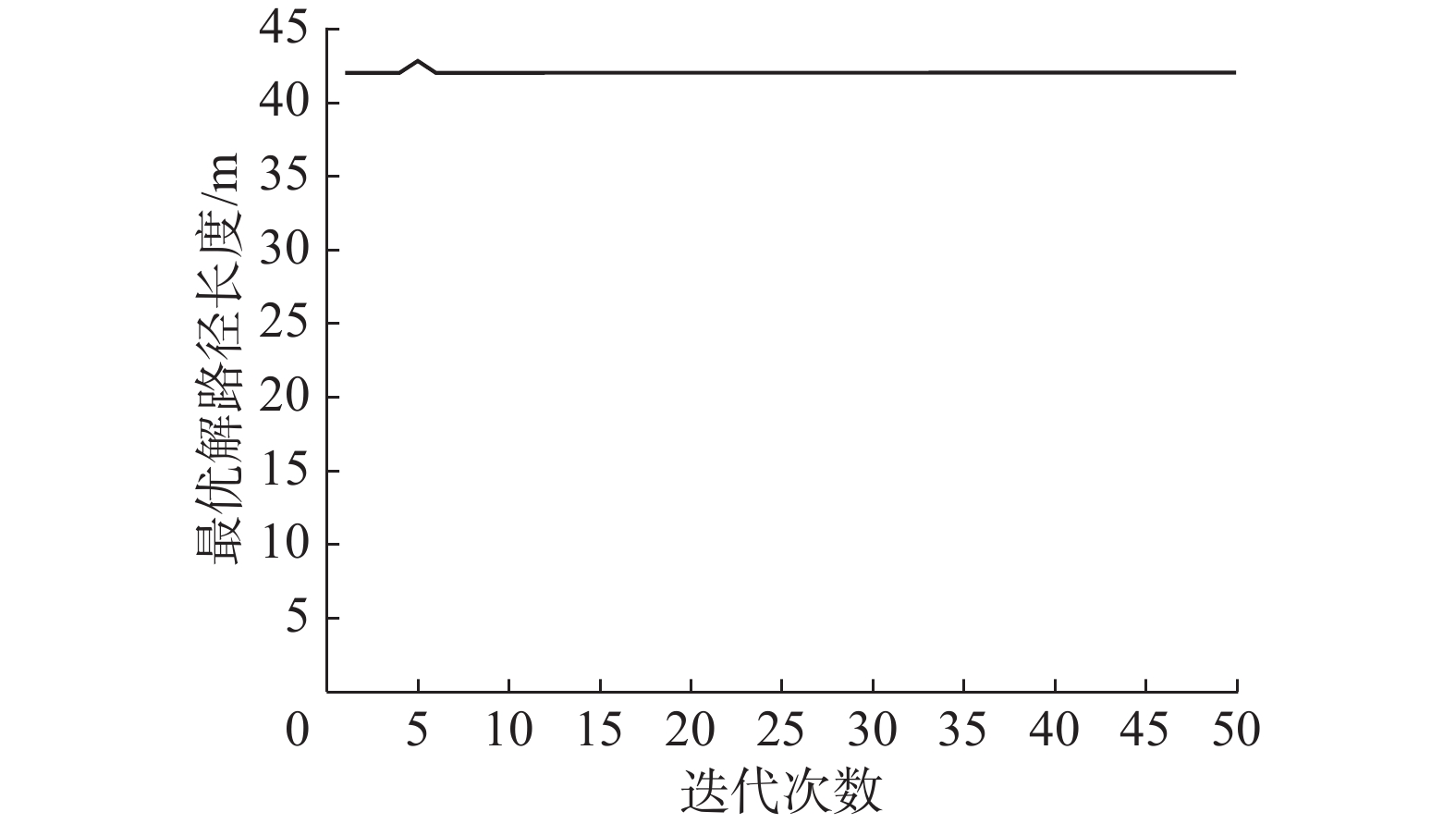
| 图 12 本文算法收敛曲线(30×30) Fig. 12 Convergence curve of the algorithm presented in this paper (30×30) | |

|
Download:
|
| 图 13 本文算法各代蚁群最优路径规划(30×30) Fig. 13 Optimal path planning of each generation of ant colony in this algorithm (30×30) | |
本文采用自主搭建的移动机器人进行实验验证,如图14及图15所示,一个纸箱代表两个正方形障碍物栅格,空白场地为自由栅格,实验场景为

|
Download:
|
| 图 14 移动机器人起点位置 Fig. 14 Starting position of mobile robot | |

|
Download:
|
| 图 15 移动机器人运行过程 Fig. 15 Mobile robot running process | |
| 表 3 各算法路径规划实验数据 Tab.3 Experimental data of path planning for each algorithm |
传统蚁群算法在移动机器人路径规划中存在搜索效率低、路径过长、收敛较慢等问题,本文在传统蚁群算法的基础上引入了变步长策略对其进行改进,扩充蚁群可以到达节点的集合,在不触碰障碍物的条件下,从蚁群当前位置的相邻位置扩大至全局地图的任意自由栅格位置,达到变步长策略,改进信息素分布策略以及调整启发函数计算方法,大幅提高本文算法的收敛速度,快速地寻找到最优路径。本文基于变步长蚁群算法在收敛速度和路径寻优方面有着较好的性能,不仅适用于简单栅格环境,也适用于复杂的栅格环境,使本文算法在实际应用场景中得到较好的应用,通过对整个地图状态空间的探索点进行采样,能够增加搜索区域,适合解决移动机器人在复杂环境下的路径规划。
| [1] |
CONFESSORE G, FABIANO M, LIOTTA G. A network flow based heuristic approach for optimising AGV movements[J]. Journal of intelligent manufacturing, 2013, 24(2): 405-419. DOI:10.1007/s10845-011-0612-7 ( 0) 0)
|
| [2] |
张毅, 权浩, 文家富. 基于独狼蚁群混合算法的移动机器人路径规划[J]. 华中科技大学学报(自然科学版), 2020, 48(1): 127-132. ZHANG Yi, QUAN Hai, WEN Jiafu. Mobile robot path planning based on the wolf ant colony hybrid algorithm[J]. Journal of Huazhong University of Science and Technology (Nature Science Edition), 2020, 48(1): 127-132. (  0) 0)
|
| [3] |
刘可, 李可, 宿磊, 等. 基于蚁群算法与参数迁移的机器人三维路径规划方法[J]. 农业机械学报, 2020, 51(1): 29-36. LIU Ke, LI Ke, SU Lei, et al. Robot 3D path planning method based on ant colony algorithm and parameter transfer[J]. Transactions of the Chinese society for agricultural machinery, 2020, 51(1): 29-36. (  0) 0)
|
| [4] |
ZHOU Zhiping, NIE Yunfeng, GAO Min. Enhanced ant colony optimization algorithm for global path planning of mobile robots[C]//Proceedings of 2013 International Conference on Computational and Information Sciences. Shiyang, China, 2013: 698−701.
( 0) 0)
|
| [5] |
HE Qiang, HU Xiangtao, REN Hong, et al. A novel artificial fish swarm algorithm for solving large-scale reliability-redundancy application problem[J]. ISA transactions, 2015, 59: 105-113. DOI:10.1016/j.isatra.2015.09.015 ( 0) 0)
|
| [6] |
WU Tao, JING Xiaojun. Exploration of multiple access interference suppression based on multi-user detection[J]. Chinese journal of electronics, 2019, 28(4): 835-840. DOI:10.1049/cje.2019.05.011 ( 0) 0)
|
| [7] |
陈军章. 改进人工鱼群算法的机器人路径规划及跟踪[J]. 机械设计与制造, 2019(04): 251-255. CHEN Junzhang. Mobile Robot Path Planning and Tracking Based on Improved Artificial Fish Swarm Algorithm[J]. Machinery Design & Manufacture, 2019(04): 251-255. DOI:10.3969/j.issn.1001-3997.2019.04.062 (  0) 0)
|
| [8] |
许凯波, 鲁海燕, 黄洋, 等. 基于双层蚁群算法和动态环境的机器人路径规划方法[J]. 电子学报, 2019, 47(10): 2166-2176. XU Kaibo, LU Haiyan, HUANG Yang, et al. Robot path planning based on double-layer ant colony optimization algorithm and dynamic environment[J]. Acta electronica sinica, 2019, 47(10): 2166-2176. DOI:10.3969/j.issn.0372-2112.2019.10.019 (  0) 0)
|
| [9] |
朱艳, 游晓明, 刘升. 基于启发式机制的改进蚁群算法[J]. 信息与控制, 2019, 48(3): 265-271. ZHU Yan, YOU Xiaoming, LIU Sheng. Improved ant colony algorithm based on heuristic mechanism[J]. Information and control, 2019, 48(3): 265-271. (  0) 0)
|
| [10] |
LIU Jianhua, YANG Jianguo, LIU Huaping, et al. An improved ant colony algorithm for robot path planning[J]. Soft computing, 2017, 21(19): 5829-5839. DOI:10.1007/s00500-016-2161-7 ( 0) 0)
|
| [11] |
HWU T, WANG A Y, OROS N, et al. Adaptive robot path planning using a spiking neuron algorithm with axonal delays[J]. IEEE transactions on cognitive and developmental systems, 2018, 10(2): 126-137. DOI:10.1109/TCDS.2017.2655539 ( 0) 0)
|
| [12] |
封声飞, 雷琦, 吴文烈, 等. 自适应蚁群算法的移动机器人路径规划[J]. 计算机工程与应用, 2019, 55(17): 35-43. FENG Shengfei, LEI Qi, WU Wenlie, et al. Mobile robot path planning based on adaptive ant colony algorithm[J]. Computer Engineering and Applications, 2019, 55(17): 35-43. DOI:10.3778/j.issn.1002-8331.1903-0401 (  0) 0)
|
| [13] |
黄琰, 李岩, 俞建成, 等. AUV智能化现状与发展趋势[J]. 机器人, 2020, 42(2): 215-231. HUANG Yan, LI Yan, YU Jiancheng, et al. State-of-the-art and development trends of AUV intelligence[J]. Robot, 2020, 42(2): 215-231. (  0) 0)
|
| [14] |
江明, 王飞, 葛愿, 等. 基于改进蚁群算法的移动机器人路径规划研究[J]. 仪器仪表学报, 2019, 40(2): 113-121. JIANG Ming, WANG Fei, GE Yuan, et al. Research on path planning of mobile robot based on improved ant colony algorithm[J]. Chinese journal of scientific instrument, 2019, 40(2): 113-121. (  0) 0)
|
| [15] |
CAO Jingang. Robot global path planning based on an improved ant colony algorithm[J]. Journal of computer and communications, 2016, 4(2): 11-19. DOI:10.4236/jcc.2016.42002 ( 0) 0)
|
| [16] |
徐玉琼, 娄柯, 李婷婷, 等. 改进自适应蚁群算法的移动机器人路径规划[J]. 电子测量与仪器学报, 2019, 33(10): 89-95. XU Yuqiong, LOU Ke, LI Tingting, et al. Path planning of mobile robot based on improved adaptive ant colony algorithm[J]. Journal of electronic measurement and instrumentation, 2019, 33(10): 89-95. (  0) 0)
|
| [17] |
AJEIL F H, IBRAHEEM I K, AZAR A T, et al. Grid-based mobile robot path planning using aging-based ant colony optimization algorithm in static and dynamic environments[J]. Sensors, 2020, 20(7): 1880. DOI:10.3390/s20071880 ( 0) 0)
|
| [18] |
杨俊成, 李淑霞, 蔡增玉. 路径规划算法的研究与发展[J]. 控制工程, 2017, 24(7): 1473-1480. YANG Juncheng, LI Shuxia, CAI Zengyu. Research and development of path planning algorithm[J]. Control engineering of China, 2017, 24(7): 1473-1480. (  0) 0)
|
| [19] |
王培良, 张婷, 肖英杰. 蚁群元胞优化算法在人群疏散路径规划中的应用[J]. 物理学报, 2020, 69(8): 234-242. WANG Peiliang, ZHANG Ting, XIAO Yingjie. Application research of ant colony cellular optimization algorithm in population evacuation path planning[J]. Acta physica sinica, 2020, 69(8): 234-242. (  0) 0)
|
| [20] |
万方, 周风余, 尹磊, 等. 基于电势场法的移动机器人全局路径规划算法[J]. 机器人, 2019, 41(6): 742-750. WAN Fang, ZHOU Fengyu, YIN Lei, et al. Global path planning algorithm of mobile robot based on electric potential field[J]. Robot, 2019, 41(6): 742-750. (  0) 0)
|
 2021, Vol. 16
2021, Vol. 16


