目标跟踪指通过目标检测或人工标记来确定目标在第一帧中的尺寸、位置，然后利用跟踪算法继续获取下一帧中目标的尺寸、位置，进而预测目标的运动轨迹^[1]。它是计算机视觉领域中重要的研究方向，在视频监控和军事领域等方面应用广泛^[2]。

生成式跟踪法^[3]主要根据目标的外观特征建立复杂跟踪模型，但它忽略了背景信息，当跟踪目标和背景信息较相似时，容易导致跟踪失败，并且该方法计算复杂度较高，实时性相对较差。而判别式跟踪法^[4-5]结合了目标和背景信息来训练分类器，在跟踪过程中通过分类器预测目标运动轨迹，其表现更为鲁棒。

核相关滤波法(kernelized correlation filter, KCF) ^[6]属于判别式跟踪法，其高效的计算能力受到国内外研究者的青睐^[7]。KCF算法将目标样本进行循环移位采集到大量训练样本，通过循环矩阵的性质将时域中的矩阵求逆转化为频域中的点积运算，降低了计算复杂度^[8]，并通过引入核函数将非线性问题转化为线性问题，使得该算法满足大多数实际应用场景的需求。但是KCF算法难以解决运动目标发生形变、尺度变化、遮挡和运动模糊等情况下的跟踪问题。近几年，CN(color name)^[9]、DSST(accurate scale estimation for robust visual tracking)^[10]、SAMF(scale adaptive with multiple features)^[11]、SRDCF (spatially regularized correlation filters)^[12-13]和CFLB (correlation filters with limited boundaries)^[14]等算法相继提出，分别从颜色特征、多尺度变化、特征融合和降低边界效应等方面不断将跟踪法进行优化，来提高算法的跟踪精度。

然而，对模糊图像中的目标进行有效跟踪仍是跟踪领域内的一个难题。为此，本文在KCF算法的基础上引入了尺度不变特征变换描述子 (scale invariant feature transform, SIFT) ^[15]，通过结合局部二值模式 (local binary pattern, LBP) ^[16]算法使得SIFT描述子可从模糊图像中提取到更多的目标特征点，并采用圆形邻域对特征点进行描述以降低特征向量的维度，综合构建出高效模糊特征检测器，并通过OTB-2013^[17]和OTB-2015^[18]数据集对所提算法进行分析与验证。

1 KCF跟踪法 1.1 训练分类器

KCF算法通过循环移位目标样本采集到大量训练样本，( ${{{x}}_i}$ , ${y_i}$ )为第  $i$  个训练样本与其对应的标签。该算法的核心是岭回归，目的是找到一个回归函数  $f({{x}}) = {{w}^{\rm{T}}}{{x}}$ ，通过最小化样本与标签之间的误差平方和，求得权重向量  ${w}$ 。计算方法如下：

$\mathop {\min }\limits_{{w}} \sum\limits_{i = 1}^n {{{(f({x_i}) - {y_i})}^2} + \lambda {{\left\| {w} \right\|}^2}} $

(1)

式中： ${w}$  为分类器权重向量； $\lambda $  是防止过拟合的正则化参数。利用最小二乘法进行求解：

${w}={{({{{X}}^{\text{T}}}{X}+\lambda {I})}^{-1}}{{{X}}^{\text{T}}}{y}$

(2)

式中： ${X}$  表示样本循环矩阵； ${{y}}$  是列向量，每个元素代表一个样本标签； ${I}$  是单位矩阵。

针对非线性问题，将样本  ${{{x}}_i}$  映射到非线性的特征空间  ${{\varphi }}({{{x}}_i})$ ，将权重向量  ${{w}}$  表示为样本的线性组合，即  ${{w}} = \displaystyle\sum\limits_i {{\alpha _i}{{\varphi }}({{{x}}_i})} $ ， ${\alpha _i}$  为第  $i$  个样本的权重系数。

利用核函数  ${{{\varphi }}^{\rm{T}}}({{x}}){{\varphi }}({{x'}}) = k({{x}},{{x'}})$  进行样本间的点积计算，计算结果保存在核循环矩阵  ${K} = $ $ C (k({{x,x'}}))$  中，其元素  ${K_{ij}} = k({{{x}}_i},{{{x}}_j})$ 。求得系数向量  ${\alpha} = {({K} + \lambda {I})^{ - 1}}{y}$ ，利用循环矩阵性质得出系数向量的傅里叶变换形式：

${{\hat \alpha }} = \frac{{{{\hat y}}}}{{{{{{\hat k}}}^{{{xx}}}} + \lambda }}$

(3)

式中： $ \wedge $  表示傅里叶变换域的值； ${{{k}}^{{xx}}}$  为核循环矩阵 ${{K}}$  的第一行元素组成的向量。本文使用的核函数为高斯核，表达式如下所示：

$k({{x,x'}}) = \exp \left( - \frac{{{{\left\| {{x}} \right\|}^2} + {{\left\| {{{x'}}} \right\|}^2} - 2{{\cal F}^{ - 1}}({{{{\hat x}}}^ * } \odot {{\hat x'}})}}{{{\sigma ^2}}}\right)$

(4)

式中： $\sigma $  表示高斯核的带宽； $ \odot $  表示向量间的点乘运算； ${{\cal F}^{ - 1}}$  表示傅里叶逆变换。

1.2 预测目标位置

计算当前图像中所有待检测样本  ${{z}}$  的回归响应值，计算公式为

${{\hat f}}({{z}}) = {{{\hat k}}^{{{xz}}}} \odot {{\hat \alpha }}$

(5)

式中： ${{{k}}^{{{xz}}}}$  表示训练样本 ${{x}}$ 与检测样本 ${{z}}$ 生成的互相关核向量。最大响应值的位置就是当前图像中目标的可能位置。

1.3 参数更新

为了防止模型发生剧烈变化，需不断地更新当前图像中的目标模板 ${\hat x}$ 以及分类器权重向量 ${{\hat \alpha }}$ ，更新的目标模板和权重向量：

${{\hat {{x}}}_{{\rm{update}}}}{\rm{ = (1 - }}\beta {\rm{)}}{{\hat x}_{{\rm{pre}}}} + \beta {\hat x}$

(6)

${{\hat a}_{{\rm{update}}}}{\rm{ = (1 - }}\beta {\rm{)}}{{\hat a}_{{\rm{pre}}}} + \beta {\hat a}$

(7)

式中： $\;\beta $  是更新参数的学习率；下标  ${\rm{pre}}$  和  ${\rm{update}}$  分别表示上一帧和当前图像更新后的参数向量。将训练和检测交替进行，实现目标的持续跟踪。

传统的KCF算法同时结合了目标和背景信息，并且引入了循环矩阵和核函数，算法运行速度快，可以满足实时跟踪的需求。但是该算法在面对模糊图像时，容易出现跟踪失败的现象。本文在KCF算法基础上结合了模糊特征检测器，通过在模糊图像上提取特征点来计算跟踪目标的位置，进一步提高KCF算法的跟踪精确度和成功率。

2 结合模糊特征检测的KCF跟踪法

跟踪过程中，若出现模糊图像，会造成跟踪模板被污染，导致KCF算法跟踪失败。本文在传统KCF算法的基础上，提出一种结合模糊特征检测的鲁棒KCF跟踪法。该算法通过在模糊图像上提取大量特征点并进行特征向量匹配来确定当前图像中跟踪目标的位置，进而提高KCF算法在模糊图像中的精确度和准确率。

2.1 目标特征点检测

SIFT描述子是一种多尺度的局部特征描述算法，对光照变化、视觉变换等具有一定的稳定性。算法主要分为4个部分^[19]：1)在原始图像的基础上，通过高斯滤波形成高斯尺度空间，将相邻高斯图像相减形成高斯差分金字塔，检测图像的局部极值点；2)确定极值点的精确位置并输出稳定的特征点；3)计算特征点邻域像素点的梯度幅值和梯度方向，根据邻域像素点的梯度方向分布，得出梯度直方图，为特征点指定主方向；4)通常在特征点周围构建  $16 \times 16$  像素大小的矩形邻域，并将其划分为  $4 \times 4$  个子区域，在每个子区域中计算8个方向的梯度累加值，形成  $4 \times 4 \times 8 = $ $ 128$  维的特征描述符向量^[20]。

但是，现有的SIFT描述子存在两方面的问题：1)SIFT描述子丢弃了一些边缘上的点和低对比度的点，导致该描述子在边缘光滑或模糊图像中提取的特征点数量较少，或提取的特征点不准确；2)SIFT描述子生成了128维的特征描述符向量，高纬度的特征向量造成该描述子运行时间过长。针对现有SIFT描述子的不足之处，本文通过构建高效模糊特征检测器来提高特征点的数量和精确度。

1)在模糊图像中提取稳定特征点

LBP算法用于提取图像的局部纹理特征，当图像变得模糊时，LBP图像可以保留原始图像的结构信息和空间信息，具有旋转不变性和灰度不变性^[21]。并且该算法参数设置较少，计算公式为

$B({x_0},{y_0}) = \sum\limits_{p = 0}^7 {{2^p}s({v_p} - {v_c})} $

(8)

式中： $B({x_0},{y_0})$  表示特征点的LBP值； ${v_c}$  表示特征点的灰度值； ${v_p}$  表示邻域像素点的灰度值； $s$  为符号函数，且  $s(x) = \left\{ \begin{gathered} 1,\;x \geqslant 0 \\ 0,\,x < 0 \\ \end{gathered} \right.$ 。将LBP算法与SIFT描述子结合，新形成的描述子在LBP图像的差分金字塔中寻找极值点。

2)降低特征描述符向量的维度

跟踪过程中目标可能会发生旋转，为使描述子依旧具有旋转不变性，本文将特征点的矩形邻域改为圆形邻域^[22]，并将特征点邻域像素的梯度幅值根据像素点与特征点的距离进行高斯加权，提高算法的精确度。通过扩大特征点邻域范围，使新形成的圆形描述符在降维的同时满足跟踪过程中所需的目标匹配精度。圆形描述符的具体模型为

${(x - {x_0})^2} + {(y - {y_0})^2} \leqslant {r^2}$

(9)

式中： $({x_0},{y_0})$  为特征点位置； $(x,y)$  为圆形邻域中像素点的位置； $r$  为同心圆区域的半径。

以特征点为圆心，形成  $n$  个同心圆子区域，在每个子区域中计算  $t$  个方向的梯度累加值。然后将每个子区域中计算出的  $t$  维向量进行循环左移，使得梯度方图中的最大值始终为向量的第1个元素，确保描述符向量具有选择不变性。最后将生成的  $n \times t = w$  维描述符向量进行归一化，减少光照变化的影响。

构建的高效模糊特征检测器，可以在模糊图像中提取到大量稳定特征点，并且不需要计算特征点的主方向，同时降低了特征描述符向量的维度，可减少后续特征点匹配的时间。

2.2 目标特征点匹配

从上一帧图像中选出跟踪目标，生成  $k$  个模板特征向量  ${{{m}}_i} = ({m_1},{m_2}, \cdots ,{m_c}, \cdots ,{m_w})$ ，其中  $i \in [1,k], $ $\;\;c \in \left[ {1,w} \right]$  且  $w$  为每个特征向量的维度。并从当前模糊图像中提取  $p$  个待匹配特征向量  ${{{n}}_j}{\rm{ = }}({n_1},{n_2}, \cdots ,{n_c}, \cdots ,{n_w})$ ，其中  ${\kern 1pt} j \in [1,p]\;,c \in \left[ {1,w} \right]$ 。利用公式  ${D_j} = \sum\limits_{c = 1}^w {\left| {{m_c} - {n_c}} \right|} \;\left( {j \in \left( {1,p} \right)} \right)$  分别计算每个模板特征向量与  $p$  个待匹配特征向量之间的绝对距离。若一组特征向量最近邻绝对距离与次近邻绝对距离的比值小于所给阈值，则接着计算两个特征向量之间的余弦相似度，若所得相似度值大于经验阈值，将这两个特征向量视为匹配对；否则，进行下一组特征向量的计算。最后得出当前图像中所有匹配点的重心位置，将此位置视为跟踪目标的中心位置。

2.3 预测目标最终位置

根据所给的视频序列，设置清晰度阈值，若当前图像清晰度高于阈值，则使用传统的KCF算法预测目标位置；若当前图像清晰度低于阈值，则启动模糊特征检测器，通过计算当前图像上所有匹配点的重心位置来得到目标的中心位置，最后标定跟踪目标，进行后续的检测。模糊图像中的目标匹配结果如图1所示。

改进算法的整体流程图如图2所示。

3 实验结果与分析 3.1 实验设置

采用OTB-2013^[17]和OTB-2015^[18]数据集测试本文算法的性能，它们分别含有50和100个标注完整的视频序列。实验中设置目标搜索区域面积为跟踪框的2.5倍，正则化参数0.0001，空间带宽0.1，更新参数的学习率  $\beta $  为0.02，高斯核函数的方差为0.5。低对比度阈值设置为170，主曲率阈值设置为18。经实验分析，圆形邻域最大半径设为9，将特征点圆形邻域分为6个同心圆子区域，梯度方向  $t = 8$ ，绝对距离阈值设为0.6，余弦相似度阈值设为0.95，并且在实验过程中所有参数值固定不变。

实验环境为Intel(R) Core(TM) i5-5200U CPU @2.20 GHz处理器，4 GB运行内存，MATLABR2014a平台。

3.2 定性分析

为了更直观的对比各算法在模糊图像上的跟踪效果，从OTB-2013和OTB-2015数据集中选取了4组代表性的视频序列，分别为Coke、Jogging、Couple和Jump序列，并将所选序列随机地进行模糊化处理。视频序列跟踪结果如图3所示，视频图中的数字表示帧数，绿色框、蓝色框、紫红色框、黑色框和红色框分别代表KCF^[6]、DSST^[10]、SRDCF^[12]、人工标注和本文算法的跟踪框。

实验1：OTB-2015数据集中的Coke序列受到不均匀的光照以及绿色树叶的遮挡。跟踪结果如图3(a)所示：第17帧，视频图像清晰，跟踪目标受到轻微光照的影响，4种算法均能正确跟踪到目标物体。从第68帧到141帧，视频图像变得模糊，导致跟踪目标外观不清晰，KCF算法出现跟踪失败的现象，DSST算法虽然能跟踪到目标，但是跟踪框包含了大量的背景信息，只有本文算法和SRDCF算法可以正确定位到跟踪目标的位置。第281帧，视频图像由模糊变得清晰，本文算法和SRDCF算法依旧可以顺利跟踪到目标，并且不受光照变化的影响，而其余两种算法均跟踪失败。

实验2：OTB-2015数据集中的Jogging序列，跟踪目标与背景较相似，并且在跟踪过程中目标受到较长时间的遮挡。跟踪结果如图3(b)所示：第66帧，视频图像清晰，4种算法均能正确跟踪到目标物体。从第86帧到116帧，跟踪目标受到了连续几帧的模糊和遮挡，本文算法依旧可以正确预测到跟踪目标的位置，而其余3种算法均跟踪失败。

实验3：OTB-2013数据集中的Couple序列受到了光照变化的影响，并且运动速度较快。图3(c)中，第21帧和第89帧的可视化跟踪结果显示：本文算法可以对模糊图像中的目标进行有效跟踪，而SRDCF算法出现跟踪丢失的现象，DSST算法刚开始可以跟踪到目标，之后跟踪模板被污染，同样出现了跟踪失败的现象。直到第125帧，视频图像再次变得清晰，但是此时跟踪目标受到了强烈光照的影响，本文算法可以跟踪到目标，而其余3种算法均出现跟踪丢失的现象。

实验4：选取OTB-2013数据集中的Jump序列。跟踪结果如图3(d)所示：视频图像第20帧和第62帧，跟踪目标外观模糊、发生旋转并且所在背景杂乱，本文算法可通过启动模糊特征检测器，在模糊图像中提取到大量稳定的特征点，从而正确跟踪到目标，而其他3种算法均出现跟踪丢失的现象。

3.3 定量分析

为进一步验证本文所提算法在各视频序列中的跟踪性能，将跟踪精确度和成功率作为算法的评价指标。其中，跟踪精确度定义为预测的目标位置与人工标注的目标位置之间的欧式距离小于所给阈值的帧数占总帧数的比值^[23]；跟踪成功率定义为预测的目标框的面积与人工标注的目标框的面积的重叠率大于给定阈值的帧数占总帧数的比值。采用经典实验数据值，将精确度阈值设为20像素，成功率阈值设为0.5。

1)跟踪序列精确度和成功率分析

4种算法对Coke、Jogging、Couple和Jump序列的跟踪精确度和成功率值如表1~2所示：与其他3种实验算法相比，本文算法的精确度和成功率均为最高或次高值。说明虽然图像模糊导致跟踪目标的边缘信息丢失，但是本文算法可通过模糊特征检测器，从模糊图像中提取出大量特征点，从而跟踪到目标，并且跟踪框包含着大量的目标信息，使得跟踪精度和准确率较高。而KCF算法、DSST算法和SRDCF算法由于不具备抗模糊性，在模糊图像中导致跟踪模板被污染，出现跟踪失败的现象。

2)模糊序列精确度和成功率分析

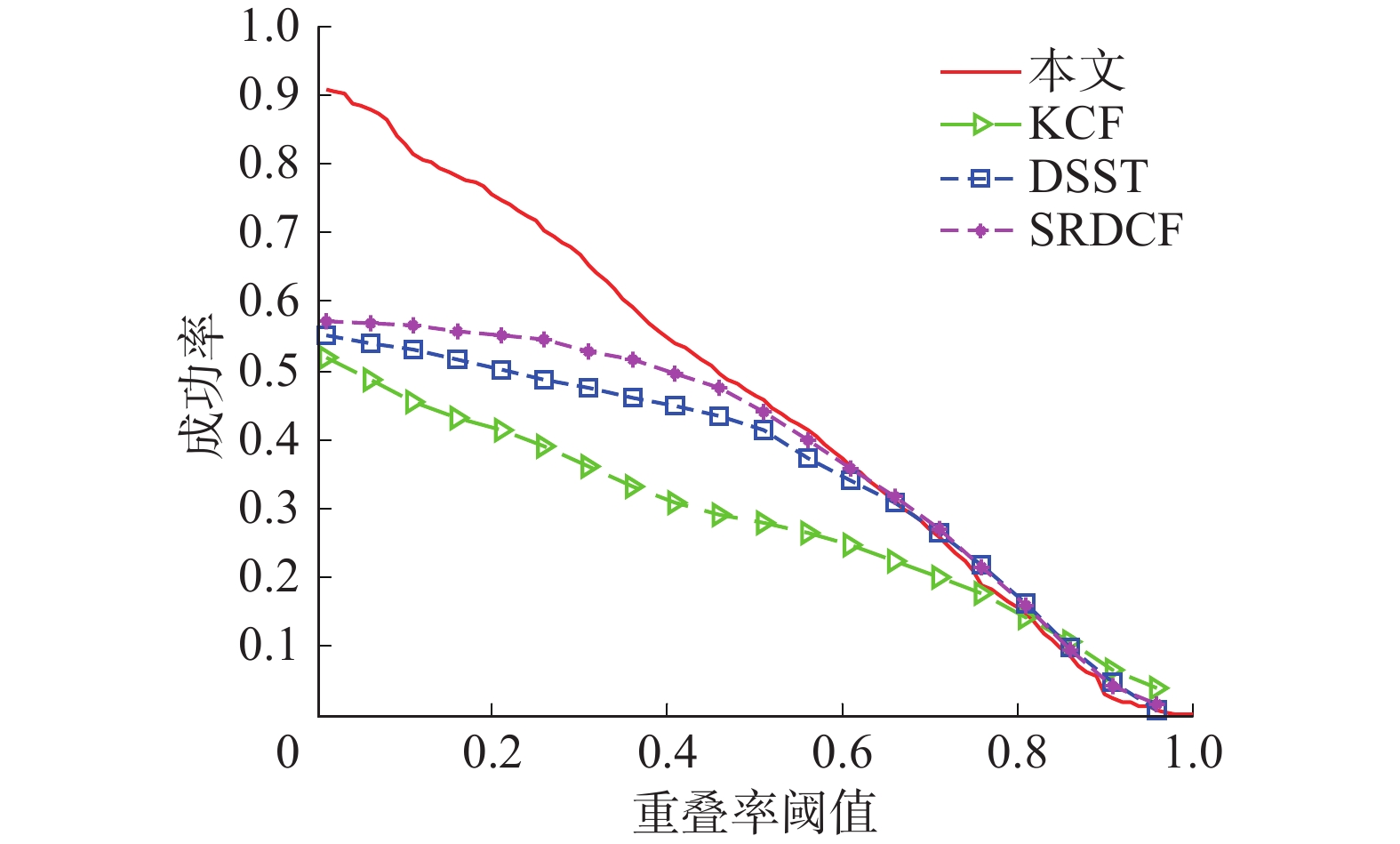
为验证本文算法在其他视频序列上的适用性，从OTB-2015数据集中选取大量不同属性的视频，并将其进行不同程度的模糊化处理。跟踪精确度和成功率曲线如图4~5所示：本文算法的精确度和成功率均居第一。本文算法的精确度为68.2%，在经典KCF算法的基础上提高了18.1%，比次优的SRDCF算法提高了5.7%；本文算法的成功率为49.5%，在经典KCF算法的基础上提高了19.2%，比次优的SRDCF算法提高了2.3%。实验数据说明，本文算法通过启动模糊特征检测器，可以在模糊图像上提取到大量目标特征点，并通过绝对距离和余弦相似度进行目标特征向量匹配，进而成功定位到目标的位置，由此提高了KCF算法在模糊图像上的精确度和成功率。

另外，模糊化处理OTB-2013数据集里的视频序列，并将其用于本文算法的测试中。测试结果表明，与现有的KCF算法相比，本文算法可以对模糊图像中的目标进行有效跟踪，且其精确度较高，从而进一步说明本文算法具有普适性。

4 结束语

对模糊图像中的目标进行有效跟踪是跟踪领域内的一个难点，本文在KCF算法的基础上，提出了一种结合模糊特征检测的鲁棒KCF跟踪法。该算法通过启动模糊特征检测器，可以在模糊图像上提取大量的目标特征点，并将降维后的目标特征向量进行匹配，提高了KCF算法的性能。视频序列可视化跟踪结果显示，本文算法在模糊图像上可以顺利跟踪到目标，且其精确度和成功率均高于对比算法，由此可说明本文算法具有抗模糊性和光照不变性，适用于大部分模糊图像的跟踪场景。但是，与经典的KCF算法相比，本文算法由于引入了LBP算法，在提高精度的同时也增加了计算量，导致跟踪速度较低。下一步研究的目标是在不影响算法精度的情况下进一步提高算法的运行速度。