2. 清华大学 深圳国际研究生院,广东 深圳 518055
2. Shenzhen International Graduate School, Tsinghua University, Shenzhen 518055, China
强化学习(reinforcement learning)是一类智能体在与环境的交互中不断试错来学习最优策略的机器学习方法[1-2],主要用于解决序贯决策问题。在最近五年时间里,AlphaGO[3]、AlphaStar[4]、OpenAIFive[5]分别在围棋、星际争霸II、Dota 2击败了人类最高水平的玩家,强化学习一度成为了人工智能最热门的研究领域之一。AlphaGo的主要作者David Silver认为[6],强化学习与深度学习相结合,是实现通用人工智能(general intelligence)的关键。
在强化学习中,奖励(reward)起到了引导智能体学习方向的作用[7-8],缺乏奖励信息将导致智能体学习缓慢甚至无法学习到最优策略,这就是稀疏奖励问题[9](sparse reward problem)。例如,在蒙特祖玛复仇游戏中,玩家需要依次执行上百个动作才能获得奖励,这使其成为了Atari游戏中最困难的任务之一[10]。此外,在很多实际任务中,不存在现成的奖励值,人为设计的奖励函数又常常陷入局部最优[11],这些问题限制了强化学习的实际应用。稀疏奖励问题的研究能够降低奖励函数的设计难度,提高学习算法的样本利用率,加速策略学习的速度,为强化学习的广泛应用与落地打下理论基础[12]。
本文总结了当前主流的稀疏奖励算法,围绕是否引入外部引导信息,将当下主流的稀疏奖励问题解决思路分为两类,分别介绍了奖励塑造[13](reward shaping)、模仿学习[14](imitation learning)、课程学习[15](curriculum learning)和事后经验回放[11](hindsight experience replay)、好奇心驱动[16](curiosity-driven algorithms)、分层强化学习[17](hierarchical reinforcement learning)等6类算法,并在Mujoco的Fetch Reach环境[18]下进行了实验验证和分析,实验代码开源在以下地址:
当强化学习问题满足马尔可夫性时,就能将其描述为由五元组
|
Download:
|
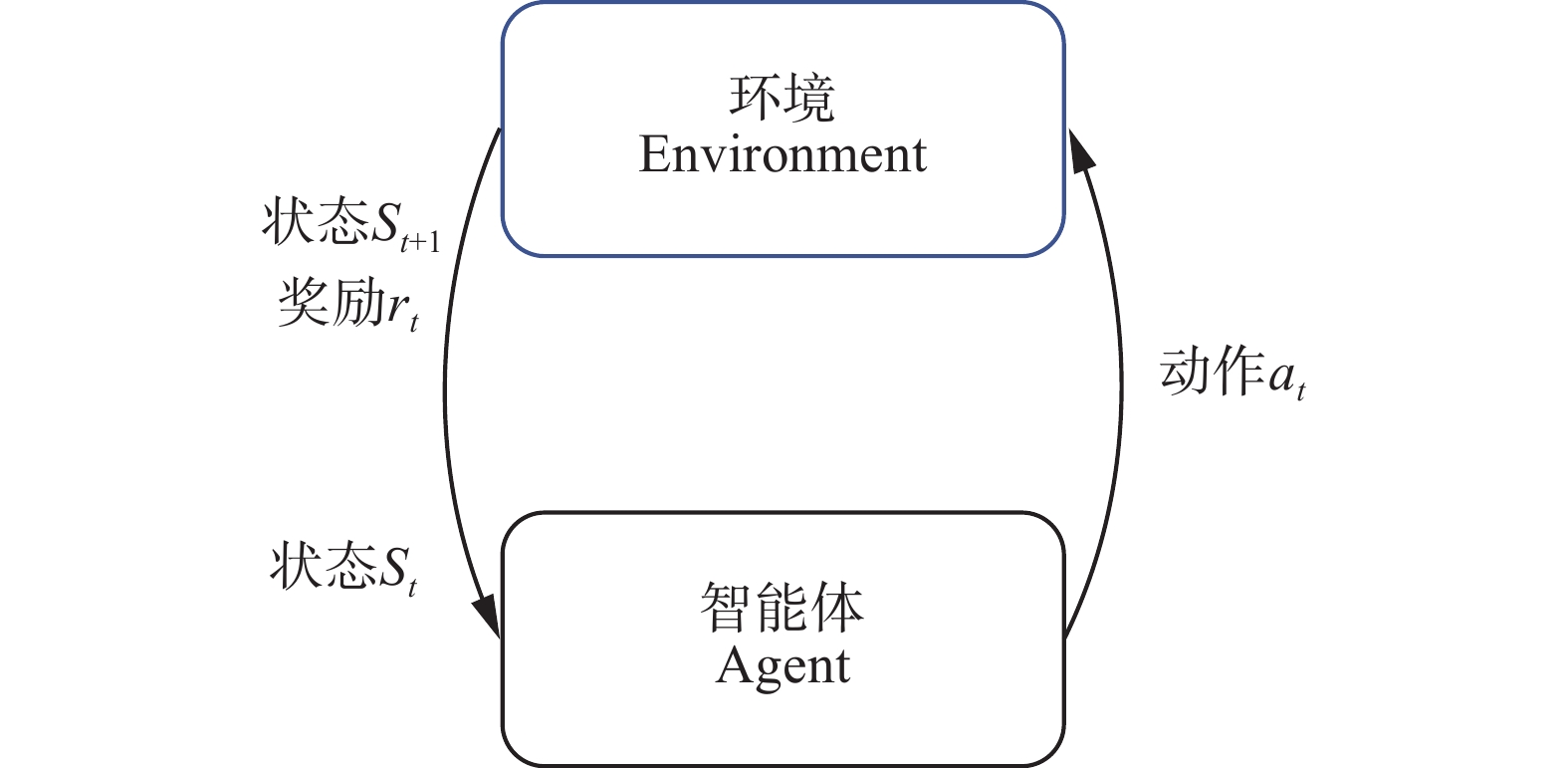
| 图 1 智能体与环境交互示意图 Fig. 1 Schematic of interactions between agent and environment | |
| $ R = \sum\limits_{k = 0}^\infty {\left( {{\gamma ^k}{r_{t + k}}} \right)} . $ | (1) |
为了完成最大化累计折扣奖励值的目标,需要引入策略(policy)和值函数(value function)两个重要概念。策略可以描述为当前状态
| $ \pi \left({a}_{t}|{s}_{t}\right)=P\left({a}_{t}|{s}_{t}\right). $ |
值函数是指从状态
| $V\left( s \right) = E\left[ {\sum\limits_{k = 0}^\infty {\left( {{\gamma ^k}{r_{t + k}}} \right)} |{s_t} = s} \right]$ | (2) |
| $Q\left( {s,a} \right) = E\left[ {\sum\limits_{k = 0}^\infty {\left( {{\gamma ^k}{r_{t + k}}} \right)} |{s_t} = s,\;{a_t} = a} \right]$ | (3) |
深度强化学习与传统强化学习的区别是使用了深度神经网络来拟合值函数、策略或环境动态模型[8]。神经网络的引入提高了强化学习解决大规模复杂问题的能力,在众多领域取得了令人瞩目的成绩[19]。目前的深度强化学习方法可以分为以下3类:基于值函数的方法、基于策略梯度(policy gradient)的方法以及Actor-Critic的方法[7]。3类方法的代表分别是DQN[20-21]、REINFORCE[22]、Actor-Critic[23],从Actor-Critic还衍生出A3C[24]、PPO[25]、DDPG[26]等一系列当前主流的强化学习算法。
基于值函数的方法,以DQN[20-21]为例,用
| ${\rm{loss}} = E\left[ {{{\left( {r + \gamma \mathop {\max }\limits_{a'} Q\left( {s',a',w} \right) - Q\left( {s,a,w} \right)} \right)}^2}} \right]$ | (4) |
根据式(1)、(3)、(4),在奖励值几乎为零的稀疏奖励情况下,值函数的估计
基于策略梯度的方法,以REINFORCE[22]为例,
| $ {\nabla }_{\theta }\pi \left(a|s;\theta \right)={\nabla }_{\theta }{\rm{log}}\pi \left(a|s;\theta \right){R}_{t} $ | (5) |
根据式(1)、(5),在稀疏奖励的条件下,累积奖励值
基于Actor-Critic[23]的方法同理,Critic部分基于值函数更新,Actor部分基于策略梯度更新,稀疏奖励的条件下两部分梯度更新均接近于零。
稀疏奖励问题除了奖励的稀疏性导致学习缓慢外,还可能存在稀疏性带来的估计不可靠的问题,由于奖励样本少,值函数估计的方差较大,这会导致模型训练难以收敛。研究者们为解决以上问题,进行了一系列的研究工作。
2 稀疏奖励研究现状目前解决稀疏奖励问题的算法主要有奖励塑造、模仿学习、课程学习、事后经验回放、好奇心驱动、分层强化学习等6类算法,我们可以根据是否引入外部引导信息将算法分为两大类,如图2所示。引入外部引导信息的算法通常针对特定问题,需要相应的领域知识或数据,泛化性较差,同时也因为先验知识的引入,降低了强化学习模型的学习难度,通常具有实现简单、学习速度快的特点,这一类型算法有奖励塑造、模仿学习、课程学习。无外部引导信息的算法通过挖掘模型、数据自身的潜能,泛化性能更好,但是模型通常更为复杂,这一类型算法包括好奇心驱动、事后经验回放、分层强化学习。接下来我们将对各个方法进行展开介绍。

|
Download:
|
| 图 2 稀疏奖励主流算法 Fig. 2 Mainstream sparse reward algorithms | |
奖励塑造通常是利用先验知识人工设计附加奖励函数[13]来引导智能体完成期望任务的一类方法。合适的附加奖励函数能够有效克服稀疏奖励问题中奖励的稀疏性,加快智能体学习速度。通常用
| $ {R}'\left(s,a,{s}'\right)=R\left(s,a,{s}'\right)+ F\left(s,a,{s}'\right) $ |
但是在新的MDP问题中学习到的最优策略不一定是原MDP的最优策略,也就可能导致奖励塑造后学习到非理论最优的策略[27-28]。Ng等[27]证明了当附加奖励函数可以表示为势能函数
| $ F\left(s,a,{s}'\right)=\gamma \varPhi \left(s{'}\right)-\varPhi \left(s\right) $ |
其中:
Ng等[27]使用距离、子目标来设计启发式的附加奖励函数,在表格问题中明显加速了学习过程;Jagodnik等[29]使用距离信息计算和人为主观评价两种方式作为奖励函数来控制手臂仿真机器人,结果均好于优化的比例微分控制器(PD controller);Ferreira等[30]将奖励塑造的强化学习方法引入对话管理任务中,显著提高了前期训练阶段的表现。
为了克服奖励塑造泛化性较差的问题,研究者们提出了一些自动化地设计奖励函数的方法。Ng等[31]提出逆强化学习(inverse reinforcement learning)的概念,将专家示例看作为最优或者次优的策略,然后从专家示例的数据中学习出奖励函数用于指导智能体训练。Marthi[32]提出基于抽象函数(abstrcat function)的自动奖励塑造方法,通过求解抽象MDP问题的势能函数,再计算势能函数的差分就得到了附加奖励函数。
2.2 模仿学习模仿学习是一类从示例数据中学习策略的方法[14]。稀疏奖励问题往往具有巨大的状态动作空间,难以直接进行探索和学习,使用示例数据进行监督式的学习能够使智能体快速掌握示例策略,极大减少了训练时间。
模仿学习中如果只使用示例数据进行监督学习,难以泛化到陌生的环境中,且长时间步的决策将导致误差累积,逐渐偏离示例策略[33]。Ross等[33]证明了误差与时间步的平方成正比,为此提出在交互中缓慢移动策略分布的SMILe (stochastic mixing iterative learning)算法,并理论证明了其收敛性。Nair等[34]在策略梯度算法中引入行为克隆损失(behavior clone loss)来学习示例策略,能够完成复杂的机械臂控制任务,其行动损失函数为
| ${L_{BC}} = \mathop \sum \limits_{i = 1}^N \left\| {\pi \left( {{s_i}{\rm{|}}{\theta _\pi }} \right) - {a_i}} \right\|_2^2$ |
其中:
| $ {E}_{\pi }\left[{{\rm{log}}}\left(D\left(s,a\right)\right)\right]+{E}_{{\pi }_{E}}\left[{{\rm{log}}}\left(1-D\left(s,a\right)\right)\right]-\lambda H\left(\pi \right) $ |
式中:
通常模仿学习中的示例状态动作对
课程学习是机器学习中逐步增加任务难度以加快学习速度的方法。在强化学习中课程学习实质上在逐步调整学习的任务分布,智能体在简单任务上更容易获得奖励,将相对简单的任务上学到的策略迁移到复杂任务中,降低了在复杂任务中探索的难度,因此课程学习能够用于解决稀疏奖励问题[14]。
Elman[38]最早提出在语法学习任务中使用逐步增加训练数据复杂度的方法来训练神经网络,能够解决直接使用全部数据难以训练的问题。Bengio等[15]认为,课程学习的本质是逐步调整学习样本的分布,在简单的样本分布上更容易学习到泛化性好的策略,并通过实验证明了课程学习能够提高训练速度和收敛到更优解。Bengio等[15]给出了课程学习的数学定义,
| $ {Q}_{\lambda }\left(z\right)\propto {W}_{\lambda }\left(z\right)P\left(z\right), \forall z $ |
其中
| $ \begin{array}{c} \int {Q}_{\lambda }\left(z\right){\rm{d}}z=1 \\ {Q}_{1}\left(z\right)=P\left(z\right),\forall z \end{array}$ |
不同课程阶段对应的分布满足熵增和权重单调增加:
| $ \begin{array}{c} H\left({Q}_{\lambda }\left(z\right)\right)<H\left({Q}_{\lambda +\epsilon }\left(z\right)\right),\forall \epsilon >0 \\ {W}_{\lambda +\epsilon }\left(z\right)<{W}_{\lambda }\left(z\right),\forall z,\forall \epsilon >0 \end{array}$ |
课程学习的一个难点在于如何自动化地设计课程的分级,解决这个问题需要考虑训练模型时的反馈。Graves等[39]提出一种自适应课程学习方法,通过预测正确率和网络复杂性的增长来自动调整课程的难度,在语言模型训练任务上显著提高了训练速度。Akkaya等[40]提出ADR(automatic domain randomization),通过设定表现阈值,当正确率高于表现阈值时就扩大训练的分布提高课程难度,反之缩小训练分布,在复杂的魔方操作任务中取得了成功。
2.4 事后经验回放事后经验回放(HER)[11]是一种从失败经历中学习的强化学习方法,通过修正失败经历的目标产生奖励信息,解决了奖励的稀疏性问题,同时对失败样本的利用极大提高了样本利用效率。
目前对于事后经验回放算法的改进主要在于降低偏差、改进目标采样方式、适配在线策略算法等。Lanka等[41]认为HER修改目标引入的新数据带来了偏差,提出通过调整真实奖励和HER的奖励的权重来降低偏差。Manela等[42]指出,在目标物体未移动的情况下,采样的目标只与初始位置有关而与策略无关,这样的样本会给训练带来偏差,于是提出Filtered-HER,通过滤去该类型目标来缓解该问题。Rauber等[43]通过重要性采样将HER运用到策略梯度方法上,实验结果表明HER明显提高了策略梯度方法的样本利用效率。
2.5 好奇心驱动好奇心驱动是一类使用内在奖励引导智能体探索环境的方法,高效的探索能够更快地获得外在奖励[16],同时能够降低环境的奖励、状态转移的不确定性,平衡探索与利用[44],因此好奇心驱动能解决稀疏奖励问题带来的稀疏性和不可靠性问题。目前的好奇心驱动算法根据内在奖励计算方式可以分为访问计数法和预测差法[45]。Bellemare等[46]通过信息增益(information gain)来联系访问计数法和预测差法,证明了两者本质是相同的。
访问计数法使用访问次数定义状态的陌生程度,鼓励智能体探索更陌生的状态,以提高探索能力和降低对奖励估计的不确定性。Strehl等[47]提出了一种基于模型的内在奖励方法,使用与状态动作对计数的平方根成反比的内部奖励,并理论证明了其最优性:
| $ {r}_{{\rm{in}}}\left(s,a\right)=\beta N{\left(s,a\right)}^{-\frac{1}{2}} $ |
式中:
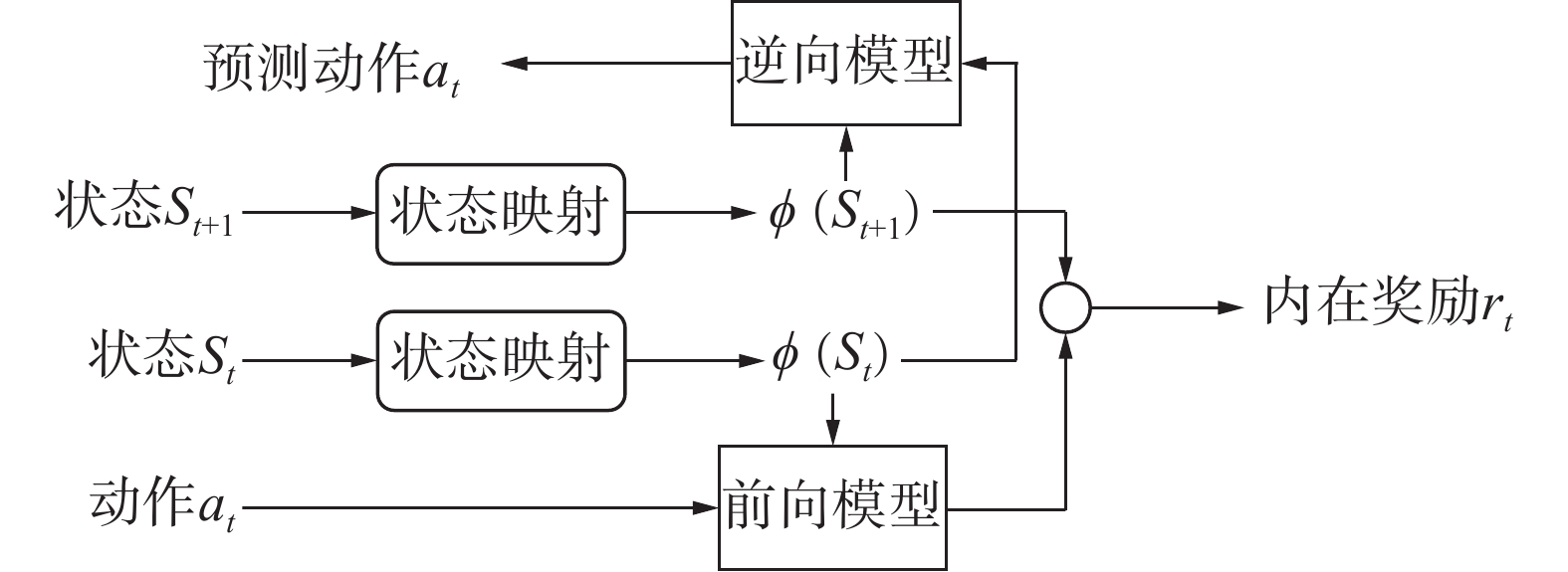
预测差法通过学习环境的状态转移,使用预测误差作为内在奖励,能降低环境动态的不确定性。预测差法中使用状态
| $e\left( {{s_t},{a_t},{s_{t + 1}}} \right) = \left\| {\phi \left( {{s_{t + 1}}} \right) - M\left( {\phi \left( {{s_t}} \right),{a_t}} \right)} \right\|_2^2$ |
其中
|
Download:
|
| 图 3 ICM原理图 Fig. 3 Schematic of ICM | |
状态编码是高维连续状态空间下的好奇心驱动算法一个重要研究内容。Burda等[16]对比了ICM、VAE[51]、Random Network、Pixels 4种编码方式在54个游戏中的实验结果,得出以下结论:ICM的泛化性最好,Random Network也足以在45%的游戏中超过ICM,意味着很多游戏只需使用固定的随机网络就能够提取足够的特征用于策略学习,对后续的研究具有启示作用。
2.6 分层强化学习分层强化学习(HRL)是一类使用分层策略结构的方法,分层的结构能够学习不同层次的策略,从而有效解决维度爆炸的问题[16, 52]。分层强化学习方法的上层策略往往能够处理更大时间尺度的决策,同时分层强化学习方法还能缩小各层策略的动作序列空间,进一步提高了解决稀疏奖励问题的能力。
目前用于稀疏奖励问题的分层强化学习算法主要有两类[52],基于选项[53](option)的方法和基于子目标[54](subgoal)的方法。
基于选项的方法结构简单,上层策略在多个下层策略中进行选择,被选择的下层策略输出动作,如图4所示。Sutton等[53]将基于选项的分层算法表述为半马尔可夫决策过程(SMDP),并推导出在动态规划、Q-Learning中基于选项方法的公式。Bacon等[55]将基于选项的分层方法和策略梯度法结合,提出了Option-Critic算法,并通过实验验证了该方法能够学习到具有实际意义的选项策略。Frans等[56]结合元学习方法来训练基于选项的分层结构,在多个连续动作控制问题中显著提高了学习速度。

|
Download:
|
| 图 4 基于选项的分层结构示意图 Fig. 4 Schematic of option-based HRL methods | |
基于子目标的方法结构则是:上层策略生成子目标,下层策略输出动作去实现子目标,如图5所示。Vezhnevets等[57]提出FeUdal Networks,将子目标设定为隐状态空间中的方向,在蒙特祖玛复仇等多个Atari游戏中的表现均超过基线算法。Nachum等[58]认为,采用离线策略训练分层结构将因为策略的改变产生偏差,可能导致训练不稳定,因此提出了使用离线数据校正的HIRO算法,在Ant-Gather、Ant-Maze等复杂的连续动作控制环境中表现均优于FeUdal Networks。Levy等[59]提出了HAC(hierarchical actor critic),该方法在基于子目标的分层算法基础上,结合了事后经验回放算法极大提升了学习速度且表现好于HIRO。

|
Download:
|
| 图 5 基于子目标的分层结构示意图 Fig. 5 Schematic of subgoal-based HRL methods | |
为了初步验证上述算法在稀疏奖励问题中作用,我们在MuJoCo的机器人环境Fetch Reach[18]下分别实现了6类算法的代表性算法(实验2~7):
1)奖励塑造:实验2实现了Ng等[27]提出的势能函数差分形式的奖励塑造方法,记为Reward Shaping;
2)模仿学习:实验3实现了Nair等[34]提出的行为克隆算法,记为Behavior Clone;
3)课程学习:实验4实现了符合Bengio等[15]定义的课程学习方法,记为Curriculum Learning;
4)事后经验回放:实验5实现了事后经验回放算法[12],记为HER;
5)好奇心驱动:实验6实现了一种基于预测差的前向动态算法[50],记为Forward Dynamic;
6)分层强化学习:实验7实现了一种基于子目标的分层强化学习算法[54],记为HDDPG。
Fetch Reach实验环境的任务是控制机械臂到达目标位置,目标范围在空间中用小红球表示,如图6所示,当机械夹顶端碰到小红球即为达到目标。对于机器人的每步操作,完成目标获得奖励

|
Download:
|
| 图 6 Fetch Reach实验环境 Fig. 6 Fetch Reach environment | |
各实验均进行10次随机试验,去除最大最小值绘制成功率均值标准差曲线,1 个epoch包括100 局仿真,其余实验参数见表1。
| 表 1 DDPG 参数 Tab.1 DDPG Parameters |
本实验采用的基线算法是基于泛化值函数估计[60]的深度确定性策略梯度算法(DDPG),DDPG是代表性的基于Actor-Critic的连续动作控制方法,后续6个算法的实现均建立在其基础上。基于泛化值函数估计的方法认为智能体的策略和值函数与目标有关,
| $ \begin{array}{c} {Q}_{{\rm{target}}}={r}_{t+1}+\gamma Q\left({s}_{t+1},\pi \left({s}_{t+1},g\right),g\right) \\ {L}_{{\rm{critic}}}={{E}_{{s}_{t}\sim {d}^{\pi }}\left({Q}_{{\rm{target}}}-Q\left({s}_{t},{a}_{t},g\right)\right)}^{2} \\ {L}_{{\rm{actor}}}={-E}_{{s}_{t}\sim {d}^{\pi }}\left[Q\left({s}_{t},\pi \left({s}_{t},g\right),g\right)\right] \end{array} $ |
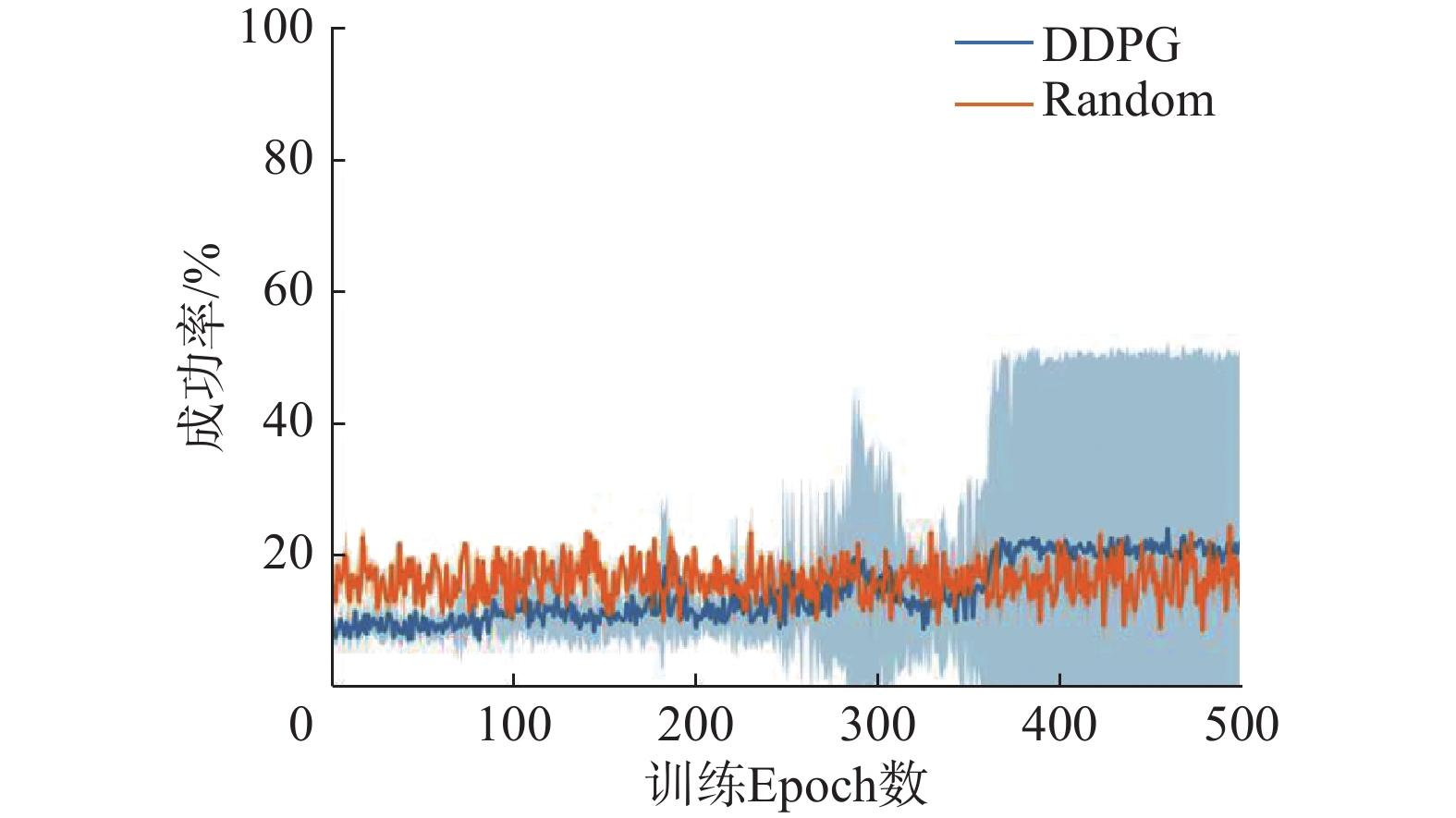
实验1比较了DDPG与随机策略(Random)的表现,实验结果如图7所示。DDPG经过370个epoch的学习平均表现才超过随机策略,在500个epoch内最高平均成功率为21%。通过实验1,我们可以验证常规的深度强化学习算法DDPG在稀疏奖励任务中学习缓慢。
|
Download:
|
| 图 7 DDPG与随机动作成功率学习曲线 Fig. 7 Performance curve of DDPG and Random | |
实验2根据机械夹顶端到目标位置的距离设计奖励函数。
| $ {{\varPhi }}\left( {{s_t},g} \right) = - \left\| {g - \phi \left( {{s_t}} \right)} \right\|_2^2 $ |
根据Ng等[27]的理论,我们设计奖励函数
| $ \begin{array}{*{20}{c}} {r\left( {{s_t},{s_{t + 1}},g} \right) = \lambda \left( {\varPhi \left( {{s_{t + 1}},g} \right) - \varPhi \left( {{s_t},g} \right)} \right)}=\\ { \lambda (\left\| {g - \varphi \left( {{s_t}} \right)} \right\|_2^2 - \left\| {g - \phi \left( {{s_{t + 1}}} \right)} \right\|_2^2)} \end{array} $ |
其中
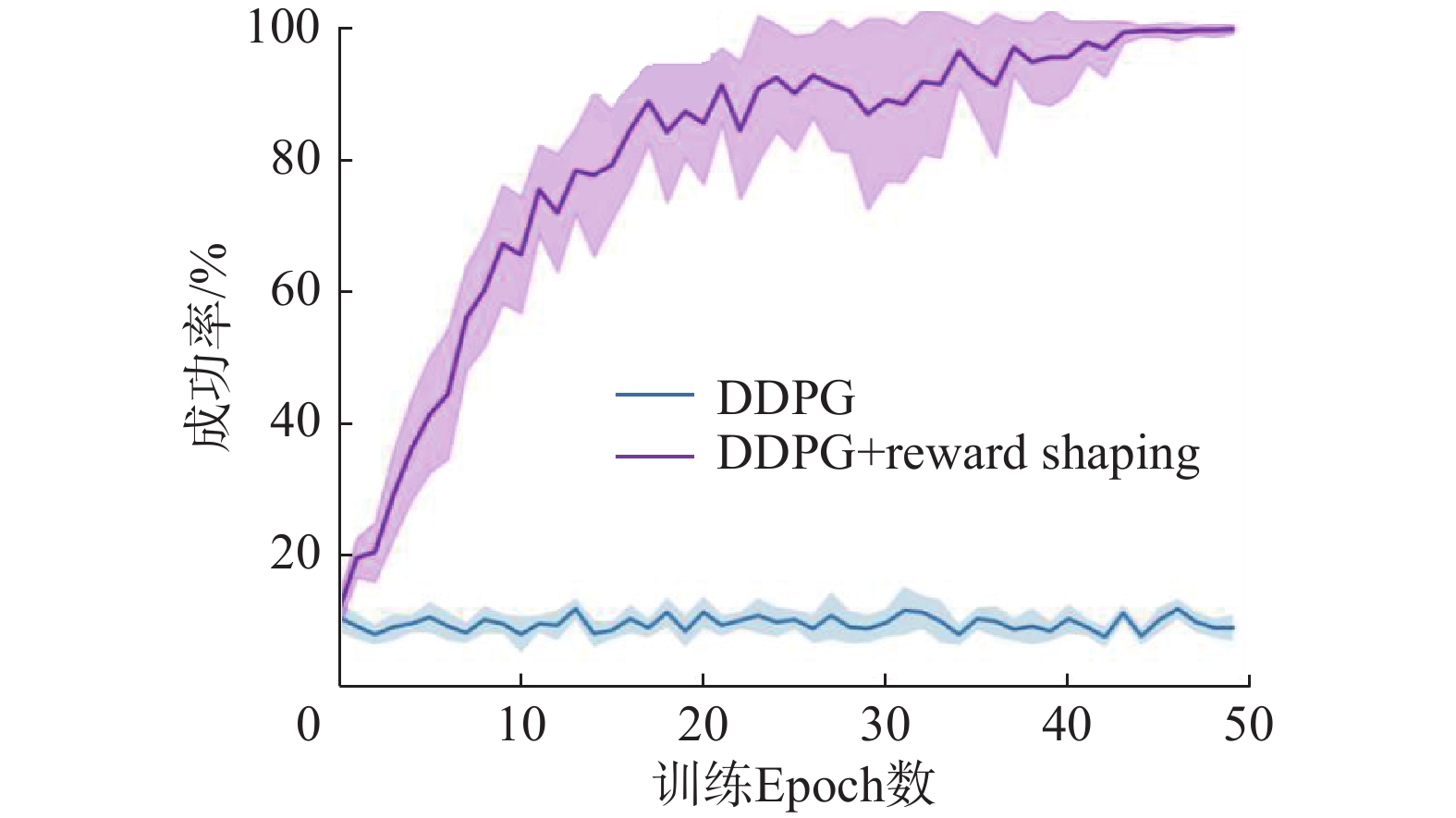
实验2比较了奖励塑造和DDPG的表现,实验结果如图8所示。奖励塑造明显加快了学习速度,40个epoch就收敛到100%成功率,验证了按照势能函数差分形式设计奖励函数的有效性。
|
Download:
|
| 图 8 奖励塑造与DDPG成功率学习曲线 Fig. 8 Performance curve of Reward Shaping and DDPG | |
实验3实现的是Nair等[34]使用的行为克隆(Behavior Clone)算法,利用HER训练的成功率100%的智能体随机产生100局的交互数据作为示例数据,同时最大化累计奖励和最小化与示例策略的误差。由于示例数据有限,不一定能获得示例策略在当前状态下的决策,为此我们使用从示例数据中的采样
| $ \begin{array}{*{20}{c}} {{L_{{\rm{actor}}}} = - {E_{{s_t}\sim {d^\pi }}}\left[ {Q\left( {{s_t},\pi \left( {{s_t},g} \right),g} \right)} \right] + }\\ {\;\;\;\;\;\;\;\;\;\;\alpha {E_{{s_e}\sim {d^{{\pi _e}}}}}\left\| {{a_e} - \pi \left( {{s_e},{g_e}} \right)} \right\|_2^2} \end{array} $ |
式中:
实验3比较了不同

|
Download:
|
| 图 9 Behavior Clone成功率学习曲线 Fig. 9 Performance curve of Behavior Clone | |
实验4通过设计目标分布范围逐渐增大的任务序列来实现课程学习,能够证明我们的设计方式符合Bengio等[15]对课程学习的定义。实验任务中目标位置在各维度变化范围是
| $ {\rm{range}}=0.05+i\times \frac{0.1}{c-1},\; i\in \left[0,c-1\right] $ |
其中
实验4比较了不同课程数

|
Download:
|
| 图 10 课程学习成功率学习曲线 Fig. 10 Performance curve of Curriculum Learning | |
实验5实现的HER[11]算法具体描述为:在每局仿真结束后,对该局的数据
本实验中,状态
实验5比较了事后经验回放与DDPG的表现,实验结果如图11所示。HER在15个epoch左右就收敛到100%成功率,且稳定性高,在无外部引导信息算法中表现最好。

|
Download:
|
| 图 11 HER与DDPG学习曲线 Fig. 11 Performance curve of HER and DDPG | |
实验6实现的好奇心驱动算法是基于预测差的Forward Dynamic[50],使用前向模型
| $ \begin{array}{c} {\rm{los}}{{\rm{s}}_{{\rm{forward}}}} = {E_{{s_t}\sim {d^\pi }}}\left\| {{s_{t + 1}} - M\left( {{s_t},{a_t};\theta } \right)} \right\|_2^2 \\ \;\;\;\;\;\;\;\;{\rm{los}}{{\rm{s}}}_{{\rm{forward}}}\stackrel{{\rm{update}}}{\to }\mu ,\sigma \\ \;\;\;\;{\rm{los}}{{\rm{s}}}_{{\rm{norm}}}=\dfrac{{\rm{los}}{{\rm{s}}}_{{\rm{forward}}}-\mu }{\sigma }\\ \;\;\;\;\;\;\;\;{r}_{{\rm{in}}}={\rm{los}}{{\rm{s}}}_{{\rm{norm}}} \end{array} $ |
其中,
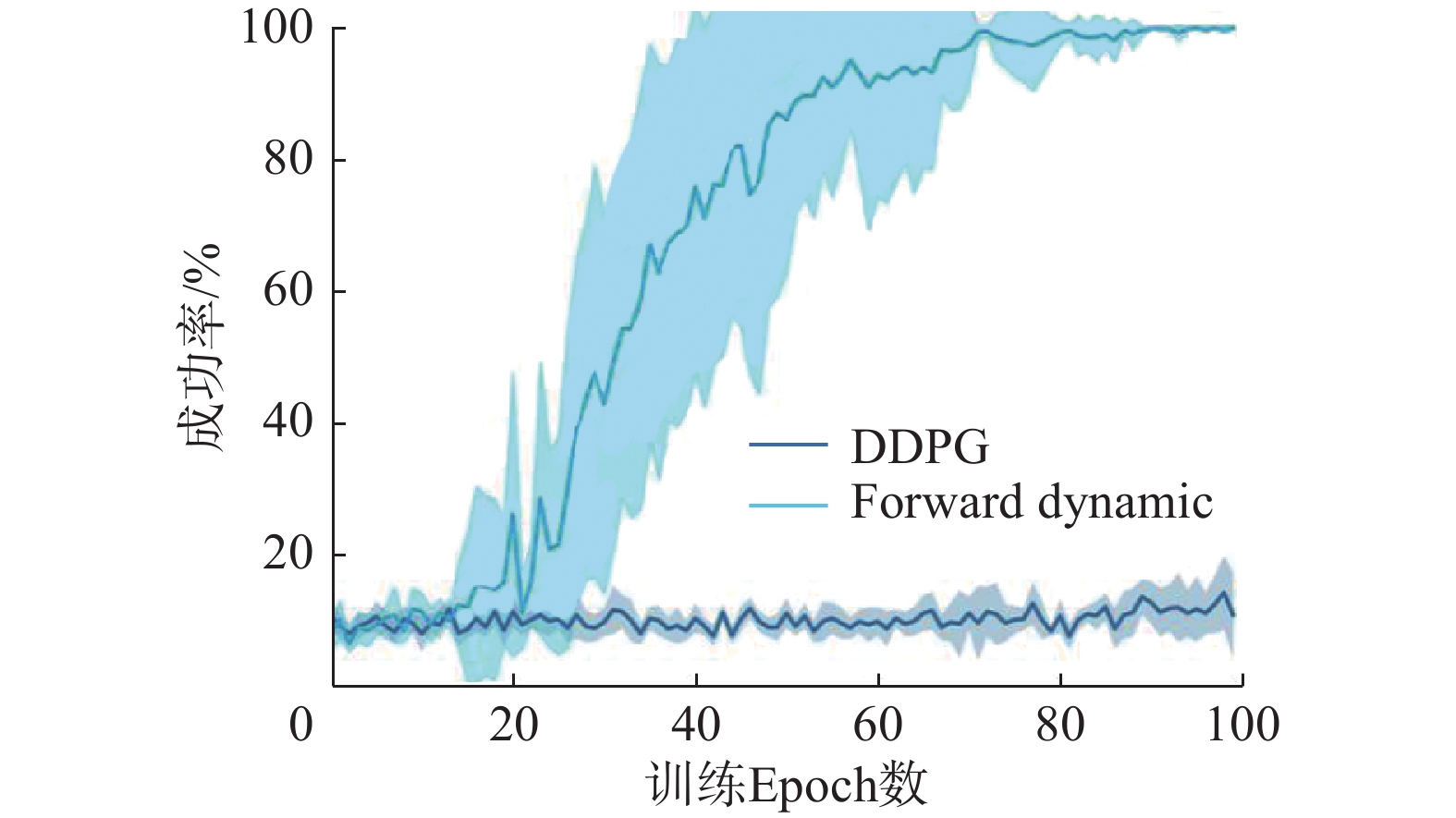
实验6比较了Forward Dynamic与DDPG的表现,实验结果如图12所示。Forward Dynamic在80个epoch左右收敛到100%成功率,验证了Forward Dynamic方法对稀疏奖励问题的有效性。
|
Download:
|
| 图 12 Forward Dynamic与DDPG成功率学习曲线 Fig. 12 Performance curve of Forward Dynamic and DDPG | |
实验7实现的分层强化学习算法HDDPG(Hierarchical DDPG)结构上和HAC[59]相近,区别在于HDDPG不使用事后经验回放。HDDPG属于基于子目标的分层强化学习方法,假设层数为
| $ {\rm{subgoa}}{{\rm{l}}}_{H}={\pi }_{H}\left({s}_{t},g\right) $ |
中间层策略输入状态、子目标,输出子目标:
| $ {\rm{subgoa}}{{\rm{l}}}_{h-1}={\pi }_{h}\left({s}_{t},{\rm{subgoa}}{{\rm{l}}}_{h}\right), h\in (1,H) $ |
最下层策略输入状态、子目标,输出动作:
| $ {a}_{t}={\pi }_{1}\left({s}_{t},{\rm{subgoa}}{{\rm{l}}}_{1}\right) $ |
各层每一步如果完成目标获得奖励
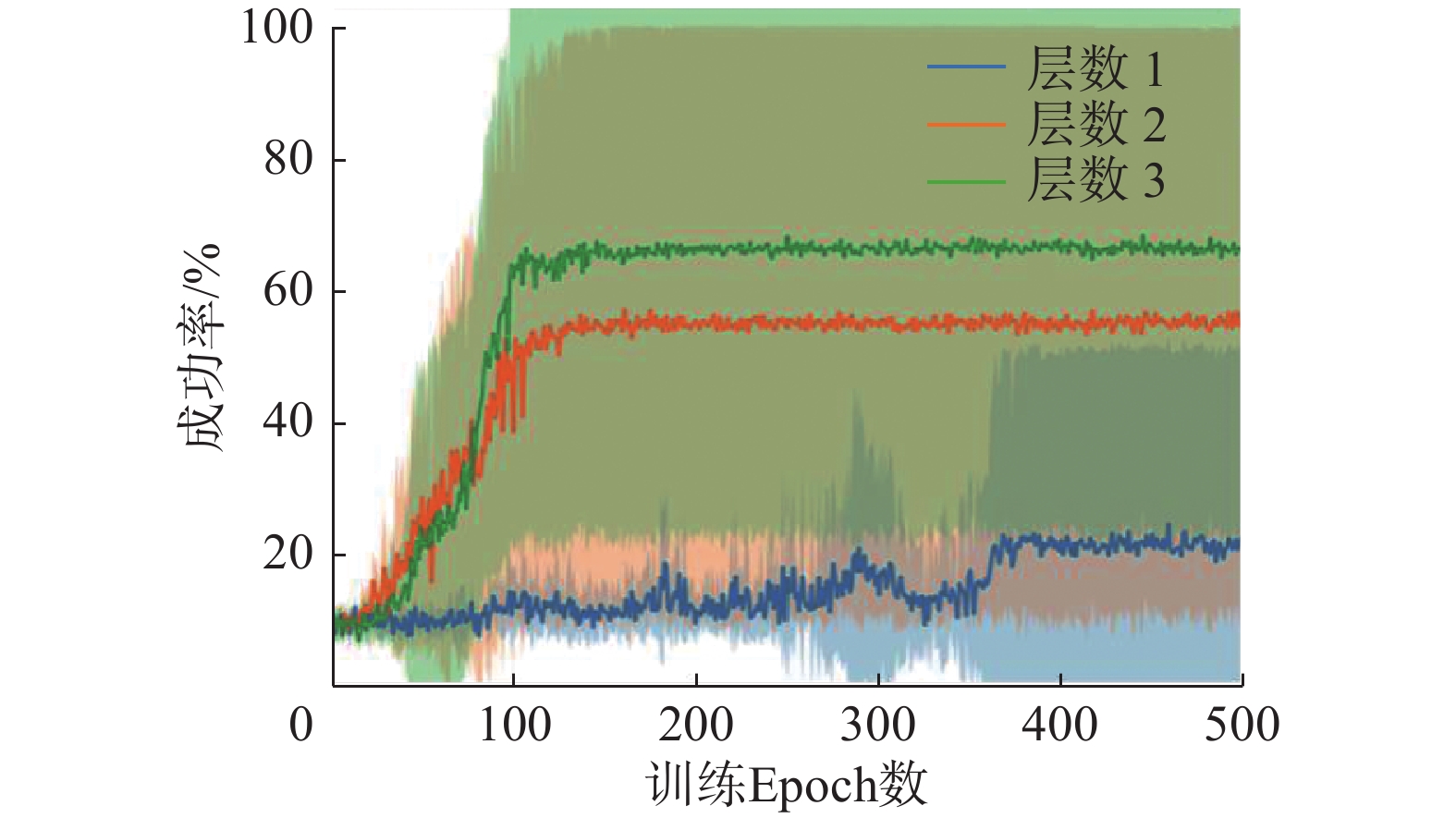
实验7比较了不同层数HDDPG的表现,其中层数为1即为DDPG,实验结果如图13所示。本实验验证了HDDPG分层的结构提高了解决稀疏奖励问题的能力,同时能够得到层数对HDDPG的影响,当层数不大于3的时候,HDDPG表现随层数增加而提高,层数为3时最高平均成功率达到66%。此外,我们也进行了层数大于3的实验,结果接近DDPG,我们认为这是因为分层的离线策略算法存在的偏差[58]随着层数增加累积,当层数过大时会导致训练不稳定,甚至难以进行策略学习。
|
Download:
|
| 图 13 不同层数HDDPG成功率学习曲线 Fig. 13 Performance curve of different layers of HDDPG | |
通过表2总结了实验实现的6类算法的代表性算法在稀疏奖励问题中的表现,相比于DDPG均有显著提升。其中,使用示例策略辅助学习的Behavior Clone表现最佳,8个epoch就收敛到100%成功率,HER没有使用外部引导信息但是表现接近Behavior Clone,15个epoch收敛到100%成功率。
从表2可以看到使用外部引导信息的算法平均表现好于无外部引导信息的算法。实际上我们使用的Fetch Reach实验环境是相对简单的,容易构建可靠的外部引导信息,在更多的稀疏奖励任务中,外部引导信息是难于构建的,这就需要无外部引导信息算法的研究。在我们的实验中,HER、Forward Dynamic等算法的表现已经接近使用外部引导信息的算法,具有重要的研究价值和意义。
| 表 2 实验结果 Tab.2 Experiment results |
稀疏奖励算法未来的研究方向可以是根据各算法存在的问题进行改进,或对多种稀疏奖励算法进行结合。自适应课程学习是重要的研究方向,结合生成对抗思想[61]或元学习[62]的自动课程学习具有广阔的研究前景。好奇心驱动存在被称作“电视噪声”的问题[45]:当环境中出现难以预测的随机噪声时,会导致智能体驻留而不去完成任务。为解决电视噪声问题,未来可以研究好奇心驱动的状态编码方式[15]或结合注意力机制[63]等方法,让智能体更关注与任务有关的状态和奖励信息。事后经验回放算法基于“存在状态到目标的映射”的假设,但是大量实际问题中并不容易找到这样的映射关系,比如视频游戏、机器人导航[64]等问题,研究通用的目标映射方法有助于将HER这种高效的稀疏奖励算法应用到更多问题中。分层强化学习还需要进一步研究分层的数据矫正[58]以及更高效的分层结构。基于目标的分层强化学习中,自动学习目标空间的表示[65]也是重要的研究内容。最后,多种稀疏奖励算法的结合算法能够融合不同算法的优势,为稀疏奖励问题提供更加强有力的解决方案,例如Levy等[59]提出的分层与HER结合的HAC、Lanier等[66]提出的好奇心驱动与HER结合的算法、Nair等[34]提出的模仿学习与HER结合的算法。
5 结束语本文将目前主流的稀疏奖励算法按是否引入外部引导信息分为两类,分别介绍了奖励塑造、模仿学习、课程学习和事后经验回放、好奇心驱动、分层强化学习等6类算法的发展和应用。本文还通过实验验证了6种算法在稀疏奖励问题中的有效性,相比于DDPG均有显著提升,部分无外部引导信息的算法表现已经接近使用外部引导信息的算法。本文的实验比较了6种算法解决稀疏奖励问题的能力,为进一步的研究提供了实验基础。
稀疏奖励问题的研究对强化学习理论的拓展以及算法的实际落地具有重要意义,我们希望在未来看到更高效的算法用于解决复杂的稀疏奖励问题,同时也希望看到更多强化学习算法的实际落地与应用,为社会创造更多价值。
| [1] |
SUTTON R S, BARTO A G. Reinforcement learning: an introduction[M]. Cambridge, USA: MIT Press, 1998.
( 0) 0)
|
| [2] |
SUTTON R S, BARTO A G. Reinforcement learning: an introduction[M]. 2nd ed. Cambridge: MIT Press, 2018.
( 0) 0)
|
| [3] |
SILVER D, HUANG A, MADDISON C J, et al. Mastering the game of Go with deep neural networks and tree search[J]. Nature, 2016, 529(7587): 484-489. DOI:10.1038/nature16961 ( 0) 0)
|
| [4] |
VINYALS O, BABUSCHKIN I, CZARNECKI W M, et al. Grandmaster level in StarCraft II using multi-agent reinforcement learning[J]. Nature, 2019, 575(7782): 350-354. DOI:10.1038/s41586-019-1724-z ( 0) 0)
|
| [5] |
BERNER C, BROCKMAN G, CHAN B, et al. Dota 2 with large scale deep reinforcement learning[EB/OL]. California, USA: arXiv, 2019. [2019-10-1] https://arxiv.org/pdf/1912.06680.pdf.
( 0) 0)
|
| [6] |
SILVER D. Tutorial: Deep reinforcement learning[C]//Proc. of the 33rd Int. Conf. on Machine Learning (ICML 2016). 2016.
( 0) 0)
|
| [7] |
LI Yuxi. Deep reinforcement learning: An overview[EB/OL]. Alberta, Canada: arXiv, 2017. [2019-10-2] https://arxiv.org/pdf/ 1701.07274.pdf.
( 0) 0)
|
| [8] |
LI Yuxi. Deep reinforcement learning[EB/OL]. Alberta, Canada: arXiv, 2018. [2019-10-5] https://arxiv.org/pdf/1810.06339.pdf.
( 0) 0)
|
| [9] |
Riedmiller M, Hafner R, Lampe T, et al. Learning by playing-solving sparse reward tasks from scratch[EB/OL]. London, UK: arXiv, 2018. [2019-10-20] https://arxiv.org/pdf/1802.10567.pdf.
( 0) 0)
|
| [10] |
HOSU I A, REBEDEA T. Playing atari games with deep reinforcement learning and human checkpoint replay[EB/OL]. Bucharest, Romania: arXiv, 2016. [2019-10-21] https://arxiv.org/pdf/1607.05077.pdf.
( 0) 0)
|
| [11] |
ANDRYCHOWICZ M, WOLSKI F, RAY A, et al. Hindsight experience replay[C]//Proceedings of the 31st International Conference on Neural Information Processing Systems. Long Beach, USA, 2017: 5048−5058.
( 0) 0)
|
| [12] |
杨惟轶, 白辰甲, 蔡超, 等. 深度强化学习中稀疏奖励问题研究综述[J]. 计算机科学, 2020, 47(3): 182-191. YANG Weiyi, BAI Chenjia, CAI Chao, et al. Survey on sparse reward in deep reinforcement learning[J]. Computer science, 2020, 47(3): 182-191. DOI:10.11896/jsjkx.190200352 (  0) 0)
|
| [13] |
GULLAPALLI V, BARTO A G. Shaping as a method for accelerating reinforcement learning[C]//Proceedings of the 1992 IEEE International Symposium on Intelligent Control. Glasgow, UK, 1992: 554−559.
( 0) 0)
|
| [14] |
HUSSEIN A, GABER M M, ELYAN E, et al. Imitation learning: A survey of learning methods[J]. ACM computing surveys, 2017, 50(2): 1-35. ( 0) 0)
|
| [15] |
BENGIO Y, LOURADOUR J, COLLOBERT R, et al. Curriculum learning[C]//Proceedings of the 26th Annual International Conference on Machine Learning. Montreal, Quebec, Canada, 2009: 41−48.
( 0) 0)
|
| [16] |
BURDA Y, EDWARDS H, PATHAK D, et al. Large-scale study of curiosity-driven learning[EB/OL]. California, USA: arXiv, 2018. [2019-10-30] https://arxiv.org/pdf/1808.04355.
( 0) 0)
|
| [17] |
周文吉, 俞扬. 分层强化学习综述[J]. 智能系统学报, 2017, 12(5): 590-594. ZHOU Wenji, YU Yang. Summarize of hierarchical reinforcement learning[J]. CAAI transactions on intelligent systems, 2017, 12(5): 590-594. (  0) 0)
|
| [18] |
Plappert M, Andrychowicz M, Ray A, et al. Multi-goal reinforcement learning: Challenging robotics environments and request for research[EB/OL]. California, USA: arXiv, 2018. [2019-11-1] https://arxiv.org/pdf/1802.09464.pdf.
( 0) 0)
|
| [19] |
万里鹏, 兰旭光, 张翰博, 等. 深度强化学习理论及其应用综述[J]. 模式识别与人工智能, 2019, 32(1): 67-81. WAN Lipeng, LAN Xuguang, ZHANG Hanbo, et al. A review of deep reinforcement learning theory and application[J]. Pattern recognition and artificial intelligence, 2019, 32(1): 67-81. (  0) 0)
|
| [20] |
MNIH V, KAVUKCUOGLU K, SILVER D, et al. Playing atari with deep reinforcement learning[EB/OL]. London, UK: arXiv, 2013. [2019-11-1] https://arxiv.org/pdf/1312.5602.pdf.
( 0) 0)
|
| [21] |
MNIH V, KAVUKCUOGLU K, SILVER D, et al. Human-level control through deep reinforcement learning[J]. Nature, 2015, 518(7540): 529-533. DOI:10.1038/nature14236 ( 0) 0)
|
| [22] |
WILLIAMS R J. Simple statistical gradient-following algorithms for connectionist reinforcement learning[J]. Machine learning, 1992, 8(3/4): 229-256. DOI:10.1023/A:1022672621406 ( 0) 0)
|
| [23] |
KONDA V R, TSITSIKLIS J N. Actor-critic algorithms[C]//Advances in Neural Information Processing Systems. Colorado, USA, 2000: 1008−1014.
( 0) 0)
|
| [24] |
MNIH V, BADIA A P, MIRZA M, et al. Asynchronous methods for deep reinforcement learning[C]//Proceedings of the 33rd International Conference on International Conference on Machine Learning. New York, USA, 2016: 1928−1937.
( 0) 0)
|
| [25] |
SCHULMAN J, WOLSKI F, DHARIWAL P, et al. Proximal policy optimization algorithms[EB/OL]. California, USA: arXiv, 2017. [2019-11-3] https://arxiv.org/pdf/1707.06347.pdf.
( 0) 0)
|
| [26] |
LILLICRAP T P, HUNT J J, PRITZEL A, et al. Continuous control with deep reinforcement learning[EB/OL]. London, UK: arXiv, 2015. [2019-12-25] https://arxiv.org/pdf/1509.02971.pdf.
( 0) 0)
|
| [27] |
NG A Y, HARADA D, RUSSELL S. Policy invariance under reward transformations: Theory and application to reward shaping[C]//Proceedings of the Sixteenth International Conference on Machine Learning. Bled, Slovenia, 1999, 99: 278−287.
( 0) 0)
|
| [28] |
RANDLØV J, ALSTRØM P. Learning to drive a bicycle using reinforcement learning and shaping[C]//Proceedings of the Fifteenth International Conference on Machine Learning. Madison, USA, 1998, 98: 463−471.
( 0) 0)
|
| [29] |
JAGODNIK K M, THOMAS P S, VAN DEN BOGERT A J, et al. Training an actor-critic reinforcement learning controller for arm movement using human-generated rewards[J]. IEEE transactions on neural systems and rehabilitation engineering, 2017, 25(10): 1892-1905. DOI:10.1109/TNSRE.2017.2700395 ( 0) 0)
|
| [30] |
FERREIRA E, LEFÈVRE F. Expert-based reward shaping and exploration scheme for boosting policy learning of dialogue management[C]//2013 IEEE Workshop on Automatic Speech Recognition and Understanding. Olomouc, Czech Republic, 2013: 108−113.
( 0) 0)
|
| [31] |
NG A Y, RUSSELL S J. Algorithms for inverse reinforcement learning[C]//Proceedings of the Seventeenth International Conference on Machine Learning. Stanford, USA, 2000, 1: 663−670.
( 0) 0)
|
| [32] |
MARTHI B. Automatic shaping and decomposition of reward functions[C]//Proceedings of the 24th International Conference on Machine Learning. Corvallis, USA, 2007: 601−608.
( 0) 0)
|
| [33] |
ROSS S, BAGNELL D. Efficient reductions for imitation learning[C]//Proceedings of the Thirteenth International Conference on Artificial Intelligence and Statistics. Sardinia, Italy, 2010: 661−668.
( 0) 0)
|
| [34] |
NAIR A, MCGREW B, ANDRYCHOWICZ M, et al. Overcoming exploration in reinforcement learning with demonstrations[C]//2018 IEEE International Conference on Robotics and Automation (ICRA). Brisbane, QLD, Australia, 2018: 6292−6299.
( 0) 0)
|
| [35] |
HO J, ERMON S. Generative adversarial imitation learning[C]//Proceedings of the 30th International Conference on Neural Information Processing Systems. Barcelona, Spain, 2016: 4565−4573.
( 0) 0)
|
| [36] |
LIU Yuxuan, GUPTA A, ABBEEL P, et al. Imitation from observation: Learning to imitate behaviors from raw video via context translation[C]//2018 IEEE International Conference on Robotics and Automation (ICRA). Brisbane, Australia, 2018: 1118−1125.
( 0) 0)
|
| [37] |
TORABI F, WARNELL G, STONE P. Behavioral cloning from observation[EB/OL]. Texas, USA: arXiv, 2018. [2019-11-1] https://arxiv.org/pdf/1805.01954.pdf.
( 0) 0)
|
| [38] |
ELMAN J L. Learning and development in neural networks: The importance of starting small[J]. Cognition, 1993, 48(1): 71-99. DOI:10.1016/0010-0277(93)90058-4 ( 0) 0)
|
| [39] |
GRAVES A, BELLEMARE M G, MENICK J, et al. Automated curriculum learning for neural networks[C]//Proceedings of the 34th International Conference on Machine Learning-Volume 70. Sydney, Australia, 2017: 1311−1320.
( 0) 0)
|
| [40] |
OpenAI, AKKAYA I, ANDRYCHOWICZ M, et al. Solving rubik's cube with a robot hand[EB/OL]. California, USA: arXiv, 2019. [2019-11-2] https://arxiv.org/pdf/1910.07113.pdf.
( 0) 0)
|
| [41] |
LANKA S, WU Tianfu. ARCHER: aggressive rewards to counter bias in hindsight experience replay[EB/OL]. NC, USA: arXiv, 2018. [2019-12-3] https://arxiv.org/pdf/1809.02070.
( 0) 0)
|
| [42] |
MANELA B, BIESS A. Bias-reduced hindsight experience replay with virtual goal prioritization[EB/OL]. BeerSheva, Israel: arXiv, 2019. [2019-12-3] https://arxiv.org/pdf/1905.05498.pdf.
( 0) 0)
|
| [43] |
RAUBER P, UMMADISINGU A, MUTZ F, et al. Hindsight policy gradients[EB/OL]. London, UK: arXiv, 2017. [2019-11-2] https://arxiv.org/pdf/1711.06006.pdf.
( 0) 0)
|
| [44] |
SCHMIDHUBER J. A possibility for implementing curiosity and boredom in model-building neural controllers[C]//Proceedings of the International Conference on Simulation of Adaptive Behavior: From Animals to Animats. Cambridge, USA, 1991: 222−227.
( 0) 0)
|
| [45] |
PATHAK D, AGRAWAL P, EFROS A A, et al. Curiosity-driven exploration by self-supervised prediction[C]//Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition Workshops. Honolulu, USA, 2017: 16−17.
( 0) 0)
|
| [46] |
BELLEMARE M, SRINIVASAN S, OSTROVSKI G, et al. Unifying count-based exploration and intrinsic motivation[C]//Proceedings of the 30th International Conference on Neural Information Processing Systems. Barcelona, Spain, 2016: 1471−1479.
( 0) 0)
|
| [47] |
STREHL A L, LITTMAN M L. An analysis of model-based interval estimation for Markov decision processes[J]. Journal of computer and system sciences, 2008, 74(8): 1309-1331. DOI:10.1016/j.jcss.2007.08.009 ( 0) 0)
|
| [48] |
TANG Haoran, HOUTHOOFT R, FOOTE D, et al. # exploration: A study of count-based exploration for deep reinforcement learning[C]//Proceedings of the 31st International Conference on Neural Information Processing Systems. Long Beach, USA, 2017: 2753−2762.
( 0) 0)
|
| [49] |
BURDA Y, EDWARDS H, STORKEY A, et al. Exploration by random network distillation[EB/OL]. California, USA: arXiv, 2018. [2019-5-20] https://arxiv.org/pdf/1810.12894.pdf.
( 0) 0)
|
| [50] |
STADIE B C, LEVINE S, ABBEEL P. Incentivizing exploration in reinforcement learning with deep predictive models[EB/OL]. California, USA: arXiv, 2015. [2019-5-2] https://arxiv.org/pdf/1507.00814.pdf.
( 0) 0)
|
| [51] |
KINGMA D P, WELLING M. Auto-encoding variational bayes[EB/OL]. Amsterdam, Netherlands: arXiv, 2013. [2019-2-2] https://arxiv.org/pdf/1312.6114.pdf.
( 0) 0)
|
| [52] |
RAFATI J, NOELLE D C. Learning representations in model-free hierarchical reinforcement learning[C]//Proceedings of the AAAI Conference on Artificial Intelligence. Honolulu, USA, 2019, 33: 10009−10010.
( 0) 0)
|
| [53] |
SUTTON R S, PRECUP D, SINGH S. Between MDPs and semi-MDPs: A framework for temporal abstraction in reinforcement learning[J]. Artificial intelligence, 1999, 112(1-2): 181-211. DOI:10.1016/S0004-3702(99)00052-1 ( 0) 0)
|
| [54] |
KULKARNI T D, NARASIMHAN K R, SAEEDI A, et al. Hierarchical deep reinforcement learning: Integrating temporal abstraction and intrinsic motivation[C]//Proceedings of the 30th International Conference on Neural Information Processing Systems. Barcelona, Spain, 2016: 3675−3683.
( 0) 0)
|
| [55] |
BACON P L, HARB J, PRECUP D. The option-critic architecture[C]//Thirty-First AAAI Conference on Artificial Intelligence. San Francisco, USA, 2017.
( 0) 0)
|
| [56] |
FRANS K, HO J, CHEN X, et al. Meta learning shared hierarchies[EB/OL]. California, USA: arXiv, 2017. [2019-11-15] https://arxiv.org/pdf/1710.09767, 2017.
( 0) 0)
|
| [57] |
VEZHNEVETS A S, OSINDERO S, SCHAUL T, et al. Feudal networks for hierarchical reinforcement learning[C]//Proceedings of the 34th International Conference on Machine Learning-Volume 70. Sydney, Australia, 2017: 3540−3549.
( 0) 0)
|
| [58] |
NACHUM O, GU Shixiang, LEE H, et al. Data-efficient hierarchical reinforcement learning[C]//Proceedings of the 32nd International Conference on Neural Information Processing Systems. Montréal, Canada, 2018: 3303−3313.
( 0) 0)
|
| [59] |
LEVY A, KONIDARIS G, PLATT R, et al. Learning multi-level hierarchies with hindsight[EB/OL]. RI, USA: arXiv, 2017. [2019-12-16] https://arxiv.org/pdf/1712.00948.pdf.
( 0) 0)
|
| [60] |
SCHAUL T, HORGAN D, GREGOR K, et al. Universal value function approximators[C]//Proceedings of the 32nd International Conference on International Conference on Machine Learning. Lille, France, 2015: 1312−1320.
( 0) 0)
|
| [61] |
SUKHBAATAR S, LIN Zeming, KOSTRIKOV I, et al. Intrinsic motivation and automatic curricula via asymmetric self-play[EB/OL]. NY, USA: arXiv, 2017. [2019-12-11] https://arxiv.org/pdf/1703.05407.pdf.
( 0) 0)
|
| [62] |
JABRI A, HSU K, EYSENBACH B, et al. Unsupervised curricula for visual meta-reinforcement learning[EB/OL]. California, USA: arXiv, 2019. [2019-12-21] https://arxiv.org/pdf/1912.04226.pdf.
( 0) 0)
|
| [63] |
VASWANI A, SHAZEER N, PARMAR N, et al. Attention is all you need[C]//Proceedings of the 31st International Conference on Neural Information Processing Systems. Long Beach, USA, 2017: 5998−6008.
( 0) 0)
|
| [64] |
SAHNI H, BUCKLEY T, ABBEEL P, et al. Visual hindsight experience replay[EB/OL]. GA, USA: arXiv, 2019. [2019-10-12] https://arxiv.org/pdf/1901.11529.pdf.
( 0) 0)
|
| [65] |
SUKHBAATAR S, DENTON E, SZLAM A, et al. Learning goal embeddings via self-play for hierarchical reinforcement learning[EB/OL]. NY, USA: arXiv, 2018. [2019-11-21] https://arxiv.org/pdf/1811.09083.pdf.
( 0) 0)
|
| [66] |
LANIER J B, MCALEER S, BALDI P. Curiosity-driven multi-criteria hindsight experience replay[EB/OL]. California, USA: arXiv, 2019. [2019-12-13] https://arxiv.org/pdf/1906.03710.pdf.
( 0) 0)
|
 2020, Vol. 15
2020, Vol. 15


