2. 广西科技大学 电气与信息工程学院,广西 柳州 545006;
3. 上海交通大学 船舶海洋与建筑工程学院,上海 200240;
4. 上海船舶工艺研究所 先进连接技术与自动化装备研究室,上海 200032
2. College of Electrical and Information Engineering, Guangxi University of Science and Technology, Liuzhou 545006, China;
3. School of Naval Architecture, Ocean and Civil Engineering, Shanghai Jiao Tong University, Shanghai 200240, China;
4. Advanced Connection Technology and Automation Equipment Research Laboratory, Shanghai Institute of Shipbuilding Technology, Shanghai 200032, China
工业过程控制领域中一些具有模糊性和随机性的复杂非线性系统, 采用二值逻辑或多值逻辑难以对其精确描述, 对于这些不确定控制对象, 较有效的处理手段是模仿人对非确定概念的判断和思维方式, 通过综合决策和似然推理来解决模糊信息处理的问题。在模糊推理领域, Zadeh等[1-5]率先给出基于合成关系的推理模式(compositional rules of inference, CRI),之后经多位学者的充实与完善,在工业领域获得成功应用。该方法虽简便易行,但它欠缺严格的公理化证明,推理结果不可还原,并在一些应用中存在输出结果与现实情况不吻合的问题[6-7]。由此,一些学者根据给定事实与规则前提的相似性,提出一种与CRI有显著差异的推理模式-基于相似度的近似推理(similarity-based approximate reasoning, SAR)[8-9]。在该算法的基础上, Chen等[10-11]讨论了相似性推理中规则后件的调整问题, 给出多种调整函数的表示形式; 何映思等[12]提出一种具有可还原性的多维模糊推理算法; 针对模糊拒取式(fuzzy modus tollens, FMT)问题, Mondal等[13]给出3种基于相似度的逆向推理算法; Raha等[14]结合模糊关系, 构造基于相似度的模糊推理算法; Li等[15]进一步讨论分析了Raha推理模型的相关性质。另一方面,研究人员将SAR推理方法拓展到区间值模糊(也称为vague或直觉模糊)环境中。Chen等[16]讨论了区间值模糊集之间的相似性度量, 提出一种新的双向近似推理方法; 李凡等[17]改进了区间值模糊集的相似性度量, 探讨一种基于相似性的多规则模糊推理方法; 石玉强等[18]针对区间值模糊集距离测度中存在的缺陷, 给出基于区间值模糊集距离的双向近似推理算法; Feng等[19-20]将相似度量引入区间值模糊关系的构造,提出一种基于约简型修正关系的近似推理模式; 王毅等[21]通过引入包含函数来定义区间值模糊相似度, 并将其应用于近似推理算法的构造。
基于相似度的推理机制是根据输入变量与前件之间的相似程度,按照一定的算法对后件进行修正来导出推理结果。修正计算的目的,是使得输出结果对输入事实和规则前提中的任意变化能作出准确的响应。本文在分析CRI与SAR推理模式不合理之处的基础上,通过定义模糊概念之间的贴近方向函数,提出一种基于相似修正关系的近似推理算法。给出包括扩展与缩减2种类型的修正计算方案,探讨用于转化条件命题(构造模糊关系)的转化算子,进而给出该方法在焊接工艺决策中的应用。
1 相似修正关系推理 1.1 CRI与SAR推理设
| $\begin{array}{l} B'(v) = {\sup _{u \in U}}T(A'(u),R(u,v))=\\ {\sup _{u \in U}}T(A'(u),{R_T}(A(u),B(v))) \end{array}$ | (1) |
式中:
| $\begin{array}{l} B'(v) = {\sup _{u \in U}}\min (A'(u),\min (A(u),B(v)))=\\ \;\;\;\;\;\;\;\; \min ({\sup _{u \in U}}\min (A'(u),A(u)),B(v)) \end{array}$ | (2) |
由式(2),给定前件
对于基于相似度的近似推理(SAR), 该算法一般可表示为
| $B'(v) = M(S(A',A),B(v))$ | (3) |
式中:
考察近似推理中相似度量的定义对推理结论的影响。设前件
| $S\left( {A',A} \right) = 1 - \frac{1}{n}\sum\limits_{i = 1}^n {\left| {A'({u_i}) - A({u_i})} \right|} $ |
由式(3)有
| $S\left( {A',A} \right) = \frac{{\displaystyle\sum\nolimits_{{u_i} \in U} {\min (A'({u_i}),A({u_i}))} }}{{\displaystyle\sum\nolimits_{{u_i} \in U} {\max (A'({u_i}),A({u_i}))} }}$ |
则由式(3)同样得
事实上, 在现有基于相似度的近似推理模式中, 相似匹配仅对输入事实与规则前件间的接近程度进行计算, 无法反映概念间隶属函数变化的趋向, 如“high”、“more or less high”、“minus high”、“plus high”、“very high”等, 为此引入一个模糊概念间贴近方向函数的定义。
定义1 设
| ${N_D}(A',A) = \frac{1}{n}\sum\limits_{i = 1}^n {(A'({u_i}) - A({u_i}))} $ | (4) |
称
由式(4)得:
根据上述讨论, 本节在现有SAR推理模式的基础上, 结合CRI转化计算的特点, 通过引入贴近方向函数, 提出一种依据输入与前提的相似性对模糊关系进行修正的推理方法, 即相似修正关系推理(similarity-modified relation inference, SMRI)。
SMRI算法:
1)根据事实
2)运用转化算子
3)根据
4)由修正关系
近似推理是由非精确前提中得出潜在非精确结论的决策过程。在人们直觉思维中推理过程往往是近似的, 例如, 据条件命题“如果苹果红了,那么苹果熟了”和2个给定的事实“苹果很红”、“苹果有点红”, 可分别得出结论“苹果很熟”、“苹果有点熟”, 由此可以推断出:
| $A' \subseteq A \Rightarrow B' \subseteq B\;\left( {\text{缩减式}} \right)$ |
| $A' \supseteq A \Rightarrow B' \supseteq B\;\left( {\text{扩展式}} \right)$ |
设
1)若
2)若
3)若
按照缩减式推理的假设, 当
4)若
5)若
6)若
根据性质1)、4), 若
简记
定义2 设
1)
2)
3)
4)
称
5)
6)
称
由定义2, 考察模糊逻辑中的剩余蕴涵(R-蕴涵)
7)
8)
9)
10)
由7)~10), 剩余蕴涵满足扩展型修正算子的性质1)~4), 主要有
另一方面, 考察t-范数
11)
12)
13)
14)
由11)~14), t-范数可满足缩减型修正算子的性质1)、2)、5)和6), 主要有
定义3 设
| $r' = M(s,r) = \left\{ \begin{array}{l} I(s,r),\quad {n_D} \geqslant 0\\ T(s,r),\quad {\text{其他}} \end{array} \right.$ | (5) |
式(5)给出修正关系
| $B'(v) = \left\{ {\begin{array}{*{20}{l}} {\mathop {\sup }\limits_{u \in U} I(s,R(u,v)),\quad {n_D} \geqslant 0}\\ {\mathop {\sup }\limits_{u \in U} T(s,R(u,v)),\quad {\text{其他}}} \end{array}} \right.$ | (6) |
就推理机制而言, SMRI算法与CRI、Turksen的SAR有显著差别。令
| $\begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;A' \wedge R(B|A) \Rightarrow B'\\ BS(A',A) \Rightarrow B'{\text{或}}B/S(A',A) \Rightarrow B' \end{array}$ |
对本文的算法, 有:
| $S(A',A) \to R(B|A) \Rightarrow B'\;\left( {\text{扩展式}} \right)$ |
| $S(A',A) \wedge R(B|A) \Rightarrow B'\;\left( {\text{缩减式}} \right)$ |
式中:
在SMRI方法的步骤2)中, 通过合适的转化算子
命题1 令
1) 如转化算子
2) 如转化算子
证明1) 由修正算子
| $\begin{array}{l} B'\left( v \right) = {\sup _{u \in U}}M\left( {s,R\left( {u,v} \right)} \right)=\\ {\sup _{u \in U}}M\left( {s,{R_T}\left( {A\left( u \right),B\left( v \right)} \right)} \right)=\\ M\left( {s,{{\sup }_{u \in U}}{R_T}\left( {A\left( u \right),B\left( v \right)} \right)} \right) \end{array}$ |
由
| $\begin{array}{c} B'\left( v \right) = M\left( {s,{R_T}\left( {{{\sup }_{u \in U}}A\left( u \right),B\left( v \right)} \right)} \right)=\\ M\left( {s,{R_T}\left( {1,B\left( v \right)} \right)} \right) = M\left( {s,B\left( v \right)} \right)=\\ M\left( {1,B\left( v \right)} \right) = B\left( v \right) \end{array}$ |
2) 由
| $\begin{array}{c} B'\left( v \right) = {\sup _{u \in U}}M\left( {s,{R_T}\left( {A\left( u \right),B\left( v \right)} \right)} \right) =\\ M\left( {s,{R_T}\left( {{{\inf }_{u \in U}}A\left( u \right),B\left( v \right)} \right)} \right) \end{array}$ |
据
| $\begin{array}{c} B'\left( v \right) = M\left( {s,{R_T}\left( {{{\inf }_{u \in U}}A\left( u \right),B\left( v \right)} \right)} \right)=\\ M\left( {1,{R_T}\left( {0,B\left( v \right)} \right)} \right)=\\ M\left( {1,1} \right) = 1{\rm{ }} \end{array}$ |
故有
据命题1中性质1), 若转化算子
| $B'\left( v \right) = \left\{ \begin{array}{l} I\left( {s,B\left( v \right)} \right),\quad {n_D} \geqslant 0\\ T\left( {s,B\left( v \right)} \right),\quad {\text{其他}} \end{array} \right.$ |
若扩展型和缩减型修正算子分别为
| $B'\left( v \right) = \left\{ \begin{array}{l} \min \left\{ {1,B\left( v \right)/s} \right\}{\rm{, }}\quad {n_D} \geqslant 0{\rm{ }}\\ sB\left( v \right){\rm{, }}\quad {\text{其他}} \end{array} \right.$ | (7) |
式(8)正是文献[8-9]中Turksen的“扩展”与“缩减”推理形式。任给
| $B'\left( v \right) = \left\{ \begin{array}{l} I(s,{R_T}(\mathop {\sup }\limits_{u \in U} Au,Bv)),\quad {n_D} \geqslant 0\\ T(s,{R_T}(\mathop {\sup }\limits_{u \in U} Au,Bv)),\quad {\text{其他}} \end{array} \right.$ | (8) |
据命题1的性质2), 若转化算子
定义4 设
1)
2)
3)
4)
5)
6)
称RT为
命题2 令
证明 据式(8), 若
| $\begin{gathered} B'\left( v \right) = I\left( {s,{R_T}\left( {{{\sup }_{u \in U}}A\left( u \right),B\left( v \right)} \right)} \right)= \\ I\left( {s,{R_T}\left( {1,B\left( v \right)} \right)} \right) \geqslant\\ I\left( {1,{R_T}\left( {1,B\left( v \right)} \right)} \right) = {R_T}\left( {1,B\left( v \right)} \right) = B\left( v \right) \\ \end{gathered} $ |
即
| $\begin{gathered} B'\left( v \right) = T\left( {s,{R_T}\left( {{{\sup }_{u \in U}}A\left( u \right),B\left( v \right)} \right)} \right) =\\ T\left( {s,{R_T}\left( {1,B\left( v \right)} \right)} \right) <\\ T\left( {1,{R_T}\left( {1,B\left( v \right)} \right)} \right) = {R_T}\left( {1,B\left( v \right)} \right) = B\left( v \right) \\ \end{gathered} $ |
故
命题2表明,若
SMRI算法中, 修正及转化算子的选用对计算结果有直接影响。为使输出结果对系统相关变量的任意变化作出明显的响应, 对于扩展式可取强蕴涵和较强的t-范数, 而对于缩减式, 则取较弱的t-范数作为操作算子。表1为几种修正算子与转化算子的组合情况。
| 表 1 修正算子与转化算子的组合 Tab.1 Combination of modification operators and translation operators |
据式(8), 因修正算子和转化算子为右递增, 且
| ${B'_{{I_G},{T_B}}} \subseteq {B'_{I,T}} \subseteq {B'_{{I_L},{T_M}}}$ |
对缩减式, 有:
| ${B'_{{T_L},{T_B}}} \subseteq {B'_{T,T}} \subseteq {B'_{{T_M},{T_M}}}$ |
算例1 设
据CRI方法, 取转化算子和t-范数均为取小运算
即
据SMRI算法, 计算
| $S({A'_1},A) = 1 - \frac{{0.19 + 0.25 + 0.19}}{4} = 0.84$ |
| ${N_D}({A'_1},A) = - \frac{{0.19 + 0.25 + 0.19}}{4} = - 0.16$ |
| $S({A'_2},A) = 1 - \frac{{0.12 + 0.21 + 0.25}}{4} = 0.86$ |
| ${N_D}({A'_2},A) = \frac{{0.12 + 0.21 + 0.25}}{4} = 0.14$ |
由
| $\begin{gathered} {{B'}_1}( {{v_1}} ) = \max ( {S( {{{A'}_1},A} ) + \max ( {\mathop {\max }\limits_{u \in U} Au + B{v_1} - 1,0} ) - 1,}\\{0} ) = \max ( {0.84 + \max ( {1 + 0.25 - 1,0} ) - 1,0} ) = 0.09 \\ \end{gathered} $ |
依次计算得:
由
| $\begin{gathered} {{B'}_2}\left( {{v_1}} \right) = \min \left( {1 - S\left( {{{A'}_1},A} \right) + \min \left( {\mathop {\max }\limits_{u \in U} A\left( u \right),B\left( {{v_1}} \right)} \right),1} \right) =\\ \min \left( {1 - 0.86 + \min \left( {1,0.25} \right),1} \right) = 0.39 \\ \end{gathered} $ |
依次可得:
即
气体保护焊以其高效作业、低成本、操作方便等特点在船舶、机械、石化、车辆等制造业有广泛应用。焊接规范参数的选取是焊接质量控制的关键环节之一, 为获得规范参数与焊缝形态之间关系的数学模型, 往往需进行大量的工艺试验, 但焊接过程的复杂性使构建精确的模型通常不易实现。理论已证明模糊逻辑作为一种万能逼近器, 能以任意精度逼近非线性对象或过程[5], 所以模糊建模在焊接领域具有较好的应用前景, 下面给出SMRI算法在CO2焊接工艺决策方面的应用。
2.1 焊接参数决策的推理模型焊接熔深是焊缝接头质量的最重要指标, 在与之相关的诸多焊接工艺参数中, 焊接电流和焊速为主要因素, 为此可构建一个在不同焊速下, 以焊缝熔深
由CO2焊接试验总结出3种焊速下熔深与电流之间关系的工艺规则, 如表2所示。
| 表 2 焊缝熔深与电流之间的工艺规则 Tab.2 Process rules between weld depth and welding current |
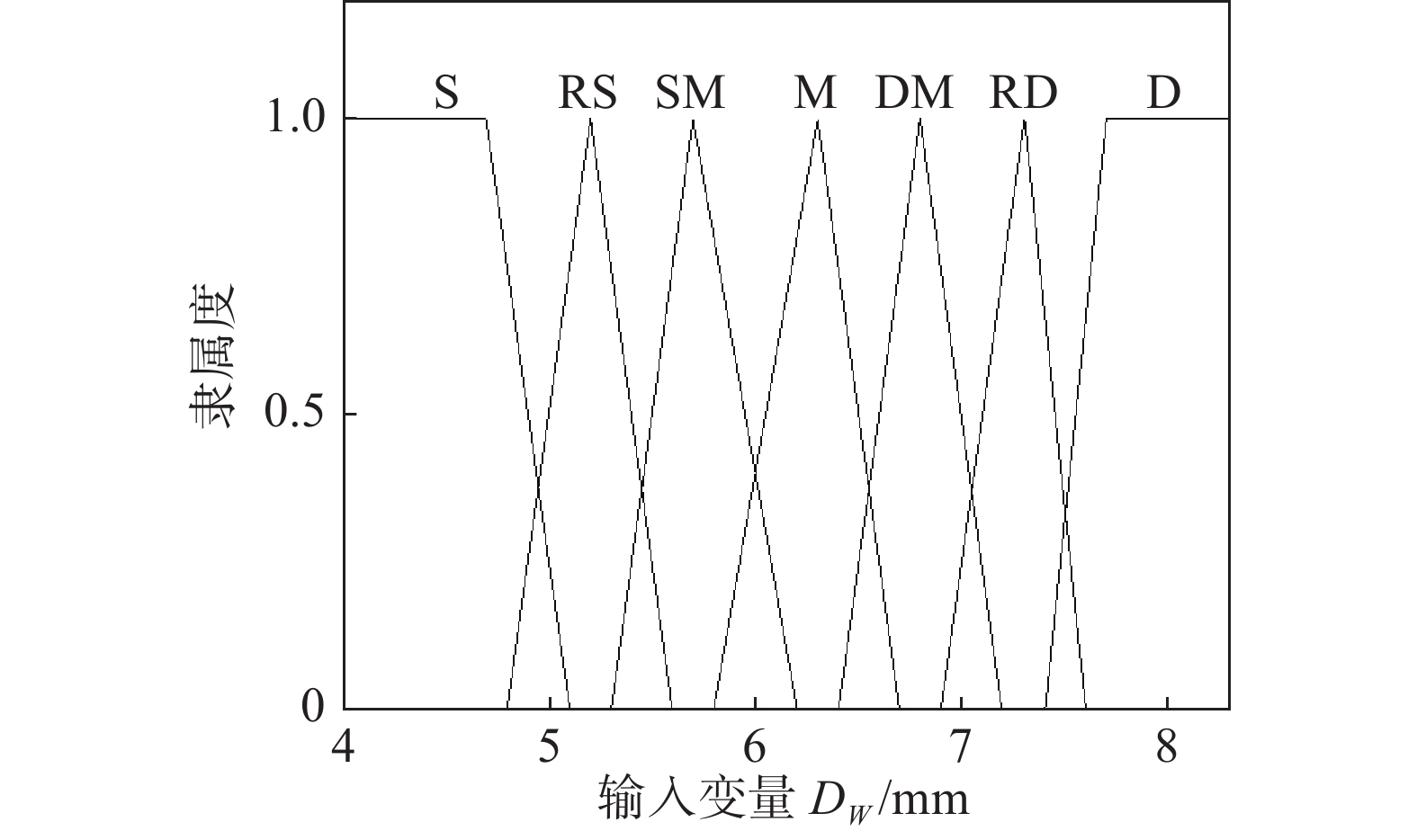
简明起见, 各模糊变量的隶属函数取三角形或梯形,
|
Download:
|
| 图 1 焊缝熔深的隶属函数 Fig. 1 Membership functions of weld depth | |
|
Download:
|
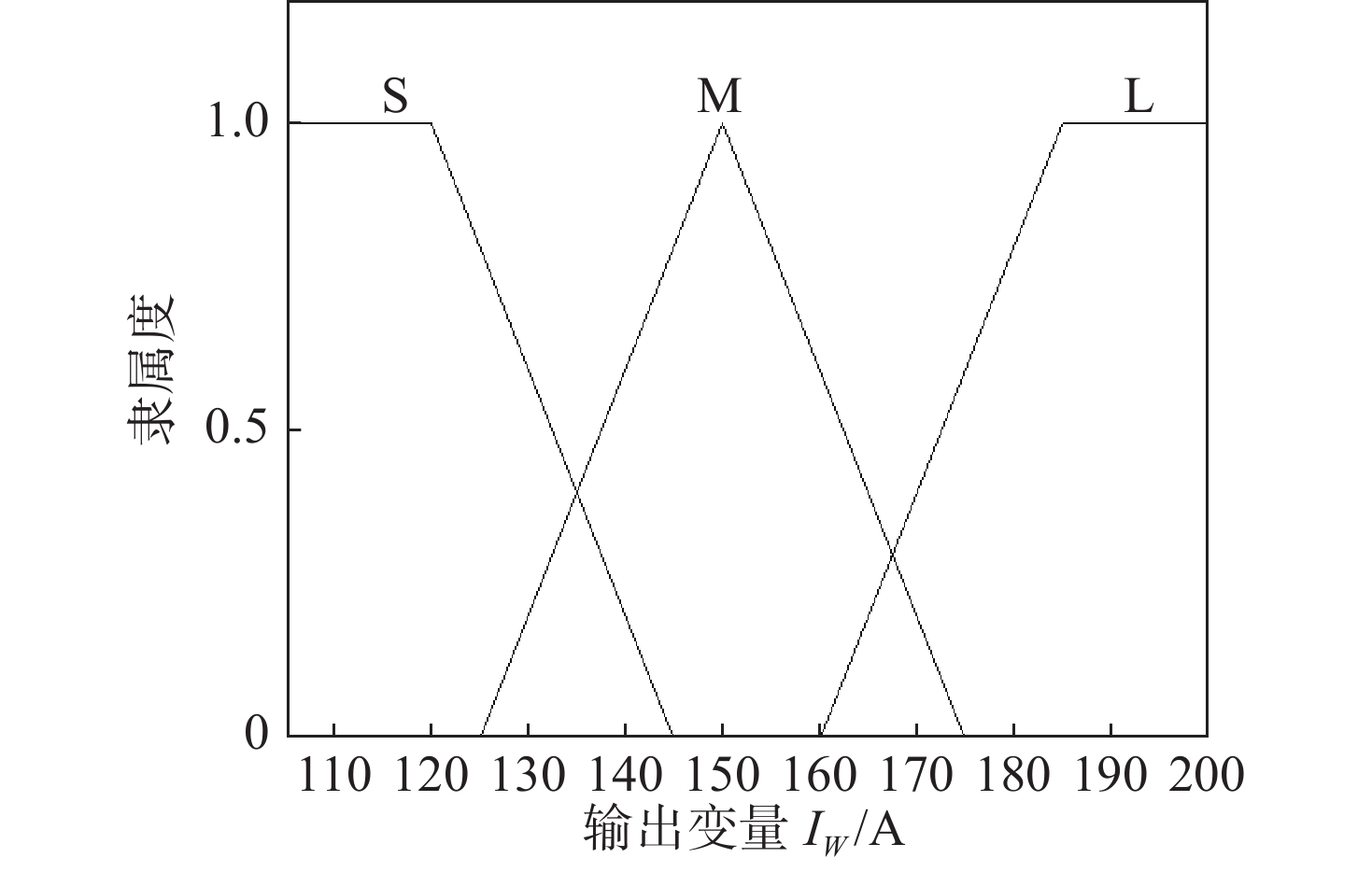
| 图 2 焊接电流的隶属函数 Fig. 2 Membership functions of welding current | |
基于SMRI方法实现焊接电流决策的主要步骤如下:
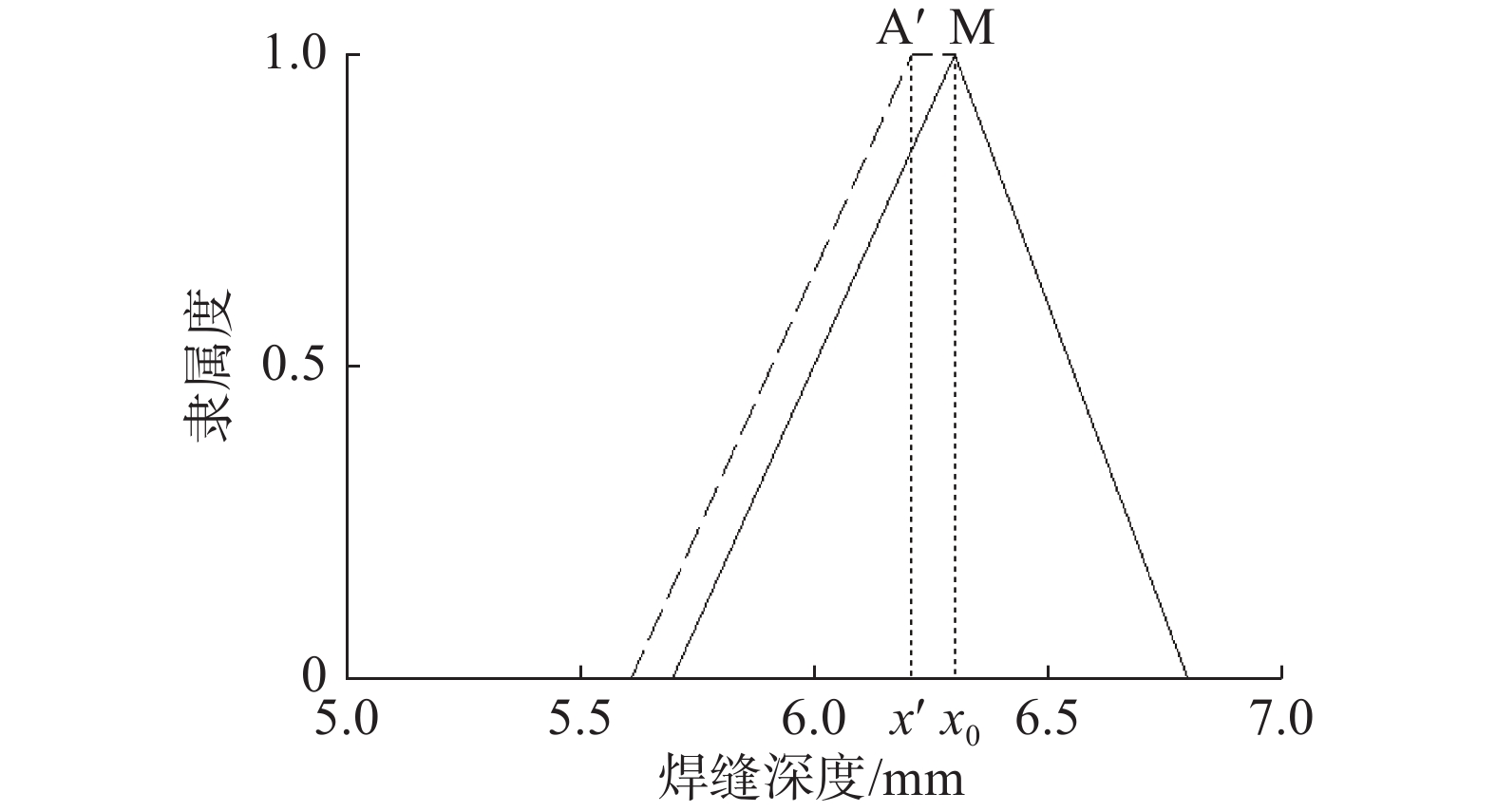
1)输入精确量的模糊化。设输入精确值
|
Download:
|
|
图 3 输入精确值
|
|
2) 计算输入与前件间的相似度和贴近方向。
| $S(A',A) = \frac{{\displaystyle\int_X {\min \left\{ {A'(x),A(x)} \right\}{\rm{d}}x} }}{{\displaystyle\int_X {\max \left\{ {A'(x),A(x)} \right\}{\rm{d}}x} }}$ |
| ${N_D}(A',A) = {{\int_X {(A'(x) - A(x)){\rm{d}}x} }/{\int_X {{\rm{d}}x} }}$ |
3) 修正关系及投影计算。据式(8), 有:
| $B'(y) = M(S(A',A),{R_T}({\sup _{x \in X}}A(x),B(y)))$ |
因
| $B'(y) = M(S(A',A),B(y))$ |
这里, 若
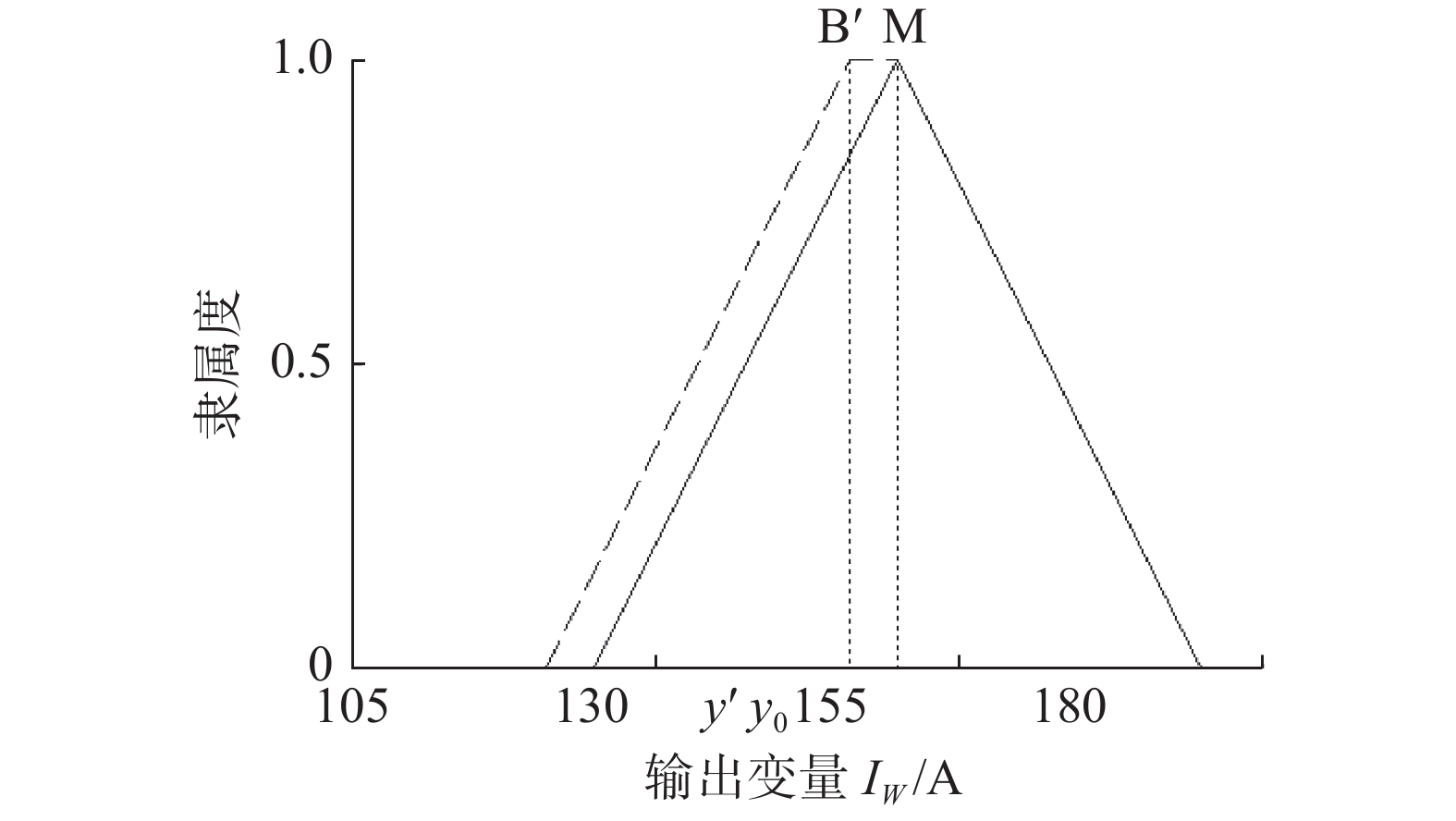
4) 输出解模糊。按最大隶属原则, 输出量y’可由
|
Download:
|
| 图 4 输出变量精确值的计算 Fig. 4 Computation of output exact value | |
按以上步骤, 通过MATLAB编程建立基于SMRI的焊接规范参数决策模型, 模型运行界面如图5所示。

|
Download:
|
| 图 5 基于SMRI的焊接规范参数计算 Fig. 5 Calculation of welding specification parameters based on SMRI | |
根据给定的焊缝熔深, 通过SMRI模型推理获得焊接电流和焊速后实施焊接, 试验条件为: 逆变NB-500焊机, 焊接母材AH36船用高强钢, 对接平焊, 焊丝直径1.0 mm, 焊接电压21±2 V。焊后切取焊缝的横截面并测量焊缝深度。模型推理和实验结果如表3所示, 其中
| 表 3 焊接参数决策工艺试验 Tab.3 Eexperiments for welding parameter decision |

|
Download:
|
| 图 6 理论值与实测值的比较 Fig. 6 Comparison of theoretical and measured values | |
在SAR推理模式的基础上, 引入贴近方向函数作为匹配计算的一个环节, 可以更准确地反映模糊概念中隶属度的变化趋向。CRI的推理过程可以看作由给定事实直接对模糊关系进行修正计算, 其修正函数对应于合成运算。对于本文的SMRI算法,计算修正关系是通过事实和前提的相似匹配来达成, 由此事实与前提中的任意变化(包括扩展和缩减变化)都可整合到修正关系之中, 这不仅改进了Turksen等人提出的基于相似度的近似推理模式,而且有助于解决CRI的推理结论在某些情况下与实际不符的问题。
在近似推理中有多种模糊算子可选择, 本文对SMRI模式中的转化算子和修正算子的选择方案进行了探讨。例如,当要求推理结论对输入事实和规则的变化作出显著响应时,可以分别选择较强和较弱的模糊算子进行扩展及缩减计算。工程化应用是近似推理算法研究的目标之一, 本文给出SMRI算法在焊接工艺参数决策的实例, 下步将研究修正算子和转化算子的性质,并将该算法应用到焊接模糊控制方面。
| [1] |
ZADEH L A. Outline of a new approach to the analysis of complex systems and decision processes[J]. IEEE transactions on systems, man, and cybernetics, 1973, SMC-3(1): 28-44. DOI:10.1109/TSMC.1973.5408575 ( 0) 0)
|
| [2] |
MAMDANI E H. Application of fuzzy logic to approximate reasoning using linguistic Synthesis[J]. IEEE transactions on computers, 1977, 26(12): 1182-1191. DOI:10.1109/TC.1977.1674779 ( 0) 0)
|
| [3] |
MIZUMOTO M, FUKAMI S, TANAKA K. Some methods of fuzzy reasoning, in: advances in fuzzy set theory and applications[M]. New York: North-Holland, 1979.
( 0) 0)
|
| [4] |
BACZYŃSKI M, JAYARAM B. Fuzzy implications[M]. Berlin: Springer, 2008.
( 0) 0)
|
| [5] |
侯健, 苑飞. 模糊推理方法及模糊系统的逼近性能[M]. 天津: 天津科学技术出版社, 2009.
( 0) 0)
|
| [6] |
李洪兴. 模糊控制的插值机理[J]. 中国科学(E缉), 1998, 41(3): 312-320. LI Hongxing. Interpolation mechanism of fuzzy control[J]. Science in China series E: technological sciences, 1998, 41(3): 312-320. DOI:10.1007/BF02919442 (  0) 0)
|
| [7] |
王国俊. 模糊推理的全蕴涵三I算法[J]. 中国科学(E缉), 1999, 29(1): 43-53. WANG Guojun. Full implication triple I algorithm of fuzzy reasoning[J]. Science in China (series E), 1999, 29(1): 43-53. (  0) 0)
|
| [8] |
TURKSEN I B, ZHONG Zhao. An approximate analogical reasoning approach based on similarity measures[J]. IEEE transactions on systems, man, and cybernetics, 1988, 18(6): 1049-1056. DOI:10.1109/21.23107 ( 0) 0)
|
| [9] |
TURKSEN I B, ZHONG Zhao. An approximate analogical reasoning schema based on similarity measures and interval-valued fuzzy sets[J]. Fuzzy sets and systems, 1990, 34(3): 323-346. DOI:10.1016/0165-0114(90)90218-U ( 0) 0)
|
| [10] |
CHEN S M. A weighted fuzzy reasoning algorithm for medical diagnosis[J]. Decision support systems, 1994, 11(1): 37-43. DOI:10.1016/0167-9236(94)90063-9 ( 0) 0)
|
| [11] |
YEUNG D S, TSANG E C C. A comparative study on similarity-based fuzzy reasoning methods[J]. IEEE transactions on systems, man, and cybernetics, Part B (cybernetics), 1997, 27(2): 216-227. DOI:10.1109/3477.558802 ( 0) 0)
|
| [12] |
何映思, 全海金, 邓辉文. 具有还原性的多重多维模糊推理算法[J]. 计算机科学, 2007, 34(4): 145-148. HE Yingsi, QUAN Haijin, DENG Huiwen. An algorithm of general fuzzy inference with the reductive property[J]. Computer science, 2007, 34(4): 145-148. DOI:10.3969/j.issn.1002-137X.2007.04.040 (  0) 0)
|
| [13] |
MONDAL B, RAHA S. Similarity-based inverse approximate reasoning[J]. IEEE transactions on fuzzy systems, 2011, 19(6): 1058-1071. DOI:10.1109/TFUZZ.2011.2159981 ( 0) 0)
|
| [14] |
RAHA S, HOSSAIN A, GHOSH S. Similarity based approximate reasoning: fuzzy control[J]. Journal of applied logic, 2008, 6(1): 47-71. DOI:10.1016/j.jal.2007.01.001 ( 0) 0)
|
| [15] |
LI Yingfang, QIN Keyun, HE Xingxing, et al. Properties of Raha’s similarity-based approximate reasoning method[J]. Fuzzy sets and systems, 2016, 294: 48-62. DOI:10.1016/j.fss.2015.05.008 ( 0) 0)
|
| [16] |
CHEN S M, HSIAO W H, JONG W T. Bidirectional approximate reasoning based on interval-valued fuzzy sets[J]. Fuzzy sets and systems, 1997, 91(3): 339-353. DOI:10.1016/S0165-0114(97)86594-3 ( 0) 0)
|
| [17] |
李凡, 田应忠, 吕泽华. 基于Vague集的近似推理方法[J]. 华中科技大学学报(自然科学版), 2004, 32(4): 44-46. LI Fan, TIAN Yingzhong, LU Zehua. An approximate reasoning approach based on the measures of similarity between Vague sets[J]. Journal of Huazhong University of Science & Technology (nature science edition), 2004, 32(4): 44-46. (  0) 0)
|
| [18] |
石玉强, 王鸿绪. 一种基于Vague集间距离的双向近似推理方法[J]. 小型微型计算机系统, 2007, 28(4): 661-665. SHI Yuqiang, WANG Hongxu. Bidirectional approxinate reasoning based on distances of vague set[J]. Journal of Chinese computer systems, 2007, 28(4): 661-665. DOI:10.3969/j.issn.1000-1220.2007.04.018 (  0) 0)
|
| [19] |
FENG Zhiqiang, LIU Cungen. On similarity-based approximate reasoning in interval-valued fuzzy environments[J]. Informatica, 2012, 36(3): 255-262. ( 0) 0)
|
| [20] |
FENG Zhiqiang, LIU Cungen, HUANG Hu. Knowledge modeling based on interval-valued fuzzy rough set and similarity inference: prediction of welding distortion[J]. Journal of Zhejiang University Science C, 2014, 15(8): 636-650. DOI:10.1631/jzus.C1300370 ( 0) 0)
|
| [21] |
王毅, 刘三阳, 张文, 等. 基于包含度的直觉模糊相似度量推理方法[J]. 系统工程与电子技术, 2014, 36(3): 494-500. WANG Yi, LIU Sanyang, ZHANG Wen, et al. Intuitionistic fuzzy similarity measures reasoning method based on inclusion degrees[J]. Systems engineering and electronics, 2014, 36(3): 494-500. (  0) 0)
|
 2020, Vol. 15
2020, Vol. 15


