系留无人机通过供电线缆连接地面供电系统与无人机端，可长时间留空^[1-3]。由于系留无人机能长时间续航，能在巡检测量过程中持续作业，目前系留无人机已被广泛应用于各领域执行复杂任务，为电力巡检、灾后搜救、隧洞勘探等带来了诸多便利^[4-7]。系留无人机定位，是系留无人机稳定飞行的关键，目前解决系留无人机在无GPS环境或弱GPS环境下的定位仍是一个难题^[8-9]。

系留无人机在空旷的户外可依靠GPS和惯性测量单元(IMU)定位^[10-12]。在弱GPS的户外或无GPS的室内，无人机的定位通常借助于激光雷达或视觉辅助定位^[13-14]。激光雷达与视觉定位易受距离、天气、雾霾、粉尘等因素影响，且实时构建二维或三维地图的数据量庞大、处理过程相对复杂。惯性测量、激光雷达与视觉定位会随时间的累积造成数据的漂移，导致系留无人机在弱GPS或无GPS环境下的定位存在不可控环境因素干扰^[15-16]。利用激光雷达、双目视觉、IMU多传感器融合定位的方式能解决系留无人机在无GPS或弱GPS环境下的定位问题，多个传感器的使用增加了系留无人机的负载，需要极大地增大系留无人机的动力。当系留无人机的功率过大时，系留线缆上的压降不可忽视，绳缆上的能量损耗以及散热会引出新的研究问题^[17-19]。文献[20]提出了系留无人机绳缆定位的方法，利用绳缆数据来代替GPS、惯性测量单元、视觉传感器的数据来实现定位，但定位误差为0.367 5 m。因定位精度不高，所用的Fotokite Pro无人机可移植性差，以至于系留无人机绳缆定位方法难以被实际应用^[21-22]。

针对上述在系留无人机室内不借助于激光雷达、视觉等定位方式下，仅仅依靠系留绳缆实现系留无人机在室内的定位。本文提出了基于力传感的系留无人机定位方法，建立了系留无人机绳缆定位物理模型，通过借助于系留绳缆与三维力传感器，能有效估计系留无人机所处空间位置。

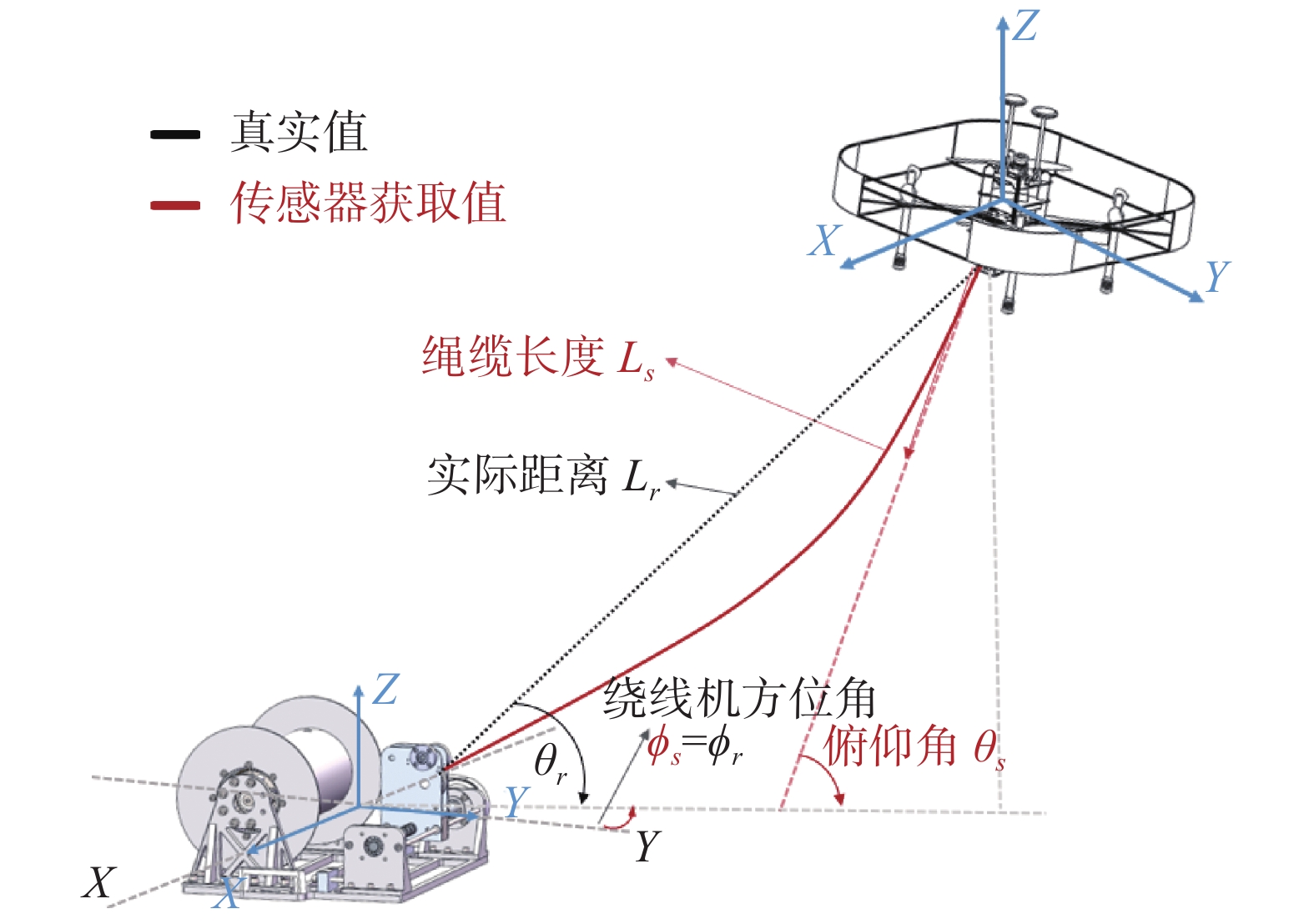
1 绳缆定位模型

在系留无人机飞行过程中，随着绳缆长度的增加，系留绳缆对飞行姿态和位置的影响越来越大，有必要研究系留绳缆在空中的重量和模型，不能直接忽略。为了计算简便，通常把模型中绳缆与绕线机的距离当作直线距离而忽略绳缆的实际状态，而在实际测试中绳缆因重力导致绳缆弯曲。尽量还原实际情况可以把系留绳缆弯曲的状态看成悬链曲线，利用系留绳缆建立悬链线模型(如图1所示)。

利用几何方法可以估计无人机与绕线机之间的直线距离^{[16, 20]}。整个系统由搭载三维力传感器的无人机、硅胶线缆、地面绕线机3个部分构成，通过测定绳缆的长度 $L_s$ 、俯仰角 $\theta _s$ 、无人机端拉力 $T$ 、绳缆的单位质量 $m_0$ 、绕线机方位角 $\phi_ s$ ，再以绕线机为坐标原点建立惯性坐标系，将测定的物理量输入MATLAB建立的数学模型中可获得无人机相对于绕线机的空间坐标位置。

1.1 空间位置模型

绕线机的末端带编码器，可测量绳缆长度，因此把绕线机的末端当作空间坐标系的原点。图1模型中系留无人机的空间坐标位置表示为

$ \left\{ {\begin{array}{*{20}{l}} {x = {L_r}\cos {\theta _r}\sin {\phi _r}}\\ {y = {L_r}\cos {\theta _r}\cos {\phi _r}}\\ {z = {L_r}\sin {\theta _r}} \end{array}} \right. $

式中： $L_r$ 表示无人机到绕线机的直线距离，由悬链线模型估计获得； $\theta _r$ 表示 $L_r$ 与水平面XOY的夹角，由悬链线三角函数关系获得； $\phi _r$ 为绕线机与初始位置的方位角，系留无人机偏离ZOY平面时，绳缆将带动绕线机一起转动，绕线机旋转的方位角可以根据绕线机相对初始位置旋转的角度的偏移测得^[20]。

1.2 系留无人机受力分析

系留无人机悬停在空中，受力如图2所示。

无人机满足平衡方程:

$ \left\{ {\begin{array}{*{20}{l}} {F\cos \beta = T\cos {\theta _s}}\\ {F\sin \beta = T\sin {\theta _s} + G} \end{array}} \right. $

(1)

式中： $F$ 表示无人机竖直向上的升力，由螺旋桨产生； $T$ 表示无人机上绳缆拉力大小； $G$ 表示无人机重力； $\;\beta $ 表示升力与水平方向的夹角； $\theta _s$ 为俯仰角。简化式(1)可得式(2)：

$ \left\{ \begin{array}{l} F{\rm{ = }}\dfrac{G}{{\sin \beta {\rm{ - }}\cos \beta \tan {\theta _s}}}\\ T{\rm{ = }}\dfrac{G}{{\cos {\theta _s}\tan \beta - \sin {\theta _s}}} \end{array} \right. $

(2)

系留无人机绳缆用悬链线模型表示，绳缆上的受力分析如图3所示。

B点表示无人机端三维力传感器末端，A点表示绕线机末端。绳缆上力受力平衡方程可表示为

$ \left\{ \begin{array}{l} {T_1}\cos {\theta _s} = {T_0}\\ {T_1}\sin {\theta _s} = W \end{array} \right. $

式中： $T_1$ 表示无人机上拉力大小； $T_0$ 表示绕线机端的拉力； $W$ 表示绳缆的重力。绳缆上的拉力由三维力传感器测得，得到的数据分别是笛卡尔坐标系下每个坐标轴的分力，在笛卡尔坐标系下已知3个分力的方向和大小可以计算合力的方向和大小，空间中3个力的合成如图4所示。

从三维力传感器上通过力的合成可以间接获得无人机上的拉力和俯仰角。无人机上的拉力大小和系留绳缆上的拉力大小相等方向相反，即

$ T=T_1 $

系留线缆上任意一小段的受力情况可表示为

$ \left\{ \begin{array}{l} {{{{\rm{d}}}} / {{\rm{d}}y}} \centerdot \left( {T_{{y}} \centerdot {\rm{sin}}\;\theta {{y}}} \right) = {{{{\rm{d}}}} / {{{{\rm{d}}}}y}} \centerdot Wy{\rm{}}\\ {{{\rm{d}}L = }}\sqrt {{{\left( {{{{\rm{d}}}}y} \right)}^2} + {{\left( {{{{\rm{d}}}}{{z}}} \right)}^2}} = \sqrt {1 + \left( {{{{{{\rm{d}}}}z} / {{{{\rm{d}}}}y}}} \right) \centerdot {{{\rm{d}}}}y} \\ {\rm{tan}}\theta {{y}}\;{\rm{ = }}{{{{{\rm{d}}}}{{z}}} / {{{{\rm{d}}}}{{y}}}} \end{array} \right. $

(3)

将任意一点拉力 $T_y$ 用 $T_0$ 表示为

$T_{{y}} = {{T_0} / {\cos \theta _y}}$

(4)

把式(4)代入式(3)简化得

$ \left\{ \begin{array}{l} \dfrac{{\rm{d}}}{{{\rm{d}}y}}\left( {{T_0}\tan {\theta _y}} \right) = \dfrac{{\rm{d}}}{{{\rm{d}}y}}{W_y} = \gamma \centerdot {\rm{d}}L\\ \gamma = \rho vg \end{array} \right. $

(5)

式中： $\gamma $ 表示系留绳缆的单位质量； $\;\rho $ 表示绳缆的密度； $g$ 为重力加速度； ${\rm{d}}L$ 为一小段绳长； $v$ 表示任意一小段绳缆体积，W_y表示任意小段绳缆的质量。绳缆上每一小段的长度用弧长公式表示：

${\rm{d}}L = \sqrt {1 + {{\left( {{\rm{d}}z/{\rm{d}}y} \right)}^{\rm{2}}}} \centerdot {\rm{d}}y$

绳缆的长度 $L_{{s}}$ 用弧长积分得到：

$L_s{\rm{ = }}\int_{\rm{0}}^{L_{{y}}} {\sqrt {1 + {{\left( {\mathop {{\rm{d}}z}\nolimits^{} /\mathop {{\rm{d}}y}\nolimits^{} } \right)}^2}} } $

(6)

式(6)代入式(5)中，并做微分处理可得：

$ \frac{{\rm{d}}}{{{\rm{d}}z}}\left( {\frac{{{\rm{d}}z}}{{{\rm{d}}y}}} \right) = \frac{{\rho g}}{{T_0}}\centerdot \sqrt {1 + {{\left( {{\rm{d}}z/{\rm{d}}y} \right)}^{\rm{2}}}} \centerdot {\rm{d}}y $

(7)

式(7)做积分分离，整理后可得到悬链线方程：

$ \left\{ \begin{array}{l} z = a \centerdot \cosh \left( {{y / a}} \right)\\ a = {{{T_0}} / \gamma }\\ \cosh \left( x \right) = {{\left( {{{\rm{e}}^x} + {{\rm{e}}^{-x}}} \right)} / 2} \end{array} \right. $

(8)

式中 $\cosh \left( x \right)$ 表示双曲余弦函数。对式(8)求导：

$\frac{{{\rm{d}}z}}{{{\rm{d}}y}} = \tan \theta _y = \sinh \left( {{\kern 1pt} \frac{y}{a}} \right)$

(9)

式(9)代入式(6)得到绳缆长度：

$ {L_s} = \int_0^{{L_y}} {\sqrt {{\rm{1 + }}\left( {\sinh \frac{y}{a}} \right)} } {\rm{d}}y = a\centerdot \sinh \frac{{{L_y}}}{a} $

式(9)是通用表示情况，系留无人机连接绳缆端的角度大小为 $\theta _{{s}}$ ，因此可得到系留无人机悬链线输入模型数学表达式：

$ \left\{ \begin{array}{l} \tan {\theta _s} = \sinh \left( {{{L_{{y}}} / a}} \right)\\ {L_s}{\rm{ = }}a \centerdot \sinh \left( {{{{L_{{y}}}} / a}} \right) - a \centerdot \sinh \left( 0 \right)\\ {L_z}{\rm{ = }}a \centerdot \cosh \left( {{{{L_{{y}}}} / a}} \right) - a \centerdot \cosh \left( 0 \right) \end{array} \right. $

2 实验平台搭建 2.1 基于力传感系留无人机

三维拉力传感器采用VARIENSE厂商的FSE103，传感器直径39 mm，重量40 g，拉力范围为在0~80 N，最小精度0.01 N。三维力传感器如图5所示，在传感器受力区施加量程范围内的力，可通过上位机读取笛卡尔坐标系下3个坐标轴上力的大小。为了统一坐标系，在安装三维力传感器时应使3个坐标轴与绕线机为原点建立的坐标轴保持一致。三维力传感器精度能达到0.01 N，在实际使用过程中微小的受力变化也能被传感器捕获，同时受力区在没有受到外力时传感器存在噪声数据，如图6所示，为了消除噪声干扰对真实数据的影响，在测量之前需要对噪声数据做预处理。传感器未受力时取1 000个带噪声的数据求取均值，若用n₀表示无外力时带噪声数据，传感器受绳缆拉力时的测量数据用N表示，那么测量数据的真实值可用N−n₀表示。

无人机使用DJI F450机架，三维力传感器悬挂于无人机底部重心位置，系留线缆通过螺纹螺栓与硅胶线缆连接。系留线缆末端与地面绕线机相连接，绕线机可控制绳缆长度变化，使绳缆始终能处于悬链线模型状态。

2.2 绕线机与绳缆

绕线机可根据绳缆上张力大小使绳缆保持自动收放。为了使实验效果明显，系留线缆选取了密度较大的硅胶线缆，并且硅胶线缆不是完全均匀，为了减小绳缆密度不均匀产生的误差，这里采用多点测量取平均值的方式获得绳缆密度。绳缆密度计算方式为

$ \left\{ \begin{array}{l} \rho {\rm{ = }}\dfrac{m}{V}\\ V = {\text{π}} {r^2} \cdot L \end{array} \right. $

式中：m表示绳缆的总质量；V表示绳缆的总体积；r表示绳缆半径；L表示绳缆总长，数据测定如表1所示。

绕线机通过张力测试控制绳缆收放的同时绕线机末端的编码器也能测量绳缆的长度 $L_S$ 。

3 实验测试

悬链线模型估计的定位数据需要与系留无人机在室内所处空间位置的真实值对比获得定位精度。系留无人机实验场地由 $3.2\;\,{\rm{m}} \times {\rm{4}}\,\;{\rm{m}} \times {\rm{2}}{\rm{.8}}\,\;{\rm{m}}$ 行架和安全网搭建。无人机在室内的真实位置采用MarveImind的Indoor “GPS”测定，Indoor “GPS”由5个基站和一个GPS调节器组成，在实验场地的4根行架柱与系留无人机上分别固定一个GPS基站，实验场地如图7所示，室内GPS调节器与PC连接，室内GPS定位系统定位稳定性高且不易受外界环境影响，在室内能达到2 cm的定位误差。

由于绕线机不能自由旋转，因此不能实现绕线机与绳缆偏角的测量，在实验过程中做以下约束，以便于实验数据的处理：

1)绕线机的角度固定，不能在任意位置偏转，即不需要考虑绕线机被系留绳缆拖拽的方位角。

2)系留无人机空间位置估计过程中忽略无人机的飞行姿态(横滚、俯仰、偏航)，把系留无人机当作质点。

3)坐标系的选取，以绕线机为原点建立笛卡尔坐标系，系留无人机的位置是相对于坐标原点的空间位置。

4 数据分析

在实验场地中分别测量绳缆长度为1.2、1.8、2.4、3.0 m时的数据。为了验证该定位方法的有效性，将Indoor “GPS”获取的数据表示系留无人机的期望位置，悬链线模型下得到的数据表示估计位置。

绳长为1.2 m时无人机位置的变化，改变的物理量只有三维力传感器上拉力的大小和方向，图8表示悬链线位置估计下系留无人机在10次测量中位置变化情况。

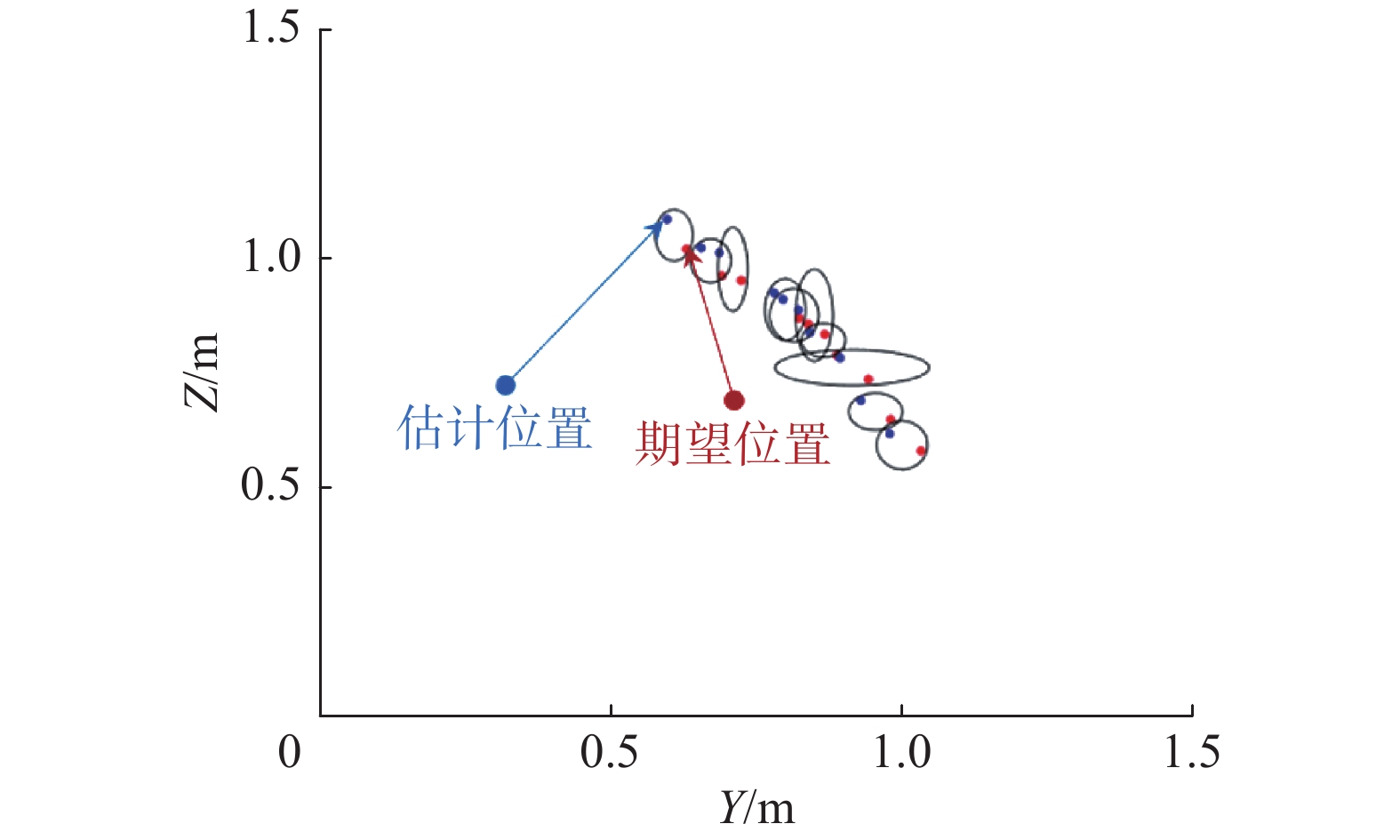
把系留无人机的空间位置在YZ坐标轴的平面上投影，对比期望位置与估计位置的误差如图9所示。红色圆点表示RTK获得的期望位置，蓝色圆点表示悬链线模型估计位置，黑色椭圆表示每一组期望值与估计值的距离范围，椭圆中红色点与蓝色点距离越近误差越小。10次实验中，测量误差取平均值，Y方向的误差为5.193%，Z方向的误差为6.341%。

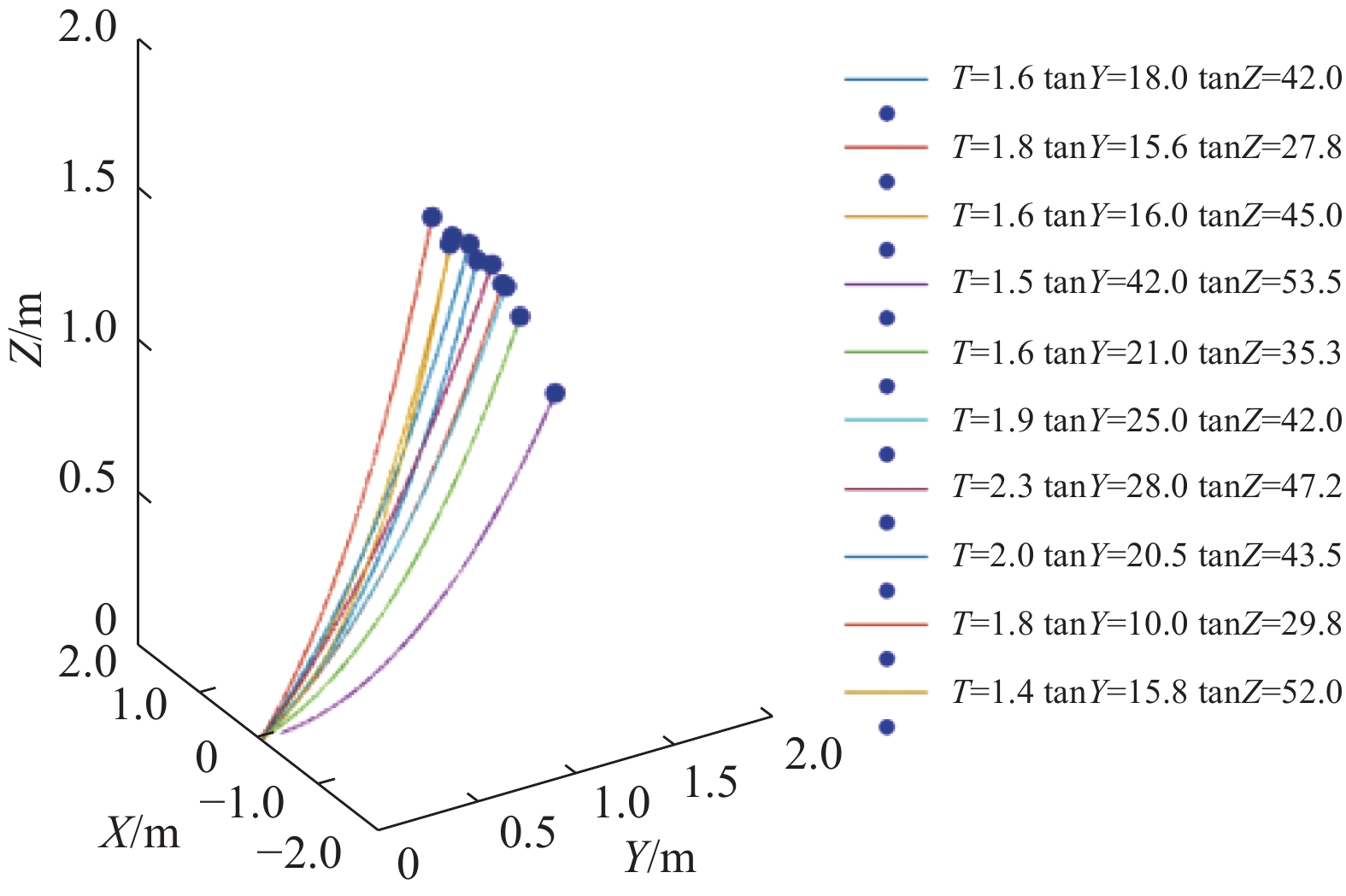
绳长为1.8 m时，悬链线模型估计位置如图10所示。期望位置与估计位置误差比较如图11所示。

绳长1.8 m的10次实验中，测量误差取平均值，Y方向的误差为4.034%，Z方向的误差为2.326%。该组数据下系留线缆Y方向的跨度在0.8~1.6 m，线缆的弯曲程度在该组数据中跨度较大，这并没有导致该模型下系留无人机估计位置的跳变，这表明悬链线模型对系留无人机空间位置的估计与悬链线的弯曲程度无关。

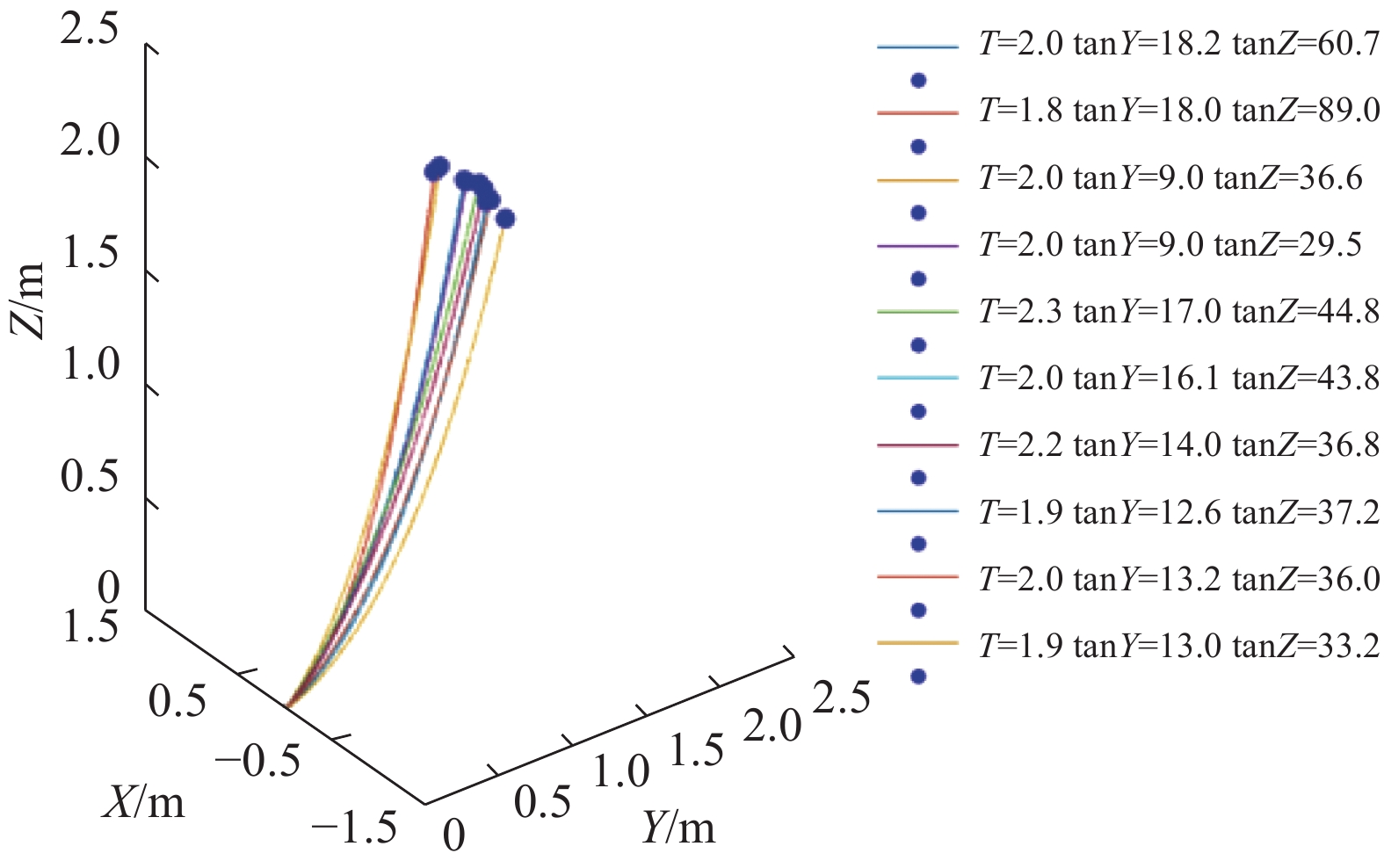
绳长L_s为2.4 m时，悬链线模型估计位置如图12所示。期望位置与估计位置误差比较如图13所示。

绳长2.4 m的10次实验中，测量误差平均值，Y方向误差为2.359%，Z方向误差为1.022%。

绳长L_s为3.0 m时，悬链线模型估计位置如图14所示。期望位置与估计位置误差比较如图15。

绳长3.0 m的10次实验中，测量误差取均值，Y方向误差为3.103%，Z方向误差为4.206%。

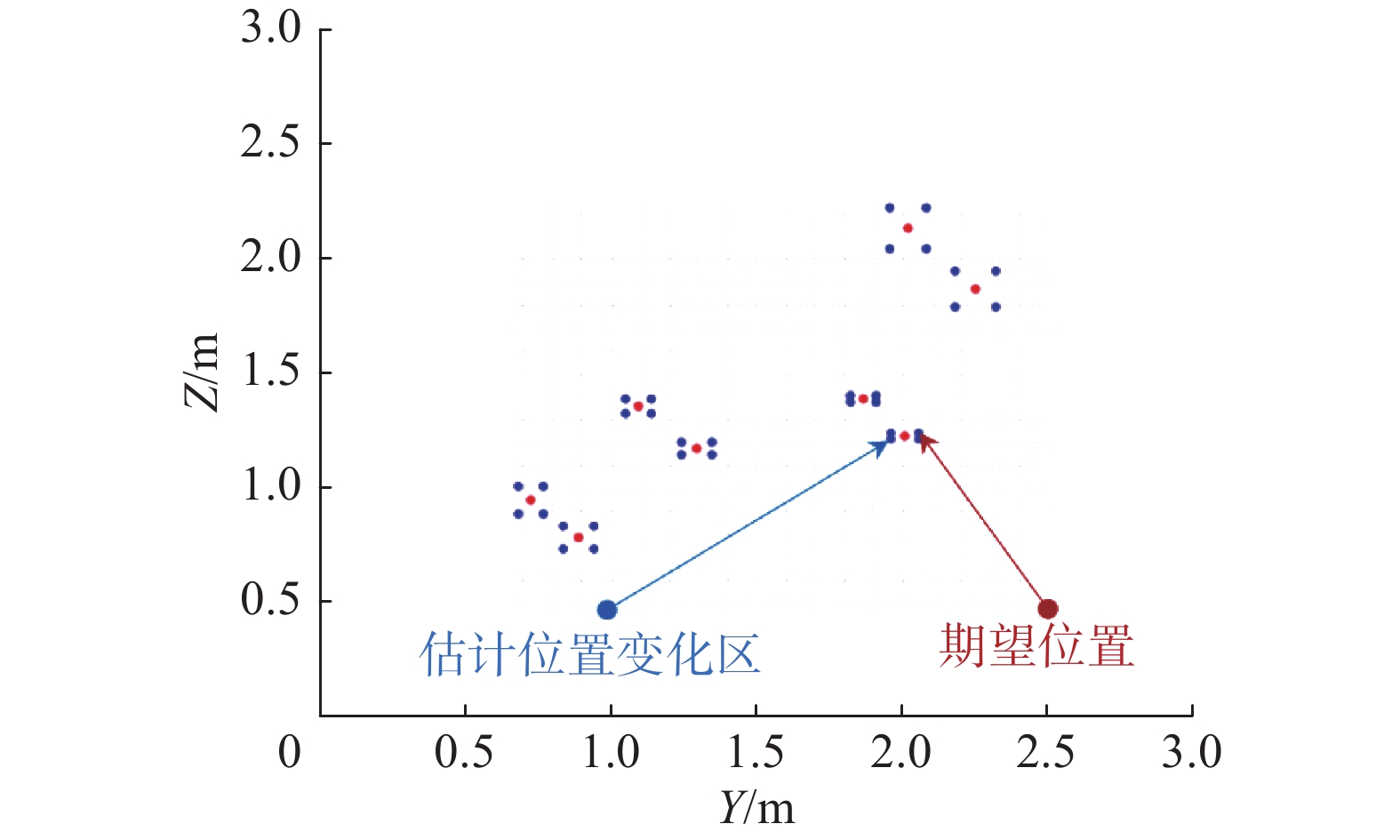
在4种不同绳缆长度下测定的数据与Indoor “GPS”对比平均误差为3.573%，误差距离为0.107 1 m。系留无人机在室内的期望位置是确定的，估计位置具有不确定性，不同绳缆长度下的估计位置与真实位置的偏差如图16所示，估计位置是在以期望位置为球的误差半径范围内波动。

基于力传感的系留无人机绳缆定位实验结果与文献[20]使用的Fotokite Pro无人机绳缆定位相对比将定位误差由0.367 5 m缩减到0.107 1 m，定位精度提升了70.86%。

5 结束语

本文建立了系留无人机悬链线模型，仅依靠系留绳缆与三维力传感器实现无人机室内定位，得益于三维力传感器能准确获得绳缆拉力，使系统定位精度达到0.107 1 m。由于三维力传感器与无人机相互独立工作，系统可复制性强，悬链线模型下获得的定位数据，将定位数据传递给飞机控制系统，可使基于力传感的系留无人机适用于更复杂的环境。未来将结合流体力学分析等进一步丰富力学模型以提高定位精度。随着系留线缆长度的增加，系留线缆对无人机飞行姿态和位置影响越来越大，非线性扰动对系留无人机的影响不可忽视，可利用深度强化学习建立系留无人机非线性扰动模型，使无人机能自适应绳缆上的非线性外力造成的影响，从而提高定位精度。