世界卫生组织在2015年发表的《全球道路安全状况报告》^[1]中指出每年约有125万人死于交通事故。通过交通大数据，识别交通事故中的规律并加以治理和预防已成为交通领域重要的研究课题。

建立有效的交通事故风险预测系统是交通事故预防的关键。如果某一区域的交通事故发生风险是可以预测的，就可以将这一信息传播给附近的司机，提醒他们选择一条不那么危险的道路；交警部门也可以在该区域有针对性地安排巡逻人员，达到减少事故发生的目的。然而交通事故发生风险的准确预测是非常困难的，交通事故的诱发因素多种多样，大致可以分为人、车、路和环境四大类^[2-3]，其中人的因素是首要因素。人的行为主观性较强，不可预测，导致虽然许多研究人员已经把注意力集中在交通事故相关的关键因素识别上，交通事故风险的有效预测仍然是一个具有挑战性的问题。

在过去，针对交通事故预测的研究主要聚焦在粗粒度、宏观方面上的研究。研究空间粒度精度聚焦在省、市层次，时间粒度聚焦在年、月份层次^[4-8]。因此研究成果的针对性不高，实用性较差，仅能提供参考性意见。近年来，随着大数据和深度学习技术的发展^[9-14]，交通事故的短期实时预测成为了可能。2016年，Chen等^[15]通过Stack去噪自动编码器来提取人的移动特征构建深度学习网络来预测日本境内交通事故风险; 2018年，Ren^[16]综合考虑交通事故的周期性和空间分布模式并结合其他重要因素如天气、空气质量等，采用LSTM模型，构建了短期北京市的交通事故风险预测系统。以上方法都对预测区域进行规则化网格划分，针对每一个网格统计其数据特征，预测网格区域短期事故发生风险。2018年，Bao等^[17]在划分的网格的基础上，利用卷积神经网络(convolutional neural networks, CNN)来计算网格的局部区域特征，从而得到了更好的预测效果。

但这些基于网格划分的交通事故短期预测方法，将规则化网格作为预测的空间单位，这些网格内包含大量的非道路区域，如居民区、商场区等。非道路区域通常不会有交通事故的发生，这在一定情况下影响了预测的准确度。交警在进行巡逻、救援等执勤任务时都以路段为单位进行划分，划分网格的预测结果只能在任务分配时提供一定程度的参考；以网格作为交通事故风险预测单位也不能满足司机根据事故发生风险来选择行进路线的需求。因此基于划分网格的短期交通事故预测方法准确度普遍不高且实用价值较低。

因此，本文提出基于路网结构的城市交通事故短期风险预测算法。该算法以真实路段而不是规则网格作为空间预测单位，使用深度学习技术预测真实路段在短期内的事故风险，完成了逐天和逐小时的交通事故风险预测任务。

路网是一个复杂的不规则网络，CNN等处理规则化数据的深度学习方法无法提取复杂网络的局部特征，因此本文引入图卷积神经网络(graph convolutional neural networks, GCNN)模型来计算路网结构的局部特征。GCNN可以处理不规则的网络数据,在深度学习领域得到了广泛的应用^[18-20]。在预测模型方面，2018年，Lin等^[20]将GCNN和LSTM结合用于纽约市共享单车站点每小时单车需求量的预测，取得良好的效果。

与迭代神经网络(recurrent neural network, RNN)相比，长短期记忆网络(long short-term memory network, LSTM)因其可以进行长时间预测的特点而在时序数据预测中广泛使用。但LSTM在处理超长序列时会导致训练时间大大增长，同时在超长的序列中进行反向传播也可能会导致梯度消失，从而削弱模型的可靠性。本文结合交通事故的时序特征，设计了双链LSTM(double link LSTM, DLSTM)，处理交通事故风险预测中超长输入的问题，取得了较好的效果。

综上所述，本文的主要贡献有以下几点：

1)提出基于路网结构、以真实路段作为空间预测单元，逐日、逐小时对城市交通事故短期风险进行预测，提高了预测结果的准确性和实际应用价值。

2)采用深度学习技术构建了基于路网的城市短期交通事故风险预测模型。在模型中使用GCNN提取交通事故预测属性的空间特征，使用优化后的DLSTM提取预测属性的时间特征，并将两者结合提取其时空特征。

3)利用杭州市的多源交通数据对模型进行了训练，并与已有的计量经济学模型和深度学习模型进行了对比，实验证明本文算法在准确度、正确率和漏报率上均优于已有算法。

1 多源交通数据及预处理 1.1 多源交通数据

本文采用浙江省杭州市西湖区总共5类与交通有关的数据进行交通事故风险的短期预测。

交通事故数据　交通事故数据由杭州市交警支队提供，数据时间跨度为2015年7月11日—2015年12月21日。交通事故数据主要包括交通事故发生的时间和位置信息，格式如表1所示。

路网结构数据　本文所使用路网结构数据从OpenStreetMap网站下载，并经过简化处理获得，其数据格式如表2所示。路网结构数据中记录各个道路路段的关键节点的经纬度坐标，及该路段邻接路段的编号。

道路微波检测数据　道路微波检测数据由杭州市交警支队提供，数据时间跨度同交通事故数据一致，为2015年7月11日—12月21日。微波检测数据由两部分构成：微波检测器分布数据和微波检测器输出数据。微波检测器分布数据如表3所示。

微波检测器每5 s记录一次道路路况，每条记录包含该路段在5 s内通过的车辆数目，以及通过车辆的平均速度，微波检测器检测数据格式如表4所示。

出租车轨迹数据　本文使用的出租车轨迹数据来自于杭州市出租车公司。时间跨度为2015年6月22日—6月30日，为期9天的数据。因为数据时间跨度很小，故本文未将其用作预测交通事故风险的属性信息，只将其作为构建路网图结构的支撑数据。出租车轨迹数据的格式如表5所示。

天气数据　本文所使用的数据由爬虫从天气后报网( http://www.tianqihoubao.com/)爬取获得，天气数据的时间跨度为2015年7月11日—12月21日，同交通事故数据一致，天气数据的主要格式如表6所示。

1.2 数据预处理

本文提出的基于路网结构的城市交通事故短期风险预测算法以真实路段作为空间预测单元，因此使用的所有属性特征应该按照路段进行划分。由2.1节可知，所有数据的位置信息以经纬度来描述，因此首先要将经纬度所代表信息绑定到相应路段。假设预测路段集合为S，待绑定的位置为 ${P_{({\rm{lng,lat}})}}$ ，位置与路段绑定的算法如下。

1)针对于路段集合S中第 $i$ 条路段，其长度为 ${l_i}$ ，位置 ${P_{({\rm{lng,lat}})}}$ 与其起点和终点的距离分别为 ${d_{i - {\rm{start}}}}$ 、 ${d_{i - {\rm{end}}}}$ ，距离采用欧几里德距离公式计算，则可得路段差值 ${d_i} = {d_{i - {\rm{start}}}} + {d_{i - {\rm{end}}}} - {l_i}$ 。

2)寻找路段m使得 ${d_m}$ 为所有路段差值的最小值。

3)定义阈值 $\varepsilon $ ，若 ${d_m}$ 小于阈值 $\varepsilon $ ，则该位置与路段m绑定；若 ${d_m}$ 不小于阈值 $\varepsilon $ ,则该位置与预测集合中的任何路段都不绑定。

根据以上位置点与路段的绑定算法，可以将交通事故、微波检测器及出租车位置信息绑定到相应路段。从而可得路段在预测交通事故时的所有属性特征。本文将路段属性数据分为3类：空间相关数据、时间相关数据、时空相关数据。

空间相关数据　仅与路段相关的特征，对于任意时间段数据值都一样。该类数据有路段长度、道路等级、车道数、道路所属区域等。

时间相关数据　仅与时间段相关联的数据，对于所有的路段数据值都一样。该类特征有天气、风力、风向、气温等。

时空相关数据　是与时间段、路段都有关联的数据。同一路段在不同时间、不同路段在相同时间都具有不同的数据值。该类数据有单位时间道路通过车辆数、单位时间道路车辆通过平均速度、单位时间内事故发生数量等。

观察数据可知，以上数据数值范围都不统一，因此并不能直接作为神经网络的输入。因此针对于所有的枚举类特征，例如天气、风向、道路所属区域等，本文采用one-hot编码。对于所有的数值型特征，本文统计最大值、最小值，然后根据最大最小值将其映射到区间 $\left[ {0,1} \right]$ 。于是所有的特征值都处在 $\left[ {0,1} \right]$ 区间内，使得深度学习框架能获得良好的效果。

在此说明，本文仅对输入特征数据进行量纲统一处理，对于预测结果，本文使用单位时间内事故发生的次数并没有映射到区间 $\left[ {0,1} \right]$ ，这也与已有算法的交通事故风险描述一致。

2 交通事故预测深度学习模型

本节首先详细地描述了基于路网的交通事故风险预测模型(traffic accidents risk prediction based on road network, TARPBRN)的总体架构，然后分别对每个主要模块进行了具体介绍。

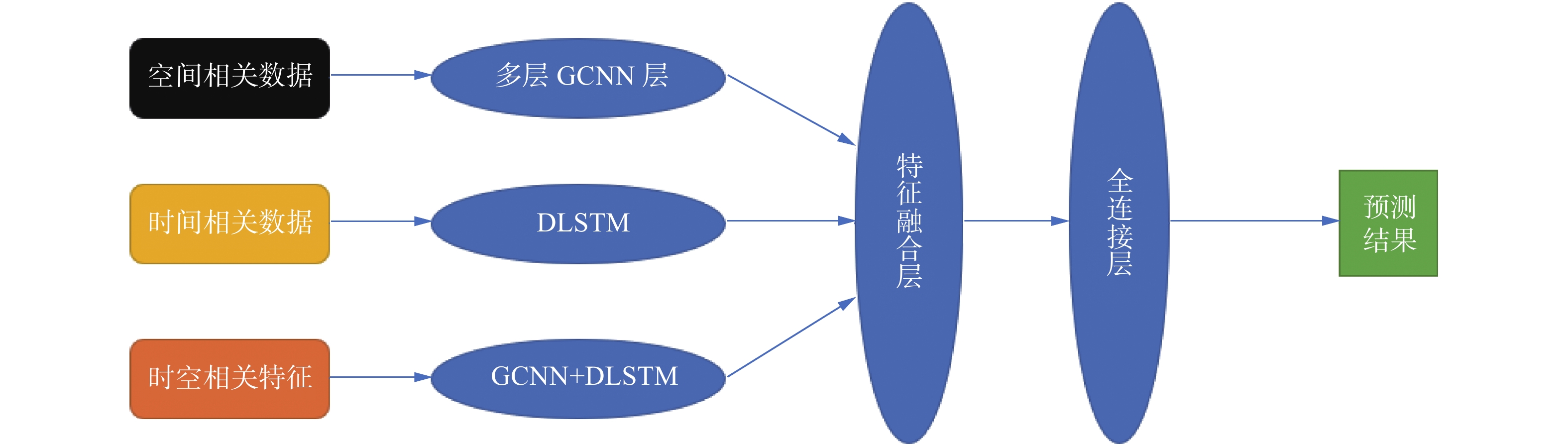
2.1 TARPBRN模型架构

由1.2节可知，本文将交通事故的诱发因素从数据特征出发主要分为三大类：时间相关特征、空间相关特征和时空相关特征，针对每一类特征，分别采用不同的网络结构进行特征提取。TARPBRN模型的总体架构如图1所示。首先，对3类属性数据进行特征提取操作。对于空间相关数据，本文使用多层GCNN来提取空间特征。对于时间相关数据采用DLSTM提取时间特征。对于时空相关数据，本文将GCNN和DLSTM相结合来提取时空特征。然后，将3类属性数据通过相应特征提取层获得的特征传入特征融合层，将3类属性特征融合为一个整体。最后，将融合后的特征传入全连接网络，通过全连接网络输出最终的预测结果。

2.2 多层GCNN层提取空间属性特征

GCNN是一种能对图数据进行深度学习的方法，在对图进行卷积神经网络学习时，可以同时考虑到节点的特征信息以及结构信息。这使得GCNN广泛用于非规则数据的深度学习。图卷积网络的主要计算方式如下：

给定图 $G = (V,{{x}},\varepsilon ,{{A}})$ ， $V$ 是N个顶点的集合, ${{x}} \in {R^N}$ 是每一个顶点特征向量的集合。 $\varepsilon $ 是边的结合，A是邻接矩阵，其中 ${A_{ij}}$ 表示两个顶点间的关联度。假设GCNN模型从输入层到输出层共有m层。图网络中的每一个顶点在 $l$ 层中都有一个长度为 ${C^l}$ 的特征向量。对于每一层 $l$ $(l=1,2,\cdots , m-1)$ ，图卷积模型GCNN以如下的规则从输入层到输出层进行传播：

$ {{{H}}^l} = \sigma ({{{D}}^{ - \frac{1}{2}}}{{A}}{{{D}}^{ - \frac{1}{2}}}{{{H}}^{l - 1}}{{{W}}^l}) $

其中D是一个对角矩阵， ${D_{ii}} = \sum {{A_{ij}}} $ ， ${{{W}}^{l - 1}} \in {R^{{C^{l - 1}} \times {C^l}}}$ 是每一层可训练的权重矩阵， $\sigma (\centerdot )$ 是一个激活函数， ${{{H}}^l} \in {R^{N\times{C^l}}}$ 是第 $l$ 层的激活输出矩阵。 ${{{H}}^{l - 1}} \in {R^{N\times{C^{l - 1}}}}$ 则是第 $l - 1$ 层的激活输出矩阵。对于第1层输入层：

$ {{{H}}^1} = \sigma ({{{D}}^{ - \frac{1}{2}}}{{A}}{{{D}}^{ - \frac{1}{2}}}{{{H}}^0}{{{W}}^1}) $

${{{H}}^0}$ 即是图网络结构中各顶点的输入特征 $x$ 。

综上可知，图卷积进行特征提取是需要输入两部分数据，图的邻接矩阵A及特征属性数据 $x$ 。特征属性数据 $x$ 由第2节经过数据预处理已经获得，图的邻接矩阵可由路网结构转化得到。

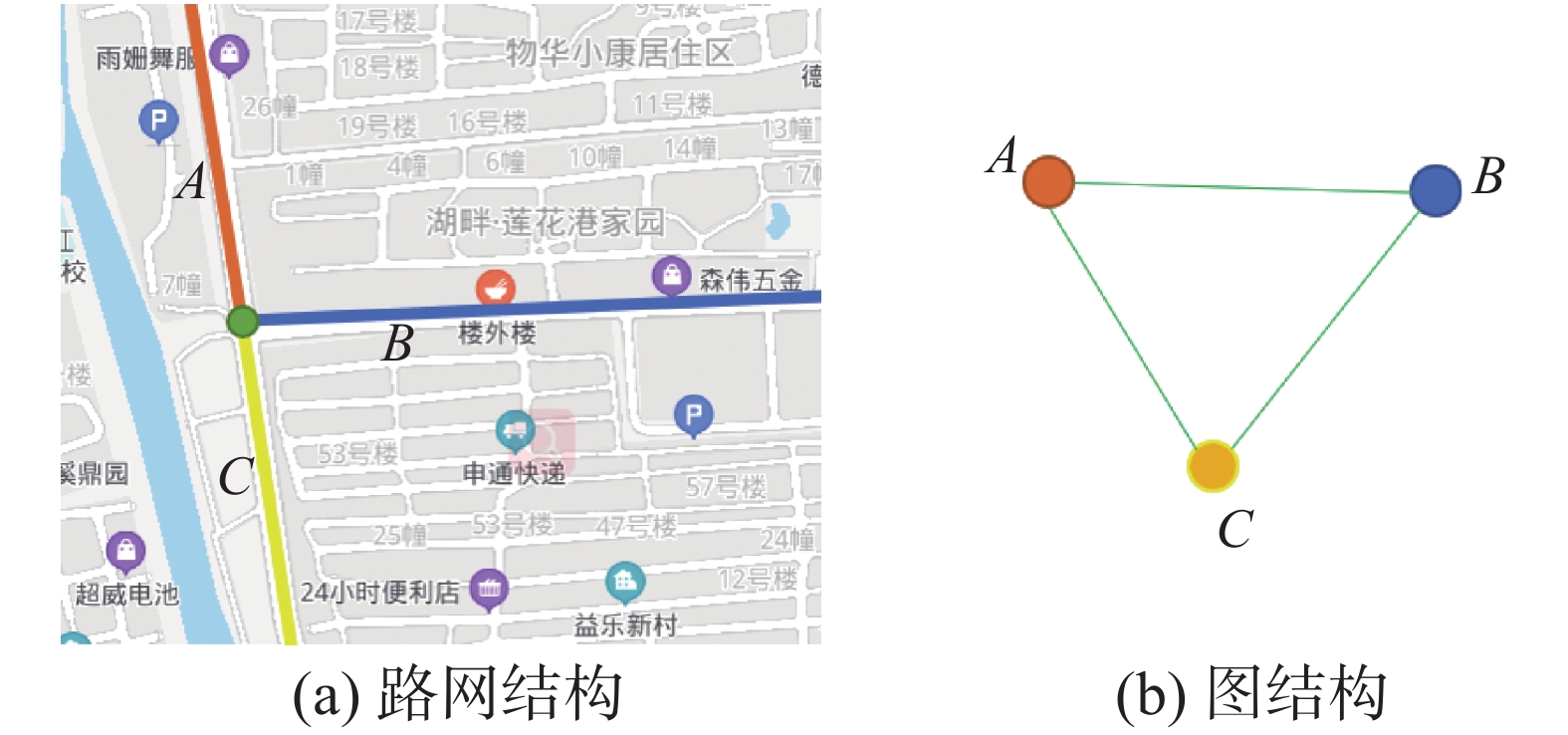
本文以路段作为空间预测单元，路段在路网结构中通常以边的形式存在，而GCNN模型主要计算图结构的顶点特征。因此本文首先要将路网中的路段转化为图结构中的顶点，将路网中的交叉点转化为边。转化方式如图2所示。

图2(a)中有3条路段A、B、C交汇于一点，当该路网结构转化为图结构时，A、B、C路段转化为3个顶点，如图2(b)所示。路段A可通过交汇点到达B，因此图结构中，顶点A与顶点B之间有边相连，同理，顶点A、B，顶点B、C之间都有边相连。

将路网结构转化为图结构后就可以得出路网结构的邻接矩阵，但此时邻接矩阵的只有0、1两个数值。0表示不连接，1表示连接。为了更明确地表示相邻路段之间的关联度，本文根据出租车轨迹数据，计算出租车经过相邻路段的次数，用该数据来描述相邻路段的关联度，在相邻路段间经过的次数越多，相邻路段之间的关联度越高，转换公式为

$ f(x) = \lg x/\lg \max $

式中：x为车辆在相邻路段经过的次数；max为车辆在相邻路段经过次数的最大值； $f(x)$ 即为转化后的关联度。

2.3 DLSTM层提取时间特征

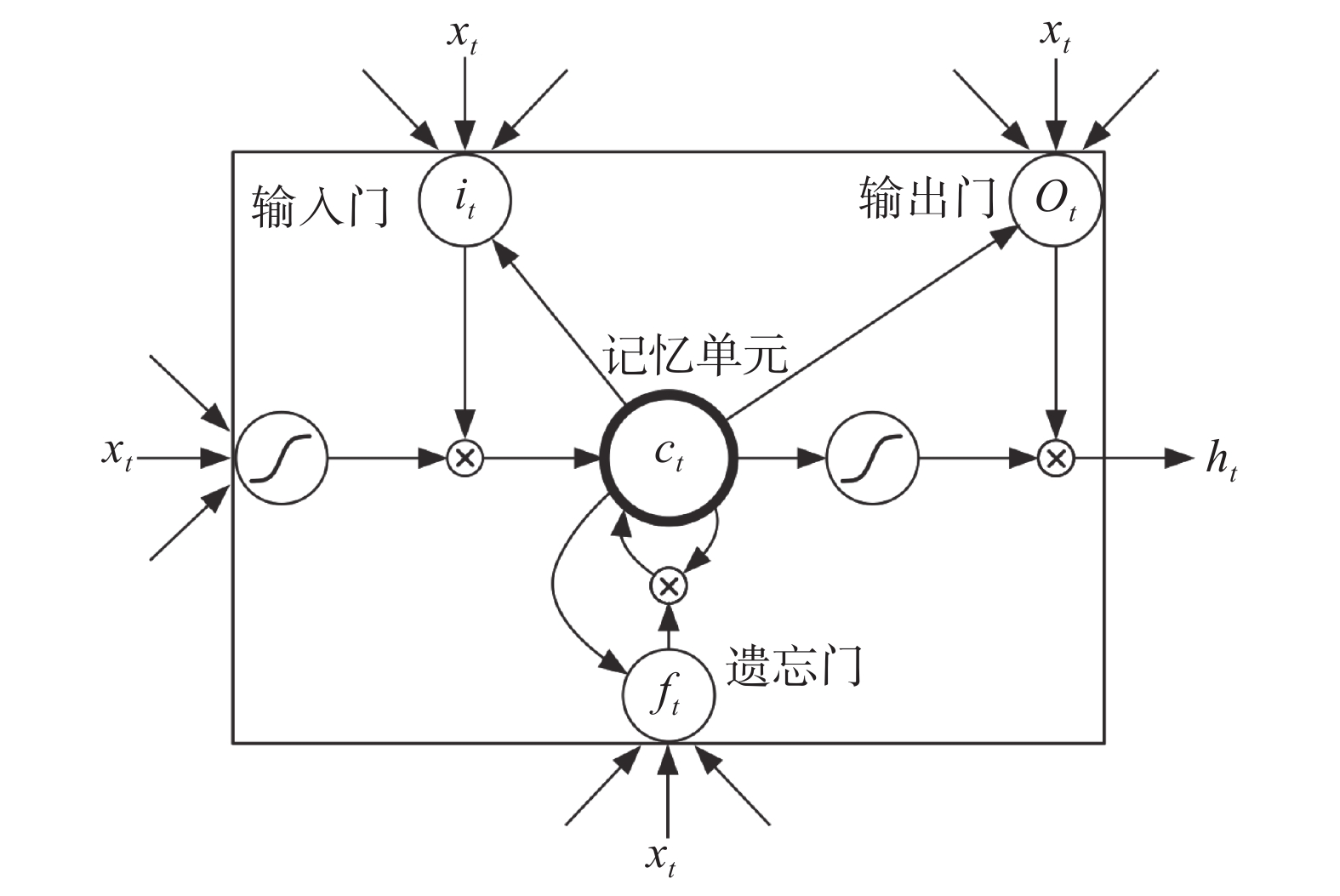
长短期记忆(long short-term memory, LSTM)是一种特殊的RNN，相比普通的RNN，LSTM能够在长序列数据中有更好的表现，它在算法中加入了一个判断信息有用与否的结构单元。如图3所示，结构单元中被放置了3扇门，即输入门、遗忘门和输出门。当一个信息进入LSTM的网络当中，可以根据规则来判断是否有用，实现信息的选择性通过。LSTM更细节的信息可以参考文献[23]。

虽然通过LSTM可以获取长期记忆的特征，但LSTM在处理超长序列时会导致训练时间大大增长，同时在超长的序列中进行反向传播也可能会导致梯度消失，从而削弱模型的可靠性。部分情况下，还可能因为冗余信息太多，无法取得良好效果。

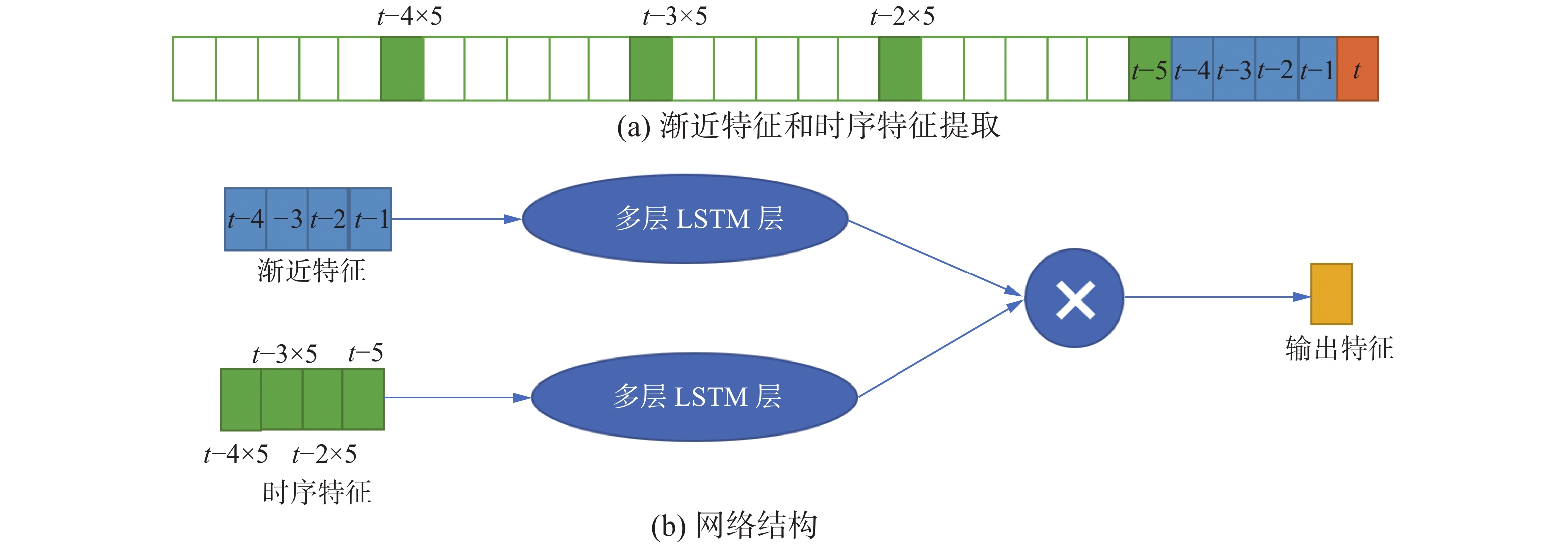
因此，基于交通事故在时序上呈现的周期性和渐近性的特征，本文提出了双链LSTM(DLSTM)网络。如图4所示。假设预测t时刻的时序特征(假设序列的周期性为5)，则提取 $t{\rm{ - }}1{\text{、}}t{\rm{ - }}2{\text{、}}t{\rm{ - }}3{\text{、}} t{\rm{ - }}4$ 时刻的特征(图中蓝色区域特征)作为渐近特征。提取 $t{\rm{ - }}5{\text{、}}t{\rm{ - }}2 \times 5{\text{、}}t{\rm{ - }}3 \times 5{\text{、}}t{\rm{ - }}4 \times 5$ 时刻的特征(图中绿色区域的特征作为周期特征)。然后将渐近特征和周期特征分别传入LSTM网络，最后将两个LSTM链中的特征进行融合，作为DLSM网络的输出特征。注意这里因为两种特征同属于多层LSTM层输出的时序特征，相互之间影响较大，故以相乘的方式进行特征融合。

2.4 GCNN与DLSTM相结合提取时空特征

在城市交通事故风险短期预测模型中，交通事故风险、道路车流量、道路行车平均速度不仅与时间相关，还与所属路段及空间有关。因此，本文将DLSTM与GCNN模型进行整合，构建了新的时空特征提取层。在整合过程中，本文提出两种方案：

1) GCNN+DLSTM模型，先对时空特征在每个时间段上进行图卷积求出局部特征，然后针对每个时间段上的图卷积特征，构建时间序列，传入到DLSTM求取其时间特征。

2) DLSTM+GCNN模型。首先根据交通事故时空特征所属路段的不同进行分类，然后将每一路段的时空序列特征传入DLSTM模型，计算其时序特征，最后将所有路段的时序特征传入GCNN模型，求取其空间特征。

本文对两种方案都进行了比较。为了介绍方便，本文在除模型对比外，将这两种方案作为一种，在下文中都采用GconvLSTM模型表示。

2.5 特征融合与全连接层

在特征融合层，将GCNN提取的空间特征、DLSTM神经网络提取的时间特征、GconvLSTM神经网络提取的时空特征串联成一个密集的向量，构建输入全连接网络的高维特征。然后通过全连接层将矢量转换为模型输出。因此，模型预测输出可转化为公式：

${\hat y_t} = {W_{{\rm{gcnn}}}}X_t^{{\rm{gcnn}}} + {W_{{\rm{DLstm}}}}X_t^{{\rm{lstm}}} + {W_{{\rm{GconvLstm}}}}X_t^{{\rm{GconvLstm}}} + {b_t}$

(1)

其中 $X_t^{{\rm{gcnn}}}$ 、 $X_t^{{\rm{lstm}}}$ 、 $X_t^{{\rm{GconvLstm}}}$ 分别表示在t时刻的空间特征、时间特征和时空特征； ${W_{{\rm{gcnn}}}}$ 、 ${W_{{\rm{DLstm}}}}$ 、 ${W_{{\rm{GconvLstm}}}}$ 、 ${b_t}$ 表示各个属性相关的权重和偏差。

2.6 损失函数

在交通事故风险预测中，绝大部分时间、绝大部分路段的交通事故发生风险值都为0，事故风险为0与事故风险非0的样本数量差距相当大，非常不平衡。为了缓解样本间的不平衡问题，本文在目标函数均方差误差的基础上进行了改进，加强事故风险不是0的样本的损失函数值。为防止在训练过程中出现过拟合现象，本文引用了L2规则化范数。因此最终的损失函数为

$ \mathop {\min }\limits_{w,b} \left( {\left\| {{y_t} - {{\hat y}_t}} \right\|_2^2} \right) \times \left( {{y_t} + 1} \right) + \alpha \left\| W \right\|_2^2 $

式中：W代表式(1)中所有的权重参数， $\alpha $ 为正则化参数。

2.7 评价函数

现有的基于深度学习的城市短期交通事故预测模型均采用划分网格的方式来进行预测，在进行方法对比时均采用MAE、MRE、RMSE这3种度量方式来对预测模型进行度量，本文同样如此。

$ \begin{array}{l} \;\;\;{\rm{MAE}} = \dfrac{1}{{{n_{}}}}\displaystyle\sum\limits_{i = 1}^n {\left| {{y_i} - {{\hat y}_i}} \right|} \\ \;\;\;\;\;{\rm{MRE}} = \dfrac{1}{n}\displaystyle\sum\limits_{i = 1}^n {\dfrac{{\left| {{y_i} - {{\hat y}_i}} \right|}}{{{y_i}}}}\\ {\rm{RMSE}} = \sqrt {\dfrac{1}{{{n_{}}}}\displaystyle\sum\limits_{i = 1}^n {{{({y_i} - {{\hat y}_i})}^2}} } \end{array} $

式中： ${y_i}$ 为路段i的交通事故真是发生风险， $\hat {{y_i}}$ 为路段i交通事故发生风险的预测值；n为所预测道路的总条数。

3 分析结果 3.1 交通事故数据的周期特征

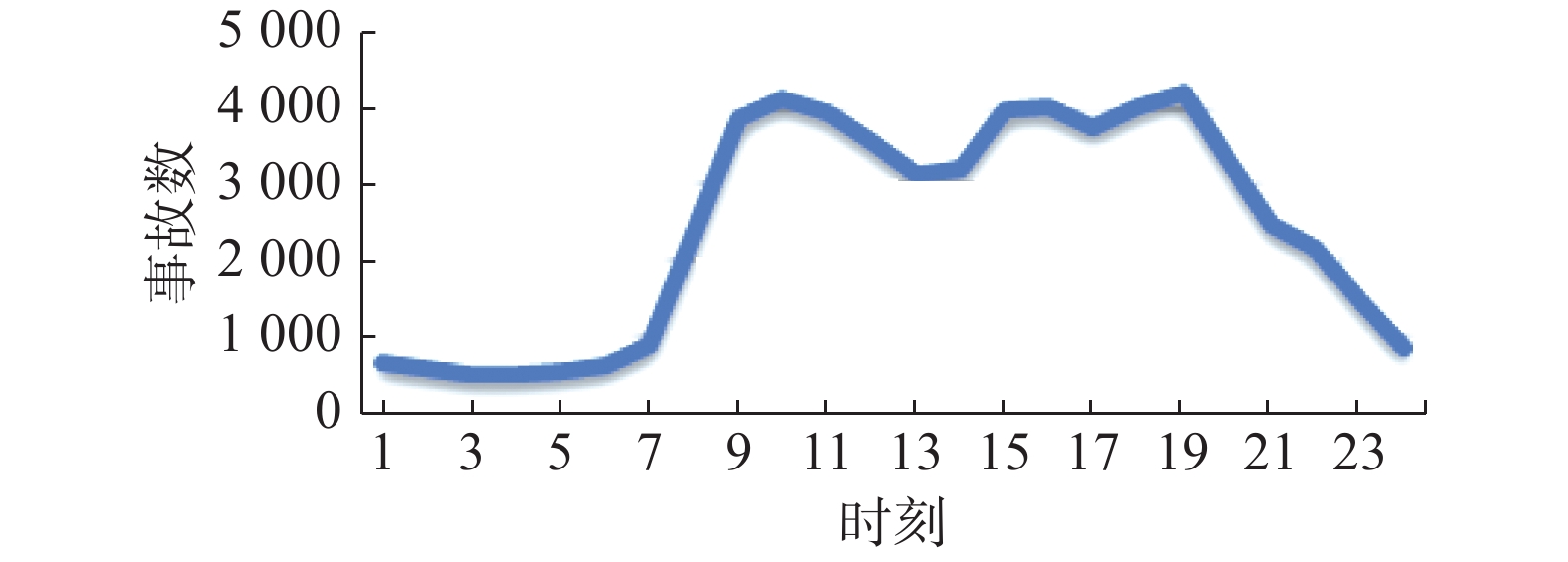
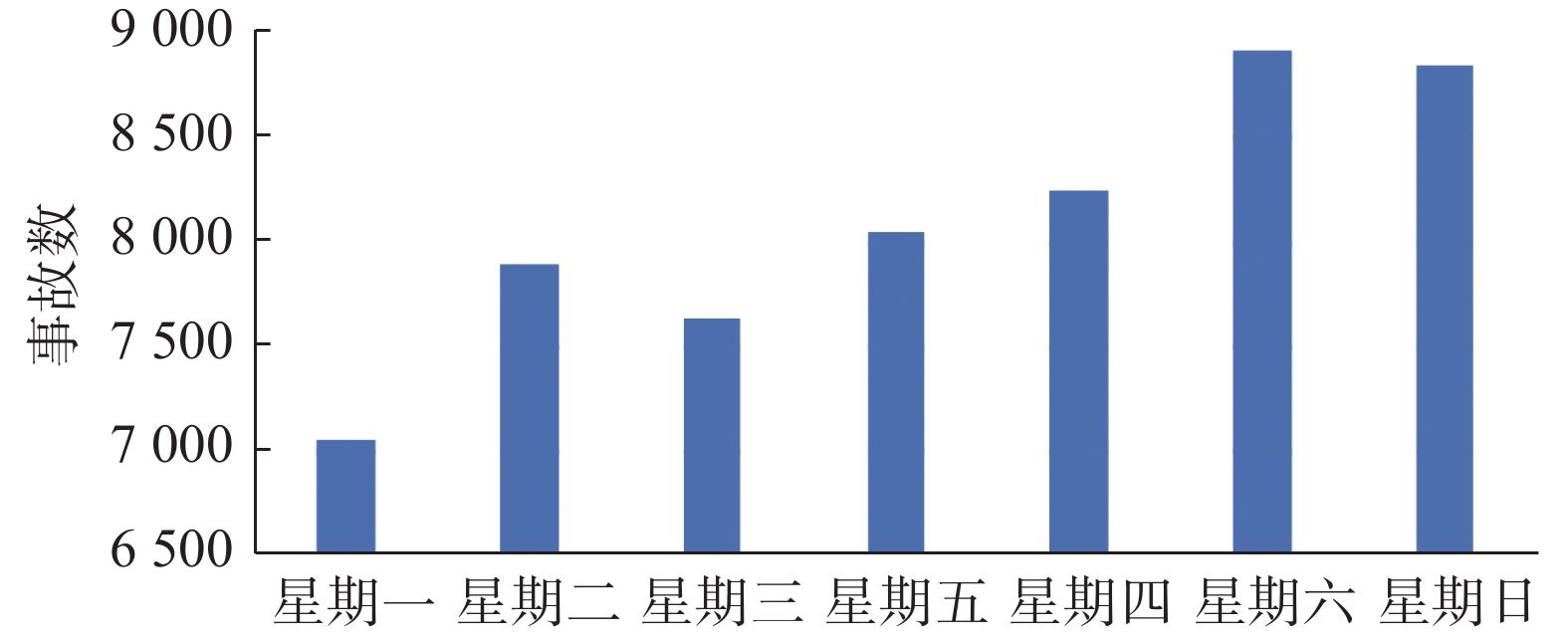
交通事故是人类活动产生的结果，因此必将在时间上呈现规律性变化。本文统计了交通事故1天和1周的分布情况，分别如图5、6所示。

由图5可知，交通事故多发生在日间，在夜间事故发生次数较少。且事故多发生在早上7~10点及晚上4~6点。由图6可知，交通事故在周末发生较多，在工作日发生事故较少。综上可知，交通事故分别以天和星期为周期呈现出一定的周期性。因此，在逐小时风险预测模型中，可以设置DLSTM的步长为24；在逐日风险预测模型中，可以设置DLSTM的步长为7。

3.2 结果分析

本研究建立了两类短期碰撞风险预测模型:逐日风险预测模型和逐小时风险预测模型。在每种预测模型中又根据时空特征提取的顺序分为GCNN+DLSTM模型和DLSTM+GCNN模型。预测数据集按7:3的比例分为训练数据集和测试数据集。在模式测试过程中，本文假设所有空间特征为S，所有时间特征为T，时空特征为ST，针对不同模型输入不同特征，则模型预测结果如表7、8所示。

分析表7、8可知，当ST特征不参与计算时，TARPBRN_CNN+DLSTM与TARPBRN_DLSTM+GCNN为同一种模型，因此结果一致。在逐小时事故风险预测结果TARPBRN_GCNN+DLSTM表现较好，而在逐天事故风险预测结果TARPBRN_DLSTM+GCNN有更好的表现，因此在进行事故预测时，可以根据预测时间的粒度，来选择合适的算法。在3类特征对比中可知，时空属性相关特征对预测结果影响最大，其次为时间相关特征，最次为空间相关特征。

3.3 模型对比

与已有的基于划分网格的城市短期交通事故风险预测系统不同，本文所提出的城市短期交通事故风险预测系统以真实的路段作为预测对象。因此本文使用的数据结构并不能直接用于已有算法，且因为预测对象不同，并不能使用MAE、MRE、RMSE 3种度量方式在不同模型间进行对比。为了在不同的预测模型间比较，经过与交警部门交流，本文提出使用准确率(acc, accuracy)，精准率(p, precision)和漏报率(FNR)3项来评估模型的预测性能。3种度量方式的计算方式如下：

$ \begin{array}{l} {\rm{acc}} = \dfrac{{{\rm{TN}} + {\rm{TP}}}}{{{\rm{TN}} + {\rm{FP}} + {\rm{FN}} + {\rm{TP}}}}\\ \;\;\;\;\;\;\;\;p = \dfrac{{{\rm{FP}}}}{{{\rm{TN}} + {\rm{FP}}}}\\ \;\;\;\;\;\;{\rm{FNR = }}\dfrac{{{\rm{FN}}}}{{{\rm{FN + TN}}}} \end{array} $

式中的变量由表9确定。

本文以几种已有模型为基准，与所提出的模型进行了比较。所选的基准测试方法可以分为两种类型：计量经济模型和深度学习模型。所选择的计量经济模型包括自回归综合移动平均模型(autoregressive integrated moving average mode, ARIMA)、随机参数(random-parameter)模型、随机效应(random-effects)模型和地理加权回归模型(geographical weighted regression，GWR)模型，所选择的机器学习模型包括堆叠降噪自动编码器(stacked denoising auto encoder, SDAE)模型、基于LSTM的交通事故风险预测模型(traffic accident risk prediction method based on LSTM, TARPML)和基于时空卷积的长短期记忆网络(spatiotemporal convolutional long short-term memory network, STCL-Net)。

ARIMA是一种应用广泛的时间序列分析方法，它可以同时集成移动平均模型、自回归部分和移动平均部分^[14]。随机效应模型假设预测结果与独立的变量不相关，可以通过观察很好地解释观测之间的空间相关性、时间相关性或者时空相关性^[15]。近年来，随机参数模型和GWR模型是解决空间异质性问题的两种潜在的碰撞建模技术，它们允许碰撞计数与预测因子之间存在不同的关系^[16]。SDAE模型是一种基于降噪编解码器的深度学习模型，在日本城市交通预测中取得了较好的效果。TARPML是一种结合多源数据，基于LSTM与全连接网络的深度学习模型，曾用于北京市的城市交通风险预测。STCL-Net在LSTM模型的基础上引入了CNN模型，充分考虑数据的空间特征对城市交通事故风险进行了预测。3种深度学习方法都基于划分网格的方法对交通事故风险进行预测。

为了进行公平的比较，所有的基准方法都采用同一批数据，并在同样的训练周期数下进行调优。但因为本文的算法为基于路段的算法，数据结构不能直接应用于基准测试方法，因此对于不同的方法数据都进行了相应的修改。例如：在划分网格的方法中，本文采用500 m×500 m网格大小对预测区域进行网格划分，并对所有网格进行预测。模型对比的预测效果如表10所示。总体来看，本文提出的算法在准确率、正确率及漏报率方面都优于其他基准模型。逐天预测模型的整体准确率要高于逐小时预测，正确率逐渐增大，但漏报率也呈变大的趋势。

4 结束语

本文以路段作为空间预测单元，预测某路段短期内的交通事故发生风险，从而给司机及交警部门在道路选择和事故治理方面提供决策依据。与已有的计量经济学模型和深度学习算法相比，本文算法在准确率、正确率和漏报率方面都表现出极大的优势。

虽然提出的基于路网的城市交通事故短期风险预测模型显示出了巨大的潜力，但在本研究中仍有几个局限性需要解决。交通事故成因复杂，涉及方方面面的因素，仅凭已有的数据能起到的预测效果有限，未来应该收集更多数据（例如车辆数据、违章数据、行人信息、司机信息等），来进行事故预测，以求取得更精确的预测效果。与传统的计量经济学模型相比，本文提出的TARPBRN模型工作起来像一个黑匣子，缺乏因子分析，这也是深度学习方法普遍存在的问题。交通事故属于小概率事件，这导致了交通事故预测中存在着严重的样本偏差问题，虽然本文通过重新构建损失函数来处理这一问题，但仍需投入大量的工作来解决这一问题。