不平衡数据的分类问题在疾病检测[1]、欺诈检测[2]以及故障诊断[3]等应用领域中受到了广泛关注。不平衡数据是指类分布明显不均衡的数据,其中样本数目多的类为多数类,而样本数目少的类为少数类。由于少数类样本数目过少,导致传统分类器的准确率偏向于多数类,即便准确率很高也无法保证少数类样本均分类正确。然而在现实生活中,少数类样本的预测结果才是人们关注的重点,如疾病检测中,人们对阳性病人检测为阴性的容忍度要远远低于阴性病人检测为阳性的容忍度。
为了提高不平衡数据的分类模型性能,近年来不少学者做了大量研究工作,主要分为算法层面和数据层面。本文重点关注数据层面的研究。在分类之前通过移除或添加一部分数据来平衡类分布是数据层面常用的做法,主要包括欠采样和过采样。传统的处理不平衡数据集的采样方法主要有随机欠采样和随机过采样。随机欠采样是指随机地移除部分多数类样本,但该方法可能会丢失部分有用的信息,导致分类器性能下降。随机过采样则是随机的复制少数类样本,使得数据的类分布平衡,但该方法由于反复复制少数类样本,增加了分类模型过拟合的可能性。为解决上述问题,Chawla等[4]提出了SMOTE(synthetic minority oversampling technique)方法,该方法通过在数据中增加人工合成的少数类样本使类分布平衡,降低了过拟合的可能性,提高了分类器在测试集上的泛化性能。
SMOTE为解决不平衡问题提供了新的方向,成为处理不平衡数据有效的预处理技术,并成功地应用于许多不同领域。SMOTE促进了解决不平衡分类问题方法的产生,同时为新的监督学习范式做出了重大贡献,如多标签分类、增量学习、半监督学习以及多实例学习等[5]。许多研究人员根据SMOTE提出了改进的算法,以克服SMOTE导致的过泛化等问题,从而提高不同应用背景下不平衡问题的分类模型性能。SMOTE方法已经成为现阶段不平衡分类领域的热点技术之一。在CNKI库与Web of Science核心集中,以“SMOTE”为关键词的近10年的发文数量总体呈逐年上升趋势,其中2018年CNKI发文量达到61篇,SCI发文量达到106篇。而以“SMOTE”和“不平衡数据”为联合关键词的近10年的发文数量总体也呈上升趋势,这种现象说明了SMOTE研究不平衡数据分类问题的重要性。此外,SMOTE论文[4]在SCI库中的引用频次逐年上升,尤其在2018年达到644次。这些数据从另一种角度说明了SMOTE方法的重要性。
1 SMOTE原理SMOTE方法是Chawla等[4]提出的应用于不平衡问题的数据预处理技术。不同于随机过采样的简单复制样本机制,SMOTE通过线性插值的方法在两个少数类样本间合成新的样本,从而有效缓解了由随机过采样引起的过拟合问题。
SMOTE的基本原理通过图1进行说明。首先从少数类样本中依次选取每个样本
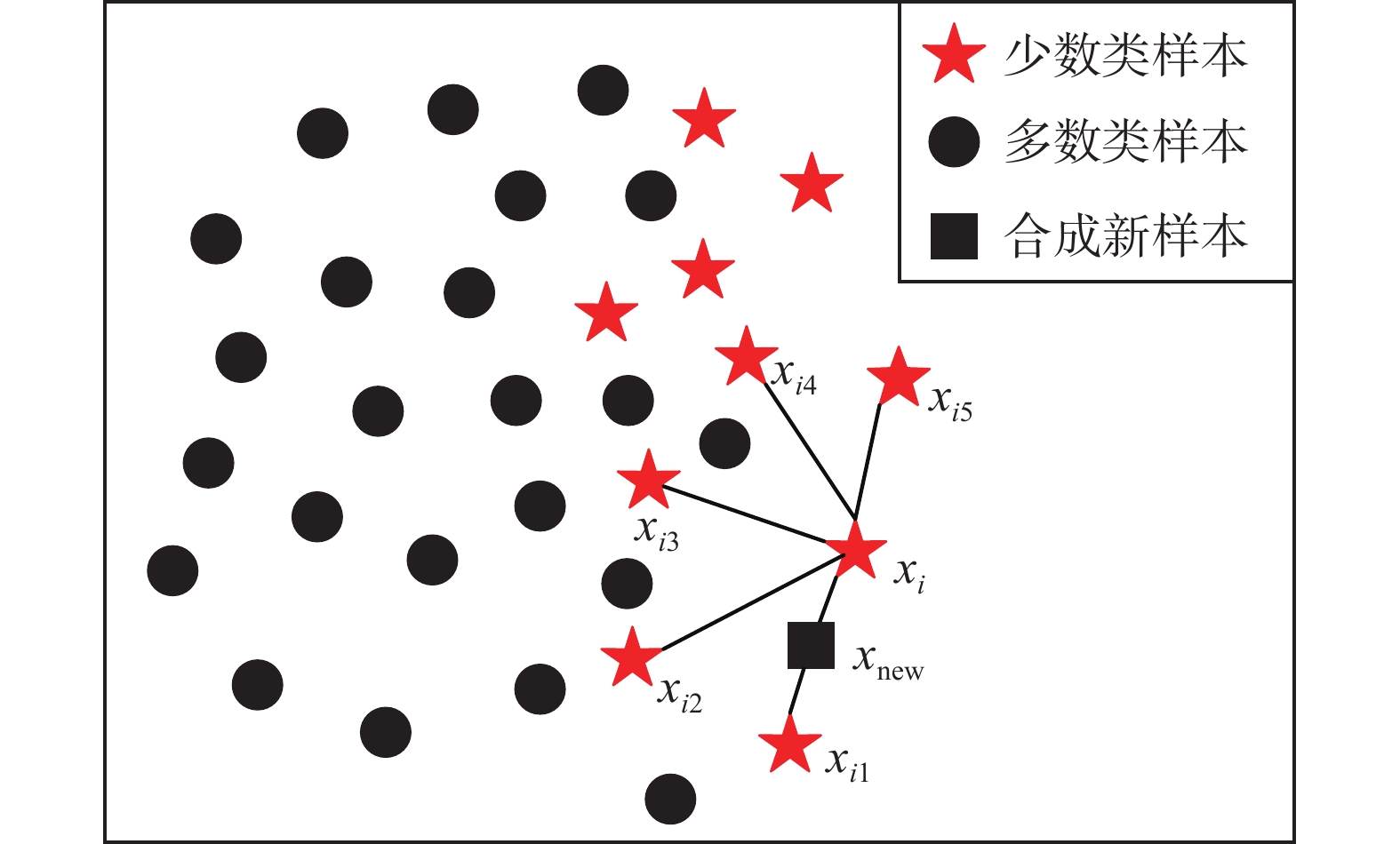
|
Download:
|
| 图 1 SMOTE算法插值说明图 Fig. 1 The interpolation illustration of SMOTE algorithm | |
| ${x_{\rm new,attr}} = {x_{i,{\rm attr}}} + ({x_{ij,{\rm attr}}} - {x_{i,{\rm attr}}}) \times \gamma $ | (1) |
其中
算法 SMOTE算法
输入 少数类样本集T,向上采样倍率n,样本近邻数k;
输出 合成少数类样本集S。
1) for i = 1 to |T| do
2) 计算
3) for l = 1 to n do
4) 从Xik中随机选取样本
5) 生成[0, 1]之间的随机数
6) 利用公式(1)合成
7) 将
8) endfor
9) endfor
SMOTE是基于特征空间的一种过采样方法,在少数类样本及其最近邻样本间合成新特征,然后组成新样本。SMOTE通过人工合成样本缓解了由随机复制样本引起的过拟合,并在许多领域得到了广泛应用,但同时也存在一些问题。
① 合成样本的质量问题
由SMOTE算法可知,新样本的合成取决于根样本与辅助样本的选择。若根样本与辅助样本均处于少数类区域,则合成的新样本被视为是合理的。然而,若根样本与辅助样本中有一个属于噪声样本,则新样本将极有可能落在多数类区域,即新样本将会成为噪声而扰乱数据集的正确分类,此时该新样本通常被视为不合理的。
② 模糊类边界问题
SMOTE算法在合成少数类样本时不考虑多数类样本的分布。如果SMOTE从处于类边界的少数类样本中合成新样本,其k近邻样本也处于类的边界,则经插值合成的少数类样本同样会落在两类的重叠区域,从而更加模糊两类的边界。
③ 少数类分布问题
少数类样本分布不均匀,既有密集区也有稀疏区时,经SMOTE过采样合成的少数类样本根据近邻原则也会分布在相应的位置,即原少数类分布密集区经SMOTE后依然相对密集,而分布稀疏区依然相对稀疏,因此,分类算法不易识别稀疏区的少数类样本而影响分类的准确性。
如果少数类样本分布稀疏且由若干碎片块组成,即使采用SMOTE方法,生成的样本也极有可能仍位于每个碎片块内,几乎不改变数据集的分布,导致识别稀疏区的样本更加困难。
2 SMOTE的改进与扩展针对上述问题,不少学者开展了新的研究,旨在提升SMOTE合成样本后数据的分类模型性能。本文搜集并整理了SMOTE算法的主要相关文献,并将其划分成SMOTE改进算法和其他方法与SMOTE相结合的算法。
2.1 SMOTE的改进算法多数SMOTE改进算法的关键在于根样本和辅助样本的选择。由于根样本是少数类样本,如果辅助样本分布在多数类周围时,则合成的新样本会加重两类的重叠。基于此,许多学者对SMOTE做了相应的改进,以提高少数类的分类效果,部分经典的改进方法见表1。
| 表 1 SMOTE改进算法 Tab.1 The improved SMOTE algorithms |
Han等[6]只考虑分布在分类边界附近的少数类样本,并将其作为根样本,提出了Borderline -SMOTE方法。首先通过k-NN方法将原始数据中的少数类样本划分成“Safe”、“Danger”和“Noise”3类,其中“Danger”类样本是指靠近分类边界的样本。根据SMOTE插值原理,对属于“Danger”类少数类样本进行过采样,可增加用于确定分类边界的少数类样本。Safe-Level-SMOTE算法[7]则关注SMOTE带来的类重叠问题,在合成新样本前分别给每个少数类样本分配一个安全系数,新合成的样本更加接近安全系数高的样本,从而保证新样本分布在安全区域内。ADASYN算法[8]根据少数类样本的分布自适应地改变不同少数类样本的权重,自动地确定每个少数类样本需要合成新样本的数量,为较难学习的样本合成更多的新样本,从而补偿偏态分布。SMOM算法是Zhu等[9]为多类不平衡问题提出的一种过采样技术,通过对辅助样本的选择,进而确定合成样本的位置。SMOM算法通过给每个少数类样本
数据集中存在噪声样本时,采用SMOTE过采样会加剧两类样本的重叠,从而影响该数据集的分类效果。文献[11-12]的实验结果表明,混合采样后数据的分类模型性能往往优于单个采样方法。融合欠采样和过采样的混合采样成为改进SMOTE方法的一种新的思路,本文介绍了部分经典的融合算法,如表2所示。
| 表 2 欠采样与SMOTE结合的方法 Tab.2 Methods combining undersampling with SMOTE |
AdaBoost-SVM-MSA算法[13]按一定规则将SVM分错的样本划分成噪声样本、危险样本与安全样本,然后直接删除噪声样本,采用约除法处理危险样本,并对安全样本进行SMOTE过采样。基于聚类的混合采样(BDSK)[14]将SMOTE的过采样与基于K-means的欠采样相结合,旨在扩大少数类样本集的同时有效剔除噪声样本。BMS算法[15]通过设置变异系数阈值将样本划分成边界域和非边界域,然后使用SMOTE以及基于欧氏距离的随机欠采样方法(OSED)[16]分别对边界域的少数类样本和非边界域的多数类样本进行采样,旨在解决在剔除噪声时由于误删少数类样本而丢失部分样本信息的问题。OSSU-SMOTEO算法[17]使用单边选择(OSS)欠采样移除多数类样本中冗余样本和边界样本,然后采用SMOTE对少数类样本过采样,从而平衡数据集,提高SVM在预测蛋白质s-磺酰化位点的分类精度。文献[18]的Hybrid Sampling使用DBSCAN和KNN剔除多数类中的模糊样本;然后采用SMOTE对重叠区域的少数类样本过采样,达到平衡数据集的目的。SDS-SMOT算法[19]利用安全双筛选丢弃远离决策边界的多数类样本和噪声样本,实现原始数据集的欠采样,采用SMOTE合成新样本实现过采样,使数据集达到基本平衡。基于 SVM 分类超平面的混合采样算法(SVM_HS)分别对多数类样本和较为重要的少数类样本进行欠采样和过采样从而平衡数据集[20]。
2.3 过滤技术与SMOTE结合的方法混合采样是克服不平衡问题中噪声样本的一种手段,然而结合噪声过滤技术同样可以消除由SMOTE合成的错误样本,如表3所示。常见的过滤技术包括基于粗糙集的过滤、数据清洗等。
| 表 3 过滤技术与SMOTE结合的方法 Tab.3 Methods combining filtering technique with SMOTE |
Ramentol等[21]将粗糙集理论的编辑技术与SMOTE算法融合,提出了SMOTE-RSB*算法。SMOTE-IPF算法[22]采用迭代分区滤波器(iterative-partitioning filter,IPF)将噪声过滤器与SMOTE融合,旨在克服不平衡问题中的噪声和边界问题。BST-CF算法[23]将SMOTE与噪声过滤器CF(classification filter)结合,在平衡数据集的同时,从多数类中消除位于边界区域的噪声样本。SSMNFOS算法[24]是一种基于随机灵敏度测量(SSM)的噪声过滤和过采样的方法,从而提高过采样方法对噪声样本的鲁棒性。NN-FRIS-SMOTE算法[25]则先筛选出代表性的样本,再使用模糊粗糙实例选择(RSIS)技术过滤噪声样本,然后使用SMOTE过采样少数类样本,从而增加了正确识别产品缺陷的可能性。基于数据清洗的过滤算法中典型的有SMOTE-Tomek和SMOTE-ENN算法[26],SMOTE-Tomek利用SMOTE对原始数据过采样来扩大样本集,移除采样后数据集中的Tome Link对,从而删除类间重叠的样本,其中Tome Link对是指分属不同类别且距离最近的一对样本,这类样本通常位于类间或者是噪声样本。SMOTE-ENN则是通过对采样后的数据集采用k-NN方法分类,进而剔除判错的样本。
2.4 聚类算法与SMOTE结合的方法聚类算法和SMOTE结合是调整数据分布的另一种思路,其主要策略通常有两种:一是直接采用聚类算法将少数类样本划分成多个簇,在簇内进行插值;二是利用聚类算法识别样本类型,对不同类型的样本采用不同的方式处理,然后再使用SMOTE进行过采样,部分算法如表4所示。
| 表 4 聚类算法与SMOTE结合的方法 Tab.4 Methods combining clustering algorithm with SMOTE |
MWMOTE算法[27]按照与多数类样本的距离对难以学习的少数类样本分配权重,采用聚类算法从加权的少数类样本合成样本,从而保证这些新样本位于少数类区域内。对于多类不平衡问题,FCMSMT算法[28]使用模糊C均值(FCM)对样本多的目标类聚类,选出与平均样本数相同数量的样本,而对样本少的目标类使用SMOTE过采样,从而降低类内与类间的错误,提高分类性能。K-means SMOTE算法[29]利用K-means对输入数据集聚类,在少数类样本多的簇内进行SMOTE过采样,从而避免噪声的生成,有效改善类间不平衡。
CB-SMOTE算法[30]根据“聚类一致性系数”找出少数类的边界样本,再根据最近邻密度删除噪声样本,同时确定合成样本的数量,然后从这些边界样本中人工合成新样本。CURE-SMOTE算法[31]采用CURE(clustering using representatives)对少数类样本聚类并移除噪声和离群点,然后使用SMOTE在代表性样本和中心样本间插值以平衡数据集。HPM算法[32]通过整合DBSCAN的离群检测、SMOTE和随机森林,从而成功预测糖尿病和高血压疾病。IDP-SMOTE算法[33]利用改进的密度峰值聚类算法(improved-DP)对各个类进行聚类,识别并剔除噪声样本,然后采用自适应的方法对每个少数类样本进行SMOTE过采样。
3 面向特定应用背景的SMOTE 3.1 面向高维数据的SMOTE高维不平横数据中的数据分布稀疏、特征冗余或特征不相关等问题是影响传统学习算法难以识别少数类样本的原因。SMOTE在处理这类问题时效果甚至不如随机欠采样方法[34],而目前常见的做法是在分类前使用现有的技术对数据进行降维,然后在新的维度空间下学习。常见的降维技术有主成分分析(PCA)[35]、特征选择、Bagging[36]、内核函数(kernel functions)[37]、流形技术(manifold techniques)[38]和自动编码器(auto-encoders)[39]等。
Li等[40]提出了基于LASSO的特征选择模型,首先使用特征选择和其他方法删除数据中冗余和不相关的特征,然后采用基于LASSO的特征权重选择模型增加关键数据的权重,再利用SMOTE平衡数据集,从而有效消除高维数据中噪声和不相关数据。Zhang等[41]通过改进的SVM-RFE[42]算法(SVM-BRFE)对高维数据进行特征选择,并采用改进的重采样PBKS算法对不平衡数据进行过采样,提出了针对高维不平衡数据二分类的BRFE-PBKS-SVM算法。在处理高维不平衡的医疗数据时,许召召等[43]将SMOTE与Filter-Wrapper特征选择算法相融合,并将其应用于支持临床医疗决策。Guo等[44]使用基于随机森林(RF)的特征选择方法降低计算复杂度,然后通过结合SMOTE和Tomek Link的重采样平衡数据集,从而提高膜蛋白预测的准确性。
3.2 面向回归问题的SMOTE不平衡数据的回归问题是指预测连续目标变量的罕见值的问题。目标变量为离散值的不平衡分类问题一直以来得到了深入的研究,而不平衡回归问题的研究成果却少之又少。回归问题可以分为两类:传统回归与序数回归。
传统回归是指在不考虑数据集有序特性的情况下,对连续型目标变量的预测问题。SMOTER算法[45]是处理不平衡回归数据的一种改进的SMOTE过采样方法,通过人为给定的阈值将极少数实例定义成极高值和极低值,并将这两种类型作为单独的情况处理,而合成样本的目标变量值则是通过两个所选样本目标变量的加权平均值确定。Moniz等[46]考虑时间序列的特性,将SMOTER算法推广到不平衡的时间序列问题中,从而提出了SM_B、SM_T和SM_TPhi 3种方法。Branco等[47]结合SMOTER方法,提出了基于bagging的集成方法(REBAGG),以解决不平衡回归问题。
序数回归则考虑数据集的有序特征,将原始数据的目标变量值按人为给定的阈值依次划分成多个有序的类标签,然后对这些类标签分类。在序数回归的有序类标签中,两端的类通常是极端情况,这类样本也占少数,因此序数回归本质上是一种类不平衡问题。Pérez-Ortiz等[48]提出了OGONI, OGOISP 和 OGOSP 3种基于图的过采样方法,旨在平衡有序信息。但是,这3种方法只考虑到少数类及其相邻类的局部排序,忽略了其他类的排序。因此,Zhu等[49]提出了SMOR算法,对每个少数类样本,找到与其类别相同和相邻的k个近邻样本,沿每个近邻样本分配不同的权重,以控制合成的样本更加靠近少数类,从而保证样本结构的有序性。
3.3 面向分类型数据的SMOTESMOTE过采样是从特征的角度生成新样本,新样本的特征是从根样本与辅助样本对应的特征间插值产生,而插值的关键在于距离的度量。SMOTE过采样所选择的欧氏距离只能处理数值型数据,而对分类型数据过采样的方法有两种:分类型数据数值化和改进距离度量公式。
分类型数据数值化方法对数值化后的数据使用SMOTE插值,是处理分类型数据常用的方法之一。然而,插值后属性值是否合理是SMOTE方法面临的问题。Chawla等[4]对含有分类型属性数据分别提出了SMOTE-NC和SMOTE-N算法,前者仍采用欧氏距离来计算,对分类型属性间的距离则采用连续属性标准差的中值来代替;后者则采用VDM(value difference metric)距离公式[50]来度量两个样本间的距离。Kurniawati等[51]也利用VDM改进了ADASYN,提出了ADASYN-N和ADASYN-KNN算法,用来处理具有分类型数据的多类数据集。针对含有分类型属性的距离度量,现阶段已经得到了广泛研究,相比VDM度量,HVDM(heterogeneous value difference metric)度量[52]在处理混合属性的数据时更具优势。其他处理含有分类型属性的距离度量包括Ahmad’s 距离度量[53]、KL散度[54]以及基于context的距离度量[55]等。图2总结了上述3种不同应用背景下处理不平衡数据的相关技术或方法。
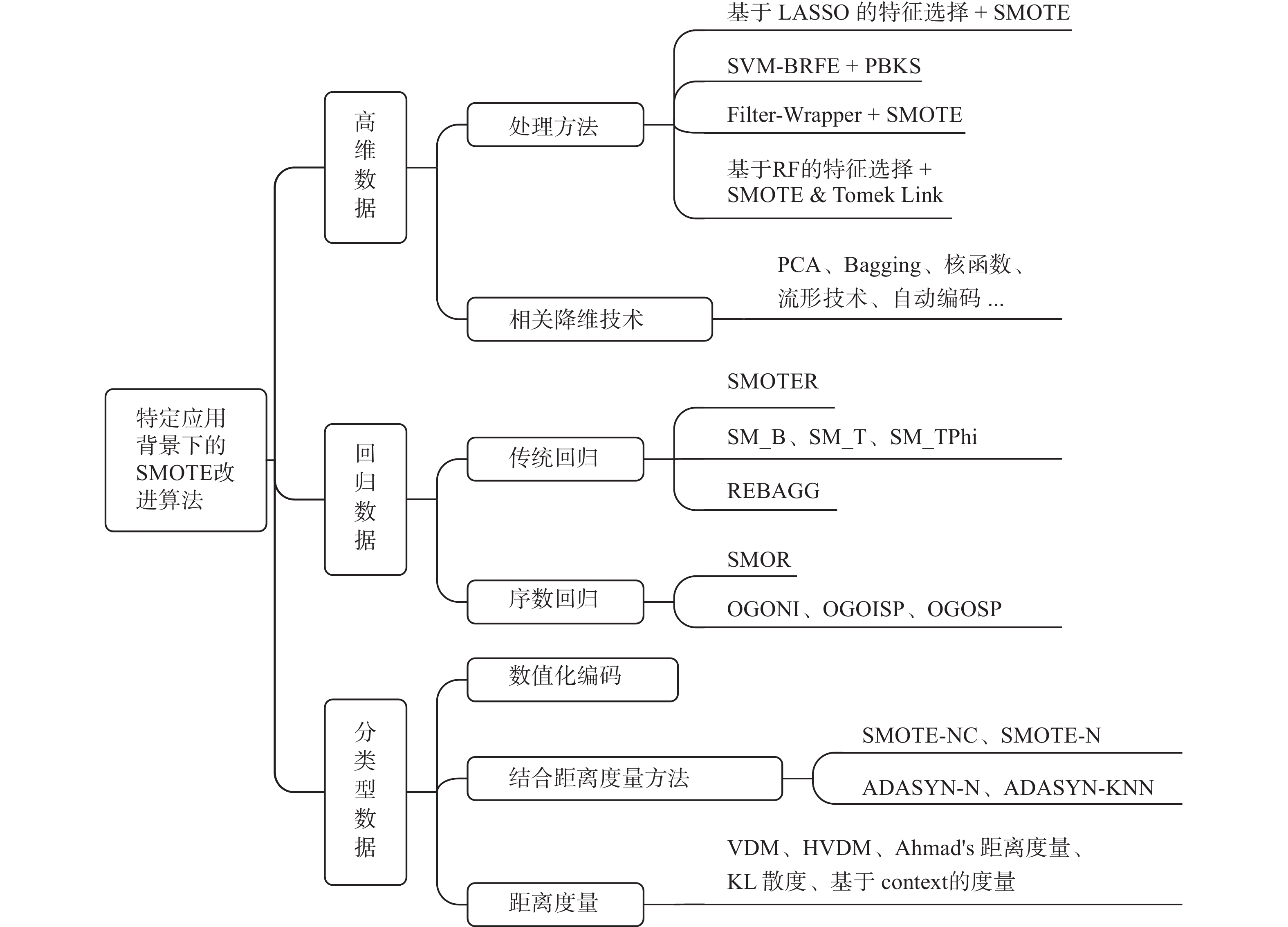
|
Download:
|
| 图 2 面向不同应用的SMOTE改进方法 Fig. 2 The improved SMOTE methods for different applications | |
SMOTE算法在处理不平衡数据时表现出良好的优势,然而现实中数据的表现形式多种多样,在面临不同类型不平衡数据(如大数据、流数据等)时,如何利用SMOTE等技术来提升学习算法性能仍需深入研究。
4.1 不平衡大数据基于分布式计算的分类算法是处理大数据的主要解决思路。典型的分布式计算技术MapReduce及其开源实现Hadoop-MapReduce为处理大数据提供了成熟的框架和平台。然而,在处理不平衡大数据时,由于高维、缺乏少数类样本等因素,以至于分布在每个站点的数据块所包含的少数类样本更少,而直接采用SMOTE过采样将变得更加困难。Rio等[56]将SMOTE算法应用于大数据的MapReduce工作流中,将输入数据分割成若干个独立的数据块并传输到各个机器,每个Map任务负责使用SMOTE从相应的分区中生成数据,Reduce阶段随机化Map阶段的输出,最终形成一个平衡的数据集。当数据集中存在小碎片时,结果可能会产生严重的偏差。SMOTE合成样本是基于k-NN算法的,对同一个少数类样本而言,其在独立数据块的近邻样本极有可能与原始数据不同,因此经过插值得到的数据很可能有偏,甚至扰乱原始数据的分布。如何改进分布式环境中的SMOTE算法,提高分布式系统中合成样本的质量需要继续探索。
4.2 不平衡流数据不平衡分类问题处理的数据通常是静态的,然而现实中的数据大多是以流的方式出现的动态数据,其数据分布也会随时间延续而不断变化。不平衡流数据在网络监控、故障检测等领域广泛出现,在线学习是处理流数据的关键技术,但在线实时学习数据流时可能会面临一些困难[57]。一方面,流数据的分布随时间而改变,导致内在结构不稳定从而产生概念漂移[58]。另一方面,由于缺乏先验知识,无法事先获取新增数据的类标签,导致数据的不平衡状态不稳定,无法确定哪个类是少数类或者多数类[59-60]。集成框架下的代价敏感学习[61-62]与SMOTE预处理技术[63]是解决上述问题的主要手段。从SMOTE预处理技术的角度而言,窗口化过程意味着只向预处理算法提供总数据的一个子集,从而影响了合成数据的质量[5]。因此如何有效利用流数据,提高合成数据质量,进而提升SMOTE算法性能是下一步需要解决的问题。
4.3 少量标签的不平衡数据监督学习的重要前提是获得足够多的有标签数据来训练预测模型。然而现实中的数据通常是未经标记的无标签数据,有标签数据只占少数,且获得大量有标签数据非常困难。特别是在不平衡数据中,从少量少数类数据中获取带标签的数据更是难上加难。如何利用少量标签数据提升学习器的泛化性能是目前不平衡分类问题的瓶颈之一。主动学习是处理这类问题的技术之一,通过引入专家知识对信息量大的无标签数据进行标记从而提高模型精度。半监督学习[57]则是另一种技术,该技术不依赖于外界交互,而是自动地利用无标签数据的内在信息改进分类模型,从而提高学习性能。此外一些学者试图在这种学习范式中,利用SMOTE生成新的数据,从而弥补由大量无标签数据引起的缺陷[64-67]。然而如何选择和使用信息量丰富的数据仍需进一步深入研究。
4.4 其他类型数据除上述3种类型的数据外,还存在其他不同类型的不平衡数据,如高维数据、数值型标签数据以及二值属性数据等。尽管关于这类型数据取得了一些成果(见第3节),但仍面临一些问题。
高维数据由于其分布稀疏、特征维数高的特点,导致传统学习算法处理起来过于困难,在预处理前对数据进行降维是目前主要解决方案。虽然已经研究出许多可用的降维技术,但是,如何扩展或修改SMOTE算法,使其能够直接应用于高维数据,避免数据降维工作,是一个值得深入研究的方向。
调整数值型标签数据的分布是回归领域中预处理所面临的问题,将数值型标签转换为离散型是一种解决思路。但对一些特殊的回归问题,经过离散化标签后的数据本质上存在一种有序关系,如何调整合成样本的区域,使得生成的新样本位于其类内或相邻类内,而不改变原始数据的本质特性是这类问题的关键。
二值属性数据是分类型数据的特殊形式,分类型数据数值化是其中一种处理方式,使用SMOTE对数值化后的数据进行过采样,是对这类问题常见的预处理解决方案。但合成的新样本通常会不合理,如某二值属性取值为0(红)和1(蓝),经过插值生成的新样本的对应特征值为0.65,则该特征值显然没有任何意义,因此,合成新样本的特征取值需要考虑其原始属性值的范围,然后对其进行调整,以符合实际意义。将分类型数据的距离度量与SMOTE融合是处理分类型不平衡数据的另一个流行方法,因此,合理考虑这类问题的本质特性,探索有效的距离度量方法是目前另一个研究热点。
5 结束语SMOTE过采样解决了随机过采样的过拟合问题,是数据层面流行的预处理技术。本文主要阐述了SMOTE过采样的研究现状与工作原理,针对SMOTE存在的问题,对一些改进的SMOTE算法进行了综述,同时概述了不同应用背景下关于SMOTE算法的研究工作,最后分析了SMOTE算法在处理不平衡大数据、不平衡流数据、少量标签的不平衡数据等数据时需要进一步探索和研究的问题。本文可为SMOTE的研究和应用提供有价值的借鉴和参考。
| [1] |
VASIGHIZAKER A, JALILI S. C-PUGP: a cluster-based positive unlabeled learning method for disease gene prediction and prioritization[J]. Computational biology and chemistry, 2018, 76: 23-31. DOI:10.1016/j.compbiolchem.2018.05.022 ( 0) 0)
|
| [2] |
JURGOVSKY J, GRANITZER M, ZIEGLER K, et al. Sequence classification for credit-card fraud detection[J]. Expert systems with applications, 2018, 100: 234-245. DOI:10.1016/j.eswa.2018.01.037 ( 0) 0)
|
| [3] |
KIM J H. Time frequency image and artificial neural network based classification of impact noise for machine fault diagnosis[J]. International journal of precision engineering and manufacturing, 2018, 19(6): 821-827. DOI:10.1007/s12541-018-0098-8 ( 0) 0)
|
| [4] |
CHAWLA N V, BOWYER K W, HALL L O, et al. SMOTE: synthetic minority over-sampling technique[J]. Journal of artificial intelligence research, 2002, 16(1): 321-357. ( 0) 0)
|
| [5] |
FERNÁNDEZ A, GARCIA S, HERRERA F, et al. SMOTE for learning from imbalanced data: Progress and challenges, marking the 15-year anniversary[J]. Journal of artificial intelligence research, 2018, 61: 863-905. DOI:10.1613/jair.1.11192 ( 0) 0)
|
| [6] |
HAN Hui, WANG Wenyuan, MAO Binghuan. Borderline-SMOTE: a new over-sampling method in imbalanced data sets learning[C]//Proceedings of International Conference on Intelligent Computing. Hefei, China, 2005: 878−887.
( 0) 0)
|
| [7] |
BUNKHUMPORNPAT C, SINAPIROMSARAN K, LURSINSAP C. Safe-level-SMOTE: safe-level-synthetic minority over-sampling TEchnique for handling the class imbalanced problem[C]//Proceedings of the 13th Pacific-Asia Conference on Knowledge Discovery and Data Mining. Bangkok, Thailand, 2009: 475−482.
( 0) 0)
|
| [8] |
HE Haibo, BAI Yang, GARCIA E A, et al. ADASYN: adaptive synthetic sampling approach for imbalanced learning[C]//Proceedings of 2008 IEEE International Joint Conference on Neural Networks. Hong Kong, China, 2008: 1322−1328.
( 0) 0)
|
| [9] |
ZHU Tuanfai, LIN Yaping, LIU Yonghe. Synthetic minority oversampling technique for multiclass imbalance problems[J]. Pattern recognition, 2017, 72: 327-340. DOI:10.1016/j.patcog.2017.07.024 ( 0) 0)
|
| [10] |
DOUZAS G, BACAO F. Geometric SMOTE a geometrically enhanced drop-in replacement for SMOTE[J]. Information sciences, 2019, 501: 118-135. DOI:10.1016/j.ins.2019.06.007 ( 0) 0)
|
| [11] |
SEIFFERT C, KHOSHGOFTAAR T M, VAN HULSE J. Hybrid sampling for imbalanced data[J]. Integrated computer-aided engineering, 2009, 16(3): 193-210. DOI:10.3233/ICA-2009-0314 ( 0) 0)
|
| [12] |
GAZZAH S, HECHKEL A, AMARA N E B. A hybrid sampling method for imbalanced data[C]//Proceedings of 2015 IEEE 12th International Multi-Conference on Systems, Signals & Devices. Mahdia, Tunisia, 2015: 1−6.
( 0) 0)
|
| [13] |
古平, 欧阳源遊. 基于混合采样的非平衡数据集分类研究[J]. 计算机应用研究, 2015, 32(2): 379-381, 418. GU Ping, OUYANG Yuanyou. Classification research for unbalanced data based on mixed-sampling[J]. Application research of computers, 2015, 32(2): 379-381, 418. DOI:10.3969/j.issn.1001-3695.2015.02.014 (  0) 0)
|
| [14] |
SONG Jia, HUANG Xianglin, QIN Sijun, et al. A bi-directional sampling based on k-means method for imbalance text classification[C]//Proceedings of 2016 IEEE/ACIS International Conference on Computer and Information Science. Okayama, Japan, 2016: 1−5.
( 0) 0)
|
| [15] |
冯宏伟, 姚博, 高原, 等. 基于边界混合采样的非均衡数据处理算法[J]. 控制与决策, 2017, 32(10): 1831-1836. FENG Hongwei, YAO Bo, GAO Yuan, et al. Imbalanced data processing algorithm based on boundary mixed sampling[J]. Control and decision, 2017, 32(10): 1831-1836. (  0) 0)
|
| [16] |
赵自翔, 王广亮, 李晓东. 基于支持向量机的不平衡数据分类的改进欠采样方法[J]. 中山大学学报(自然科学版), 2012, 51(6): 10-16. ZHAO Zixiang, WANG Guangliang, LI Xiaodong. An improved SVM based under-sampling method for classifying imbalanced data[J]. Acta Scientiarum Naturalium Universitatis Sunyatseni, 2012, 51(6): 10-16. (  0) 0)
|
| [17] |
JIA Cangzhi, ZUO Yun. S-SulfPred: a sensitive predictor to capture S-sulfenylation sites based on a resampling one-sided selection undersampling-synthetic minority oversampling technique[J]. Journal of theoretical biology, 2017, 422: 84-49. DOI:10.1016/j.jtbi.2017.03.031 ( 0) 0)
|
| [18] |
HANSKUNATAI A. A new hybrid sampling approach for classification of imbalanced datasets[C]//Proceedings of 2018 International Conference on Computer and Communication Systems. Nagoya, Japan, 2018: 67−71.
( 0) 0)
|
| [19] |
SHI Hongbo, GAO Qigang, JI Suqin, et al. A hybrid sampling method based on safe screening for imbalanced datasets with sparse structure[C]//Proceedings of 2018 International Joint Conference on Neural Networks. Rio de Janeiro, Brazil, 2018: 1−8.
( 0) 0)
|
| [20] |
吴艺凡, 梁吉业, 王俊红. 基于混合采样的非平衡数据分类算法[J]. 计算机科学与探索, 2019, 13(2): 342-349. WU Yifan, LIANG Jiye, WANG Junhong. Classification algorithm based on hybrid sampling for unbalanced data[J]. Journal of frontiers of computer science and technology, 2019, 13(2): 342-349. DOI:10.3778/j.issn.1673-9418.1804041 (  0) 0)
|
| [21] |
RAMENTOL E, CABALLERO Y, BELLO R, et al. SMOTE-RSB*: a hybrid preprocessing approach based on oversampling and undersampling for high imbalanced data-sets using SMOTE and rough sets theory
[J]. Knowledge and information systems, 2012, 33(2): 245-265. DOI:10.1007/s10115-011-0465-6 ( 0) 0)
|
| [22] |
SÁEZ J A, LUENGO J, STEFANOWSKI J, et al. SMOTE–IPF: addressing the noisy and borderline examples problem in imbalanced classification by a re-sampling method with filtering[J]. Information sciences, 2015, 291: 184-203. DOI:10.1016/j.ins.2014.08.051 ( 0) 0)
|
| [23] |
RADWAN A M. Enhancing prediction on imbalance data by thresholding technique with noise filtering[C]//Proceedings of 2017 International Conference on Information Technology. Amman, Jordan, 2017: 399−404.
( 0) 0)
|
| [24] |
ZHANG Jianjun, NG W. Stochastic sensitivity measure-based noise filtering and oversampling method for imbalanced classification problems[C]//Proceedings of 2018 IEEE International Conference on Systems, Man, and Cybernetics. Miyazaki, Japan, 2018: 403−408.
( 0) 0)
|
| [25] |
BISPO A, PRUDENCIO R, VÉRAS D. Instance selection and class balancing techniques for cross project defect prediction[C]//Proceedings of 2018 Brazilian Conference on Intelligent Systems. Sao Paulo, Brazil, 2018: 552−557.
( 0) 0)
|
| [26] |
BATISTA G E A P A, PRATI R C, MONARD M C. A study of the behavior of several methods for balancing machine learning training data[J]. ACM SIGKDD explorations newsletter, 2004, 6(1): 20-29. DOI:10.1145/1007730.1007735 ( 0) 0)
|
| [27] |
BARUA S, ISLAM M M, YAO Xin, et al. MWMOTE-majority weighted minority oversampling technique for imbalanced data set learning[J]. IEEE transactions on knowledge and data engineering, 2014, 26(2): 405-425. DOI:10.1109/TKDE.2012.232 ( 0) 0)
|
| [28] |
PRUENGKARN R, WONG K W, FUNG C C. Multiclass imbalanced classification using fuzzy C-mean and SMOTE with fuzzy support vector machine[C]//Proceedings of the 24th International Conference on Neural Information Processing. Guangzhou, China, 2017: 67−75.
( 0) 0)
|
| [29] |
DOUZAS G, BACAO F, LAST F. Improving imbalanced learning through a heuristic oversampling method based on k-means and SMOTE[J]. Information sciences, 2018, 465: 1-20. DOI:10.1016/j.ins.2018.06.056 ( 0) 0)
|
| [30] |
楼晓俊, 孙雨轩, 刘海涛. 聚类边界过采样不平衡数据分类方法[J]. 浙江大学学报(工学版), 2013, 47(6): 944-950. LOU Xiaojun, SUN Yuxuan, LIU Haitao. Clustering boundary over-sampling classification method for imbalanced data sets[J]. Journal of Zhejiang University (Engineering Science), 2013, 47(6): 944-950. DOI:10.3785/j.issn.1008-973X.2013.06.003 (  0) 0)
|
| [31] |
MA Li, FAN Suohai. CURE-SMOTE algorithm and hybrid algorithm for feature selection and parameter optimization based on random forests[J]. BMC bioinformatics, 2017, 18(1): 169. DOI:10.1186/s12859-017-1578-z ( 0) 0)
|
| [32] |
IJAZ M F, ALFIAN G, SYAFRUDIN M, et al. Hybrid prediction model for type 2 diabetes and hypertension using DBSCAN-based outlier detection, synthetic minority over sampling technique (SMOTE), and random forest[J]. Applied sciences, 2018, 8(8): 1325. DOI:10.3390/app8081325 ( 0) 0)
|
| [33] |
盛凯, 刘忠, 周德超, 等. 面向不平衡分类的IDP-SMOTE重采样算法[J]. 计算机应用研究, 2019, 36(01): 115-118. SHENG Kai, LIU Zhong, ZHOU Dechao, et al. IDP-SMOTE resampling algorithm for imbalanced classification[J]. Application research of computers, 2019, 36(01): 115-118. (  0) 0)
|
| [34] |
BLAGUS R, LUSA L. SMOTE for high-dimensional class-imbalanced data[J]. BMC bioinformatics, 2013, 14: 106. DOI:10.1186/1471-2105-14-106 ( 0) 0)
|
| [35] |
ABDI L, HASHEMI S. To combat multi-class imbalanced problems by means of over-sampling techniques[J]. IEEE transactions on knowledge and data engineering, 2016, 28(1): 238-251. DOI:10.1109/TKDE.2015.2458858 ( 0) 0)
|
| [36] |
WANG Jin, YUN Bo, HUANG Pingli, et al. Applying threshold SMOTE algorithm with attribute bagging to imbalanced datasets[C]//Proceedings of the 8th International Conference on Rough Sets and Knowledge Technology. Halifax, NS, Canada, 2013: 221–228.
( 0) 0)
|
| [37] |
MATHEW J, LUO Ming, PANG C K, et al. Kernel-based SMOTE for SVM classification of imbalanced datasets[C]//Proceedings of IECON 2015-41st Annual Conference of the IEEE Industrial Electronics Society. Yokohama, Japan, 2015: 1127–1132.
( 0) 0)
|
| [38] |
BELLINGER C, DRUMMOND C, JAPKOWICZ N. Beyond the boundaries of SMOTE-A framework for manifold-based synthetically oversampling[C]//Proceedings of Joint European Conference on Machine Learning and Knowledge Discovery in Databases. Riva del Garda, Italy, 2016: 248−263.
( 0) 0)
|
| [39] |
BELLINGER C, JAPKOWICZ N, DRUMMOND C. Synthetic oversampling for advanced radioactive threat detection[C]//Proceedings of 2015 IEEE International Conference on Machine Learning and Applications. Miami, FL, USA, 2015: 948−953.
( 0) 0)
|
| [40] |
LI Xiao, ZOU Beiji, WANG Lei, et al. A novel LASSO-based feature weighting selection method for microarray data classification[C]//Proceedings of 2015 IET International Conference on Biomedical Image and Signal Processing. Beijing, China, 2015: 1–5.
( 0) 0)
|
| [41] |
ZHANG Chunkai, GUO Jianwei, LU Junru. Research on classification method of high-dimensional class-imbalanced data sets based on SVM[C]//Proceedings of the 2nd IEEE International Conference on Data Science in Cyberspace. Shenzhen, China, 2017: 60−67.
( 0) 0)
|
| [42] |
GUYON I, WESTON J, BARNHILL S, et al. Gene selection for cancer classification using support vector machines[J]. Machine learning, 2002, 46(1/2/3): 389-422. ( 0) 0)
|
| [43] |
许召召, 李京华, 陈同林, 等. 融合SMOTE与Filter-Wrapper的朴素贝叶斯决策树算法及其应用[J]. 计算机科学, 2018, 45(9): 65-69, 74. XU Zhaozhao, LI Jinghua, CHEN Tonglin, et al. Naive Bayesian decision tree algorithm combining SMOTE and Filter-Wrapper and it's application[J]. Computer science, 2018, 45(9): 65-69, 74. (  0) 0)
|
| [44] |
GUO Lei, WANG Shunfang F. Membrane protein type prediction for high-dimensional imbalanced datasets[C]//Proceedings of 2018 International Conference on Information Technology in Medicine and Education. Hangzhou, China, 2018: 847−851.
( 0) 0)
|
| [45] |
TORGO L, BRANCO P, RIBEIRO R P, et al. Resampling strategies for regression[J]. Expert systems, 2015, 32(3): 465-476. DOI:10.1111/exsy.12081 ( 0) 0)
|
| [46] |
MONIZ N, BRANCO P, TORGO L. Resampling strategies for imbalanced time series[C]//Proceedings of 2016 IEEE International Conference on Data Science and Advanced Analytics. Montreal, QC, Canada, 2016: 282−291.
( 0) 0)
|
| [47] |
BRANCO P, TORGO L, RIBEIRO R P. REBAGG: REsampled BAGGing for imbalanced regression[C]//Proceedings of International Workshop on Learning with Imbalanced Domains: Theory and Applications. Dublin, Ireland, 2018: 67−81.
( 0) 0)
|
| [48] |
PÉREZ-ORTIZ M, GUTIÉRREZ P A, HERVÁS-MARTÍNEZ C, et al. Graph-based approaches for over-sampling in the context of ordinal regression[J]. IEEE transactions on knowledge and data engineering, 2015, 27(5): 1233-1245. DOI:10.1109/TKDE.2014.2365780 ( 0) 0)
|
| [49] |
ZHU Tuanfei, LIN Yaping, LIU Yonghe, et al. Minority oversampling for imbalanced ordinal regression[J]. Knowledge-based systems, 2019, 166: 140-155. DOI:10.1016/j.knosys.2018.12.021 ( 0) 0)
|
| [50] |
COST S, SALZBERG S. A weighted nearest neighbor algorithm for learning with symbolic features[J]. Machine learning, 1993, 10(1): 57-78. ( 0) 0)
|
| [51] |
KURNIAWATI Y E, PERMANASARI A E, FAUZIATI S. Adaptive synthetic-nominal (ADASYN-N) and adaptive synthetic-KNN (ADASYN-KNN) for multiclass imbalance learning on laboratory test data[C]//Proceedings of 2018 International Conference on Science and Technology. Yogyakarta, Indonesia, 2018: 1−6.
( 0) 0)
|
| [52] |
WILSON D R, MARTINEZ T R. Improved heterogeneous distance functions[J]. Journal of artificial intelligence research, 1997, 6: 1-34. DOI:10.1613/jair.346 ( 0) 0)
|
| [53] |
AHMAD A, DEY L. A method to compute distance between two categorical values of same attribute in unsupervised learning for categorical data set[J]. Pattern recognition letters, 2007, 28(1): 110-118. DOI:10.1016/j.patrec.2006.06.006 ( 0) 0)
|
| [54] |
KULLBACK S, LEIBLER R A. On information and sufficiency[J]. The annals of mathematical statistics, 1951, 22(1): 79-86. DOI:10.1214/aoms/1177729694 ( 0) 0)
|
| [55] |
IENCO D, PENSA R G, MEO R. Context-based distance learning for categorical data clustering[C]//Proceedings of the 8th International Symposium on Intelligent Data Analysis. Lyon, France, 2009: 83−94.
( 0) 0)
|
| [56] |
DEL RÍO S, LÓPEZ V, BENÍTEZ J M, et al. On the use of MapReduce for imbalanced big data using Random Forest[J]. Information sciences, 2014, 285: 112-137. DOI:10.1016/j.ins.2014.03.043 ( 0) 0)
|
| [57] |
GUO Haixiang, LI Yijing, SHANG J, et al. Learning from class-imbalanced data: review of methods and applications[J]. Expert systems with applications, 2017, 73: 220-239. DOI:10.1016/j.eswa.2016.12.035 ( 0) 0)
|
| [58] |
GHAZIKHANI A, MONSEFI R, YAZDI H S. Online neural network model for non-stationary and imbalanced data stream classification[J]. International journal of machine learning and cybernetics, 2014, 5(1): 51-62. DOI:10.1007/s13042-013-0180-6 ( 0) 0)
|
| [59] |
WANG Shuo, MINKU L L, YAO Xin. A multi-objective ensemble method for online class imbalance learning[C]//Proceedings of 2014 International Joint Conference on Neural Networks. Beijing, China, 2014: 3311−3318.
( 0) 0)
|
| [60] |
WANG Shuo, MINKU L L, YAO Xin. Resampling-based ensemble methods for online class imbalance learning[J]. IEEE transactions on knowledge and data engineering, 2015, 27(5): 1356-1368. DOI:10.1109/TKDE.2014.2345380 ( 0) 0)
|
| [61] |
MIRZA B, LIN Zhiping, LIU Nan. Ensemble of subset online sequential extreme learning machine for class imbalance and concept drift[J]. Neurocomputing, 2015, 149: 316-329. DOI:10.1016/j.neucom.2014.03.075 ( 0) 0)
|
| [62] |
GHAZIKHANI A, MONSEFI R, YAZDI H S. Ensemble of online neural networks for non-stationary and imbalanced data streams[J]. Neurocomputing, 2013, 122: 535-544. DOI:10.1016/j.neucom.2013.05.003 ( 0) 0)
|
| [63] |
DITZLER G, POLIKAR R. Incremental learning of concept drift from streaming imbalanced data[J]. IEEE transactions on knowledge and data engineering, 2013, 25(10): 2283-2301. DOI:10.1109/TKDE.2012.136 ( 0) 0)
|
| [64] |
ERTEKIN Ş. Adaptive oversampling for imbalanced data classification[C]//Proceedings of the 28th International Symposium on Computer and Information Sciences. Paris, France, 2013: 261−269.
( 0) 0)
|
| [65] |
MOUTAFIS P, KAKADIARIS I A. GS4: generating synthetic samples for semi-supervised nearest neighbor classification[C]//Proceedings of Pacific-Asia Conference on Knowledge Discovery and Data Mining. Tainan, China, 2014: 393−403.
( 0) 0)
|
| [66] |
TRIGUERO I, GARCIA S, HERRERA F. SEG-SSC: a framework based on synthetic examples generation for self-labeled semi-supervised classification[J]. IEEE transactions on cybernetics, 2015, 45(4): 622-634. DOI:10.1109/TCYB.2014.2332003 ( 0) 0)
|
| [67] |
DONG Aimei, CHUNG F L, WANG Shitong. Semi-supervised classification method through oversampling and common hidden space[J]. Information sciences, 2016, 349-350: 216-228. DOI:10.1016/j.ins.2016.02.042 ( 0) 0)
|
 2019, Vol. 14
2019, Vol. 14


