在机器学习领域，距离(distance)的概念从诞生之日起就一直有着广泛的应用。它提供了一种数据间相似性的度量，即距离近的数据要尽可能相似，距离远的数据要尽可能不同^[1-2]。这种相似性学习的思想应用在分类问题上是著名的最近邻(nearest neighbors, NN)^[3]分类，该方法将待测样本的类别分配为距其最近的训练样本的类别。这种最近邻分类思想催生了距离度量学习(distance metric learning)的产生^[4]。

欧氏距离作为一种简洁有效的度量工具得到了度量学习算法的广泛青睐，然而，单一形式的距离度量无法普适所有实际问题。因此，度量学习希望能够结合数据自身特点，学习一种有效的度量方式，用于求解目标问题。

早期度量学习算法的产生，极大地改善了基于距离分类器的分类性能^[5-6]、基于距离聚类的无监督问题^[1]以及特征降维^[7]的表现。而后，随着深度学习^[8-14]的飞速发展，结合深度神经网络在语义特征抽取、端到端训练优势的深度度量学习，逐步进入人们的眼帘。

相比于经典度量学习，深度度量学习可以对输入特征做非线性映射，在计算机视觉领域得到了广泛的应用，例如：图像检索^[15-16]、图像聚类^[17]、迁移学习^[18-19]、验证^[20]、特征匹配^[21]。除此之外，对于一些极端分类^[22-24]任务(类别数目很多，但每类仅有几个样本)，深度度量学习仍有不错的表现。例如，基于深度度量学习，FaceNet^[25]在8 M个个体、260 M张图像的人脸识别任务中，表现结果已经超越了人类水平。

标准的深度度量学习通过挖掘2个^[26]或3个^[25]正负样本对来约束类内距、扩大类间距。这为训练样本的采样带来了挑战：由于训练样本数量极多，因此只能挖掘有意义的样本参与训练。若负样本选取过难，则易导致训练不稳定；若选取过简单，则易导致损失函数无梯度，不利于模型的收敛。

代理损失^[16]的提出为每种类别分配了一个代理点，由于代理点数量远远小于样本集合，因而可以完整存储起来，在训练过程中参与梯度回传，从而为训练过程提供了全局的语义信息，取得了更好的结果。

此外，我们发现改进后的代理近邻损失与标准的分类任务有些相似：一方面，损失函数同时优化所有类别实现缩小类内距、扩大类间距；另一方面，如果我们移除了softmax线性变换的偏置项^[27]，权重W的物理含义即为该类别的代理点。

标准分类任务结合softmax与交叉熵建立损失函数，可以输出特征向量分别属于每一类的概率。然而softmax不具有较强的判别性，因而很多算法提出温度值概念^[27-29]，从特征梯度层面改进其性能，具体细节我们将在后文展开综述。

度量学习起源于分类问题的最近邻思想，经历了逐步演化最终至代理近邻损失函数。已有文献[27]证明移除偏置项、正则化输入特征x和权重W后的softmax分类任务可视为基于代理点的度量学习。考虑到代理近邻损失与softmax的相关性—softmax的权值可视为该类别学到的代理点，我们借鉴了带温度值的softmax分类思想，将温度值引入代理损失，从而进一步扩大类间距，提高了度量学习的判别性能。至此，我们将度量学习与分类这两条看似独立的分支建立了联系，深入挖掘出二者背后统一的思想，可谓“殊途同归”。

1 深度度量学习

在人脸识别、指纹识别等开集分类的任务中，类别数往往很多而类内样本数比较少，在这种情况下基于深度学习的分类方法常表现出一些局限性，如缺少类内约束、分类器优化困难等。这些局限可以通过深度度量学习来解决：深度度量学习通过特定的损失函数，学习到样本到特征的映射f_θ(∙)。在该映射下，样本特征间的度量d_(i,j)(通常为欧式距离 ${\left\| {{f_\theta }\left( {{x_i}} \right) - {f_\theta }\left( {{x_j}} \right)} \right\|_2}$ )便可以反映样本间的相似程度：类内样本对应的特征距离更近，类间样本对应的特征距离更远。

1.1 对比损失

对比损失(contrastive loss)^[26,30] 是深度度量学习的开篇之作，它首次将深度神经网络引入度量学习。在此之前，经典度量学习最早应用于聚类问题^[1]，如：局部线性嵌入(locally linear embedding, LLE)^[31]、Hessian局部线性嵌入(Hessian LLE)^[32]、主成分分析(principal component analysis, PCA)^[33]等。它们通过定义样本x和样本y之间的马氏距离d(x, y)=(x−y)^TM(x−y)，约束相似样本马氏距离小，不相似样本马氏距离大。其中M为马氏距离，为d×d的半正定矩阵。相比于欧氏距离，马氏距离考虑了特征之间的权重与相关性，且凸问题易被优化，因而得到了广泛应用。

然而，传统方法主要存在两个弊端：一是依赖于原始输入空间进行距离度量；二是不能很好地映射与训练样本关系未知的新样本的函数。作者利用深度学习特征提取的优势，将原始的输入空间映射到欧氏空间，直接约束类内样本的特征尽可能接近而类间样本的特征足够远如式(1):

${l_{\ \rm contrast}}({{{X}}_{{i}}},{{{X}}_{{j}}}) = {{{y}}_{{{i}},{{j}}}}d_{i,j}^2 + (1 - {{{y}}_{{{i}},{{j}}}}){[\alpha - d_{i,j}^2]_ + }$

(1)

其中，若X_i与X_j类别编号相同则y_(i,j)=1，否则y_(i,j)=0。d_(i,j)即为欧式距离，α控制类间样本足够远的程度。

1.2 三元组损失

对比损失仅仅只约束类内对的特征尽量近而类间对的特征尽量远，三元组损失(triplet loss)^[5,25]在对比损失的基础上进一步考虑了类内对与类间对之间的相对关系：首先固定一个锚点样本(anchor),希望包含该样本的类间对(anchor-negative)特征的距离能够比同样包含该样本的类内对(anchor-positive)特征的距离大一个间隔(margin)，如式(2)：

${l_{\ \rm triplet}}({{{X}}_{{a}}},{{{X}}_{{b}}},{{{X}}_{{n}}}) = {[d_{a,p}^2 + m - d_{a,n}^2]_ + }$

(2)

式中X_a、X_p、X_n分别为锚点样本、与锚点样本同类的样本以及与锚点样本异类的样本；m即为间隔。

然而，对于三元组的选取，采样策略是至关重要的：假设训练集样本数为n，那么所有的三元组组合数为O(n³)，数量非常庞大。其中存在大量的平凡三元组，这些平凡三元组类间对的距离已经比类内对的距离大一个间隔，它们对应的损失为0。简单的随机采样会导致模型收敛缓慢，特征不具有足够的判别性^{[14, 34-35]}。因此一种合理的解决方案是仅挖掘对训练有意义的正负样本，也称为“难例挖掘”^[25,36-39]。例如：HardNet^[36]旨在在一个训练batch中挖掘一些最难的三元组。然而如果每次都针对锚点样本挖掘最困难的类间样本，模型又很容易坍缩。因此，文献[25]提出了一种半难例(semi-hard)挖掘的方式：选择比类内样本距离远而又不足够远出间隔的类间样本来进行训练。

1.3 提升结构化损失

由于三元组损失一次采样3个样本，虽然能够同时考虑类内距、类间距以及二者的相对关系，但该损失没有充分利用训练时每个batch内的所有样本，因此文献[18]提出在一个batch内建立稠密的成对(pair-wise)的连接关系，具体实现是：对于每一个类内对，同时选择两个难例，一个距离x^a最近，一个距离x^p最近。提升结构化损失(lifted structured loss)^[18]对应的损失函数为

$\begin{gathered} \displaystyle J = \frac{1}{{2|\hat P|}}\sum\limits_{(i,j) \in \hat P} {\max {{(0,{J_{i.j}})}^2}} \\[-3pt] {J_{i,j}} = \max (\mathop {\max }\limits_{(i,j) \in \hat N} \alpha - {D_{i,k}},\mathop {\max }\limits_{(j,l) \in \hat N} \alpha - {D_{j,l}}) + {D_{i,j}} \\ \end{gathered} $

(3)

式中： $\hat P$ 为batch内所有的正样本对集合； $\hat N$ 为batch内所有的负样本对集合。

这种设计结构性损失函数，以在一个训练batch中考虑所有可能的训练对或三元组并执行“软化的”难例挖掘在文献[40]中也得到了相似的应用。

1.4 多类N元组损失

Sohn等^[15]将对比损失和三元组收敛比较慢的原因归结于训练时每次只挖掘一个负样本，缺少了与其他负样本交互过程。因此他们提出多类N元组损失(multi-class N-pair loss)^[15]：同类样本的距离不应每次只小于一组类间距，而应同时小于n-1组类间距离，从而实现类内对相似度显著高于所有类间对相似度。损失函数的设计借鉴了(neighborhood component analysis, NCA)^[6]的表达形式，具体如式(4)所示：

$\begin{gathered} l({{X}},{{y}}) = \frac{{ - 1}}{{|{{P}}|}}\sum\limits_{(i,j) \in P} {\log \frac{{\exp \{ {{{S}}_{{{i}},{{j}}}}\} }}{{\exp \{ {{{S}}_{{{i}},{{j}}}}\} + \displaystyle\sum\limits_{k:{{y}}[k] \ne {{y}}[i]} {\exp \{ {{{S}}_{{i}},{{k}}}}\} } }} + \\ \frac{\textit{λ}}{m} {\sum\limits_i^m {||f({{{X}}_{{i}}})||} _2} \end{gathered}$

(4)

式中：i, j表示同类样本；k表示不同类样本；P为一个batch内的所有正样本；m为batch size的大小。另一方面，为了使分类面只与向量X_i的方向有关，与模长无关，作者对一个batch内的所有输入特征X_i利用L₂正则化。

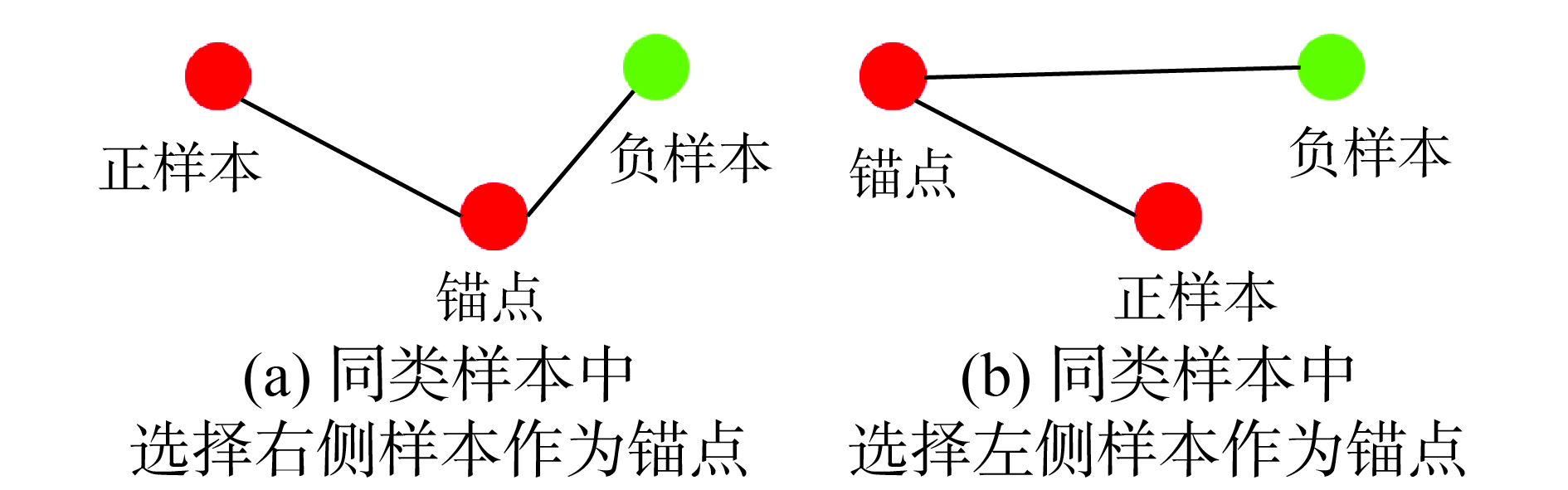
1.5 成对聚类损失

由于三元组损失^[25]在锚点选取时的任意性，因此有些不满足类间距>类内距+间隔的样本，可能并没有被挖掘到，如图1所示。

若样本以左侧方式组合，则负样本很易被检测到，从而距离得到优化；但若以右边方式设置锚点、正样本，则负样本由于满足约束，因而loss为0，导致同类物体的距离没有被拉近，这一定程度上减缓了收敛的速度。这说明三元组损失对锚点的选取十分敏感，考虑到相似样本应该聚集成簇^[42]，不同类样本应保持相对较远，因此他们^[36]提出成对聚类损失函数(coupled clusters loss, CCL)为同类样本估计了一个类内中心c ^p：

${{{c}}^{{p}}} = \frac{1}{{{N^p}}}\sum\limits_i^{{N^p}} {f({{X}}_{{i}}^{{p}})} $

(5)

从而希望所有的正样本X_i^p到聚类中心c ^p的距离加间隔 $\alpha $ 小于其他类间样本到聚类中心c ^p的距离，对应的损失函数为

$ \begin{array}{*{20}{c}} {L({{W}},{{{X}}^{{p}}},{{{X}}^{{n}}}) = }\\ \displaystyle{\sum\limits_i^{{N^p}} {\frac{1}{2}\max \{ 0,||f({{X}}_{{i}}^{{p}}) - {{{c}}^{{p}}}|{|^2} + \alpha - |f({{X}}_*^n) - {{{c}}^{{p}}}|{|^2}\} } } \end{array}$

(6)

式中：X_i^p为正样本； ${X_*}^n$ 为负样本； ${N^p}$ 为同类正样本的数目；c ^p为正样本的聚类中心。

1.6 中心损失

处理开集识别问题的深度特征，不仅需要具有可分离性(separable)，还应具有判别性(discriminative)。可判别性特征可以很好地容忍类内变化、分离类间变化，进而可以应用在最近邻(nearest neighbor, NN)^[3]和k近邻(k-nearest neighbor, k-NN)^[43]算法中。然而，softmax loss仅能约束特征具有可分离性、不具有判别性，因此为CNN设计一个有效的损失函数是极为重要的。

中心损失(center loss)^[44]结合了成对聚类损失(CCL)和softmax loss的优势，用CCL约束类内，softmax约束类间。具体做法是：为每一类特征学习一个聚类中心，随着训练的进行，同步更新类内中心以及最小化特征与对应中心的距离。将聚类的loss与softmax联合训练，利用超参平衡两个监督信号的权重。主观上，softmax损失可以分离不同类别特征，center loss可以使同类特征聚在一起中心点周围，从而扩大类间距、缩小类内距，学到了更具有判别性的深度特征。对应的损失函数为

$\begin{gathered} L = {L_S} + {L_C} = \\ \;\;\;\;\;\; \displaystyle\sum\limits_{i = 1}^m {\log \frac{{\exp \{ {{W}}_{{{{y}}_{{i}}}}^{\rm{T}}{{{X}}_{{i}}} + {{{b}}_{{{{y}}_{{i}}}}}\} }}{{ \displaystyle\sum\limits_{j = 1}^n {\exp \{ {{W}}_{{{{y}}_{{i}}}}^{\rm{T}}{{{X}}_{{i}}} + {{{b}}_{{{{y}}_{{i}}}}}\} } }} + \frac{{\textit{λ}}}{2}} \sum\limits_i^m {|{{{X}}_{{i}}} - {{{c}}_{{{{y}}_{{i}}}}}||} _2^2 \\ \end{gathered} $

(7)

其中 ${{ c}_{{y_i}}}$ 表示第y_i类深度特征中心。

1.7 设备定位损失

Oh等^[45]认为，当前存在的大多数方法^{[15, 18, 25, 46]}通常只关注数据的局部区域(如：二元组、三元组或n元组)，并没有考虑到全局的结构信息，因而降低了聚类和检索的表现。

作者指出，一旦正样本对距离较远且二者之间被其他类别的负样本间隔开，那么正样本对间相互吸引的梯度信号被负样本相互排斥的梯度信号所超过，从而同类样本很难聚成一类，而被错误地分开成了两类。因此，他们提出一组聚类损失—设备定位损失(facility location loss)^[45]来解决这个问题。

对于一组输入样本 ${{X}}=\{{{X}}_1,{{X}}_2, \cdots, {{{X}}_n} \} $ ，以k-mediods^[47]思想为基础，我们期望从中选取的聚类中心{X_S}(其中 $S \subset \{1, \cdots, n \}$ )满足在特征空间中与同类样本距离尽可能接近：

$F({{X}},{{S}};\theta ) = - \sum\limits_{i \in |{{X}}|} {\mathop {\min }\limits_{j \in S} ||f({{{X}}_{{i}}};\theta ) - f({{{X}}_{{j}}};\theta )||} $

(8)

式(8)也被称为设备定位函数(facility location function)，现已被广泛应用于数据求和^[48-49]与聚类。

由于最大化式(8)是一个NP-hard问题^[50-51]，因此作者通过对子模块的贪婪求解，找到了一个完备的优化下界，复杂度为 $\displaystyle O(1 - \frac{1}{e})$ 。具体方法是：通过设计一个打分函数 $\tilde F$ ，基于真实类别标签y^*来评估聚类的好坏，对应的公式为

$\tilde F({{X}},{{{y}}^*};\theta ) = - \sum\limits_{i \in |{{Y}}|} {\mathop {\max }\limits_{j \in \{ i:{y^*}[i] = k\} } F({{{X}}_{\{ i:{y^*}[i] = k\} }},\{ j\} ;\theta )} $

(9)

其中， $\{ i:{y^*}[i] = k\} $ 表示当真实类别标签为第k类时，对应的{1, $2, \; \cdots $ , n}的元素构成的集合。

由于希望打分函数 $\tilde F$ 越大越好，因此借鉴三元组损失的间隔思想，F比 $\tilde F$ 相差一个间隔 $\Delta ({{y}},{{{y}}^*})$ ，即

$l({{X}},{{{y}}^*}) = [\mathop {\max }\limits_{S \subset \{ 1, \cdots ,n\} } \{ F({{X}},{{S}};\theta ) + \gamma \Delta ({{y}},{{{y}}^*})\} - \tilde F({{X}},{{{y}}^*};\theta )]$

(10)

其中，

${{y}}[i] = \mathop {\arg \min }\limits_j ||f({{{X}}_{{i}}};\theta ) - f({{{X}}_{\left\{ {{{j}}| \in {{S}}} \right\}}};\theta )||$

$\begin{array}{l} \;\;\;\;\Delta ({{y}},{{{y}}^*}) = 1 - {\rm NMI}({{y}},{{{y}}^*}) \\ \displaystyle {\rm NMI}({{{y}}_{{1}}},{{{y}}_{{2}}}) = \frac{{{\rm MI}({{{y}}_{{1}}},{{{y}}_{{2}}})}}{{\sqrt {H({{{y}}_{{1}}})H({{{y}}_2})} }} \\ \end{array} $

(11)

其中，NMI表示正则化互信息(normalized mutual information, NMI)^[52]。由于这种聚类方法在特征空间中有一个全局的感受野，因此可以解决局部最优的问题。聚类的损失函数可以约束全局样本向类内中心靠拢、间隔项中的NMI矩阵可以使不同类别远离。

1.8 代理损失

为了克服三元组样本对采样困难的问题，代理损失^[16]提出了一种用小规模的代理点来代替大规模的原始样本点的方法：将原始样本用代理点来近似，这样约束类内对和类间对的距离便可以转化为约束锚点样本与同类样本对应代理点和锚点与异类样本对应代理点的距离。随着训练的进行，样本的特征与代理点都获得更新。

假设原始样本点和代理点的集合分别为X, P，且|X|=n, |P|=m, m $ \ll $ n。有如下两种分配代理点的方式：1)动态分配策略：选取距该样本最近的代理点作为代表该样本的代理点(式(12))；2)静态分配策略：选取与样本类别数相同的代理点数目，某一类样本被固定分配至对应该类别的代理点。

${{p}}(x) = \arg {\min _{p \in P}}{d^2}({{X}},{{p}})$

(12)

代理损失借鉴了近邻成分分析(neighborhood component analysis, NCA)^[6]的思路，希望锚点样本与其同类代理点的距离尽可能近而与其异类代理点的距离尽可能远：

$\displaystyle{l^{\ \rm proxy}}({{X}},{{P}}) = - \log (\frac{{\exp ( - {d^2}({{X}},{{p}}(x)))}}{{\displaystyle\sum\nolimits_{z \in {{P}}\backslash \{ {{p}}(x)\} } {\exp ( - {d^2}({{X}},{{z}})} }})$

(13)

图2展示了三元组损失与代理损失在优化时的差别，代理点的设定使得“样本对”的数量大大减少：对于每一个锚点样本，图(a)中可以组成12个三元组，而图(b)中仅存在2个锚点−代理点对，样本挖掘的困难很大程度被克服了。

另一方面，作者也论证了代理损失与三元组损失的优化目标是一致的，通过三角不等式证明了代理损失是三元组损失的上界。

1.9 其他损失

除此之外，最近还有一些使用深度网络进行度量学习的工作。Hershey等^[17]在二值化的真实标签和成对估计的亲和度矩阵之间的残差上使用了Frobenius范数；他们将此应用于语音谱信号聚类。然而，直接使用Frobenius范数是次优的，因为它忽略了亲和矩阵是正定的这一事实。为了克服这个问题，矩阵反向传播^[53]首先将真实和预测的亲和度矩阵投影到欧氏空间。然而，这种方法需要计算数据矩阵的特征值分解，具有数据样本量三次方的时间复杂度，因此对于大数据问题不适用。Ranked loss^[54]则是从秩的角度优化距离度量。

2 深度度量学习与softmax分类

利用深度神经网络的倒数第二层(也叫瓶颈层)特征，搭配softmax与交叉熵损失训练得到的分类器，同样适用于许多基于深度度量学习的应用^[55]，例如诸如：物体识别^{[17, 51-58]}、人脸验证^[59-61]、手写数字识别^[62]等。然而，分类器训练与度量学习的目标实际是不同的^[29]。前者旨在寻找最佳分类面，而后者旨在学习特征嵌入，使得相同类别的样本嵌入是紧凑的，而不同类别的样本嵌入是远离的。这促使我们研究度量学习和分类器训练之间的关系。

2.1 代理损失与softmax的关系

如果我们将代理近邻损失式(13)的分母中加入正样本项，则变为

$l({{X}},{{P}}) = - \log (\frac{{\exp ( - {d^2}({{X}},{{p}}(x)))}}{{\displaystyle\sum\limits_{z \in {{P}}} {\exp ( - {d^2}({{X}},{{z}}))} }})$

(14)

这样log函数内的式子可以看成是样本被分配到其对应代理点的概率，这里用q来表示概率即：

$q({{{p}}_{{i}}}|{{X}}) = \frac{{\exp ( - {d^2}({{X}},{{{p}}_{{i}}}))}}{{\displaystyle\sum\limits_{j = 1}^m {\exp ( - {d^2}({{X}},{{{p}}_{{j}}}))} }}$

(15)

这样式(14)可以看作上述后验概率结合交叉熵损失以及类别标签所得。

代理损失与softmax不同之处在于，softmax将样本经过线性变换wx+b之后进行归一化作为后验概率，而此处则是将样本与对应代理点的距离d²(x, p_i)进行归一化作为后验概率。如果我们将样本特征以及代理点的模长固定为常数s，有：

${d^2}({{X}},{{{p}}_{{i}}}) = ||{{X}}||_2^2 + ||{{{p}}_{{i}}}||_2^2 - 2{{{X}}^{\rm{T}}}{{{p}}_{{i}}} = 2{{{s}}^2} - 2{{{X}}^{\rm{T}}}{{{p}}_{{i}}}$

(16)

代入到式(15)中：

$q({{{p}}_{{i}}}|{{X}}) = \frac{{\exp (2{{{X}}^{\rm{T}}}{{{p}}_{{i}}} - 2{{{s}}^2})}}{{\displaystyle\sum\limits_{j = 1}^m {\exp (2{{{X}}^{\rm{T}}}{{{p}}_{{j}}} - 2{{{s}}^2})} }} = \frac{{\exp (2{{{X}}^{\rm{T}}}{{{p}}_{{i}}})}}{{\displaystyle\sum\limits_{j = 1}^m {\exp (2{{{X}}^{\rm{T}}}{{{p}}_{{j}}})} }}$

(17)

可以看作将线性变换参数的模长固定且去掉偏置项的softmax，这与Zhai等^[27]的发现也是一致的。由此，我们在度量学习中的代理损失与softmax分类之间建立了联系。

2.2 温度放缩

softmax损失函数对不同类别的特征有着较好的分离性，却不具有足够的判别性。因此，现阶段的工作提出了几种变体^{[44, 63-71]}来增强其判别性。最早在2015年，Hinton为解决模型压缩^[72]、知识迁移等问题，提出了温度值^[28]的概念。他认为不同类别间的关系不应是非0即1的问题(如：将猫误判为狗的损失直观上应该要比将猫误判为汽车的损失小)，因此，粗暴地使用one-hot编码丢失了类间和类内关联性的额外信息。由此作者提出带温度值的softmax函数，弱化不同类别之间的差异。损失函数：

${L_{\rm soft}} = - \sum\limits_{i = 1}^K {{{{p}}_{{i}}}\log {{{q}}_{{i}}} = - \sum\limits_{i = 1}^K {{{{p}}_{{i}}}\log \frac{{{{\rm{e}}^{{{{z}}_{{i}}}/T}}}}{{\displaystyle\sum\limits_j {{{\rm{e}}^{{{{z}}_{{j}}}/T}}} }}} } $

(18)

式中：z_i为logit，即 ${{{z}}_{{i}}} = {{WX}} + b$ ; p_i为软化后的类别标签；q_i为压缩模型的输出。由式(14)可知，当T=1时，恢复到普通的softmax变换。文中令T>1，就得到了软化后的softmax。这一思想在Zhai等^[27]的实验中得到了进一步验证。

文献[27]通过移除最后一层的偏置项，并对权重与输入特征施加L₂正则，从而完成了将任意分类网络向基于代理损失的度量学习转换的过程。考虑到在高维空间中，单位球面上两个样本点之间的距离接近正态分布 $\displaystyle N\left( {\sqrt 2 ,\frac{1}{{2\dim }}} \right)$ ，其中dim表示特征维数^[28]。为了使网络对类别差异变化更敏感，他们引入温度值 $\sigma $ 放缩余弦距离：

${L_{\rm cls}}({{X}},{{{p}}_{{y}}},{{{p}}_{{Z}}},\sigma ) = - \log (\frac{{\exp ({{{X}}^{\bf{T}}}{{{p}}_{{y}}}/\sigma )}}{{\displaystyle\sum\limits_{{{{p}}_{{z}}} \in ({{{p}}_{{z}}} \cup {{{p}}_{{y}}})} {\exp ({{{X}}^{\bf{T}}}{{{p}}_{{z}}}/\sigma )} }})$

(19)

作者在CUB-200-2011^[73]数据集上，探索了不同温度参数 $\sigma $ 对实验结果的影响，如表1所示。

由表1可知，与Hinton^[28]的思想一致，当温度值 $\sigma $ <1时，类别间差异放大，学到的特征具有更强的判别性，当温度值 $\sigma $ =1时，判别性能急剧下降；类似地，温度值太低也会降低性能。然而，针对这一现象，本文作者并未做出合理的解释。

Zhang等^[29]从样本特征梯度的角度分析了温度值如何影响特征分布。为方便起见，作者令 $\alpha = 1/T$ ，即：

$q(m|x) = \log \frac{{{{\rm{e}}^{{{{z}}_{{m}}}/T}}}}{{\displaystyle\sum\limits_{j = 1}^M {{{\rm{e}}^{{{{z}}_{{j}}}/T}}} }} = \log \frac{{{{\rm{e}}^{\alpha {{{z}}_{{m}}}}}}}{{\displaystyle\sum\limits_{j = 1}^M {{{\rm{e}}^{\alpha {{{z}}_{{j}}}}}} }}$

(20)

式中：m为类别数，m $ \in $ {1, $2, \;\cdots $ , M}。q(m|x)为模型softmax预测概率输出。假设p(m|x)为训练样本真实分布，则可得到交叉熵损失函数：

$L({{X}},\alpha ) = - \sum\limits_{m = 1}^M {\log (q(m|{{X}},\alpha ))p(m|{{X}})} $

(21)

损失函数 $L\left( {x,\alpha } \right)$ 对logit z_m的梯度为

$\frac{{\partial L}}{{\partial {{{z}}_{{m}}}}} = \alpha (q(m|{{X}}) - p(m|{{X}}))$

(22)

进而得到对特征f的梯度：

$\frac{{\partial L}}{{\partial { f}}} = \sum\limits_{m = 1}^M {\frac{{\partial L}}{{\partial {{{z}}_{{m}}}}}\frac{{\partial {{{z}}_{{m}}}}}{{\partial { f}}}} = \alpha \sum\limits_{m = 1}^M {(q(m|{{X}}) - p(m|{{X}})){{{w}}_{{m}}}} $

(23)

由此，作者观察到不同的 $\alpha $ 值为不同的样本(难例、边界样本且被分对、内部易被分对样本)分配不同大小的梯度，从而改变了最终特征表达的分布。换句话说，随着 $\alpha $ 的增大(温度值T减小)，难例的梯度增大、而易分对样本梯度先增大后减小，因而选择合适的 $\alpha $ 实际是在不同样本的梯度间做一种权衡。

3 结束语

本文综述了最近的一系列具有代表性的深度度量学习算法的文章，并探讨了其与softmax分类的关系。深度度量学习最早源于对比损失，由于未同时兼顾类内与类间的相对关系，进而衍生出改进后的三元组损失。由于成对的二元组、三元组样本数量极多，难例挖掘、半难例挖掘等采样策略针对正负样本采样问题起着关键作用。为减轻采样负担，许多结构化的损失函数，利用batch内更丰富的样本间结构关系来设计损失函数，约束特征。还有一些基于聚类思想的损失函数，如：中心损失、代理损失等，为每类样本学习一个代理点，从而大大减少了类间样本数量，使模型更易优化。

综述中，我们发现搭配softmax与交叉熵损失训练得到的分类器，同样适用于许多基于深度度量学习的任务，这促使我们研究度量学习和分类器训练之间的关系。随着研究的深入，我们发现代理损失与softmax分类这两条看似平行的研究思路，实则背后有着一致的思想。针对softmax判别性不高的缺点，许多算法引入温度值概念，对原始的softmax logit作出改造，并取得了很好的实验结果。在未来的研究中，我们希望继续深入探索二者之间的关系。例如，我们可以将softmax变体中间隔margin的概念引入代理近邻损失，从而进一步缩小类内距离、扩展类间距。