为了建模实际问题中信息存在的不完整性、不确定性与模糊性，Yang等^[1]提出了基于证据理论的置信规则库推理方法(belief rule-based inference methodology using the evidence reasoning，RIMER)。该方法将传统IF-THEN规则同决策理论^[2]、模糊集理论^[3]、D-S证据理论^[4-5]等理论相结合，使其具有处理不完整、不确定、模糊信息的能力。以RIMER为基础构建的专家系统称为置信规则库系统^[6]，它将置信规则库作为载体来表达知识，并且利用证据推理(evidence reasoning，ER)算法实现知识的推理。置信规则库系统已经成功应用于输油管道检漏^[7]、出租车乘车概率预测^[8]、消费者偏好预测^[9-10]等方面。

早期的置信规则库(belief rule base，BRB)系统需要根据领域知识人为设定系统参数，无法推广到大规模规则库的构建上，因此一些学者提出了梯度下降优化、差分进化、变速粒子群优化等基于参数学习的优化方法^[11-15]。参数学习的引入虽然提高了规则库的推理精度，但是大多数参数学习方法需要反复迭代得出最终结果，无法保证推理的效率。由于BRB的规则数量与条件属性及条件属性候选值呈指数相关，BRB的规模易出现“组合爆炸”，于是一些学者利用主成分分析、关联系数标准差融合、粗糙集约减等方法对BRB的结构进行优化^[16-18]，这有助于提高规则库的推理效率，但要求条件属性具有可约减性。

因此，Liu等^[19]提出了基于数据驱动的扩展置信规则库(extended belief rule base，EBRB)系统，它既不需要进行繁复的参数训练，又能更好解决“组合爆炸”问题。EBRB系统在传统BRB系统的基础上，扩展了规则的前提属性部分，引入类似于BRB系统中结果属性的置信分布形式，使得规则库的条件部分对模糊性、不确定性信息具有更强的表达能力，由此引发了众多学者的关注并产生了一系列研究成果。Yang等^[20]通过分析规则的不完整性和不一致性，提出了适用于规则推理过程的激活规则筛选方法。林燕清等^[21]利用NSGA-II多目标优化智能算法来寻找最佳激活规则子集，改进了EBRB系统的整体效果。为了解决EBRB系统中每条规则无序存储导致推理效率低下的问题，苏群等^[22]提出对EBRB系统规则库构建BK树索引，提高了EBRB系统的推理性能；在此基础上，Yang等^[23]针对不同条件属性维度的规则库提出基于多属性搜索框架的EBRB系统，增强EBRB系统在多场景下的适用性；Lin等^[24]提出了基于VP、MVP索引结构的EBRB系统，并且通过聚类算法实现了索引参数的自动化选择。

采用Liu等^[19]所提方法来构建EBRB系统，相比传统BRB系统，无需训练大量参数，同时能取得较好的推理效果。但仍存在以下问题：1)EBRB系统的激活规则存在规则的不一致性与不完整性问题，影响了EBRB系统的推理效率与推理精度；2)当输入数据与所有规则的激活权重都较低时，推理出现异常，无法得出结果，即规则零激活问题。Calzada等^[25]提出了动态规则激活方法，通过调节激活规则的一致性与完整性来提高EBRB系统的推理精度，但是未从本质上解决规则零激活问题，并且推理效率受算法迭代次数影响。林燕清等^[26]提出改进的个体匹配度计算方法来解决规则零激活问题，但同时加剧了激活规则的不一致性，每一次输入都要通过反复迭代选取最优子集的方式来降低不一致性，限制了EBRB系统的推理效率。

为解决这些问题，本文提出基于改进规则激活率的扩展置信规则库方法，主要贡献有：1)在EBRB系统中，输入数据与规则库的相似性度量会直接影响到系统的推理过程，因此本文引入基于高斯核的动态个体匹配度计算方法，以提高EBRB系统的推理能力；2)本文利用k近邻方法，对产生零激活的输入数据进行二次处理，在保证系统效率的前提下，解决零激活问题；3)本文对EBRB系统激活规则的一致性与完整性进行讨论，结合新的个体匹配度计算方法，通过控制规则激活率来平衡激活规则的一致性与完整性，提高EBRB系统的推理性能。

1 EBRB专家系统 1.1 EBRB表示

EBRB系统中的置信规则格式如式(1)所示：

$ \begin{array}{l} {R_k}:{\rm IF}\;{U_1}\;{\rm is}\;\{ ({A_{11}},\alpha _{11}^k),({A_{12}},\alpha _{12}^k), \cdots ,({A_{1{J_1}}},\alpha _{1{J_1}}^k)\} \wedge \\ \;\;\;\;\;\;\;\;\;\;\;{U_2}\;{\rm is}\;{\rm{\{ }}({A_{21}},\alpha _{21}^k),({A_{22}},\alpha _{22}^k), \cdots ,({A_{2{J_2}}},\alpha _{2{J_2}}^k)\} \wedge \cdots \wedge \\ \;\;\;\;\;\;\;\;\;\;\;{U_T}\;{\rm is}\;\{ ({A_{T1}},\alpha _{T1}^k),({A_{T2}},\alpha _{T2}^k), \cdots ,({A_{T{J_T}}},\alpha _{T{J_T}}^k)\} \\ \;\;\;\;\;\;{\rm THEN}\;\{ ({D_1},\beta _1^k),({D_2},\beta _2^k), \cdots ,({D_N},\beta _N^k)\} \\ \;\;\;\;\;\;{\rm with\;a\;rule\;weight}\;{\theta _k}\; {\rm and\;attribute\;weights}\\ \;\;\;\;\;\;{\delta _1},{\delta _2}, \cdots ,{\delta _T};\\ \;\;\;\;\;\;\displaystyle{\rm{s}}{\rm{.t}}{\rm{.}}\;\sum\limits_{j = 1}^N {\beta _j^k \leqslant 1} ,\;\sum\limits_{{\rm{j}} = 1}^{{J_i}} {\alpha _{ij}^k \leqslant 1} \end{array} $

(1)

式中：k表示当前描述的是第k条规则； ${U_i}$ 表示第i个属性； $({A_{ij}},\alpha _{ij}^k)$ 为属性U_i的置信分布形式；A_ij表示第i个属性的第j个参考值； $\alpha _{ij}^k$ 为其对应的置信度；T表示属性总数；J_i表示第i个属性的参考值的个数；θ_k表示第k条规则的规则权重；δ_i表示第i个属性的属性权重；D_j表示第j个结果属性参考值， $\beta _j^k$ 为D_j对应的置信度；N表示结果属性参考值的总数。

1.2 EBRB规则构建

有别于BRB系统的规则库构建方式，EBRB系统中的规则可依据数据生成。假设有L条数据，且每条数据有T个条件属性与一个结果属性：

$ {\rm{\{ (}}x_1^k,x_2^k, \cdots ,x_T^k;{y^k})|k = 1,2, \cdots ,L\} $

以下给出EBRB系统的规则生成步骤：

1) 根据领域专家的经验得到^[1]，或者通过模糊隶属函数^[27]确定每个条件属性参考值 $\left\{ {{A_{ij}},i = } \right. $ $\left. { 1,2, \cdots ,T,j = 1,2, \cdots ,{J_i}} \right\} $ 和结果属性参考值 $\left\{ {{D_j},j = } \right.$ $ \left. { 1,2, \cdots ,N} \right\} $ 。

2) 利用1)确定的条件属性参考值和结果属性参考值，将训练数据的输入X以及输出y分别转化为对应的置信分布形式。本文针对数值型数据给出置信分布转化方法：

首先，考虑生成规则库条件属性的置信分布。对第k条数据的输入部分 ${X^k} = (x_1^k,x_2^k, \cdots ,x_T^k)$ ，考虑将第i个分量 $x_i^k$ 转化成如下置信分布形式：

$ E(x_i^k) = \{ ({A_{ij}},\alpha _{ij}^k),j = 1,2, \cdots ,{J_i}\} $

(2)

令γ_ij表示属性参考值A_ij对应的数值，且保证 $ \left\{ {{\gamma _i}_{(j + 1)} > {\gamma _{ij}}, j = 1,2, \cdots ,J_i - 1} \right\} $ 。则 $\alpha _{ij}^k$ 的计算公式如下：

$ \alpha _{ij}^k = \frac{{{\gamma _{i(j + 1)}} - x_i^k}}{{{\gamma _{i(j + 1)}} - {\gamma _{ij}}}}, \;{\gamma _{ij}} \leqslant x_i^k \leqslant {\gamma _{i(j + 1)}},\;j = 1,2, \ldots ,{J_i} - 1 $

(3)

$\alpha _{i(j + 1)}^k = 1 - \alpha _{ij}^k,\;{\gamma _{ij}} \leqslant x_i^k \leqslant {\gamma _{i(j + 1)}},\;j = 1,2, \cdots ,{J_i} - 1 $

(4)

$ \alpha _{it}^k = 0,\; t = 1,2, \cdots ,j - 1,j + 2, \cdots ,{J_i} $

(5)

同理，根据第k条数据的输出值 ${y^k}$ ，我们也可计算得到规则的结果属性的置信分布形式：

$E({y^k}) = \{ ({D_j},\beta _j^k),j = 1,2, \cdots ,N\} $

3) 利用2)的方法，本文可将数据 ${\rm{(}}x_1^k,x_2^k, \cdots , $ $x_T^k;{y^k})$ 转化成如式(1)所示的规则，从而得到初步的规则库。

4) 确定EBRB中每条规则的权重以及条件属性权重。由于EBRB的每条规则都由数据生成的，因此规则权重的设定需要考虑到数据质量引起的规则之间的冲突与不一致，将不一致性指标^[19]引入规则权重的计算可以缓解规则的冲突性。

1.3 EBRB推理机制

EBRB系统规则库生成之后，即可进行EBRB推理。给定一个T维输入数据 $X = ({x_1},{x_2}, \cdots ,{x_T})$ ，根据式(2)~(5)可得输入对应的置信分布形式：

$ E\left( {{x_i}} \right) = \left\{ {\left( {{A_{ij}},{\alpha _{ij}}} \right),i = 1,2, \cdots T,j = 1,2, \cdots ,{J_i}} \right\} $

由此，可计算第k条规则与该输入关于第i个条件属性的个体匹配度：

$ d_i^k = \sqrt {\sum\limits_{j = 1}^{{J_i}} {{{({\alpha _{i,j}} - \alpha _{i,j}^k)}^2}} } $

(6)

$ S_i^k = 1{\rm{ - }}d_i^k $

(7)

第k条规则的激活权重计算公式如下：

$ \begin{gathered} \displaystyle{\omega _k} = \frac{{{\theta _k}\prod\limits_{i = 1}^{{T_k}} {{{\left( {S_i^k} \right)}^{{{\bar \delta }_i}}}} }}{{\sum\limits_{l = 1}^L {\left[ {{\theta _l}\prod\limits_{i = 1}^{{T_l}} {{{\left( {S_i^l} \right)}^{{{\bar \delta }_i}}}} } \right]} }}\;\;,\;\;{{\bar \delta }_i} = \frac{{{\delta _i}}}{{\begin{array}{*{20}{c}} {\max } \\ {j = 1,2, \cdots ,{T_k}} \end{array}\left\{ {{\delta _j}} \right\}}} \\ \displaystyle{\rm{s}}{\rm{.t}}.\;0 \leqslant {\omega _k} \leqslant 1(k = 1,2, \cdots ,L),\sum\limits_{i = 1}^L {{\omega _i}} = 1 \\ \end{gathered} $

(8)

接下来对激活权重不为零的规则进行ER合成，并获得推理结果。首先将式(1)中的 $\beta _j^k$ 转化为对应的基本概率值：

$ \begin{array}{l} \displaystyle m_j^k = {\omega _k}\beta _j^k\\ \displaystyle m_D^k = 1 - {\omega _k}\sum\limits_{j = 1}^N {\beta _j^k} \\ \displaystyle \bar m_D^k = 1 - {\omega _k}\\ \displaystyle \tilde m_D^k = {\omega _k}\left( {1 - \sum\limits_{j = 1}^N {\beta _j^k} } \right) \end{array} $

式中： $m_j^k$ 表示第j个结果属性参考值的基本可信度； $\bar m_D^k$ 表示规则激活权重未分配给任何结果属性参考值的基本可信度； $\tilde m_D^k$ 表示结果属性参考值的不完备性所导致的基本可信度。根据以上公式可推导出 $m_D^k = \bar m_D^k{\rm{ + }}\tilde m_D^k$ 。

接着对所有的规则进行ER合成，得到结果属性参考值D_j的置信度：

$ {C_j} = t\left[ {\prod\limits_{l = 1}^L {\left( {m_j^l + \bar m_D^l + \tilde m_D^l} \right)} - \prod\limits_{l = 1}^L {\left( {\bar m_D^l + \tilde m_D^l} \right)} } \right] $

$ {\tilde C_D} = t\left[ {\prod\limits_{l = 1}^L {\left( {\bar m_D^l + \tilde m_D^l} \right)} - \prod\limits_{l = 1}^L {\bar m_D^l} } \right] $

$ {\bar C_D} = t\prod\limits_{l = 1}^L {\bar m_D^l} $

$ {t^{ - 1}} = \sum\limits_{j = 1}^N {\prod\limits_{l = 1}^L {\left( {m_j^l + \bar m_D^l + \tilde m_D^l} \right)} } - \left( {N - 1} \right)\prod\limits_{l = 1}^L {\left( {\bar m_D^l + \tilde m_D^l} \right)} $

$ {\beta _j} = \frac{{{C_j}}}{{1 - {{\bar C}_D}}}, \; j = 1,\ 2,\ \cdots ,N $

$ {\beta _D} = \frac{{{{\tilde C}_D}}}{{1 - {{\bar C}_D}}} $

当最终的输出结果要求为单一数值时，可以通过计算规则库的期望效用值来获取最后结果：

$ f\left( {{x_t}} \right) = \sum\limits_{j = 1}^N {\left( {\mu \left( {{D_j}} \right){\beta _j}} \right)} + \frac{{\left( {\mu \left( {{D_1}} \right) + \mu \left( {{D_N}} \right)} \right)}}{2}\left( {1 - \sum\limits_{j = 1}^N {{\beta _j}} } \right) $

2 EBRB激活方法优化 2.1 一致性与完整性问题

EBRB属于数据驱动的置信规则库，因此规则库质量会受数据质量的影响。当被激活的规则中存在冲突规则，或者包含大量与输入相关度低的规则时，证据推理的效果会受影响，EBRB系统存在规则不一致性问题。相反，当被激活的规则中只包含少量规则，一些相关度高的规则未被激活时，同样也会影响最终的推理结果，即EBRB系统存在规则不完整性问题。

被激活的规则范围越大，越容易造成规则不一致性问题；被激活的规则范围越小，则规则不完整性问题会突显。因此，为了达到更好的推理效果，需要对规则的一致性与完整性进行权衡。

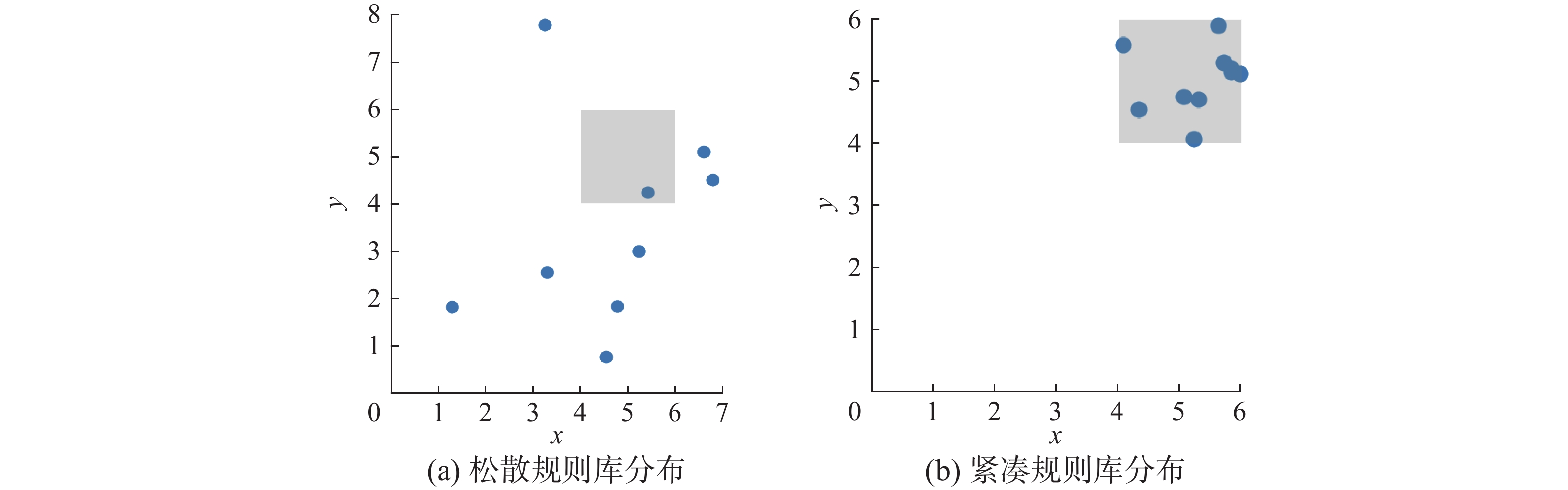
2.2 个体匹配度计算方法改进

根据1.3节中EBRB系统的推理框架，可以发现式(7)中个体匹配度 $S_i^k$ 需要满足如下条件：1)非负性，即 $S_i^k \in [0,1]$ ，其中 $S_i^k=0$ 表示输入数据与规则完全不匹配， $S_i^k{\rm{ = 1}}$ 表示输入数据与规则完美匹配；2)单调性，输入数据与规则的相似度越高，对应的个体匹配度的值越大。

结合式(1)中α的约束条件，可知式(7)中 $S_i^k \in [1{\rm{ - }}\sqrt 2 ,1]$ ，不符合非负性条件，EBRB系统存在隐患，不具备良好的鲁棒性。此外，式(7)中个体匹配度计算方法是静态的，无法控制规则激活率以适应不同EBRB系统对激活规则的一致性与完整性要求。本文以二维数据为例，利用Calzada等^[25]所提方法，将生成的规则库映射到二维空间中，如图1所示，其中结点代表规则库的分布，图1(a)的规则库分布密度较小，图1(b)的规则库分布密度较大。阴影区域表示利用式(7)计算得到的某一特定输入对应的激活域，位于激活域内的规则将会被激活。观察图1(a)，10条规则仅有1条规则位于激活域内，易造成规则不完整性问题；相反，图1(b)中10条规则全部位于激活域内，易造成规则不一致性问题。可见，静态的个体匹配度计算方法无法适应不同分布下的EBRB系统。

为了解决上述问题，本文将高斯核函数作为新的个体匹配度计算公式，通过引入参数σ来控制规则激活率，对规则的一致性与完整性进行权衡：

$ S_i^k = \exp {\rm{( - }}{(d_i^k)^2}/(2{\sigma ^2}){\rm{)}}, \sigma {\rm{ > 0}} $

(9)

易知式(9)中 $S_i^k \in [\exp ( - 1/{\sigma ^2}),1]$ ，符合非负性；且 $S_i^k$ 随 $d_i^k$ 的减小而增大， $d_i^k$ 越小说明个体匹配度越高，因此 $S_i^k$ 满足单调性。

如图2所示，函数S₁、S₂分别来自文献[19,26]，函数S₃为本文所提方法。观察可知，S₃相对于S₁与S₂，有如下优点：1)函数S₁在 $d \in [1,\sqrt 2 ]$ 时取值小于0，会使EBRB无法正常运作，而函数S₃的取值始终不小于零；2)函数S₂取值区间为 $[1/(1{\rm{ + }}\sqrt 2 ),{\rm{ 1]}}$ ，无法保证激活规则的一致性，而函数S₃取值区间为 $[0,1]$ ，因此激活规则的一致性可以得到保证；3)函数S₁、S₂都是静态的，无法适应基于不同数据分布构建的规则库，而如图3所示，函数S₃能够通过调整参数σ，对个体匹配度计算方法进行调整，从而使其适应不同分布的规则库。

2.3 规则零激活处理方法

观察式(8)，可知个体匹配度连乘得到规则激活权重，因此如果有一个属性的个体匹配度计算结果为零，则对应规则的激活权重为零。当所有规则激活权重都为零时，EBRB系统瘫痪，无法得到对应输出结果。

为了解决上述问题，林燕清等^[26]提出新的个体匹配度计算方法：

$ S_i^k = 1/(1 + d_i^k) $

(10)

由式(1)和式(6)可知式(10)中 $S_i^k$ 的取值范围为 $[1/(1{\rm{ + }}\sqrt 2 ),{\rm{ 1]}}$ ，虽然可以解决“零激活”问题，但 $S_i^k$ 最小值也会超过0.4，这导致激活规则集合存在严重的不一致性，特别是在规则的条件属性较少的情况下。因此，林燕清等^[26]通过反复迭代选取最优激活子集的方式来降低不一致性，但这导致系统的推理效率得不到保障。

分析以上问题可以发现，主要原因是因为没有将发生零激活的输入与正常的输入分开处理。因此本文提出针对规则零激活的二次处理方法，结合k近邻思想^[28]，在权衡规则的一致性与完整性的前提下，解决“零激活”问题。具体实现如算法1所示，其中参数t通过对训练数据进行多则交叉的方式获取。

算法1　零激活输入二次处理算法

输入　产生零激活的输入 $X = {\rm{ }}({x_1},{x_2}, \cdots ,{x_T}) $ ；

输出　激活权重前t大的规则集合Rules2 。

1) W = [] /*数组初始化为空*/

2) for R_k in Rules do

3) for U_i in R_k do

4) calculate similarity of (x_i,U_i) /*依据式(9), σ取较大值, 保证规则全激活*/

5) end for

6) calculate w_k /*式(8)*/

7) W.append(w_k)

8) end for

9) sort(W) (descending)

10) threshod = W[t]

11) Rules2 = []

12) for R_k in Rules do

13) if w_k > threshod do

14) Rules2.append(R_k)

15) end if

16) end for

17) return Rules2

2.4 EBRB推理方法改进

以第1节的EBRB框架为基础，结合第2.2和2.3节基于规则激活率优化的个体匹配度计算方法以及零激活输入二次处理算法，本节将介绍改进后的扩展置信规则库的推理过程。

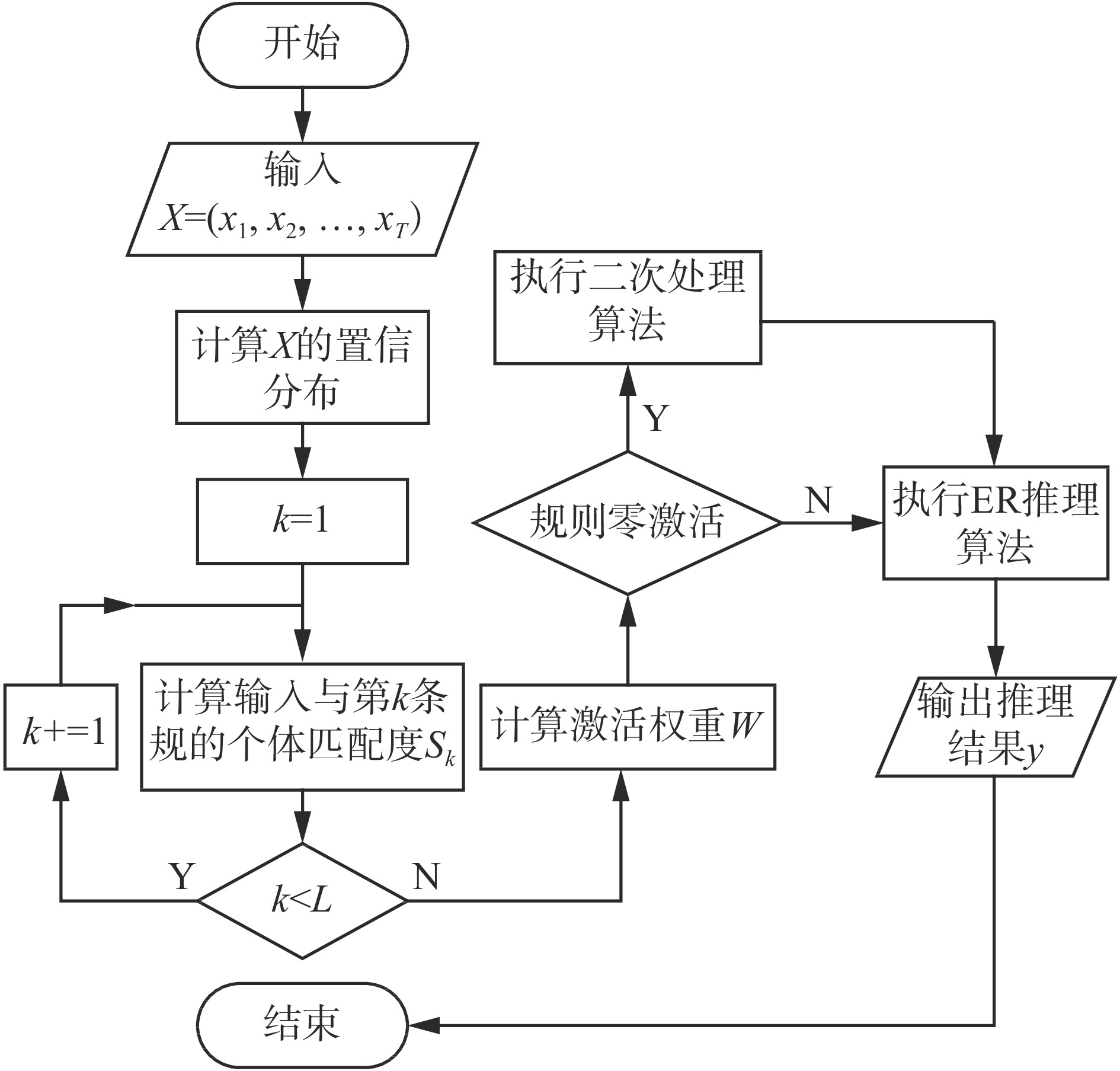
图4为改进后的扩展置信规则库的推理过程，具体步骤描述如下。

1) 给定输入 $X = ({x_1},{x_2}, \cdots ,{x_T})$ ，首先根据式(2)~(5)计算得X的置信分布表示：

$ \begin{array}{*{20}{l}} {\alpha {\rm{ }} = \left\{ {{\alpha _{ij}},i = {\rm{ }}1,2, \cdots ,T,j = 1,2, \cdots ,{J_i}} \right\}} \end{array} $

2) 根据式(9)得到该输入与第k条规则对应的每个条件属性的个体匹配度：

$ {S^k} = \{ S_1^k({x_1},{U_1}),S_2^k({x_2},{U_2}), \cdots ,S_T^k({x_T},{U_T})\} $

3) 循环执行2)，得到输入X与规则库中所有规则的个体匹配度；

4) 以步骤2)、3)得到的结果为基础，按照公式(8)计算出每条规则对应的激活权重，如下所示：

$ W(X) = \{ {W_1}(X),{W_2}(X), \cdots ,{W_L}(X)\} $

5) 如果步骤4)中出现规则零激活问题，则执行步骤6)；否则执行步骤7)；

6) 执行2.3节提出的二次处理算法，重新计算个体匹配度，并且只选择激活权重前t大的规则进行ER推理；

7) 运行ER算法融合所有激活规则，得到EBRB系统的输出结果。

2.5 时间复杂度分析

本文提出的基于改进规则激活率的EBRB系统的时间复杂度主要体现在规则库构建与规则推理两个部分。其中规则库构建部分，假设条件属性的个数为T，每个条件属性的候选值个数为J，规则总数为L，结果属性参考值数为N，则每条规则生成的时间为O(TJ)，规则初始权重调节时间为O(L²TJ)，因此规则库总的构建时间为O(L²TJ)。

EBRB系统推理部分，将输入转变为对应的置信分布形式需要O(TJ)；计算个体匹配度的时间需要O(LTJ)，规则权重的计算需要O(LT)，若出现规则零激活，需执行二次处理算法，处理时间变为O(LTJ+LlogL)。由于只有激活权重超过零的规则才会进入ER推理，这里假设有αL条规则进入ER推理，其中 $\alpha \in \left[ {0,1} \right]$ ，则有EBRB的推理时间为O(NαL)。因此本文改进的EBRB系统处理每一条输入数据的时间复杂度为O(L(TJ+αN+logL))。

与文献[19]对比可知本文方法的规则库构建部分复杂度与其相同。规则推理部分，Liu^[19]的时间复杂度为O(L(TJ+N))。当输入未发生零激活时，本文方法的推理复杂度为O(L(TJ+αN))，要优于Liu^[19]的方法。当输入发生零激活时，Liu^[19]的方法会出现异常，而本文以较小时间代价，解决了零激活问题。

3 实验与结果

本文首先介绍函数仿真实验，研究参数σ对EBRB系统的影响，接着选取输油管道检漏作为实验案例，与其他方法进行对比分析，验证本文方法的有效性。实验环境为：Intel(R) Core i7-6700@ 3.40 GHz；16 GB内存；Windows 10 操作系统；算法在Python3.6环境下编写。

3.1 非线性函数拟合

林燕清等^[19]表明EBRB系统可以拟合任意非线性函数，为了验证本文方法的效果，将通过一个常用非线性函数进行测试，其数学表达式为

$ f(x) = x\sin ({x^2}),0 \leqslant x \leqslant 3 $

(11)

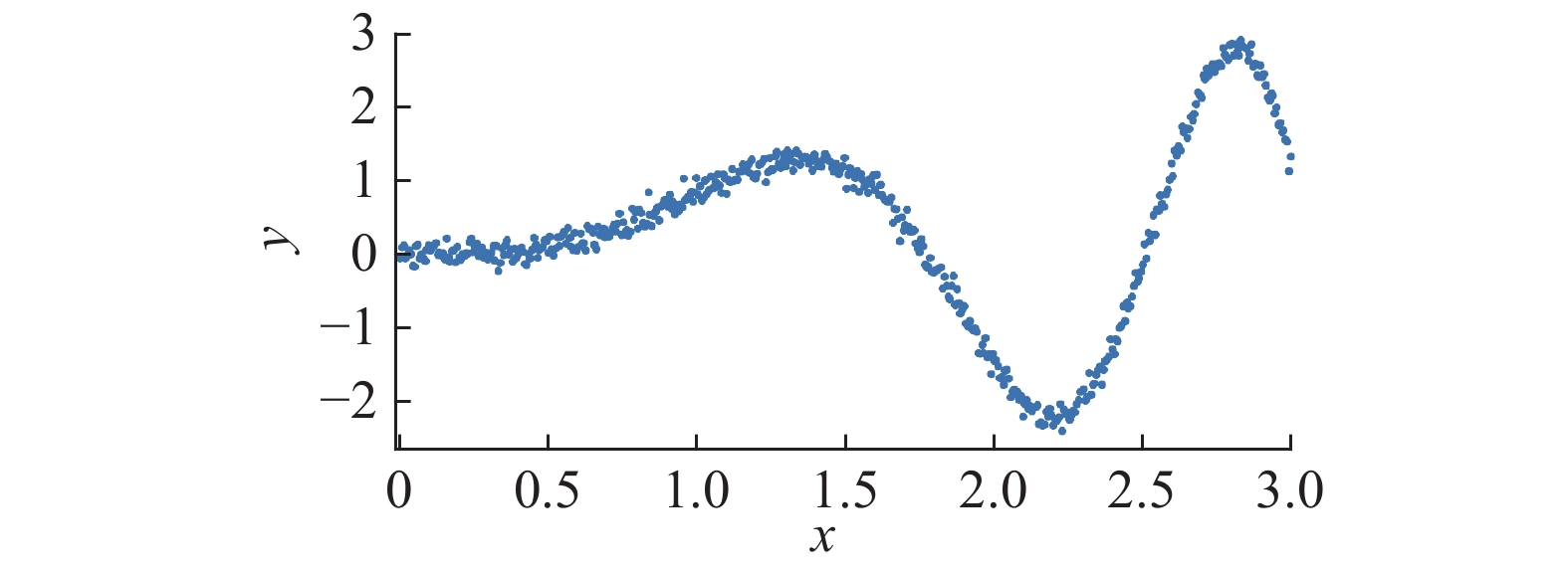
构建EBRB系统的过程中，令x为条件属性，并且在区间 $[0,3]$ 内均匀选取7个点当作参考值，分别为{0,0.5,1,1.5,2,2.5,3}。函数值 $f(x)$ 作为输出结果，其评价等级效用值设为{−2.5,−1,1,2,3}。在区间 $[0,3]$ 中均匀选择500个点作为训练数据中x的取值，计算出 $f(x)$ 并且加入高斯随机数噪声作为训练数据的输出结果，训练数据如图5所示。利用训练数据构建出EBRB系统规则库之后，在区间[0,3]中均匀选择1 000个点作为测试数据，计算EBRB系统的输出与真实值 $f(x)$ 之间的损失，用均方误差(mean square error，MSE)作为评价依据。

对式(9)中的σ取不同的值，观察改进后的EBRB系统对非线性函数的拟合效果，实验结果如表1所示，其中平均处理时间是指处理一个输入需要耗费的平均时间。从表1中，可观察出随着σ的减小，MSE呈现出先下降后上升的趋势。σ从1变化到0.05的过程中，MSE下降是因为当σ较大时，平均激活规则数较多，这容易引起规则的不一致性与不相关性问题，因此随着σ的减小，平均激活规则数也随之减小，规则的一致性与相关性得到一定保障，EBRB系统的预测精度提升；当σ从0.05变化到0.002时，平均激活规则数的过度减小引起了规则的不完整性问题，EBRB系统的预测能力也逐渐降低。同时可以观察出随着平均激活规则数的降低，平均处理时间也跟随下降，这是因为进入证据推理环节的规则变少导致推理的时间减少。

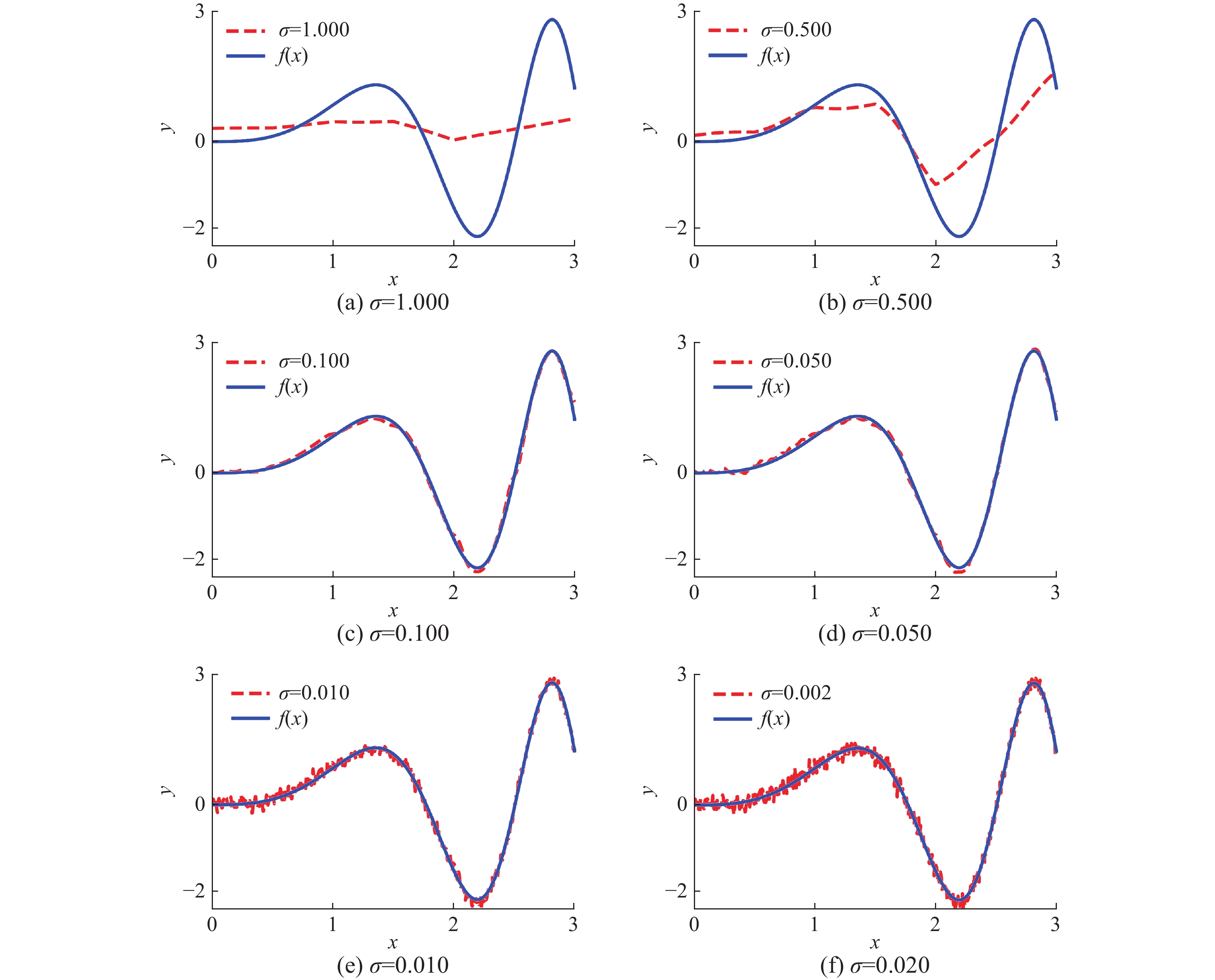
图6为表1对应的函数拟合曲线对比图。当σ较大时，EBRB系统的预测结果未能拟合式(11)，但随着σ的减小，预测结果在不断逼近式(11)；当σ位于区间 $[0.05,0.1]$ 时，预测结果已经能够基本拟合式(11)，且可以看出虽然σ = 0.05时的MSE更小，但σ = 0.1时曲线要更加光滑，因此可以判断出预测结果已经过拟合；随着σ的进一步减小，预测结果出现锯齿状，且MSE也开始回升，EBRB系统过拟合现象更加明显。

为了验证本文所提个体匹配度计算方法的有效性，本文将其与文献[19,26]中的个体匹配度计算方法进行对比。为了保证对比结果的可靠性，本文对文献[19,26]的方法也引入零激活输入二次处理算法，并且将个体匹配度小于零的值上调为零。

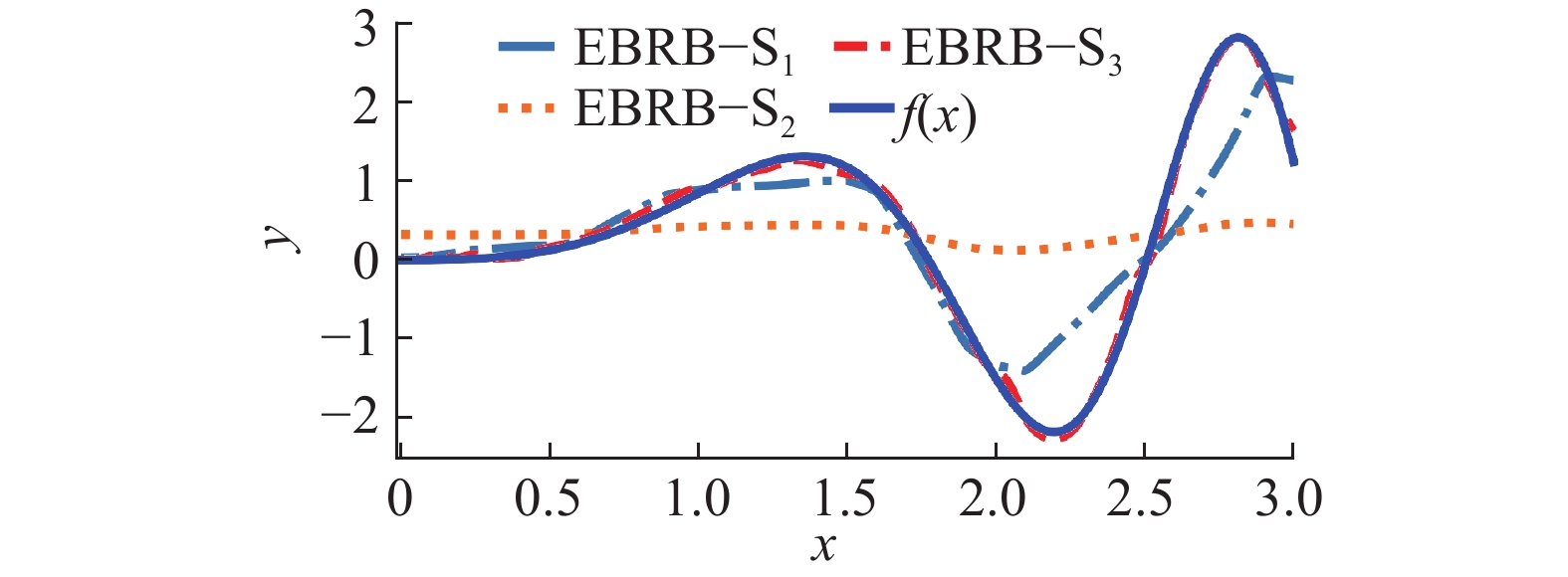
表2列出了3种方法的函数拟合输出结果，其中EBRB-S₁、EBRB-S₂分别代表文献[19,26]中个体匹配度计算方法构建的EBRB系统，EBRB-S₃代表本文所提方法。从表2中可得出EBRB-S₃的MSE值要远低于EBRB-S₁、EBRB-S₂，并且EBRB-S₁方法中出现个体匹配度小于零的输入有1 000条，EBRB-S₁中所使用的个体匹配度计算方法存在较大缺陷。EBRB-S₃方法不仅精度高，而且运行效率良好，其平均处理时间比EBRB-S₁降低了9.1%，比EBRB-S₂降低了33.3%。

图7为表2对应的函数拟合曲线，从中可观察出EBRB-S₂基本未拟合函数，主要是因为其对应的个体匹配度计算方法引起的规则不一致与不相关程度较大；EBRB-S₁的拟合效果要比EBRB-S₂好，但在函数的极值部分，拟合效果仍不理想；只有EBRB-S₃基本拟合了曲线的走势，并且曲线的走势也比较光滑。

通过非线性函数拟合实验，验证了EBRB-S₃系统的重要性质。接下来将通过实际生活中的输油管道检漏实验进一步验证本文方法的有效性。

3.2 输油管道检漏

输油管道检漏实验的研究对象为英国一条长达一百多公里的输油管道，领域专家通过管道的入口与出口流量差异(flow difference，FD)以及输油管道内的平均压力差(pressure difference，PD)这两个因素来检测输油管道发生泄漏的大小(leak size，LS)，因此该实验以FD和PD作为EBRB系统的两个条件属性，泄露大小LS作为输出结果。根据领域专家的经验给出两个条件属性参考值分别为A_FD = {−10, −5, −3, −1, 0, 1, 2, 3}、A_PD = {−0.042, −0.025, −0.010, 0.000, 0.010, 0.025, 0.042}，设定输出结果属性参考值为D_LS={0, 2, 4, 6, 8}。

为了同文献[19,25-26]进行比较，本文选择出500组数据作为训练数据，然后利用本文所提方法构建EBRB-S₃规则库。最后用构建好的系统预测2 008组测试数据，并将实验结果的平均绝对误差(mean absolute error，MAE)作为评价依据，同其他的EBRB系统进行对比。

表3为3.1节所提到的EBRB-S₁、EBRB-S₂、EBRB-S₃3种EBRB系统的输油管道检漏实验结果，EBRB-S₃的MAE值相比EBRB-S₁下降了32.5%，并且远小于EBRB-S₂。这表明本文所提个体匹配度计算方法能够提高EBRB系统的性能。观察3种方法的平均处理时间，与表2相比差距变小，主要原因是输油管道检漏实验的规则库条件属性数量与参考值数量都比非线性函数拟合多，因此置信分布转化、个体匹配度计算等初始化时间占了主要部分，激活规则数量变化导致的时间差异被弱化。

表4列出了Liu-EBRB系统^[19]、DRA-EBRB系统^[25]、SRA-EBRB系统^[26]以及本文方法的输出结果与真实结果之间的MAE值，系统处理每条输入需要花费的平均时间、出现零激活的输入个数(Failed)。其中EBRB-S₃的MAE值最小，比排名第二小的SRA-EBRB降低了19.7%。并且EBRB-S₃的平均处理时间仅次于Liu-EBRB，比SRA-EBRB降低了62.3%，比DRA-EBRB降低了87.0%，这主要是因为SRA-EBRB与DRA-EBRB都是基于迭代的方法，需要反复扫描EBRB系统，因此平均处理时间相对较长。Liu-EBRB出现了一条引起规则零激活的输入，而EBRB-S₃对每一条输入都能够给出合理输出，这主要归功于EBRB-S₃引入了零激活输入二次处理算法，从根本上解决规则零激活问题。综上所述，EBRB-S₃在保证系统运行效率的前提下，提高了EBRB系统的推理精度，增强了EBRB系统的鲁棒性。

图8为EBRB-S₃的预测值与真实观测值的三维对比图，可以发现EBRB-S₃能够得到接近真实值的结果。

4 结束语

本文针对现有EBRB系统激活规则的不一致性与不完整性，以及无法处理“零激活”输入的问题，提出了基于改进规则激活率的扩展置信规则库方法。该方法将高斯核函数作为新的个体匹配度计算方法，对规则的激活率进行调整，保证EBRB系统激活规则的一致性与完整性的权衡；对于出现规则零激活现象的输入，本文提出了基于k近邻思想的二次处理算法，解决了规则零激活问题。为了验证本文方法的有效性，通过非线性函数拟合和输油管道检漏两个实验与其他EBRB系统进行了对比分析，研究结果表明本文所提方法取得了预期效果。