粗糙集^[1-2]是Pawlak提出的一种用以刻画不确定性的建模方法。由于经典粗糙集所使用的等价关系仅仅适用于符号型数据，为了弥补这一不足，涌现出了一批可以处理复杂类型数据的拓展粗糙集模型^[3-5]。

众所周知，无论是在经典粗糙集还是在众多拓展粗糙集研究中，属性约简^[6-10]一直扮演着核心角色。根据问题求解需求的不同，属性约简可以使用不同的度量准则加以定义，因此其具有丰富的解释与含义。例如近似质量可以用来度量数据中的确定性程度，条件熵可以用来描述条件属性相对于决策属性的鉴别能力。属性约简，就可以依据这些度量准则，找到数据中的冗余属性并加以删除，以达到满足度量准则所对应的约束条件。通过这一策略，还能够使得后续的学习过程仅需在一部分属性上构建模型，从而达到降低学习难度以及降低学习时间消耗的目的。

目前在粗糙集理论中，穷举法与启发式方法被公认为是求解约简的两大类基本方法。然而很多穷举搜索与启发式搜索策略都将数据集中的所有样本视为同等重要，当样本量非常巨大时，这会带来较低的约简求解效率。为解决这一问题，已有众多学者将样本选择的概念引入到约简求解过程中。样本选择的概念最早是由Hart提出，他提出了压缩近邻规则^[11]，随后亦有学者提出了很多改进策略，如缩减最近邻^[12]、有序最近邻^[13]和快速压缩最近邻^[14]等。当涉及约简求解的问题时，已有学者^[15-19]关注到不同的样本对属性重要度评价的贡献是不同的，如王熙照等^[15]提出的K-means样本选择算法将远离类簇中心点的样本视为重要的；随后Xu等^[19]将这种方法应用到多标记数据的维度压缩问题中。但他们在追求时间效率的同时忽略了约简在测试集上的分类性能。

基于以上分析，笔者提出了一种基于样本一致性原则的样本选择算法(以下简称为一致性采样)，一致性采样的主要思想为：1)给定一个样本，找到距离自己最近的邻居；2)判断这一邻居是否与自身属于同一类别，若属于同一类别，则将该样本选中；3)最后将所有选中的样本组成一个新的数据集。

1 基础知识

在粗糙集理论中，一个决策系统可表示为一个二元组DS=<U, AT∪D>,U是所有样本构成的非空有限集合，即论域；AT是所有条件属性的集合；D是决策属性的集合且AT∩D= ${\textit{Ø}} $ 。当D的取值都为离散型时，可得U/IND (D)={X₁, X₂, $\cdots $ , X_q}，其表示根据决策属性D所诱导出的论域上的划分，对于 $\forall $ X_p∈U/IND(D), X_p表示第p个决策类，其中[x]_D表示与x属于同一个决策类的样本的集合。

定义1　给定一个决策系统DS, $\forall $ A $\subseteq $ AT, 则邻域关系定义为

$ {N_A}={\rm{ }}\{ (x,y) \in U \times U:r(x,y) \leqslant \delta \} $

(1)

其中， $\forall $ x, y∈U, r(x, y)表示样本x与y之间的欧氏距离，δ>0称为邻域半径。

则由式(1)，容易得到关于A样本x的邻域：

$ {\delta _A}\left( x \right){\rm{ }}={\rm{ }}\left\{ {{y_{}}|{\rm{ }}r(x,y) \leqslant \delta } \right\} $

(2)

定义2 　给定一个决策系统DS, U/IND(D)={X₁, X₂, $\cdots $ , X_q}, $\forall $ A $\subseteq $ AT, $\forall $ X_p∈U/IND(D), X_p关于A的下近似集和上近似集分别定义为

$ {{\underline {N_A}}{{X_p}} }=\{ x \in U|{\delta _A}\left( x \right) \subseteq {X_p}\} $

(3)

$ {{\overline {N_A}} {{X_p}}}=\{ x \in U|{\delta _A}\left( x \right) \cap {X_p} \ne \phi \} $

(4)

定义3^[20] 　给定一个决策系统DS, U/IND(D)={X₁, X₂, $\cdots $ , X_q}, $\forall $ A $\subseteq $ AT, D关于A的近似质量定义如下：

$ \gamma \left( {A,D} \right){\rm{=}}\frac{{\left| {\bigcup\limits_{p=1}^q {{{{\underline {N_A}}{{X_p}} }}} } \right|}}{{\left| U \right|}} $

(5)

其中|U|表示集合X的基数。

显然0≤γ(A, D)≤1成立。γ(A, D)表示根据条件属性A, 那些确定属于某一决策类别的样本占总体样本的比例。

条件熵是属性约简中另外一种常用的度量准则，它能反映条件属性相对于决策属性的鉴别能力。根据不同的需求，很多学者设计并定义了多种形式的条件熵^[21-25]，一种经典的形式可定义为：

定义4^[25] 　给定一个决策系统DS, $\forall $ A $\subseteq $ AT, D关于A的条件熵定义如下：

$ {\rm{ENT}}\left( {A,D} \right){\rm{ }}=- \frac{1}{{\left| U \right|}}\mathop {\sum\limits_{x \in U} {{\rm{log}}} }\limits_{} \frac{{\left| {{\delta _A}(x) \cap {{[x]}_D}} \right|}}{{\left| U \right|}} $

(6)

显然，条件熵的值越小，条件属性相对于决策属性鉴别能力越大。

2 属性约简

属性约简作为粗糙集领域的一个核心内容，其主要目的是根据某一给定的约束条件来去除全部属性中的冗余、不相关的属性。目前求解约简的常用策略包括穷举式算法和启发式算法。虽然前者可以得到一个数据中的所有约简，但当数据维数急剧升高时，它的时间消耗随之增大，过大的时间消耗导致算法并不适用于处理实际问题。与穷举式算法不同，启发式算法因其较高的时间效率得到了众多学者的青睐，它运用贪心策略，每次迭代过程中其将属性重要度最大的属性加入到潜在约简集合中，直至满足约束条件则终止算法。因此，接下来需要给出属性重要度的表达式。

$ {\rm Sig}{_\gamma }\left( {{a_i},A,D} \right){\rm{ }}=\gamma (A \cup \left\{ {{a_i}} \right\},D) - \gamma \left( {A,D} \right) $

(7)

$ \begin{array}{*{20}{l}} {{\rm{Si}}{{\rm{g}}_{{\rm{ENT}}}}\left( {{a_i},A,D} \right)={\rm{ENT}}\left( {A,D} \right) - {\rm{ENT}}(A \cup \left\{ {{a_i}} \right\},D){\rm{ }}} \end{array} $

(8)

对于近似质量(利用式(7)来计算属性重要度)，a_i的重要度越大，表示a_i对其值的提升效果越明显。而对于条件熵而言(利用式(8)来计算属性重要度)，a_i的重要度越大，则表示a_i对其值的降低效果越明显。

定义5　给定一个决策系统DS, $\forall $ A $\subseteq $ AT, A是DS中的一个关于φ的约简当且仅当：

(1) φ(A, D)满足约束条件；

(2) $\forall $ A' $\subseteq $ A, φ(A', D)不满足约束条件。

在定义5中，“φ”可以是“γ”也可以是“ENT”。当φ=γ时，约束条件可以定义为γ(A, D)≥γ(AT, D), 它表示利用约简A中的属性计算的近似质量值应不低于利用全部属性(AT)计算的近似质量值；而当φ=ENT时，约束条件则定义为ENT(A, D)≤ENT (AT, D), 它表示利用约简A中的属性计算的条件熵值应不高于利用全部属性(AT)计算的条件熵值。

算法1给出了一个求解定义5所示φ约简的启发式框架型描述。

算法1　启发式算法

输入　决策系统DS=<U, AT∪D>, 半径δ

输出　一个关于φ的约简：A

1) 计算φ(AT, D);

2) A←ϕ;

3)：

(1) $\forall $ a_i∈AT−A,计算属性a_i的重要度Sig_φ(a_i, A, D);

(2) 选出一个重要度最大的属性b, 令A=A∪{b};

(3) 计算φ(A, D);

4) 如果φ(A, D)满足约束条件，则直接转至5)

5) 返回A

算法1的时间复杂度为O(|U|²·|AT|²)，其中|U|为论域中样本数目，|AT|为条件属性数目。

算法1是基于单准则设计的，而运用基于单准则的算法得到的约简往往仅能满足一个约束条件，而此约简结果可能无法满足其他约束条件。例如：仅使用近似质量得到的约简满足自身的约束条件，但它往往无法同时提高分类能力，这主要是因为近似质量是用来描述数据中的确定性程度，而与数据的分类关系不大。为了弥补这一局限，近年来，根据多准则设计的约简也开始受到学者的重视。如Yang与Yao^[26]提出的集成选择器极大地丰富了约简的求解策略；随后，Li等^[27]利用这一思想设计了基于调和平均的多准则属性约简。Liu等^[21]进一步利用集成思想，将其扩展应用到半监督领域中。一般来说，多准则启发式算法可由算法2实现。

算法2　多准则启发式算法

输入　决策系统DS=<U, AT∪D>, 半径δ

输出　一个多准则约简：A

1) 计算φ₁(AT, D), φ₂(AT, D), $ \cdots$ , φ_m(AT, D);

2) A←ϕ;

3)

(1) For 1 ≤ k ≤ m

$\forall $ a_i∈AT−A，计算属性a_i的重要度 ${\rm{Si}}{{\rm{g}}_{{\varphi _{_k}}}}({a_i},A,D)$ ; 选出重要度最大的属性 $a_k^j$ ;

End For

(2) 在{ $a_1^j$ , $a_2^j,\ \cdots $ , $a_m^j$ }中选择一个出现频次最高的属性b;

(3) A=A∪{b};

(4) 计算φ₁(A, D), φ₂(A, D), $\cdots $ , φ_m(A, D);

4) 如果对于任意的k(1≤k≤m), φ_k(A, D)满足约束条件，则直接转至步骤5); 否则转至步骤3);

5) 返回A。

算法2的时间复杂度为O(m·|U|²·|AT|²)。在每次迭代过程，3)将m个准则下重要度最大的属性分别选择出来并记录每个属性出现的频次，选取频次最高的属性加入到潜在约简集合中：1)如果出现频次最高的属性是唯一的，则直接将其加入到潜在约简集合中；2)否则，出现频次最高的属性发生冲突情况，即两个或多个属性的频次同时达到最高，则需要进行选择，为了保证算法的稳定性，将位置靠前的属性加入到潜在约简集合中。

3 一致性采样约简

显然，第2节所示的两个算法都是基于扫描数据中的全部样本来实现的。但当数据体量较大时，这种求解策略的时间消耗较高。为了进一步压缩算法的时间消耗，可以将样本选择的方法引入到约简求解过程中。不同的样本选择方法会选取不同的样本，进而产生不同的分类效果。本文将一致性从样本间距离与样本的决策属性值角度出发，目的是使得算法可以利用选择出的样本获取更高的分类精度。算法大致分为两个主要部分：1)要全部样本组成的决策系统上进行采样处理以构建含有较少样本个数的新决策系统；2)随后，将一致性采样的思想应用到属性约简的求解过程中。具体算法流程如下所示。

算法3　一致性采样约简算法

输入　决策系统DS=<U, AT∪D>, 半径δ；

输出　一个约简A。

1)

(1) 令U'=Ø;

(2) $\forall $ y∈U, 计算样本之间距离r(x, y);

(3) 对r(x, y)进行排序；

(4) 取距离测试样本y最近的样本，若二者的决策值相同，则选中该测试样本并将其加入到U'中；

(5)将新选中的样本组成新的决策系统DS'=<U', AT∪D>;

2) 在新的决策系统DS'中计算φ₁(AT, D), φ₂(AT, D), $\cdots $ , φ_m(AT, D);

3) A←Ø;

4)

(1) For 1≤k≤m

$ \forall$ a_i∈AT−A，计算属性a_i的重要度 ${\rm{Si}}{{\rm{g}}_{{\varphi _{_k}}}}({a_i},A,D)$ ; 选出重要度最大的属性 $a_k^j$ ;

End For

(2) 在{ $a_1^j$ , $\cdots $ , $a_m^j$ }中选择一个出现频次最高的属性b;

(3) A=A∪{b};

(4) 计算φ₁(A, D), φ₂(A, D), $\cdots $ , φ_m(A, D);

5) 如果对于任意的k(1≤k≤m), φ_k(A, D)满足约束条件，则直接转至步骤6) ; 否则转至步骤4) ;

6) 返回A。

算法3的时间复杂度为O(|U|²+m·|U'|²·|AT|²)。其中，|U'|为新的决策系统中样本的个数。步骤1为样本选择的过程，将一致性样本选择出来的时间复杂度为O(|U|²)。而之后的步骤则是用启发式算法求解约简，由于使用的是新的决策系统，则时间复杂度为O(m·|U'|²·|AT|²)。这里的启发式算法可以为单准则属性约简算法也可以为多准则属性约简算法，当m=1时则简化为单准则属性约简算法。换言之，无论单准则还是多准则约简算法，都可先经过采样后再根据具体需求设计相应的属性约简算法。

4 实验分析

为了验证算法3的有效性，笔者从UCI数据集中选取了8组数据，数据的基本描述如表1所列。实验环境为PC机，双核2.60 GHz CPU，8 GB内存，windows 10操作系统，Matlab R2016a实验平台。

实验采用了5折交叉验证的方法，并且选取了10个不同的半径δ, 其值分别为0.03，0.06， $\cdots $ ，0.3。5折交叉验证的具体实施过程是将实验数据中的样本平均分成5份，即U₁, U₂, ∪ $\cdots $ , U₅。第一次使用U₂∪U₃∪ $\cdots $ ∪U₅作为训练集求得约简A₁，使用U₁作为测试集并在其中利用A₁中的属性计算分类精度；第2次使用U₁∪U₃∪…∪U₅作为训练集求得约简A₂，使用U₂作为测试集并在其中利用A₂中的属性计算分类精度；依次类推，第5次使用U₁∪U₂∪ $\cdots $ ∪U₄作为训练集求得约简A₅，使用U₅作为测试集并在其中利用A₅中的属性计算分类精度。

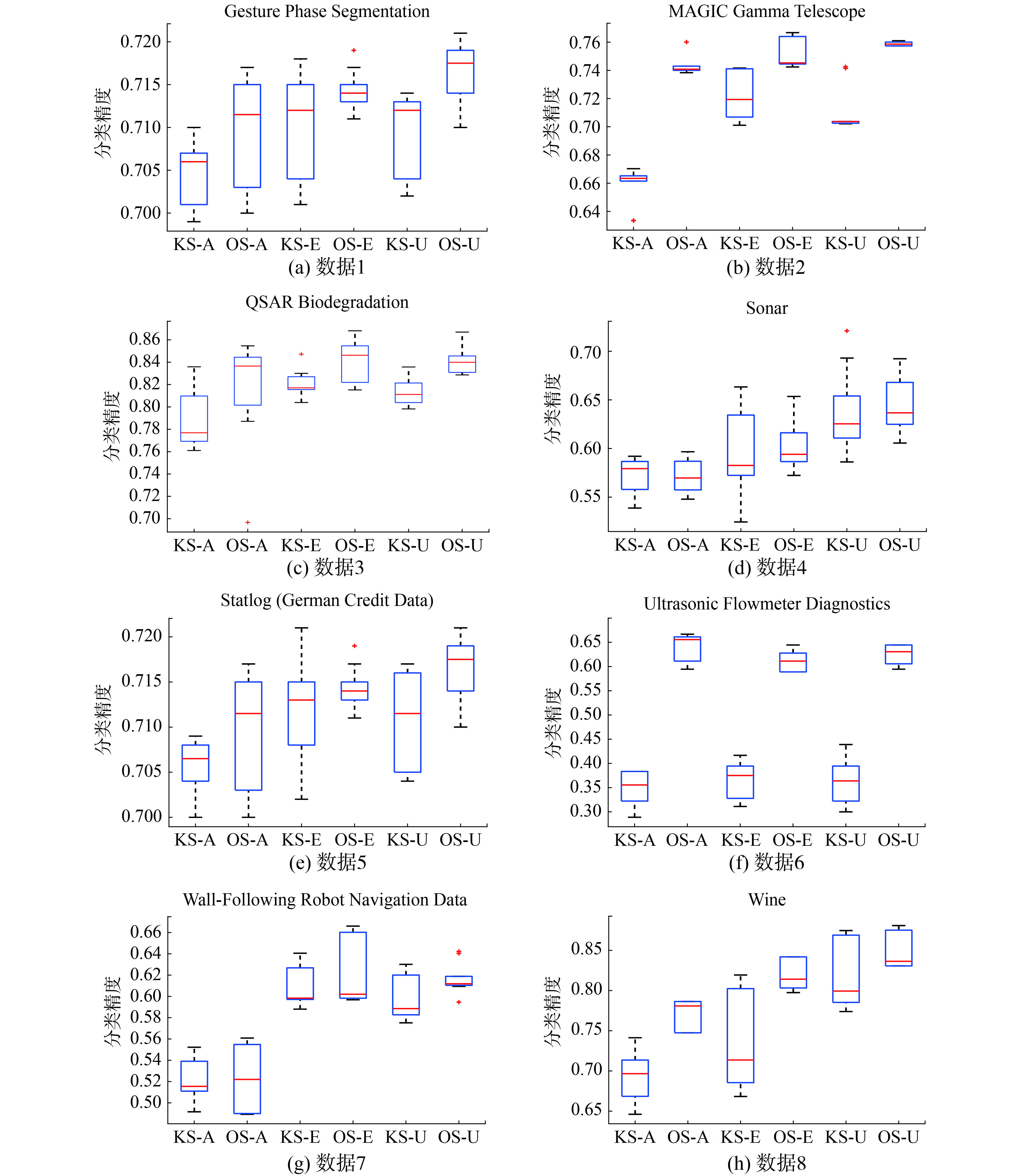
本组实验选取了近似质量、条件熵以及多准则(同时满足近似质量和条件熵的约束条件)作为约简的度量准则。实验将一致性采样属性约简算法与基于K-means采样^[15]的属性约简算法(这里K的取值等于数据的决策类数目)进行对比分析。在上述8组数据集上分别计算并比较了基于这3种约简的分类精度。其中，在计算分类精度时，分别采用了邻域分类器(NEC)^[28]和SVM分类器^[29]，实验结果如图1、图2所示。

在以下的结果图中，用KS-A、KS-E、KS-U分别表示基于K-means采样的近似质量约简、条件熵约简、多准则约简，OS-A、OS-E、OS-U分别表示基于一致性采样的近似质量约简、条件熵约简、多准则约简。

观察图1可以发现，在10个半径下，不难得出如下结论：

1) 相较于基于K-means采样的约简，利用基于一致性采样的约简在测试样本上可以获得更好的分类效果；

2) 在3个度量准则的比较中，利用条件熵约简能够大体上使得分类精度达到最高。此外，一致性采样相较于K-means采样来说，当利用近似质量作为约简的度量准则时，约简在测试样本上分类效果的提升最为明显。这主要是因为相较于K-means采样来说，一致性采样能够使得较多的样本落入下近似集中，从而较大幅度地提升近似质量的值，使得在约简迭代过程中，需要更多的属性被加入到约简集合中。

观察图2，不难得出如下结论：

1) 由于SVM分类器在计算分类精度时没有使用半径这一参数，所以本文主要比较两者的分类精度的平均值，可以发现相较于基于K-means采样的约简，基于一致性采样的约简在测试样本上能够提供较高的分类精度；

2) 在3个度量准则的比较中，利用多准则策略大体上可以使得分类精度达到最高，这主要是因为多准则约简同时满足近似质量与条件熵的约束条件，较多的约束条件需要较多的属性才能完成目标。

观察图3可以发现，相较于K-means采样，利用一致性采样进行约简求解，大体上需要更多的时间消耗，这主要是因为利用一致性采样得到的样本数量往往比利用K-means采样所得到的样本数量多，这一事实可以参照表2。

5 结束语

为了提高约简的求解效率，本文提出一种基于一致性原则的采样方法。进一步地，将基于一致性采样与基于聚类采样所求得的约简结果进行对比分析，实验结果表明，相较于聚类采样，一致性采样的约简结果可以有效地提升分类器的分类性能。在这一工作的基础上，本文将就以下问题展开进一步探讨：

1) 本文仅仅从整体角度考虑度量准则，在之后的研究中可以进一步引入一些局部度量准则^[30]如：局部近似质量、局部条件熵等。

2) 本文算法及所使用的对比算法都仅仅是建立在一种采样技术的基础上的，今后可以尝试使用混合采样的方法^[31]以进一步地提升约简的性能。