支持向量机(SVM)是Vapnik等人于1995年提出，以统计学习理论为基础建立起来的一类新的机器学习算法^[1]。它以最小化结构风险^[2]为原则来提高学习机泛化能力，实现期望风险的最小化，从而达到在统计样本量较少的情况下，亦能获得良好统计规律的目的。SVM能够很好地解决小样本、非线性、高维度、局部极小等问题，现已被应用到很多领域，如文本分类、语音识别、情感分析、回归分析等。

随着SVM的不断发展和应用，其部分局限性也逐渐显露出来，在很多方面的研究还有待探索和改进。例如，SVM易受到噪声和孤立点影响，为解决此问题，Lin等^[3]提出了模糊支持向量机(fuzzy support vector machine，FSVM)的概念，即将模糊隶属度引入到支持向量机中。FSVM降低了噪声和孤立点对最终决策函数的影响，提高了分类精度，现在也应用到了风险预测、故障诊断、手写字符串识别等领域。

此外，SVM中核函数和核参数的选择对最终的学习结果有着重要影响，然而目前还没有关于核函数以及核参数选取的有效手段。作为核方法的重要成果，多核学习(multiple kernel learning，MKL)^[4-5]近年来已成为机器学习领域广大学者的研究热点。单一核函数往往无法充分刻画数据间的相似性，尤其是复杂数据间的相似性，不同的核函数对应于不同的相似性表示，多核相结合可以较准确的表达数据间的相似性，同时也克服了核函数选择这一难题。受模糊支持向量机和多核学习的启发，为了同时解决这两大问题，本文提出模糊多核支持向量机模型。

本文的主要工作有：1)将基于核对齐^[6]的多核学习方法引入到模糊支持向量机中，提出了基于核对齐的模糊多核支持向量机，同时解决了核函数选择难题和对噪声数据敏感问题；2)利用基于Gaussian核的模糊粗糙集下近似算子来确定每个样本点的隶属度^[7]，更有效地减小噪声点和孤立点对分类超平面的影响；3)根据最大化组合核与理想核之间的相似性，计算核权重，使组合核更精确地刻画数据间的相似性；4)实验结果验证了本文所提方法比经典支持向量机(SVM)、模糊支持向量机(FSVM)和多核支持向量机(MSVM)表现更为优异。

1 相关工作 1.1 经典支持向量机

对于给定数据 ${{T}} = \left\{ {\left( {{{{x}}_1},{y_1}} \right),\left( {{{{x}}_2},{y_2}} \right), \cdots ,\left( {{{{x}}_l},{y_l}} \right)} \right\}$ ，其中 ${{{x}}_i} \in {{\bf{R}}^n}$ ， ${y_i} \in \left\{ { - 1,1} \right\}$ ， $i = 1,2, \cdots ,l$ 。SVM的目标是得到最优超平面 $f\left( {{x}} \right) = {{{\omega}} ^{\rm T}}{{x}} + {{b}}$ ，其不仅能将这组数据正确分为两类，同时能够保证两类样本到分类超平面的距离之和最大。根据结构风险最小化原则，可将寻找最优超平面的过程归结为如下的优化问题^[1-2]：

$\begin{array}{l} \displaystyle \min \;\;\frac{1}{2}{\left\| {{\omega }} \right\|^2} + C\sum\limits_{i = 1}^l {{\xi _i}} \\ \displaystyle {\rm{s.t.}}{y_i}\left( {{{{\omega }}^{\rm T}} \cdot {{{x}}_i} + b} \right) \geqslant 1 - {\xi _i} \\ \displaystyle {\xi _i} \geqslant 0,i = 1,2, \cdots ,l \\ \end{array} $

(1)

式中： ${\xi _i}$ 为误差项； $C$ 为惩罚系数。

利用Lagrange乘子法，上述优化问题可转化为如下对偶问题：

$\begin{gathered} \max \;\;\sum\limits_{i = 1}^l {{\alpha _i}} - \frac{1}{2}\sum\limits_{i = 1}^l {\sum\limits_{j = 1}^l {{\alpha _i}{\alpha _j}{y_i}{y_j}\left\langle {{{{x}}_i},{{{x}}_j}} \right\rangle } } \\[-6pt] {\rm{s.t.}}\;\;\sum\limits_{i = 1}^l {{\alpha _i}{y_i} = 0,\;\;0 \leqslant {\alpha _i} \leqslant C} ,\;\;i,j = 1,2, \cdots ,l \\ \end{gathered} $

(2)

式中： ${\alpha _i}$ 是样本点 ${{{x}}_i}$ 的Lagrange乘子； $\left\langle \cdot ,\cdot \right\rangle $ 表示内积。最终得到的分类决策函数有如下形式：

$f({{x}}) = {\rm{sign}}(\sum\limits_{i = 1}^l {{\alpha _i}{y_i} < {{{x}}_i},{{x}} > +b)} $

(3)

对于线性不可分数据，虽然通过引入误差项 ${\xi _i}$ 可以得到分割超平面，然而其并无法实现对所有样例的正确划分。引入非线性映射 $\varphi :{{\bf{R}}^n} \to H$ ，将数据从原空间映射到高维特征空间中，并在该空间中构造最优分割超平面。由SVM模型可知，只需要计算出 $\varphi \left( {{x}} \right)$ 和 $\varphi \left( {{{x'}}} \right)$ 的内积。通过核函数 $k({{x}},{{x'}})$ ^[2]可以获得两点在特征空间中的内积：

$k({{x}},{{x'}}) = \left\langle {\varphi ({{x}}),\varphi ({{x'}})} \right\rangle $

(4)

则(2)式可转化为

$\begin{gathered} \max \;\;\sum\limits_{i = 1}^l {{\alpha _i}} - \frac{1}{2}\sum\limits_{i = 1}^l {\sum\limits_{j = 1}^l {{\alpha _i}{\alpha _j}{y_i}{y_j}k\left( {{{{x}}_i},{{{x}}_j}} \right)} } \\[-6pt] {\rm{s.t.}}\;\;\sum\limits_{i = 1}^l {{\alpha _i}{y_i}} = 0,\;0 \leqslant {\alpha _i} \leqslant C,\;i,j = 1,2, \cdots ,l \\ \end{gathered} $

(5)

所以在实际应用中并不需要知道 $\varphi $ ，只通过核函数 $k\left( {{{x}},{{x'}}} \right)$ 就可以得到相应的决策函数：

$f\left( {{x}} \right) = {\rm{sgn}}\left( {\sum\limits_{i = 1}^l {{y_i}{\alpha _i}k\left( {{{{x}}_i},{{x}}} \right)} +b} \right)$

(6)

常用的核函数主要有线性核、多项式核和Gaussian核^[1-2]。

1.2 模糊支持向量机

在实际问题中，数据易受到噪声等各种因素的干扰，SVM往往难以获得令人满意的学习效果。为了有效地排除不确定环境中野点（标签错误的训练样本）的干扰，2002年Lin将样本隶属度引入SVM，使样本由于隶属度的不同而对超平面有不同的影响，得到模糊支持向量机(FSVM)^[3,8]。野点和噪声数据往往被赋予较小的隶属度，从而削弱其对于分类超平面的影响。FSVM对应如下优化问题：

$\begin{array}{l}\displaystyle \min \;\;\frac{1}{2}{\left\| {{\omega }} \right\|^2} + C\sum\limits_{i = 1}^l {{s_i}{\xi _i}} \\ \displaystyle {\rm{s.t.}}{y_i}\left( {{{{\omega }}^{\rm T}} \cdot {{{x}}_i} + b} \right) \geqslant 1 - {\xi _i} \\ \displaystyle {\xi _i} \geqslant 0,i = 1,2, \cdots ,l \\ \end{array} $

(7)

这里 ${s_i}$ 是样例 ${{{x}}_i}$ 属于类别 ${y_i}$ 的隶属度。显然 ${s_i}$ 对目标函数中的 ${\xi _i}$ 起加权作用，使得噪声点对最终得到的超平面有较小的影响。该算法增强了SVM的鲁棒性。

由Lagrange乘子法可将式(7)转化为对偶形式：

$\begin{array}{l}\displaystyle \qquad \max \;\;\sum\limits_{i = 1}^l {{\alpha _i}} - \frac{1}{2}\sum\limits_{i = 1}^l {\sum\limits_{j = 1}^l {{\alpha _i}{\alpha _j}{y_i}{y_j}\left\langle {{{{x}}_i},{{{x}}_j}} \right\rangle } } \\[-2pt] \displaystyle {\rm{s.t.}}\;\;\;\sum\limits_{i = 1}^l {{\alpha _i}{y_i}} = 0,\;0 \leqslant {\alpha _i} \leqslant C{s_i},\;i,j = 1,2, \cdots ,l \\ \end{array} $

(8)

分类决策函数为

$f\left( {{x}} \right) = {\rm{sgn}} \left( {\sum\limits_{i = 1}^l {{\alpha _i}{y_i}\left\langle {{{{x}}_i},{{x}}} \right\rangle } + b} \right)$

(9)

经过不断发展，基于上述FSVM算法，其他学者也提出了各种模糊SVM来处理不同的具体问题。这些方法都是针对实际问题中的某种不确定性而提出的，是对传统SVM的改进与完善。

2 多核学习

在支持向量机处理分类问题时，核函数的选择对分类效果有非常重要的影响。在核函数选择的过程中，普遍采用试算方法，核函数与核参数选择的计算代价较大。多核学习将多个核函数组合在一起，取代了经典支持向量机的单个核函数。多核组合往往能够更加准确地刻画样本间的相似性，从而使得SVM在相对较小的计算开销前提下，获得了较好的分类性能。

多核支持向量机(MSVM)主要研究问题为核函数的组合方式和相关权系数的计算。目前来说，核函数的组合方式可以分为以下3种：

　　1）线性组合方式^[9]，也是现在使用最广泛的方式，如简单单核相加和加权线性组合：

${k_{{\eta }}}\left( {{{{x}}_i},{{{x}}_j}} \right) = \sum\limits_{m = 1}^p {{\eta _m}{k_m}\left( {{{x}}_i^m,{{x}}_j^m} \right)} $

(10)

式中： ${\eta _{_m}}$ 为核权重， ${\eta _{_m}}$ 都为1时即为简单单核相加； $p$ 为核函数个数。

　　2）非线性组合方式^[10]，例如乘积、点积和幂：

${k_{{\eta }}}\left( {{{{x}}_i},{{{x}}_j}} \right) = \prod\limits_{m = 1}^p {{k_m}\left( {{{x}}_i^m,{{x}}_j^m} \right)} $

(11)

　　3）数据相关组合方式^[11]，这种方式会对每个数据样本分配一个特定的权重，这样可以得到数据的局部分布状况，进而根据分布情况对每个区域学习到合适的组合规则。

多核权系数的计算在多核学习研究中是关键问题，目前，相关权系数的计算方式具体来说有以下5类：固定规则学习方式^[12]、启发式学习方式^[6,13]、最优化求解方式^[14]、贝叶斯学习方式^[11]和Boosting学习方式^[15]。

本文中采用启发式学习方式来获得核权重，通过核对齐^[6,16-18]的方式计算多核权系数，即计算核函数相应核矩阵之间的相似性来确定权系数。基于训练集 ${{T}}$ ，两个核函数 ${k_1}$ 和 ${k_2}$ 对应的核矩阵 ${{{{ K}}}_1}$ 与 ${{{K}}_2}$ 之间的核对齐定义为

$A\left( {{{T}},{{{K}}_1},{{{K}}_2}} \right) = \frac{{{{\left\langle {{{{{ K}}}_1},{{{K}}_2}} \right\rangle }_F}}}{{\sqrt {{{\left\langle {{{{{ K}}}_1},{{{K}}_1}} \right\rangle }_F}{{\left\langle {{{{K}}_2},{{{K}}_2}} \right\rangle }_F}} }}$

(12)

其中 $\displaystyle{\left\langle {{{{K}}_1},{{{K}}_2}} \right\rangle _F} = \sum\limits_{i = 1}^l {\sum\limits_{j = 1}^l {{{{K}}_1}\left( {{{{x}}_i},{{{x}}_j}} \right){{{K}}_2}\left( {{{{x}}_i},{{{x}}_j}} \right)} } $ 。

多核SVM的优化问题由(1)转化为

$\begin{array}{l}\displaystyle \min \;\;\frac{1}{2}\left\| {{{{\omega }}_{{\eta }}}} \right\|_2^2 + C\sum\limits_{i = 1}^l {{\xi _i}} \\ \displaystyle {\rm{s.t.}}{y_i}\left( {{{{{\textit{ω}}}}_{{\eta }}}^{\rm T} \cdot {\varPhi _{{\eta }}}\left( {{{{x}}_i}} \right) + b} \right) \geqslant 1 - {\xi _i} \\ \displaystyle {\xi _i} \geqslant 0,i = 1,2, \cdots ,l \\ \end{array} $

(13)

式中： ${{{\textit{ω}}}_{{\eta }}}$ 为高维特征空间中分类超平面的法向量，映射 ${\varPhi _{{\eta }}}$ 将数据由原空间映射到高维特征空间。分类决策函数变为

$f\left( {{x}} \right) = {\rm{sgn}} \left( \sum\limits_{i = 1}^l {{\alpha _i}{y_i}{k_{{\eta }}}\left( {{{{x}}_i},{{x}}} \right) + b} \right)$

(14)

3 模糊多核支持向量机

针对核函数选择难题和对噪声数据敏感问题，本文将基于核对齐加权求和多核学习方法引入到模糊支持向量机模型中，并利用模糊粗糙集方法得到样例隶属度，提出了基于核对齐的模糊多核支持向量机(multiple kernel fuzzy support vector machine, MFSVM)。

粗糙集(RS)是20世纪80年代波兰学者Pawlak提出的一种不确定性数学理论^[19]，可以对数据进行分析和推理，从中发现隐含的知识。经典的RS理论建立在等价关系基础上，其只能处理符号数据。作为RS的推广，模糊粗糙集(FRS)技术可以处理实值数据。FRS理论最早是由Dubois和Prade提出^[20-21]，之后得到了快速发展。现有的FRS方法已经被成功应用于很多实际问题。本文中，使用基于Gaussian核的FRS的下近似算子来作为事例的隶属度^[7,22]。取 $k\left( {{{x}},{{x}}'} \right)$ 为Gaussian核函数。对样例 ${{{x}}_i} \in {{A}}$ ，令 ${s_i}$ 为 ${{{x}}_i}$ 属于 ${{A}}$ 的隶属度，则 ${s_i} = {\inf _{{{x}}' \notin {{A}}}}\sqrt {1 - {{\left( {k\left( {{{x}},{{x}}'} \right)} \right)}^2}} $ 。

本文采用基于核对齐加权求和的多核组合方式，多核组合公式为

${{{K}}_{{\eta }}}\left( {{{{x}}_i},{{{x}}_j}} \right) = \sum\limits_{m = 1}^p {{\eta _m}{{{K}}_m}\left( {{{{x}}_i},{{{x}}_j}} \right)} $

(15)

式中： ${{\eta }_{m}}$ 是核权重， $m=1,2,\cdots ,p $ ； ${{{K}}_{m}}$ 是一组基础核矩阵， $m=1,2,\cdots ,p $ ，优化目标为最大化组合核与理想核的相似性，即可得到如下公式^[6,23]：

$\begin{gathered} \max \;A \left( {{{T}},{{{K}}_{{\eta }}},{{y}}{{{y}}^{\rm T}}} \right)= \\[-6pt] \displaystyle\frac{{{{\left\langle {\displaystyle\sum\limits_{m = 1}^p {{\eta _m}{{{K}}_m}} ,{{y}}{{{y}}^{\rm T}}} \right\rangle }_F}}}{{\sqrt {{{\left\langle {\displaystyle\sum\limits_{m = 1}^p {{\eta _m}{{{K}}_m}} ,\displaystyle\sum\limits_{m = 1}^p {{\eta _m}{{{K}}_m}} } \right\rangle }_F}{{\left\langle {{{y}}{{{y}}^{\rm T}},{{y}}{{{y}}^{\rm T}}} \right\rangle }_F}} }}= \\[-6pt] \displaystyle\frac{{\displaystyle\sum\limits_{m = 1}^p {{\eta _m}{{\left\langle {{{{K}}_m},{{y}}{{{y}}^{\rm T}}} \right\rangle }_F}} }}{{l\sqrt {\displaystyle\sum\limits_{m = 1}^p {\displaystyle\sum\limits_{j = 1}^p {{\eta _m}{\eta _j}{{\left\langle {{{{K}}_m},{{{K}}_j}} \right\rangle }_F}} } } }} \\[-6pt] {\rm{s.t.}}\;\;{{\eta }} \in {\rm{R}} _ + ^{p} \\ \end{gathered} $

(16)

其中 ${{y}} = {\left[ {{y_1}\,{y_2}\, \cdots \,{y_l}} \right]^{\rm T}}$ ， ${{y}}{{{y}}^{\rm T}}$ 是基于训练集 ${{T}}$ 的二分类任务的理想核。为了解决此优化问题，可以令 $A\left( {{{T}},{{{K}}_{{\eta }}},{{y}}{{{y}}^{\rm T}}} \right)$ 中的分母为常数，即式(16)等价于：

$\begin{gathered} \displaystyle\mathop {\max }\limits_{{\eta }} \;\sum\limits_{m = 1}^p {{\eta _m}{{\left\langle {{{{K}}_m},{{y}}{{{y}}^{\rm T}}} \right\rangle }_F}} \\ \displaystyle {\rm{s.t.}}\;\sum\limits_{m = 1}^p {\sum\limits_{j = 1}^p {{\eta _m}{\eta _j}{{\left\langle {{{{K}}_m},{{{K}}_j}} \right\rangle }_F}} } = C, \\ \displaystyle{\eta _m} \geqslant 0,m = 1,2, \cdots ,p \\ \end{gathered} $

(17)

通过Lagrange乘子法，转化为其对偶问题：

$\begin{gathered} \mathop {\max }\limits_{{\eta }} \;\sum\limits_{m = 1}^p {{\eta _m}{{\left\langle {{{{K}}_m},{{y}}{{{y}}^{\rm T}}} \right\rangle }_F}} - \\ {\textit{λ}} \left( {\sum\limits_{m = 1}^p {\sum\limits_{j = 1}^p {{\eta _m}{\eta _j}{{\left\langle {{{{K}}_m},{{{K}}_j}} \right\rangle }_F}} } - C} \right)\; \\ {\rm{s.t.}}\;{\eta _m} \geqslant 0,m = 1,2, \cdots ,p \\ \end{gathered} $

(18)

　　观察式 (18)， $\lambda $ 随着 $C$ 的变化而变化，根据核对齐的定义，当核权重 ${\eta _m}$ 做线性变化时，核对齐的值保持不变，所以可考虑 ${\textit{λ}} = 1$ ，那么式 (18) 优化问题变为

$\begin{gathered} \mathop {\max }\limits_{{\eta }} \;\sum\limits_{m = 1}^p {{\eta _m}{{\left\langle {{{{K}}_m},{{y}}{{{y}}^{\rm T}}} \right\rangle }_F}} - \sum\limits_{m = 1}^p {\sum\limits_{j = 1}^p {{\eta _m}{\eta _j}{{\left\langle {{{{K}}_m},{{{K}}_j}} \right\rangle }_F}} } \\ {\rm{s.t.}}\;{\eta _m} \geqslant 0,m = 1,2, \cdots ,p \\ \end{gathered} $

(19)

　　为了避免核函数在训练集中过拟合，在优化问题中添加对 ${\eta _m}$ 的约束，即变为

$\begin{gathered} \mathop {\max }\limits_{{\eta }} \;\sum\limits_{m = 1}^p {{\eta _m}{{\left\langle {{{{K}}_m},{{y}}{{{y}}^{\rm T}}} \right\rangle }_F}} - \\[-6pt] \sum\limits_{m = 1}^p {\sum\limits_{j = 1}^p {{\eta _m}{\eta _j}{{\left\langle {{{{K}}_m},{{{K}}_j}} \right\rangle }_F}} } - \delta \sum\limits_{m = 1}^p {\eta _m^2} \\[-4pt] {\rm{s.t.}}\;{\eta _m} \geqslant 0,m = 1,2, \cdots ,p \\ \end{gathered} $

(20)

其中 $\delta > 0$ ，定义一个矩阵 ${{{O}}_{mj}} = \left\{ \begin{gathered} 1\;\;m = j \\ 0\;\;m \ne j \\ \end{gathered} \right.$ ，式 (20) 即可变为^[23]

$\begin{gathered} \mathop {\max }\limits_{{\eta }} \;\sum\limits_{m = 1}^p {{\eta _m}{{\left\langle {{{{K}}_m},{{y}}{{{y}}^{\rm T}}} \right\rangle }_F}} - \\[-6pt] \sum\limits_{m = 1}^p {\sum\limits_{j = 1}^p {{\eta _m}{\eta _j}} } \left( {{{\left\langle {{{{K}}_m},{{{K}}_j}} \right\rangle }_F} + \delta {O_{mj}}} \right) \\[-4pt] {\rm{s.t.}}\;{\eta _m} \geqslant 0,m = 1,2, \cdots ,p \\ \end{gathered} $

(21)

由于式 (21) 是凸二次规划问题，所以可求得 $\eta $ 的唯一解，代入式(15)后得到合成核，再将其引入到上述基于模糊粗糙集隶属度的模糊支持向量机中，优化问题即变为

$\begin{gathered} \min \;\;\frac{1}{2}{\left\| {{{{\omega }}_{{\eta }}}} \right\|^2} + C\sum\limits_{i = 1}^l {{s_i}{\xi _i}} \\[-4pt] {\rm{s.t.}}\;\;{y_i}\left( {{{{\textit{ω}}}_{{\eta }}}^{\rm T} \cdot {\varPhi _{{\eta }}}\left( {{{{x}}_i}} \right) + b} \right) \geqslant 1 - {\xi _i} \\[-4pt] \;\;\;\;\;\;\;{\xi _i} \geqslant 0,i = 1,2, \cdots ,l \\ \end{gathered} $

(22)

引入Langrange乘子，其对偶问题由式(8)可转化为

$\begin{gathered} \max \;\;\sum\limits_{i = 1}^l {{\alpha _i}} - \frac{1}{2}\sum\limits_{i = 1}^l {\sum\limits_{j = 1}^l {{\alpha _i}{\alpha _j}{y_i}{y_j}{k_{{\eta }}}\left\langle {{{{x}}_i},{{{x}}_j}} \right\rangle } } \\[-6pt] {\rm{s.t.}}\;\;\sum\limits_{i = 1}^l {{\alpha _i}{y_i}} = 0,0 \leqslant {\alpha _i} \leqslant C{s_i},\;\;i,j = 1,2, \cdots ,l \\ \end{gathered} $

(23)

决策函数为

$\begin{gathered} f\left( {{x}} \right) = {\rm{sgn}} \left( {\sum\limits_{i = 1}^l {{\alpha _i}{y_i}{k_{{\eta }}}\left( {{{{x}}_i},{{x}}} \right)} + b} \right)= \\[-4pt] {\rm{sgn}} \left( {\sum\limits_{i = 1}^l {\sum\limits_{m = 1}^p {{\alpha _i}{y_i}{\eta _m}{k_m}\left( {{{{x}}_i},{{x}}} \right)} } + b} \right) \\ \end{gathered} $

(24)

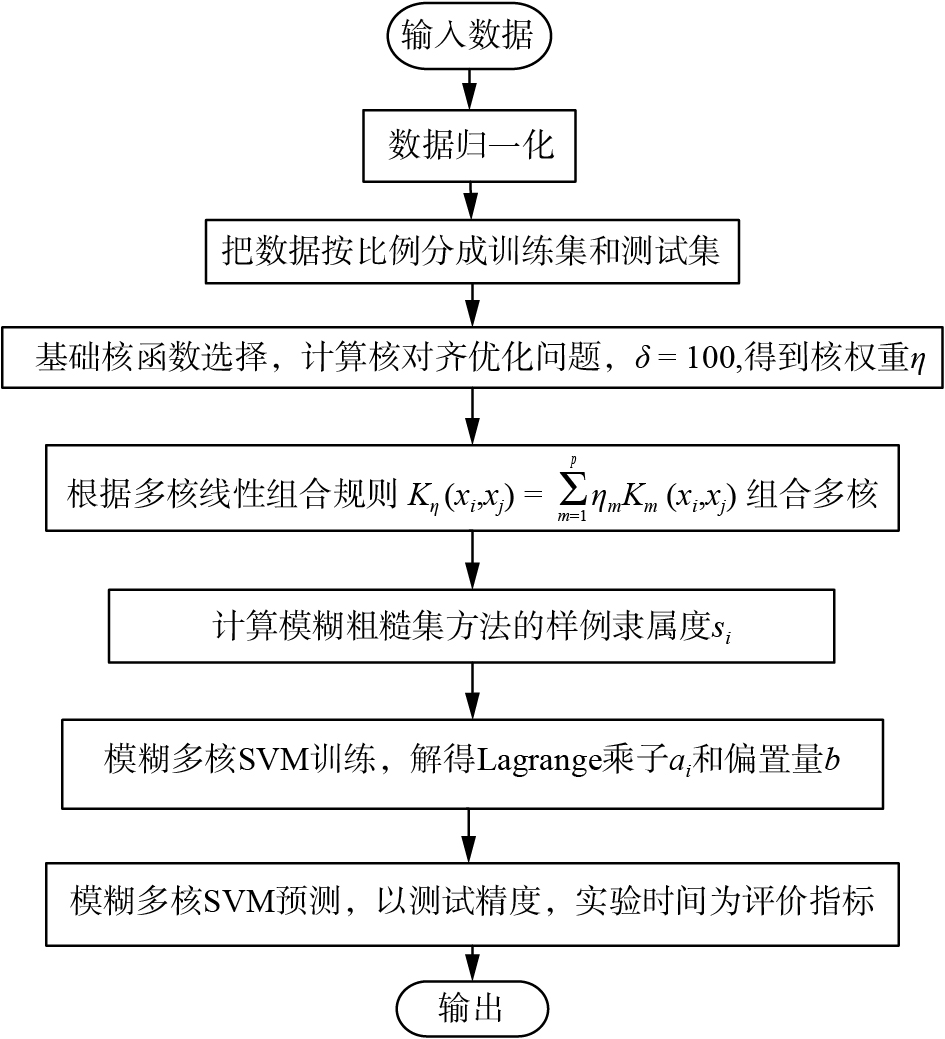
基于核对齐的模糊多核支持向量机的算法实现流程图如图1所示。

4 实验仿真

UCI数据库是加州大学欧文分校提出的用于机器学习的数据库，是常用的标准测试数据库集，为了验证本文所提出方法的可行性与有效性，本文在UCI中选取了9个数据集，有关信息如表1所示。由于本文只考虑两类分类问题，所以对于wine数据集，将类别2与3视为一类处理。

实验在一台PC机（CPU：2.6 GHz，内存4 GB）上进行，操作系统为Windows 8.1，实验工具为Matlab R2014b。实验中将所有数据都做归一化处理，核函数采用的是不同核参数的Gaussian核。给定惩罚系数 $C = 100$ ，解核对齐优化问题时的参数 $\delta = 10^2$ 。选择7个参数 $\sigma $ 不同的Gaussian核作为基础核，每个数据集对应的核参数如表2所示。所有精度都采用10折交叉验证方式获得，其中单核支持向量机结果为不同参数Gaussian核精度最大值。实验对本文提出的基于粗糙集隶属度的模糊多核支持向量机(MFSVM)和经典支持向量机(SVM)、模糊支持向量机(FSVM)、多核支持向量机(MSVM)的分类性能进行对比。

无噪声情况下实验结果如表3所示。从实验结果可以看出，在无噪声的情况下，本文提出的MFSVM方法在9个数据集中分类精度最高，其中在lymphography数据集和wine数据集中，MFSVM和MSVM分类精度一样，并且比SVM和FSVM的分类精度高，而且在计算效率方面，MSVM与MFSVM比SVM和FSVM显著提高。

为了进一步验证MFSVM在噪声环境中的表现，接下来在所有9个数据集中都随机选择一定比例的分类超平面附近训练样本改变其类标签。通过这样的方式构造了带有10%、20%的噪声水平的数据。表4和表5分别是噪声比例为10%和20%时，4种算法的测试精度比较结果。

从实验结果可以看出，当加入10%的噪声时，MFSVM方法在所有9个数据集中的分类精度均高于其他3种方法，具有最高的分类精度。在噪声比例为20%的情况下，虽然4种方法的分类精度较于表4中都相对变低，但在所有数据库上，MFSVM都具有最高的分类精度。该结果也进一步验证了，本文所提出的MFSVM方法在抗噪声能力与计算开销两方面集中了MSVM与FSVM的优势，不仅避免了核选择难题，而且具有较强的抗噪声能力。从而MFSVM不仅可行，且有更广的应用范围。

5 结论

本文是在模糊支持向量机和多核学习的基础之上，通过将基于核对齐的多核方法引入到模糊支持向量机中，提出了基于核对齐的模糊多核支持向量机模型。实验仿真表明此方法综合了模糊支持向量机和多核学习的优点，在分类性能上有一定程度的提升，特别是在有噪声的样本中表现更为突出，证实了本文方法在解决核函数选择难和对噪声数据敏感问题上的可行性和有效性。由于本文方法中涉及到了多核组合和隶属度的计算，因此下一步将进一步研究更优的核组合方式以及如何改进样本隶属度的计算。