2. 山西大学 计算智能与中文信息处理教育部重点实验室,山西 太原 030006;
3. 山西大学 计算机与信息技术学院,山西 太原 030006
2. Key Laboratory of Computational Intelligence and Chinese Information Processing of Ministry of Education, Shanxi University, Taiyuan 030006, China;
3. School of Computer and Information Technology, Shanxi University, Taiyuan 030006, China
数字序列逻辑学习的发展可以说是经历了漫长的岁月,其可以追溯到人类早期历史。例如,古时满月的预测[1],并且其仍然是当今研究的活跃领域,在股市中,我们经常会听到有神奇数字时间之窗这一说法,其用到的波浪理论的数字基础就是一系列的数列,此数列称为fibonacci序列。大自然中还有很多与fibonacci序列有关的奇妙现象,如蜘蛛网、水流的旋涡、蜗牛壳的螺纹以及星系内星球的分布等。
数字序列逻辑学习问题是归纳推理和模式发现的经典问题之一[2-3],这些问题在哲学和数学领域中已经研究了数千年,在心理学和计算机科学领域中也已经研究了数十年[4]。近些年来随着机器学习和深度学习的不断发展[5-8],序列预测问题更是吸引了大家的广泛研究。数字序列预测问题在各个领域的应用也是相当的广泛。其可以编码渐进矩阵问题[9],该问题是用二维矩阵表示的,科学预测问题包括股票的预测、智商测试等,以及许多归纳推理问题[10-12]。早在1963年,Simon等[13]就提出了针对一系列字母序列来预测的模式描述程序,并解释了人类如何从记忆中的概念或规则产生连续模式。Sanghi等[14]提出了一种用于智力测试的程序,该程序还解决了各种数字序列预测问题。且针对数字序列预测问题的解决已有很多方法,例如:反统一算法成功应用于交替序列和斐波纳契序列。Siebers等[15]提出了一种半分析方法用以解决自然数序列归纳问题,这实则是一种典型的智力测试任务,该方法通过术语结构的启发式枚举来猜测给定数字序列的术语结构,最后利用数字序列评估系统来评估该方法,最终结果精度达到93.2%。然而,其缺点是枚举和搜索受到一种看似合理的偏见的严格限制。Strannegard等[16]提出了IQ测试中数字序列预测问题的计算方法。该计算方法是通过开发ASolver来实现的,ASolver是一种基于有限工作记忆思想的拟人化认知系统,其利用了人类推理的模型。结果表明,该算法的性能优于Maple和WolframAlpha等数学工具。Hofmann等[17]证明了归纳程序系统IGOR2可以解决数字序列预测问题,其不同于上述专门用于解决数字序列域中问题的系统,IGOR2可以解决不同问题解决域中的问题。IGOR2是一个从小组输入/输出示例中学习功能程序的系统。但不足之处在于其无法很好地处理负数和交替序列。Ragni等[18-19]提出了一种基于人工神经网络(ANNs)的动态学习方法来解决数字序列的预测问题。其总体结果与人类水平相当,但误差分布差异很大,且无法解决Nested序列问题(见2.1)。
上述方法都是传统的方法,它是基于已知的数字和规则来构建模式,然后预测数字。然而,传统数字序列逻辑学习也存在一定的不足,它很难解决未知数字和规则的模式构建的数字序列预测问题。例如,每月的天数序列、Nested序列、交替序列、带负数的序列等。举一个更为具体的例子:
针对传统数字序列逻辑学习的不足,本文提出了图像数字序列逻辑学习任务,以从另一个角度来解决数字序列预测问题,其可以很好地解决传统数字序列难以解决的未知数字和规则的模式构建的序列预测问题。在传统数字序列逻辑学习中,数字的含义及其规则都已被事先定义。而本文提出的图像数字序列逻辑学习是在不知道图像间关系和图像内包含的内容的意义的前提下,仍可以自动学习出其包含的内在逻辑模式。在本文中,图像序列中的所有图像都是15×85像素的黑白图像,且每张图像包含一个多位数。然后将图像传递给计算机,且并不告诉计算机图像中包含的内容是什么,让计算机自动学习图像之间的内在逻辑模式,并且预测下一张图像中的内容。由此看来,图像数字序列逻辑学习不仅可以解决数字序列预测问题,更是为解决一系列未知逻辑模式构建任务提供了一种可能。
1 研究方法本节主要介绍了图像数字序列逻辑学习的基本任务,并详细描述了4种有代表性的深度神经网络的网络结构(MLP、LSTM、CNN_MLP、ResNet)。
1.1 基本任务图像数字序列逻辑学习是从另一个角度来解决数字序列预测问题,其与传统数字序列解决方案不同。传统数字序列技术是在已知数字和规则的前提下构建模式。而本文的方法是在不知道图像间关系和图像内包含的内容的意义下来预测序列,然后利用深度神经网络来完成数字序列逻辑学习任务,该任务的输入是几张相关的图像序列,其输出仍然是图像,展示的是下一张图像序列预测的结果。
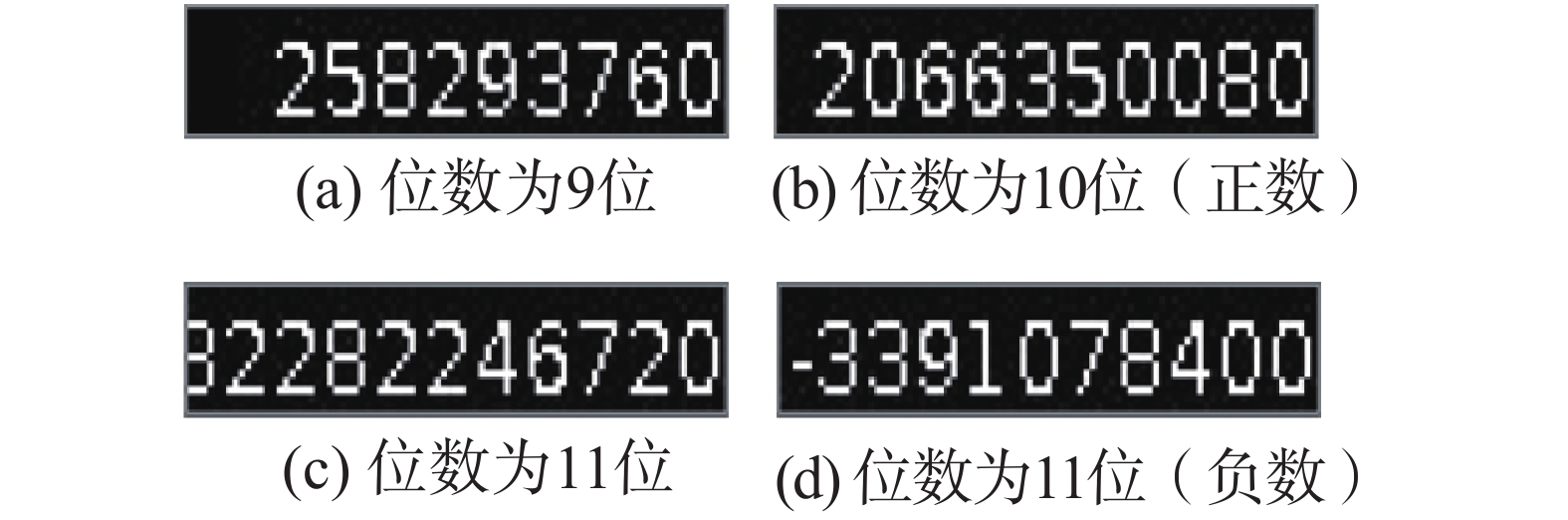
首先将图像序列传送给计算机,让计算机在不知道图像间关系和图像内包含的内容的意义的前提下自动学习出其内在逻辑模式,从而进行数字序列的预测。所有这些图像都是黑白图像,右对齐,大小归一化(15×85),每张图像包含一个多位数,其可以是正数或负数,每张图像中的最大位数设置为10。如图1所示,其中图1(a)的位数设置为9位,图1(b)位数设置为10位,图1(c)位数设置为11位,原本数字为32 282 246 720,由于超出位数的设定,图像中最左位的数字无法完全显示,图1(d)为负数情形,位数设置为10位(除符号位)。然后本文使用几种代表性的深度神经网络来完成数字序列逻辑学习任务,并加以比较分析。给出网络结构的详细描述。最后,为了测试本文的网络性能,本文以某种逻辑关系随机生成一批测试样本,每个样本包括k张图像,将前k−1张图像传入模型中,测试生成的图像是否正确。
|
Download:
|
| 图 1 图像展示 Fig. 1 Image display | |
本文在构造的数据集上比较了几种有代表性的深度神经网络的性能(MLP、LSTM、CNN_MLP、ResNet)。数据集的构造详见2.1。全部模型均使用均方误差(MSE)损失作为优化函数,ADAM[20]作为优化器,衰减率参数设置为β1=0.9,β2=0.999。每个网络的详细结构和超参数设置如图2。

|
Download:
|
| 图 2 4种神经网络结构 Fig. 2 Four neural network structures. | |
多层感知机(MLP) 在本文中,使用一个4层的多层感知机网络来构建模型,该模型包含输入层、隐藏层和输出层。采用一个3层架构的隐藏层,每个隐藏层将线性整流函数(ReLU)[21]作为激活函数。使用Sigmoid函数作为网络的输出层。网络结构如图2(a)所示。
长短期记忆网络(LSTM) 本文采用标准的LSTM网络结构,它是一种特殊的RNN,主要是为了解决长序列训练过程中的梯度消失等问题[22]。而且由于LSTM是按顺序地接收输入数据,这非常适合于本文的序列预测问题。本文将图像特征向量
| ${c_t}(\phi ({x_t}),{c_{t - 1}}) = f \cdot {c_{t - 1}} + i \cdot {\overline c _{t}}$ | (1) |
| ${h_t}(\phi ({x_t}),{h_{t - 1}}) = o \cdot \tanh ({c_t})$ | (2) |
式中:
卷积-全连接神经网络(CNN-MLP) 本文使用一个标准的4层卷积神经网络[23-24],并将ReLU非线性函数作为卷积层的激活函数,在卷积输出层后连接一个2层的全连接层(MLP)。为防止过拟合在第一个全连接层上使用丢失率为0.5的dropout[25]技术。结构及其超参数设置如图2(c)所示。
深度残差网络(ResNet) 深度残差网络有很多不同的结构[26],包括ResNet18、34、50、101、152等,在本文实验中,这几种网络的实验效果相差无几,所以在这里仅展示了ResNet18的实验结果。其结构如图2(d)所示。
本文的具体步骤如下:在训练阶段,传递给计算机N张图像,每张图像包含一个多位数,如图3所示(假设N=4),而且并不告知计算机每张图像中包含的内容是什么,然后使用以上所提及的深度神经网络来完成数字序列逻辑学习任务,以便计算机可以从前3张图像间的逻辑模式自动学习第4张图像。在测试阶段,以某种逻辑关系随机生成一批测试样本,每个样本包括4张图像,将前3张图像放入模型中,以查看是否可以生成正确的预测图像。
|
Download:
|
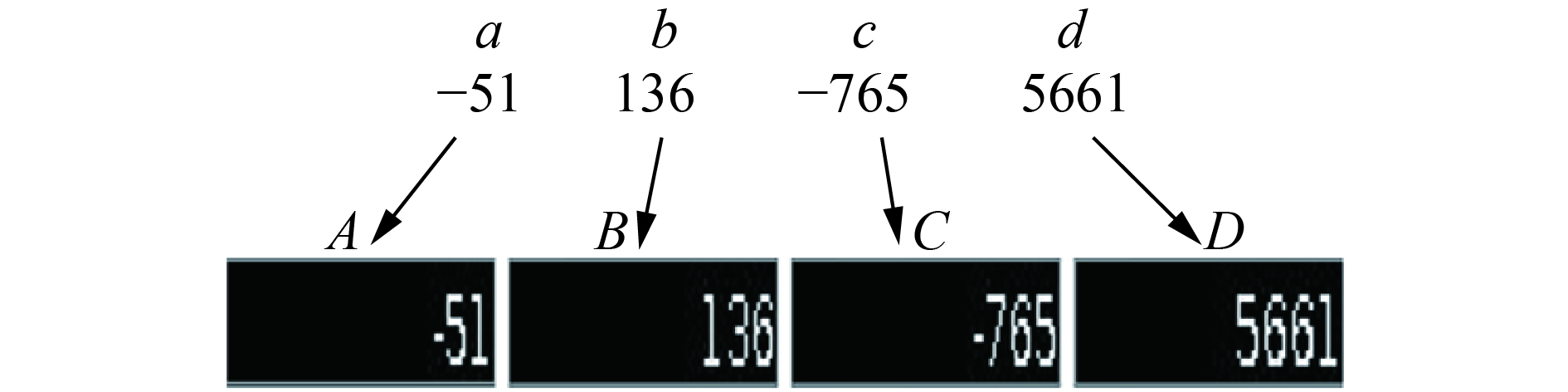
| 图 3 计算机不知道给定图像中所包含的内容是什么 Fig. 3 The computer doesn't know what the content in the given image is | |
对于数据分析,本文系统地改变学习速率、批量大小、隐藏节点的数量和训练迭代等。这些变化应该允许将不同的神经网络模型与经验结果进行比较。此外,本文将在所构造的数据集上对比分析不同的深度神经网络模型的性能,进一步验证本文所提出的图像数字序列逻辑学习对未知数字和规则的模式构建的序列预测的有效性。
2 实验及分析本节详细介绍了图像序列数据集的构造过程及原则,并在所构造数据集上利用深度神经网络对各维度的图像数字序列的预测加以分析比较。
2.1 数据集正如本文前面所提及,图像数字序列预测问题的解决方法与传统数字序列的解决方法不同,它从另一种角度来解决数字序列预测问题。传统数字序列是在已知数字的意义下,然后根据序列背景知识、结构复杂性等进行模式的构建,从而求解数字序列,而本文的方法是计算机在不知道如图3所示的a、b、c、d以及A、B、C、D间关系的前提下自动地学习出其中所包含的内在逻辑模式,进而预测出所要求解的图像。
本文构造了4个大的数据集,其包含各种图像序列,在本文中,根据其解决方案的不同将数据集分为4种不同的类型,分别为:Linear、Multiplication、Fio和Nested。各类型图像序列的详细描述如下:1)Linear序列下一张图像的生成仅与前一张图像内容相关联,与其他项内容无关,其仅涉及“+”和“−”两种数学运算,例如等差序列就是Linear序列的一个特例;2)Multiplication序列仅包含“×”运算符,并且其每张图像的生成原理与Linear序列的生成原理相同,即仅与前一张图像内容相关;3)Fio序列不仅与前一张图像的内容相关联,而且与前2张图像的内容相关联,所涉及的运算符包括“+”和“−”。例如Fibonacci序列就是Fio序列的一个特例;4)对于Nested序列而言,其包含更多的操作运算符:“+”、“−”和“×”,并且其运算不仅仅与前2项相关,还与任意的随机常数项相关联。用数学公式可以表述为:
| $f(n) = f(n - 1) \pm f(n - 2) \pm b $ | (3) |
| $ f(n) = [f(n - 1) \pm f(n - 2)] \times b $ | (4) |
式中:
本文整个数据集的构造原则:1)为方便构造数据集,本文只考虑整数图像序列,图像序列可以包含正数或负数;2)每张图像都包含一个多位数,且每张图像中的最大位数设置为10。所有这些图像均是黑白图像,对齐和尺寸标准化(15×85);3)每张图像位数的设置最大为10位,本文选择的数据集仅是一个小样本集,其在总集(即我们数据的变动范围[−999 999 999 9, 999 999 999])中的占比很小,也就是说,本文确保训练集、测试集互不相交。本文为每种类型的数据集均选择了60 000的图像数字序列,其中50 000用于训练,10 000用于测试。Linear序列、Multiplication序列、Fio序列和Nested序列的部分数据集如图4~7所示(以4维的图像数字序列为例)。

|
Download:
|
| 图 4 Linear序列 Fig. 4 Linear sequences | |

|
Download:
|
| 图 5 Multiplication序列 Fig. 5 Multiplication sequences | |

|
Download:
|
| 图 6 Fio序列 Fig. 6 Fio sequences | |

|
Download:
|
| 图 7 Nested序列 Fig. 7 Nested sequences | |
到目前为止,解决数字序列预测的方法几乎都是在基于给定数字的含义下,通过归纳序列的潜在规律,构建出满足该数字序列规律的模式,从而预测数字。而且,对于传统数字序列而言,其模式的长度与最终的预测结果有很大的关系,即输入节点的数量对最终预测结果的准确率有极大的影响。Ragni等[18]提出了一种基于人工神经网络的动态学习方法来解决数字序列预测问题,该实验结果表明:输入节点的最佳配置为4个节点。因此,本文对输入维度,即输入的图像数进行了实验并加以分析比较。
本文对已构建的4个数据集进行了维度上的扩展,分别扩展为4维图像序列、5维图像序列和6维图像序列,这里并没有扩展3维图像序列,因为它的不确定性太大,例如本文的Fio序列,其并非简单地与最后一个数字有关,而是与最后2个数字相关联。关于数据集及其分类部分在3.1节中已有详细介绍,此处将不再赘述。
对于实验1,首先给定计算机4张图像,与此同时并不告知计算机每张图像中包含的内容是什么,在学习过程中,本文利用4种代表性的深度神经网络(MLP、LSTM、CNN_MLP、ResNet)来完成数字序列逻辑学习任务,以便计算机可以从前3张图像间的逻辑模式自动学习出第4张图像。在测试阶段,本文任意输入4维图像序列,并将前3张图像放入模型中进行测试,使用OCR工具[27]来识别得到的预测图像,将OCR的结果与期望输出进行比较,并计算预测正确的百分比。
对于实验2,其步骤与实验1几乎相同。区别之处在于:在学习阶段,本文给计算机提供5张图像,让计算机自动学习每张图像间的内在逻辑模式。在测试阶段,输入5维图像序列,并将前4张图像传递到模型中以预测结果的正确性。
对于实验3,步骤与前2个实验几乎相同。不同的是,在学习阶段,本文给计算机提供6张图像,让计算机自动学习出每张图像间的逻辑模式。在测试阶段,本文输入6维图像序列,并将前5张图像传入模型进行测试,以检测本文是否可以生成具有正确结果的图像。
本文利用上述提及的4种深度神经网络模型对每个实验进行了准确度的测试,实验结果如表1所示,从表1可以看到4种神经网络模型可以很好地预测Linear序列和Fio序列,且维度越高,预测准确率越高。对Multiplication序列和Nested序列而言,MLP模型和LSTM模型对这2种序列的预测均呈现一种维度越高准确率越低的趋势。相反,CNN_MLP模型和ResNet模型呈现一种维度越高,预测的准确率越高的情形,且ResNet模型对于这2种序列的预测结果总体而言要优于其他的模型。
| 表 1 4种神经网络模型在本文数据集上的实验结果 Tab.1 Experimental results on the our own dataset for the four neural network models |
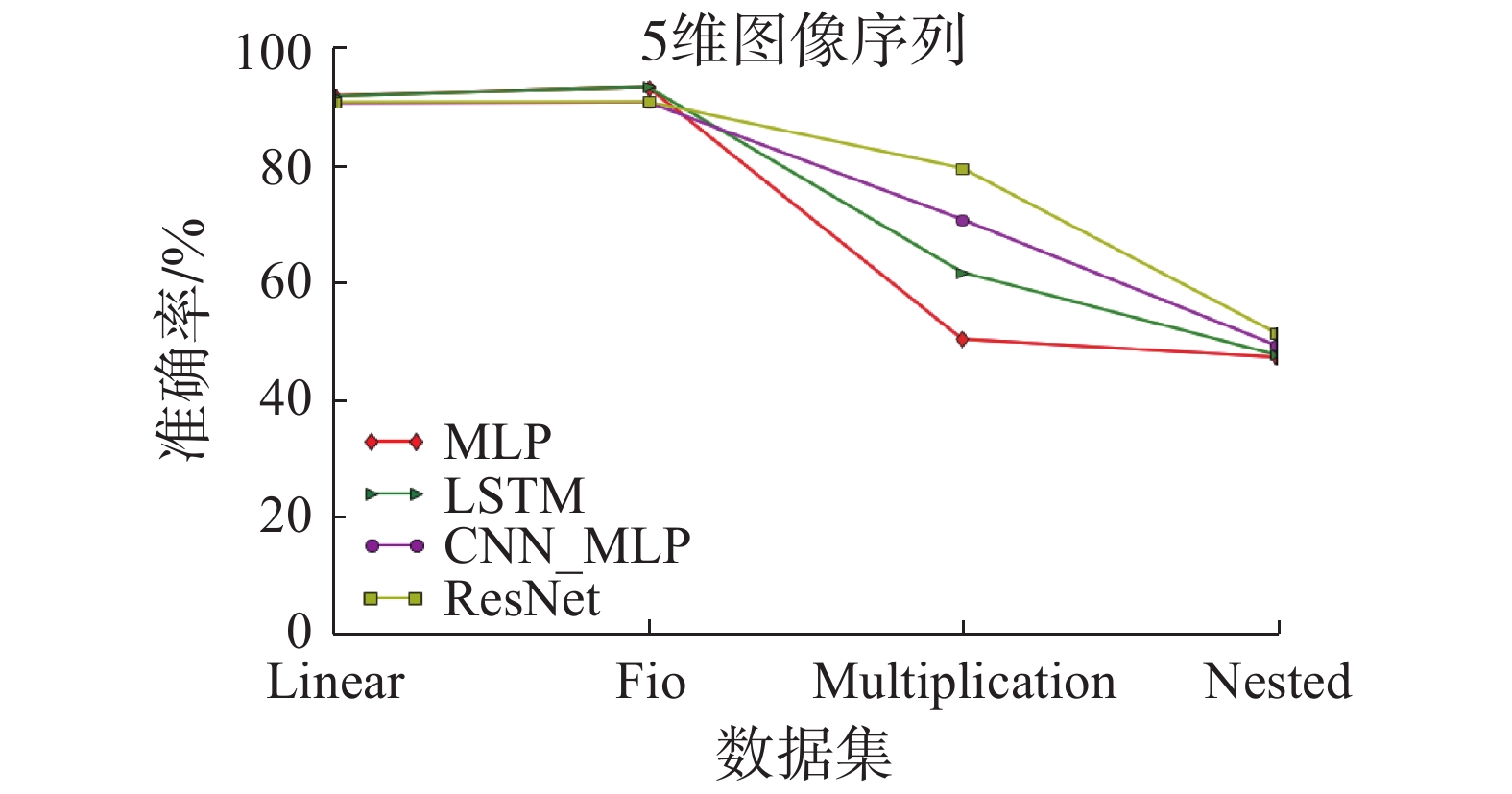
本文对4种深度神经网络模型在4维、5维和6维图像序列的性能比较见图8~10。从各个维度图像序列的折线图中可以明显观察到,4种模型可以很好地预测Linear序列和Fio序列的结果,无论它们是4维、5维还是6维图像序列,且维度越高,准确率越高。这可能是由于Linear序列和Fio序列自身规律较为简单,例如,给定Linear图像序列5、7、9,预测结果11,计算机可以很明显知道是一个加2的规律,进而可以很容易地学到内在逻辑模式,从而进行序列的预测。
4种深度神经网络模型在4维图像序列的性能比较见图8,LSTM对Multiplication序列的预测准确率明显高于其它模型,但当维度升高时,如图9~10所示,可以看到LSTM模型对该序列的预测下降了,而ResNet和CNN_MLP模型对于该序列的预测效果呈现越来越好的趋势,这可能是由于ResNet和CNN_MLP网络模型较为复杂,当维度越高其获得的信息就会越多,越是可以较为准确的学到该图像序列的逻辑模式。而LSTM模型可能由于维度越高,其更易受到其子序列的影响。例如6维图像序列:1、2、4、8、16,预测32,该图像序列中包含子序列1、4、16和2、8等。在LSTM模型中其极易受到子序列的影响,从而致使预测结果有误,如子序列1、4、16,其是一个乘4的规律,有可能下一个数预测为64,而当只给定4维图像序列时,如2、4、8,预测结果16,其反而较易进行该序列的预测。

|
Download:
|
| 图 8 4种深度神经网络模型在4维图像序列中的性能比较 Fig. 8 A comparison on performance of four kinds of deep neural network models in 4-dimensional image sequences | |
|
Download:
|
| 图 9 4种深度神经网络模型在5维图像序列中的性能比较 Fig. 9 A comparison on performance of four kinds of deep neural network models in 5-dimensional image sequences | |

|
Download:
|
| 图 10 4种深度神经网络模型在6维图像序列中的性能比较 Fig. 10 A comparison on performance of four kinds of deep neural network models in 6-dimensional image sequences | |
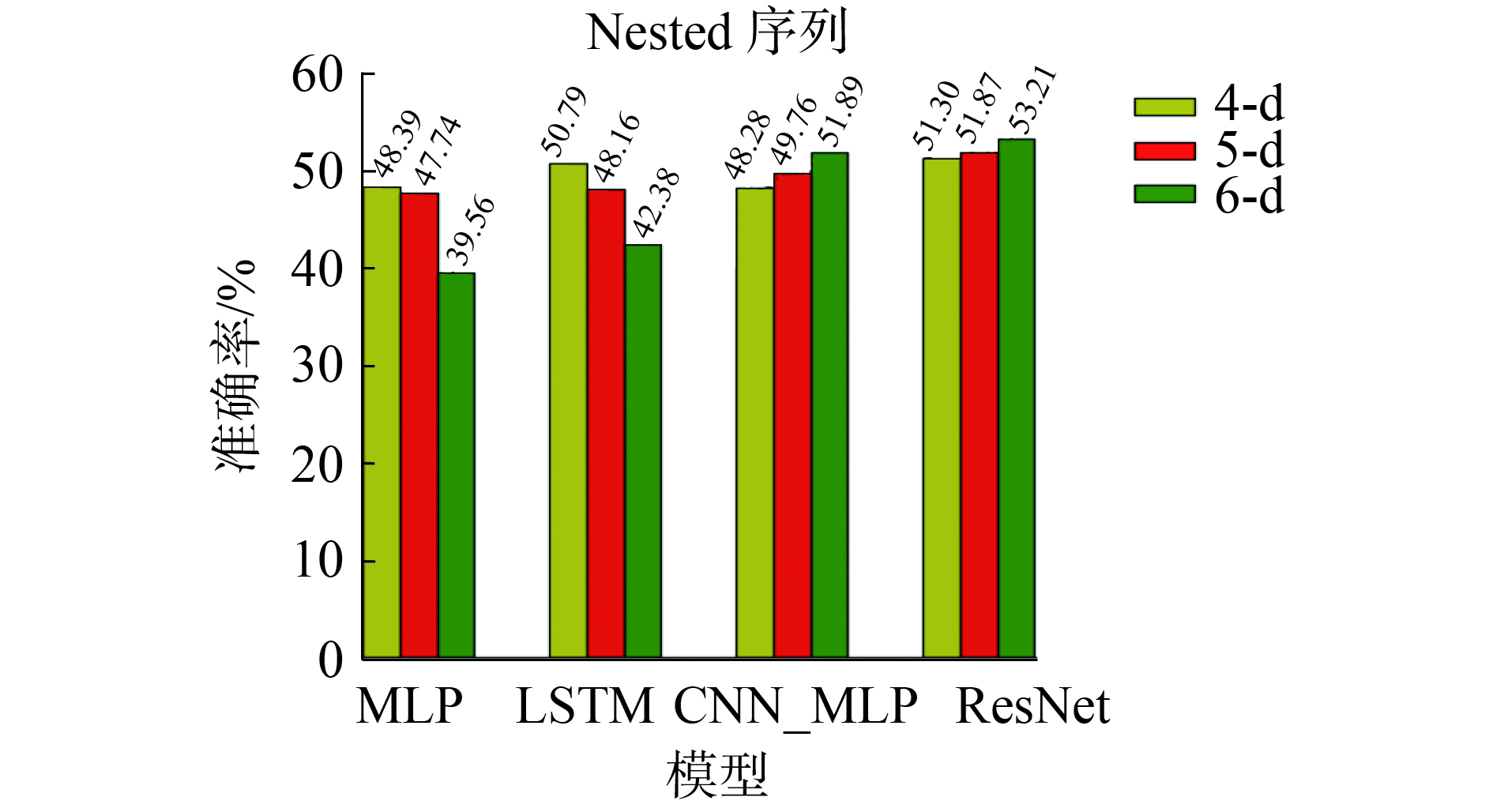
对4维和5维图像序列的性能比较见图8~9,各模型对于Nested序列的预测均集中在一定的范围,这可能是由于Nested序列较为复杂,所有模型在该序列上的性能没有太大区别,但随着维度增高,从图10可以发现ResNet和CNN_MLP模型对于该序列的预测稍有提升,而MLP和LSTM模型对于此序列的预测又有所下降,这可能是由于MLP和LSTM模型较为简单,而ResNet和CNN_MLP模型较为复杂,对于这种复杂序列,随着维数增高,复杂模型在图像序列的预测上其准确率极有可能上升,而简单模型的准确率极易下降。
此外,本文分析比较4种深度神经网络模型在Linear序列、Fio序列、Multiplication序列和Nested序列上的性能,如图11~14。从图11可以发现:随着维数的增高,各模型对于Linear序列预测的准确率提升并不明显,这可能是与Linear序列自身的规律有关,其规则是仅与前一项内容相关联,而与其他项无关,所以当维数增高时,计算机所获得的序列的内在逻辑模式的信息实则是没有太大的变化,例如,给定序列2、3、4,预测结果5,计算机可以很明显知道其是一个加1的规律,当再给定序列1、2、3、4预测下一个内容时,计算机并没有从中得到更多的信息,故而维度虽然增高了,但其准确率的变化并没有很大改变。

|
Download:
|
| 图 11 4种深度神经网络模型在Linear序列上的性能比较 Fig. 11 A comparison on performance of four kinds of deep neural network models in Linear sequences | |

|
Download:
|
| 图 12 4种深度神经网络模型在Fio序列上的性能比较 Fig. 12 A comparison on performance of four kinds of deep neural network models in Fio sequences | |
|
Download:
|
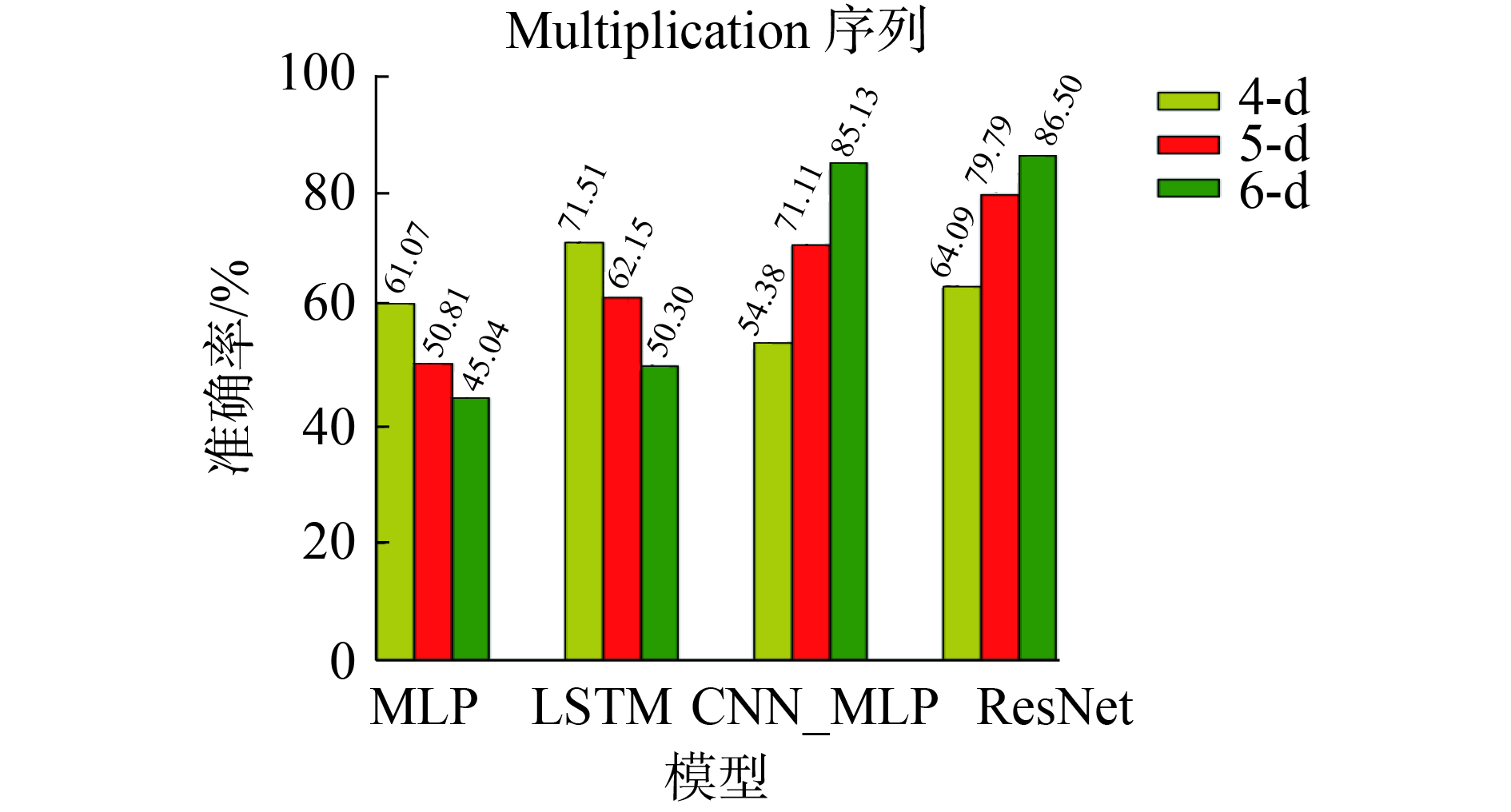
| 图 13 4种深度神经网络模型在Multiplication序列上的性能比较 Fig. 13 A comparison on performance of four kinds of deep neural network models in Multiplication sequences | |
|
Download:
|
| 图 14 4种深度神经网络模型在Nested序列上的性能比较 Fig. 14 A comparison on performance of four kinds of deep neural network models in Nested sequences | |
对比图12的Fio序列,其规则是不仅仅与前一项内容相关联,而且与前两项的内容相关,这就使得当维数越高,即给定的图像数越多,计算机得到的图像间的信息就会越多,就越易预测该序列,可以很明显地看到图12中准确率的提升随着维数的增高越来越明显。
Multiplication序列和Nested序列的性能比较见图13~14,从图中可以看出维度越高,对于CNN_MLP和ResNet模型而言预测的准确率越高。相反,MLP和LSTM模型对于这2种序列的预测均呈现一种维度越高准确率越低的趋势。这可能是由于CNN_MLP和ResNet模型自身较为复杂,其对于这种复杂序列来说,其预测精度反而是易于随着维数增高而增大。而对于MLP和LSTM模型而言,其模型自身较为简单,加之Multiplication序列和Nested序列又较为复杂,相当于是个模型简单任务难的问题,其对于此序列的预测难度就会加大,容易导致维度越高准确率越低的情况。
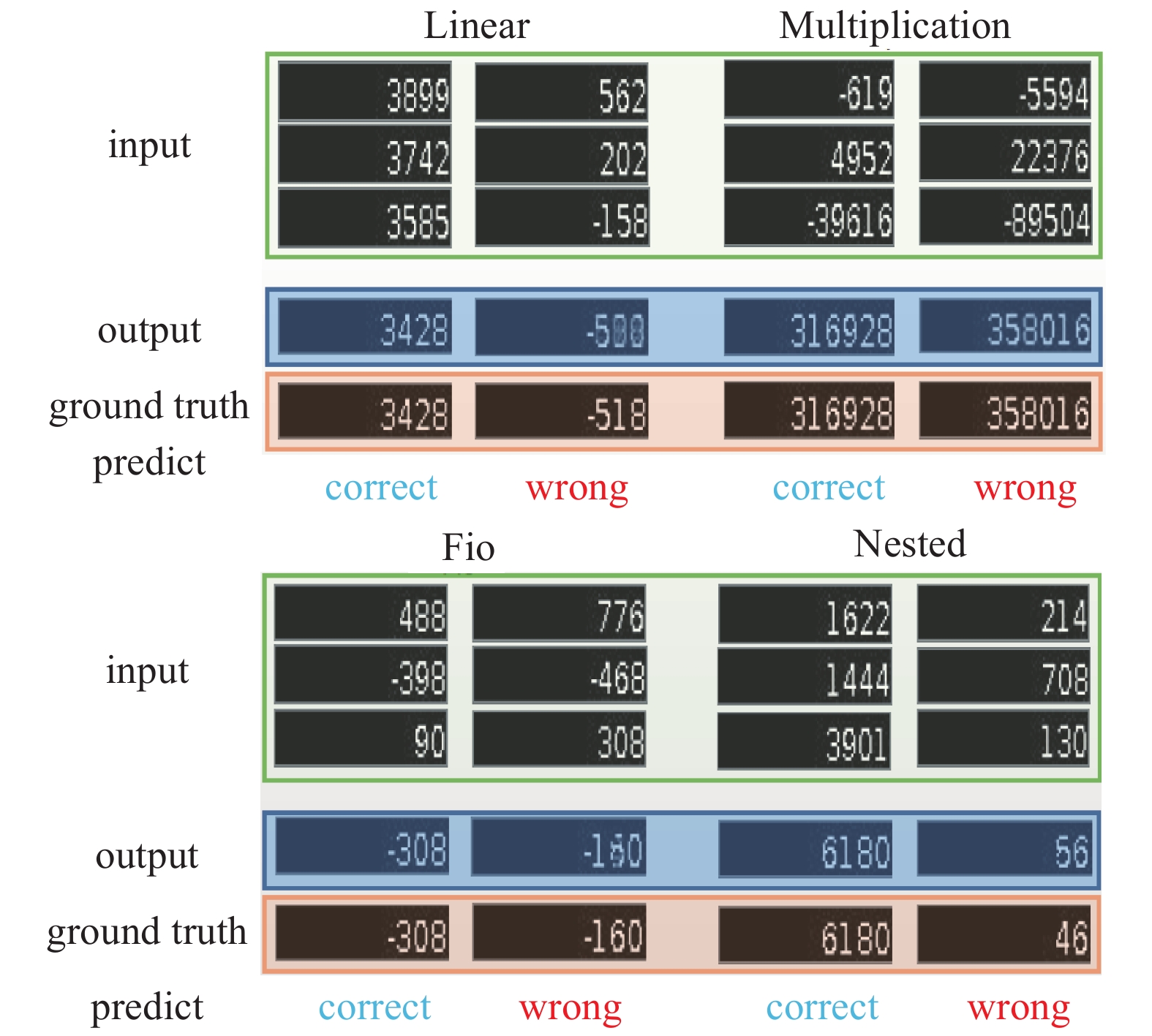
2.3 结果分析本小节从视觉效果的角度展示了每种类型图像序列在不同维度上的实验结果,如图15~17所示(其中包括正确的预测和错误的预测)。
|
Download:
|
| 图 15 4维图像序列 Fig. 15 4-dimensional image sequences | |
|
Download:
|
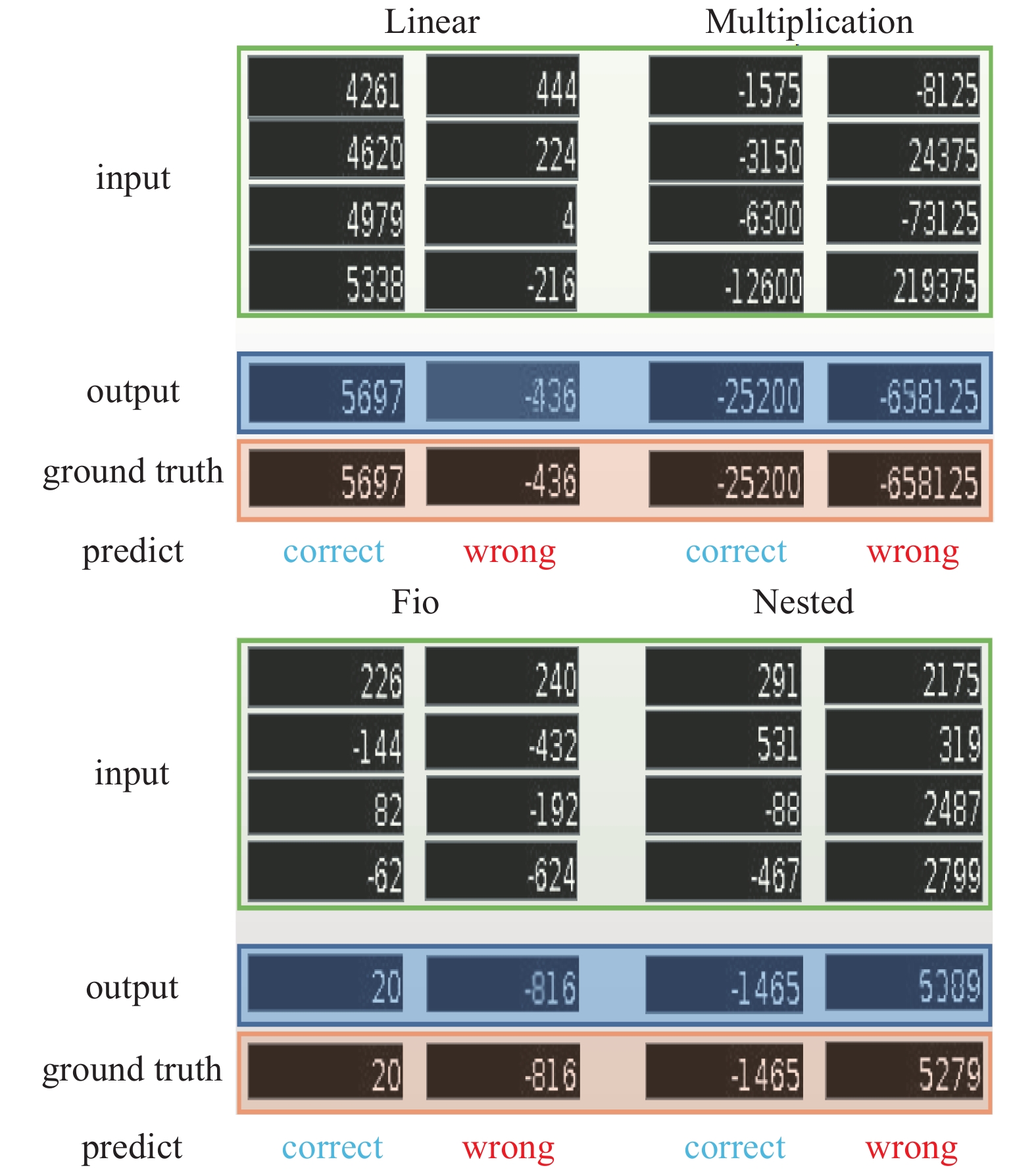
| 图 16 5维图像序列 Fig. 16 5-dimensional image sequences | |
本文仅展示了4维、5维、6维图像序列的部分实验结果。从这些实验结果发现预测误差的原因可能如下:1) 当输出图像模糊时,很容易引起OCR工具识别错误,例如图15中的Fio序列,观察错误的那一栏,当输出图像模糊时,图像中输出结果的第2位(从右往左)有可能是6或8,这就极易导致OCR的识别出错,再如,图15~16中的Multiplication序列,图16中的Linear序列和Fio序列等。2) 其对负号的图像预测有时是不准确的,例如图17中的Multiplication序列和Nested序列等。3) 结果输出中的位数越大,其预测出错的可能性就会越大,因为计算位数越大,相对而言,其难度就会越大,预测错误的可能性就会加大。

|
Download:
|
| 图 17 6维图像序列 Fig. 17 6-dimensional image sequences | |
数字序列逻辑学习任务一直以来都是人工智能的一个研究热点。而且未知的数字和规则的模型构建数字序列问题的预测始终是一个具有挑战性的任务。传统的数字序列技术是基于已知数字的含义下,并根据序列本身的规律特征构造满足该规律的模式,以便进行数字序列的预测。本文的方法是在不知道图像间关系和图像内包含的内容的意义的情况下利用深度学习的方法完成数字序列逻辑学习任务来预测下一张图像内容。同时,人类对于这种未知的数字和规则的模型构建的数字序列极易限制其中,无法快速计算出结果甚至无法得到正确结果。而本文所提出的方法为解决此类序列问题提供了一种可能。
在未来的工作中,我们将进一步探索如何提高精度及对缺失数据的预测,同时期望可以对任意位置的图像内容进行预测,而非单一地对下一张的图像内容进行预测,特别地,下一步希望可以提出更适用于数字预测逻辑学习任务的模型以求精度上面的突破。
| [1] |
BOGOSHI J. The oldest mathematical artefact[J]. The mathematical gazette, 1987, 71(458): 294-294. DOI:10.2307/3617049 ( 0) 0)
|
| [2] |
SCHMID U, KITZELMANN E. Inductive rule learning on the knowledge level[J]. Cognitive systems research, 2011, 12(3/4): 237-248. DOI:10.1016/j.cogsys.2010.12.002 ( 0) 0)
|
| [3] |
FLENER P, SCHMID U. An introduction to inductive programming[J]. Artificial intelligence review, 2008, 29(1): 45-62. DOI:10.1007/s10462-009-9108-7 ( 0) 0)
|
| [4] |
COLTON S, BUNDY A, WALSH T. Automatic Invention of Integer Sequences[M]// The fertility of the soil /. Cambridge University Press AAAI/IAAI, 2000: 558-563.
( 0) 0)
|
| [5] |
QIAN Y, LI F J, LIANG J Y, et al. Space structure and clustering of categorical data[J]. IEEE transactions on neural networks and learning systems, 2016, 27(10): 2047-2059. DOI:10.1109/TNNLS.2015.2451151 ( 0) 0)
|
| [6] |
QIAN Y, XU H, LIANG J Y, et al. Fusing monotonic decision trees[J]. IEEE transactions on knowledge and data engineering, 2015, 27(10): 2717-2728. DOI:10.1109/TKDE.2015.2429133 ( 0) 0)
|
| [7] |
QIAN Y, LI Y, LIANG J, et al. Fuzzy granular structure distance[J]. IEEE transactions on fuzzy systems, 2015, 23(6): 2245-2259. DOI:10.1109/TFUZZ.2015.2417893 ( 0) 0)
|
| [8] |
QIAN Y, LIANG J, PEDRYCZ W, et al. Positive approximation: An accelerator for attribute reduction in rough set theory[J]. Artificial intelligence, 2010, 174(9/10): 597-618. DOI:10.1016/j.artint.2010.04.018 ( 0) 0)
|
| [9] |
RAVEN J, et al. Raven progressive matrices[M]. Handbook of Nonverbal Assessment, 2003, 223-237.
( 0) 0)
|
| [10] |
MUGGLETON S, CHEN J. Guest editorial: special issue on inductive logic programming (ILP 2011)[J]. Machine learning, 2012, 89(3): 213-214. DOI:10.1007/s10994-012-5315-6 ( 0) 0)
|
| [11] |
HOLZMAN T G, PELLIGRINO J W, GLASER R. Cognitive dimensions of numerical rule induction[J]. Journal of educational psychology, 1982, 74(3): 360-373. DOI:10.1037/0022-0663.74.3.360 ( 0) 0)
|
| [12] |
STERNBERG R.J. Handbook of Intelligence[M]. Cambridge University Press, 2000.
( 0) 0)
|
| [13] |
SIMON H A, KOTOVSKY K. Human acquisition of concepts for sequential patterns[J]. Psychological review, 1963, 70(6): 534-546. DOI:10.1037/h0043901 ( 0) 0)
|
| [14] |
SANGHI P, DOWE D.L, A computer program capable of passing I.Q. tests[C]//4th Int. Conf. on Cognitive Science(ICCS'03), Sydney, 2003: 570−575.
( 0) 0)
|
| [15] |
SIEBERS M, SCHMID U. Semi-analytic natural number series induction[J]. Advances in artificial intelligence, 2012, 7526: 249-252. DOI:10.5220/0003719902490255 ( 0) 0)
|
| [16] |
STRANNEGARD C, AMIRGHASEMI M, ULFSBACKER S. An anthropomorphic method for number sequence problems[J]. Cognitive systems research, 2013, 22-23: 27-34. DOI:10.1016/j.cogsys.2012.05.003 ( 0) 0)
|
| [17] |
HOFMANN J, KITZELMANN E, SCHMID U. Applying inductive program synthesis to induction of number series a case study with IGOR2[J]. Joint german/austrian conference on artificial intelligence(Künstliche Intelligenz).Springer, Cham, 2014: 25-36. ( 0) 0)
|
| [18] |
RAGNI M, KLEIN A. Predicting numbers: An AI approach to solving number series[C]// German Conference on Advances in Artificial Intelligence. Springer, Berlin, Heidelberg, 2011:255−259.
( 0) 0)
|
| [19] |
RAGNI M, KLEIN A. Solving number series - architectural properties of successful artificial neural networks[C]// NCTA 2011- Proceedings of the International Conference on Neural Computation Theory and Applications, 2011: 224-229.
( 0) 0)
|
| [20] |
KINGMA D P, BA J. Adam: A method for stochastic optimization. [C]//Proceedings of the 3rd International Comference on Learning Representations, San Diego, arXiv prerint arXiv: 1412.6980, 2014.
( 0) 0)
|
| [21] |
LECUN Y, BENGIO Y, Hinton G. Deep learning[M]. Nature, 2015, 521(7553):436.
( 0) 0)
|
| [22] |
HOCHREITER S, SCHMIDHUBER, JÜRGEN. Long short-term memory[J]. Neural computation, 1997, 9(8): 1735-1780. DOI:10.1162/neco.1997.9.8.1735 ( 0) 0)
|
| [23] |
CHUMERIN N. Convolutional neural network[J]. Neurocomputing, 2015, 148: 136-142. DOI:10.1016/j.neucom.2012.10.043 ( 0) 0)
|
| [24] |
KRIZHEVSKY A, SUTSKEVER I, HINTON G E. Imagenet classification with deep convolutional neural networks[J]. In: advances in neural information processing systems, 2012: 1097-1105. ( 0) 0)
|
| [25] |
SRIVASTAVA N, HINTON G, KRIZHEVSKY A, et al. Dropout: a simple way to prevent neural networks from overfitting[J]. Journal of machine learning research, 2014, 15(1): 1929-1958. ( 0) 0)
|
| [26] |
HE K, ZHANG X, REN S, et al. Deep residual learning for image recognition[J]. In proceedings of the IEEE conference on computer vision and pattern recognition, 2016: 770-778. ( 0) 0)
|
| [27] |
SMITH R. An overview of the tesseract OCR engine[C]// icdar. IEEE Computer Society, 2007, 2: 629-633.
( 0) 0)
|
 2019, Vol. 14
2019, Vol. 14


