货位优化是对仓储货品储存位置的优化分配，以合理利用存储空间，实现最佳货位布局与降低仓库运营成本。现代仓储管理系统的需求复杂，考虑动态资源约束及多样目标的货位决策优化问题^[1-2]，更具实际应用价值。

现有研究中，Dijkstra等^[3]以作业路径最短为单目标，Ning等^[4]以仓储作业时间、货架重心及产品关联性为多目标，分别开展货位决策优化研究。研究表明，多目标优化模型更符合仓储管理系统的实际需求。Yan^[5]等采用层次分析法（analytic hierarchy process，AHP）获得权重，并通过简单加权将多目标转化为单目标。但上述研究只解决了单批次作业下货位决策优化，对多批次作业优化目标值变化规律、货位持续优化能力是否稳定没有作进一步探讨。在构建约束时，Augustyn 等^[6]考虑了仓库规模等环境因素对货位决策优化的影响，但没有考虑库存及可分配货位等因素的动态性。在模型算法实现方面，近年来采用遗传算法^[7]、机器学习^[8]的货位优化研究不断涌现，差分进化算法（differential evolution，DE）因其卓越的优化性能而备受关注^[9]，在仓储优化中也有一定的应用^[10]。基于差分进化与Pareto^[11]最优的货位决策优化研究还相对较少。

综上，以提高货架稳定性、均衡巷道作业及提高仓储效率为目标，考虑动态库存与可分配货位等约束条件，基于变异参数自适应差分进化，提出响应动态约束条件的多目标货位优化算法。进一步基于层次分析法对Pareto解集进行评价，研究多目标权重对多批作业货位持续优化的影响规律。

1 问题描述 1.1 立库货位分配问题

如图1所示自动化立体仓库（automated storage and retrieval system, AS/RS）有N个巷道，每个巷道被一台堆垛机占用，在执行出、入库作业时，各巷道的堆垛机可同时工作。假定沿货架垂直方向为y方向，沿货架水平方向为x方向，沿货架排列方向为z方向。

多巷道立体库作业货位优化分配，需考虑货架稳定性、巷道作业均衡及作业路径最短等因素，并满足动态变化库存、货位占用状态及托盘使用情况等复杂约束条件，以实现高稳定性、高效率、高准确率的精益仓储目标。

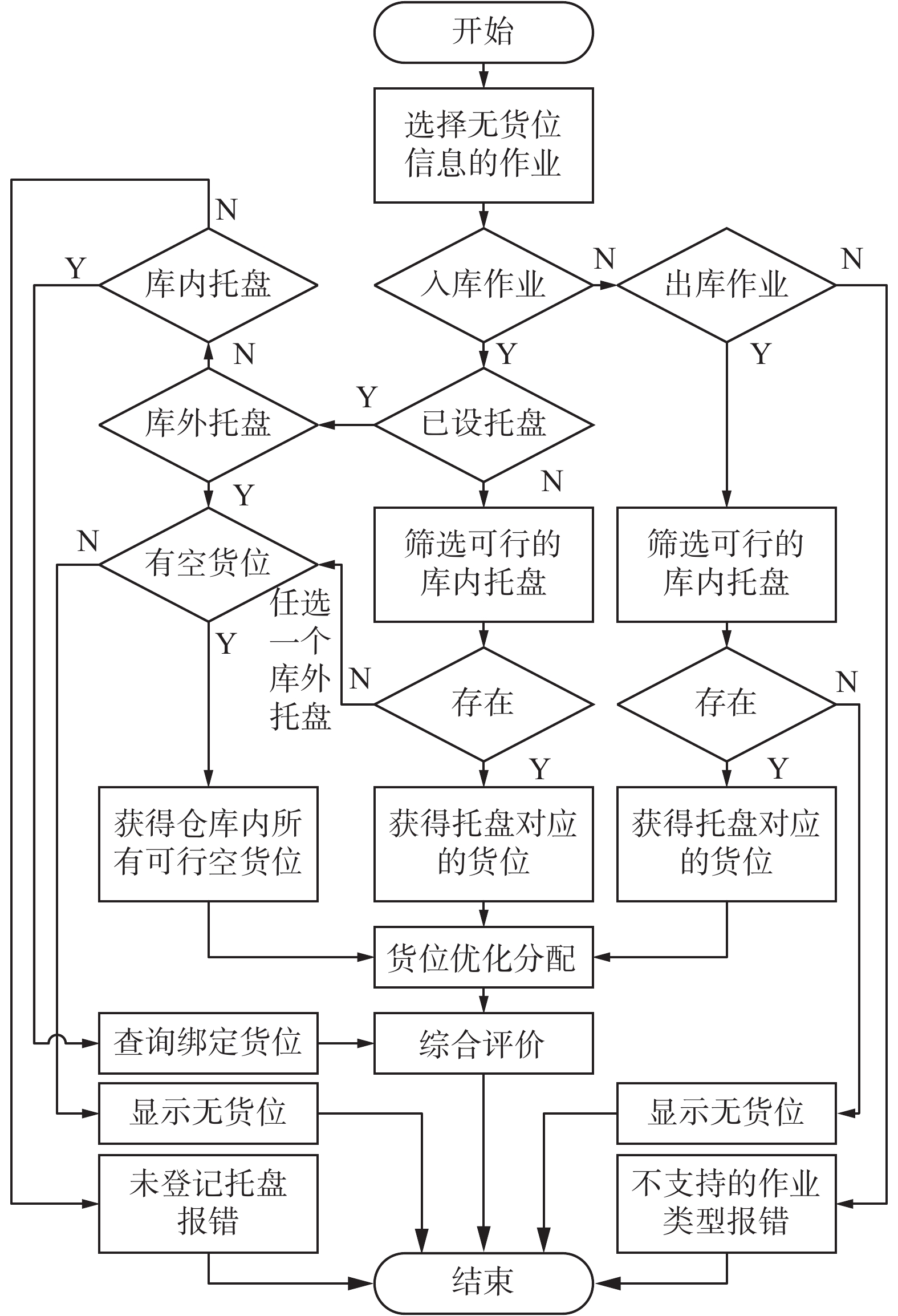
由于托盘使用状态复杂，货位优化的同时还需进行托盘决策。如图2所示为货位分配流程，若是未与货位绑定的库外托盘入库，则需为该作业分配空货位；若是与货位绑定的库内托盘入库，则应优先考虑包含该作业所需物料、且承载能力足够的库内托盘，使同种物料尽量聚集，若无满足条件的托盘，则任选一个库外托盘；在执行出库作业时，应为作业分配包含该作业下所有物料、且数量足够的库内托盘，否则应提示库存不足，无法分配货位。多批作业过程中，作业的货位可行域会动态变化。

目前大多数仓储管理系统中，出入库作业不会在同批次内混杂，且入库作业对应的货位可行域比出库作业大、货位可行域筛选规则复杂，由于出库作业流程相对简单，简化起见，将重点研究入库作业多目标货位优化与评价，以及多批作业货位持续优化规律等问题。

1.2 假设条件

1）同种物料可存放在多个托盘上，一个托盘可存放多种物料，一个货位只能放置一个托盘；

2）同一批作业为单纯的出库或者入库；

3）一个作业对应一个货位，一个货位可被不同批次的作业重复使用；

4）只考虑物料重量，不考虑货架、托盘重量，且各巷道的出入库口在同一侧。

2 多目标货位优化模型

$T{\rm{ = }}\left( {{T_{\rm{1}}}{\rm{, }}{T_{\rm{2}}}{\rm{, }} \cdot \cdot \cdot {\rm{ , }}{T_{{n}}}} \right)$ 表示单批作业，n表示该批作业总数； ${T_q} = \left\{ {{t_{qm}}|m = 1,2, \cdot \cdot \cdot ,M} \right\}$ 为第q个作业， ${t_{qm}}$ 表示作业q中物料m的总质量，M表示该物料种类数。 $A = \left\{ {\left( {{r_q},{c_q},{k_q}} \right)|q = 1,2, \cdot \cdot \cdot ,n} \right\}$ 为货位集合，通过作业q对应货位的排、列、层 $\left( {{r_q},{c_q},{k_q}} \right)$ ，可从仓储管理系统中获得该货位上的库存信息。考虑自动化立体仓库货架重心稳定、巷道作业均衡及就近存放等原则，建立以下多目标优化模型。

2.1 货架重心稳定

货架质量偏心、重心较高等会影响货架的力学性能及稳定性，考虑托盘存放“均匀分布”、“上轻下重”等原则，一方面使货架x方向重心接近其几何中心，避免出现货物“一边倒”、货架倾覆等现象，另一方面使y方向重心低。

${f_{\rm{1}}}\left( A \right) = |{G_x} - 0.5CL|$

${f_2}\left( A \right) = {G_y}$

${G_x} = \frac{{\displaystyle\sum\limits_{r = 1}^R {\displaystyle\sum\limits_{c = 1}^C {\displaystyle\sum\limits_{k = 1}^K {\left[ {{G_{rck}} \left( {c - 0.5} \right)L} \right]} } } }}{{\displaystyle\sum\limits_{r = 1}^R {\displaystyle\sum\limits_{c = 1}^C {\displaystyle\sum\limits_{k = 1}^K {{G_{rck}}} } } }}$

${G_y} = \frac{{\displaystyle\sum\limits_{r = 1}^R {\displaystyle\sum\limits_{c = 1}^C {\displaystyle\sum\limits_{k = 1}^K {\left[ {{G_{rck}} \left( {r - 0.5} \right)H} \right]} } } }}{{\displaystyle\sum\limits_{r = 1}^R {\displaystyle\sum\limits_{c = 1}^C {\displaystyle\sum\limits_{k = 1}^K {{G_{rck}}} } } }}$

${G_{rck}} = \sum\limits_{m = 1}^M {({q_{mrck}}{w_{mrck}} + {x_{qm}}{t_{qm}}),\begin{array}{*{20}{c}} {q = 1,2, \cdot \cdot \cdot ,n}&{} \end{array}} $

${x_{qm}} = \left\{ \begin{array}{l} 1, \quad {{{\text{入库作业}}q{\text{分配到货位}}}}\left( {r,c,k} \right){\text{上}}\\ 0 ,\quad {\text{作业}}q{\text{未分配到货位}}\left( {r,c,k} \right){\text{上}}\\ - 1,\quad {\text{出库作业}}q{\text{分配到货位}}\left( {r,c,k} \right){\text{上}} \end{array} \right.$

式中：K、C、R分别为货架的排、列、层总数；L、W、H分别为货架的长、宽、高； ${G_x}$ 为货架x方向的重心； ${f_1}$ 表示x方向重心偏离其几何中心的程度； ${f_2}$ 、 ${G_y}$ 为货架在y方向的重心； ${G_{rck}}$ 表示在第k排r层c列货位上的物料总质量（ ${\rm{1}} \leqslant c \leqslant C$ ， ${\rm{1}} \leqslant r \leqslant R$ ， ${\rm{1}} \leqslant k \leqslant K$ ，且c、r、k∈Z）； ${q_{mrck}}$ 为该托盘上物料m的数量， $m = 1,2, \cdot \cdot \cdot ,M;{w_{mrck}}$ 为该托盘上物料m的单位质量；M为该托盘存放物料的种类数； ${x_{qm}}$ 为决策变量。

2.2 巷道作业均衡

为了避免托盘在一个巷道内堆积、堆垛机超负荷工作，影响作业效率及堆垛机寿命，以货架中占用货位的标准差 ${f_3}$ 来反映作业的均衡程度，其值越小作业越均衡：

${f_3}\left( A \right) = \sqrt {\frac{1}{{K - 1}}\sum\limits_{k = 1}^K {{{\left( {{P_k} - \bar P} \right)}^2}} } $

式中： ${P_k}$ 表示分配货位后第k排货架被占货位数量， ${P_k} \in {{\bf{N}}^{{*}}}$ ； $\bar P$ 表示优化分配后平均每货架占用货位数量。

2.3 仓储作业路径最短

若不考虑堆垛机存取货物的时间，则堆垛机在巷道作业路径越短，仓储运行效率越高。假设出入库口 ${S_{\rm{0}}}$ 的坐标为（0,0,0），巷道的宽度忽略不计， ${f_4}$ 表示堆垛机的工作总路径：

${f_4}\left( A \right) = \frac{1}{n}\sum\limits_{q = 1}^n {\sqrt {{r_q}^2 + {c_q}^2 + {k_q}^2} } $

式中：n为作业总数； $\left( {{r_q},{c_q},{k_q}} \right)$ 为作业q对应的目标货位坐标。

2.4 货位优化数学模型

由于目标函数的数值范围大小存在差异，为了后期更好地评价Pareto解，如式（1）所示，将多目标函数 ${f_i}$ 归一化处理为 $f_i^*$ ：

${f_1}^* = \frac{{{f_1} - \min {f_1}}}{{\max {f_1} - \min {f_1}}}$

${f_2}^* = \frac{{{f_2} - \min {f_2}}}{{\max {f_2} - \min {f_2}}}$

${f_3}^* = \frac{{{f_3}}}{{\bar P}}$

${f_4}^* = \frac{{{f_4} - \min {f_4}}}{{\max {f_4} - \min {f_4}}}$

$\max {f_1} = \left( {{\rm{0}}{\rm{.5}}C - 0.5} \right)L,\min {f_1} = 0.5L$

(1)

$\max {f_2} = \left( {R - 0.5} \right)H,\min {f_2} = 0.5H$

$\max {f_4} = \sqrt {{K^2} + {R^2} + {C^2}} ,\min {f_4} = 0$

${{F}} = {\left[ {{f_1}^*,\quad {f_2}^*,\quad {f_3}^*,\quad {f_4}^*} \right]^{\rm{T}}}$

${\rm{s}}{\rm{.t}}{\rm{.}}\left\{ \begin{array}{l} \left( {{r_q},{c_q},{k_q}} \right) \in {{{D}}_q},\quad q = 1,2, \cdot \cdot \cdot ,n \\ {G_{rck}} \leqslant {G_{\max }} \end{array} \right.$

式中： $\max {f_i}$ 与 $\min {f_i}$ 分别为 ${f_i}$ 的上下限；多排货架中占用货位的离散程度 $f_{\rm{3}}^*$ ，用来反映各巷道作业均衡； ${{F}}$ 为优化目标矢量； $\left( {{r_q},{c_q},{k_q}} \right)$ 表示作业q所分配的货位； ${{{D}}_q}$ 表示作业q的动态货位可行域；每个托盘存放的物料总重量应小于托盘的最大承载重量 ${G_{\max }}$ 。

3 响应动态约束的多目标优化算法 3.1 基于自适应差分进化的货位优化算法

自适应差分进化算法^[12]是通过自适应调整进化参数与进化操作算子，以提高算法的收敛性能。本文采用的多目标差分进化算法^[13]（multi-objective adaptive differential evolution algorithm, MOA-DEA），通过变异参数自适应调整，个体解码时根据货位实时可行域响应动态约束条件，以及多目标Pareto解集综合评价，获得最优作业货位。算法原理如下：

1）初始化及编码

个体采用0~1的浮点编码，长度等于作业个数D，个体基因索引号为作业编号。初始化Pareto解集 ${X_P}$ 为空集，随机生成NP个维度为D的初始个体，对应于每个基因的 $\left( {{r_q},{c_q},{k_q}} \right)$ 是货位排、列、层。

2）响应动态约束条件的个体解码

通过作业q对应的基因值 ${x_i}_{_q}$ 、货位实时可行域 ${{{D}}_q}\left\{ {\left( {{r_1},{c_1},{k_1}} \right),\left( {{r_2},{c_2},{k_2}} \right), \cdot \cdot \cdot ,\left( {{r_j},{c_j},{k_j}} \right)} \right\}$ ，可获得对应的目标货位 $\left( {{r_q},{c_q},{k_q}} \right)$ 。通过货位集合 ${A_i}$ 计算目标函数值，具体解码过程如算法1所示。

算法1　响应动态约束条件的个体解码算法

输入　个体编码 ${X_i} = \left\{ {{x_i}_{_q}|q = 1,2, \cdot \cdot \cdot ,n} \right\}$ ，n个作业。

输出　货位集合 ${A_i} = \left\{ {\left( {{r_q},{c_q},{k_q}} \right)|q = 1,2, \cdot \cdot \cdot ,n} \right\}$ 。

1）已分配的货位集合 $C$ 初始化为 $\phi $

2） for 作业q=1 to n do

3）    设作业q的可行域 ${{{D}}_q} = \phi $

4） if 作业q为库外托盘入库

5）    库内所有的未占用的空货位为 ${{{D}}_q}$

6） else if 作业q为库内托盘入库

7）库内所有包含作业q所需物料，且承载能力足够的货位为 ${{{D}}_q}$

8） else if 作业q为出库

9）    库内所有包含作业q所需物料，且数量足够的货位为 ${{{D}}_q}$

10）     ${{{D}}_q} \leftarrow {{{D}}_q} - C$ //从 ${{{D}}_q}$ 中去除前q-1个作业已分配的货位

11）    if ${{{D}}_q} \ne \phi $

12）     ${\rm{inde}}{{\rm{x}}_q} = \left\lceil {{\rm{card}}\left( {{{{D}}_q}} \right){{x_i}_{_{q}}}} \right\rceil {\rm{ - 1}}$ //获得货位索引号

13）     $\left( {{r_q},{c_q},{k_q}} \right) \leftarrow {{D}}\left[ {{\rm{inde}}{{\rm{x}}_q}} \right]$ //获得目标货位

14）    将 $\left( {{r_q},{c_q},{k_q}} \right)$ 添加到 $C$ 中

15）    else $\left( {{r_q},{c_q},{k_q}} \right) = ( - 1, - 1, - 1)$ //未分配货位

16）  end for

17）  return ${A_i} $

3）变异操作

式（2）为个体变异公式，变异缩放因子 $F$ 按式（3）~（5）自适应产生，由 ${F_{i_1}}$ 和 ${F_{i_{\rm{2}}}}$ 2部分组成。其中 ${F_{i_1}}$ 按时间呈非线性自适应衰减，使算法在进化前期有较好的全局搜索能力，进化后期有较好的局部勘探能力； ${F_{i_{\rm{2}}}}$ 按每个体自身与种群最优个体目标函数值差异来自适应调整^[14]；r₁、r₂、r₃ 为从 $\left\{ {1,2, \cdot \cdot \cdot ,{\rm{NP}}} \right\}$ 集合中随机选择的两两互不相同且不等于i的整数； ${F_l}$ 为 ${F_i}$ 的下限； ${F_u}$ 为 ${F_i}$ 的上限；T为最大迭代次数； $t \in [0,T - 1]$ 为当前迭代次数； ${f_i}$ 为个体目标函数值； ${f_{\min }}$ 为种群内最小目标函数值； ${f_{\max }}$ 为种群内最大目标函数值。

$V_i^t = X_{r_1}^t + F\left( {X_{r_2}^t - X_{r_3}^t} \right)$

(2)

${F_{i_1}} = {F_u}\exp \left( {\frac{{\ln \left( {{F_l}/{F_u}} \right)}}{{T{\rm{ - 1}}}}t} \right)$

(3)

${F_{i_{\rm{2}}}}{\rm{ = }}\frac{{{f_i} - {f_{\min }}}}{{{f_{\max }} - {f_{\min }}}}$

(4)

$F = \frac{{{F_{i_{\rm{1}}}} + {F_{i_{\rm{2}}}}}}{2}$

(5)

4）交叉操作

为增加种群的多样性，采用二项式交叉操作获得实验向量 ${{U}}_i^t = \left[ {u_{1,i}^t,\quad u_{2,i}^t, \quad \cdots ,\quad u_{D,i}^t} \right]$ ，如式（6）所示， ${R_{i,{\rm{rand}}}} \in \left( {{\rm{1,2,}} \cdot \cdot \cdot ,D} \right)$ ，可保证 $u_{j,i}^t$ 至少有一个参数来自 $V_i^t$ ；交叉算子 ${\rm{CR}} \in \left[ {0,1} \right]$ 。

$u_{j,i}^t = \left\{ \begin{array}{l} v_{j,i}^t, \quad {\rm{rand}}\left( {0,1} \right) \leqslant {\rm{CR}} {\text{或}} j = {R_{i,{\rm{rand}}}}\\ x_{j,i}^t, \quad {\text{其他}} \end{array} \right.$

(6)

5）选择操作

基于多目标算法中的占优关系，选择算子如式（7）所示， ${\rm{LC}}(U_i^{t + 1},X_i^t)$ 表示 $U_i^{t + 1}$ 与 $X_i^t$ 中拥挤熵较小的个体^[15]。

$X_i^{t + 1} = \left\{ \begin{array}{l} \begin{array}{*{20}{c}} {X_i^t,}&{X_i^t{\text{占优或强占优}}U_i^{t{\rm{ + 1}}}} \end{array}\\ \begin{array}{*{20}{c}} {U_i^{t{\rm{ + 1}}},}&{U_i^{t{\rm{ + 1}}}{\text{占优或强占优}}X_i^t} \end{array}\\ \begin{array}{*{20}{c}} {{\rm{LC(}}U_i^{t{\rm{ + 1}}},X_i^t),}&{U_i^{t{\rm{ + 1}}}{\text{与}}X_i^t{\text{互不占优}}} \end{array} \end{array} \right.$

(7)

6）获取Pareto解集

${x^{\rm{*}}} \in \Omega $ 是Pareto最优解，是指 $\nexists x \in \Omega $ 使得 $f(x) < f({x^*})$ ， $\Omega $ 为变量x的可行域，Pareto最优解集 ${X_P}$ 是指所有Pareto最优解的集合。将第t代的Pareto解集与第t+1代的种群合并，用于求解第t+1代的Pareto解集，以获得足够多样性且分布在整个Pareto前沿的最优解集。

3.2 基于层次分析法的Pareto最优解评价与选择

从仓储实际应用出发，需从Pareto解集中遴选出合理的单个解。因此，通过常用的层次分析法^[16]计算权重，利用该权重将多目标加权求解，获得综合目标函数值最小的个体，观察多目标权重与货位持续优化能力间的关系。根据重要性标度构建判断矩阵 ${{B}}{\rm{ = }}{\left( {{b_{ij}}} \right)_{n \times n}}$ ，按列归一化得到矩阵 ${{C}}{\rm{ = }}{\left( {{c_{ij}}} \right)_{n \times n}}$ ，C矩阵的行元素之和除以元素总和可求得各目标的权重。

${c_{ij}} = \frac{{{b_{ij}}}}{{\displaystyle\sum\limits_{k = 1}^n {{a_{kj}}} }}$

${\omega _i} = \frac{{\displaystyle\sum\limits_{k = 1}^n {{c_{ik}}} }}{{\displaystyle\sum\limits_{j = 1}^n {\displaystyle\sum\limits_{i = 1}^n {{c_{ij}}} } }}$

通过层次分析法确定x方向重心的权重 ${\omega _{\rm{1}}}$ 、y方向重心的权重 ${\omega _{\rm{2}}}$ 、多排货架中占用货位的离散程度权重 ${\omega _{\rm{3}}}$ 及作业距离的权重 ${\omega _{\rm{4}}}$ 。MOADEA求解获得Pareto解集后，根据式（8）计算Pareto解集中所有个体的综合目标函数值F，选择F最小的个体为最优个体；若以式（8）为单目标进行优化求解，则称之为简单加权差分进化算法（simple weighted adaptive differential evolution algorithms，SWADEA），后续实验中将对2种方法优化结果进行对比。

$F = \min ({\omega _{\rm{1}}}{f_1} + {\omega _{\rm{2}}}{f_2} + {\omega _{\rm{3}}}{f_3} + {\omega _{\rm{4}}}{f_4})$

(8)

3.3 算法的流程

所提算法基本流程如图3所示，具体步骤如下：

1) 设置种群规模NP，最大迭代次数T，终止条件，交叉算子CR；初始化种群，个体向量维度D等于作业数量n，对个体进行随机数编码，初始化Pareto解集为空集。

2) 判断是否达到最大迭代次数T，若是，则从Pareto解中遴选出综合目标函数值最小的个体；若不是，则进行下一步。

3) 进行变异交叉操作，并计算目标函数值。

4) 判断 $U_i^{t + 1}$ 与 $X_i^t$ 的占优关系，并选择个体 $X_i^{t + 1}$ 。

5) 比较目标向量 $X_i^t$ 与Pareto解集 ${X_P}$ 中所有向量，更新Pareto解集。

6) 迭代次数t=t+1，种群中合并第t代获取的Pareto解，转到2)。

4 实验与分析

以图1所示的仓储环境为例进行实验，仓库共有6排货架、3条巷道，每排货架4层4列，共96个货位。相邻2货位之间间隔为1个距离单位，相邻2巷道之间间隔为2个距离单位。实验计算机配置为Intel(R)Core(TM)/i7CPU/1.8GHZ/8GB内存，操作系统为Windows10，使用C#、MATLAB作为编程及分析工具。

4.1 多批次作业货位持续优化实验与分析

库内托盘入库、出库作业对货位占有率影响不大，且出入库混合比例等影响因素难以控制，为了观察多批次作业下，随着货位占有率的增加，多目标权重对货位持续优化的影响规律。随机生成96个库外托盘入库作业，每8个作业为一批共12批，每个作业随机包含1~15种物料，每种物料存储数量随机。每个方案采用简单加权单目标SWADEA及多目标自适应MOADEA，分别单独实验10次，通过多批作业的综合目标函数值分析货位持续优化能力。

选取算法最大迭代次数T=500，种群规模NP=50，变异参数F为自适应变化，范围是0.1~0.5交叉概率CR为0.5。如表1所示，基于层次分析法仅选择同样重要、略重要2个重要性标度，设置了所有可能的权重方案。

实验结果如图4所示，每个子图的横坐标为作业批次，纵坐标为10次测试下，综合目标函数值F的平均值。方案2、4、8、9、10、14的综合目标函数值F随作业批次增加不断增加，其波动范围大、不稳定，货位持续优化能力差；方案1、3、7，综合目标函数值F随作业批次增加而趋于平稳，其波动范围小，货位持续优化能力强；且MOADEA的综合目标函数值F明显优于SWADEA，而不同权重会影响货位的持续优化能力。方案7中12批作业F的均值 $\mu $ =0.188，标准差 $\sigma $ =0.036均较小，解的质量好且稳定，即货位持续优化能力好，适用于AS/RS中对货位持续优化要求较高的作业场景，以减少盘点周期、降低仓储成本、提高作业效率。

当选择y方向重心的权重 ${\omega _{\rm{2}}}$ 、作业路径的权重 ${\omega _{\rm{4}}}$ 较大的方案时，综合优化目标函数值F不断增加，优化结果越来越差，货位的持续优化能力差。相反，选择x方向重心与货架中心偏离程度的权重 ${\omega _{\rm{1}}}$ 、多排货架中占用货位的离散程度的权重 ${\omega _{\rm{3}}}$ 较大时，货位的持续优化能力较强，更符合仓储持续、动态作业的需求。

为了进一步分析影响货位持续优化能力的因素，并更好地观察SWADEA与MOADEA优化结果的差异，选择持续优化能力较好的4组权重方案（方案1、3、7、11），分析SWADEA与MOADEA各子目标函数值。如图5所示，随着作业批次的增加，x方向重心偏离货架中心程度 $f_1^*$ 越小，y方向重心 $f_{\rm{2}}^*$ 越高，占用货位离散程度 $f_{\rm{3}}^*$ 在达到较优后趋于平稳，作业路径 $f_{\rm{4}}^*$ 越长。对比2种方法，MOADEA求解结果显著优于SWADEA，且MOADEA综合目标函数值F的均值更加平稳。可见，相比SWADEA，MOADEA更易获得最优解。

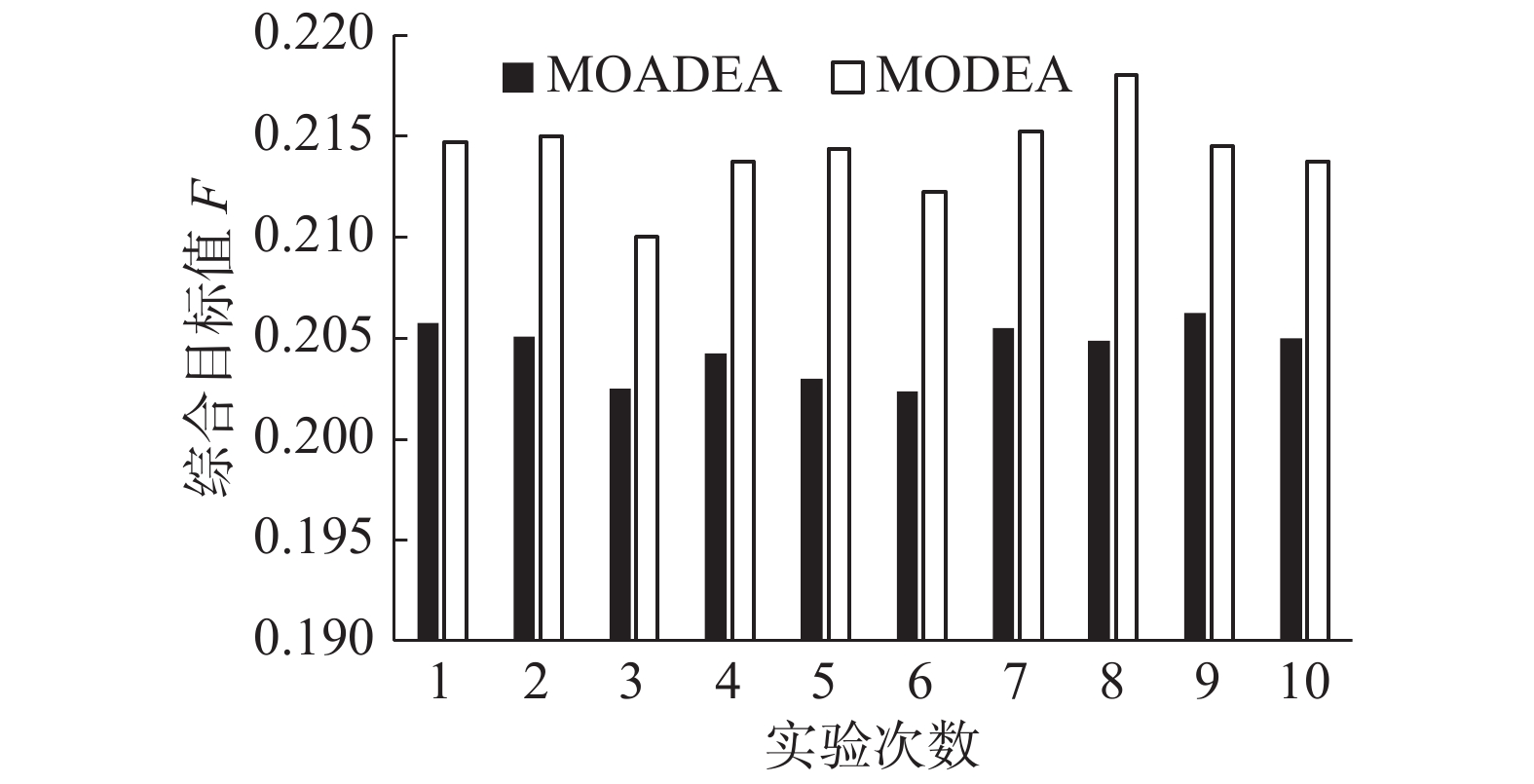
为了观察变异系数自适应DE算法的改进效果，与基于标准DE的多目标算法MODEA相比，MODEA的固定参数F=0.5，CR=0.5，采用方案7的权重，在同样初始库存、单批作业下，对2种算法分别进行10次独立试验。如图6所示，采用式（2）~（5）中的变异参数自适应方法，综合目标函数值F显著优于标准DE算法。

4.2 算法结果

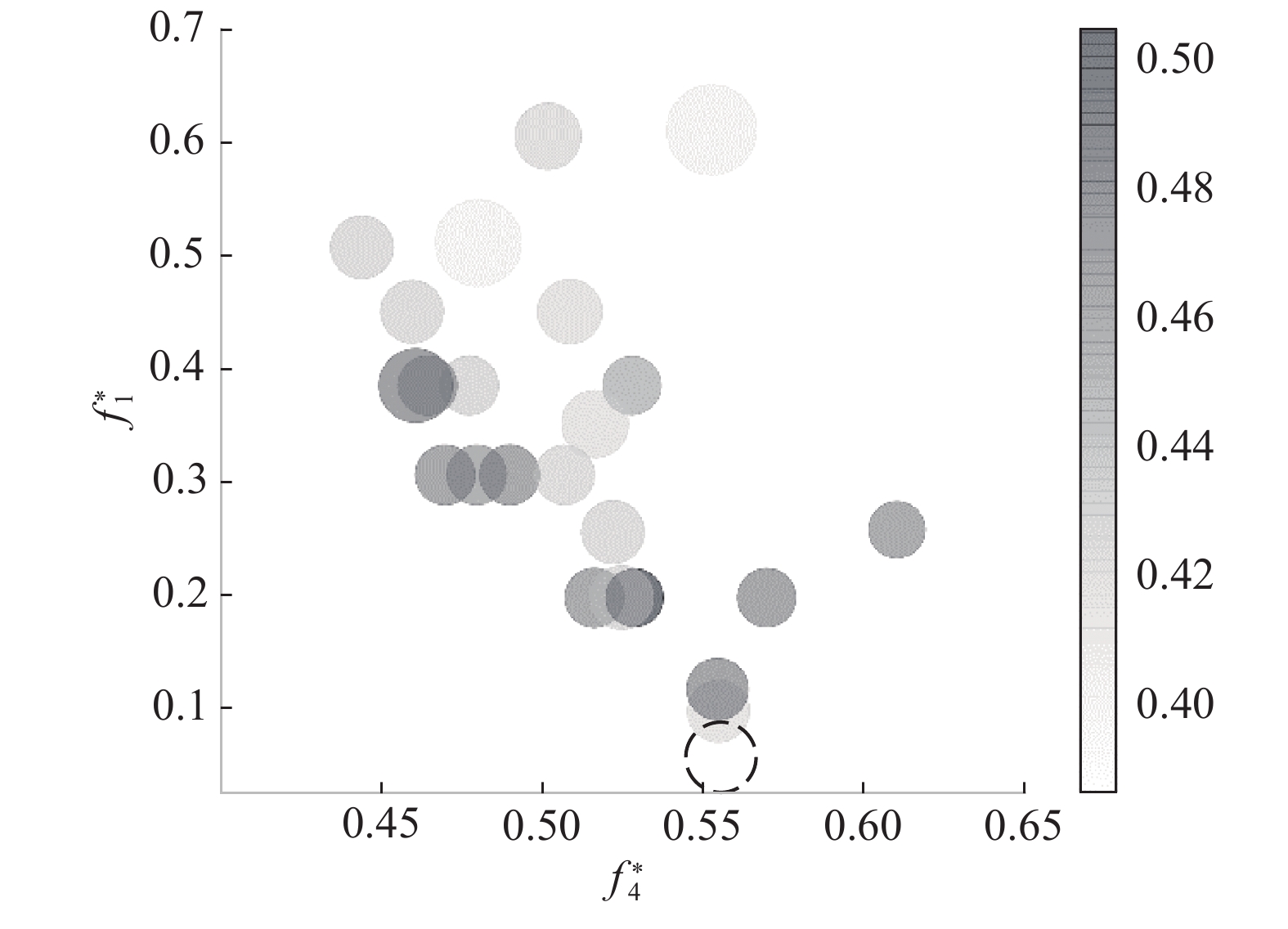
为验证所提模型及算法在实际仓储作业中的有效性，在仓库单元设置初始库存的情况下，随机生成库内托盘入库、库外托盘入库共20个作业，而出库作业优化求解过程与库内托盘入库基本类似，在此不再赘述。如图7所示，气泡表示经MOADEA求解后获得的Pareto解集，横坐标为 $f_{\rm{4}}^*$ ，纵坐标为 $f_{\rm{1}}^*$ ，气泡越小表示 $f_{\rm{3}}^*$ 值越小，气泡颜色越浅表示 $f_{\rm{2}}^*$ 值越小，虚线圈出的气泡表示采用方案7权重选择出的最优个体。

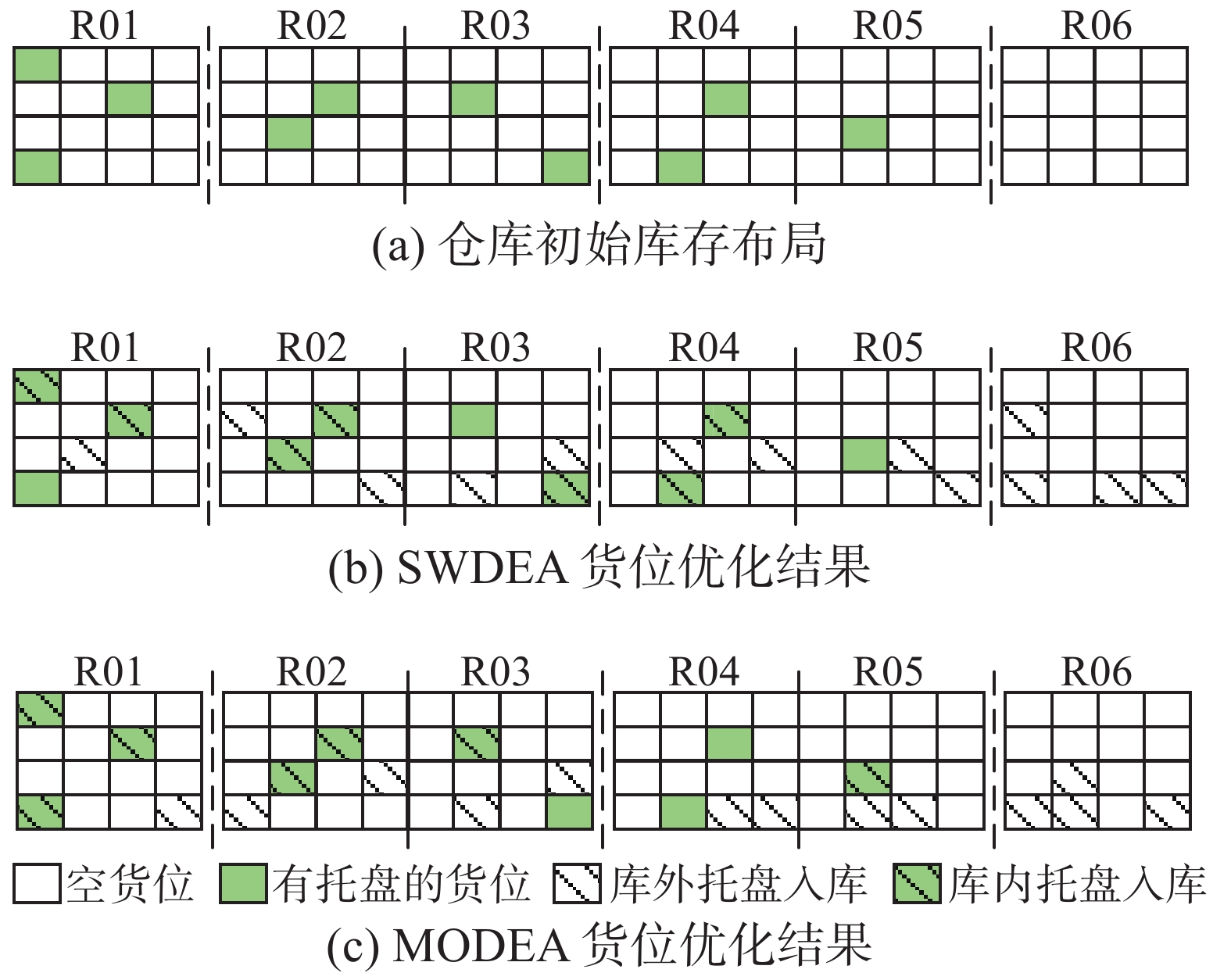
从图8及表2可看出，MOADEA优化后的库位布局达到了理想的结果，分配的作业货位均匀分布在各巷道，货位更接近于货架底层，离出入库口更近，更靠近货架中心。相比于SWADEA，经MOADEA优化后，货架垂直方向重心降低了11%，水平方向重心改善了6%，作业路径缩短了7%，综合目标函数值优化了4.7%。实验中单批作业平均优化时间约为3~4 s。MOADEA在企业中已得到初步应用，能够有效解决动态货位优化问题。

5 结束语

考虑仓储作业中资源约束的动态性，采用多目标差分进化算法求解动态货位决策优化问题，进而基于层次分析法从Pareto解中遴择最符合需求的个体，并分析目标权重与货位持续优化能力间的关系。实验结果表明：

1）所提优化算法能够响应货位可行域等动态约束条件，符合实际仓储作业需求；

2）相比于简单加权差分进化算法，所提算法的解更优，分配货位后货架重心稳定，作业均衡且路径短；

3）优化目标的权重将影响货位持续优化能力，当货架x方向稳定性与货位占有离散程度权重取较大时，货位优化持续稳定。

综上所述，所提算法可有效解决动态货位决策优化问题，但未考虑出入库混批等复杂情形，出入库混批作业货位决策优化有待进一步研究，算法性能也有待进一步提高。