近年来,在理论或工程上的诸多应用,包括控制器设计、高级过程仿真、软计算以及故障诊断等,都离不开对被研究的复杂非线性系统的建模[1]。因此,建立被研究对象的非线性动态数学模型在实际工程应用中变得尤为重要。由于诸多不确定性的存在,例如模型结构以及参数等,导致非线性系统的机理建模出现了巨大挑战[2-3]。因此,出现了基于数据的两种经典方法:1)基于经验风险最小化的神经网络(neural network,NN);2)采用结构风险最小化理论的支持向量机(support vector machine, SVM)及其变体最小二乘支持向量机(least squares SVM),都被广泛应用于非线性系统的建模研究。
从理论上来讲,神经网络可以以任意的精度逼近任意的非线性系统[4],在非线性系统的建模领域有着大量的研究[5]。例如,在文献[6-7]中提出的带随机权值分配的级联神经网络,从某种程度上其建模精度得到了较大改善。为了能实现非线性系统建模过程中的快速鲁棒收敛,一种自适应二阶算法[8]被提出用于训练模糊神经网络,获取了满意的建模结果。分层径向基函数神经网络[9-10]作为NN的另一种变体,通过对污水处理的非线性建模,在实际应用中的预测性能上都达到了较好的效果。然而,上述提到的这些方法仅仅考虑了单隐层结构,在建模精度上仍缺乏显著改进。根据统计学一致逼近理论理可知[11],当NN的隐神经元个数选取较多时,甚至等于训练样本的数量时,单隐层NN就能以足够高的精度去逼近任意的非线性系统;然而,较多的样本数量会引起神经元个数的增加,导致NN的模型结构复杂,泛化性能变差。此外,众多神经网络在参数求解过程中,主要还是采用经验风险最小化理论[12],即神经网络的参数最终解是以模型预测输出与实际输出之间的平方和达到最小作为标准,进而导致训练获取的神经网络模型复杂,容易产生局部极小与过拟合问题。由Vapnik提出的SVM,通过执行结构风险最小化来代替经验风险最小化,理论上保证了SVM在非线性系统建模上的全局最优,已成为分类和回归应用中的一种重要学习方法。在非线性回归领域,通过大量的实验研究表明,SVM的泛化性能优于神经网络及其变体的非线性建模方法。基于此,在SVM基础上,文献 [13-14]提出了基于支持向量学习方法的模糊回归分析,该方法较传统神经网络方法在泛化性能上做了较好的改进。基于此,基于数据的另一种模糊建模方法,也将基于增量平滑SVR的结构风险最小化作为优化问题[15],进而提高模型泛化性能。近年来,深度学习俨然成为研究的热点,文献[16-17]围绕非线性系统的建模问题,提出了一种基于改进型深度学习的非线性建模方法。
目前,各种数据建模方法主要集中在确定性数学模型建模的研究,其鲁棒性差,易受外界干扰,很少有针对来自模型结构、参数以及测量数据的不确定性等因素引起的最优下界建模;此外,如何控制所建立模型的结构复杂性,提高泛化性能,也是需要考虑的重点。在本文中,考虑到基于结构风险最小化的支持向量机所具有的优良特性,将其转化为
随着Vapnik的不敏感损失函数的引入[18-19],支持向量机的分类问题被扩展到回归问题,即支持向量回归(SVR),已在最优控制、时间序列预测、区间回归分析等方面得到了广泛应用。SVR方法是对一组带有噪声的测量数据
| $f({{x}},{{\theta }}) = \sum\limits_{k = 1}^m {{\theta _k}{g_s}({{x}})} + b$ | (1) |
式中:
| $\min :\;\;\;R(f) = \sum\limits_{k = 1}^N {{L_\varepsilon }\left( {{y_k} - f({{{x}}_k})} \right)} + \gamma \left\| {{w}} \right\|\;_2^2$ | (2) |
| ${L_\varepsilon }({y_k} - f({y_k} - f({{{x}}_k})) = \left\{ \begin{array}{l} 0\;,\;\;\;\;\;\;\;|{y_k} - f({{{x}}_k})| \leqslant \varepsilon \\ |{y_k} - f({{{x}}_k})| - \varepsilon ,\;\;{\text{其他}} \end{array} \right.$ |
从上述
通过应用拉格朗日乘子方法,对式(2)的最小化可转化为它的对偶优化问题:
| $\begin{array}{c} \min :\;\;\;W({{{\alpha }}^ + },{{{\alpha }}^ - }) = \varepsilon \displaystyle\sum\limits_{k = 1}^N {{L_\varepsilon }\left( {\alpha _k^ - + \alpha _k^ + } \right)} - \displaystyle\sum\limits_{k = 1}^N {{y_k}\left( {\alpha _k^ + - \alpha _k^ - } \right)} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \dfrac{1}{2}\displaystyle\sum\limits_{k,i = 1}^N {\left( {\left( {\alpha _k^ + - \alpha _k^ - } \right)\left( {\alpha _k^ + - \alpha _k^ - } \right)\displaystyle\sum\limits_{s = 1}^m {{g_s}({{{x}}_k}){g_s}({{{x}}_i})} } \right)} \; \\ {\rm{s}}.{\rm{t}}\;\;\;\;\displaystyle\sum\limits_{k = 1}^N {\alpha _k^ + } = \;\displaystyle\sum\limits_{k = 1}^N {\alpha _k^ - ,\;\;\;\;\;0 \leqslant \alpha _k^ + \;,\alpha _k^ - \leqslant \gamma },\;\;\; \\ {\rm{for}}\;\;{k = 1,2, \cdots ,N} \end{array} $ | (3) |
| $K({{{x}}_k},{{{x}}_i}) = \sum\limits_{s = 1}^m {{g_s}({{{x}}_k}){g_s}({{{x}}_i})} $ |
核函数确定了解的平滑特性,选取时应该更好的反映数据的先验知识。式(3)的优化问题可从写为
| $\begin{array}{c} \min :\;\;\;W({{\bf{\alpha }}^ + },{{\bf{\alpha }}^ - }) = \varepsilon \displaystyle\sum\limits_{k = 1}^N {{L_\varepsilon }\left( {\alpha _k^ - + \alpha _k^ + } \right)} - \displaystyle\sum\limits_{k = 1}^N {{y_k}\left( {\alpha _k^ + - \alpha _k^ - } \right)} + \\ \dfrac{1}{2}\displaystyle\sum\limits_{k,i = 1}^N {\left( {\left( {\alpha _k^ + - \alpha _k^ - } \right)\left( {\alpha _k^ + - \alpha _k^ - } \right)K({{{x}}_k},{{{x}}_i})} \right)} \end{array} $ |
基于Vapnik的研究,SVR方法的解以核函数的线性展开描述为
| $f({{x}},{{{\alpha }}^ + },{{{\alpha }}^ - }) = \sum\limits_{k = 1}^m {({{{\alpha }}^ + } - {{{\alpha }}^ - })K({{x}},{{{x}}_i})} + b$ | (7) |
其中常量
| $b = {y_k} - \sum\limits_{k = 1}^N {\left( {\alpha _k^ + - \alpha _k^ - } \right)K({{{x}}_k},{{{x}}_i}) + \varepsilon \cdot {\rm{sign}}\left( {\alpha _k^ - - \alpha _k^ + } \right)} $ |
显然,仅当
| $f({{x}},{{\bf{\alpha }}^ + },{{\bf{\alpha }}^ - }) = \sum\limits_{k = 1}^m {\left( {\alpha _k^ + - \alpha _k^ - } \right)\exp \left\{ {\frac{{ - {{\left\| {{{x}} - {{{x}}_k}} \right\|}^2}}}{{2{\sigma ^2}}}} \right\}} + b$ | (5) |
式中
SVR采用结构风险最小化理论建立求解模型参数的凸二次规划问题,不仅保证了模型建模精度,而且模型结构的稀疏特性也得到了保证,被广泛应用于模式识别以及非线性内动态系统建模。然而,正如1.1节的SVR回归问题那样,其传统的二次规划-SVR(quadric programming-support vector regression,QP-SVR)在执行参数的求解过程中,容易产生模型的冗余描述及昂贵的计算成本[18]。对于QP-SVR,基于式(2)的优化问题,
| $\begin{array}{l} \min :\;\;\;R(f) = C\displaystyle\sum\limits_{k = 1}^N {{L_\varepsilon }\left( {{\xi _k} + \xi _k^*} \right)} + \dfrac{1}{2}\left\| {{w}} \right\|\;_2^2 \\ \;\;{\rm{s}}.{\rm{t}}.\;\;\;\;\;\;\;\;\;\;\;\;\;\left\{ \begin{array}{l} {y_k} - \left\langle {{{w}},\;\varphi ({{{x}}_k})} \right\rangle - b \leqslant \varepsilon + {\xi _k}, \\ \left\langle {{{w}},\;\varphi ({{{x}}_k})} \right\rangle + b - {y_k} \leqslant \varepsilon + \xi _k^* \\ {\xi _k},\xi _k^* \geqslant 0 \\ \end{array} \right. \\ \end{array} $ |
其中
| $f({{x}},{\bf{\beta }}) = \sum\limits_{k = 1}^N {{\beta _k}\exp \left( {\frac{{ - {{\left\| {{{x}} - {{{x}}_k}} \right\|}^2}}}{{2{\sigma ^2}}}} \right)} + b$ | (6) |
| $\min :\;\;\;R(f) = \sum\limits_{k = 1}^N {{L_\varepsilon }\left( {{y_k} - f({{{x}}_k})} \right)} + \gamma {\left\| {\bf{\beta }} \right\|_{\;1}}$ |
其中,
| $\begin{array}{c} \min :\;\;\;R(f) = C\displaystyle\sum\limits_{k = 1}^N {\left( {{\xi _k} + \xi _k^*} \right)} + {\left\| {\bf{\beta }} \right\|_{\;1}} \\ \;\;{\rm{s}}.{\rm{t}}.\;\;\;\;\;\;\;\;\;\;\;\;\;\left\{ \begin{array}{l} {y_k} - \displaystyle\sum\limits_{k = 1}^m {{\beta _k}\exp \left\{ {\dfrac{{ - {{\left\| {{{x}} - {{{x}}_k}} \right\|}^2}}}{{2{\sigma ^2}}}} \right\} - } b \leqslant \varepsilon + \xi _k^* \\ \displaystyle\sum\limits_{k = 1}^m {{\beta _k}\exp \left\{ {\dfrac{{ - {{\left\| {{{x}} - {{{x}}_k}} \right\|}^2}}}{{2{\sigma ^2}}}} \right\}} + b - {y_k} \leqslant \varepsilon + \xi _k^* \\ {\xi _k},\xi _k^* \geqslant 0 \end{array} \right. \end{array} \!\!\!$ | (7) |
从几何的角度来看,
| $\begin{array}{c} \min :\;\;\;R(f) = C\displaystyle\sum\limits_{k = 1}^N {{\xi _k}} + {\left\| {\bf{\beta }} \right\|_{\;1}} \\ \;\;{\rm{s}}.{\rm{t}}.\;\;\;\;\;\;\;\;\;\;\;\;\;\left\{ \begin{array}{l} {y_k} - \displaystyle\sum\limits_{k = 1}^m {{\beta _k}\exp \left\{ {\dfrac{{ - {{\left\| {{{x}} - {{{x}}_k}} \right\|}^2}}}{{2{\sigma ^2}}}} \right\} - } b \leqslant \varepsilon + {\xi _k} \\ \displaystyle\sum\limits_{k = 1}^m {{\beta _k}\exp \left\{ {\dfrac{{ - {{\left\| {{{x}} - {{{x}}_k}} \right\|}^2}}}{{2{\sigma ^2}}}} \right\}} + b - {y_k} \leqslant \varepsilon + {\xi _k} \\ {\xi _k} \geqslant 0 \end{array} \right. \end{array} $ | (8) |
为了转化上述优化问题为线性规划问题,将
| $\begin{array}{l} {\beta _k} = \alpha _k^ + - \alpha _k^ - \\ |{\beta _k}| = \alpha _k^ + + \alpha _k^ - \\ \end{array} $ | (9) |
基于式(9),优化问题(8)进一步变成:
| $ \begin{array}{c} \min :\;\;\;R(f) = C\displaystyle\sum\limits_{k = 1}^N {{\xi _k}} + \displaystyle\sum\limits_{i = 1}^N {(\alpha _k^ + + \alpha _k^ - )} \\ \;\;{\rm{s}}.{\rm{t}}\;\;\;\left\{ \begin{array}{l} {y_k} - \displaystyle\sum\limits_{k = 1}^m {(\alpha _k^ + - \alpha _k^ - )\exp \left\{ {\dfrac{{ - {{\left\| {{{x}} - {{{x}}_k}} \right\|}^2}}}{{2{\sigma ^2}}}} \right\} - } b \leqslant \varepsilon + {\xi _k} \\ \displaystyle\sum\limits_{k = 1}^m {(\alpha _k^ + - \alpha _k^ - )\exp \left\{ {\dfrac{{ - {{\left\| {{{x}} - {{{x}}_k}} \right\|}^2}}}{{2{\sigma ^2}}}} \right\}} + b - {y_k} \leqslant \varepsilon + {\xi _k} \\ {\xi _k} \geqslant 0 \\ \end{array} \right. \\ \end{array} $ | (10) |
现定义向量
| $\begin{array}{c} \min \;\;\;\;\;\;{{{c}}^{\rm{T}}}\left( \begin{array}{l} {{{\alpha }}^ + } \\ {{{\alpha }}^ - } \\ {{\xi }} \\ \end{array} \right) \\ {\rm{s}}.{\rm{t}}.\;\;\;\;\;\left\{ \begin{array}{l} \left( \begin{array}{l} \;{{K}}\;\;\; - {{K}}\;\;\; - {{I}} \\ - {{K}}\;\;\;\;{{K}}\;\;\;\; - {{I}} \\ \end{array} \right) \cdot \left( \begin{array}{l} {{{\alpha }}^ + } \\ {{{\alpha }}^ - } \\ {{\xi }} \\ \end{array} \right) \leqslant \left( \begin{array}{l} {{y}} + \varepsilon \\ \varepsilon - {{y}} \\ \end{array} \right) \\ {{{\alpha }}^ + },\;{{{\alpha }}^ - }\; \geqslant 0,\;\;\;{{\xi }} \geqslant 0 \end{array} \right. \end{array} $ | (11) |
其中
| ${{{K}}_{ij}} = k({{{x}}_i},{{{x}}_j}) = {\rm{exp}}\left\{ {\frac{{ - {{\left\| {{{{x}}_i} - {{{x}}_j}} \right\|}^2}}}{{2{\sigma ^2}}}} \right\}。$ |
线性规划问题(11)可通过单纯型算法或原−对偶内点算法进行求解[22]。对于二次规划−SVR(QP-SVR),在
基于第1节介绍的支持向量回归及优化问题转化的基础上,该部分将讨论模型参数估计的另一种方法,即使用
| ${y_k} = g({{{x}}_k}),\;\;\;\;\;\;k = 1,2, \cdots ,N$ |
根据统计学理论理可知[12],存在以式(6)描述的非线性回归模型
| $\mathop {\sup }\limits_{{{{x}}_k} \in {{S}}} \left| {f({{{x}}_k}) - g({{{x}}_k})} \right| < \eta \;\;\;\;\;\;\;\;\;\;\forall k$ |
值得指出的是,较小的
| ${e_k} = {y_k} - f({{{x}}_k})\;\;\;\;\;\;\forall k$ | (12) |
为了估计SVR模型的最优参数,考虑所有建模误差的最小化:
| $\mathop {\min }\limits_{{{{x}}_k} \in Z} \left| {{y_k} - f({{{x}}_k})} \right|\;\;\;\;\;\;\forall k$ | (21) |
| ${\bf{\beta }} = \arg \;\mathop {\min }\limits_{{\bf{\beta }}\;,\;{{{x}}_k} \in Z} \;\;\left| {{y_k} - \sum\limits_{i = 1}^N {{\beta _i}\exp \left( {\frac{{ - {{\left\| {{{{x}}_i} - {{{x}}_k}} \right\|}^2}}}{{2{\sigma ^2}}}} \right)} - b} \right|$ |
假定不确定非线性函数或非线性系统属于函数簇
| $\varGamma = \{ g:{{S}} \to {{R}^1}|\;g({{x}}) = {g_{{\rm{nom}}}}({{x}}) + \Delta g({{x}}),\;{{x}} \in {{S}}\} $ |
| $f({{{x}}_k}) \leqslant g({{{x}}_k})\;\;\;\;\forall {{{x}}_k} \in {{S}}$ | (14) |
在式(14)约束的意义下,来自函数簇的任一成员函数总能在LBRM上方中找到。显然,这样的LBRM有无穷多个,本文的目的就是根据提出的约束(14),确定尽可能逼近成员函数的下界。为了确定LBRM的最优逼近,提出的方法将逼近误差的
| $f({{x}},{{\beta }},b) = \sum\limits_{k = 1}^N {{\beta _k}\exp \left( {\frac{{ - {{\left\| {{{x}} - {{{x}}_k}} \right\|}^2}}}{{2{\sigma ^2}}}} \right)} + b$ |
下界回归模型
| $\mathop {\min }\limits_{f,\;\;{{{x}}_k} \in S} \;\;\sum\limits_{k = 1}^N {({y_k} - f({{{x}}_k}))} \;\;\;{\rm{s}}.{\rm{t}}.\;\;\;{y_k} - f({{{x}}_k})\geqslant 0$ | (15) |
因此,模型
| $\begin{array}{c} \;\;\;\min :\;\;\;\;\;\;\lambda \; = \displaystyle\sum\limits_{k = 1}^N {{\lambda _k}} \\ \left\{ \begin{array}{l} {y_k} - \displaystyle\sum\limits_{i = 1}^N {\beta _i^{}\exp \left( {\dfrac{{ - {{\left\| {{{{x}}_i} - {{{x}}_k}} \right\|}^2}}}{{2{\sigma ^2}}}} \right)} - {b_{}} \leqslant {\lambda _k},\;\;\;\;k = 1,2, \cdots ,N \\ {y_k} - \displaystyle\sum\limits_{i = 1}^N {\beta _i^{}\exp \left( {\dfrac{{ - {{\left\| {{{{x}}_i} - {{{x}}_k}} \right\|}^2}}}{{2{\sigma ^2}}}} \right)} - \beta _i^{} \geqslant 0\;\;\;k = 1,2, \cdots ,N \\ {\lambda _k} \geqslant 0 \end{array} \right. \end{array} $ | (16) |
其中
证明 上述定理2直接通过定理1推出。
从上述回归模型辨识的思想来看,仅考虑上边模型输出与实际输出之间的逼近误差,而回归模型本身的结构复杂性却没有被考虑,这样一来,通过上述优化问题获取的参数解有可能出现不全为零的情况,不具有稀疏特性,对应N个样本数据可能都是支持向量,导致模型结构复杂。为了解决模型稀疏解的问题,在求解下边回归模型的优化问题中,有必要将结构风险最小化的思想融合其中,在保证回归模型逼近精度的同时,尽可能让模型结构复杂性得到有效控制。基于此,将下界回归模型优化问题(16)(式(16)),融合到基于结构风险最小化的优化问题(10)(式(10))。因此,对于下界回归模型
| $\begin{array}{c} \;\;\;\min :\;\;\;C\displaystyle\sum\limits_{k = 1}^N {{\xi _k}} + \displaystyle\sum\limits_{i = 1}^N {(\alpha _k^ + + \alpha _k^ - )} + \displaystyle\sum\nolimits_{k = 1}^N {{\lambda _k}} + b \\ \left\{ \begin{array}{l} \displaystyle\sum\limits_{k = 1}^m {(\alpha _k^ + - \alpha _k^ - )\exp \left\{ {\dfrac{{ - {{\left\| {{{x}} - {{{x}}_k}} \right\|}^2}}}{{2{\sigma ^2}}}} \right\}} + b - {y_k} \leqslant \varepsilon + {\xi _k}, \\ {y_k} - \displaystyle\sum\limits_{k = 1}^m {(\alpha _k^ + - \alpha _k^ - )\exp \left\{ {\dfrac{{ - {{\left\| {{{x}} - {{{x}}_k}} \right\|}^2}}}{{2{\sigma ^2}}}} \right\} - } b \leqslant \varepsilon + {\xi _k}, \\ {y_k} - \displaystyle\sum\limits_{i = 1}^N {(\alpha _k^ + - \alpha _k^ - )\exp \left( {\dfrac{{ - {{\left\| {{{{x}}_i} - {{{x}}_k}} \right\|}^2}}}{{2{\sigma ^2}}}} \right)} - b \leqslant {\lambda _k}, \\ \displaystyle\sum\limits_{i = 1}^N {(\alpha _k^ + - \alpha _k^ - )\exp \left( {\dfrac{{ - {{\left\| {{{{x}}_i} - {{{x}}_k}} \right\|}^2}}}{{2{\sigma ^2}}}} \right)} + b - {y_k} \leqslant 0, \\ \;\;\;\;\;\;{\xi _k} \geqslant 0,\;\;{\lambda _k} \geqslant 0,\;\;k = 1,2, \cdots ,N \\ \end{array} \right. \\ \end{array} $ | (17) |
式中:
从优化问题(17)可知,为典型的线性规划问题,可用向量及矩阵形式表述如下:
| $\begin{array}{c} \min \;\;\;\;\;\;{{{c}}^{\rm{T}}}\left( \begin{array}{l} {{\alpha }}_{}^ + \\ {{\alpha }}_{}^ - \\ \;{{\xi }} \\ \;{{{\lambda }}_{}} \\ \;{b_{}} \\ \end{array} \right) \\ {\rm{s}}.{\rm{t}}.\;\;\;\;\;\left\{ \begin{array}{l} \left( \begin{array}{l} \;{{K}}\;\;\; - {{K}}\;\;\; - {{I}}\;\;\;{{Z}}\;\;\;{{E}} \\ - {{K}}\;\;\;\;{{K}}\;\;\;\; - {{I}}\;\;\;{{Z}}\;\;\;{{E}} \\ - {{K}}\;\;\;\;{{K}}\;\;\;\;\;\;{{Z}}\;\; - {{I}}\;\;{{E}} \\ \;{{K}}\;\;\; - {{K}}\;\;\;\;\;{{Z}}\;\;\;{{Z}}\;\;\;{{E}} \\ \end{array} \right) \cdot \left( \begin{array}{l} {{\alpha }}_{}^ + \\ {{\alpha }}_{}^ - \\ \;{{\xi }} \\ \;{{{\lambda }}_{}} \\ \;{b_{}} \\ \end{array} \right) \leqslant \left( \begin{array}{l} {{y}} + \varepsilon \\ \varepsilon - {{y}} \\ \; - {{y}} \\ \;\;\;\;{{y}} \\ \end{array} \right) \\ {{\alpha }}_{}^ + ,\;{{\alpha }}_{}^ - \; \geqslant 0,\;{{\xi }} \geqslant 0,\;\;0 \leqslant {\lambda _k} \leqslant 1 \\ \end{array} \right. \\ \end{array} $ | (18) |
其中,
| $f({{x}}) = \sum\limits_{k = 1}^N {(\alpha _k^ + - \alpha _k^ - )\exp \left( {\frac{{ - {{\left\| {{{x}} - {{{x}}_k}} \right\|}^2}}}{{2{\sigma ^2}}}} \right)} + b$ | (19) |
从应用提出方法来建立
将通过如下实验分析,论证所提出方法的最优性与稀疏性;同时为了更直观地去评判提出的方法,将考虑如下两个性能指标,即均方根误差(root man square error,RMSE)和支持向量占整个样本数据的百分比
| ${\rm{RMSE}} = \frac{1}{N}\sqrt {\sum\limits_{k = 1}^N {{{\left( {y_k - {\hat y}_k} \right)}^2}} } \;$ |
式中:
| ${\rm{SVs}}\% = \frac{{{N_k}}}{N} \times 100\% $ |
显然,在保证下界模型建模精度的同时,指标
接下来将对提出的方法从下边界回归模型的辨识精度以及稀疏特性展开实验分析。当被建模的非线性系统由噪声引起的不确定性输出时,论证带稀疏特性的最优下边界回归模型辨识。
先考虑如下的非线性动态系统:
| $\begin{array}{c} y(t + 1) = \dfrac{{y(t)y(t - 1)[y(t) + 2.5]}}{{1 + {y^2}(t) + {y^2}(t - 1)}} + u(t) + {\rm{noise}} \\ y(0) = y(1) = 0,\;\;\;u(t) = \sin (2\pi t/50) \end{array} $ | (20) |
其中,
LBRM的最优性,除了应用提出方法在辨识精度与稀疏特性之间取其平衡得以体现之外,超参数集的选取对LBRM的稀疏特性也起着至关重要的作用。在实验分析中,超参数集的4种取值主要是基于SVR方法的经验来获取[23],其中不敏感域
|
Download:
|
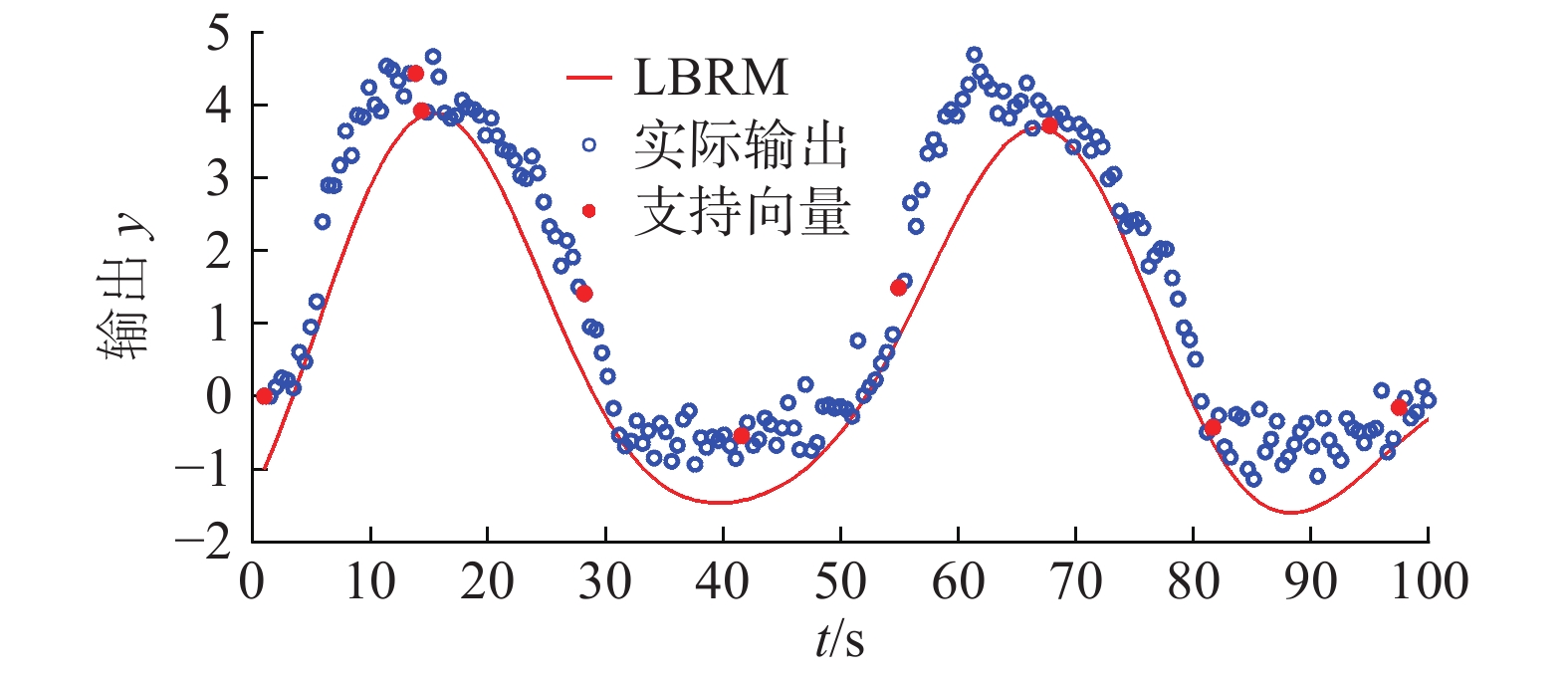
| 图 1 提出方法所建立的最优下界回归模型(核宽度为5.0) Fig. 1 Optimal LBRM constructed by our approach, where σ=5.0 | |
可知,应用提出方法所建立的最优LBRM仅仅需要9个支持向量,即从这201个数据中,建立LBRM只用到了其中的9个数据,表明稀疏特性较好,对应的指标

|
Download:
|
| 图 2 提出方法所对应的逼近误差 Fig. 2 Approximation error of the proposed method | |

|
Download:
|
| 图 3 提出方法所建立的最优下界回归模型(核宽度为0.1) Fig. 3 Optimal LBRM constructed by our approach, where σ=0.1 | |

|
Download:
|
| 图 4 过拟合所对应的逼近误差 Fig. 4 Approximation error of the proposed method when the over-fitting appeared. | |
| 表 1 当超参数
|
接下来,考虑由模型结构参数的变化所引起的,不确定性输出的LBRM辨识。描述的不确定非线性系统为
| ${f_{{\rm{norm}}}}({{x}}) = \cos {{x}}\sin {{x}}$ |
| $\Delta f({{x}}) = \tau \cos (8{{x}})$ |
| $g({{x}}) = {f_{{\rm{norm}}}}({{x}}) + \Delta f({{x}})$ | (21) |
式中:
|
Download:
|
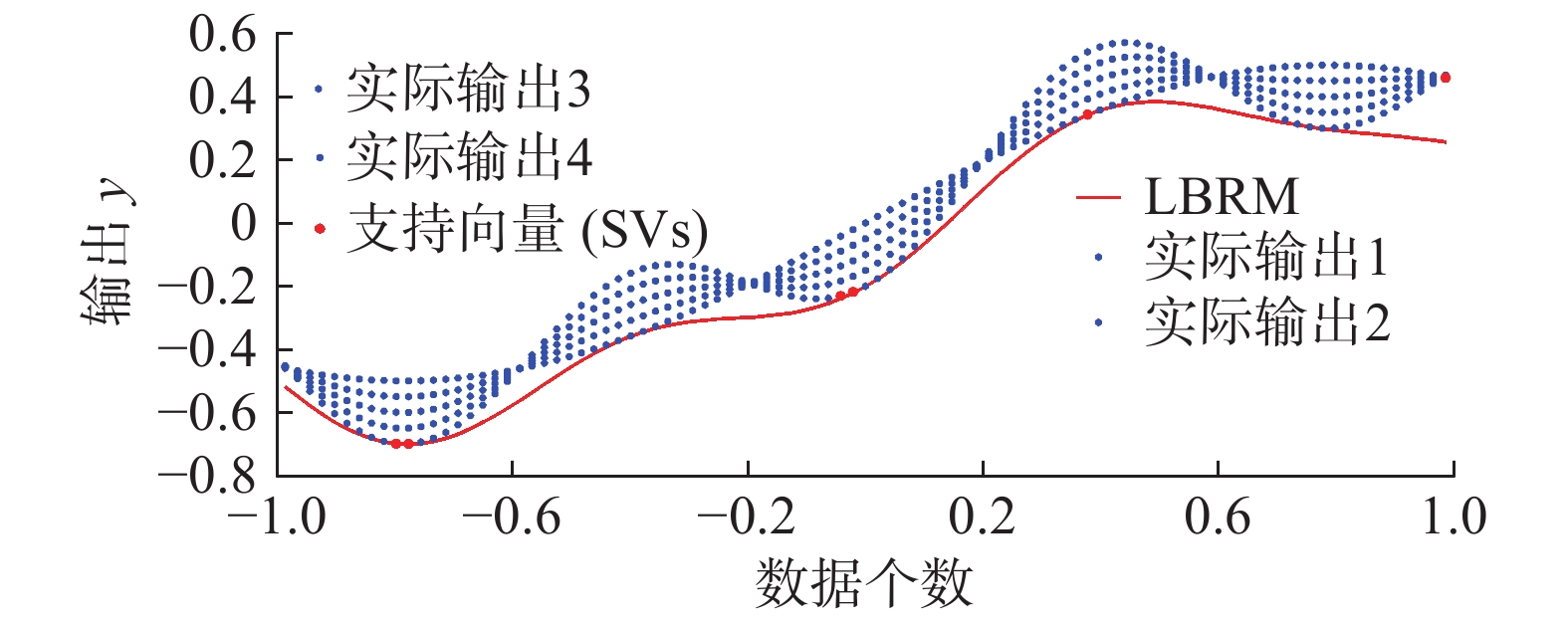
| 图 5 提出方法所建立的最优下界回归模型(核宽度为10.5) Fig. 5 Optimal LBRM constructed by our approach, where σ=10.5 | |
当超参数集
|
Download:
|
|
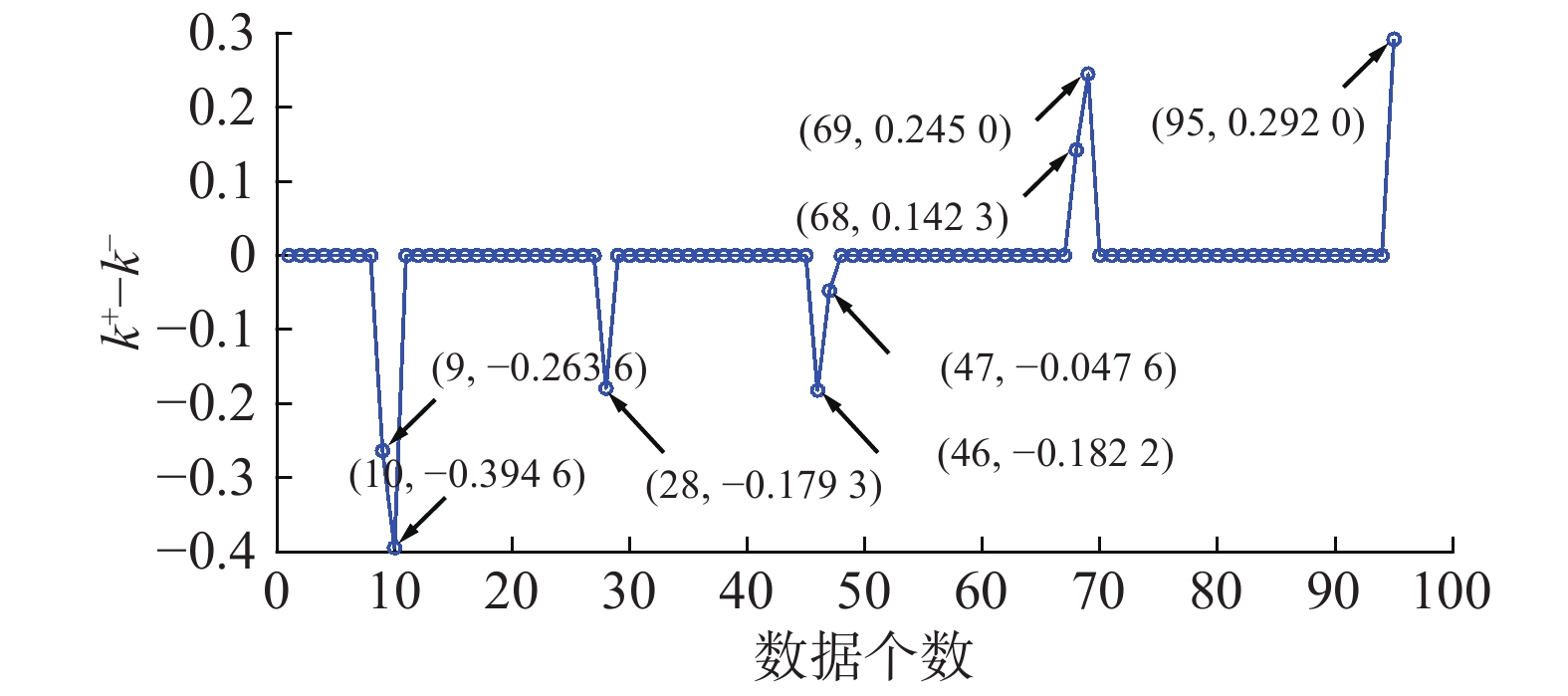
图 6 第k个支持向量所对应的
|
|
| 表 2 第k个支持向量(SV)对应的
|
基于式(19)可列出LBRM的数学模型为
| $\begin{array}{c} f({{x}}) = - 0.26 \cdot \exp \left( {\dfrac{{ - {{\left\| {{{x}} + 0.691\;69} \right\|}^2}}}{{2 \times {{10.5}^2}}}} \right) \; - \\0.40 \cdot \exp \left( {\dfrac{{ - {{\left\| {{{x}} + 0.70} \right\|}^2}}}{{2 \times {{10.5}^2}}}} \right) - 0.18 \cdot \exp \left( {\dfrac{{ - {{\left\| {{{x}} + 0.37} \right\|}^2}}}{{2 \times {{10.5}^2}}}} \right) \; -\\ 0.18 \cdot \exp \left( {\dfrac{{ - {{\left\| {{{x}} + 0.23} \right\|}^2}}}{{2 \times {{10.5}^2}}}} \right) - 0.05 \cdot \exp \left( {\dfrac{{ - {{\left\| {{{x}} + 0.22} \right\|}^2}}}{{2 \times {{10.5}^2}}}} \right) \; +\\ 0.14 \cdot \exp \left( {\dfrac{{ - {{\left\| {{{x}} + 0.37} \right\|}^2}}}{{2 \times {{10.5}^2}}}} \right) + 0.25 \cdot \exp \left( {\dfrac{{ - {{\left\| {{{x}} + 0.39} \right\|}^2}}}{{2 \times {{10.5}^2}}}} \right) \; + \\0.29 \cdot \exp \left( {\dfrac{{ - {{\left\| {{{x}} + 0.46} \right\|}^2}}}{{2 \times {{10.5}^2}}}} \right) \end{array} $ |
当超参数集

|
Download:
|
| 图 7 提出方法所建立的最优下界回归模型(核宽度为4.5) Fig. 7 Optimal LBRM constructed by our approach, where σ=4.5 | |
| 表 3 当超参数
|
基于数据的传统辨识方法主要从模型辨识精度进行研究,是一种确定性建模方法,对应点输出,同时易产生较复杂的模型结构,致使模型的泛化性能变差。从模型结构参数以及测量数据的不确定性出发,本文研究了由不确定性引起的下边界回归模型辨识方法,具有如下显著特点:1)建立了不确定性的边界输出,提高建模的鲁棒性;2)边界模型结构可通过引入的结构风险最小化原理进行调整,提高其泛化性能;3)提出方法的最优性体现在模型结构与辨识精度之间的平衡,即在保证模型稀疏特性的情况下,尽可能提高模型辨识精度,该方法可以应用到信息压缩、故障检测等。
| [1] |
HAN Honggui, GUO Yanan, QIAO Junfei. Nonlinear system modeling using a self-organizing recurrent radial basis function neural network[J]. Applied soft computing, 2018, 71: 1105-1116. DOI:10.1016/j.asoc.2017.10.030 ( 0) 0)
|
| [2] |
FRAVOLINI M L, NAPOLITANO M R, DEL CORE G, et al. Experimental interval models for the robust fault detection of aircraft air data sensors[J]. Control engineering practice, 2018, 78: 196-212. DOI:10.1016/j.conengprac.2018.07.002 ( 0) 0)
|
| [3] |
FANG Shengen, ZHANG Qiuhu, REN Weixin. An interval model updating strategy using interval response surface models[J]. Mechanical systems and signal processing, 2015, 60−61: 909-927. ( 0) 0)
|
| [4] |
LEUNG F H F, LAM H K, LING S H, et al. Tuning of the structure and parameters of a neural network using an improved genetic algorithm[J]. IEEE transactions on neural networks, 2003, 14(1): 79-88. DOI:10.1109/TNN.2002.804317 ( 0) 0)
|
| [5] |
赵文清, 严海, 王晓辉. BP神经网络和支持向量机相结合的电容器介损角辨识[J]. 智能系统学报, 2019, 14(1): 134-140. ZHAO Wenqing, YAN Hai, WANG Xiaohui. Capacitor dielectric loss angle identification based on a BP neural network and SVM[J]. CAAI transactions on intelligent systems, 2019, 14(1): 134-140. (  0) 0)
|
| [6] |
刘道华, 张礼涛, 曾召霞, 等. 基于正交最小二乘法的径向基神经网络模型[J]. 信阳师范学院学报(自然科学版), 2013, 26(3): 428-431. LIU Daohua, ZHANG Litao, ZENG Zhaoxia, et al. Radial basis function neural network model based on orthogonal least squares[J]. Journal of Xinyang Normal University (natural science edition), 2013, 26(3): 428-431. DOI:10.3969/j.issn.1003-0972.2013.03.030 (  0) 0)
|
| [7] |
刘道华, 张飞, 张言言. 一种改进的RBF神经网络对县级政府编制预测[J]. 信阳师范学院学报(自然科学版), 2016, 29(2): 265-269. LIU Daohua, ZHANG Fei, ZHANG Yanyan. A prediction for the preparation of county government based on improved RBF neural networks[J]. Journal of Xinyang Normal University (natural science edition), 2016, 29(2): 265-269. DOI:10.3969/j.issn.1003-0972.2016.02.027 (  0) 0)
|
| [8] |
HAN Honggui, GE Luming, QIAO Junfei. An adaptive second order fuzzy neural network for nonlinear system modeling[J]. Neurocomputing, 2016, 2014: 837-847. ( 0) 0)
|
| [9] |
LI Fanjun, QIAO Junfei, HAN Honggui, et al. A self-organizing cascade neural network with random weights for nonlinear system modeling[J]. Applied soft computing, 2016, 42: 184-193. DOI:10.1016/j.asoc.2016.01.028 ( 0) 0)
|
| [10] |
HAN Honggui, QIAO Junfei. Hierarchical neural network modeling approach to predict sludge volume index of wastewater treatment process[J]. IEEE transactions on control systems technology, 2013, 21(6): 2423-2431. DOI:10.1109/TCST.2012.2228861 ( 0) 0)
|
| [11] |
VAPNIK V N. An overview of statistical learning theory[J]. IEEE transactions on neural networks, 1999, 10(5): 988-999. DOI:10.1109/72.788640 ( 0) 0)
|
| [12] |
唐波, 彭友仙, 陈彬, 等. 基于BP神经网络的交流输电线路可听噪声预测模型[J]. 信阳师范学院学报(自然科学版), 2015, 28(1): 136-140. TANG Bo, PENG Youxian, CHEN Bin, et al. Audible noise prediction model of ac power lines based on BP neural network[J]. Journal of Xinyang Normal University (natural science edition), 2015, 28(1): 136-140. DOI:10.3969/j.issn.1003-0972.2015.01.033 (  0) 0)
|
| [13] |
HAO Peiyi. Interval regression analysis using support vector networks[J]. Fuzzy sets and systems, 2009, 160(17): 2466-2485. DOI:10.1016/j.fss.2008.10.012 ( 0) 0)
|
| [14] |
HAO Peiyi. Possibilistic regression analysis by support vector machine[C]//Proceedings of 2011 IEEE International Conference on Fuzzy Systems. Taipei, China, 2011: 889−894.
( 0) 0)
|
| [15] |
石磊, 侯丽萍. 基于改进PSO算法参数优化的模糊支持向量分类机[J]. 信阳师范学院学报(自然科学版), 2013, 26(2): 288-291. SHI Lei, HOU Liping. Parameter optimization of fuzzy support vector classifiers based on the improved PSO[J]. Journal of Xinyang Normal University (natural science edition), 2013, 26(2): 288-291. DOI:10.3969/j.issn.1003-0972.2013.02.031 (  0) 0)
|
| [16] |
SOUZA L C, SOUZA R M C R, AMARAL G J A, et al. A parametrized approach for linear regression of interval data[J]. Knowledge-based systems, 2017, 131: 149-159. DOI:10.1016/j.knosys.2017.06.012 ( 0) 0)
|
| [17] |
DE A LIMA NETO E, DE A T DE CARVALHO F. An exponential-type kernel robust regression model for interval-valued variables[J]. Information sciences, 2018, 454−455: 419-442. ( 0) 0)
|
| [18] |
BASAK D, PAL S, PATRANABIS D C. Support vector regression[J]. Neural information processing-letters and reviews, 2007, 11(10): 203-224. ( 0) 0)
|
| [19] |
SMOLA A J, SCHÖLKOPF B. A tutorial on support vector regression[J]. Statistics and computing, 2004, 14(3): 199-222. DOI:10.1023/B:STCO.0000035301.49549.88 ( 0) 0)
|
| [20] |
SOARES Y M G, FAGUNDES R A A. Interval quantile regression models based on swarm intelligence[J]. Applied soft computing, 2018, 72: 474-485. DOI:10.1016/j.asoc.2018.04.061 ( 0) 0)
|
| [21] |
LU Zhao, SUN Jing, BUTTS K. Linear programming SVM-ARMA2K with application in engine system identification[J]. IEEE transactions on automation science and engineering, 2011, 8(4): 846-854. DOI:10.1109/TASE.2011.2140105 ( 0) 0)
|
| [22] |
RIVAS-PEREA P, COTA-RUIZ J. An algorithm for training a large scale support vector machine for regression based on linear programming and decomposition methods[J]. Pattern recognition letters, 2013, 34(4): 439-451. DOI:10.1016/j.patrec.2012.10.026 ( 0) 0)
|
| [23] |
HSU C W, CHANG C C, LIN C J. A practical guide to support vector classification. Technical report. Department of Computer Science, National Taiwan University (2003)[EB/OL](2010-4-15). http://www.csie.ntu.edu.tw/~cjlin/papers/guide/guide.pdf.
( 0) 0)
|
 2020, Vol. 15
2020, Vol. 15


