近年来，视觉里程计(visual odometry, VO)^[1]作为视觉SLAM的前端，利用单个或多个视觉传感器，获取图像的信息进而估计出相机运动，给后端提供良好的初始值。视觉传感器因其获取信息丰富、成本低、易携带等诸多优点，被广泛用于机器人、自动驾驶^[2]等领域。随着RGB-D深度相机的产生，如微软的kinect、Pmdtec的Camcube等，利用RGB-D的视觉里程计方法得到越来越广泛的研究。

视觉里程计的实现方法一般按是否需要提取特征分为两种：1) 特征点法的前端即基于特征的视觉里程计(FVO)；2) 不提特征的直接法前端即稠密视觉里程计(DVO)。DVO一般用图像帧的所有像素信息去估计相机位姿，用到了图像一致性假设，最早由Steinbruecker等^[3]提出,将问题转化为能量最小化处理，但是由于其数据及计算量巨大，无法达到实时目的。相对于直接法前端，基于特征点法的前端一直以来被认为是视觉里程计的主流方法，它具备运行稳定、计算量较小、对光照及动态物体相对不敏感等优点，是目前较为成熟的视觉里程计方案。

FVO通过寻找图像帧的特征点，通过匹配特征点来估计相机位姿，特征点拥有稳定的局部图像特征，如著名的尺度不变特征变换(scale-invariant feature transform，SIFT)^[4]、加速鲁棒特征(speed-up robust features，SURF)^[5]、ORB^[6]等，根据匹配的特征采用迭代最近点(ICP)算法^[7]进行位姿估计，为了减少噪声及误匹配带来的影响，往往采用由Fischler和Bolles^[8]提出的随机误差一致性(RANSAC)算法来进行优化，剔除误差匹配。SIFT充分考虑了图像在变换过程中的尺度旋转等变换，但伴随的极大计算量是里程计无法接受的，至今普通的CPU还无法实时计算SIFT特征，而ORB特征通过改进FAST检测子^[9]，并使用速度极快的二进制描述子BRIEF^[10]使得实时SLAM变成了可能，但ORB也存在尺度光照不变性缺失的问题，文献[11]提出了改进FAST特征，将图像结合高斯金字塔模型实现了FAST角点的尺度不变性。文献[12-13]提出通过缩小抽样点总量来保证匹配点选取质量，有效地减少迭代次数。

然而，kinect相机所捕获的深度图像由于遮挡、吸收、散斑、反射等原因导致深度区域缺失，在实际测试中发现，缺失特征点数在最差情况下将近占总特征点数的三分之一，这就使得单纯使用ICP算法产生很大的误差。

针对以上，本文提出一种基于kinect相机的改进RGB-D视觉里程计方法，由改进ORB算法进行RGB-D图像特征匹配，对kinect所得深度图进行处理，先用RANSAC筛选出可靠内点，得到位姿初始估计，接着对深度缺失的3D-2D特征点对进行PnP优化，对其他3D-3D特征点对进行ICP优化，并将两者转化为一个BA(bundle adjustment)问题建立优化模型，使用g2o求解器同时进行特征点及相机位姿优化，最后实验结果证明了该方法的有效性。

1 改进的RGB-D视觉里程计

本文提出的基于kinect相机的改进RGB-D视觉里程计框架如图1所示，对相机捕获的彩色图用改进的ORB算法进行检测与匹配，并对所得深度图进行分析，当检测深度不为0时，利用RANSAC算法剔除3D-3D误差点得到初始位姿估计，采用ICP算法进行优化；当检测深度为0时，利用RANSAC算法剔除3D-2D误差点得到初始位姿估计，采用PnP算法进行优化。最后，将两者误差项混合转化为一个BA问题建立优化模型，使用g2o求解器进行特征点及位姿的优化。

1.1 改进的ORB算法

ORB算法是由Rublee等提出的一种改进FAST角点和BRIEF描述子的描述算法，其在特征提取上具有良好的性能。它改进了FAST检测子不具有方向性的问题，采用二进制描述子BRIEF使得算法具有极快的运算速度，大大加速了图像的特征提取环节，其实时性能远远高于SURF与SIFT，并且在质量与性能之间也有较好的折中，本文在其尺度与光照上的缺陷做了一些改进，使得ORB算法在尺度及光照变化上具有一定的健壮性。

在旋转不变性上，ORB特征采用灰度质心法(intensity centroid)实现，具体步骤如下：

1) 在图像块中定义图像矩为

${m_{pq}} =\displaystyle \sum\limits_{x,y \in B} {{x^p}{y^q}I(x,y)} ,\;\quad p,q = \left\{ {0,1} \right\}$

(1)

式中： ${m_{pq}}$ 为区域的阶矩表示； $I(x,y)$ 为角点的灰度值。

2) 得到图像的质心C：

$C = \Bigg(\dfrac{{{m_{10}}}}{{{m_{00}}}},\dfrac{{{m_{01}}}}{{{m_{00}}}}\Bigg)$

(2)

3) 连接几何中心与质心，得到一个方向向量，定义特征点的方向为

$\theta = \arctan ({m_{01}}/{m_{10}})$

(3)

以上方法使得FAST角点具有了旋转描述，大大提升了在不同图像之间表达的健壮性，这种改进的FAST角点称为Oriented FAST。

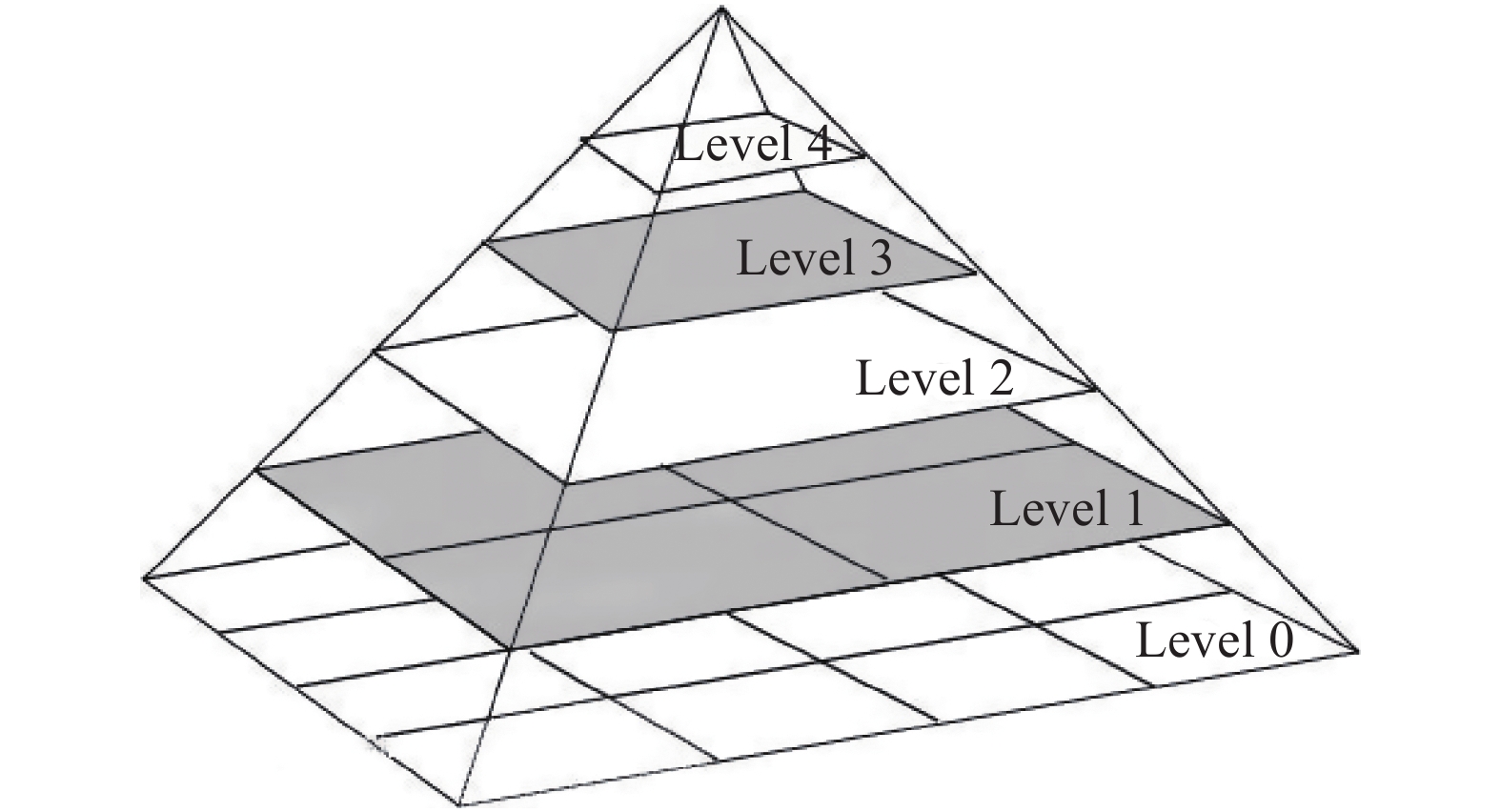
尺度问题上，构建高斯图金字塔，如图2，对图像进行不同层次的采样，以获得不同分辨率图像，并在金字塔的每一层上检测角点进而实现ORB对尺度的健壮性。

在光照问题上，FAST关键点所选用的灰度阈值T是固定的，这就使得当周边环境对比度变化时特征点的提取会受到很大的影响，采用文献[14-15]的方法，选用一种根据图像对比度的自适应阈值方法，首先计算图像的对比度：

$C =\displaystyle \sum\limits_\delta {\delta {{(i,j)}^2}{P_\delta }(i,j)} $

(4)

式中： $\delta (i,j) = \left| {i - j} \right|$ ，即相邻像素灰度差； ${P_\delta }(i,j)$ 为相邻像素间的灰度差为 $\delta $ 的像素分布概率。

由得到的对比度 $C$ 设计自适应阈值 ${T^*}$ :

${T^*} = \alpha C$

(5)

1.2 RANSAC算法完成初始化

PnP和ICP的迭代优化算法都依赖良好的初值选取，初值选取不当会导致迭代陷入局部最优或无法收敛，不能达到全局最优效果。RANSAC是一种随机参数估计算法，通过反复选取数据中的一组子集来建立参数化模型，并通过设置阈值来进行内点的筛选，剔除误差数据，从而获得最佳模型参数。本文通过RANSAC算法分别对3D-2D点对和3D-3D点对进行粗匹配与初始位姿估计，采用直接线性变换(DLT)建立和求解参数模型。

1) 3D-2D模型

现考虑空间点 $P$ ，它的齐次坐标为

$ {{P}} = {{\rm{[}}X\; Y\;Z{\rm{\;1]}}^{\rm{T}}}$

由于在相邻帧中由于匹配点深度信息未知，但由于相机的内参 ${{K}}$ 一般都由厂家标定，为已知信息，故设其归一化平面齐次坐标为 ${{p}} = {[u\;v\;1]^{\rm{T}}}$ ，此时相机的位姿 ${{R}}$ 、 ${{t}}$ 未知，定义增广矩阵 $\left[ {{{R}}\left\| {{t}} \right.} \right]$ 为3×4矩阵，包含了旋转与平移信息，形式为

$s\left[ {\begin{array}{*{20}{c}} u \\ v \\ 1 \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{t_1}}&{{t_2}}&{{t_3}}&{{t_4}} \\ {{t_5}}&{{t_6}}&{{t_7}}&{{t_8}} \\ {{t_9}}&{{t_{10}}}&{{t_{11}}}&{{t_{12}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} X \\ Y \\ Z \\ 1 \end{array}} \right]$

(6)

假设有个3D-2D特征点，则可以列出如下的线性方程组：

$\left[ {\begin{array}{*{20}{c}} {{{P}}_{{1}}^{\bf{T}}}&0&{ - {u_{{1}}}{{P}}_{{1}}^{\bf{T}}} \\ 0&{{{P}}_{{1}}^{\bf{T}}}&{ - {v_{{1}}}{{P}}_{{1}}^{\bf{T}}} \\ \vdots & \vdots & \vdots \\ {{{P}}_{{N}}^{\bf{T}}}&0&{ - {u_N}{{P}}_{{N}}^{\bf{T}}} \\ 0&{{{P}}_{{N}}^{\bf{T}}}&{ - {v_N}{{P}}_{{N}}^{\bf{T}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{{T}}_{{1}}}} \\ {{{T}}{}_{{2}}} \\ {{{{T}}_{{3}}}} \end{array}} \right] = 0$

(7)

由于 ${{t}}$ 一共有12维，因此只需要6组匹配点即可实现矩阵的线性求解，得到变换矩阵后测试其他匹配对，通过设定阈值选取模型内点并剔除误差点，当内点足够多时则完成特征点的优化并得到3D-2D的初始位姿估计 ${{{\xi }}_{{P}}}$ ( ${{{\xi }}_{{P}}}$ 为李代数表达)。

2) 3D-3D模型

相比于3D-2D点对，3D-3D点对的参数模型建立则简单了许多，现有空间点 ${{{Q}}_{{1}}} = {[{X_1}\;{Y_1}\;{Z_1}]^{\rm{T}}}$ ，与之匹配的3D点 ${{{Q}}_{{2}}} = {[{X_2}\;{Y_2}\;Z_2^{}]^{\rm{T}}}$ ，想要找一个欧式变换 ${{R,t}}$ ，使得：

${{{Q}}_{{1}}} = {{R}}{{{Q}}_{{2}}} + {{t}}$

(8)

类似于3D-2D模型， ${{R,t}}$ 共有12维，而3D点对存在3个约束，故只需4对匹配点即可完成线性求解，得到3D-3D位姿初始估计 ${{{\xi }}_{{Q}}}$ ，求解方法类似3D-2D模型。

1.3 BA模型与位姿优化

PnP和ICP算法都是指通过多对3D与2D或3D与3D匹配点，在已知或者未知相机内参的情况下，利用最小化误差函数来求解相机外参的算法。在得到由RANSAC进行优化后的点对和位姿初始估计后，本文提出一种基于PnP和ICP的融合BA优化的算法。

在PnP问题中,考虑 $N$ 个三维空间点 ${{P}}$ 及其对应的归一化平面点，希望得到相机的位姿 ${{R{\text{、}}t}}$ ，在进行PnP问题时本文采用李代数的方法，因为使用李代数可以构建无约束的优化问题，从而更方便地通过高斯牛顿法、列文伯格—马夸尔特方法等优化算法进行求解。假设空间点坐标为 ${{{P}}_{{i}}} = {{\rm{[}}{X_i}\;{Y_i}\;Z_i^{}{\rm{]}}^{\rm{T}}}$ ，其对应像素坐标为 ${{{p}}_{{i}}} = {[{u_i}\;{v_i}]^{\rm{T}}}$ ，像素位置与空间点的李代数关系如下：

${s_i}{{{p}}_{{i}}} = {{K}}\exp ({{{\xi }}^ {\wedge} }){{{P}}_{{i}}}$

(9)

由于相机位姿及观测点的噪声，式(9)存在一个误差，将误差求和构建最小二乘问题，然后优化相机位姿：

${{{e}}_P} = \mathop {\min }\limits_{{\xi }} = \displaystyle {\sum\limits_{i = 1}^N {\left\| {{{{p}}_{{i}}} - \frac{1}{{{s_i}}}{{K}}\exp ({{{\xi }}^ {\wedge} }){{{P}}_i}} \right\|} ^2}$

(10)

式中 ${{{e}}_P}$ 为像素坐标误差，是二维向量。

在ICP问题中，考虑一组数量为 $M$ 的筛选后的匹配点对 ${{Q}} = {[{X_i}\;{Y_i}\;{Z_i}]^{\rm{T}}}$ 和 ${{Q'}} = {[{X'_i}\;{Y'_i}\;{Z'_i}]^{\rm{T}}}$ ，它的李代数位姿表达式为

${{{Q}}_i} = \exp ({{{\xi }}^ {\wedge} }){{{Q'}}_i}$

(11)

类似式(10)，可以构建误差函数：

${{{e}}_Q} = \mathop {\min }\limits_{{\xi }} =\displaystyle \sum\limits_{i = 1}^M {{{\left\| {{{{Q}}_i} - \exp ({{{\xi }}^ {\wedge} }){{{{Q'}}}_i}} \right\|}^2}} $

(12)

式中 ${{{e}}_Q}$ 为空间坐标误差，是三维向量。

将式(10)与(12)融合为一个BA问题，构成五维代价函数：

${{e}} = \mathop {{\rm{min}}}\limits_{{\xi }} = \left( {\begin{array}{*{20}{c}} {\dfrac{{\rm{1}}}{N}{{{e}}_P}} \\ {\dfrac{1}{M}{{{e}}_Q}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {\dfrac{1}{N}\displaystyle \sum\limits_{i = 1}^N {{{\left\| {{{{p}}_i} - \dfrac{1}{{{s_i}}}{{K}}\exp ({{{\xi }}^ {\wedge} }){{{P}}_i}} \right\|}^2}} } \\ {\dfrac{1}{M}\displaystyle \sum\limits_{i = 1}^M {{{\left\| {{{{Q}}_i} - \exp ({{{\xi }}^ {\wedge} }){{{{Q'}}}_i}} \right\|}^2}} } \end{array}} \right)$

(13)

其中， ${{e}}$ 为五维向量，下面对式(13)进行优化求解。

在使用高斯牛顿法求解之前，需要知道每个误差项关于优化变量 ${{\xi }}$ 的一阶导数，即雅克比矩阵 ${{J}}$ 以及 ${{\xi }}$ 的初始位姿 ${{{\xi }}_0}$ 。 ${{{\xi }}_0}$ 的取值为

${{{\xi }}_0} = \dfrac{N}{{M + N}}{{{\xi }}_P} + \dfrac{M}{{M + N}}{{{\xi }}_Q}$

(14)

关于 ${{J}}$ 的形式是本文关键所在，在 ${{{e}}_P}$ 中，像素坐标误差为二维，位姿为六维， ${{{J}}_P}$ 将是2×6的矩阵；在 ${{{e}}_Q}$ 中，空间坐标误差为三维 ， ${{{J}}_Q}$ 将是3×6的矩阵，故误差 ${{e}}$ 的雅克比矩阵为5×6矩阵。

首先分析 ${{{J}}_P}$ 的形式，记变换到相机坐标系下的空间坐标为 ${{P'}} = {[X'\;Y'\;Z']^{\rm{T}}}$ ，它的相机投影模型为

$u = {f_x}\dfrac{{X'}}{{Z'}} + {c_x},\quad v = {f_y}\dfrac{{Y'}}{{Z'}} + {c_y}$

(15)

其中， ${f_x}{\text{、}}{f_y}{\text{、}}{c_x}{\text{、}}{c_y}$ 为相机内参，为相机出厂时标定。

在求导上本文使用李代数的左乘扰动模型^[16]，对 ${{{\xi }}^ {\wedge} }$ 左乘扰动量 $\delta {{\xi }}$ ，然后使用链式法则，列写如下：

$\dfrac{{\partial {{{e}}_P}}}{{\partial \delta {{\xi }}}} = \mathop {\lim }\limits_{\delta {{\xi }} \to 0} \dfrac{{{{{e}}_P}(\delta {{\xi }} \oplus {{\xi }})}}{{\delta {{\xi }}}} = \dfrac{{\partial {{{e}}_P}}}{{\partial {{P'}}}}\dfrac{{\partial {{P'}}}}{{\partial \delta {{\xi }}}}$

(16)

式中： $ \oplus $ 指李代数上的左乘扰动；右边两项，其中第1项是关于投影点的导数，由式(15)可得

$\dfrac{{\partial {{{e}}_P}}}{{\partial {{P'}}}} = - \left( {\begin{array}{*{20}{c}} {\dfrac{{{f_x}}}{{Z'}}}&0&{ - \dfrac{{{f_x}X'}}{{{{Z'}^2}}}} \\ 0&{\dfrac{{{f_y}}}{{Z'}}}&{ - \dfrac{{{f_y}Y'}}{{{{Z'}^2}}}} \end{array}} \right)$

(17)

第2项是误差关于位姿李代数的导数，由文献[12]可推导出：

$\dfrac{{\partial {{P'}}}}{{\partial \delta {{\xi }}}} = [{{I}}, - {{{P'}}^ {\wedge} }]$

(18)

将式(17)与(18)相乘即可得单个误差雅克比矩阵 ${{{J}}_P}$ ：

$\dfrac{{\partial {{{e}}_P}}}{{\partial \delta {{\xi }}}} = - \left( {\begin{array}{*{20}{c}} {\dfrac{{{f_x}}}{{Z'}}}\!\!\!&\!\!\!0&\!\!\!{ - \dfrac{{{f_x}X'}}{{{{Z'}^2}}}}\!\!\!&\!\!\!{ - \dfrac{{{f_x}X'Y'}}{{{{Z'}^2}}}}\!\!\!&\!\!\!{{f_x} + \dfrac{{{f_x}{{X'}^2}}}{{{{Z'}^2}}}}\!\!\!&\!\!\!{ - \dfrac{{{f_x}Y'}}{{{{Z'}^2}}}} \\ \!\!\!0&\!\!\!{\dfrac{{{f_y}}}{{Z'}}}\!\!\!&\!\!\!{ - \dfrac{{{f_y}Y'}}{{{{Z'}^2}}}}\!\!\!&\!\!\!{ - {f_y} - \dfrac{{{f_y}{{Y'}^2}}}{{{{Z'}^2}}}}\!\!\!&\!\!\!{\dfrac{{{f_y}X'Y'}}{{{{Z'}^2}}}}\!\!\!&\!\!\!{\dfrac{{{f_y}X'}}{{{{Z'}^2}}}} \end{array}} \right)$

${{{J}}_Q}$ 的推导与之相似，空间点 ${{Q'}} = {[X'\;Y'\;Z']^{\rm{T}}}$ 经位姿变换为 ${{Q''}} = {[X''\;Y''\;Z'']^{\rm{T}}}$ ，使用李代数扰动模型即可得

$\dfrac{{\partial {{{e}}_Q}}}{{\partial \delta {{\xi }}}} = - \left( {\begin{array}{*{20}{c}} 1&0&0&0&{ - Z''}&{Y''} \\ 0&1&0&{Z''}&0&{ - X''} \\ 0&0&1&{ - Y''}&{X''}&0 \end{array}} \right)$

综上，可得由 $N$ 个3D-2D点对与 $M$ 个3D-3D点对组成的BA代价函数 ${{e}}$ 的雅克比矩阵 ${{J}}$ 为

$ { J}=\left( {\begin{array}{*{20}{c}} \displaystyle {\sum\limits_{i = 1}^N {\dfrac{{{f_x}}}{{{{Z'}_i}}}} }&0&\displaystyle{ - \sum\limits_{i = 1}^N {\dfrac{{{f_x}{{X'}_i}}}{{Z_i^{'2}}}} }&\displaystyle{ - \sum\limits_{i = 1}^N {\dfrac{{{f_x}{{X'}_i}{{Y'}_i}}}{{Z_i^{'2}}}} }&{N{f_x} +\displaystyle \sum\limits_{i = 1}^N {\dfrac{{{f_x}X_i^{'2}}}{{Z_i^{'2}}}} }&\displaystyle{ - \sum\limits_{i = 1}^N {\dfrac{{{f_x}{{Y''}_i}}}{{Z_i^{'2}}}} } \\ 0&\displaystyle{\sum\limits_{i = 1}^N {\dfrac{{{f_Y}}}{{{{Z'}_i}}}} }& \displaystyle{ - \sum\limits_{i = 1}^N {\dfrac{{{f_y}{{Y'}_i}}}{{Z_i^{'2}}}} }&{ - N{f_y} -\displaystyle \sum\limits_{i = 1}^N {\dfrac{{{f_y}Y_i^{'2}}}{{Z_i^{'2}}}} }&\displaystyle{\sum\limits_{i = 1}^N {\dfrac{{{f_y}{{X'}_i}{{Y'}_i}}}{{Z_i^{'2}}}} }&\displaystyle{\sum\limits_{i = 1}^N {\dfrac{{{f_y}{{X'}_i}}}{{Z_i^{'2}}}} } \\ M&0&0&0&\displaystyle { - \sum\limits_{i = 1}^M {{{Z''}_i}} }&\displaystyle{\sum\limits_{i = 1}^M {{{Y''}_i}} } \\ 0&M&0&\displaystyle{\sum\limits_{i = 1}^M {{{Z''}_i}} }&0&\displaystyle{ - \sum\limits_{i = 1}^M {{{X''}_i}} } \\ 0&0&M&\displaystyle{ - \sum\limits_{i = 1}^M {{{Y''}_i}} }&\displaystyle{\sum\limits_{i = 1}^M {{{X''}_i}} }&0 \end{array}} \right) $

得到了初始位姿 ${{{\xi }}_0}$ 与雅克比矩阵 ${{J}}$ 后调用高斯牛顿法，算法流程如下：

1) 给定初始值 ${{{\xi }}_0}$ 。

2) 对于第k次迭代，求出当前的雅克比矩阵 ${{J}}$ 与误差 ${{e}}$ 。

3) 求解增量方程 ${{H}}\Delta {{{\xi }}_k} = {{g}}$ 。

4) 若 $\Delta {{{\xi }}_k}$ 足够小，则停止。否则，令 ${\xi _{k + 1}} = {\xi _k} + \Delta {\xi _k}$ ，返回2)。

2 实验与结果 2.1 实验环境

为了对本文算法的有效性进行验证，实验计算机的配置为：Intel i5双核1.8 GHz CPU，4 GB内存，500 GB硬盘，NVIDIA独立显卡，操作系统为64位的ubuntu14.04，算法基于C++、OpenCV3.0和g2o库进行编写。

2.2 改进ORB特征点对比

在基于稀疏特征点法的里程计中，特征点的数量是反映计算准确性的重要指标之一。与传统ORB相比，本文采用改进ORB算法在FAST特征点提取上具有更好的适应性。原FAST特征点识别方法与改进后的特征点识别方法如图3所示。

从图3可以看出，对于同一关键帧，当光照强度不是很强时，改进之后的算法明显适应性更强，相比原算法多检测出了约20%的特征点，增强了整个系统的鲁棒性。

2.3 RANSAC内点筛选

在基于稀疏特征点法的里程计中，特征点匹配精度决定了里程计的性能，图4为室外道路环境的两帧图像，图4(a)为未经RANSAC筛选的ORB特征点匹配，可以看到有许多特征点的误匹配，这会对优化算法造成极大的误差，图4(b)为经RANSAC筛选后的特征匹配，匹配精度得到很大提高。

2.4 直线运动实验

本实验是在Turtlebot移动机器人平台上进行的，设定直线运动速度0.3 m/s，运动距离为3 m。分别进行传统ICP算法、RANSAC+ICP算法和融合算法估计移动机器人运动轨迹，并使用g2o求解器进行位姿优化求解。g2o是一个在SLAM领域广为使用的优化库，可以将非线性优化与图论相结合，大大提高系统的实时性与精确性，运动轨迹如图5所示，结果表明，融合算法的平均误差为1.98%，相比于传统ICP的8.64%与改进后的RANSAC+ICP算法的5.28%有着更小的误差。

从表1可以看出，在匹配点对上，直接ICP将所有ORB特征点都进行迭代优化，RANSAC筛选后去除了近乎三分之一的误差点，本文算法在此基础上加上了被剔除的深度缺失的特征点；在迭代次数上可以看到相比直接ICP算法RANSAC筛选过的ICP与本文算法都有了迭代次数明显地减少；在收敛成功次数上本文算法存在显著优势，几乎达到了百分百成功率，大大提高了里程计的鲁棒性；在优化时间上本次实验取的为单一迭代优化的时间，并没有加上特征提取与匹配所花的时间，3种方法优化时间相对比较接近，整体里程计算法一般为30 ms左右；在3种方法的相对误差上可以看出，相比直接ICP与RANSAC+ICP，本文算法在估计相机误差精度上有着显著提高。

3 结束语

本文提出一种融合PnP与ICP的RGB-D视觉里程计方法，有效针对kinect深度相机深度区域丢失的缺点，利用改进ORB算法进行特征点提取与匹配，再利用RANSAC算法得到良好的相机位姿估计初始值，根据特征点深度值的大小进行PnP和ICP模型建立，并得到一个BA优化模型，利用g2o进行迭代求解，实验证明了该方法优秀的收敛成功率以及匹配相机位姿的精度，大大提高了视觉里程计的精确性与鲁棒性。