数字水印可根据水印嵌入方式的不同分为空间域水印和变换域水印。前者是将水印信息直接嵌入载体图像像素中，后者是对载体图像做适当变换后嵌入水印信息。由于后者具有更强的抗攻击能力且鲁棒性能较优，通常选择后者。快速响应二维码(quick response code，QR码)，是二维条码的一种，通过扫描可以迅速获得其所携带的信息，主要特点是自身容量大、纠错能力强^[1]。如果将QR码作为水印信息嵌入变换域中，则能够增加水印信息的嵌入量和加强水印算法的鲁棒性^[2]。

Zhang等^[3]提出对载体图像实施一级离散小波变换（discrete wavelet transform,DWT），选择其低频子图实施8×8分块，再进行离散余弦变换(discrete cosine transform, DCT)，并从4×4左上变换系数矩阵中提取组织新的矩阵实施奇异值分解(singular value decomposition,SVD)操作获得对角矩阵，最后在对角矩阵中嵌入水印。由实验数据可知，鲁棒性较强，但实验选取的载体图像非彩色图像，水印图像非QR码，因此实用性不足且嵌入量较小。徐江峰等^[4]提出对载体图像进行DWT操作，并对其低高频子带进行4×4分块DCT操作，将混沌加密后的QR码水印嵌入其中，实验选取的载体图像非彩色图像，实用性不强，在高斯噪声攻击和JPEG压缩攻击上，归一化相关系数（normalized correlation, NC）值略低。因此，鉴于以上问题，本文提出一种适用于QR码的彩色图像数字水印算法，该方案通过对QR码实施Logistic映射和Arnold变换来完成双重加密，用以增强水印的安全性能；对彩色载体图像从RGB空间转换到YCbCr空间，使用DWT、DCT和SVD技术在其亮度分量图中嵌入QR码，用来提高水印的嵌入量、不可见性和鲁棒性。

1 QR码水印的处理 1.1 Logistic映射

Logistic映射的定义为

${x_{k + 1}} = u{x_k}\left( {1 - {x_k}} \right)$

式中： $0 \leqslant u \leqslant 4;\;{x_k} \in \left( {0,1} \right),\;k = 0,1,2, \cdots $ ； $u$ 为Logistic的参数， $u$ 的取值影响映射的效果，当 $3.569\;945\;6 \leqslant u \leqslant 4$ 时，Logistic映射处在混沌的状态^[5]； ${x_k}$ 为映射前的状态； ${x_{k + 1}}$ 为映射后的状态。初值 $x$ 的选择对图像的映射效果也有影响。本文对QR码进行加密是通过实施logistic映射来完成的，参数 $u$ 为4，初始值 $x$ 为0.2345。

1.2 Arnold变换

Arnold变换实现加密的手段是将图像的像素点进行置乱^[6]。二维Arnold置乱为

$\left[ \begin{array}{l} {x'} \\ {y'} \\ \end{array} \right] = \left[ \begin{array}{l} {\rm{1 1}} \\ {\rm{1 2}} \\ \end{array} \right]\left[ \begin{array}{l} x \\ y \\ \end{array} \right]\left( {{\rm{mod}}N} \right)$

式中： $x,y \in \left\{ {\left. {0,1, \cdots ,N - 1} \right\}} \right.$ ； $\left( {x,y} \right)$ 表示置乱前的具体像素坐标； $\left( {x',y'} \right)$ 表示置乱后的具体像素坐标；N为图像矩阵的阶数，代表着图像的像素；mod()是取模运算。

图像实施T次Arnold操作后回到初始状态的特性称为Arnold置乱的周期性，且周期T与图像的像素大小N×N有关系。本文中QR码像素为64×64，置乱周期为48，当QR码实施30次Arnold操作后达到一定置乱状态进而实现加密，由Arnold的周期性可知，再对其实施18次Arnold操作即可恢复到原QR码。

2 彩色载体图像的处理

彩色载体图像的处理需要DWT、DCT和SVD。它们的结合均衡了水印的不可见性和鲁棒性。

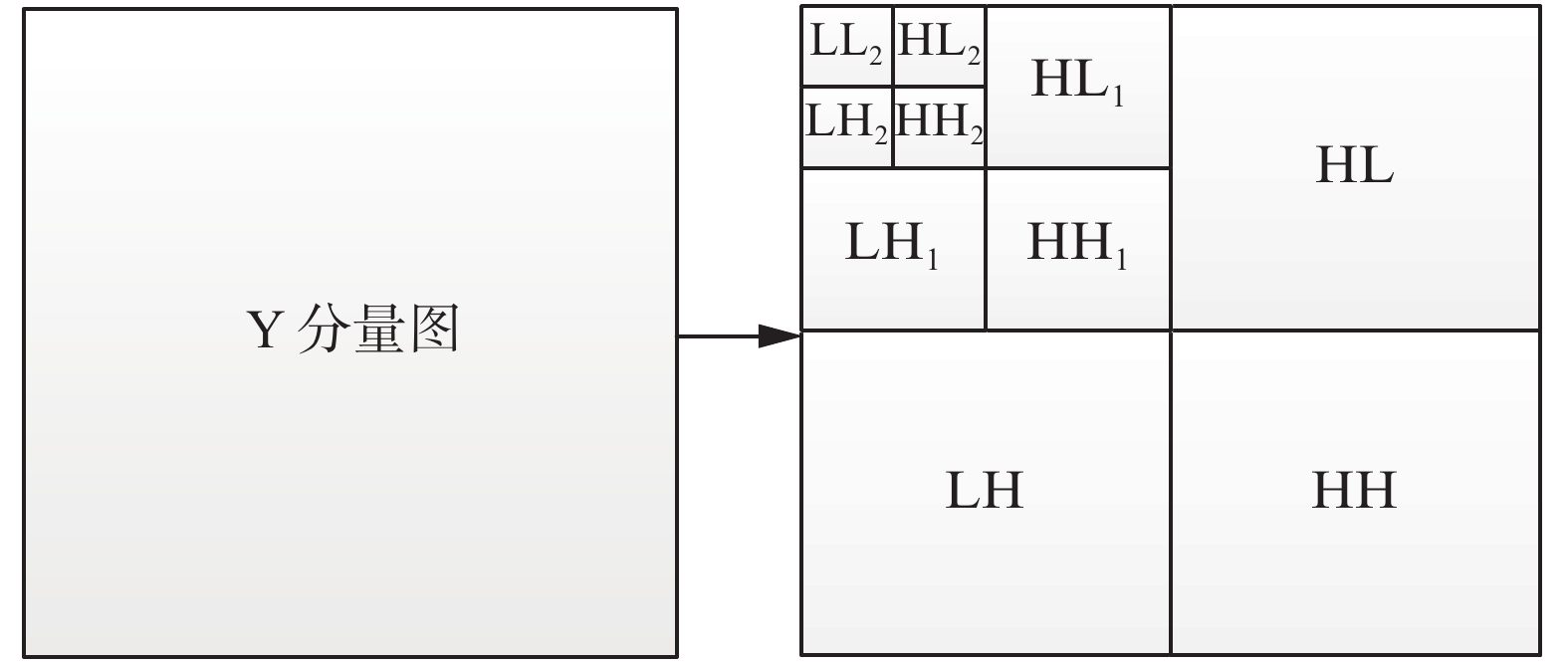
2.1 离散小波变换(DWT)

对原始彩色图像进行处理，即从RGB颜色空间到YCrCb颜色空间，提取YCrCb空间的Y分量，会得到一个灰度图像，对其进行小波变换，经过1级DWT后的灰度图像会分解为LL、LH、HL、HH 4个大小相等的子图，且在之后的小波变换中，低频子图采用如上完全相同的方式进行变化，生成更小的子图，小波变换分解图见图1^[7-8]。从图1中可看出，经过3级DWT后，生成了10个子图，其中，LL₂为低频子图，其余均为高频子图，低频子图代表了灰度图像的基本特征和大部分能量，高频子图体现了原灰度图像的细节部分，如边缘、纹理等^[9]。

由于低频分量代表灰度图像的基本特征，如果将水印嵌入低频子图LL₂中，不仅具有抵抗压缩攻击的能力，并且能够有效地提取水印，使得水印的鲁棒性较强^[10]。

2.2 离散余弦变换(DCT)

离散余弦变换又叫作DCT变换，经过该变换得到的DCT系数相关性较空间域降低，主要信号能量聚集在左上角几个低频变换系数上^[11]。DCT算法具有很强的抗干扰能力，图像遭受攻击后会有一定的失真，但是主要信息还存在，嵌入的水印信息依然可以提取出来。目前在水印算法中有2种DCT变换方式，其一是将像素大小为M×N的图像看作是一个二维矩阵，对此矩阵直接实施DCT变换，将水印嵌入其中；另一种是将大小为M×N的图像分割成X个小块，生成X个二维矩阵，对X个二维矩阵分别进行DCT变换，将水印嵌入其中。本文采用的DCT变换方式是第一种，像素大小为512×512的Y分量图进行3级DWT后，可以得到一个64×64的低频子图，对该图实施DCT变换，可以得到64×64的矩阵用于水印的嵌入。

2.3 奇异值分解(SVD)

奇异值分解是一种正交变换，可以将矩阵对角化。假设一幅图像A的大小为M×N，则可以看作是M×N的矩阵。那么A的奇异值分解定义为

${{A}} = {{US}}{{{V}}^{\bf{T}}}$

式中：U和V均为正交矩阵；S为对角矩阵，且非对角线上的元素均为0，对角线上的元素满足 ${S_1} \geqslant {S_2} \geqslant \cdots \geqslant {S_r} \geqslant {S_{r + 1}} = \cdots = {S_n} = 0$ (r是A的秩)^[12-13]。

本文选用奇异值分解主要有2个原因：1)由于图像的奇异值比较稳定，使其在遭受攻击时，奇异值变化不至于过大，有助于提高水印的攻击能力^[14-17]；2)图像的本质特征是由奇异值体现的，并非视觉特征^[18-20]。低频子图经过DCT变换后，会得到64×64的矩阵，对其实施奇异值分解，可以使得水印的不可见性和鲁棒性较强。

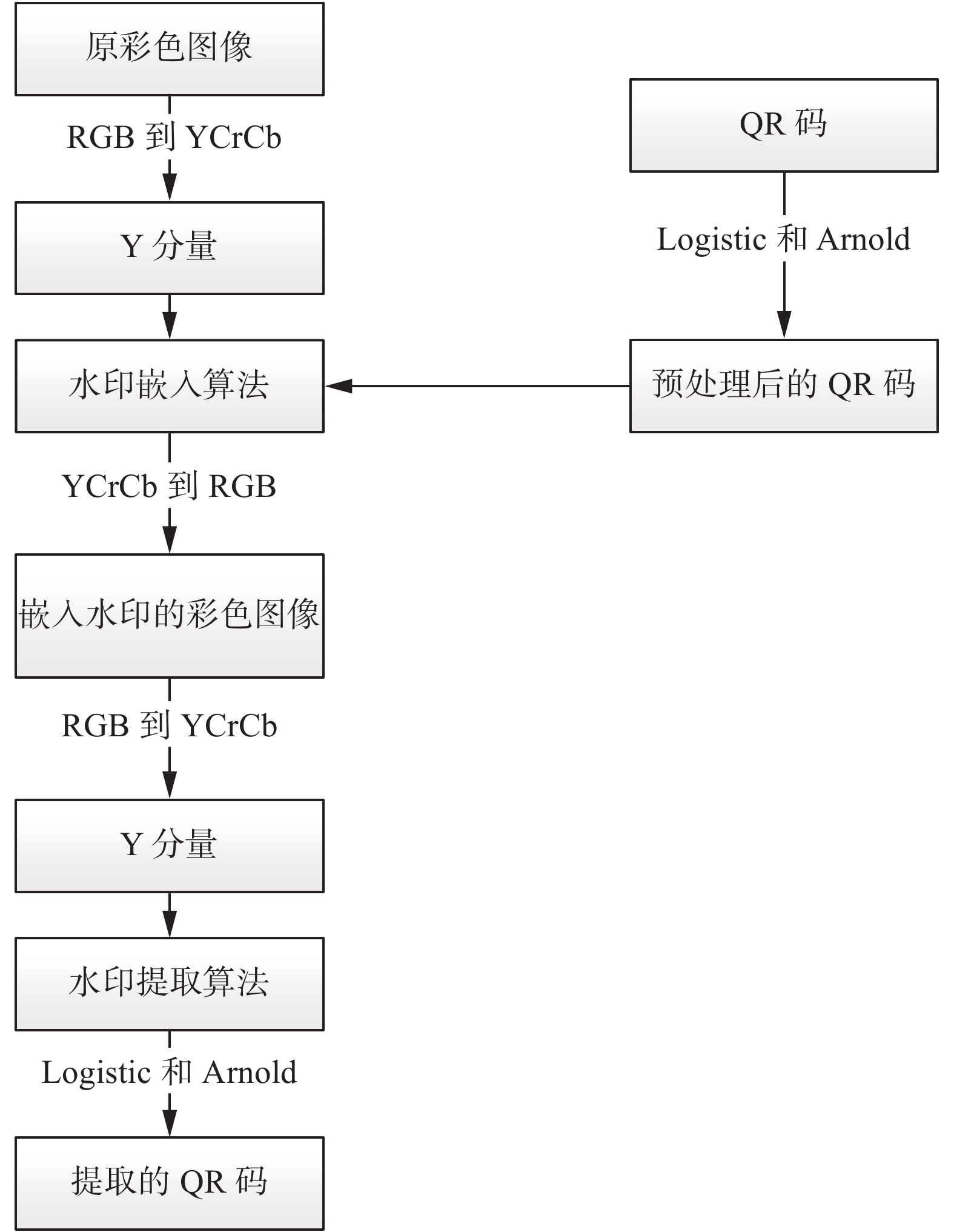
3 水印的嵌入和提取

本文选用QR码为水印图像，彩色图像为载体图像。采用QR码使得水印嵌入量增大和鲁棒性增强。图2为水印算法的总框架。

3.1 水印的嵌入

1)对QR码先实施Logistic映射，后进行Arnold操作，获得双重加密后的QR码序列W；

2)把彩色载体图像从RGB空间转换到YCbCr空间，提取其Y分量得到亮度分量图；

3)对亮度分量图实施3级DWT，获得低频子图LL，对LL实施DCT变换，即 ${\rm{dct}} = {\rm{dct}}2\left( {{\rm{LL}}} \right)$ ，得到变换后dct系数矩阵；

4)对dct系数矩阵实施奇异值分解，即 $\left[ {{{U}},{{S}},{{V}}} \right] =$ $ {\rm{SVD}}\left( {{\rm{dct}}} \right)$ ，引入强度因子 $\alpha $ ，利用加性法则嵌入QR码信息，为

${{W}}a = {{S}} + \alpha {{W}}$

式中：S为嵌入QR码前的对角矩阵；W为QR码信息； $ {{W}}\alpha$ 为嵌入QR码后的对角矩阵； $\alpha $ 为强度因子，随着 $\alpha $ 的增大，不可见性变差，相似度增加，经过多次实验，确定该算法中 $\alpha = 60$ 。

5)对 $ {{W}}\alpha$ 矩阵实施奇异值分解，即 $\left[ {{{{U}}_1},{{{S}}_1},{{{V}}_1}} \right] = $ ${\rm{SVD}}\left( {{{W}}\alpha } \right)$ ，利用 ${{U}}{\text{、}}{{{S}}_1}{\text{、}}{{V}}$ 完成奇异值重构，即 ${\rm{dct}}1$ $ = {{U}}{{{S}}_1}{{V}}$ 。最后实施DCT逆变换和3级小波逆变换，获得嵌入QR码的亮度分量图。

6)将嵌入QR码的亮度分量图从YCbCr空间转换到RGB空间，最终获得嵌入QR码的彩色载体图像。

3.2 水印的提取

1)将嵌入QR码的彩色载体图像从RGB空间转换到YCbCr空间，提取其Y分量获得亮度分量图；

2)对亮度分量图实施3级DWT，获得低频子图LL₁，对LL₁实施DCT变换，即 ${\rm{dct}}2 = {\rm{dct}}2\left( {{\rm{L}}{{\rm{L}}_1}} \right)$ ，得到dct系数矩阵；

3)对dct系数矩阵实施奇异值分解， $\left[ {{{{U}}_2},{{{S}}_2},{{{V}}_2}} \right]=$ $ {\rm{SVD}}\left( {{\rm{dct}}2} \right)$ ，将 ${{{U}}_1},{{{S}}_2},{{{V}}_1}$ 进行逆奇异值变换，即 ${{SS}} = {{{U}}_1}{{{S}}_2}{{{V}}_1}$ ；

4)利用 ${{S}},{{SS}},\alpha $ 提取双层加密后的QR码，即 ${{{W}}_b}$ $ = \left( {{{SS}} - {{S}}} \right)/\alpha $ ，可以得到水印信息；

5)建立一个新的空矩阵W_c用于存放水印信息，当发现水印信息时，将其存入矩阵W_c中，因此，可得到加密后的QR码序列W_c。

6)将QR码序列W_c实施解密操作，先实施Arnold变换，再实施Logistic映射，获得最终提取的QR码水印W_w。

4 实验结果分析 4.1 水印评价标准

1) 该实验中，嵌入QR码的图像与未嵌入的原始图像之间的区别由峰值信噪比(peak signal-to-noise ratio, PSNR)来衡量。均方误差(mean-square error, MSE)、峰值信噪比PSNR的表达公式为

${\rm{MSE}} = \frac{1}{{MN}}\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^N {\left[ {{{I}}'\left( {i,j} \right) - {{I}}\left( {i,j} \right)} \right]} } $

(1)

${\rm{PSNR}} = 10\log \frac{{{{255}^2} \times 3}}{{{E_{{\rm{MES}}}}\left( R \right) + {E_{{\rm{MES}}}}\left( G \right) + {E_{{\rm{MES}}}}\left( B \right)}}$

(2)

式中： ${{I}}$ 为原始彩色图像； ${{I}}'$ 为含QR码的彩色图像。不可见性随着PSNR值的增加而增加，当PSNR>30 dB时，表明该算法的不可见性较优。

2)提取出的QR码与原QR码之间的相似性由归一化相关系数NC来衡量，为

${\rm{NC}} = \dfrac{{\displaystyle\sum\limits_{i = 1}^M {\displaystyle\sum\limits_{j = 1}^N {{{w}}(i,j){{w}}'(i,j)} } }}{{\displaystyle\sum\limits_{i = 1}^M {\displaystyle\sum\limits_{j = 1}^N {{{{w}}^2}(i,j)} } }}$

(3)

式中： ${{w}}$ 表示原始QR码图像； ${{w}}'$ 表示提取出的QR码图像。相似性随着NC值的增加而增加，当NC值靠近1时，说明提取出的QR码与原始QR码之间的相似性较强。

4.2 实验结果分析

本测试以彩色图像为载体图像，像素为512×512，以携带“山西师范大学沈艳冰”信息的QR码为水印图像，像素为64×64，Logistic映射参数u为4，初始值x为0.2345，Arnold置乱周期为48，置乱次数为30，强度因子α的值为60。

4.2.1 未受攻击的实验结果

图3(a)为彩色载体图像，图3(b)为加入QR码的彩色载体图像，图3(c)为原QR码，图3(d)为提取的QR码。比较图3(a)和图3(b)，用式(1)和(2)可以算出本算法PSNR值为59.4919，说明本算法不可见性较好。比较图3(c)和图3(d)，用式(3)可以算出本算法NC值为1，说明该算法能提取完整的QR码和识别QR码。

4.2.2 受攻击的实验结果

检验算法鲁棒性的方法是对嵌入QR码的彩色图像施加攻击。表1~5列举了10种攻击，分别为JPEG压缩、图像变暗、图像增亮、对比度降低、对比度增加、高斯噪声、盐椒噪声、乘积噪声、剪切和旋转攻击。

1) JPEG压缩测试

由表1可看出，在JPEG压缩实验中，即使JPEG压缩至10%也可以提取出可识别的有效QR码，且NC值在0.998以上，说明该算法在JPEG压缩上有很强的鲁棒性。

2)图像对比度和明暗变化测试

从表2测试结果可得，无论是图像明暗变化或是对比度变化，提取的QR码的PSNR值和NC值都可以保持较高数值，且NC值始终保持在0.98以上。由此可以得知该算法可以抵抗图像明暗变化和对比度变化，有较强的抗攻击能力。

3)噪声测试

通过表3可看出，对嵌入QR码的彩色图像添加高斯噪声(方差各为0.01、0.02、0.04)、盐椒噪声(噪声密度各为0.05、0.10、0.15)以及乘积噪声(方差各为0.01、0.05)，受噪声攻击后的PSNR值和NC值仍各自保持在30和0.90以上，提取的QR码都能识别其携带原始信息，这说明该算法鲁棒性较好，可以有效抵抗噪声攻击。

4)剪切测试

由表4测试结果可看到，对QR码进行剪切时，即使剪切1/8，其PSNR值和NC值也不会发生很大的变化，分别保持在40和0.99以上，QR码仍可以提取并识别。通过该测试可知该算法能抵抗剪切，鲁棒性性能较优。

5)旋转测试

由表5旋转测试结果可知，该算法可以抵抗旋转，当旋转达到70°时QR码水印仍然可以提取并识别，且NC值保持在0.98以上。

4.2.3 与其他算法相比较的实验结果

彩色图像由RGB空间转换到YCrCb空间，提取Y分量进行水印嵌入算法，Y分量图为灰度图像，因此，该算法也适合于灰度图像。文献[4]使用灰度图像进行鲁棒性实验，所以本文选择与文献[4]进行对比实验，表6为本文与文献[4]的实验结果比较。由表6中数据可以看出，本文在高斯噪声参数为0.01、0.02和0.04的攻击上的NC值分别为0.9960、0.9945和0.9931；在JPEG压缩参数为30%、50%、70%的攻击上的NC值分别为1.0000、1.0000和1.0000；在剪切1/8的攻击上的NC值为0.9921，在中值滤波[3,3]的攻击上的NC值为0.9990，均高于文献[4]中的NC值，由此可知本文算法在高斯噪声、JPEG压缩、剪切和中值滤波下，相比于文献[4]的算法，鲁棒性更优。

5 结束语

提出一种适用于QR码的彩色图像数字水印算法。对QR码实施Logistic映射和Arnold变换，对彩色载体图像实施DWT、DCT和SVD操作，实现了不可见性和鲁棒性之间的均衡。实验数据表明：该算法经过JPEG压缩、图像亮暗变化、对比度变化、噪声、剪切和旋转后的彩色图像PSNR值均在30以上，提取出的QR码NC值均在0.98以上，且清晰可见，都能通过手机扫描识别。并与文献[4]相比较，该算法在噪声、JPEG压缩、剪切和滤波攻击上有一定提升，因此，该算法鲁棒性和实用性较强。