随着社交网络中信息量的快速增长，信息传播速度的不断加快，其信息传播构建了一种分布式传播机制^[1]以及节点的合作机制^[2]，即信息在用户之间的扩散会受到用户影响力的影响^[3]。因此，开展影响力分析研究显得十分重要。影响力最大化问题是影响力分析的重要课题之一。2015年，Morone和Makse在Nature上对社交网络中影响力最大化问题进行了深入探讨^[4]。影响力最大化问题解决的是如何衡量网络中节点重要性的问题，其经典应用之一是病毒营销^[5-8]，也就是通过口口相传效应进行产品的销售^[9-10]。

影响力最大化问题最早由Kempe等^[11]率先提出。Kempe等使用独立级联模型与线性阈值模型对社交网络中影响力的传播进行建模，并且证明在社交网络中寻找具有最佳影响力的种子节点集合是NP-Hard问题。而且他们提出使用简单的贪婪算法寻找具有最佳影响力的种子节点集合，获得了(1-1/e)的近似保证。影响力最大化问题中的关键问题是如何衡量节点传播影响力的能力，也就是节点所具有的影响力。在最初的影响力最大化问题研究中，一些基于网络拓扑结构的中心性方法被提出，例如度中心性和点介数中心性。在随后的影响力最大化问题研究中，多数算法使用次模性质^[12-15]，即通过大量迭代来计算边际收益，从而近似求得问题的最优解，但是存在算法时间复杂度较高的问题。Chen等^[16]提出了度折损启发式算法，即优先选择度大的节点作为种子节点，一旦某节点被选取为种子节点，那么其邻居节点被选为种子节点的概率将大大降低。Lee等^[17]利用多数节点平均只能影响到2阶邻居节点的现象，提出了2-hop贪婪算法，即利用节点在2阶邻居范围内的影响力更新节点的边际收益。Chen等^[16] 提出MIA(maximum influence arborescence)最大影响力树算法，利用MIIA(maximum influence in-arborescence)影响力最大入树和MIOA(maximum out-arborescence)影响力最大出树构建节点的影响力传播路径，通过节点的影响力最大化路径计算得分并选取种子节点，相较于原始的贪婪算法取得了较低的时间复杂度，但因为MIA需要对每个节点建立树，所以空间复杂度相较于其他算法较高。JUNK等^[18]提出IRIE(influence ranking influence estimation)算法，即算法整体被分为两部分，影响力排名使用一种算法，影响力模拟再使用一种算法。在最近影响力最大化问题的研究中，许多优秀的算法被提出，其中Kitsak等^[19]提出最具影响力的节点往往不是具有较大连接的节点，而是处于网络核心位置的节点，通过k-shell分解^[20]分析网络中节点核数与节点影响力的关系，为影响力最大化问题提供了新的解决思路。Gao等^[21]根据节点的影响力与其局部结构的关系，提出了一种局部结构中心性的方法，利用节点以及其邻居的拓扑结构和中心性来衡量节点的影响力，此算法在评估节点影响力方面更加准确。王等^[22]提出的多种群随机差分粒子群优化算法和刘等^[23]提出的改进萤火虫算法也可很好的应用到影响力最大化问题当中。

在上述的影响力最大化算法中，研究人员只关注所选种子节点影响力是否最佳，旨在研究更加优秀的算法近似求得影响力最优的种子节点集合，而忽略了种子节点集合的大小和网络固有的传播影响力能力的关系。本文从网络传播影响力能力的角度出发研究影响力最大化问题，从而得出网络所适合的种子节点集合的大小。本文提出种子节点集合大小并不是越大越好，而是每个网络都存在一个种子节点个数的上限，一旦超过这个上限，随着种子节点个数大小的增加，种子节点集合的影响力是趋于饱和的。为研究网络传播影响力的固有能力，本文使用渗流^[24-26]的思想，即对网络进行渗流模拟，得出网络由大量零散的团块趋向于形成一个主团块的相变值，从而得出网络所适合的种子节点集合的大小，即提出一种基于渗流模型的影响力最大化种子节点集合大小选取算法来获得最优的种子节点集合大小，并对算法结果进行了分析。

1 问题描述 1.1 影响力最大化问题

本文主要研究无向网络传播影响力的能力，定义无向网络G=(V,E)，其中V为无向网络G中的节点集合，E为无向网络G中边的集合。定义n=|V|为网络G的节点个数，m=|E|为网络G边的个数。影响力最大化问题就是在网络G中寻找大小为k的种子节点集合，使得这k个种子节点在网络G中传播的影响力是最大的，我们定义种子节点集合为S。在影响力最大化问题中，我们面临着两个尤为重要的问题，即影响力是如何定义的，以及影响力在网络中是如何传播的。独立级联模型(independent cascade model)是经典的模拟影响力传播的模型，在之前多数影响力最大化问题的研究中，研究人员都使用独立级联模型作为影响力传播模型。而节点或者节点集合的影响力，我们使用影响力函数进行求解。

1.2 独立级联模型

独立级联模型^[27-28]是经典的用于模拟影响力传播的算法，模型描述如下：在网络G中，节点集合V中的节点v存在两种状态，即一种是激活状态另一种是未激活状态。假设t时刻，节点v已经处于激活状态，那么节点v会尝试以概率p去激活其邻居节点u，如果激活成功，那么节点u会从t+1时刻开始，一直处于激活状态。如果激活失败，那么从t+1时刻开始，节点u再也不能被节点v尝试激活。我们定义影响力传播模型的初始时刻为t=0时刻，定义集合A₀中的节点处于激活状态，那么集合A_t为t时刻被激活的节点集合。如果存在某一时刻c+1，集合A_c+1为空集，那么独立级联模型终止运行。当独立级联模型终止时，我们可以获得在此过程中激活的节点集合 $A_{\rm total}=$ $\{A_0,A_1,A_2,\cdots,A_c\}$ 。

1.3 影响力函数

定义影响力函数为I(x)：将有限集合映射到非负整数域上的函数。在网络中使用独立级联模型模拟影响力传播的过程当中，种子集合S为初始时刻已经激活的节点集合，在影响力传播过程的每个离散时刻都会因集合S激活一些未激活的节点，在影响力传播过程结束时我们可以得到在此过程中激活的节点集合A_total，即集合A_total是被种子节点集合S影响的节点集合。我们令种子节点集合S的影响力为I(S)，其值为|A_total|，即种子节点集合S的影响力是在影响力传播过程中被集合S影响到的节点的个数。

2 算法思想与步骤

本文主要研究影响力最大化问题中种子节点集合大小选取的问题。在之前的研究中，研究人员一般选取5~50个节点作为种子节点，并观察算法选取出的种子节点集合的影响力，旨在通过改进算法得到更优的种子节点集合。而本文从网络传播影响力的固有能力的角度出发，发现网络在选取种子节点时，并非越多越好，而是一定数量的种子节点就能达到最优的影响力，即在网络中存在一个最优大小的种子节点集合，即我们所说的网络传播影响力的固有能力。为了研究网络传播影响力的固有能力，本文借助渗流模型对网络进行模拟分析，提出一种基于渗流模型的影响力最大化算法，即在不同的传播概率p下对网络进行渗流模拟，通过建立传播概率p与渗流模拟后网络的最大连通子图大小的函数关系，最终求得当前网络所适合的种子节点集合的大小。具体算法步骤如下：

算法　基于渗流模型的影响力最大化种子节点集合大小选取算法

输入　上三角邻接矩阵G' ，传播概率数组p_list，网络中节点的数量n，矩阵C，模拟次数R;

输出　最优种子节点集合大小k'

1) For i=1:1:len(p_list)

2) 　For j=1:1: R

3) 　　根据p_list (i)对G'进行渗流模拟，形成　　　渗流后网络GP，并且获得GP的最大连通　　　子图GP'；

4) 　　 C(j,i)=num(GP')；

　　End

　End

5) C' =avg(C)；

6) 对p_list和C进行多项式拟合，求得拟合　　　函数F(x)；

7) 求F(x)的导函数dF(x)；

8) 通过函数dF(x)求得相变值p_c；

9) 最优种子集合大小 $k' = {p_c} \times n$

本文提出一种基于渗流模型的影响力最大化种子节点集合大小选取算法。算法的输入为：无向网络G的上三角邻接矩阵G' ，传播概率数组p_list，网络中节点的数量n，矩阵C和模拟次数R。因为本文主要研究无向网络，在对网络进行渗流模拟时，为了保持边的一致性，所以使用网络G的上三角邻接矩阵G' 。p_list是大小为 $1 \times 1\;000$ 的一维数组，其中数组元素为0.001~1的数字，且相邻元素相差0.001。C是大小为 $100 \times 1\;000$ 的矩阵。因为在网络G上进行渗流的结果具有随机性，所以我们在传播概率 $p \in {p_{\rm list}}$ 的情况下进行R次渗流。算法的输出为最优种子节点集合大小k'。具体的算法步骤描述如下：

1)函数len(x)用来计算数组的长度，所以len(p_list)的值等于1 000，此步骤具体是：在传播概率 $p \in {p_{list}}$ 的情况下，对网络G' 进行渗流；

2)采用当前传播概率p对网络G' 进行R次渗流；

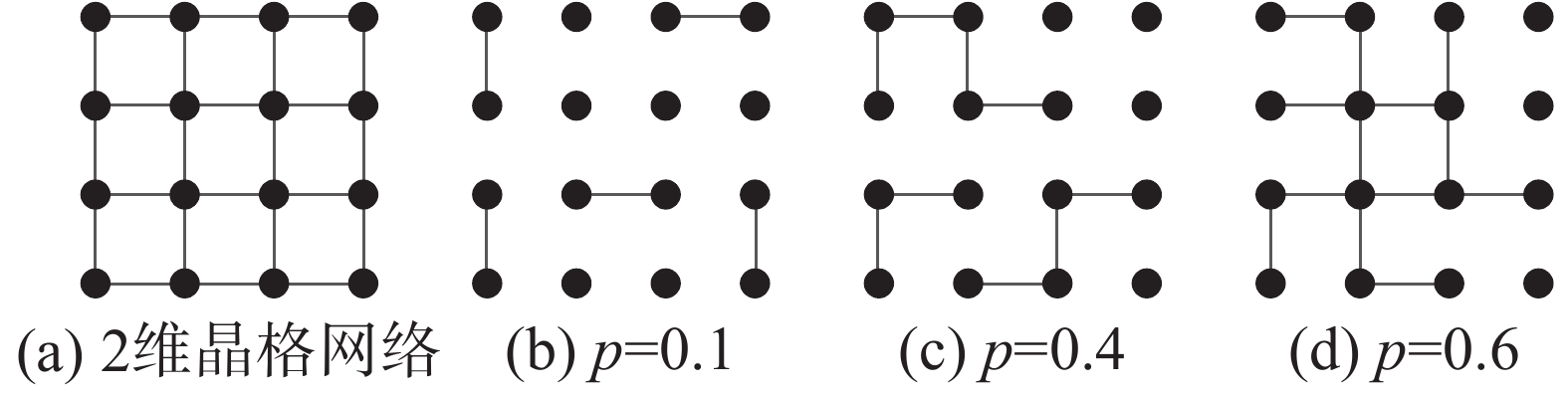
3)渗流模型的定义如下：在网络G' 中，网络每条边具有统一的传播概率值p。我们对每条边产生独立的随机值p_r，如果p_r<p，那么此边处于占有状态，如果p_r>p，那么此边处于非占有状态，也就是此边从网络中删除。通过改变统一的传播概率值p，那么存在一个值p_c，当p>p_c时，GP中的节点倾向于紧密的连接在一起，形成一个主团块。当p<p_c时，GP中的节点倾向于形成多个零散的小团块。p_c便称为网络G'的相变值。图1为渗流实验例图，图1(a)为2维晶格网络，网络中边的概率统一为p。图1(b)到图1(d)为渗流模拟后的网络，并且边的概率逐渐提高，我们发现当边的概率较低时，渗流模拟后的网络倾向于形成零散的团块，当边的概率较大时，渗流模拟后的网络倾向于形成一个主团块，其存在一个过度值，即网络由零散的团块到形成一个主团块的值，即相变值。图1(d)为2维晶格网络发生渗流时的状态，相变值p_c=0.6。在3)中，通过对网络G' 进行渗流模拟，可以得到渗流后的网络GP并且计算求得GP的最大连通子图GP'；

4)函数num(x)用于计算网络中节点的个数，所以此步骤是将GP'的节点个数存入到C中；

5)函数avg(x)用于计算矩阵每列的平均值，所以此步骤是对传播概率p下R个num(GP')求平均值，并且存入到C' 中，也就是说，每个传播概率p，我们都会对G' 进行R次渗流模拟，从而产生R个num(GP')，最后将其求平均，即得到每个传播概率p所对应GP'的平均大小；

6)采用多项式拟合的方法对p_list和C' 进行拟合。多项式拟合是使用多项展开式去近似数据点的函数关系，并使用最小二乘法来得到多项展开式的系数，最终求得数据点函数关系的方法。多项式拟合公式为

$F(x) = {a_0} + {a_1}x + {a_2}{x^2} + \cdots + {a_l}{x^l}，$

(1)

式中： ${a_0}$ 到 ${a_l}$ 为使用最小二乘法求取的系数；l为多项式的阶数。本文式(1)中的x为p_list中的元素，C' 中的元素为F(x)的函数值，通过多项式拟合函数求得F(x)的系数，从而求得p_list和C' 的拟合函数F(x)；

7)求函数F(x)的导函数dF(x)；

8)相变值p_c在p_m的左邻域中，其中dF(p_m)的值为函数dF(x)的最大值，dF(p_c)的值为靠近dF(p_m)最近的最小值，相变值p_c为函数F(x)变化速率开始加快的起点位置；

9)求取最优种子集合大小。

3 实验结果及分析

本文提出的一种基于渗流模型的影响力最大化种子节点集合大小选取算法在4个公共数据集上进行实验，数据集分别为KarateClub^[29]、Football^[30]、HighSchool^[31]和SocDolphins^[32]。因本文主要研究无向网络，所以必要时对数据集进行了无向化处理。KarateClub数据集是1970年美国大学生空手道俱乐部34名成员之间朋友关系的社交网络。Football是2000年美式足球秋季常规赛大学之间的比赛网络。HighSchool是2013年12月法国马赛高中学生友谊联系的社交网络。SocDophins是宽吻海豚之间的社交网络。其中数据集KarateClub、HighSchool和SocDophins中的边表示成员之间拥有相对频繁的联系，Football数据集中的边表示球队之间会有比赛安排。不同数据集的拓扑属性如表1中所示，其中节点数为网络中节点的总数，边数为网络中边的总数，最大度数为网络中边数的最大值，平均度为度的平均值。同配系数是描述大度节点之间相连接的能力，其值越靠近1说明其同配性越好；聚类系数是描述节点之间连接成团的能力，其值越大说明网络中的节点更有可能产生连接；网络密度描述了网络实际存在边数与网络可容纳边数的比值，也就是节点之间相互连边的密集程度，其值越大说明网络越密集。

在现有影响力最大化问题的研究中，大多数研究人员主要关注如何在网络中选取具有最佳影响力的种子节点集合，也就是通过研究创造出更先进的影响力最大化算法来近似选取种子节点集合，并不关注种子节点集合大小的问题，即网络传播影响力的固有能力的问题。本文主要研究网络传播影响力的能力，提出网络传播影响力的能力是有限的，也就是在网络中选择种子节点的时候并不是越多越好，每个网络存在一个最优的种子集合大小，一旦种子集合大小超过了最优值，其多出的种子节点所带来的影响力几乎不能起到积极的作用，反而会增加实验的成本。因为本文主要研究种子节点集合的大小，所以需要获得种子节点的算法作为载体来求得种子节点，本文使用4种经典的算法来选取种子节点，4种算法分别为：贪婪算法、度中心性、点介数中心性和基于k核过滤核覆盖算法。使用上述方法分别选出4个数据集具有最佳影响力的10种子节点，并对其影响力做出分析。

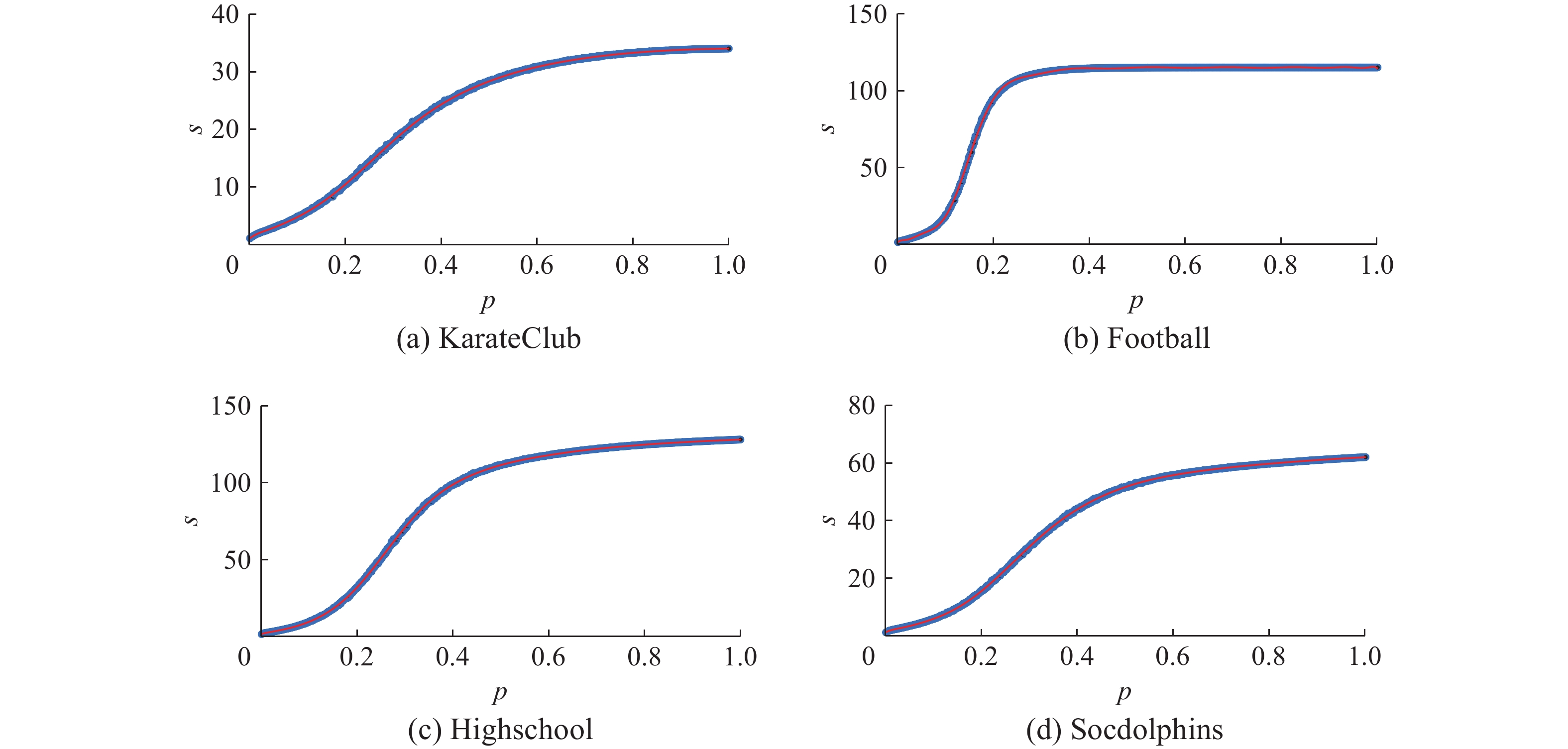
3.1 渗流实验

我们提出网络传播影响力的固有能力与相变值p_c有关，所以在网络G上进行渗流实验。通过改变传播概率p，对网络G进行多次渗流实验，建立传播概率p与渗流后网络GP的最大连通子图GP'平均大小s的函数关系。在具体实验中，设定传播概率p为0.001~1的数，且为0.001的倍数，也就是说传播概率p有1 000种情况。然后根据不同的传播概率p对网络进行渗流实验，并且每个传播概率p进行R次独立的渗流实验，因为渗流实验具有随机性，本文中通过设置较高的R值来获取足够的实验结果，本文设置R=1 000。渗流实验后，计算得到渗流后网络GP的最大连通子图GP'的平均大小s，通过多项式拟合的方法对p和s进行拟合，形成p和s的拟合函数F(x)。渗流模拟实验具体结果如图2所示。在图2中，p表示网络的传播概率，s表示每个传播概率p下R次渗流模拟后所得的最大连通子图大小均值。图2中蓝色部分是由1 000个点构成的散点图，每个点对应了一个传播概率p以及一个最大连通子图大小均值s。图中红色曲线是对p和s进行拟合得到的拟合函数F(x)的曲线。由图2发现随着p值的增大，曲线逐渐平缓，在p值较小的时候，s的增长速率较大。即p值较小时，GP由零散的小团块组成，当p值越来越大时，GP趋向由主团块组成。

3.2 相变值

为了计算网络G的相变值p_c，需要计算函数F(x)的变化速率。在图3中，p为传播概率，r为函数F(x)的变化速率，即函数dF(x)的值。我们可以得到函数dF(x)的最大值dF(p_m)，点p_m为图3中绿色的点，也就是函数F(x)变化最快的时候。所有找的相变点p_c，在p_m的左邻域中，也就是图3中红色的点，其中dF(p_c)为距离dF(p_m)最近的最小值，也就是函数dF(x)变化增长到最快时的起点位置。当网络的传播概率p小于相变值p_c时，变化速率r还处于较低水平，GP由零散的小团块组成，当传播概率p大于p_c时，GP趋向由主团块组成，GP逐渐呈现出以最大连通子图为主的图结构。本文提出相变值p_c反应了网络G传播影响力的固有能力，也就是相变值反应网络G中边被激活的能力，即在影响力传播模型下，被激活边占总边数的比例。因此可以得到网络G最优的种子节点集合的大小k'。

因此可以计算出4个数据集的相变值与最优的种子节点集合的大小，其中KarateClub、Football、HighSchool和SocDolphins的相变值分别为0.034、0.059、0.022和0.029。KarateClub、Football、HighSchool和SocDolphins的最优的种子节点集合的大小分别为2、7、3和2。

3.3 影响力模拟

本文使用4种影响力最大化算法来选取种子节点集合，4种算法分别是：简单贪婪算法^[11]、度中心性、点介数中心性^[33]以及基于k核过滤核覆盖算法^[34]。其中，简单贪婪算法通过迭代的方式逐节点计算 $I(S \cup \{ v\} )$ ，并在每轮迭代中将使函数值最大的节点v加入到种子节点集合S中，直到选满k个种子节点，迭代结束。度中心性和点介数中心性则选择度最大的k个节点作为种子节点。基于k核过滤核覆盖算法则是通过预先计算出最优的核数k_opt，通过k核分解出最小核数为k_opt的子图，在子图中选择核数最大的节点作为种子节点。

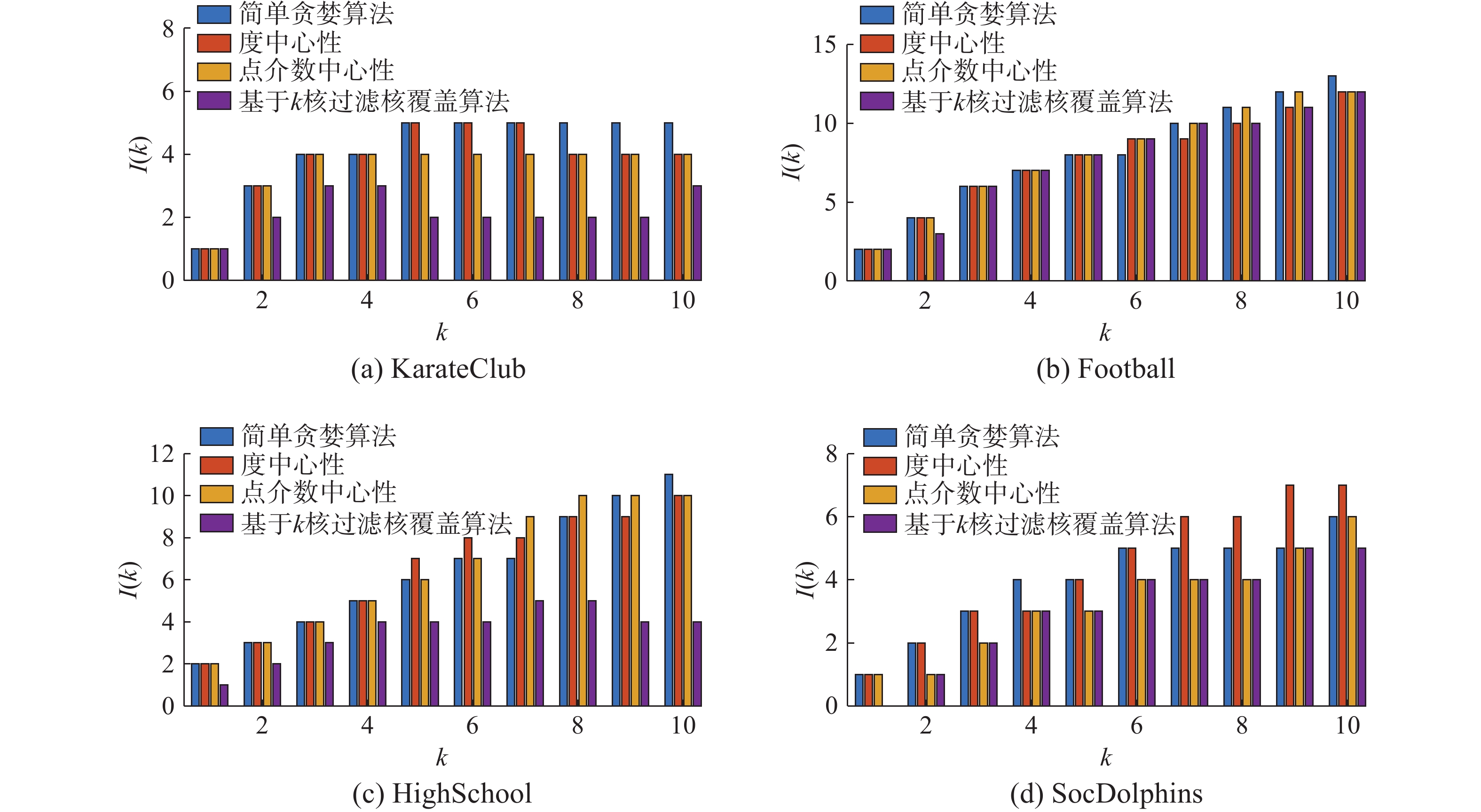
在影响力模拟实验中，我们使用独立级联模型作为影响力模拟算法以及使用I(x)计算影响力，并且使用上述4种算法选取影响力最大的10个种子节点，分别对1~10大小种子节点集合进行影响力模拟。4个数据集种子节点集合影响力实验结果如图4所示。在图4中，k为种子节点个数，I(k)为种子节点集合的影响力。图4(a)为KarateClub数据集种子节点集合影响力的实验结果，在图中我们可以发现4种算法选出的种子节点集合在大小为3时，影响力大小几乎趋于平衡，说明当前数据集适合3个以下种子节点作为种子节点集合。图4(b)为Football数据集种子节点集合影响力的实验结果，4种算法的影响力呈逐渐上升趋势，并且在种子节点个数为6时，增长趋势逐渐变缓。图4(c)为HighSchool数据集种子节点集合影响力的实验结果，4种算法的影响力呈逐渐上升趋势，图像在种子节点个数k分别为6时上升趋势逐渐放缓。图4(d)为SocDolphins数据集种子节点集合影响力的实验结果，4种算法的影响力波动较大，总体呈上升趋势，但我们可以观察到当k=5开始，影响力已经开始小于种子节点的个数。

3.4 平均影响力分析

在图5中，k为种子节点个数，纵坐标为当前种子节点集合单个节点的平均影响力。从图5(a)中可以发现，当k=2时单个种子节点的平均影响力是最高的，1个种子节点平均影响力1.5个节点左右。当k>4时，单个种子节点的影响力不足于1个节点。所以KarateClub数据集适合选择2个种子节点作为种子节点集合较合适。从图5(b)中可以发现，当k为1~3时，种子节点的平均影响力最大，1个种子节点平均影响2个节点，当k>6时，发现种子节点的平均影响力已经不足1.5个，所以我们认为Football数据集适合选取7个种子节点作为种子节点集合比较合适。从图5(c)中可以发现，当k=1时单个种子节点的平均影响力是最高的，1个种子节点平均影响力为2个节点左右，当k>3时，我们发现种子节点的平均影响力已经不足1.5个，所以我们认为HighSchool数据集适合选取3个种子节点作为种子节点集合比较合适。从图5(d)中可以发现，1个种子节点平均影响力最高为1个节点左右。点介数算法选取的种子节点在k>1时就出现了平均影响力的下降，贪婪算法和度中心性算法选出的种子节点的影响力分别在k为4和3时出现下降，因此SocDolphins数据集适合选择2个种子节点作为种子节点集合比较合适。

通过实验可以看出，一个网络的种子节点集合大小并不是越大越好，而是存在一个上限，当种子节点集合的大小超出了这个上限，多出的种子节点并不能带来很好的边际收益。根据我们所提出的算法计算出的最优种子节点集合大小k'，基本反映了一个网络传播影响力能力的上限，因此为种子节点个数的选取提供了很好的参考，并且可以用于一些选取最优种子节点集合算法中，减少额外的时间开支。

4 结束语

本文主要对无向网络传播影响力的固有能力进行研究，通过对网络进行渗流模拟得到网络的相变值，发现相变值可以反应网络传播影响力的能力，并提出一种基于渗流模型的影响力最大化算法来选取网络所适合的种子节点集合的大小。在算法中，我们建立传播概率与渗流模拟后网络最大连通子图大小的关系，得到网络相变值p_c。当传播概率p大于p_c时，渗流后网络倾向于由一个主团块组成，当传播概率p等于p_c时，网络由多个大型团块组成。算法通过相变值与种子节点集合大小的换算，得到当前网络最优的种子节点集合大小。实验结果表明该临界点对影响力最大化种子节点集合的大小选取起着重要的指导性作用。