2. 广西民族大学 广西高校复杂系统与智能计算重点实验室,广西 南宁 530006
2. Guangxi Higher School Key Laboratory of Complex Systems and Intelligent Computing, Guangxi University for Nationalities, Nanning 530006, China
支持向量机(support vector machine, SVM)自1995年由Vapnik提出以来就受到理论研究和工程应用2方面的重视,是机器学习的一个研究方向和热点,已经成功应用到很多领域中[1-3]。SVM的基本算法是一个含有不等式约束条件的二次规划(quadratic programming problem, QPP)问题,然而,如果直接求解QPP问题,当数据集较大时,算法的效率将会下降,所需内存量也会增大[4-8]。因此,如何克服SVM在处理大规模数据集时的效率低下问题,一直是学者们研究的热点。
为了更好地解决大规模样本的分类问题,基于粒度计算理论[9-10]和统计学习理论的思想,Tang等于2004年首次提出粒度支持向量机(granular support vector machine, GSVM)这个术语。GSVM的总体思想是在原始空间将数据集进行划分,得到数据粒。然后提取出有用的数据粒,并对其进行SVM训练 [11-12]。与传统支持向量机相比,GSVM学习机制具有以下优点:针对大样本数据,通过数据粒化和对有用粒子(支持向量粒)的提取,剔除了无用冗余的样本,减少了样本数量,提高了训练效率。然而,Tang只是给出了GSVM学习模型的一些设想,没有给出具体的学习算法。2009年,张鑫[13]在 Tang提出的GSVM思想的基础上,构建了一个粒度支持向量机的模型,并对其学习机制进行了探讨。此后,许多学者对支持向量机和粒度计算相结合的具体模型进行了研究,比如模糊支持向量机[13]、粗糙集支持向量机[14]、决策树支持向量机[15]和商空间支持向量机[16]等。但这些模型的共同点都是在原始空间直接划分数据集,然后再映射到高维空间进行SVM学习。然而,这种做法很有可能丢失了大量包含有用信息的数据粒,其学习算法的性能会受到影响。为此,本文采用模糊核聚类的方法将样本直接在核空间进行粒的划分和提取,然后在相同的核空间进行GSVM训练,这样保证了数据分布的一致性,提高了算法的泛化能力。最后,在标准UCI数据集和NDC大数据上的实验结果表明,本文算法是可行的且效果更好。
1 粒度支持向量机张鑫[17]在Tang提出的GSVM思想的基础上,构建了一个粒度支持向量机的模型。
设给定数据集为
| $({{{X}}_1},{{{Y}}_1}),({{{X}}_2},{{{Y}}_2}), \cdots ,({{{X}}_i},{{{Y}}_i}), \cdots ,({{{X}}_l},{{{Y}}_l})$ |
若每个粒包含
| ${{X}} = \{ ({{{X}}_i},{{{Y}}_i}),i = 1,2, \cdots ,l\} $ |
其中:
| ${{{X}}_1} = \left\{ \begin{array}{l} {{{x}}_1} \\ {{{x}}_2} \\ \; \vdots \\ {{{x}}_{{l_1}}} \\ \end{array} \right\},{{{X}}_2} = \left\{ \begin{array}{l} {{{x}}_{{l_1} + 1}} \\ {{{x}}_{{l_1} + 2}} \\ \;\;\;\vdots \\ {{{x}}_{{l_1} + {l_2}}} \\ \end{array} \right\}, \cdots ,{{{X}}_l} = \left\{ \begin{array}{l} {{{x}}_{{l_1} + {l_2} + \cdots + {l_{l - 1}} + 1}} \\ {{{x}}_{{l_1} + {l_2} + \cdots + {l_{l - 1}} + 2}} \\ \;\;\;\;\;\;\;\;\; \vdots \\ {{{x}}_{{l_1} + {l_2} + \cdots + {l_{l - 1}} + {l_l}}} \\ \end{array} \right\}$ |
则在GSVM中,最优化问题变为:
| $\begin{array}{l} {\min _{{{w}},b}}\;\; \dfrac{1}{2}{{{w}}^2} \\ {\rm{s.t.}}\;\; \;\; \;{{{Y}}_j}(({{w}} \cdot {{{X}}_j}) + b) \geqslant 1,\quad j = 1,2, \cdots ,l \\ \end{array} $ | (1) |
将上述问题根据最优化理论转化为其对偶问题:
| $\begin{aligned} \displaystyle \mathop {\max }\limits_a {{W}}(a) = \mathop {\max }\limits_a - \frac{1}{2}\sum\limits_{i = 1}^l {\sum\limits_{j = 1}^l {{a_i}} } {a_j}{{{Y}}_i}{{{Y}}_j}({{{X}}_i} {{{X}}_j}) + \sum\limits_{i = 1}^l {{a_i}} \\ \displaystyle {\rm{s.t.}}\;\; \;\; \sum\limits_{i = 1}^l {{a_i}} {{{Y}}_i} = 0 , \quad 0 \leqslant {a_i} \leqslant C \\ \end{aligned} $ | (2) |
解得最优解
| $\begin{aligned} f({{x}}) = &{\rm sgn} \{ ({{{w}}^*} {{X}}) + {b^*}\}= \\& \displaystyle {\rm sgn} \{ (\sum\limits_{j = 1}^l {{{a}}_j^*{y_j}({{{X}}_j} {{{X}}_i})} ) + {b^*}\} ,{{X}} \in {{\bf{R}}^n} \\ \end{aligned} $ | (3) |
当数据集是线性不可分时,GSVM不是在原始空间构造最优分类面,而是映射到高维特征空间,然后再进行构造,具体为:
将
| ${{X}}\xrightarrow{{}}{{\varPhi}} ({{X}}) = {[{{{\varPhi}} _1}({{X}})\,{\varPhi _2}({{X}})\, \cdots \,{{{\varPhi}} _l}({{X}})]^{\rm{T}}}$ |
以特征向量
| $\begin{aligned} f({{X}}) =& {\rm sgn} ({{w}} {{\varPhi}} ({{X}}) + b) = \\& \displaystyle {\rm sgn} (\sum\limits_{i = 1}^l {{{{a}}_{{i}}}{y_i}{{\varPhi}} ({{{X}}_i}) {{\varPhi}} ({{X}})} + b) \\ \end{aligned} $ | (4) |
利用核函数来求解向量的内积,则最优分类函数变为:
| $\begin{aligned} f({{X}}) = &{\rm sgn} ({{w}} {{\varPhi}} ({{X}}) + b) = \\ & \displaystyle{\rm sgn} (\sum\limits_{i = 1}^l {{{{a}}_{{i}}}{y_i}k({{{X}}_i},{{X}})} + b) \\ \end{aligned} $ | (5) |
其中,
在研究中发现,只有支持向量才对SVM的训练起积极作用,它们是非常重要的,对于SVM是不可或缺的,而其余的非支持向量对于分类超平面是不起作用的,甚至可能产生负面影响,比如增加了核矩阵的容量,降低了SVM的效率。GSVM也存在同样的问题,只有支持向量粒才对GSVM的训练起决定性作用。可以通过理论证明来说明这个观点的正确性。
定理1 粒度支持向量机的训练过程和训练结果与非支持向量粒无关。
证明 定义
| $\begin{array}{l} \displaystyle \mathop {\max }\limits_{{a}} g({{a}}) = \mathop {\max }\limits_{{a}} - \frac{1}{2}\sum\limits_{i = 1}^{l'} {\sum\limits_{j = 1}^{l'} {{a_i}} } {a_j}{{{Y}}_i}{{{Y}}_j}({{{X}}_i} {{{X}}_j}) + \sum\limits_{i = 1}^{l'} {{a_i}} \\ \displaystyle {\rm{s.t.}}\;\; \;\; \sum\limits_{i = 1}^l {{a_i}} {{{Y}}_i} = 0 , \; 0 \leqslant {a_i} \leqslant C,\; i = 1,2, \cdots ,\; l' \in {{\rm{I}}_{{\rm{sv}}}} \\ \end{array} $ | (6) |
要证明定理1,只需要证明式(2)和式(6)同解。用反正法,假设式(6)存在一个最优解
| $\begin{aligned} \displaystyle w({{{a}}'}) = \mathop {\max {\rm{ - }}}\limits_{{a}} \frac{1}{2}\sum\limits_{i = 1}^l {\sum\limits_{j = 1}^l {a_i'} } a_j'{y_i}{y_j}k({{{X}}_i},{{{X}}_j}) + \sum\limits_{i = 1}^l {{{a}}'}{\rm{ = }} \\ \displaystyle\mathop {\max }\limits_{{a}} {\rm{ - }}\frac{1}{2}\sum\limits_{i = 1}^{l'} {\sum\limits_{j = 1}^{l'} {a_i'} } a_j'{y_i}{y_j}k({{{X}}_i},{{{X}}_j}) + \sum\limits_{i = 1}^{l'} {{{a}}'}= {{ g(}}{{a}}'{\rm{)}} \\ \end{aligned} $ |
| $\begin{aligned} \displaystyle w({{{a}}^*}) = \mathop {\max {\rm{ - }}}\limits_{{a}} \frac{1}{2}\sum\limits_{i = 1}^l {\sum\limits_{j = 1}^l {a_i^*} } a_j^*{y_i}{y_j}k({{{X}}_i},{{{X}}_j}) + \sum\limits_{i = 1}^l {{{{a}}^*}}{\rm{ = }} \\ \displaystyle \mathop {\max }\limits_{{a}} {\rm{ - }}\frac{1}{2}\sum\limits_{i = 1}^{l'} {\sum\limits_{j = 1}^{l'} {a_i^*} } a_j^*{y_i}{y_j}k({{{X}}_i},{{{X}}_j}) + \sum\limits_{i = 1}^{l'} {{{{a}}^*}} = {{ g(}}{{{a}}^*}{\rm{)}} \end{aligned} $ |
可得
要想迅速地得到支持向量粒,节省粒化的时间,首先了解支持向量的特征,文献[13]对其特征做了归纳总结。
1)现实中,支持向量一般都是稀疏地聚集在训练数据集的边缘。
2)根据第一个特征,则每个类中心附近的数据不会是支持向量,即,离支持向量机超平面较近的数据比较可能是支持向量,这就为支持向量的选取提供了快速的获取方法。
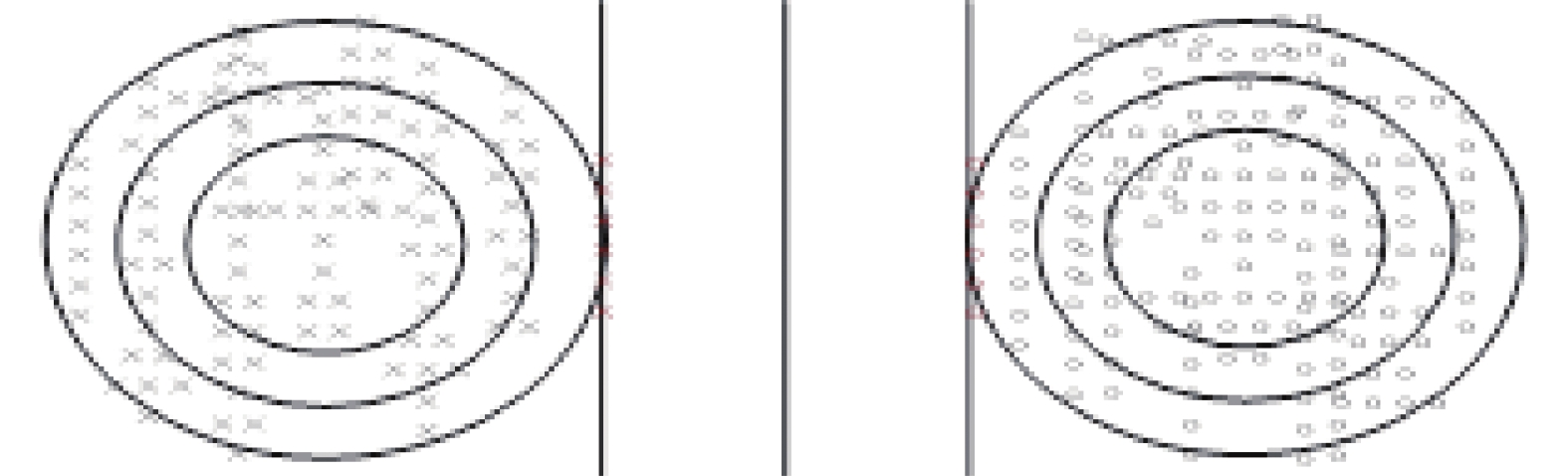
2.2 问题分析图1中,红色部分的数据是GSVM的支持向量粒,它们决定了分类超平面。并且从中可以看出,对于每一类,离类中心越远的点,就越有可能是支持向量粒。并且,从图1中还可以看出,落在每一个环上的样本,它们离类中心的距离差不多相等。离类中心越远的环就越有可能含有多的支持向量粒。基于这个思想,本文先把样本映射到核空间,按类标签的个数进行粗粒划分,确保相同标签的样本都在同一个粗粒中。然后,对于每一个粗粒,采用模糊聚类的方法进行粒化,具有相同隶属度的样本归为一个粒,进行细粒划分。每一个细粒就对应图1中的一个环,从图中可以看出,离粗粒中心越远的环,越靠近分类超平面,其是支持向量粒的可能性越大。而离粗粒中心越远的环,其隶属度越小。因此,给定一个阈值,当细粒的隶属度小于给定的阈值,就说明其处于粗粒的边缘,是支持向量粒,进而提取出支持向量粒.
|
Download:
|
| 图 1 支持向量分布图 Fig. 1 The distribution of support vectors | |
模糊核聚类(fuzzy kernel cluster, FKC)的主要思想是先将数据集映射到高维空间,然后直接在高维空间进行模糊聚类。而一般的聚类算法是直接在原始空间进行聚类划分。与其他的聚类算法相比,模糊核聚类引入了非线性映射,能够在更大程度上提取到有用的特征,聚类的效果会更好。
设原空间样本集为
| $\begin{aligned} {J_m} =& ({{X,U,V}}) = \\& \displaystyle \sum\limits_{i = 1}^C {\sum\limits_{j = 1}^N {u_{ij}^m} } {\left\| {{{\textit{Ø}}} ({x_j}) - {{\textit{Ø}}} ({v_i})} \right\|^2}{\rm{ = }} \\ & \displaystyle\sum\limits_{i = 1}^C {\sum\limits_{j = 1}^N {u_{ij}^m} } [k({x_j},{x_j}) - 2k({x_j},{v_i}) + k({v_i},{v_i})] =\\& \displaystyle \sum\limits_{i = 1}^C {\sum\limits_{j = 1}^N {u_{ij}^m} } d_{Kij}^2({x_j},{v_i}) ,\; 2 \leqslant C < N \\ \end{aligned} $ | (7) |
式中:
按模糊
| ${u_{ij}} = \frac{{{{[1/d_{Kij}^2({x_j},{v_i})]}^{1/(m - 1)}}}}{{\displaystyle\sum\limits_{j = 1}^C {{{[1/d_{Kij}^2({x_j},{v_i})]}^{1/(m - 1)}}} }}$ | (8) |
且有
| $ {{\textit{Ø}}} ({v_i}) = \frac{{\displaystyle\sum\limits_{k = 1}^N {u_{ik}^m} {{\textit{Ø}}} ({x_k})}}{{\displaystyle\sum\limits_{k = 1}^N {u_{ik}^m} }},\;\;\;i = 1,2, \cdots ,C $ | (9) |
为了最小化目标函数,需要计算
| $ k({x_j},{v_i}) = < {{\textit{Ø}}} ({x_j}),{{\textit{Ø}}} ({v_i}) > = \frac{{\displaystyle\sum\limits_{k = 1}^N {u_{ik}^m} k({x_k},{x_j})}}{{\displaystyle\sum\limits_{k = 1}^N {u_{ik}^m} }} $ | (10) |
| $ k({v_i},{v_i}) = < {{\textit{Ø}}} ({v_i}),{{\textit{Ø}}} ({v_i}) > = \frac{{\displaystyle\sum\limits_{k = 1}^N {\displaystyle\sum\limits_{s = 1}^N {u_{ik}^m} } u_{is}^mk({x_k},{x_s})}}{{{{\left( \displaystyle\sum\limits_{k = 1}^N {u_{ik}^m} \right)^2}}}} $ | (11) |
把式(9)~(11)代入式(7),可以求出模糊核
模糊核
1) 初始化参数:
2) 对训练数据集进行预处理;
3) 设置
4)计算隶属度
5) 计算新的
6) 若
目前,已有的粒度支持向量机算法模型大都是直接在原始空间对数据集进行粒化和提取,然后映射到核空间进行SVM的训练。然而,不同空间的转换,很有可能丢失了数据集的有用信息,降低学习器的性能。为了避免因数据在不同空间分布不一致而导致泛化能力不高的问题,本文采用模糊核聚类的方法直接在核空间对数据集进行粒化、提取和SVM的训练。基于以上思想,本文提出了基于模糊核聚类粒化的粒度支持向量机(fuzzy kernel cluster granular support vector machine, FKC-GSVM)。FKC-GSVM算法包括3部分:采用模糊核聚类进行粒度的划分;设定阈值,当每个粒子的隶属度大于规定的阈值时,认为这个粒子为非支持向量粒,丢弃,而剩余的粒子为支持向量粒;在核空间对支持向量粒进行SVM训练。具体的算法步骤如下:
1) 粗粒划分:以类标签个数
2) 细粒划分:采用模糊核聚类分别对
3) 支持向量粒的提取:给定一个阈值,当一个粒子的隶属度小于给定的阈值,提取这个粒子(支持向量粒),提取出来的支持向量粒组成了一个新的训练集;
4) 支持向量集的训练:在新的训练样本集上进行GSVM训练;
5) 泛化能力的测试:利用测试集测试泛化能力。
2.5 FKC-GSVM算法性能分析下面,从2个方面对FKC-GSVM的算法性能进行分析:
1) FKC-GSVM的收敛性分析
与SVM相比,FKC-GSVM采用核空间代替原始空间进行粒化,提取出支持向量粒后在相同的核空间进行GSVM训练,其训练的核心思想依然是采用支持向量来构造分类超平面,这与标准支持向量机相同。既然标准支持向量机是收敛的,则FKC-GSVM也是收敛的。但是由于FKC-GSVM剔除了大量对训练不起积极作用的非支持向量,直接采用支持向量来训练,所以它的收敛速度要快于标准支持向量机。
2) FKC-GSVM的泛化能力分析
评价一个学习器性能好坏的重要指标是其是否具有较强的泛化能力。众所周知,由于SVM采用结构风险最小(SRM)归纳原则,因此,与其他学习机器相比,SVM的泛化能力是很突出的。同样,FKC-GSVM也执行了SRM归纳原则,并且直接在核空间选取支持向量,确保了数据的一致性,具有更好的泛化性能。
3 实验结果及分析 3.1 UCI数据集上的实验为了验证FKC-GSVM的学习性能,本文在Matlab7.11的环境下对5个常用的UCI数据集进行实验,这5个数据集的描述如表1所示。在实验中,采用的核函数为高斯核函数,并且采用交叉验证方法选取惩罚参数
| 表 1 实验采用的数据集 Tab.1 Datasets used in experiments |
为了比较数据集在原空间粒化和在核空间粒化的不同效果,本文采用基于模糊聚类的粒度支持向量机(FCM-GSVM)、基于模糊核聚类的粒度支持向量机(FKC-GSVM)和粒度支持向量机(GSVM)等3种算法对5个典型的UCI数据集进行了测试,测试结果如表2所示。为了更直观地看出FKC-GSVM在不同阈值条件下的分类效果,给出了Contraceptive Method Choice数据集在不同阈值条件下采用FKC-GSVM分类的效果图,如图2~图5所示。
| 表 2 FCM-GSVM与FKC-GSVM测试结果比较 Tab.2 Comparison of test results between FCM-GSVM and FKC-GSVM |
FCM-GSVM和GSVM是在原空间进行粒度划分和支持向量粒的提取,然后把支持向量粒映射到高维空间进行分类,而FKC-GSVM是直接在核空间进行粒度划分和支持向量粒的提取,然后在相同的核空间进行分类。从表2的测试结果可以看出,由于FCM-GSVM和GSVM可能导致数据在原空间和核空间分布不一致,在相同的阈值条件下,其分类效果要比FKC-GSVM的分类效果差,这说明FKC-GSVM的泛化能力比FCM-GSVM的泛化能力强。
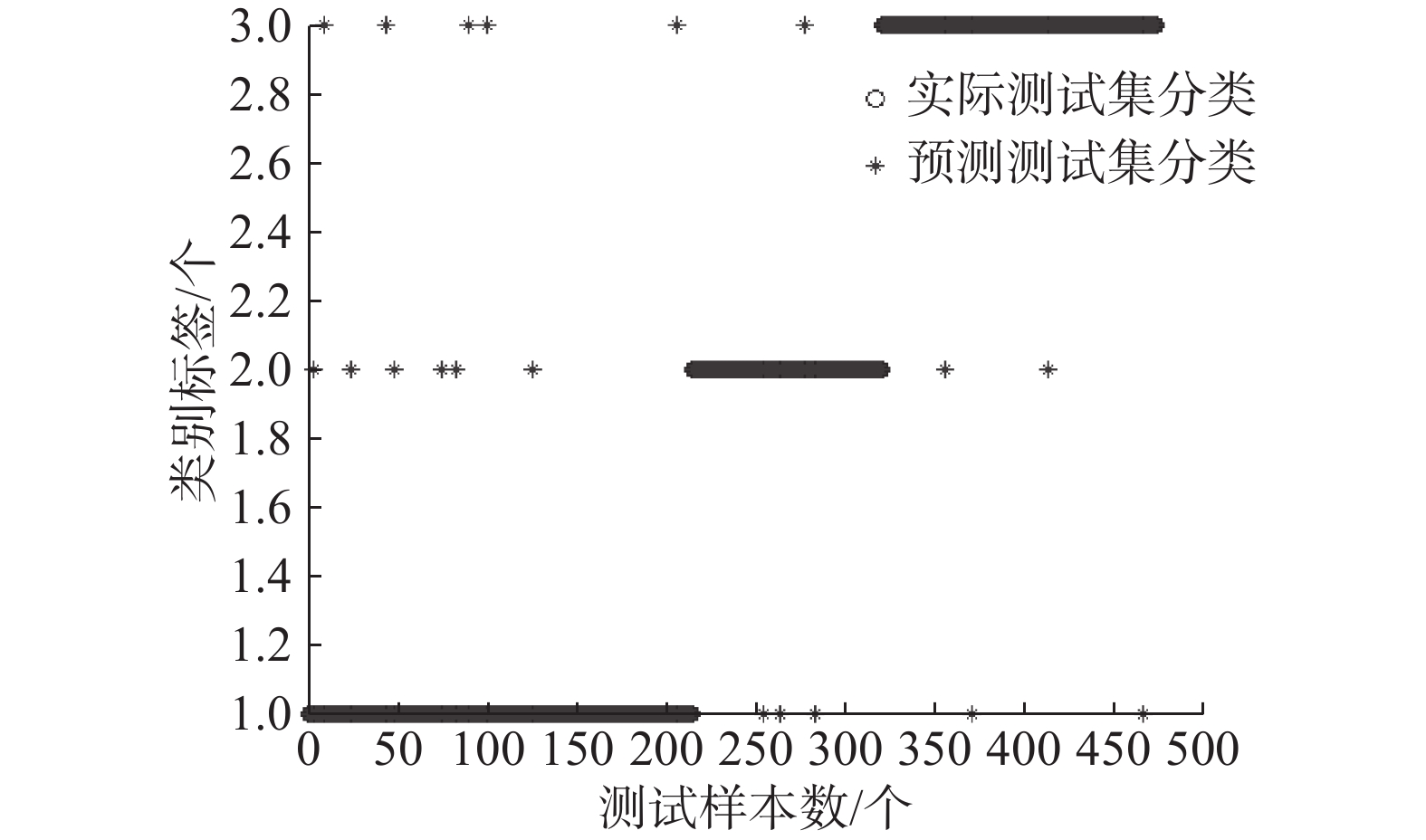
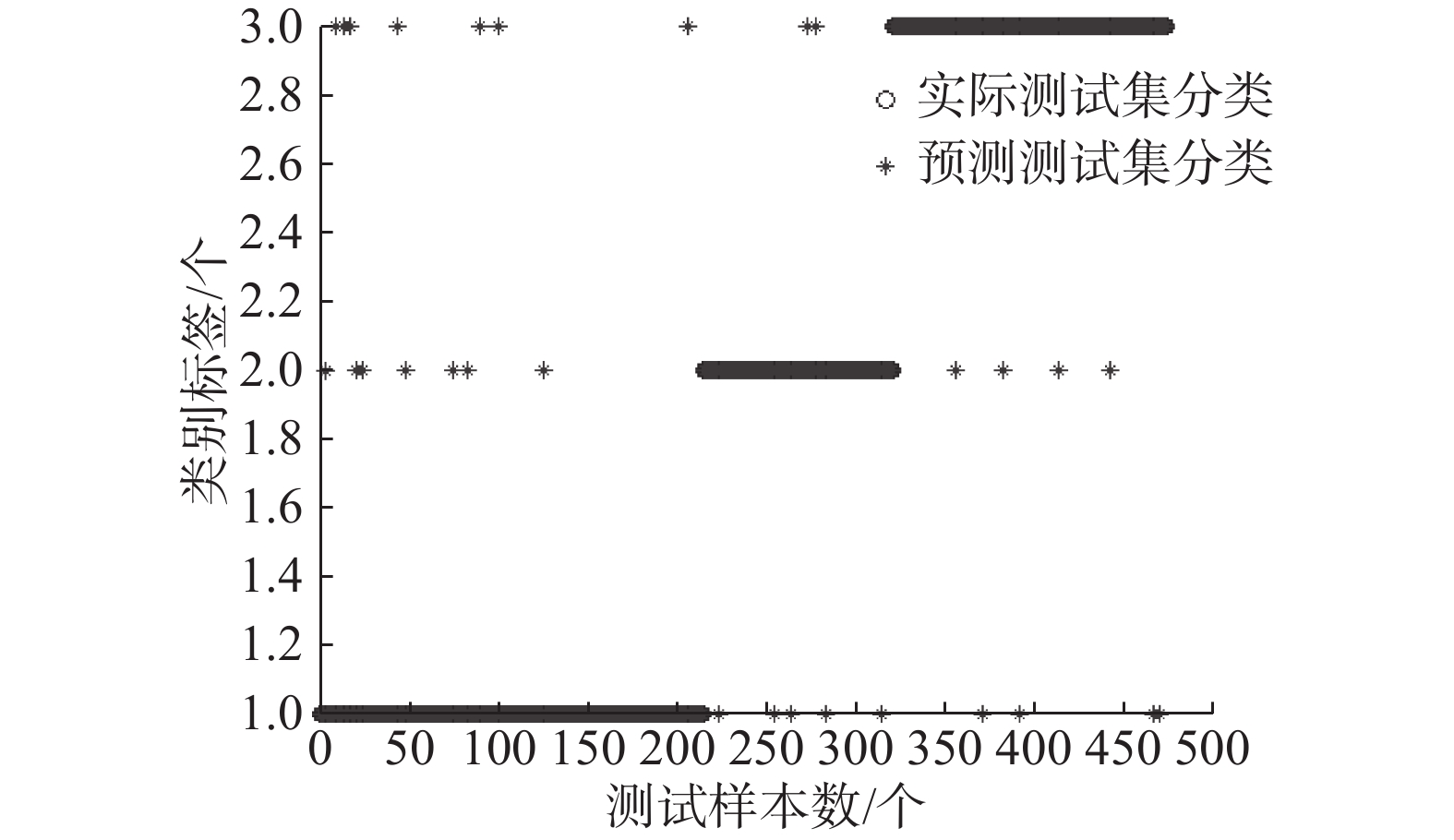
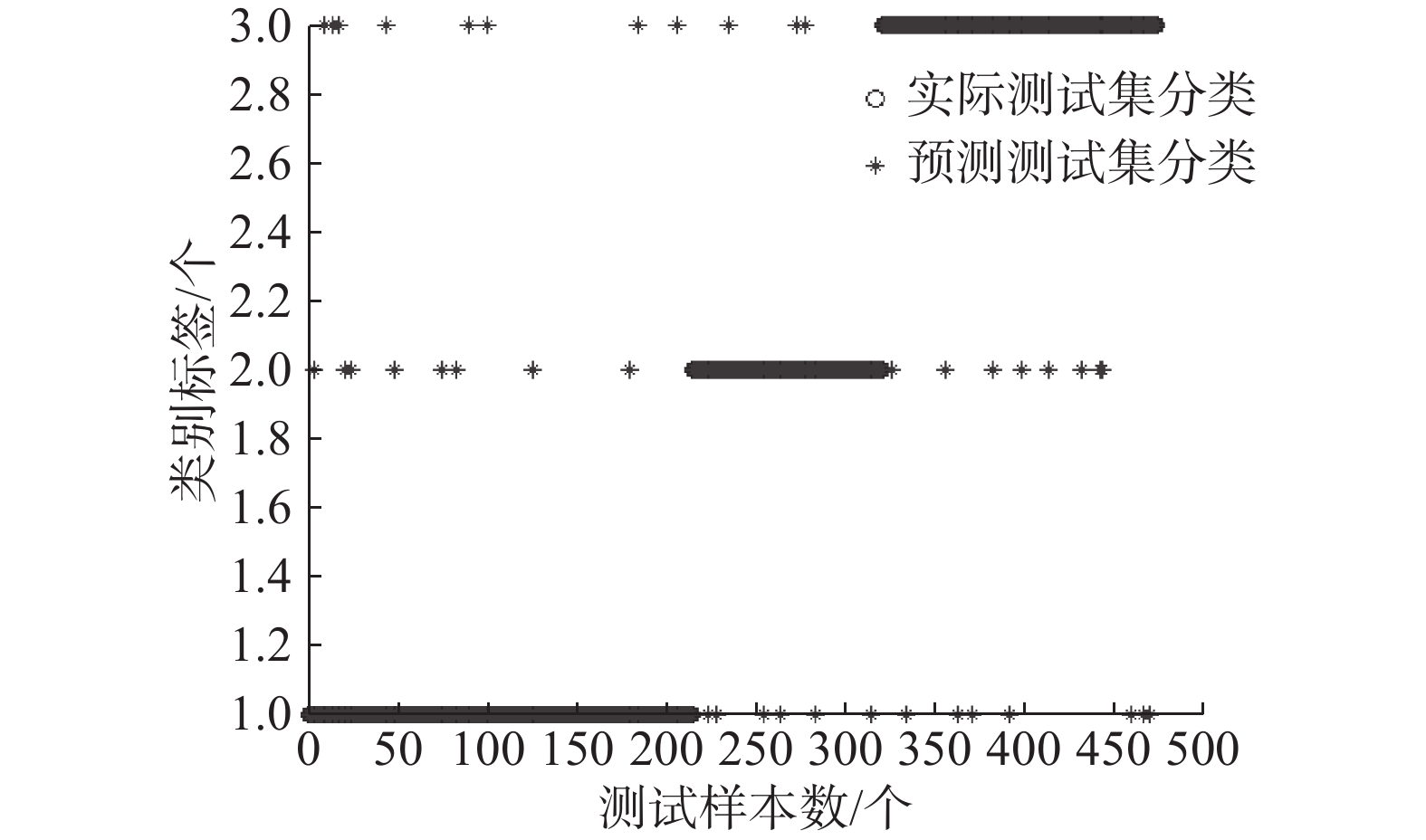
为了分析在不同阈值条件下FKC-GSVM的泛化性能,本文给出了0.9、0.85、0.8、0.75四个不同阈值条件下的实验。从表2可以看出,阈值越小,FKC-GSVM的分类效果越差,这是因为阈值越小,选取的支持向量粒就越少,这一过程可能丢失了一些支持向量,影响了分类效果。但是阈值越小,大大压缩了训练样本集,算法训练的速度得到了很大的提高。因此,对于大规模样本来说,只要在能接受的分类效果的范围内,选取合适的阈值,采用FKC-GSVM就能快速地得到需要的分类效果。图2~5是Contraceptive Method Choice数据集在不同阈值条件下采用FKC-GSVM分类的效果图,从这几个图中可以很直观地看出,FKC-GSVM的分类效果还是比较令人满意的。
|
Download:
|
| 图 2 FKC-GSVM在阈值为0.9条件下的分类效果 Fig. 2 The classification results of FKC-GSVM under the threshold 0.9 | |
|
Download:
|
| 图 3 FKC-GSVM在阈值为0.85条件下的分类效果 Fig. 3 The classification results of FKC-GSVM under the threshold 0.85 | |
|
Download:
|
| 图 4 FKC-GSVM在阈值为0.8条件下的分类效果 Fig. 4 The classification results of FKC-GSVM under the threshold 0.8 | |
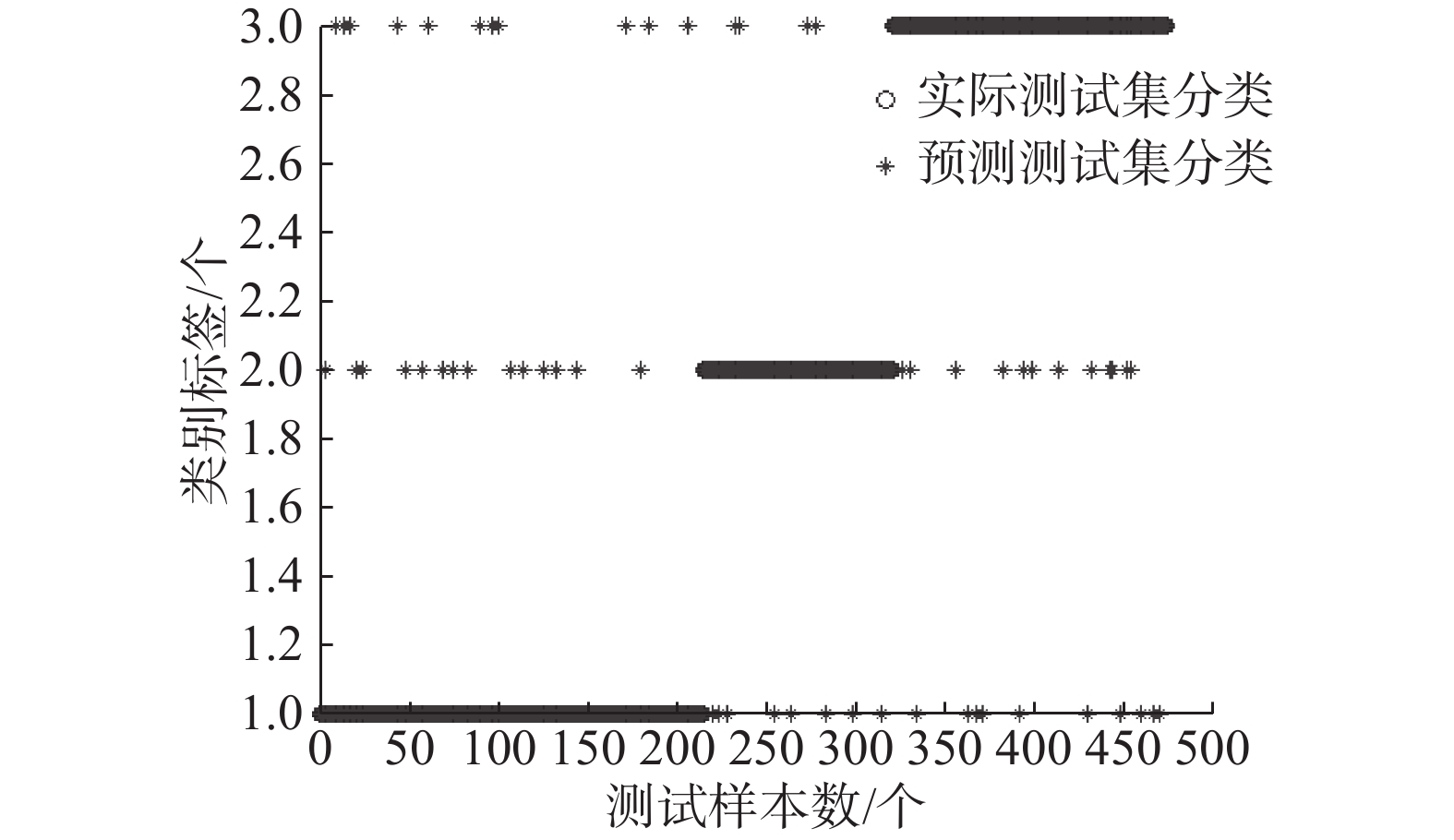
|
Download:
|
| 图 5 FKC-GSVM在阈值为0.75条件下的分类效果 Fig. 5 The classification results of FKC-GSVM under the threshold 0.75 | |
为了测试FKC-GSVM处理大数据集的性能,在实验中,采用的数据集是NDC大数据集 [20],是由David Musicant’s NDC数据产生器产生的,NDC数据集的描述如表3所示。在实验中,FKC-GSVM的测试结果将与现在比较流行的孪生支持向量机(twin support vector machines, TWSVM)的测试结果[20]从测试精度和运行时间2方面进行对比。其中,FKC-GSVM的运行环境、参数设置方法和实验3.1一样,阈值
| 表 3 实验采用的NDC数据集 Tab.3 NDC datasets used in experiments |
| 表 4 2种算法对NDC数据集的测试结果 Tab.4 Comparison of two algorithms on NDC datasets |
从表3中可以看出,本实验测试的对象为5种数据集,NDC-3L的训练样本数为300 000个,而NDC-1m的样本增加到了1 000 000个,同样,测试样本也从30 000增加到了100 000,特征数都是32维。这3个数据集主要是为了测试算法在处理维度一样而数据量不断增加时候的学习性能。为了进一步测试学习算法处理高维样本的性能,NDC1和NDC2这2个数据集的维数分别是100和1 000,设置他们的训练样本量和测试样本量都一样,都是5 000。
实验结果如表4所示,从中可以看出,当数据集为NDC-1m时,由于训练时间过高,采用TWSVM算法无法将实验进行下去。然而,FKC-GSVM在处理NDC-1m数据集时能够在合理的运行时间内得到较满意的精度解,这表明了FKC-GSVM在处理大数据时是具有优势的。同样,在处理NDC1和NDC2这2个高维数据集时,从表4可以明显看出,FKC-GSVM处理高维数据的效果也是不错的。实验结果充分说明了FKC-GSVM的学习能力比TWSVM的强,更适合于处理大数据集。
4 结束语GSVM是将训练样本在原空间粒化后再映射到核空间,这将导致数据与原空间的分布不一致,从而降低了GSVM的泛化能力。为了解决这个问题,本文提出了一种基于模糊核聚类粒化的粒度支持向量机方法(FKC-GSVM)。FKC-GSVM通过利用模糊核聚类直接在核空间对数据进行粒的划分和支持向量粒的选取,然后在相同的核空间中进行支持向量粒的GSVM训练,在标准数据集的实验说明了FKC-GSVM算法的有效性。但是阈值参数的选取仍具有一定的随意性,影响了FKC-GSVM的性能。如何自适应地调整合适的阈值,将是下一步要研究的工作内容。
| [1] |
VAPNIK V N. The nature of statistical learning theory[M]. New York: Springer-Verlag, 1995.
( 0) 0)
|
| [2] |
丁世飞, 张健, 张谢锴, 等. 多分类孪生支持向量机研究进展[J]. 软件学报, 2018, 29(1): 89-108. DING Shifei, ZHANG Jian, ZHANG Xiekai, et al. Survey on multi class twin support vector machines[J]. Journal of software, 2018, 29(1): 89-108. (  0) 0)
|
| [3] |
AN Yuexuan, DING Shifei, SHI Songhui, et al. Discrete space reinforcement learning algorithm based on support vector machine classification[J]. Pattern recognition letters, 2018, 111: 30-35. DOI:10.1016/j.patrec.2018.04.012 ( 0) 0)
|
| [4] |
谢娟英, 谢维信. 基于特征子集区分度与支持向量机的特征选择算法[J]. 计算机学报, 2014, 37(8): 1704-1718. XIE Juanying, XIE Weixin. Several feature selection algorithms based on the discernibility of a feature subset and support vector machines[J]. Chinese journal of computers, 2014, 37(8): 1704-1718. (  0) 0)
|
| [5] |
YAO Y Y. Granular computing: basic issues and possible solution[C]//Proceedings of the 5th Joint Conference on Information Sciences. Atlantic City, USA, 2000: 186–189.
( 0) 0)
|
| [6] |
DING Shifei, XU Li, ZHU Hong, et al. Research and progress of cluster algorithms based on granular computing[J]. International journal of digital content technology and its applications, 2010, 4(5): 96-104. DOI:10.4156/jdcta.vol4.issue5.11 ( 0) 0)
|
| [7] |
TANG Yuchun, JIN Bo, SUN Yi, et al. Granular support vector machines for medical binary classification problems[C]//Proceedings of 2004 IEEE Symposium on Computational Intelligence in Bioinformatics and Computational Biology. La Jolla, CA, USA, 2004: 73–78.
( 0) 0)
|
| [8] |
TANG Yuchun, JIN Bo, ZHANG Yanqing. Granular support vector machines with association rules mining for protein homology prediction[J]. Artificial intelligence in medicine, 2005, 35(1/2): 121-134. ( 0) 0)
|
| [9] |
冯昌, 廖士中. 随机傅里叶特征空间中高斯核支持向量机模型选择[J]. 计算机研究与发展, 2016, 53(9): 1971-1978. FENG Chang, LIAO Shizhong. Model selection for Gaussian kernel support vector machines in random Fourier feature space[J]. Journal of computer research and development, 2016, 53(9): 1971-1978. DOI:10.7544/issn1000-1239.2016.20150489 (  0) 0)
|
| [10] |
段丹青, 陈松乔, 杨卫军, 等. 使用粗糙集和支持向量机检测入侵[J]. 小型微型计算机系统, 2008, 29(4): 627-630. DUAN Danqing, CHEN Songqiao, YANG Weiping, et al. Detect intrusion using rough set and support vector machine[J]. Journal of Chinese computer systems, 2008, 29(4): 627-630. (  0) 0)
|
| [11] |
李涛, 刘学臣, 张帅, 等. 基于混合编程模型的支持向量机训练并行化[J]. 计算机研究与发展, 2015, 52(5): 1098-1108. LI Tao, LIU Xuechen, ZHANG Shuai, et al. Parallel support vector machine training with hybrid programming model[J]. Journal of computer research and development, 2015, 52(5): 1098-1108. DOI:10.7544/issn1000-1239.2015.20131492 (  0) 0)
|
| [12] |
丁世飞, 黄华娟. 最小二乘孪生参数化不敏感支持向量回归机[J]. 软件学报, 2017, 28(12): 3146-3155. DING Shifei, HUANG Huajuan. Least squares twin parametric insensitive support vector regression[J]. Journal of software, 2017, 28(12): 3146-3155. (  0) 0)
|
| [13] |
张鑫. 粒度支持向量机学习方法研究[D]. 太原: 山西大学, 2009. ZHANG Xin. Research on granular support vector machine learning method[D]. Taiyuan: Shangxi University, 2009. (  0) 0)
|
| [14] |
DING Shifei, AN Yuexuan, ZHANG Xiekai, et al. Wavelet twin support vector machines based on glowworm swarm optimization[J]. Neurocomputing, 2017, 225: 157-163. DOI:10.1016/j.neucom.2016.11.026 ( 0) 0)
|
| [15] |
KUMAR M A, GOPAL M. Application of smoothing technique on twin support vector machines[J]. Pattern recognition letters, 2008, 29(13): 1842-1848. DOI:10.1016/j.patrec.2008.05.016 ( 0) 0)
|
| [16] |
黄华娟. 孪生支持向量机关键问题的研究[D]. 徐州: 中国矿业大学, 2014. HUANG Huajuan. Research on the key problems of twin support vector machines[D]. Xuzhou: China University of Mining and Technology, 2014. (  0) 0)
|
| [17] |
郭虎升, 王文剑, 张鑫. 基于粒度核的支持向量机学习算法[C]// 第三届中国粒计算联合会议. 河北, 石家庄, 2009.95−97: 155.
( 0) 0)
|
 2019, Vol. 14
2019, Vol. 14


