当前,LSTM作为深度学习的一种处理序列数据最为流行的解决方案,拥有着较传统方案更加实用性强且准确率高的特点[1-2]。但是,基于深度学习的代价敏感决策仍未得到主流的研究关注。当前的研究重点多集中于如何更高效的获得精确的整体准确率。在有关于深度学习的代价敏感分类或决策问题上,当前的算法常见解决方案多集中于通过对数据的预处理和运行参数调整的方式来使分类器获得对某一类代价敏感类别更高的关注从而实现减少整体的代价[3]。但是这种方法的缺点如前文所述。为了训练对高代价分类敏感的模型,筛选出的数据集将会面临严重的数据不平衡问题。而无论是填充或者再平衡的方式,都会使原数据集的结构改变[4]。其次,无论是对数据集的预处理还是对运行参数或者模型结构的调整,都与具体问题相关性较大[5-7]。对于不同的具体问题,数据清洗和参数调整或模型调整的优劣与模型设计者的经验与对问题的了解有着较大的关系。并且,对于不同的问题,相同的解决方案并不能保证稳定的表现。在不同的数据集之间,相同的数据清洗和参数调整所带来的模型上的改变影响是不同的。
基于此,本文提出的将三支决策运用于深度学习模型能够一定程度上解决上述问题。1) 三支决策算法的理论基础为粗糙集理论,以分类置信度为基础判断决策或分类代价。从算法逻辑的角度,三支决策算法要求更高的全局分类的准确性而不是对单独高代价类的分类,此特点使得三支决策算法与更高的更广泛的分类算法优点相结合,在前置分类器不用做出改动或者调整的情况下降低决策的风险。2) 三支决策算法倾向于判断单独决策。因此,新改进的算法将避免在正常预处理的前提下,将避免因平衡特殊分类类别而造成的数据重新扩展或裁剪,从而进一步影响数据平衡问题。综上,结合三支决策的LSTM模型可以在原先的深度模型的基础上,进一步增强模型在代价敏感问题上的表现。
1 相关工作 1.1 三支决策三支决策[8]是Y.Y.Yao由概率粗糙集理论提出的一种新决策思想。相较于传统的“是,否”二支决策而言,三支决策提出了一种不同但是更合理的决策思想,即当对象当前提供的信息不足以支撑决策时,采用延迟决策,等待更多信息来完成最终决策。所以,三支决策可以规避分类信息不足时盲目决策造成的风险。
三支决策在进行分类决策前,需对样本进行域的划分。划分的原理基于粗糙集理论。按照粗糙集的定义,根据元素
在决策粗糙集公式化描述中,
| 表 1 三支决策的损失函数 Tab.1 Loss function of 3WD |
根据最小风险决策规则:
(P)当
(B)当
(N)当
其中
| $ {\rm{\alpha }} = \frac{{{{\rm{{\textit{λ}} }}_{{\rm{PN}}}} - {{\rm{{\textit{λ}} }}_{{\rm{BN}}}}}}{{\left( {{{\rm{{\textit{λ}} }}_{{\rm{PN}}}} - {{\rm{{\textit{λ}} }}_{{\rm{BN}}}}} \right) + \left( {{{\rm{{\textit{λ}} }}_{{\rm{BP}}}} - {{\rm{{\textit{λ}} }}_{{\rm{PP}}}}} \right)}} $ | (1) |
| $ {\rm{\beta }} = \frac{{{{\rm{\textit{λ} }}_{{\rm{BN}}}} - {{\rm{\textit{λ} }}_{{\rm{NN}}}}}}{{\left( {{{\rm{\textit{λ} }}_{{\rm{BN}}}} - {{\rm{\textit{λ} }}_{{\rm{NN}}}}} \right) + \left( {{{\rm{\textit{λ} }}_{{\rm{NP}}}} - {{\rm{\textit{λ} }}_{{\rm{NP}}}}} \right)}} $ | (2) |
且
| $ 0 \leqslant {\rm{\beta }} < \alpha \leqslant 1 $ | (3) |
LSTM是由Hoehreiterhe与Schmiduhber于1997年提出后经过大量的改进,目前被广泛应用[9],成为目前处理序列与时序问题上的热门方案。LSTM是由一般的RNN改进而来。LSTM与一般的RNN的主要区别是在LSTM中的神经元不再是由单纯的神经元组成而是由4个功能不同的门来共同作用。其中包括了输入门、输出门、状态门,以及遗忘门。具体的结构如图1所示。
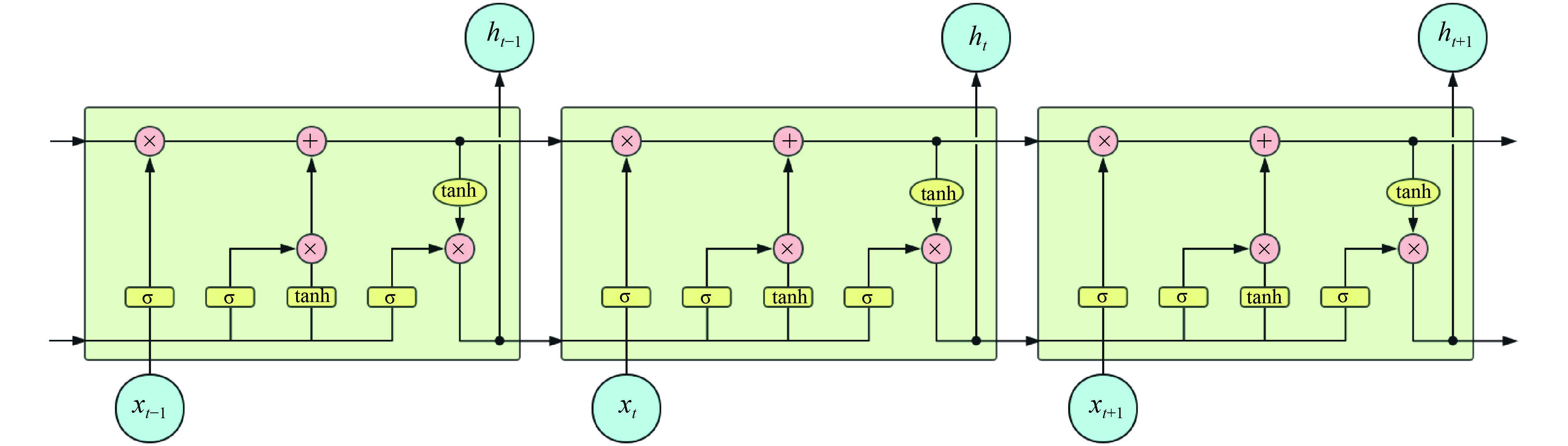
|
Download:
|
| 图 1 LSTM网络结构 Fig. 1 LSTM network structure | |
LSTM的独特结构是为了使其能够解决长期依赖问题而专门设计的。不同于RNN网络,LSTM的重复结构是由更加复杂的3个门相互连接而成。包括遗忘门、输入门与输出门。
式(4)~(9)描述了细胞内各个门的处理流程。
| $ {f_t} = \sigma \left( {{W_f} \cdot \left[ {{h_{t - 1}},{x_t}} \right] + {b_f}} \right) $ | (4) |
| $ {i_t} = {\rm{\sigma }}\left( {{W_i} \cdot \left[ {{h_{t - 1}},{x_t}} \right] + {b_i}} \right) $ | (5) |
| $ \widetilde {{C_t}} = {\rm tanh}\left( {{W_C} \cdot \left[ {{h_{t - 1}},{x_t}} \right] + {b_C}} \right) $ | (6) |
| $ {C_t} = {f_t}{\cdot }{C_{t - 1}} + {i_t}{\cdot}\widetilde {{C_t}} $ | (7) |
| $ {o_t} = {\rm{\sigma }}\left( {{W_o} \cdot \left[ {{h_{t - 1}},{x_t}} \right] + {b_o}} \right) $ | (8) |
| $ {h_t} = {o_t}{\cdot}{\rm tanh}\left( {{C_t}} \right) $ | (9) |
式(4)描述了遗忘门决定了当细胞更新时细胞状态会丢弃什么信息。该门会读取
式(5)描述输入门决定了让多少新的信息加入到细胞状态中。第一步,细胞输入
式(6)描述了更新内容
式(7)描述了更新内容
最终输出数据由式(8)的输出与当前细胞状态的一部分共同决定输出的最终值,如式(9)描述。
以上为LSTM模型的基本工作流。
1.3 代价敏感分类一般的,对于分类算法的研究的核心与重点为如何取得更高的分类准确率,但事实上,只要有误差存在,分类过程总会产生代价。而代价敏感分类就是关注如何使分类过程中产生的代价最小。根据问题的难易程度,代价敏感问题常被分为二分类与多分类问题。对于二分类问题,目前大部分的代价敏感分类多是从非代价敏感分类算法加以转化得到的。
结合上述,可将代价敏感分类等价于一个优化问题: 将实例使用分类算法
| $L\left( {x,i} \right) = \mathop \sum \limits_j P\left( {j{\rm{|}}x} \right)c\left( {i,j} \right) $ | (10) |
式中:
对于每个类别
在如何使算法获得倾向性的问题上,有两种经典算法:1)通过预处理,使算法对某些结果具有敏感性,此方法称为rescaling[11];2)希望通过以代价为基准修改不同分类在算法中的成员可能性,从而产生不同的倾向性。此方法称为reweighted[12]。
2 基于LSTM的三支决策分类算法基于三支决策的LSTM算法在原有的LSTM基础上,增加了三支决策步骤,对前端分类器给出的预测结果做出接受、拒绝、延迟3种不同的方案,算法流程如图2所示。
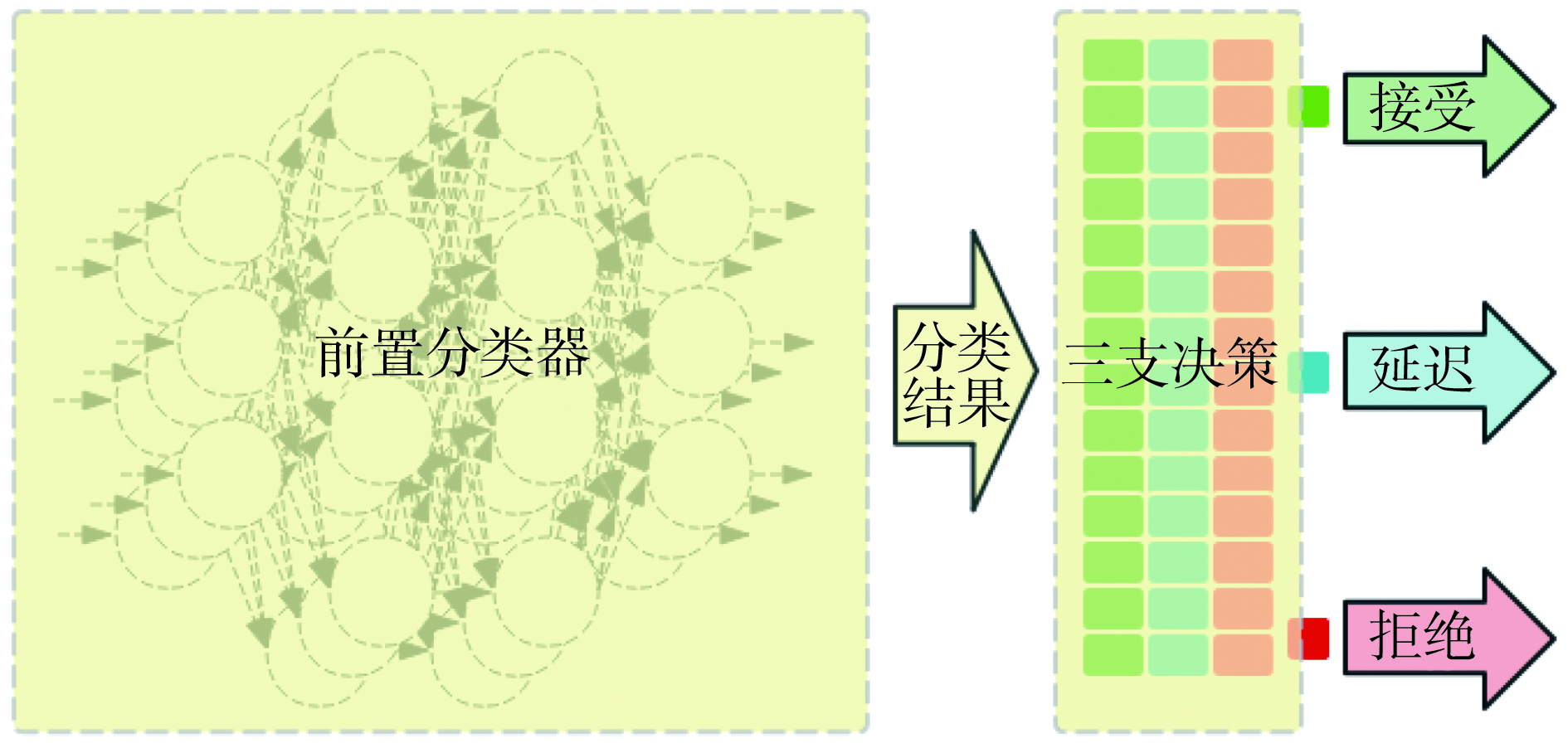
|
Download:
|
| 图 2 基于LSTM的三支决策算法流程 Fig. 2 Flow of 3WD based on LSTM | |
算法包括两部分:1) 前置分类器,用于初步分类;2) 三支决策,考虑决策风险,通过算法的判断降低决策风险。
2.1 前置分类器前置分类器的作用主要体现在前置分类器的分类精度最终决定了整体上的分类效果。此后的三支决策对前置分类器的分类结果做出评判,决定接受、拒绝、或者延迟推断。对于LSTM分类器,主要用来解决分类和时序问题预测。输出包括预测结果
三支决策对前置分类器给出的结果进行分析。根据式(1)~(3),可以得出相应的判断代价
将根据前置分类器的分类结果
| $ \begin{array}{l} \left( {\rm Pli} \right){\rm IF}\;\;{\rm Pr}\left( {X{\rm{|}}{u_i}} \right) \geqslant {\alpha _i},\;\;{\rm THEN}\;\;{u_i} \in {\rm POS}\left( X \right)\\ \left( {\rm Bli} \right)\;{\rm IF}\;{\beta _i} < Pr\left( {X{\rm{|}}{u_i}} \right) < {\alpha _i},\;{\rm THEN}\;{u_i} \in {\rm BND}\left( X \right)\\ \left( {\rm Nli} \right)\;{\rm IF}\;{\rm Pr}\left( {X{\rm{|}}{u_i}} \right) \leqslant {\beta _i},\;{\rm THEN}\;{u_i} \in {\rm NEG}\left( X \right) \end{array} $ |
结合上述分析,本文提出基于LSTM与三支决策的代价敏感分类算法,算法描述如下:
BEGIN:
1) 输入
2)
3) 输入
4) 计算边界
5) FOR 样本
计算分类概率
IF
ELSE IF
ELSE:
6)
7) IF
GOTO 2
END
3 实验与结果实验在自建实验平台中运行。实验平台包括4台服务器,每台服务器均使用相同的配置。每台服务器有6个CPU,主频2.5 GHz,运行内存16 GB。
测试数据集来自UCI开放数据集中的Beijing PM2.5 Data Set与International airline passengers。数据集均为分类任务。
PM2.5数据集来自于UCI数据库,该数据集记录了从2010年1月1日至2014年12月31日北京市的空气质量指数和气象数据。数据集为时间序列数据,特征为连续特征,任务可作为分类或回归任务。数据一共43 824条记录,特征共13个,部分数据缺失。
数据集中包括了时间,当日的温度、湿度、气压、风向、累计风速、累计降雨/降雪量、PM2.5指数共13个数据。其中的PM2.5指数为当日PM2.5值,为连续实数。当预测PM2.5值时,问题为回归问题。若以判断PM2.5区间作为空气质量判断时,问题为分类问题。本例中,将原数据集中的PM2.5均分为4个区间,从小到大分别标记为[优,良,一般,差]4类。根据前
图3表示了原数据集中,PM2.5与气象数据的关系。图4表示了两段分类结果的分布信息。

|
Download:
|
| 图 3 原始数据集中的特征分布 Fig. 3 Frequency of features in this dataset | |

|
Download:
|
| 图 4 原数据集中分类结果与时间的变化关系 Fig. 4 Relations between classify result and time change | |
从图4可以看出,空气质量与时间有明显的关系,并且呈现出一定的周期规律。
国际旅行旅客数据集包括了1949—1960年12年之间每个月的国际航线航班旅客人数。共144个数据,单位为1千人。图5为原数据集中数据的分布。
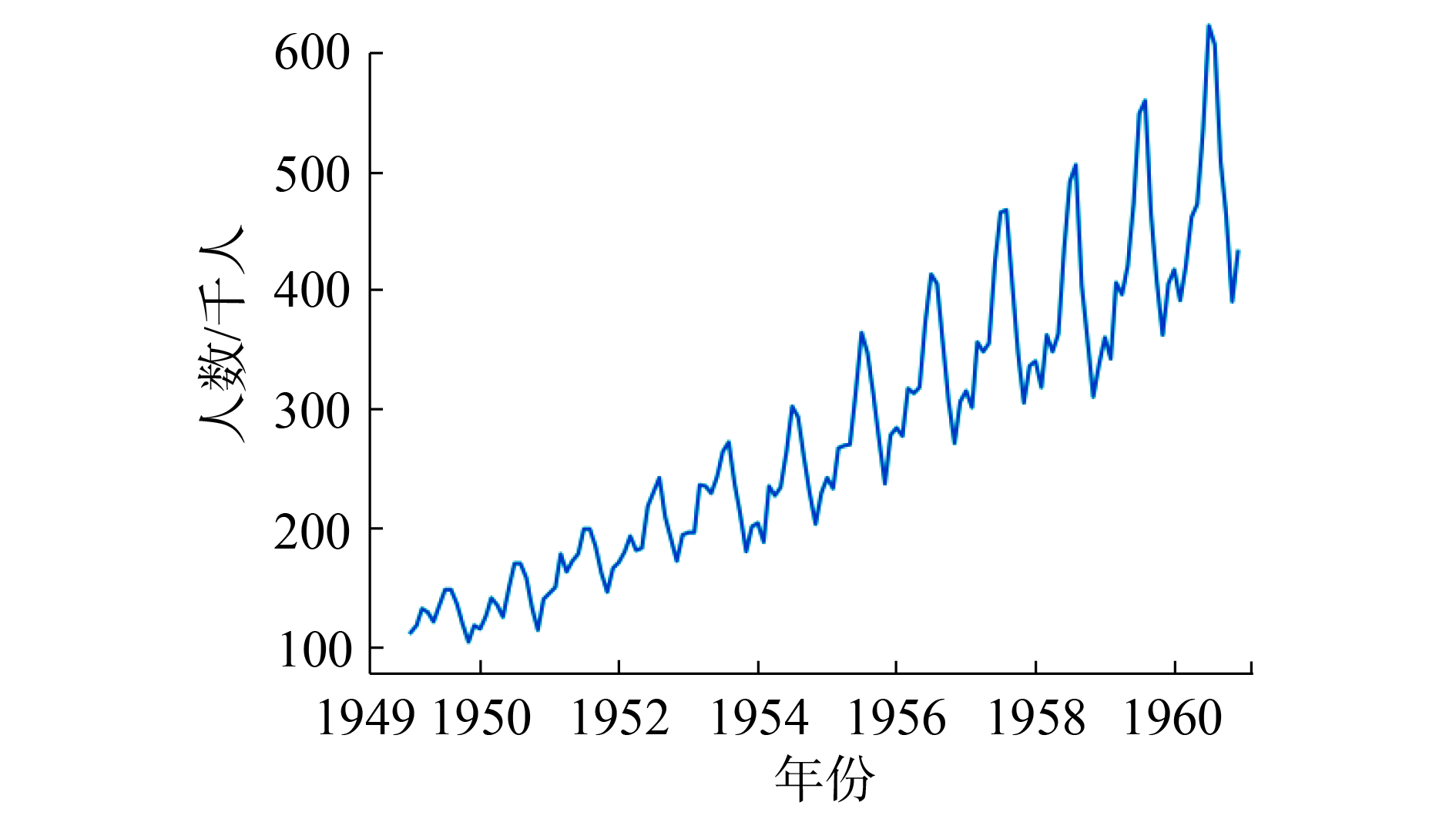
|
Download:
|
| 图 5 1949—1960年国际航班旅客人数 Fig. 5 Number of international airline traveler between 1949—1960 | |
根据前述对数据集的分析,将数据通过前置分类器进行回归分析,得到分类结果。此LSTM分类器在数据集上的分类准确率为0.997。由于为多分类问题,参考指标由准确率−召回率改为混淆矩阵。此分类器在测试数据上的结果混淆矩阵见图6。图7为分类器训练的最终损失函数。
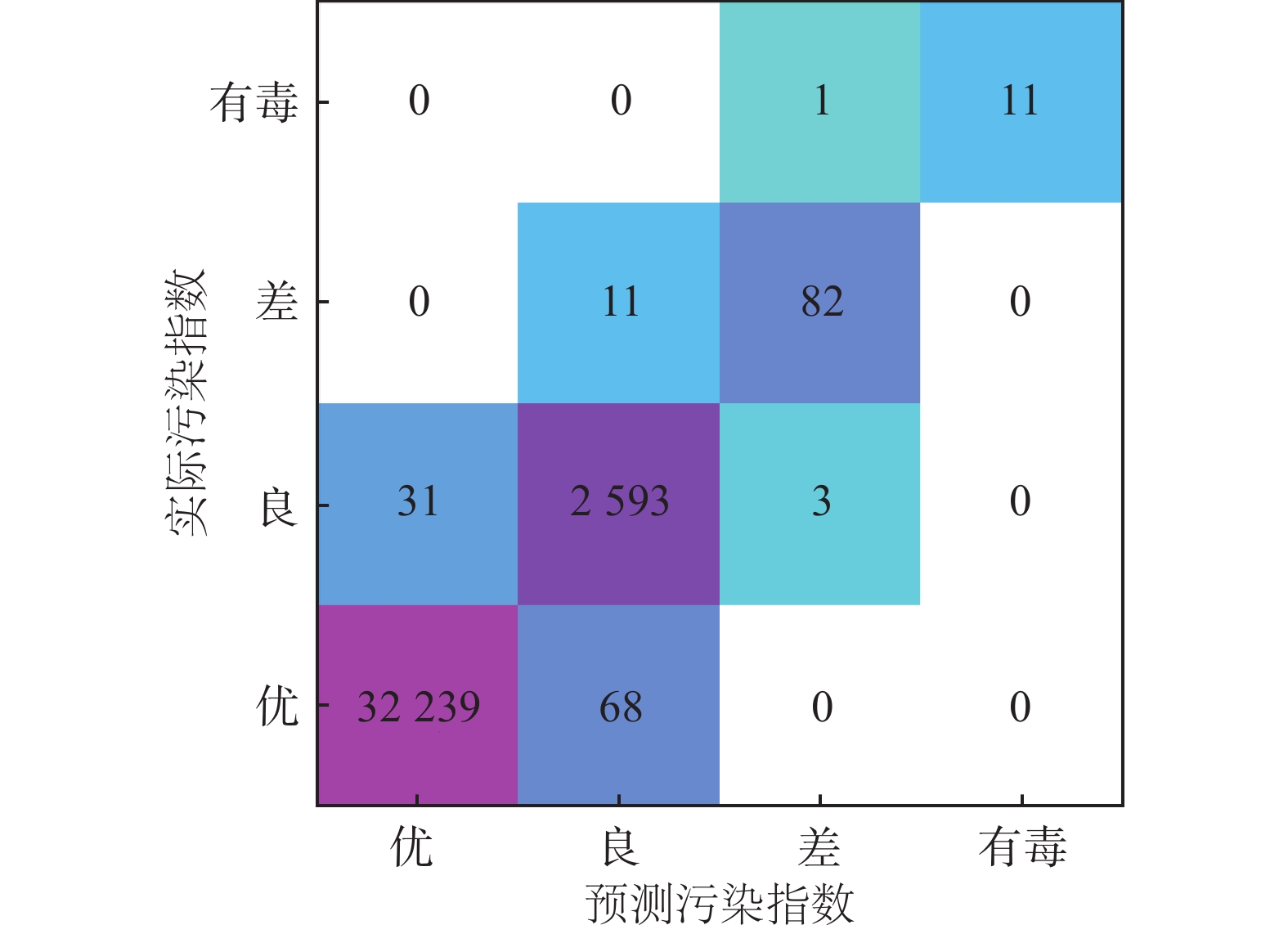
|
Download:
|
| 图 6 分类结果的混淆矩阵 Fig. 6 Confusion matrix of classification result | |

|
Download:
|
| 图 7 LSTM训练损失 Fig. 7 Loss of LSTM training | |
设代价函数为:
| $ {\rm{\lambda }} = \mathop \sum \limits_{{i}} {{\rm{\lambda }}_{{{ix}}}}{{{w}}_{{{ix}}}} + {{b}} $ | (11) |
式中:
将预测结果代入式(11)后, 得到原分类器的决策代价。
将得到的损失偏差与代入三支决策的决策规则 (Pli、Bli、Nli) 中,对明显偏离预测中心的值进行标记,得到新的分类代价。
表2可知,使用三支决策算法进行判断的分类任务在代价优化上有显著作用。
| 表 2 使用三支决策的分类代价与未使用三支决策的分类代价对比 Tab.2 Compara of cost of classification between 3WD and non-3WD |
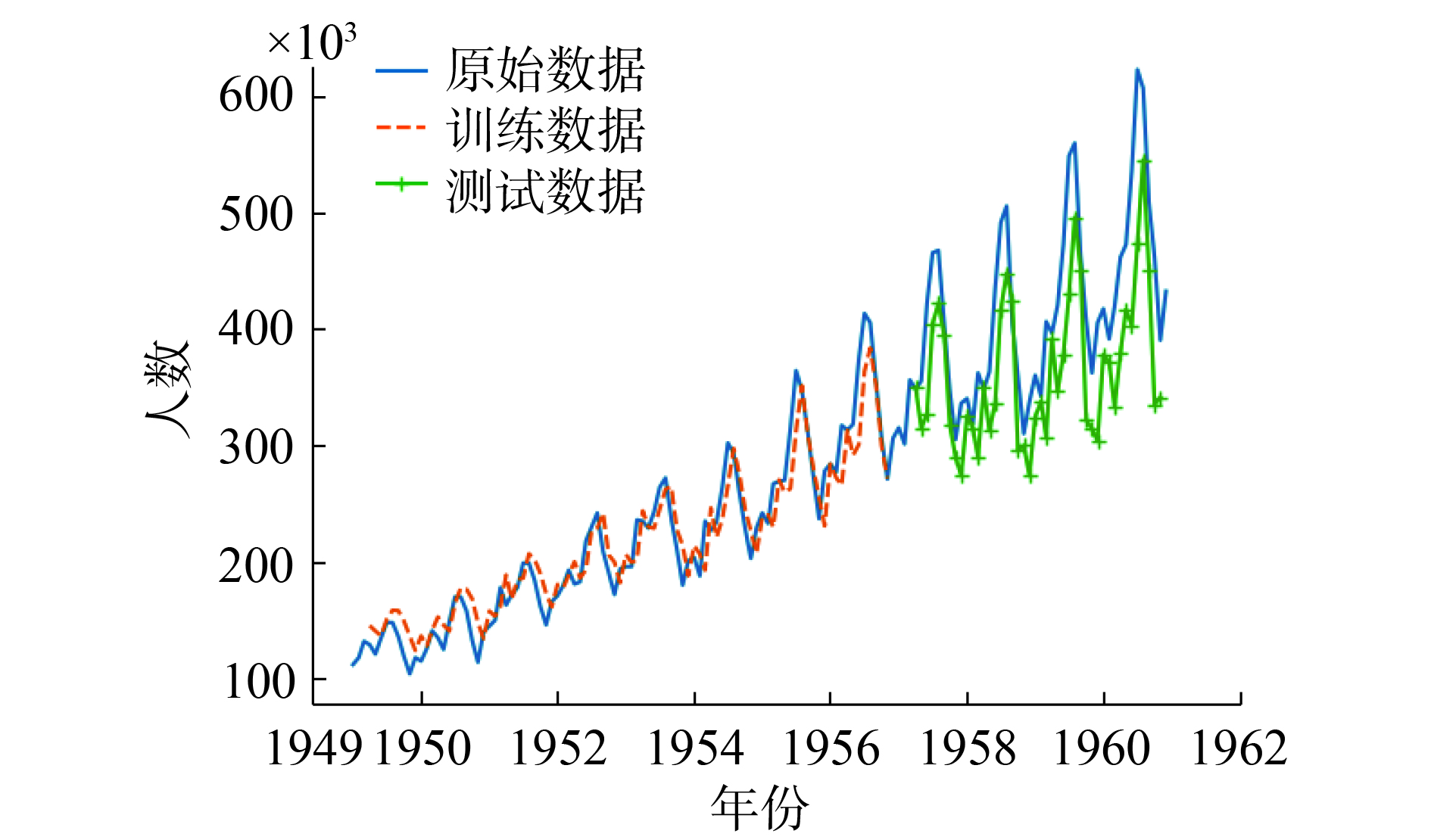
根据前述数据集的基本信息,将数据集进行前期分类。图8为LSTM作为前置分类器的预测数据。取预测步长为3,预测网络两层,每层含128个LSTM单元。
|
Download:
|
| 图 8 经过前置分类器的预测数据 Fig. 8 Predict data after preprocessing | |
显然,随着时间推移,距预测点较远的点预测误差越大。在整个数据集上,前置分类器的测试数据均方误差为28.03。
对于回归问题,由于没有直接的方式判断分类的正误,本文使用均方误差
| $\textit{λ} = \mathop \sum \limits_{i \in \left\{ {P,B,N} \right\},j \in \left\{ {X,\neg X} \right\}} {\textit{λ} _{i,j}}{w_{i,j}} + b $ | (12) |
但是与前述判断规则(Pli、Bli、Nli)不同,此时的分类不再是由有限的状态集合
| $ {{\rm{\textit{λ} }}_{{{i}},{{j}}}} \sim {{f}}\left( {{\hat{\rm \theta }},{{{t}}_{{n}}}} \right) $ | (13) |
式中:
本例中,为方便计算,假设分布
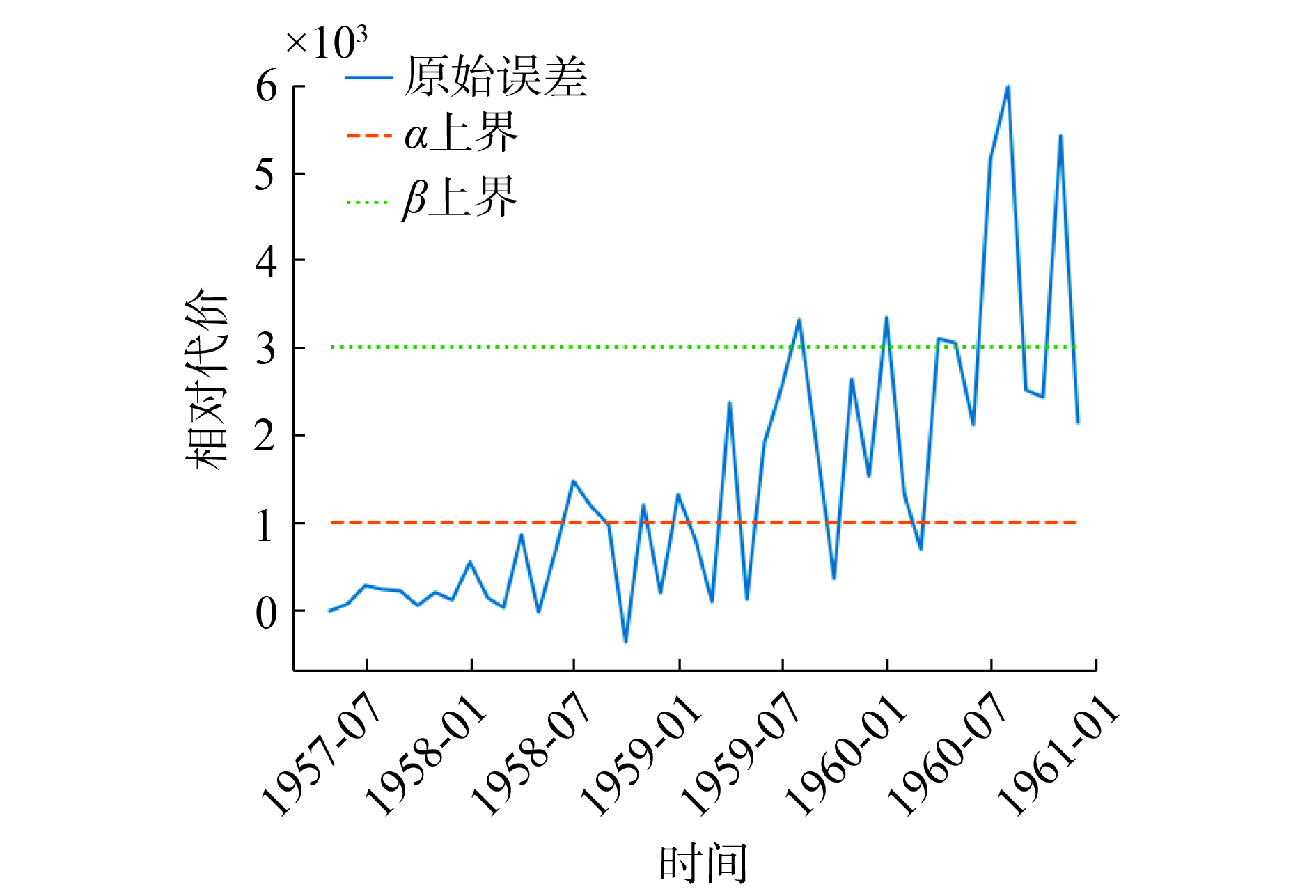
将代入三支决策算法结果如图9。由结果可知,对于问题中给定时刻

|
Download:
|
|
图 9 随
|
|
|
Download:
|
| 图 10 代价判断决定的三支决策结果 Fig. 10 Discarding costly predictions given by 3WD | |
本文通过两个实验的验证,提出了基于LSTM的三支决策分类算法。实验1在LSTM分类的基础上,增加三支决策分类后明显地降低了决策风险;实验2在原先分类器中引入三支决策后,也有了代价上的优化。实验表明:1)三支决策的决策准确率受前端分类器准确率的较大影响;2)三支决策算法可以结合深度学习模型解决代价敏感分类问题,而非仅限于非贝叶斯模型的分类器;3)三支决策在解决代价敏感分类问题的同时,可以通过扩展代价定义的方式,为回归模型建立可信度判据。结合三支决策理论,在时间序列分析问题中,三支决策模型可以为预测结果增加可信度的判据,使得预测结果更加具有分析和处理的价值。
但是当前的工作只是初步的验证有关于深度学习与三支决策相结合形成新的代价敏感分类的初步研究。本文的研究尚处于初步的阶段。未来,对于模型的改进仍有许多研究空间。例如,对于三支决策算法,可以结合新的边界理论,形成自动化的边界确定;在整体模型中,可以借助boost或专家分类器等模型,提出更完善的理论;以及结合Alex-net等其他更高效的分类器来进一步提高前置分类器的性能等。这些改进都将能够进一步提高三支决策在在代价敏感分类领域的应用频率。
| [1] |
KARIM F, MAJUMDAR S, DARABI H, et al. LSTM fully convolutional networks for time series classification[J]. IEEE access, 2018, 6: 1662-1669. DOI:10.1109/ACCESS.2017.2779939 ( 0) 0)
|
| [2] |
KARIM F, MAJUMDAR S, DARABI H, et al. Multivariate LSTM-FCNs for time series classification[J]. Neural networks, 2019, 116: 237-245. DOI:10.1016/j.neunet.2019.04.014 ( 0) 0)
|
| [3] |
KHAN S H, HAYAT M, BENNAMOUN M, et al. Cost-sensitive learning of deep feature representations from imbalanced data[J]. IEEE transactions on neural networks and learning systems, 2018, 29(8): 3573-3587. DOI:10.1109/TNNLS.2017.2732482 ( 0) 0)
|
| [4] |
FERNÁNDEZ A, GARCÍA S, GALAR M, et al. Cost-sensitive learning[M]//FERNÁNDEZ A, GARCÍA S, GALAR M, et al. Learning from Imbalanced Data Sets. Cham: Springer, 2018: 63-78.
( 0) 0)
|
| [5] |
YAN Ke, MA Lulu, DAI Yuting, et al. Cost-sensitive and sequential feature selection for chiller fault detection and diagnosis[J]. International journal of refrigeration, 2018, 86: 401-409. DOI:10.1016/j.ijrefrig.2017.11.003 ( 0) 0)
|
| [6] |
JIANG Xinxin, PAN Shirui, LONG Guodong, et al. Cost-sensitive parallel learning framework for insurance intelligence operation[J]. IEEE transactions on industrial electronics, 2019, 66(12): 9713-9723. DOI:10.1109/TIE.2018.2873526 ( 0) 0)
|
| [7] |
CHEN Jie, WU Zhongcheng, ZHANG Jun. Driving safety risk prediction using cost-sensitive with Nonnegativity-constrained Autoencoders based on imbalanced naturalistic driving data[J/OL]. IEEE transactions on intelligent transportation systems: (2019-01-17). https://ieeexplore.ieee.org/document/8617709. DOI: 10.1109/TITS.2018.2886280.
( 0) 0)
|
| [8] |
YAO Yiyu. Three-way decision: an interpretation of rules in rough set theory[C]//Proceedings of the 4th International Conference on Rough Sets and Knowledge Technology. Gold Coast, Australia, 2009: 642–649.
( 0) 0)
|
| [9] |
GERS F A, SCHMIDHUBER J, CUMMINS F. Learning to forget: continual prediction with LSTM[J]. Neural computation, 2000, 12(10): 2451-2471. DOI:10.1162/089976600300015015 ( 0) 0)
|
| [10] |
ELKAN C. The foundations of cost-sensitive learning[C]//Proceedings of the 17th International Joint Conference of Artificial Intelligence. Morgan Kaufmann, Seattle, 2001: 973–978.
( 0) 0)
|
| [11] |
LIU Xuying, ZHOU Zhihua. The influence of class imbalance on cost-sensitive learning: an empirical study[C]//Proceedings of the 6th International Conference on Data Mining. Hong Kong, China, 2006: 970–974.
( 0) 0)
|
| [12] |
ZADROZNY B, LANGFORD J, ABE N. Cost-sensitive learning by cost-proportionate example weighting[C]//Proceedings of the 3rd IEEE International Conference on Data Mining. Melbourne, FL, USA, 2003: 435–442.
( 0) 0)
|
 2019, Vol. 14
2019, Vol. 14


